1 Introduction

Dynamic systems are generally subjected to various types of excitation. A frequently encountered excitation is direct excitation, also called forced excitation. Vibration amplitudes of a system under direct excitation depend on the system parameters, particularly damping and excitation amplitude. In directly excited systems, large responses can be achieved in the presence of strong nonlinearities or when the excitation frequency is close to one of the natural frequencies of the system, where these large vibration amplitudes can be bounded by damping or nonlinearity itself. On the other hand, parametrically excited systems, where the excitation appears as time-varying coefficients in the equation of motion, are subjected to large vibration amplitudes when the excitation frequency is close to \(2\omega_{0} /n\), where \(\omega_{0}\) is the undamped natural frequency of the system and \(n\) is a positive integer representing the order of the parametric resonance, e.g., the first-order parametric resonance, called the principal parametric resonance, is achieved when \(n = 1\).

Interaction between the parametric excitation and properties of the system, such as its natural frequencies, plays a crucial role in determining the stability of structural systems. A small excitation amplitude might lead to a significant response when the system is excited in a frequency range close to the principal parametric resonance. As a result, the resulting large vibrations amplitude can damage components of the system, leading to severe dynamic instability and potential system failure. Cable-stayed bridges are generally subjected to parametric excitation caused by wind, traffic and earthquakes [1]. Strong coupling between the parametric excitation and the vibration of the bridge can lead to catastrophic effects if not taken into account [2,3,4,5]. The roll motion of a ship may, in some situations, reach dangerously large amplitudes. The highest possible amplitudes occur when wave height exceeds a given threshold and the excitation frequency from the waves is close to twice the natural frequency of the ship. This rapid change of vibrational amplitude is called parametric roll and can endanger safe operation and even capsize the ship [6]. On the other hand, it has been pointed out that parametric vibration of risers in realistic sea conditions is a stochastic process. When an offshore platform is subjected to waves, it will heave with the rhythm of the wave motion; as a result, the tension of the top displacement of the riser fluctuates with the rhythm of the platform motion. Therefore, under the action of wave load, the stochastic heave motion of the platform can be excited, along with the vibration of the riser experiencing time-varying axial tension, which will cause a significant effect on the fatigue damage and lifetime of the riser [7]. Also, interaction between the internal moving components of rotating machines such as gears, shafts and rolling element bearings is considered as the primary source of excitation in these systems [8].

Parametric excitation has been exploited extensively in various applications, including vibration energy harvesting, response amplification, vibration suppression and signal sensing. Vibration energy harvesters convert the mechanical energy of ambient vibration into usable electrical power. When implemented correctly, vibration energy harvesting has proved to provide a sustainable and efficient energy supply for the daily use of electronic devices [9]. The most common mechanical to electrical transduction mechanisms in vibration energy harvesting are electromagnetic [10], electrostatic [11], piezoelectric and magnetostrictive [12]. Exploiting parametric excitation for response amplification can be achieved by adding the parametric excitation to a directly excited system, called parametric amplification [13]. It has been pointed out that interaction between the parametric excitation and the direct harmonic excitation can increase the vibrational amplitude of the system several times compared to the case when the system is only under pure direct excitation [14]. Parametric excitation has also proved to be an effective approach for vibration suppression. The mechanism of parametric vibration suppression is mainly based on reducing the vibrational amplitudes of the main (hosting) system. The most common structure exploited as parametric vibration suppression is the pendulum [15]. On the other hand, the large vibrational amplitudes achieved at principal parametric resonance have been extensively exploited in sensing applications [16]. The principal parametric resonance is triggered at twice the system's natural frequency if the magnitude of the parametric excitation is large enough to overcome energy dissipation in the system. The vibrations are eventually damped due to nonlinearities in the system.

Parametrically excited cantilever beams (PECBs) have been studied extensively in various applications to investigate the dynamic behaviour of parametrically excited systems [17,18,19,20,21,22,23]. Two different aspects of these systems have been of interest to researchers: avoiding or controlling the unwanted effects due to parametric excitation and exploiting parametric excitation, particularly parametric resonance, in these systems to increase their performance. In order to investigate any of these two aspects of PECB systems, understanding their dynamic behaviour is of crucial significance. The best way to achieve this goal is to obtain an accurate analytical solution of the equation of motion of these systems. This will provide useful insight into the behaviour of these systems, enabling optimizing system parameters to achieve optimal performance. This is one aim of this paper.

Perturbation methods such as the Method of Multiple Scales (MMS) [24,25,26,27,28,29] and averaging methods [30, 31] have been widely applied to the investigation of the dynamic behaviour of parametrically excited systems. It has been shown that these methods can be useful techniques for predicting the response of such systems, in particular in a frequency range close to the principal parametric resonance [32]. It has been pointed out that the conventional MMS can predict the response accurately only when the essential assumptions such as the system parameters being small, weak excitations and narrow frequency ranges around the principal parametric resonance are satisfied [18, 32,33,34,35,36,37,38,39].

The Method of Varying Amplitudes (MVA) has been seen to be able to accurately predict the dynamic behaviour of parametrically excited systems. Most importantly, it has been shown that MVA can accurately predict the response over the whole frequency range considered without restricting the system parameters to be small [40,41,42,43].

While many studies have focused on different aspects of modelling to predict the dynamic behaviour of PECB systems in various applications, a thorough investigation to provide a useful insight into the response of these systems, in particular the effects of nonlinear inertia and Duffing-type nonlinearity on the response of these systems and the hardening and softening characteristics of the response, is of key importance. The originality of the work presented in this paper is to use the link between the system parameters, including damping, parametric excitation amplitude, the nonlinear inertia term, the nonlinear curvature term and the mass added at the cantilever tip, to provide a better understanding of the dynamic behaviour of PECB systems. The main aspects investigated in this paper are summarized as the following:

  • Closed-form analytical expressions for the steady-state response of the system are developed and the stability of the response is analysed using the MMS and the MVA, where the main focus is on providing a criterion for determining the hardening and softening behaviours.

  • Effects of the system parameters including the nonlinear inertia, duffing nonlinearity, damping, parametric excitation amplitude and the tip mass on the dynamic behaviour of the PECB are investigated.

  • Experimental measurements of the response of a PECB with a tip mass for different values of the excitation acceleration amplitude are taken. The experimental results for the displacement and acceleration of the cantilever tip are presented and compared with the results obtained from the MMS, the MVA, and numerical results obtained from Direct Integration (DI) of the equation of motion.

The paper is organized as follows: Sect. 2 introduces the mathematical formulation of a PECB with a tip mass followed by the reduced-order model. Section 3 presents frequency response equations of the motion of the PECB with a tip mass considered, where the first-order MMS and the single-term MVA are employed to develop approximate solutions for the response and analyse the stability of the system. Effects of the system parameters on the response of the PECB with a tip mass are discussed in Sect. 4. Section 5 presents experimental measurements of the response of a PECB with a tip mass for various values of excitation acceleration, where the experimental results obtained are compared with analytical results of the MMS and the MVA, and numerical results of Direct Integration (DI) of the equation of motion. Finally, the conclusions are drawn in Sect. 6.

2 Mathematical model

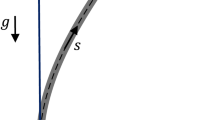
Figure 1 illustrates a cantilever beam with a tip mass \(m\) under parametric excitation, where \(L\) indicates the length of the cantilever, \(w(t)\) is the displacement of the clamped end providing parametric excitation, \(u(s,t)\) and \(v(s,t)\) are the axial and transverse deflections of the cantilever, respectively, \(s\) is the coordinate along the middle plane of the cantilever representing the arc length, \(\rho_{c}\) is the density of the cantilever, \(b_{c}\) represents the width, \(t_{c}\) is the thickness, \(A_{c}\) is the cross-sectional area, \(E_{c}\) indicates the elastic modulus, \(I_{c}\) is the area moment of inertia, \(\rho\) is the radius of curvature and \(\theta\) is the angle of rotation. The tip mass \(m\) is considered to be a point mass added at the cantilever tip (\(s = L\)). Its moment of inertia is assumed to be negligible. The beam is assumed to be uniform. Also, the thickness of the beam is assumed to be small compared to its length, and the cantilever beam is treated as a Euler–Bernoulli beam. Therefore, the effects of rotary inertia and shear deformation are ignored. Additionally, the damping in the system is assumed to be linear viscous damping with a coefficient \(c\). Furthermore, the neutral axis of the cantilever is assumed to be inextensible.

Fig. 1
figure 1

Configuration of a parametrically excited cantilever system with a tip mass

Full size image

Considering the homogenous boundary conditions, exploiting the extended Hamilton variational principle, after applying a series of simplifications, the governing equation of motion for the cantilever beam is obtained as [17, 44,45,46]

$$ \begin{aligned} &\rho_{c} A_{c} v_{tt} + cv_{t} + E_{c} I_{c} \left( {v_{ssss} + v_{s}^{2} v_{ssss} + 4v_{s} v_{ss} v_{sss} + v_{ss}^{3} } \right)\\ &\quad- \rho_{c} A_{c} \left( {v_{s} w_{tt} + v_{ss} \int_{L}^{s} {w_{tt} {\text{d}}\zeta } } \right) \hfill \\ &\quad + \frac{1}{2}\rho_{c} A_{c} \left( {v_{s} \int_{0}^{s} {\left( {v_{\gamma }^{2} } \right)_{tt} {\text{d}}\gamma } + v_{ss} \int_{L}^{s} {\int_{0}^{\varsigma } {\left( {v_{\gamma }^{2} } \right)_{tt} {\text{d}}\gamma } {\text{d}}\zeta } } \right) \\ &\quad - m\delta_{D} \left( {s - L} \right)\left( {v_{s} w_{tt} + v_{ss} \int_{L}^{s} {w_{tt} {\text{d}}\zeta } } \right) \hfill \\ &\quad + \frac{1}{2}m\delta_{D} \left( {s - L} \right)\left( {v_{s} \int_{0}^{s} {\left( {v_{\gamma }^{2} } \right)_{tt} {\text{d}}\gamma } + v_{ss} \int_{L}^{s} {\int_{0}^{\zeta } {\left( {v_{\gamma }^{2} } \right)_{tt} {\text{d}}\gamma } {\text{d}}\zeta } } \right) = 0, \hfill \\ \end{aligned} $$
(1)

where \(\delta_{D}\) is the Dirac delta function, and the subscripts \(t\) and \(s\) represent derivatives with respect to these variables, respectively. Introducing

$$ Y = \sqrt {\frac{{E_{c} I_{c} }}{{\rho_{c} A_{c} L^{4} }}} , $$
(2)

and the non-dimensional parameters

$$ \hat{s} = \frac{s}{L}, \, \hat{v} = \frac{v}{L}, \, \hat{w} = \frac{w}{L}, \, \hat{\gamma } = \frac{\gamma }{L}{, }\,\hat{\zeta }{ = }\frac{\zeta }{L}{, }\,\hat{t} = tY, \, \hat{c} = \frac{c}{{\rho_{c} A_{c} Y}}, \, \hat{\omega }_{0} = \frac{{\omega_{0} }}{Y}, \, \hat{m} = \frac{1}{{\rho_{c} A_{c} L}}m, $$
(3)

where \(\omega_{0}\) is the lowest undamped natural frequency of the system, Eq. (1) can be expressed in the non-dimensional form

$$ \begin{aligned} & \hat{v}_{{\hat{t}\hat{t}}} + \hat{c}\hat{v}_{{\hat{t}}} + \hat{v}_{{\hat{s}\hat{s}\hat{s}\hat{s}}} + \hat{v}_{{\hat{s}}}^{2} \hat{v}_{{\hat{s}\hat{s}\hat{s}\hat{s}}} + 4\hat{v}_{{\hat{s}}} \hat{v}_{{\hat{s}\hat{s}}} \hat{v}_{{\hat{s}\hat{s}\hat{s}}} \\ & \quad + \hat{v}_{{\hat{s}\hat{s}}}^{3} - \hat{v}_{{\hat{s}}} \left( {1 + \hat{m}\delta _{D} \left( {\hat{s} - 1} \right)} \right)\hat{w}_{{\hat{t}\hat{t}}} \\ & \quad - \hat{v}_{{\hat{s}\hat{s}}} \left( {1 + \hat{m}\delta _{D} \left( {\hat{s} - 1} \right)} \right)\int_{1}^{{\hat{s}}} {\hat{w}_{{\hat{t}\hat{t}}} {\text{d}}\hat{\zeta }} \\ & \quad + \hat{v}_{{\hat{s}}} \left( {1 + \hat{m}\delta _{D} \left( {\hat{s} - 1} \right)} \right)\int_{0}^{{\hat{s}}} {\left( {\hat{v}_{{\hat{t}\hat{s}}}^{2} + \hat{v}_{{\hat{s}}} \hat{v}_{{\hat{t}\hat{t}\hat{s}}} } \right)} {\text{d}}\hat{\gamma } \\ & \quad + \hat{v}_{{\hat{s}\hat{s}}} \left( {1 + \hat{m}\delta _{D} \left( {\hat{s} - 1} \right)} \right)\int_{1}^{{\hat{s}}} {\int_{0}^{{\hat{\zeta }}} {\left( {\hat{v}_{{\hat{t}\hat{s}}}^{2} + \hat{v}_{{\hat{s}}} \hat{v}_{{\hat{t}\hat{t}\hat{s}}} } \right){\text{d}}\hat{\gamma }} } {\text{d}}\hat{\zeta } = 0. \\ \end{aligned} $$
(4)

2.1 Single-mode approximation

The nonlinear governing differential Eq. (4) does not admit a closed-form solution. To develop a reduced-order model for the parametrically excited cantilever, the transverse deflection \(\hat{v}\left( {\hat{s},\hat{t}} \right)\) can be assumed as a linear combination of the contributions from \(N\) vibration modes. Hence, \(\hat{v}\left( {\hat{s},\hat{t}} \right)\) can be represented in the form [47]

$$ \hat{v}\left( {\hat{s},\hat{t}} \right) = \sum\limits_{r = 1}^{N} {\psi_{r} \left( {\hat{s}} \right)Z_{r} \left( {\hat{t}} \right)} , $$
(5)

where \(\psi_{r} (\hat{s})\) and \(Z_{r} (\hat{t})\) are the linear mass-normalized mode shape functions for the Euler–Bernoulli cantilever beam with a tip mass and the non-dimensional displacement response of the \(r{\text{th}}\) vibration mode, respectively. Considering only the first vibration mode (\(N = 1\)) in Eq. (5) and omitting subscript 1 for clarity which is valid if the excitation frequency is considerably lower than the second natural frequency of the system, \(\psi (\hat{s})\) is expressed as

$$ \psi \left( {\hat{s}} \right) = R\overline{\psi }\left( {\hat{s}} \right), $$
(6)

where

$$ R = \frac{1}{{\sqrt {\int_{0}^{1} {\left( {\overline{\psi }\left( {\hat{s}} \right)} \right)^{2} {\text{d}}\hat{s} + \hat{m}\left( {\overline{\psi }\left( {\hat{s} = 1} \right)} \right)^{2} } } }}, $$
(7)
$$ \overline{\psi }\left( {\hat{s}} \right) = \left( {\cos (\lambda \hat{s}) - \cosh (\lambda \hat{s})} \right) + Q\left( {\sin (\lambda \hat{s}) - \sinh (\lambda \hat{s})} \right)\;[46], $$
(8)
$$ Q = \frac{{\sin \left( \lambda \right) - \sinh \left( \lambda \right) + \lambda \hat{m}\left( {\cos \left( \lambda \right) - \cosh \left( \lambda \right)} \right)}}{{\cos \left( \lambda \right) + \cosh \left( \lambda \right) - \lambda \hat{m}\left( {\sin \left( \lambda \right) - \sinh \left( \lambda \right)} \right)}}. $$
(9)

In Eqs. (8) and (9) \(\lambda\) is the eigenvalue of the first vibration mode for which the relation

$$ \lambda = \sqrt {\hat{\omega }_{0} } , $$
(10)

holds. Additionally, \(\lambda\) satisfies the characteristic equation

$$ 1 + \cosh \left( \lambda \right)\cos \left( \lambda \right) + \hat{m}\lambda \left( {\cos \left( \lambda \right)\sinh \left( \lambda \right) - \sin \left( \lambda \right)\cosh \left( \lambda \right)} \right) = 0. $$
(11)

The axial motion of the clamped end of the cantilever beam is assumed to be harmonic, with an acceleration amplitude \(a_{p}\), i.e., \(w_{tt}\) can be expressed as

$$ w_{tt} = a_{p} \cos \left( {\varOmega_{p} t} \right), $$
(12)

where \(\varOmega_{p}\) is the parametric excitation frequency which can be expressed in the non-dimensional form

$$ \hat{\varOmega }_{p} = \frac{{\varOmega_{p} }}{Y}. $$
(13)

Therefore, considering Eq. (3), the non-dimensional acceleration of the clamped end (\(\hat{w}_{{\hat{t}\hat{t}}}\)) is obtained as

$$ \hat{w}_{{\hat{t}\hat{t}}} = \hat{a}_{p} \cos \left( {\hat{\varOmega }_{p} \hat{t}} \right), $$
(14)

where \(\hat{a}_{p}\) is the non-dimensional acceleration amplitude defined as

$$ \hat{a}_{p} = \frac{1}{{LY^{2} }}a_{p} . $$
(15)

Consequently, substituting Eq. (5) for the first vibration mode into Eq. (4), multiplying the resultant equation by \(\psi (\hat{s})\), and integrating over the non-dimensional length, the final, reduced-order equation of motion for the system is obtained as [48]

$$ \ddot{Z} + \beta \dot{Z} + \hat{\omega }_{0}^{2} \left( {1 + P\cos \left( {\hat{\varOmega }_{p} \hat{t}} \right)} \right)Z + \eta Z^{3} + \alpha \left( {\dot{Z}^{2} + Z\ddot{Z}} \right)Z = 0, $$
(16)

where the derivatives are with respect to \(\hat{t}\), and \(\beta\), \(P\), \(\eta\) and \(\alpha\) are the coefficients of damping, parametric excitation amplitude, Duffing-type nonlinearity and nonlinear inertia term, respectively, which are defined as

$$ \beta = \hat{c}, \, P = \frac{{h_{2} }}{{\hat{\omega }_{0}^{2} h_{1} }}\hat{a}_{p} , \, \eta = \frac{{h_{3} }}{{h_{1} }}, \, \alpha = \frac{{h_{4} + h_{5} }}{{h_{1} }}, $$
(17)

where

$$ h_{1} = \int_{0}^{1} {\psi^{2} {\text{d}}\hat{s}} , $$
(18)
$$ h_{2} = \int_{0}^{1} {\left( {\left( {1 - \hat{s}} \right)\psi \psi_{{\hat{s}\hat{s}}} - \psi \psi_{{\hat{s}}} } \right){\text{d}}\hat{s}} - \hat{m}\psi \left( 1 \right)\psi_{{\hat{s}}} \left( 1 \right), $$
(19)
$$ h_{3} = \int_{0}^{1} {\psi \left( {\psi_{{\hat{s}}}^{2} \psi_{{\hat{s}\hat{s}\hat{s}\hat{s}}} + 4\psi_{{\hat{s}}} \psi_{{\hat{s}\hat{s}}} \psi_{{\hat{s}\hat{s}\hat{s}}} + \psi_{{\hat{s}\hat{s}}}^{3} } \right)} {\text{d}}\hat{s}, $$
(20)
$$ h_{4} = \int_{0}^{1} {\psi \psi_{{\hat{s}}} \left( {\int_{0}^{{\hat{s}}} {\left( {\psi_{{\hat{\gamma }}} \left( {\hat{\gamma }} \right)} \right)^{2} {\text{d}}\hat{\gamma }} } \right){\text{d}}\hat{s}} , $$
(21)
$$ h_{5} = \int_{0}^{1} {\psi \psi_{{\hat{s}\hat{s}}} \left( {\int_{1}^{{\hat{s}}} {\int_{0}^{{\hat{\zeta }}} {\left( {\psi_{{\hat{\gamma }}} \left( {\hat{\gamma }} \right)} \right)^{2} {\text{d}}\hat{\gamma }{\text{d}}\hat{\zeta }} } } \right){\text{d}}\hat{s}} . $$
(22)

3 Frequency response approximations

The mathematical model for a PECB with a tip mass was developed in Sect. 2. In this section, approximate solutions for Eq. (16) are developed using the first-order approximation of the MMS and the single-term MVA approximation.

3.1 First-order MMS solution

Assuming the system parameters including \(\beta\), \(P\), \(\eta\) and \(\alpha\) to be small and of the same order \(\varepsilon\), Eq. (16) is scaled as

$$ \ddot{Z} + \varepsilon \beta_{\varepsilon } \dot{Z} + \hat{\omega }_{0}^{2} \left( {1 + \varepsilon P_{\varepsilon } \cos \left( {\hat{\varOmega }_{p} \hat{t}} \right)} \right)Z + \varepsilon \eta_{\varepsilon } Z^{3} + \varepsilon \alpha_{\varepsilon } \left( {\dot{Z}^{2} + Z\ddot{Z}} \right)Z = 0, $$
(23)

where [49]

$$ \varepsilon \beta_{\varepsilon } = \beta , \, \varepsilon P_{\varepsilon } = P, \, \varepsilon \eta_{\varepsilon } = \eta , \, \varepsilon \alpha_{\varepsilon } = \alpha . $$
(24)

In the first-order approximation of the MMS, the response \(Z\) is approximated as [49]

$$ Z\left( {\hat{t},\varepsilon } \right) = Z_{0} \left( {T_{0} ,T_{1} } \right) + \varepsilon Z_{1} \left( {T_{0} ,T_{1} } \right) + O\left( {\varepsilon^{2} } \right) , $$
(25)

where \(T_{0} = t\) and \(T_{1} = \varepsilon t\) represent time scales. Substituting Eq. (25) into Eq. (23) and taking only terms of order \(O(\varepsilon^{0} )\) and \(O(\varepsilon^{1} )\) into account results in the equation

$$ \begin{aligned} & D_{0}^{2} Z_{0} + \varepsilon \left( {D_{0}^{2} Z_{1} + 2D_{0} D_{1} Z_{0} } \right) \\ & \quad + \varepsilon \beta _{\varepsilon } \left( {D_{0} Z_{0} } \right) + \varepsilon \eta _{\varepsilon } Z_{0}^{3} \\ & \quad + \hat{\omega }_{0}^{2} \left( {1 + \varepsilon P_{\varepsilon } {\text{cos}}\left( {\hat{\varOmega }_{p} \hat{t}} \right)} \right)\left( {Z_{0} + \varepsilon Z_{1} } \right) \\ & \quad + \varepsilon \alpha _{\varepsilon } Z_{0} \left( {\left( {D_{0} Z_{0} } \right)^{2} + Z_{0} \left( {D_{0}^{2} Z_{0} } \right)} \right) = 0, \\ \end{aligned} $$
(26)

where the derivatives are with respect to \(\hat{t}\). Equating terms of the same order of \(\varepsilon\) in Eq. (26) yields

$$ O{(}\varepsilon^{0} {)}: D_{0}^{2} Z_{0} + \hat{\omega }_{0}^{2} Z_{0} = 0, $$
(27)
$$ \begin{aligned} & O(\varepsilon ^{1} ): D_{0}^{2} Z_{1} + \hat{\omega }_{0}^{2} Z_{1} = - 2D_{0} D_{1} Z_{0} \\ & \quad - \beta _{\varepsilon } D_{0} Z_{0} - \eta _{\varepsilon } {\text{Z}}_{0}^{3} - \alpha _{\varepsilon } Z_{0} \left( {D_{0} Z_{0} } \right)^{2} \\ & \quad - \alpha _{\varepsilon } Z_{0}^{2} D_{0}^{2} Z_{0} - \frac{1}{2}\hat{\omega }_{0}^{2} P_{\varepsilon } \left( {e^{{i\hat{\varOmega }_{p} T_{0} }} + e^{{ - i\hat{\varOmega }_{p} T_{0} }} } \right)Z_{0} . \\ \end{aligned} $$
(28)

The solution for Eq. (27) can be expressed in the form

$$ Z_{0} = a_{{{\text{MMS1}}}} \left( {T_{1} } \right)e^{{i\hat{\omega }_{0} T_{0} }} + \overline{a}_{{{\text{MMS1}}}} \left( {T_{1} } \right)e^{{ - i\hat{\omega }_{0} T_{0} }} . $$
(29)

Substituting Eq. (29) into Eq. (28) yields

$$ \begin{aligned} & D_{0}^{2} Z_{1} + \hat{\omega }_{0}^{2} Z_{1} = \left( { - 2i\hat{\omega }_{0} D_{1} a_{{{\text{MMS1}}}} - i\hat{\omega }_{0} \beta _{\varepsilon } a_{{{\text{MMS1}}}} } \right. \\ & \quad - \frac{1}{2}\hat{\omega }_{0}^{2} P_{\varepsilon } \bar{a}_{{{\text{MMS1}}}} e^{{i\left( {\hat{\varOmega }_{p} - 2\hat{\omega }_{0} } \right)T_{0} }} - 3\eta _{\varepsilon } a_{{{\text{MMS1}}}}^{2} \bar{a}_{{{\text{MMS1}}}} \\ & \quad + 2\alpha _{\varepsilon } \hat{\omega }_{0}^{2} a_{{{\text{MMS1}}}}^{2} \left. {\bar{a}_{{{\text{MMS1}}}} } \right)e^{{i\hat{\omega }_{0} T_{0} }} \\ & \quad + {\text{NST}} + {\text{CC, }} \\ \end{aligned} $$
(30)

where NST represents the non-secular terms and CC is the complex conjugate of the preceding terms. Considering the case of principal parametric resonance, where \(\hat{\varOmega }_{p} \approx 2\hat{\omega }_{0}\), the frequency detuning parameter \(\hat{\sigma }_{p}\) for the parametric excitation frequency is defined as

$$ \hat{\varOmega }_{p} - 2\hat{\omega }_{0} = \varepsilon \hat{\sigma }_{p} . $$
(31)

Considering Eqs. (24) and (31), eliminating the secular terms in Eq. (30) yields

$$ 2i\hat{\omega }_{0} \frac{{da_{{{\text{MMS1}}}} }}{{d\hat{t}}} + i\hat{\omega }_{0} \beta a_{{{\text{MMS1}}}} + \frac{1}{2}\hat{\omega }_{0}^{2} P\overline{a}_{{{\text{MMS1}}}} e^{{i\left( {\hat{\varOmega }_{p} - 2\hat{\omega }_{0} } \right)\hat{t}}} + 3\eta a_{{{\text{MMS1}}}}^{2} \overline{a}_{{{\text{MMS1}}}} - 2\alpha \hat{\omega }_{0}^{2} a_{{{\text{MMS1}}}}^{2} \overline{a}_{{{\text{MMS1}}}} = 0. $$
(32)

In order to solve Eq. (32), \(a_{{{\text{MMS1}}}} (\hat{t})\) is expressed in the polar form

$$ a_{{{\text{MMS1}}}} (\hat{t}) = \frac{1}{2}A_{{{\text{MMS1}}}} (\hat{t})e^{{i\lambda_{{{\text{MMS1}}}} (\hat{t})}} , $$
(33)

where \(A_{{{\text{MMS1}}}} (\hat{t})\) and \(\lambda_{{{\text{MMS1}}}} (\hat{t})\) are real. Substituting Eq. (33) into Eq. (32) yields

$$ \begin{gathered} \left( {i\hat{\omega }_{0} A^{\prime}_{{{\text{MMS1}}}} - \hat{\omega }_{0} A_{{{\text{MMS1}}}} \lambda^{\prime}_{{{\text{MMS1}}}} + \frac{1}{2}i\hat{\omega }_{0} \beta A_{{{\text{MMS1}}}} } \right. + \frac{1}{4}\hat{\omega }_{0}^{2} PA_{{{\text{MMS1}}}} e^{{i\left( {\left( {\hat{\varOmega }_{p} - 2\hat{\omega }_{0} } \right)\hat{t} - 2\lambda_{{{\text{MMS1}}}} } \right)}} + \frac{3}{8}\eta A_{{{\text{MMS1}}}}^{3} \hfill \\ \left. {\quad - \frac{1}{4}\alpha \hat{\omega }_{0}^{2} A_{{{\text{MMS1}}}}^{3} } \right)e^{{i\lambda_{{{\text{MMS1}}}} }} = 0, \hfill \\ \end{gathered} $$
(34)

where the derivatives are with respect to \(\hat{t}\). Separating the real and imaginary parts in Eq. (34) yields

$$ A_{{{\text{MMS1}}}} \lambda^{\prime}_{{{\text{MMS1}}}} = \frac{3}{8}\frac{{\eta A_{{{\text{MMS1}}}}^{3} }}{{\omega_{0} }} + \frac{1}{4}\hat{\omega }_{0} PA_{{{\text{MMS1}}}} {\text{cos}}\left( {\left( {\hat{\varOmega }_{p} - 2\hat{\omega }_{0} } \right)\hat{t} - 2\lambda_{{{\text{MMS1}}}} } \right) - \frac{1}{4}\alpha \hat{\omega }_{0} A_{{{\text{MMS1}}}}^{3} , $$
(35)
$$ A^{\prime}_{{{\text{MMS1}}}} = - \frac{1}{2}\beta A_{{{\text{MMS1}}}} - \frac{1}{4}\hat{\omega }_{0} PA_{{{\text{MMS1}}}} {\text{sin}}\left( {\left( {\hat{\varOmega }_{p} - 2\hat{\omega }_{0} } \right)\hat{t} - 2\lambda_{{{\text{MMS1}}}} } \right). $$
(36)

In order to eliminate the presence of time explicitly in Eqs. (35) and (36), and make this system of equations autonomous, a new function \(\hat{\tau }\) is defined as

$$ \hat{\tau } = \left( {\hat{\varOmega }_{p} - 2\hat{\omega }_{0} } \right)\hat{t} - 2\lambda_{{{\text{MMS1}}}} . $$
(37)

Therefore, the system of Eqs. (35) and (36) is simplified as

$$ A_{{{\text{MMS1}}}} \hat{\tau^{\prime}} = A_{{{\text{MMS1}}}} \left( {\hat{\varOmega }_{p} - 2\hat{\omega }_{0} } \right) - \frac{{\left( {3\eta - 2\alpha \hat{\omega }_{0}^{2} } \right)A_{{{\text{MMS1}}}}^{3} }}{{4\hat{\omega }_{0} }} - \frac{1}{2}\hat{\omega }_{0} PA_{{{\text{MMS1}}}} {\text{cos}}\left( {\hat{\tau }} \right), $$
(38)
$$ A^{\prime}_{{{\text{MMS1}}}} = - \frac{1}{2}\beta A_{{{\text{MMS1}}}} - \frac{1}{4}\hat{\omega }_{0} PA_{{{\text{MMS1}}}} {\text{sin}}\left( {\hat{\tau }} \right). $$
(39)

Consequently, solving Eqs. (38) and (39) for the steady-state response \(\left( {A^{\prime}_{{{\text{MMS1}}}} = 0, \, \hat{\tau }^{\prime} = 0} \right)\), the frequency response equation is obtained as

$$ A_{{{\text{MMS1}}}} = \sqrt {\frac{{4\hat{\omega }_{0} }}{{3\left( {\eta - \frac{2}{3}\alpha \hat{\omega }_{0}^{2} } \right)}}\left( {\left( {\hat{\varOmega }_{p} - 2\hat{\omega }_{0} } \right) \pm \sqrt {\left( {\frac{1}{2}\hat{\omega }_{0} P} \right)^{2} - \beta^{2} } } \right)} . $$
(40)

It can be found from Eq. (40) that for a steady-state nontrivial solution \(\left( {A_{{{\text{MMS1}}}} \ne 0} \right)\) to exist, the condition

$$ \beta \le \frac{1}{2}\hat{\omega }_{0} P $$
(41)

should hold. Furthermore, it can be seen that the second radicand in Eq. (40) does not depend on the excitation frequency \(\hat{\varOmega }_{p}\). Therefore, Eq. (40) does not provide a bounded response.

3.1.1 Stability analysis of MMS solution

The stability of the nontrivial solution can be investigated by considering the Jacobian matrix

$$ J_{{{\text{MMS\_NT}}}} = \left( {\begin{array}{*{20}c} {\frac{{\partial A^{\prime}_{{{\text{MMS1}}}} }}{{\partial a_{{{\text{MMS1}}}} }}} & {\frac{{\partial A^{\prime}_{{{\text{MMS1}}}} }}{{\partial \hat{\tau }}}} \\ {\frac{{\partial \hat{\tau^{\prime}}}}{{\partial A_{{{\text{MMS1}}}} }}} & {\frac{{\partial \hat{\tau^{\prime}}}}{{\partial \hat{\tau }}}} \\ \end{array} } \right). $$
(42)

Therefore, considering Eqs. (38) and (39), \(J_{{{\text{MMS\_NT}}}}\) for the steady-state solution \(\left( {A^{\prime}_{{{\text{MMS1}}}} = 0, \, \hat{\tau }^{\prime} = 0} \right)\) is obtained as

$$ J_{{{\text{MMS\_NT}}}} = \left( {\begin{array}{*{20}c} {J_{{{\text{MMS\_NT}},11}} } & {J_{{{\text{MMS\_NT}},12}} } \\ {J_{{{\text{MMS\_NT}},21}} } & {J_{{{\text{MMS\_NT}},22}} } \\ \end{array} } \right), $$
(43)

where

$$ J_{{{\text{MMS\_NT}},11}} = 0, \, J_{{{\text{MMS\_NT}},22}} = - \beta , \, J_{{{\text{MMS\_NT}},12}} = \frac{{\left( {3\eta - 2\alpha \hat{\omega }_{0}^{2} } \right)A_{{{\text{MMS1}}}}^{3} }}{{8\hat{\omega }_{0} }} - \frac{1}{2}\left( {\hat{\varOmega }_{p} - 2\hat{\omega }_{0} } \right)A_{{{\text{MMS1}}}} , $$
(44)
$$ J_{{{\text{MMS\_NT,21}}}} = - \frac{{\left( {3\eta - 2\alpha \hat{\omega }_{0}^{2} } \right)A_{{{\text{MMS1}}}} }}{{2\hat{\omega }_{0} }}. $$
(45)

For \(\beta > 0\), the trace of the Jacobian matrix in Eq. (43) is negative. Therefore, the response is stable only if \(Det(J_{{{\text{MMS\_NT}}}} ) > 0\). Consequently, for the case when \(\eta - {{2\alpha \hat{\omega }_{0}^{2} } \mathord{\left/ {\vphantom {{2\alpha \hat{\omega }_{0}^{2} } 3}} \right. \kern-0pt} 3} > 0\), the response of the system shows a hardening behaviour, and the positive and negative signs in the frequency response Eq. (40) represent the stable and unstable solutions starting from the critical frequencies

$$ \hat{\varOmega }_{p,s1} = 2\hat{\omega }_{0} - \sqrt {\left( {\frac{1}{2}\hat{\omega }_{0} P} \right)^{2} - \beta^{2} } , \, \hat{\varOmega }_{p,s2} = 2\hat{\omega }_{0} + \sqrt {\left( {\frac{1}{2}\hat{\omega }_{0} P} \right)^{2} - \beta^{2} } , $$
(46)

respectively. On the other hand, for the case when \(\eta - {{2\alpha \hat{\omega }_{0}^{2} } \mathord{\left/ {\vphantom {{2\alpha \hat{\omega }_{0}^{2} } 3}} \right. \kern-0pt} 3} < 0\), the response of the system shows a softening behaviour, and the positive and negative signs in the frequency response Eq. (40) represent the unstable and stable solutions, respectively; the unstable solution starts from the frequency \(\hat{\varOmega }_{p,s1}\) while the stable solution starts at the frequency \(\hat{\varOmega }_{p,s2}\).

To analyse the stability of the trivial solution \(\left( {A_{{{\text{MMS1}}}} = 0} \right)\), the Cartesian form of the response is used as

$$ A_{{{\text{MMS1}}}} (\hat{t}) = \frac{1}{2}\left( {M - iN} \right)e^{{\frac{1}{2}i\left( {\hat{\varOmega }_{p} - 2\hat{\omega }_{0} } \right)\hat{t}}} , $$
(47)

where \(M\), \(N\) are real. Applying Eq. (47) to the modulation Eq. (32) and separating the real and imaginary parts leads to the system of equations

$$ M^{\prime} = - \frac{1}{2}\left( {\hat{\varOmega }_{p} - 2\hat{\omega }_{0} } \right)N - \frac{1}{2}\beta M + \frac{{\left( {3\eta - 2\alpha \hat{\omega }_{0}^{2} } \right)N}}{{8\hat{\omega }_{0} }}\left( {M^{2} + N^{2} } \right) - \frac{1}{4}\hat{\omega }_{0} PN, $$
(48)
$$ N^{\prime} = \frac{1}{2}\left( {\hat{\varOmega }_{p} - 2\hat{\omega }_{0} } \right)M - \frac{1}{2}\beta N - \frac{{\left( {3\eta - 2\alpha \hat{\omega }_{0}^{2} } \right)M}}{{8\hat{\omega }_{0} }}\left( {M^{2} + N^{2} } \right) - \frac{1}{4}\hat{\omega }_{0} PM $$
(49)

Therefore, the Jacobian matrix for the trivial solution is obtained as

$$ J_{{\text{MMS - T}}} = \left( {\begin{array}{*{20}c} {\frac{{\partial M^{\prime}}}{\partial M}} & {\frac{{\partial M^{\prime}}}{\partial N}} \\ {\frac{{\partial N^{\prime}}}{\partial M}} & {\frac{{\partial N^{\prime}}}{\partial N}} \\ \end{array} } \right). $$
(50)

Consequently, the trivial solution is stable for frequencies \(\hat{\varOmega }_{p} < \hat{\varOmega }_{p,s1} , \, \hat{\varOmega }_{p} > \hat{\varOmega }_{p,s2}\), and is unstable for frequencies within the range \(\hat{\varOmega }_{p,s1} < \hat{\varOmega }_{p} < \hat{\varOmega }_{p,s2}\). Introducing the new parameter \(\eta_{{{\text{MMS}}}}^{*}\), where

$$ \eta_{{{\text{MMS}}}}^{*} = \eta - \frac{2}{3}\alpha \hat{\omega }_{0}^{2} , $$
(51)

it can be found that when \(\eta_{{{\text{MMS}}}}^{*}\) is replaced by \(\eta\), Eq. (40) reduces to the frequency response equation for the nonlinear Mathieu equation with a Duffing-type nonlinearity [32]. From Eq. (51) it follows that for a fixed value of \(\eta\), the value of the nonlinear inertia term \(\alpha\) determines whether the dynamic behaviour of the PECB is hardening or softening.

3.2 Single-term MVA solution

In the single-term approximation of the MVA, the response of the system is expressed as [41]

$$ Z\left( {\hat{t}} \right) = B\left( {\hat{t}} \right)\cos \left( {\frac{1}{2}\hat{\varOmega }_{p} \hat{t}} \right) + C\left( {\hat{t}} \right)\sin \left( {\frac{1}{2}\hat{\varOmega }_{p} \hat{t}} \right), $$
(52)

where \(B\left( {\hat{t}} \right)\) and \(C\left( {\hat{t}} \right)\) are time-varying amplitudes. Substituting Eq. (52) into Eq. (16), separating the coefficients of \(\cos (\hat{\varOmega }_{p} \hat{t}/2)\) and \(\sin (\hat{\varOmega }_{p} \hat{t}/2)\) in the resultant equation, while neglecting the higher-order harmonics, results in

$$ \begin{gathered} \ddot{B} + \beta \dot{B} + \hat{\varOmega }_{p} \dot{C} + \frac{1}{2}\beta \hat{\varOmega }_{p} C + \frac{3}{4}B\left( {B^{2} + C^{2} } \right)\left( {\eta - \frac{1}{6}\alpha \hat{\varOmega }_{p}^{2} } \right) + \left( {\hat{\omega }_{0}^{2} \left( {1 + \frac{1}{2}P} \right) - \frac{1}{4}\hat{\varOmega }_{p}^{2} } \right)B \hfill \\ \quad + \frac{1}{4}\left( {\left( {C^{2} + 3B^{2} } \right)\ddot{B} + 2BC\ddot{C}} \right. + 2C\dot{B}\dot{C} + 3B\dot{B}^{2} + 2\hat{\varOmega }_{p} \left( {B^{2} + C^{2} } \right)\dot{C} + \left. {B\dot{C}^{2} } \right) = 0, \hfill \\ \end{gathered} $$
(53)
$$ \begin{gathered} \ddot{C} - \hat{\varOmega }_{p} \dot{B} + \beta \dot{C} - \frac{1}{2}\beta \hat{\varOmega }_{p} B + \frac{3}{4}C\left( {B^{2} + C^{2} } \right)\left( {\eta - \frac{1}{6}\alpha \hat{\varOmega }_{p}^{2} } \right) + \left( {\hat{\omega }_{0}^{2} \left( {1 + \frac{1}{2}P} \right) - \frac{1}{4}\hat{\varOmega }_{p}^{2} } \right)C \hfill \\ \quad + \frac{1}{4}\left( {\left( {B^{2} + 3C^{2} } \right)\ddot{C} + 2BC\ddot{B}} \right. + 2B\dot{B}\dot{C} + 3C\dot{C}^{2} - 2\hat{\varOmega }_{p} \left( {B^{2} + C^{2} } \right)\dot{B} + \left. {C\dot{B}^{2} } \right) = 0. \hfill \\ \end{gathered} $$
(54)

The steady-state solution is obtained by setting the all derivatives in Eqs. (53) and (54) to zero (\(\dot{B} = \dot{C} = \ddot{B} = \ddot{C} = 0\)), yielding

$$ \frac{1}{2}\beta \hat{\varOmega }_{p} C + \frac{3}{4}B\left( {B^{2} + C^{2} } \right)\left( {\eta - \frac{1}{6}\alpha \hat{\varOmega }_{p}^{2} } \right) + \left( {\hat{\omega }_{0}^{2} \left( {1 + \frac{1}{2}P} \right) - \frac{1}{4}\hat{\varOmega }_{p}^{2} } \right)B = 0, $$
(55)
$$ - \frac{1}{2}\beta \hat{\varOmega }_{p} B + \frac{3}{4}C\left( {B^{2} + C^{2} } \right)\left( {\eta - \frac{1}{6}\alpha \hat{\varOmega }_{p}^{2} } \right) + \left( {\hat{\omega }_{0}^{2} \left( {1 - \frac{1}{2}P} \right) - \frac{1}{4}\hat{\varOmega }_{p}^{2} } \right)C = 0. $$
(56)

Solving the system of Eqs. (55) and (56) with respect to the constant coefficients \(B\) and \(C\), the steady-state response of the system can be obtained, which can be expressed as

$$ Z(\hat{t}) = A_{{{\text{MVA1}}}} (\hat{t})\cos \left( {\frac{1}{2}\hat{\varOmega }_{p} \hat{t} + \theta_{{{\text{MVA1}}}} (\hat{t})} \right). $$
(57)

\(A_{{{\text{MVA1}}}} (\hat{t})\) and \(\theta_{{{\text{MVA1}}}} (\hat{t})\) in Eq. (57) are the amplitude and phase, where

$$ A_{{{\text{MVA1}}}} (\hat{t}) = \sqrt {B(\hat{t})^{2} + C(\hat{t})^{2} } , \, \theta_{{{\text{MVA1}}}} \left( {\hat{t}} \right) = \tan^{ - 1} \frac{{ - C(\hat{t})}}{{B(\hat{t})}} $$
(58)

Consequently, the frequency response equation of the system described by Eq. (16) is obtained as.

From Eqs. (57) and (59), \(\theta_{{{\text{MVA1}}}} (\hat{t})\) is such that \(\sin \left( {2\theta_{{{\text{MVA1}}}} } \right) = {{\beta \hat{\varOmega }_{p} } \mathord{\left/ {\vphantom {{\beta \hat{\varOmega }_{p} } {\hat{\omega }_{0}^{2} P}}} \right. \kern-0pt} {\hat{\omega }_{0}^{2} P}}\). It can be found from Eq. (59) that the nontrivial solution exists only if

$$ A_{{{\text{MVA1}}}} = \sqrt {\frac{1}{{3\left( {\eta - \frac{1}{6}\alpha \hat{\varOmega }_{p}^{2} } \right)}}\left( {\hat{\varOmega }_{p}^{2} - 4\hat{\omega }_{0}^{2} \pm 2\sqrt {\left( {\hat{\omega }_{0}^{2} P} \right)^{2} - \left( {\beta \hat{\varOmega }_{p} } \right)^{2} } } \right)} . $$
(59)
$$ \hat{\varOmega }_{p} \le \frac{{\hat{\omega }_{0}^{2} P}}{\beta }. $$
(60)

3.2.1 Stability analysis of MVA solution

In order to investigate the stability of the solutions in the frequency response Eq. (59), the following parameters are defined:

$$ x_{1} = B, \, x_{3} = C, \, \dot{x}_{1} = x_{2} , \, \dot{x}_{3} = x_{4} . $$
(61)

The Jacobian matrix \(J_{{{\text{MVA}}}}\) is then expressed as the \(4 \times 4\) matrix whose \((i,j){\text{th}}\) element is \(J_{{{\text{MVA}},ij}} = {{\partial \dot{x}_{i} } \mathord{\left/ {\vphantom {{\partial \dot{x}_{i} } {\partial x_{j} }}} \right. \kern-0pt} {\partial x_{j} }}\). Consequently, for the nontrivial solution, the trace \(Tr\left( {J_{{\text{MVA - NT}}} } \right)\) and the determinant \(Det\left( {J_{{\text{MVA - NT}}} } \right)\) of the Jacobian matrix are obtained as

$$ Tr\left( {J_{{\text{MVA - NT}}} } \right) = - 2\beta , $$
(62)
$$ Det\left( {J_{{\text{MVA - NT}}} } \right){ } = \frac{3}{4}\left( {\eta - \frac{1}{6}\alpha \hat{\varOmega }_{p}^{2} } \right)\left( {x_{1} + x_{3} } \right)^{2} \left( {3\left( {\eta - \frac{1}{6}\alpha \hat{\varOmega }_{p}^{2} } \right)\left( {x_{1} + x_{3} } \right)^{2} - \left( {\hat{\varOmega }_{p}^{2} - 4\hat{\omega }_{0}^{2} } \right)} \right){.} $$
(63)

For \(\beta > 0\), \(Tr\left( {J_{{\text{MVA - NT}}} } \right) < 0\). Therefore, the response is stable only if \(Det\left( {J_{{\text{MVA - NT}}} } \right) > 0\). Consequently, for the frequency range such that \(\eta - {{\alpha \hat{\varOmega }_{p}^{2} } \mathord{\left/ {\vphantom {{\alpha \hat{\varOmega }_{p}^{2} } 6}} \right. \kern-0pt} 6} > 0\), the response of the system shows a hardening behaviour, and the positive and negative signs in the frequency response Eq. (59) represent the stable and unstable solutions beginning at the frequencies

$$ \hat{\varOmega }_{p,c1} = \sqrt {4\hat{\omega }_{0}^{2} - 2\beta^{2} - 2\sqrt {\beta^{2} \left( {\beta^{2} - 4\hat{\omega }_{0}^{2} } \right) + \left( {P\hat{\omega }_{0}^{2} } \right)^{2} } } , $$
(64)
$$ \hat{\varOmega }_{p,c2} = \sqrt {4\hat{\omega }_{0}^{2} - 2\beta^{2} + 2\sqrt {\beta^{2} \left( {\beta^{2} - 4\hat{\omega }_{0}^{2} } \right) + \left( {P\hat{\omega }_{0}^{2} } \right)^{2} } } , $$
(65)

respectively. Otherwise, if \(\eta - {{\alpha \hat{\varOmega }_{p}^{2} } \mathord{\left/ {\vphantom {{\alpha \hat{\varOmega }_{p}^{2} } 6}} \right. \kern-0pt} 6} < 0\), the response of the system shows a softening behaviour. For this case, the positive and negative signs in the frequency response Eq. (59) represent the unstable and stable solutions, respectively; the unstable solution starts from the frequency \(\hat{\varOmega }_{p,c1}\) while the stable solution starts at the frequency \(\hat{\varOmega }_{p,c2}\).

The stability of the trivial solutions can be investigated using the Jacobian matrix for \(x_{1} = x_{3} = 0\). Therefore, the trace and the determinant of the Jacobian matrix for the trivial solution are obtained as

$$ Tr\left( {J_{{\text{MVA - T}}} } \right) = - 2\beta , $$
(66)
$$ Det\left( {J_{{\text{MVA - T}}} } \right) = \frac{1}{16}\left( {\hat{\varOmega }_{p}^{4} + \hat{\varOmega }_{p}^{2} \left( {4\beta^{2} - 8\hat{\omega }_{0}^{2} } \right) + 4\hat{\omega }_{0}^{4} \left( {4 - P^{2} } \right)} \right). $$
(67)

Consequently, the trivial solution is stable for frequencies \(\hat{\varOmega }_{p} < \hat{\varOmega }_{p,c1} , \, \hat{\varOmega }_{p} > \hat{\varOmega }_{p,c2}\), and is unstable when \(\hat{\varOmega }_{p,c1} < \hat{\varOmega }_{p} < \hat{\varOmega }_{p,c2}\). This is in contrast to the stability analysis for the MMS solution which resulted in the critical frequencies \(\hat{\varOmega }_{p,s1}\) and \(\hat{\varOmega }_{p,s2}\) in Eq. (46).

4 Effects of system parameters on the response

The frequency response equations for the PECB illustrated in Fig. 1 were developed and presented in Sect. 3. This section aims to discuss the effects of the system parameters including nonlinear inertia, Duffing-type nonlinearity, damping, parametric excitation amplitude, and the added mass at the cantilever tip on the dynamic behaviour of PECB systems.

4.1 Effect of nonlinear inertia and Duffing nonlinearity

From the frequency response Eq. (59) obtained from the MVA it can be found that, in the absence of the nonlinear inertia term \(\alpha\), the Duffing nonlinearity term \(\eta\) will determine the hardening or softening characteristics of the behaviour of the system, which is in accordance with the frequency response equation for the nonlinear parametrically excited system modelled as Mathieu equation [32]. This is while, for the PECB, the parameter

$$ \eta_{{{\text{MVA}}}}^{*} = \eta - \frac{1}{6}\alpha \hat{\varOmega }_{p}^{2} , $$
(68)

is the criterion determining hardening or softening behaviour. If, for a certain value of the excitation frequency, \(\eta_{{{\text{MVA}}}}^{*} \simeq 0\), the vibrations will grow exponentially, which is in agreement with results of direct numerical integration of the equation of motion (16) [50]. As a result, a bounded response cannot be achieved. When \(\hat{\varOmega }_{p} \simeq 2\hat{\omega }_{0}\), if \(\eta_{{{\text{MVA}}}}^{*} > 0\) (hardening behaviour), increasing \(\hat{\varOmega }_{p}\) to frequencies away from the principal parametric resonance, the term \(\hat{\varOmega }_{p}^{2}\) can decrease \(\eta_{{{\text{MVA}}}}^{*}\) significantly such that \(\eta_{{{\text{MVA}}}}^{*} \simeq 0\). Consequently, the vibrations will grow rapidly (Fig. 2). Similarly, for a system with a softening behaviour (\(\eta_{{{\text{MVA}}}}^{*} < 0\) at \(\hat{\varOmega }_{p} \simeq 2\hat{\omega }_{0}\)), for a positive value of \(\eta\), moving away from the principal parametric resonance, \(\eta_{{{\text{MVA}}}}^{*} \simeq 0\), resulting in an exponential growth of the vibrations (Fig. 3). It can be seen from Figs. 2 and 3 that unlike the MVA results and the numerical results obtained from Direct Integration (DI) of the equation of motion, the analytical results predicted by the MMS do not show a rapid increase in the response amplitude at frequencies around which \(\eta_{{{\text{MVA}}}}^{*} \simeq 0\). This is consistent with the frequency response Eq. (40) and the fact that \(\eta_{{{\text{MMS}}}}^{*}\) does not depend on the excitation frequency \(\hat{\varOmega }_{p}\). As seen from Figs. 2 and 3, the MVA captures qualitative behaviour of the system, but there is some quantitative difference compared to the numerical results for frequencies when \(\eta_{{{\text{MVA}}}}^{*}\) is close to zero. To get a better quantitative agreement, one needs to take more harmonics in the MVA approximation, as has been discussed in [41].

Fig. 2
figure 2

Steady-state frequency–response diagrams for a PECB with a hardening behaviour; comparing the results obtained from the MMS1 using Eq. (40) (red coloured results), the MVA1 using Eq. (59) (blue coloured results), and numerical results obtained from Direct Integration (DI) of the equation of motion (16) (black coloured data points). Solid lines and dashed lines represent the stable and unstable solutions, respectively, obtained from MMS1 and MVA1. The system parameters are \(\hat{\omega }_{0} = 1\), \(\beta = 0.005\), \(P = - 0.02\), \(\eta = 11\), and \(\alpha = 10\)

Full size image
Fig. 3
figure 3

Steady-state frequency–response diagrams for a PECB with a softening behaviour. Comparing the results obtained from the MMS1 using Eq. (40) (red coloured results), the MVA1 using Eq. (59) (blue coloured results), and numerical results obtained from Direct Integration (DI) of the equation of motion (16) (black coloured data points). Solid lines and dashed lines represent the stable and unstable solutions, respectively, obtained from MMS1 and MVA1. The system parameters are \(\hat{\omega }_{0} = 1\), \(\beta = 0.005\), \(P = - 0.02\), \(\eta = 6\), \(\alpha = 16\)

Full size image

4.2 Effect of damping and parametric excitation amplitude

While the Duffing nonlinearity \(\eta\) and the nonlinear inertia \(\alpha\) play crucial roles in determining the hardening or softening characteristics of the behaviour of the PECB, the damping term \(\beta\) and the parametric excitation term \(P\) affect the critical frequencies at which the stable and unstable analytical solutions begin and the amplitude response of the PECB.

Considering the critical frequencies \(\hat{\varOmega }_{p,s1}\), \(\hat{\varOmega }_{p,s2}\) in Eq. (46) obtained from the MMS, and \(\hat{\varOmega }_{p,c1}\), \(\hat{\varOmega }_{p,c2}\) in Eqs. (64) and (65) obtained from the MVA, it can be seen that these frequencies are functions of \(\hat{\omega }_{0}\), \(\beta\), and \(P\). Therefore, for a fixed value of \(\hat{\omega }_{0}\), \(\beta\) and \(P\) can be chosen such that desired values of \(\hat{\varOmega }_{p,s1}\), \(\hat{\varOmega }_{p,s2}\), \(\hat{\varOmega }_{p,c1}\), and \(\hat{\varOmega }_{p,c2}\) are achieved, both in a hardening behaviour (Fig. 4) and in a softening behaviour (Fig. 5). Furthermore, as can be seen in these figures, within the frequency range considered, increasing \(P\) or decreasing \(\beta\) will increase the amplitude response of the PECB, which can be found from the frequency response Eqs. (40) obtained from the MMS and (59) obtained from the MVA, and is in agreement with the numerical results obtained from direct integration of the equation of motion (16).

Fig. 4
figure 4

Steady-state frequency–response diagrams for a PECB with a hardening behaviour. Comparing the results obtained from the MMS1 using Eq. (40) (red coloured results), the MVA1 using Eq. (59) (blue coloured results), and numerical results obtained from DI (black coloured data points) for \(\hat{\omega }_{0} = 3\), \(\eta = 35\), \(\alpha = 2\), and different values of \(\beta\) and \(P\); a \(\beta = 0.02\), \(P = - 0.02\), b \(\beta = 0.02\), \(P = - 0.06\), c \(\beta = 0.07\), \(P = - 0.06\). Solid lines and dashed lines represent the stable and unstable solutions, respectively, obtained from MMS1 and MVA1

Full size image
Fig. 5
figure 5

Steady-state frequency–response diagrams for a PECB with a softening behaviour. Comparing the results obtained from the MMS1 using Eq. (40) (red coloured results), the MVA1 using Eq. (59) (blue coloured results), and numerical results obtained from DI (black coloured data points) for \(\hat{\omega }_{0} = 3\), \(\eta = 25\), \(\alpha = 8\), and different values of \(\beta\) and \(P\); a \(\beta = 0.02\), \(P = - 0.02\), b \(\beta = 0.02\), \(P = - 0.06\), c \(\beta = 0.07\), \(P = - 0.06\). Solid lines and dashed lines represent the stable and unstable solutions, respectively, obtained from MMS1 and MVA1

Full size image

4.3 Effect of tip mass

It was shown that the parameters \(\eta\), \(\alpha\), \(\hat{\omega }_{0}\), \(\beta\) and \(P\) determine the hardening or softening behaviour of the PECB, or change the amplitude response, and the critical frequencies at which the stable and unstable analytical solutions begin.

It can be seen from Eqs. (7), (10), and (11) that the point mass added at the cantilever tip will change the mode shape functions \(\psi (\hat{s})\) and the non-dimensional undamped natural frequency \(\hat{\omega }_{0}\). As a result, the system parameters \(\eta\), \(\alpha\), and \(P\) expressed in Eqs. (17)-(22) will change, altering the dynamic behaviour of the PECB.

To investigate the effect of tip mass on the response of the PECB, a cantilever beam with the material and geometric properties presented in Table 1 is considered. The non-dimensional acceleration amplitude and the non-dimensional damping \(\beta\) are chosen to be \(\hat{a}_{p} = 0.2361\), \(\beta = 0.05\), respectively. For different values of the non-dimensional tip mass (\(\hat{m} = 0.0569\), \(\hat{m} = 0.0854\), and \(\hat{m} = 0.1139\)), and for a narrow frequency range around the principal parametric resonance, the frequency response diagrams are illustrated in Fig. 6.

Table 1 Material and geometric properties of the cantilever beam
Full size table
Fig. 6
figure 6

Amplitude response as a function of the frequency ratio for the parametrically excited cantilever beam with the material and geometric properties presented in Table 1. Comparing the results obtained from the MMS1 (red coloured results), MVA1 (blue coloured results), and DI (black coloured data points) for \(\hat{a}_{p} = 0.2361\) and different values of \(\hat{m}\); a \(\hat{m} = 0.0569\), b \(\hat{m} = 0.0854\), c \(\hat{m} = 0.1139\). Solid lines and dashed lines represent the stable and unstable solutions, respectively, obtained from MMS1 and MVA1

Full size image

For \(\hat{m} = 0.0569\) (Fig. 6a), using Eqs. (30), (10), and (11), the undamped natural frequency of the system is obtained as \(f_{0} = \hat{\omega }_{0} /2\pi = 4.2000{\text{ HZ}}\). The other system parameters are obtained as \(\hat{\omega }_{0} = 3.1712\), \(P = - 0.0445\), \(\eta = 27.5099\) and \(\alpha = 6.6884\) using Eqs. (18)-(22). For the frequency range considered \(\eta_{{{\text{MVA}}}}^{*}\) is negative, leading to a softening behaviour. At the principal parametric resonance frequency \(\eta_{{{\text{MVA}}}}^{*} = - 17.3314\). It can be seen that the MVA results show good agreement with the numerical results obtained from DI; the amplitude response obtained from DI, MVA, and MMS at the frequency ratio \(\hat{\varOmega }_{p} /\hat{\omega }_{0} = 1.95\) is found to be 0.2612, 0.2520, and 0.2363, respectively.

Increasing the value of the non-dimensional tip mass to \(\hat{m} = 0.0854\), the values of \(f_{0}\), \(\hat{\omega }_{0}\) and \(\eta\) decrease to 4.0158 Hz, 3.0322, and 21.7987, respectively. Also, the nonlinear inertia term and the parametric excitation amplitude are obtained as \(\alpha = 7.3077\), \(P = - 0.0530\). As a result, the magnitude of \(\eta_{{{\text{MVA}}}}^{*}\) will increase, enhancing the softening behaviour (at the principal parametric resonance frequency \(\eta_{{{\text{MVA}}}}^{*} = - 22.9937\)). Therefore, as can be seen in Fig. 6b, within the frequency range considered, \(\hat{\varOmega }_{p,s1}\), \(\hat{\varOmega }_{p,c1}\) decrease, \(\hat{\varOmega }_{p,s2}\), \(\hat{\varOmega }_{p,c2}\) increase, while the amplitude response decreases.

Consequently, increasing the value of \(\hat{m}\) increases the frequency range in which the stable solution can exist and decreases the amplitude response of the PECB. The frequency response diagram for \(\hat{m} = 0.1139\) is illustrated in Fig. 6c. For this case, the system parameters are \(f_{0} = 3.8535{\text{ HZ}}\), \(\hat{\omega }_{0} = 2.9096\), \(P = - 0.0623\), \(\eta = 16.2577\), and \(\alpha = 8.1286\). It can be seen that, as expected, the softening behaviour is enhanced, which is due to the larger magnitude of \(\eta_{{{\text{MVA}}}}^{*}\) within the frequency range considered; for this case, at the principal parametric resonance frequency \(\eta_{{{\text{MVA}}}}^{*} = - 29.6188\).

5 Experiments on a PECB system with a tip mass

This section concerns the experimental measurements of the response of a PECB with a tip mass. The main aspects investigated in this section are summarized as the following: the criteria presented in Eqs. (51) and (68) are investigated experimentally for a cantilever beam with a tip mass and with a positive value of the Duffing nonlinearity \(\eta\). Experimental measurements of the response of a PECB with a tip mass for different values of the excitation acceleration amplitude (\(a_{p} = 1.7g, \, 1.8g, \, 1.9g{\text{ and }}2.0g\)) are taken. Then, the experimental results for the displacement and acceleration of the cantilever tip are presented and compared with the results obtained from the MMS, the MVA and DI.

5.1 Experimental set-up and methodology

A schematic block diagram of the experimental set-up used to conduct the experiments, consisting of a vibration controller, power amplifier, shaker, cantilever beam, signal analyser, data acquisition computer, and two accelerometers, is illustrated in Fig. 7 and the set-up is shown in Fig. 8.

Fig. 7
figure 7

A schematic block diagram of the experimental set-up

Full size image
Fig. 8
figure 8

Configuration of a parametrically excited cantilever system with a tip mass

Full size image

To excite the cantilever beam system, a time harmonic signal with a constant acceleration amplitude was generated using the vibration controller VR9500 and VibrationView software. The generated signal was then routed to a power amplifier type APS125 and in turn to the APS113 shaker. The three-axis piezoelectric accelerometer type PCB356A32, attached to the shaker, was used to measure the reference signal. A cantilevered stainless-steel beam with material and geometric properties presented in Table 2 was connected to the shaker using a fixture, such that the generated acceleration signal was transferred to the clamped end of the cantilever, exciting the cantilever in the longitudinal direction (parametric excitation). The transverse vibration of the beam was then measured using a piezoelectric accelerometer type PCB352C22, attached to the free end of the cantilever beam, which was considered as a tip mass (\(m = 0.5g\)). The real time acceleration data of the tip accelerometer was measured using a Data Physics Quattro-DP240 signal analyser and SignalCalc ACE 900 series software installed in a data acquisition computer.

Table 2 Material and geometric properties of the cantilever beam used in experiments
Full size table

The free vibration response of the system was used to estimate the natural frequency and the damping ratio (\(\xi\)) of the system. Tapping the tip of the beam, from the corresponding FFT of the transient response of the system, the natural frequency of the first mode of vibration of the cantilever beam was estimated as \(9.40{\text{ HZ}}\). Also, using the logarithmic decrement method, the damping ratio for this vibration mode was estimated as 0.561%. To investigate the response of the system to harmonic excitation, the steady-state acceleration and displacement of the cantilever beam tip in a frequency range close to the principal parametric resonance was obtained using the SignalCalc software, applying a Flat-Top window, with the measurement time long enough for any transient disturbance to decay (Fig. 9). Furthermore, 100 measurements of the acceleration were taken at each excitation frequency and averaged. First, the excitation frequency was swept up slowly within the frequency range considered, and the results were obtained and recorded. Then, the results for the case when the excitation was swept down slowly within the frequency range considered were obtained.

Fig. 9
figure 9

Experimental measurements of the cantilever beam tip response when driven at \(a_{p} = 2.0g\) and \(\varOmega_{p} = 18.70{\text{ Hz}}\) at which the maximum response for the case when the excitation frequency was swept up slowly from \(18.61{\text{ Hz}}\) to \(18.99{\text{ Hz}}\) (\(\varOmega_{p} /\omega_{0} \simeq 1.98\) to \(\varOmega_{p} /\omega_{0} \simeq 2.02\)) was obtained. Frequency spectra for (a) displacement and (b) acceleration of the cantilever tip

Full size image

A photograph of the cantilever beam when it was driven axially at an acceleration amplitude \(a_{p} = 2.0g\) and excitation frequency \(\varOmega_{p} = 18.70{\text{ HZ}}\) is shown in Fig. 10. The frequency spectrums for the displacement and acceleration of the cantilever for this case are shown in Fig. 9. As can be seen in this figure, the response of the system is dominated by a frequency equal to half the excitation frequency, which is the main characteristic of parametrically excited systems.

Fig. 10
figure 10

Photograph of the cantilever beam when driven axially at \(a_{p} = 2.0g\) and \(\varOmega_{p} = 18.70{\text{ Hz}}\) at which the maximum response for the case when the excitation frequency was swept up from \(18.61{\text{ Hz}}\) to \(18.99{\text{ Hz}}\) (\(\varOmega_{p} /\omega_{0} \simeq 1.98\) to \(\varOmega_{p} /\omega_{0} \simeq 2.02\)) was obtained

Full size image

6 Results and discussion

The steady-state displacement and acceleration of the cantilever beam with the material and geometric properties presented in Table 2, were measured for different values of excitation acceleration amplitude (\(a_{p} = 1.7g, \, 1.8g, \, 1.9g{\text{ and }}2.0g\)) using the approach described in Sect. 5.1. The small accelerometer attached at the cantilever tip is considered to be a \(0.5g\) tip mass and effects of its rotational inertia are assumed to be very small. To compare the experimental results with the analytical results of the MMS and MVA, and the numerical results of DI, using Eqs. (2), (3), and (5), the magnitude of the displacement \(w\) and acceleration \(a\) of the cantilever tip are expressed as

$$ w = L\psi (1)A, $$
(69)
$$ a = \frac{1}{4}LY^{2} \psi (1)\hat{\varOmega }_{p}^{2} A, $$
(70)

where \(\psi (1)\) is the value of the fundamental mode shape of the beam at the tip (\(s/L = 1\)), and \(A\) is the non-dimensional amplitude obtained from the MMS and the MVA using the frequency–response Eqs. (40) and (59), respectively, and DI.

Using Eqs. (10) and (17)-(22), the system parameters are \(\hat{\omega }_{0} = 3.4548\), \(\eta = 36.2329\), and \(\alpha = 5.5682\). Also \(\beta = 2\xi \hat{\omega }_{0} = 0.0387\), where \(\xi = 0.561\%\) is the damping ratio of the first vibration mode. As can be seen, both the nonlinear curvature term \(\eta\) and the nonlinear inertial term \(\alpha\) are positive. Nevertheless, at \(\hat{\varOmega }_{p} \simeq 2\hat{\omega }_{0}\), both \(\eta_{{{\text{MMS}}}}^{*}\) and \(\eta_{{{\text{MVA}}}}^{*}\) obtained from the MMS and the MVA in Eqs. (51) and (68), respectively, are negative. Therefore, a softening behaviour for the cantilever beam considered for the experiments is predicted by both the MMS and the MVA.

For a frequency range around the principal parametric resonance (\(\varOmega_{p} /\omega_{0} \simeq 1.98\) to \(\varOmega_{p} /\omega_{0} \simeq 2.02\)), and for \(a_{p} = 1.7g, \, 1.8g, \, 1.9g{\text{ and }}2.0g\), both conditions (41) and (60) hold true: for these values of the acceleration amplitude, using Eqs. (17)-(19), \(P\) is obtained as \(- 0.0268\), \(- 0.0284\), \(- 0.0300\), and \(- 0.0316\), respectively.

For the values of the input acceleration amplitude considered, the experimental results are presented and compared with the results obtained from the MMS, the MVA and DI in Figs. 11, 12, 13 and 14, respectively. It can be seen that, as predicted by the MVA and the MMS, the cantilever beam shows a softening behaviour. The experimental results for all cases are in good agreement with the theoretical results obtained from the MVA and the MMS, and the numerical results obtained from DI. The measured critical frequencies at which the stable solution begins, for the cases when the excitation frequency was both swept up and swept down, show good agreement with \(\hat{\varOmega }_{p,s2}\) and \(\hat{\varOmega }_{p,c2}\) predicted by the MMS and the MVA in Eqs. (46) and (65), respectively. Additionally, as predicted by the analysis presented in Sect. 4.2, it can be seen that increasing the value of \(P\) within the frequency range considered increases the magnitude of the response amplitude and the frequency range in which stable solutions can exist. Experimental results show that the response of the system is bounded. However, the corresponding maximum response value is lower than predicted theoretically. This is believed to be due to other effects such as the nonlinear damping effects not included in the employed theoretical model. As discussed in Sect. 4, when linear damping is considered, the term containing a linear combination of the Duffing nonlinearity term and the nonlinear inertia term in the frequency response equation obtained by the MVA can tend to zero around the principal parametric resonance, resulting in an exponential growth of vibrations which was validated by the numerical results obtained from DI.

Fig. 11
figure 11

Steady-state frequency–response diagrams for the parametrically excited cantilever beam with the material and geometric properties presented in Table 2 and the acceleration amplitude \(a_{p} = 1.7g\). Comparing the results obtained from the MMS1 (red), MVA1 (blue), DI (black data points), the experimental results when the excitation frequency was swept up (green triangles), and the experimental results when the excitation frequency was swept down (brown squares); a displacement at the cantilever tip, b acceleration at the cantilever tip. Solid lines and dashed lines represent the stable and unstable solutions, respectively, obtained from MMS1 and MVA1. The system parameters \(\hat{\omega }_{0} = 3.4548\), \(\beta = 0.0387\), \(\eta = 36.2329\), \(\alpha = 5.5682\), \(P = - 0.0268\)

Full size image
Fig. 12
figure 12

Steady-state frequency–response diagrams for the parametrically excited cantilever beam with the material and geometric properties presented in Table 2 and the acceleration amplitude \(a_{p} = 1.8g\). Comparing the results obtained from the MMS1 (red), MVA1 (blue), DI (black data points), the experimental results when the excitation frequency was swept up (green triangles), and the experimental results when the excitation frequency was swept down (brown squares); a displacement at the cantilever tip, b acceleration at the cantilever tip. Solid lines and dashed lines represent the stable and unstable solutions, respectively, obtained from MMS1 and MVA1. The system parameters \(\hat{\omega }_{0} = 3.4548\), \(\beta = 0.0387\), \(\eta = 36.2329\), \(\alpha = 5.5682\), \(P = - 0.0284\)

Full size image
Fig. 13
figure 13

Steady-state frequency–response diagrams for the parametrically excited cantilever beam with the material and geometric properties presented in Table 2 and the acceleration amplitude \(a_{p} = 1.9g\). Comparing the results obtained from the MMS1 (red), MVA1 (blue), DI (black data points), the experimental results when the excitation frequency was swept up (green triangles), and the experimental results when the excitation frequency was swept down (brown squares); a displacement at the cantilever tip, b acceleration at the cantilever tip. Solid lines and dashed lines represent the stable and unstable solutions, respectively, obtained from MMS1 and MVA1. The system parameters \(\hat{\omega }_{0} = 3.4548\), \(\beta = 0.0387\), \(\eta = 36.2329\), \(\alpha = 5.5682\), \(P = - 0.0300\)

Full size image
Fig. 14
figure 14

Steady-state frequency–response diagrams for the parametrically excited cantilever beam with the material and geometric properties presented in Table 2 and the acceleration amplitude \(a_{p} = 2.0g\). Comparing the results obtained from the MMS1 (red), MVA1 (blue), DI (black data points), the experimental results when the excitation frequency was swept up (green triangles), and the experimental results when the excitation frequency was swept down (brown squares); a displacement at the cantilever tip, b acceleration at the cantilever tip. Solid lines and dashed lines represent the stable and unstable solutions, respectively, obtained from MMS1 and MVA1. The system parameters \(\hat{\omega }_{0} = 3.4548\), \(\beta = 0.0387\), \(\eta = 36.2329\), \(\alpha = 5.5682\), \(P = - 0.0316\)

Full size image

7 Conclusions

The response of a parametrically excited cantilever beam (PECB) with a tip mass was investigated in this paper. The paper focused on prediction of the response of the system, in particular its hardening or softening characteristics when linear damping was considered. The Method of Varying Amplitudes (MVA) and the Method of Multiple Scales (MMS) were employed to develop steady-state frequency–response approximations for the response of the system and investigate the stability of the solutions. The analytical results were validated by numerical results obtained from Direct Integration (DI) of the equation of motion. Furthermore, experimental measurements of the response of a PECB with a tip mass were presented and the experimental results were compared with theoretical results obtained from the MMS and the MVA and numerical results obtained from DI. These investigations led to the following main findings:

  • The analytical results obtained from the MVA showed that the response of the system is highly dependent on the values of the Duffing-type nonlinearity term and the nonlinear inertia term. It was shown that, for frequency ranges around the principal parametric resonance, the term containing a linear combination of these parameters in the frequency response equation can tend to zero, resulting in an exponential growth of the vibrations. The MVA results were validated by numerical results obtained from DI, while the MMS failed to predict this critical frequency.

  • It was shown that the mass added at the cantilever tip can change the system parameters, enhancing the softening behaviour of the PECB. It was shown that, within the frequency range considered, increasing the value of the tip mass decreases the amplitude response of the system and broadens the frequency range in which a stable response can exist.

  • The experimental results of the displacement and acceleration of the cantilever tip showed good agreement with the theoretical results of the MMS and the MVA, and the numerical results of DI. Furthermore, the theoretical expressions presented for the critical frequency at which the nonzero stable solution begins were demonstrated to be capable to predict this frequency with a good accuracy.