Nonlinear dynamics of a tubular beam considering distortion of the cross sections and internal resonances

Abstract

The nonlinear dynamics of a thin tube under the action of a harmonic external load is addressed in the paper. Use is made of a beam-like model which extends the Timoshenko beam model with further kinematic descriptors, related to the change in shape of the cross section. The external load is applied in half cap of the pipe, directly triggering both the bending of the axis-line and the flattening of the cross sections. The equations of motion are projected on a reduced basis constituted by the first three linear modes, and then the solutions are sought via the multiple scale method, for two different external resonance conditions. Internal resonances among the modes are considered as well. The outcomes, compared with pure numerical solutions, highlight the possible energy exchange between local modes, i.e., those describing flattening and warping of the cross sections, and global modes, i.e., those related to bending of the axis-line and rotation of the cross section of the pipe.

1 Introduction

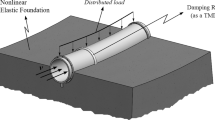
The use of tubes as structural members is widespread in lots of engineering applications, ranging from civil to industrial, aerospace and many other contexts. Hence, the evaluation of their carrying capacity is a compelling step in the design development, as the typical thin-walled nature of pipes makes this aspect a key point. Indeed, demanding cares are requested to consistently deal with the possible lack of validity of the Saint Venant principle and the significant contribution of the distortion of the cross sections. In this framework, the possibility to model tubes as beams or beam-like structures would represent an undoubted asset, as compared to more demanding bi-dimensional or three-dimensional continuum theories. However, classical beam theories like Euler–Bernoulli and Timoshenko [1] require to be enriched, in order to overtake the hypothesis of rigid cross section.

For instance, the Vlasov theory [2], introduced to address non-uniform torsion of tubular beams, serves as main instrument in including the effect of warping of cross sections in shaft models, as well as in providing advanced and reliable contributions in the mechanics of pipes. As a further example, the nonlinear interaction between bending of pipes and flattening of their cross sections is the main focus of the Brazier theory [3, 4], which provides physical explanations and functional tools to engineers to address the softening behavior of bent tubular beams. In some cases, soft elastic cores are included to prevent flattening [5].

Many other efforts have been made in the last decades by scholars in developing high-level beam theories [6,7,8,9]. The generalized beam theory (GBT) lies in this line of research [10,11,12,13,14], introducing linear combinations of assumed shape functions to describe bending, torsion and cross-section distortion of thin-walled beams. Recently, in [15], the Euler–Bernoulli beam model was endowed with descriptors for the distortion of the cross section, to deal with multi-layered pipes under flexural static actions. Lately, in [16, 17], the same idea, which originally comes from GBT, was broadened to the Timoshenko beam model, including effects of flattening and warping of the cross sections as assumed shapes, amplified by unknown variables. The same pipe model was then used to analyze the nonlinear dynamic response in [18], after consistent evaluation of the inertial contributions. In that specific case, the nonlinear coupling came both from stiffness and inertial terms, and triggered internal resonances between modes, which were related both to global (bending) and local (cross-section distortion) behavior. External resonance due to a load covering the whole cross section was considered as well, and the effects of the softening contribution provided by the cross-section change in shape were analyzed.

In this paper, starting from the pipe model proposed in [18], a different external load is considered: Here, it is assumed to be distributed only on half cap of the cross sections. This specific aspect induces a direct loading toward the flattening modes of the cross sections of the tube. Hence, 1:1 external resonance conditions with one of the local modes, combined with internal resonances between local and global modes, may potentially cause energy transfers from cross-section distortion to bending, occurrence which is worthy of investigation. The analysis is addressed by the multiple scale method (MSM), applied to the equations of motion which are made discrete by a Galerkin projection. Two different implementations of the MSM are carried out, depending on the local mode involved in the considered external resonance condition. Numerical integration of the equations of motion are used to compare and validate the asymptotic solutions.

The paper is organized as follows. In Sect. 2, the beam-like model is briefly described, in Sect. 3, the discretized nonlinear equations of motion are obtained via a Galerkin projection, in Sect. 4, the two different implementations of the MSM are described, and in Sect. 5, the numerical results are presented and discussed. Finally, the conclusions are drawn in Sect. 6.

2 Model description

The formulation of the beam-like model used here to address the nonlinear dynamics of a pipe with thin annular cross section is extensively described in [18]. For the sake of completeness, here its main features are only briefly recalled, leaving the details in [18], but highlighting the differences related to the load and resonance conditions.

An in-plane Timoshenko beam model is introduced (Fig. 1a), as constituted by a straight axis-line spanned by the abscissa $s\in [0,l]$ in direction $\bar{{\textbf{a}}}_1$, where l is the initial length, and by infinite initially transverse cross sections, parallel to the plane spanned by $\bar{{\textbf{a}}}_2,\bar{{\textbf{a}}}_3$. The unitary vectors $\bar{{\textbf{a}}}_1,\bar{{\textbf{a}}}_2,\bar{{\textbf{a}}}_3$ are mutually orthogonal. The beam is clamped at $s=0$ (cross-section A) and free at $s=l$ (cross-section B). The kinematic variables are u(s), v(s), $\vartheta (s)$, where the first two variables represent $\bar{{\textbf{a}}}_1$- and $\bar{{\textbf{a}}}_2$-components of the displacement ${\textbf{u}}$ of the axis-line points, respectively, whereas the third one describes the cross-section rotation about $\bar{{\textbf{a}}}_3$. Moreover, as an extension of the Timoshenko beam model, further kinematic variables are introduced, referred to as $a_p(s)$, $a_w(s)$, which describe in-plane and out-of-plane change in shape of the cross section, respectively. The physical meaning of $a_p(s)$, $a_w(s)$ comes from an identification procedure of the beam-like model through a three-dimensional realization of the pipe, seen as an assembly of infinite longitudinal fibers and transversal ribs (Fig. 1b), and having length l, mid radius R, and thickness $h\ll R$. In particular, $a_p(s)$, $a_w(s)$ turn out to be the amplitudes of assumed flattening (Fig. 2a) and warping (Fig. 2b) shapes of the annular cross section of the pipe at the generic abscissa, respectively.

The strain measures of the Timoshenko beam are consistently introduced: the longitudinal strain $\varepsilon _0(s)$, the transversal strain $\gamma _0(s)$, the bending curvature $\kappa _0(s)$, as well as strain components relevant to the cross-section change in shape, namely $\alpha _p(s)$, $\beta _p(s)$, $\alpha _w(s)$, $\beta _w(s)$, referred to as local components. Hence, the nonlinear strain–displacement relationship, series-expanded up to the third order, is:

$$\begin{aligned} \begin{aligned}&\begin{aligned} \varepsilon _0\mathrel {\mathop :}=\,&u'-\frac{\vartheta ^2}{2}+\vartheta v'\\ \gamma _0\mathrel {\mathop :}=\,&v'-\vartheta -u'\vartheta +\frac{1}{6}(\vartheta ^3-3\vartheta ^2v')\\ \kappa _0\mathrel {\mathop :}=\,&\vartheta ' \end{aligned}\\&\begin{aligned} \alpha _{j}\mathrel {\mathop :}=\,&a_{j}\\ \beta _{j}\mathrel {\mathop :}=\,&a_{j}' \end{aligned}\qquad \qquad \textrm{for }j=p,w, \end{aligned} \end{aligned}$$

(1)

where prime stands for s-derivative. Boundary conditions for clamp at cross-section A read:

$$\begin{aligned} u_A=0,\quad v_A=0,\quad \vartheta _A=0,\quad a_{pA}=0,\quad a_{wA}=0,\nonumber \\ \end{aligned}$$

(2)

Fig. 1

Initial configuration of the beam: a beam-like structure; b pipe with longitudinal fibers and annular ribs highlighted

Fig. 2

Local distortion on the cross section: a assumed shape for the flattening and amplitude $a_p$; b assumed shape for the warping and amplitude $a_w$

The virtual work theorem allows one to determine the weak form of the dynamic equilibrium equations. More specifically, the internal virtual work for the beam-like structure reads:

$$\begin{aligned} \begin{aligned} \delta {\mathcal {W}}_{\textrm{int}}&=\intop _{0}^{l}\Bigg (\lambda \delta \varepsilon _0+T\delta \gamma _0+M\delta \kappa _0 \\&\quad +\sum _{j=p,w}(D_{j}\delta \alpha _{j}+B_{j}\delta \beta _{j})\Bigg )\textrm{d}s \end{aligned}\nonumber \\ \end{aligned}$$

(3)

where $\delta$ is the variational operator, T, M are the shear force and bending moment of the planar Timoshenko beam, $D_{j},B_{j}$ are distortion and bi-distortion force components, dual to the local strain components, for $j=p,w$, and $\lambda$ is a Lagrange multiplier, introduced in order to nullify the longitudinal strain $\varepsilon _0$, as it is usual in case of cantilevers [19,20,21,22,23,24]. Moreover, the external virtual work for the beam-like structure reads:

$$\begin{aligned} \begin{aligned} \delta {\mathcal {W}}_{\textrm{ext}}&=\intop _{0}^{l}\Bigg ((f_u-{\tilde{f}}_u)\delta u+(f_v-{\tilde{f}}_v)\delta v \\&\quad +(c-{\tilde{c}})\delta \vartheta +\sum _{j=p,w} (g_j-{\tilde{g}}_j)\delta a_{j}\Bigg )\textrm{d}s \end{aligned}\nonumber \\ \end{aligned}$$

(4)

where $f_u,f_v,c,g_j$ represent the external distributed forces and couples, work-conjugate of the generalized displacements, and ${\tilde{f}}_u,{\tilde{f}}_v,{\tilde{c}},{\tilde{g}}_j$ are the inertial counterparts. Substitution of Eq. (1) in Eq. (3), imposition of the virtual work equation $\delta {\mathcal {W}}_{\textrm{int}}=\delta {\mathcal {W}}_{\textrm{ext}}$, for all kinematically consistent $\delta u,\delta v,\delta \vartheta ,\delta a_p,\delta a_w,\delta \lambda$, provides the weak form of the dynamical equilibrium equations.

The constitutive law in case of linear elastic material of Young modulus E and transversal elastic modulus G is obtained after the application of the identification procedure from the three-dimensional model and assumes the following expression:

$$\begin{aligned} T= & {} c_{1} \gamma _{0}-\frac{1}{2} c_{1} \alpha _{w} \kappa _0 \nonumber \\ M= & {} c_{2} \kappa _0+c_{3} \alpha _{p} \kappa _0+c_{4} \alpha _{p}^2\kappa _0-\frac{1}{2} c_{1} \alpha _{w} \gamma _{0}\nonumber \\{} & {} \quad +\frac{1}{2} c_{1} \alpha _{w}^2 \kappa _0 \nonumber \\ D_p= & {} c_{5} \alpha _{p}+c_{4} \alpha _{p} \kappa _0^2+c_{6} \kappa _0^2+c_{8} \alpha _{p} \alpha _{w} \beta _{p}\nonumber \\{} & {} \quad +c_{7} \alpha _{p} \alpha _{w}^2+c_{9} \alpha _{w}^2 \beta _{w} \nonumber \\ B_p= & {} \frac{1}{4} c_{1} \beta _{p}+c_{10} \alpha _{w}+c_{12}\alpha _{p}^2 \alpha _{w}+c_{11} \alpha _{w}^3 \nonumber \\ D_w= & {} c_{13} \alpha _{w}+c_{10} \beta _{p}+c_{7} \alpha _{p}^2\alpha _{w}+c_{12} \alpha _{p}^2\beta _{p} \nonumber \\{} & {} \quad +c_ {15} \alpha _{w}^2 \beta _{p}+\frac{1}{2} c_ {1} \alpha _{w}\kappa _0^2+c_{14}\alpha _{w}^3 \nonumber \\{} & {} \quad -\frac{1}{2} c_{1}\gamma _{0} \kappa _0+c_{16} \alpha _{p} \alpha _{w} \beta _{w} \nonumber \\ B_w= & {} c_{17} \beta _{w}+c_{9} \alpha _{p} \alpha _{w}^2 \end{aligned}$$

(5)

where the elastic coefficients are:

$$\begin{aligned} \begin{aligned} c_{1}&= \pi G h R,&c_{2}&= \pi E h R^3,&\\ c_{3}&= -\frac{3}{2} \pi E h R^2,&c_{4}&= \frac{5}{8} \pi E h R,&\\ c_{5}&= \frac{9 \pi E J}{R^3},&c_{6}&= -\frac{3}{4} \pi E h R^2,&\\ c_{7}&= \frac{27 \pi G h}{2 R^3},&c_{8}&= -\frac{9 \pi G h}{8 R^2},&\\ c_{9}&= \frac{36 \pi E h}{R^2},&c_{10}&= -G\pi h,&\\ c_{11}&= \frac{7 \pi G h}{2 R^2},&c_{12}&= -\frac{9 \pi G h}{16 R^2},&\\ c_{13}&=\frac{4 \pi G h}{R},&c_{15}&=\frac{21 \pi G h}{2 R^2},&\\ c_{16}&= \frac{72 \pi E h}{R^2},&c_{17}&=\pi E h R,{} & {} &\\ c_{14}&= \frac{118 \pi E h}{R^3}-\frac{56 \pi G h}{R^3}. \end{aligned} \end{aligned}$$

(6)

Here, the Poisson ratio is assumed as $\nu =0$, in order to highlight the pure effect of the coupling between bending and flattening.

It is worth mentioning that the three-dimensional model used for the determination of the constitutive law (5), sketched in Fig. 1b, is assumed to allow extension and shear deformation of the longitudinal fibers, as well as bending of the transversal annular ribs. More details on this aspect are given in [16, 18].

Consistently, the expressions for the inertial forces and couples are identified as well:

$$\begin{aligned} {\tilde{f}}_u&=m_{1} \ddot{u}=m_{1}\int _{0}^{s}\Biggl (\frac{\vartheta ^2}{2}-\vartheta v'\Biggr )^{\bullet \bullet }\textrm{d}\xi \end{aligned}$$

(7)

$$\begin{aligned} {\tilde{f}}_v&=m_{1} \ddot{v} \end{aligned}$$

(8)

$$\begin{aligned} {\tilde{c}}&=m_{2} \ddot{\vartheta }+m_{3} {\dot{a}}_p {\dot{\vartheta }}+m_{3} a_p \ddot{\vartheta }+m_{4} {\dot{a}}_p a_p {\dot{\vartheta }}\nonumber \\&\quad +m_{5} a_p^2 \ddot{\vartheta } +m_{1} a_w {\dot{a}}_w {\dot{\vartheta }}+m_{6} a_w^2 \ \ddot{\vartheta } \end{aligned}$$

(9)

$$\begin{aligned} {\tilde{g}}_p&=m_{4} \ddot{a}_p-\frac{5}{8} m_{6} a_p {\dot{\vartheta }}^2+m_{7} \ {\dot{\vartheta }}^2 \end{aligned}$$

(10)

$$\begin{aligned} {\tilde{g}}_w&=m_{6} \ddot{a}_w-m_{6} a_w {\dot{\vartheta }}^2 \end{aligned}$$

(11)

with the coefficients:

$$\begin{aligned} \begin{aligned} m_{1}&= 2 \pi h \rho R,&m_{2}&= \pi h \rho R^3,&m_{3}&= -\frac{3}{2} \pi h \rho R^2,\\ m_{4}&= \frac{5}{4} \pi h \rho R,&m_{5}&= \frac{5}{8} \pi h \rho R,&m_{6}&= \pi h \rho R,\\ m_{7}&= \frac{3}{4} \pi h \rho R^2 \end{aligned} \end{aligned}$$

(12)

where the dot stands for differentiation with respect to time, indicated as t.

In Eq. (7), the condensation of the variable u is applied, as a consequence of the condition $\varepsilon _0=0$ which provides, by Eq. (1-1):

$$\begin{aligned} u=\int _{0}^{s}\Biggl (\frac{\vartheta ^2}{2}-\vartheta v'\Biggr )\textrm{d}\xi . \end{aligned}$$

(13)

Correspondingly, the expression of the Lagrangian multiplier is obtained as well:

$$\begin{aligned} \lambda =T\vartheta +\int _{s}^{l}\!\!(f_u-{\tilde{f}}_u)\textrm{d}\xi . \end{aligned}$$

(14)

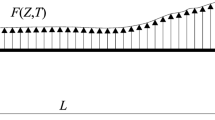
The identification procedure also provides the expression for the external forces. Here, a time-dependent load per unit volume $b_v=b_0\cos ({\varOmega } t)$, in the direction $\bar{{\textbf{a}}}_2$, is uniformly applied on the upper cap of the cross sections, as shown in Fig. 3. Therefore, the load condition is different than the one applied in [18], where the load was applied in the whole cross section. Hence, in the analyzed case and with reference to Eq. (4), the load provides both $f_v$ and $g_p$ components in the beam-like model, of expression: $f_v=f_0\cos ({\varOmega } t)$, $g_p=-\frac{4}{3\pi }f_0\cos ({\varOmega } t)$, with $f_0=\pi h R b_0$ whereas $f_u=0$, $c=0$, $g_w=0$. In other words, the load produces nonzero work both in the transversal displacement and in the flattening component of displacement.

The theorem of virtual work, after localization and use of Eqs. (1), (5), (7)–(11), allows one to evaluate the nonlinear equations of motion in terms of kinematic variables, which are reported in Appendix A (Eqs. (59)–(61)).

If free linear vibrations are sought, Eqs. (59)–(61) are written retaining only linear terms and neglecting the external forcing contributions, namely:

$$\begin{aligned}&c_{1}(v'-\vartheta )'-m_{1} \ddot{v}=0 \end{aligned}$$

(15)

$$\begin{aligned}&c_{2} \vartheta ''+ c_{1}(v'-\vartheta )-m_{2} \ddot{\vartheta }=0 \end{aligned}$$

(16)

$$\begin{aligned}&c_{10} a'_{w}+\frac{1}{4} c_{1} a''_{p}-c_{5} a_{p}-m_{4} \ddot{a}_p=0 \end{aligned}$$

(17)

$$\begin{aligned}&c_{17} a''_{w}-c_{13} a_{w}-c_{10} a'_{p}-m_{6} \ddot{a}_w=0 \end{aligned}$$

(18)

with boundary conditions at A:

$$\begin{aligned} u_A=0,\quad v_A=0,\quad \vartheta _A=0,\quad a_{pA}=0,\quad a_{wA}=0\nonumber \\ \end{aligned}$$

(19)

and at B:

$$\begin{aligned}&c_{1}(v'_{B}-\vartheta _{B})=0 \end{aligned}$$

(20)

$$\begin{aligned}&c_{2} \vartheta '_{B}=0 \end{aligned}$$

(21)

$$\begin{aligned}&c_{10} a_{wB}+\frac{1}{4} c_{1} a'_{pB}=0 \end{aligned}$$

(22)

$$\begin{aligned}&c_{17} a'_{wB}=0. \end{aligned}$$

(23)

It is worth noticing that Eqs. (15)–(23) are uncoupled in the global ($v,\vartheta$) and local ($a_p,a_w$) problems, since coupling only occurs through nonlinear terms. As a consequence, linear modes for the global problem (i.e., those of the Timoshenko beam) are unmodified by the local motion and vice versa. Furthermore, a class of local modes, i.e., involving $a_p$ and $a_w$ only, is obtained.

Fig. 3

Distributed force per unit volume in the pipe, applied to the upper cap

3 Reduced-order model

A Galerkin projection of the nonlinear problem is performed here, using as trial functions the first three modes of the linear problem Eqs. (15)–(23), where one is global (frequency $\omega _1$) and two are local (frequencies $\omega _2,$ $\omega _3$). Moreover, the frequencies of the higher modes are assumed quite far from the considered ones, so as to neglect their contributions in the response. These assumptions will be lately fulfilled in the numerical example.

The following expressions are hence introduced:

$$\begin{aligned} \begin{aligned} \begin{pmatrix} v(s,t)\\ \vartheta (s,t)\\ a_p(s,t)\\ a_w(s,t) \end{pmatrix}&=q_1(t) \begin{pmatrix} \phi _{v,1}(s)\\ \phi _{\vartheta ,1}(s)\\ 0\\ 0 \end{pmatrix}+q_2(t) \begin{pmatrix} 0\\ 0\\ \phi _{p,2}(s)\\ \phi _{w,2}(s) \end{pmatrix}\\&\quad +q_3(t) \begin{pmatrix} 0\\ 0\\ \phi _{p,3}(s)\\ \phi _{w,3}(s) \end{pmatrix} \end{aligned} \nonumber \\ \end{aligned}$$

(24)

where $q_j(t)$, $j=1,2,3$ represent the unknown time-dependent amplitudes, and $(\phi _{v,1}(s),\phi _{\vartheta ,1}(s))$, $(\phi _{p,k}(s),\phi _{w,k}(s))$, $k=2,3$ are the modal components. Substitution of Eq. (24) in the virtual work equation, calculation of the integrals in ds and collection of the terms multiplying $\delta q_j$, $j=1,2,3$, produces the reduced ordinary differential equations of motions. In the state space form, they appear as:

$$\begin{aligned} \begin{aligned}&\dot{{\textbf{q}}}-{\textbf{p}}={\textbf{0}} \\&\dot{{\textbf{p}}}+{\textbf{C}}{\textbf{p}}+{\textbf{K}}{\textbf{q}}+{\mathcal {N}}({\textbf{q}},{\textbf{p}})+{\textbf{F}}\cos ({\varOmega } t)={\textbf{0}} \end{aligned} \end{aligned}$$

(25)

where ${\textbf{q}}(t)=(q_1(t),q_2(t),q_3(t))^T$ collects the amplitudes and ${\textbf{p}}(t)=(p_1(t),p_2(t),p_3(t))^T$ their velocities. According to the choice of the trial functions and their normalization, ${\textbf{K}}=\text {diag}(\omega _j^2)$, $j=1,2,3$ is the (diagonal) stiffness matrix listing on its diagonal the square of the natural frequencies; a linear damping operator ${\textbf{C}}=\text {diag}(2\zeta _j\omega _j)$ is inserted in Eq. (25), being $\zeta _j$ the damping factors. The load column vector ${\textbf{F}}$ is defined as:

$$\begin{aligned} {\textbf{F}}=f_0\int _0^l\!\! \begin{pmatrix} \phi _{v,1}(s)\\ -\frac{4}{3\pi }\phi _{p,2}(s)\\ -\frac{4}{3\pi }\phi _{p,3}(s) \end{pmatrix}\textrm{d}s =\mathrel {\mathop :} f_0 \begin{pmatrix} c_{f,1}\\ c_{f,2}\\ c_{f,3} \end{pmatrix} \end{aligned}$$

(26)

and ${\mathcal {N}}$ is the column vector collecting the quadratic and cubic nonlinear terms:

$$\begin{aligned} \begin{aligned} {\mathcal {N}}({\textbf{q}},{\textbf{p}})&={\textbf{N}}_{2,1}({\textbf{q}},{\textbf{q}})+{\textbf{N}}_{2,2}({\textbf{p}},{\textbf{p}})+{\textbf{N}}_{2,3}({\textbf{q}},\dot{{\textbf{p}}}) \\&\quad + {\textbf{N}}_{3,1}({\textbf{q}},{\textbf{q}},{\textbf{q}})+{\textbf{N}}_{3,2}({\textbf{q}},{\textbf{p}},{\textbf{p}})\\&\quad + {\textbf{N}}_{3,3}({\textbf{q}},{\textbf{q}},\dot{{\textbf{p}}}) \end{aligned}\nonumber \\ \end{aligned}$$

(27)

where the single functions are explicitly defined in Appendix B.

4 Perturbation method

An asymptotic solution of Eq. (25) is sought via the multiple scale method [25]. To this end, the dependent variables are expressed as series expansion, after introducing the small scaling parameter $0<\epsilon \ll 1$:

$$\begin{aligned} \begin{aligned}&{\textbf{q}}(t)=\epsilon {\textbf{q}}_1(t_0,t_1,t_2)+\epsilon ^2 {\textbf{q}}_2(t_0,t_1,t_2)\\&\quad \quad \quad +\,\epsilon ^3 {\textbf{q}}_3(t_0,t_1,t_2)\\&{\textbf{p}}(t)=\epsilon {\textbf{p}}_1(t_0,t_1,t_2)+\epsilon ^2 {\textbf{p}}_2(t_0,t_1,t_2)\\&\quad \quad \quad +\,\epsilon ^3 {\textbf{p}}_3(t_0,t_1,t_2) \end{aligned}\nonumber \\ \end{aligned}$$

(28)

where the different time scales are defined as $t_0=t, t_1=\epsilon t,t_2=\epsilon ^2 t$. The linear damping ratios are assumed to be small so that they appear directly at the highest order, i.e., $\zeta _j=\epsilon ^2\tilde{\zeta _j}$ (tilde is omitted in the follow).

Internal resonance conditions are considered as well, namely $\omega _2\simeq 2\omega _1$, $\omega _3\simeq 3\omega _1$ in order to possibly address energy exchange between global and local modes. Furthermore, as the external action provides a direct excitation also toward the local modes (Eq. (26)), the following two load cases are considered, inducing different external resonances:

• Case 1: ${\varOmega }\simeq \omega _2$;

• Case 2: ${\varOmega }\simeq \omega _3$.

To analyze the aforementioned cases, two distinct perturbation schemes are developed to take into account the proper external detunings. It is worth noting that the case ${\varOmega }\simeq \omega _1$ was addressed in [18].

4.1 Case 1: ${\varOmega }\simeq \omega _2$

For the specified case, the following scaling is adopted for the forcing terms defined in Eq. (26):

$$\begin{aligned} \begin{aligned} c_{f,1}&=\epsilon {\tilde{c}}_{f,1},&c_{f,2}&=\epsilon ^3 {\tilde{c}}_{f,2},&c_{f,3}&=\epsilon {\tilde{c}}_{f,3}, \end{aligned} \end{aligned}$$

(29)

so that the resonant term will appear at the cubic order, while the non-resonant forcing terms at the linear order. Moreover, external detuning $\sigma$ is considered as:

$$\begin{aligned} {\varOmega }=\omega _2+\epsilon ^2\sigma \end{aligned}$$

(30)

and the internal detuning parameters $\rho _2,\rho _3$ are defined so that:

$$\begin{aligned} \begin{aligned} \omega _2&=2\omega _1+\epsilon ^2\rho _2\\ \omega _3&=3\omega _1+\epsilon ^2\rho _3. \end{aligned} \end{aligned}$$

(31)

Under these assumptions, the following perturbation equations are obtained:

Order $\epsilon$:

$$\begin{aligned} \begin{aligned}&\partial _0{\textbf{q}}_1-{\textbf{p}}_1={\textbf{0}} \\&\partial _0{\textbf{p}}_1+{\textbf{K}}{\textbf{q}}_1=-{\textbf{F}}_1\cos {{\varOmega } t_0}, \end{aligned} \end{aligned}$$

(32)

Order $\epsilon ^2$:

$$\begin{aligned} \begin{aligned}&\partial _0{\textbf{q}}_2-{\textbf{p}}_2=-\partial _1{\textbf{q}}_1 \\&\partial _0{\textbf{p}}_2+{\textbf{K}}{\textbf{q}}_2=-\partial _1\textbf{p }_1-{\textbf{N}}_{2,1}({\textbf{q}}_1,{\textbf{q}}_1)\\&\qquad \qquad \qquad \quad \quad -{\textbf{N}}_{2,2}({\textbf{p}}_1,{\textbf{p}}_1)-{\textbf{N}}_{2,3}({\textbf{q}}_1,\partial _0{\textbf{p}}_1), \end{aligned}\nonumber \\ \end{aligned}$$

(33)

Order $\epsilon ^3$:

$$\begin{aligned} \begin{aligned}&\partial _0{\textbf{q}}_3-{\textbf{p}}_3=-\partial _2{\textbf{q}}_1 -\partial _1{\textbf{q}}_2 \\&\partial _0{\textbf{p}}_3+{\textbf{K}}{\textbf{q}}_3=-\partial _2{\textbf{p}}_1 -\partial _1{\textbf{p}}_2-{\textbf{C}}{\textbf{q}}_1-{\textbf{F}}_3\cos ({\varOmega } t_0)\\&\quad -{\textbf{N}}_{3,1}({\textbf{q}}_1,{\textbf{q}}_1,{\textbf{q}}_1)-{\textbf{N}}_{3,1}({\textbf{q}}_1,{\textbf{p}}_1,{\textbf{p}}_1) \\&\quad -{\textbf{N}}_{3,1}({\textbf{q}}_1,{\textbf{q}}_1,\partial _0{\textbf{p}}_1) \\&\quad -{\textbf{N}}_{2,1}({\textbf{q}}_1,{\textbf{q}}_2) -{\textbf{N}}_{2,1}({\textbf{q}}_2,{\textbf{q}}_1) \\&\quad -{\textbf{N}}_{2,2}({\textbf{p}}_1,{\textbf{p}}_2) -{\textbf{N}}_{2,2}({\textbf{p}}_2,{\textbf{p}}_1) \\&\quad -{\textbf{N}}_{2,3}({\textbf{q}}_1,\partial _1{\textbf{p}}_1) -{\textbf{N}}_{2,3}({\textbf{q}}_1,\partial _0{\textbf{p}}_2) \\&\quad -{\textbf{N}}_{2,3}({\textbf{q}}_2,\partial _0{\textbf{p}}_1), \end{aligned}\nonumber \\ \end{aligned}$$

(34)

where $\partial _j=d/dt_j$ with $j=0,1,2$. The nonlinear terms are expressed according to the functions defined in Appendix B, while the forcing terms are defined as follows:

$$\begin{aligned} \begin{aligned} {\textbf{F}}_1&\mathrel {\mathop :}=\,f_0\begin{pmatrix}c_{f,1}\\ 0\\ c_{f,3}\end{pmatrix} ,&{\textbf{F}}_3&\mathrel {\mathop :}=\,f_0\begin{pmatrix}0\\ c_{f,2}\\ 0\end{pmatrix}. \end{aligned} \end{aligned}$$

(35)

4.1.1 Linear-order problem

The solution of the linear-order problem (32), beside the complementary solution, is characterized by the presence of the particular solution related to ${\textbf{F}}_1$. Accordingly, it is defined by the following expression:

$$\begin{aligned} \begin{aligned} \begin{pmatrix} {\textbf{q}}_1\\ {\textbf{p}}_1 \end{pmatrix}=&\sum _{k=1}^{3}A_k(t_1,t_2) \begin{pmatrix} {\textbf{z}}_k\\ i\omega _k{\textbf{z}}_k \end{pmatrix}e^{i\omega _k t_0} \\ {}&+f_0\sum _{j=1}^{3}\begin{pmatrix} \varvec{{\varLambda }}_j \\ i{\varOmega }\varvec{{\varLambda }}_j \end{pmatrix}e^{i{\varOmega } t_0}+{\textit{cc}}, \end{aligned}\nonumber \\ \end{aligned}$$

(36)

where $({\textbf{z}}_k, i\omega _k{\textbf{z}}_k)^T$ is the k-th right eigenvector of the eigenvalue problem given by Eq. (32) made homogeneous. More specifically, it is:

$$\begin{aligned} ({\textbf{z}}_1,{\textbf{z}}_2,{\textbf{z}}_3)=\begin{pmatrix} 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 1 \end{pmatrix}. \end{aligned}$$

(37)

Moreover, cc stands for complex conjugate, and the components of the vectors $\varvec{{\varLambda }}_j$ are:

$$\begin{aligned} \varvec{{\varLambda }}_1\mathrel {\mathop :}=\,\begin{pmatrix} \frac{1}{2}\frac{\,c_{f,1}}{\omega _1^2-{\varOmega }^2 }\\ 0\\ 0 \end{pmatrix},\;\varvec{{\varLambda }}_2\mathrel {\mathop :}=\,{\varvec{0}},\; \varvec{{\varLambda }}_3\mathrel {\mathop :}=\,\begin{pmatrix} 0\\ 0\\ \frac{1}{2}\frac{\,c_{f,3}}{\omega _3^2-{\varOmega }^2 } \end{pmatrix}. \nonumber \\ \end{aligned}$$

(38)

4.1.2 Quadratic-order problem

After substituting expressions (36) into Eq. (33), the following solvability condition is imposed to eliminate the secular producing terms:

$$\begin{aligned} \int _0^{2\pi /\omega _k}\begin{pmatrix}i\omega _k{\textbf{z}}_k\\ {\textbf{z}}_k\end{pmatrix}^T {\textbf{R}}_2 e^{-i\omega _k t}dt_0=0, \end{aligned}$$

(39)

with $k=1,2,3$, being $(i\omega _k{\textbf{z}}_k,{\textbf{z}}_k)^T$ the k-th left eigenvector and ${\textbf{R}}_2$ the right-end side of Eq. (33). From Eq. (39), the following amplitude modulation equations are derived:

$$\begin{aligned} \begin{aligned} \partial _1 A_1&=id_1A_2 {\bar{A}}_1 e^{i \rho _2 t_2}+id_2 f_0 {\bar{A}}_1 e^{i \left( \rho _2+\sigma \right) t_2} \\&\quad +id_3 f_0 A_3 e^{-i \left( \rho _2-\rho _3+\sigma \right) t_2},\\ \partial _1 A_2&= id_4 A_1^2e^{-i \rho _2 t_2},\\ \partial _1 A_3&=id_5 f_0 A_1 e^{i \left( \rho _2-\rho _3+\sigma \right) t_2 }, \end{aligned}\nonumber \\ \end{aligned}$$

(40)

where the coefficients $d_j$ ($j=1,\dots ,6$) are defined in Appendix C.

Equation (40), substituted into Eq. (33), allows one to determine the particular solution of the quadratic order problem that can be written in the following form:

$$\begin{aligned} \begin{aligned} \begin{pmatrix} {\textbf{q}}_2\\ {\textbf{p}}_2 \end{pmatrix}&= A_2{\bar{A}}_1\begin{pmatrix} {\textbf{w}}_1\\ -i\omega _1{\textbf{w}}_1 \end{pmatrix}e^{i\omega _1t_0+i\rho _2t_2} \\&\quad +f_0{\bar{A}}_1\begin{pmatrix} {\textbf{w}}_2\\ -i\omega _1{\textbf{w}}_2 \end{pmatrix}e^{i\omega _1t_0+i(\sigma +\rho _2)t_2} \\&\quad +f_0 A_3\begin{pmatrix} {\textbf{w}}_3\\ -i\omega _1{\textbf{w}}_3 \end{pmatrix}e^{i\omega _1t_0-i(\sigma +\rho _2-\rho _3)t_2} \\&\quad +A_1^2\begin{pmatrix} {\textbf{w}}_4\\ i\omega _2{\textbf{w}}_4 \end{pmatrix}e^{2i\omega _1t_0-i\rho _2t_2} \\&\quad +f_0{\bar{A}}_1\begin{pmatrix} {\textbf{w}}_5\\ -i\omega _1{\textbf{w}}_5 \end{pmatrix} e^{i\omega _1t_0+i(\sigma +\rho _2)t_2} \\ {}&\quad +{\hbox {NRT}}+{\textit{cc}}, \end{aligned}\nonumber \\ \end{aligned}$$

(41)

where ${\hbox {NRT}}$ represents the non-resonant terms that are not reported here for sake of brevity, while the vectors ${\textbf{w}}_j$ are defined in Appendix D.

4.1.3 Cubic-order problem

After substituting expressions (36) and (41) into Eq. (34), in order to eliminate secular producing terms, the following solvability condition is imposed:

$$\begin{aligned} \int _0^{2\pi /\omega _k}\begin{pmatrix}i\omega _k{\textbf{z}}_k\\ {\textbf{z}}_k\end{pmatrix}^T{\textbf{R}}_3 e^{-i\omega _k t}dt_0=0 \end{aligned}$$

(42)

with $k=1,2,3$ and being ${\textbf{R}}_3$ the right-end side of Eq. (34). From the latter expression, the following amplitude modulation equations at the third order are derived:

$$\begin{aligned} \partial _2 A_1= & {} id_6A_1^2 {\bar{A}}_1+d_7 A_1 A_2 {\bar{A}}_2+id_8 f_0 A_1 A_2 e^{-i \sigma t_2} \nonumber \\{} & {} \quad +id_9 f_0A_1 {\bar{A}}_2 e^{i \sigma t_2}+id_{10}A_1 A_3 {\bar{A}}_3 \nonumber \\{} & {} \quad +id_{11} f_0^2A_1 +id_{12}\zeta A_1 \nonumber \\{} & {} \quad +id_{13} f_0 A_2 {\bar{A}}_3 e^{i \left( 2 \rho _2-\rho _3+\sigma \right) t_2}\nonumber \\{} & {} \quad +id_{14} f_0^2 {\bar{A}}_3 e^{i \left( 2 \rho _2-\rho _3+2 \sigma \right) t_2 },\nonumber \\ \partial _2 A_2= & {} id_{15} A_1 A_2 {\bar{A}}_1 +id_{16} f_0 A_1 {\bar{A}}_1 e^{i \sigma t_2} \nonumber \\{} & {} \quad +id_{17} f_0 A_1 A_3 e^{-i \left( 2\rho _2-\rho _3+\sigma \right) t_2} +id_{18} A_2^2 {\bar{A}}_2 \nonumber \\{} & {} \quad + id_{19} f_0 A_2^2e^{-i \sigma t_2} +id_{20} f_0 A_2 {\bar{A}}_2 e^{i \sigma t_2 } \nonumber \\{} & {} \quad +i d_{21} A_2 A_3 {\bar{A}}_3 +id_{22} f_0^2A_2\nonumber \\{} & {} \quad + i d_{23}\zeta A_2 +i d_{24} f_0^2 {\bar{A}}_2 e^{2i \sigma t_2} \nonumber \\{} & {} \quad + id_{25} f_0 A_3 {\bar{A}}_3 e^{i \sigma t_2}+d_{26} f_0^3 e^{i \sigma t_2}\nonumber \\{} & {} \quad +id_{27} f_0 e^{i \sigma t_2}, \nonumber \\ \partial _2 A_3= & {} id_{28} A_1 A_3 {\bar{A}}_1+id_{29} f_0A_2 {\bar{A}}_1 e^{i\left( 2 \rho _2-\rho _3+\sigma \right) t_2 } \nonumber \\{} & {} \quad + i d_{30} f_0^2 {\bar{A}}_1 e^{ i \left( 2\rho _2+2\sigma -\rho _3\right) t_2}+id_{31}A_2 A_3 {\bar{A}}_2 \nonumber \\{} & {} \quad +id_{32} f_0 A_2 A_3 e^{-i \sigma t_2}+id_{33} f_0A_3 {\bar{A}}_2 e^{i \sigma t_2 }\nonumber \\{} & {} \quad +i d_{34} A_3^2 {\bar{A}}_3 +id_{36} f_0^2 A_3 +id_{35} \zeta A_3 .\nonumber \\ \end{aligned}$$

(43)

The coefficients appearing in Eq. (43) are explicitly defined in Appendix C and their numerical values are shown in Appendix E, with reference to the case study proposed in Sect. 5.1. The reconstructed amplitude modulation equations in the true time t can be written in the form:

$$\begin{aligned} {\dot{A}}_k=\epsilon \partial _1A_k+\epsilon ^2\partial _2A_k \quad \text {with}\quad k=1,2,3 \end{aligned}$$

(44)

where the terms $\partial _1A_k$ and $\partial _2A_k$ are given in Eqs. (40) and (43), respectively. Equation (44) is transformed in a set of real equations, by introducing the following definitions:

$$\begin{aligned} A_k=\frac{1}{2}(x_k+i y_k)e^{i \gamma _k} \quad \textrm{with}~ k=1,2,3 \end{aligned}$$

(45)

where the phases are set to make the system autonomous as:

$$\begin{aligned} \begin{aligned} \gamma _1&=\frac{1}{2}(\sigma +\rho _2)t\\ \gamma _2&=\sigma t\\ \gamma _3&=\gamma _1+(\sigma +\rho _2-\rho _3) t. \end{aligned} \end{aligned}$$

(46)

Then, real and imaginary parts of the equations are collected, giving rise to the following set of six first-order differential equations in the variables $x_k,y_k$:

$$\begin{aligned} {\dot{x}}_1= & {} \left( \frac{ \rho _2}{2}+\frac{ \sigma }{2}\right) y_1+d_{11} f_0^2 x_1+d_2 f_0 x_1 \nonumber \\{} & {} \quad +\frac{1}{2} d_8 f_0 (x_2 x_1-y_1y_2)\nonumber \\{} & {} \quad +\frac{1}{2} d_9 f_0 (x_2 x_1+y_2y_1)\nonumber \\{} & {} \quad +d_{14} f_0^2 x_3+d_3 f_0 x_3+d_{12} \zeta x_1\nonumber \\{} & {} \quad +\frac{1}{2} d_{13} f_0 (x_2 x_3+ y_2 y_3)+\frac{1}{4} d_6 x_1\big ( x_1^2+y_1^2\big )\nonumber \\{} & {} \quad +\frac{1}{4} d_{10} x_1 \big (x_3^2+y_3^2\big )\nonumber \\{} & {} \quad +\frac{1}{4} d_7 x_1\big (x_2^2+y_2^2\big )+\frac{1}{2} d_1 (x_2 x_1+ y_1 y_2),\nonumber \\ {\dot{y}}_1= & {} -\left( \frac{ \rho _2}{2}+\frac{ \sigma }{2}\right) x_1+\frac{1}{2} d_8 f_0 x_2 y_1\nonumber \\{} & {} \quad +\frac{1}{2} d_9 f_0 x_2 y_1+\frac{1}{2} d_8 f_0 x_1 y_2-\frac{1}{2} d_9 f_0 x_1 y_2\nonumber \\{} & {} \quad +\frac{1}{2} d_{13} f_0( x_3 y_2- x_2 y_3)+d_{11} f_0^2 y_1-d_2 f_0 y_1\nonumber \\{} & {} \quad -d_{14} f_0^2 y_3+d_3 f_0 y_3 \nonumber \\{} & {} \quad +\frac{1}{4} d_6 x_1^2 y_1 +\frac{1}{4} d_7 x_2^2 y_1\nonumber \\{} & {} \quad +\frac{1}{4} d_{10} x_3^2 y_1+\frac{1}{2} d_1 (x_1 y_2-x_2 y_1)\nonumber \\{} & {} \quad +d_{12} \zeta y_1 +\frac{1}{4} d_6 y_1^3+\frac{1}{4} d_7 y_2^2 y_1+\frac{1}{4} d_{10} y_3^2 y_1, \nonumber \\ {\dot{x}}_2= & {} y _2 \sigma +d_{22} f_0^2 x_2+d_{24} f_0^2 x_2+\frac{1}{2} d_{16} f_0 \big (x_1^2+y_1^2\big )\nonumber \\{} & {} \quad +\frac{1}{2} d_{20} f_0 \big (x_2^2+y_2^2\big )+\frac{1}{2} d_{17} f_0 (x_1 x_3-y_1 y_3)\nonumber \\{} & {} \quad +\frac{1}{2} d_{19} f_0 \big (x_2^2-y_2^2\big )+\frac{1}{2} d_{25} f_0 \big (x_3^2+y_3^2\big )\nonumber \\{} & {} \quad +\frac{1}{2} d_4 \big (x_1^2-y_1^2\big )\nonumber \\{} & {} \quad +2 d_{26} f_0^3+2 d_{27} f_0+d_{23} \zeta x_2+\frac{1}{4} d_{15} x_2 \big (x_1^2+y_1^2\big )\nonumber \\{} & {} \quad +\frac{1}{4} d_{21} \big (x_2 y_3^2+ x_2 x_3^2\big )+\frac{1}{4} d_{18} x_2\big (x_2^2+y_2^2\big ), \nonumber \\ {\dot{y}}_2= & {} -x _2 \sigma +d_{19} f_0 x_2 y_2+\frac{1}{2} d_{17} f_0 (x_3 y_1+ x_1 y_3)\nonumber \\{} & {} \quad +d_{22} f_0^2 y_2\nonumber \\{} & {} \quad -d_{24} f_0^2 y_2+\frac{1}{4} d_{15} x_1^2 y_2+\frac{1}{4} d_{21} \big (x_3^2 y_2+y_3^2 y_2\big )\nonumber \\{} & {} \quad +d_4 x_1 y_1+d_{23} \zeta y_2+\frac{1}{4} d_{18}y_2\big (x_2^2+ y_2^2\big )\nonumber \\{} & {} \quad +\frac{1}{4} d_{15} y_1^2 y_2, \nonumber \\ {\dot{x}}_3= & {} \left( \frac{3 \rho _2}{2}- \rho _3+\frac{3 \sigma }{2}\right) y_3+d_{36} f_0^2 x_3+\frac{1}{2} d_{32} f_0 x_2 x_3\nonumber \\{} & {} \quad +\frac{1}{2} d_{33} f_0 (x_2 x_3+y_2y_3)+d_{30} f_0^2 x_1\nonumber \\{} & {} \quad +d_5 f_0 x_1+d_{35} \zeta x_3\nonumber \\{} & {} \quad -\frac{1}{2} d_{32} f_0 y_2 y_3+\frac{1}{4} d_{28} x_3 \big (x_1^2+y_1^2\big )\nonumber \\{} & {} \quad +\frac{1}{2} d_{29} f_0 (x_1 x_2+ y_1 y_2)\nonumber \\{} & {} \quad +\frac{1}{4} d_{31} x_3 \big (x_2^2+y_2^2\big )+\frac{1}{4} d_{34} x_3\big ( y_3^2+x_3^2\big ),\nonumber \\ {\dot{y}}_3= & {} \left( -\frac{3 \rho _2}{2}+ \rho _3-\frac{3 \sigma }{2}\right) x_3+\frac{1}{2} d_{32} f_0 (x_2 y_3+x_3y_2)\nonumber \\{} & {} \quad +\frac{1}{2} d_{33} f_0 (x_2 y_3-x_3 y_2)+\frac{1}{2} d_{29} f_0 (x_1 y_2-x_2 y_1)\nonumber \\{} & {} \quad +d_{36} f_0^2 y_3-d_{30} f_0^2 y_1+d_5 f_0 y_1+\frac{1}{4} d_{28} x_1^2 y_3\nonumber \\{} & {} \quad +\frac{1}{4} d_{31} y_3\big (x_2^2+y_2^2)+\frac{1}{4} d_{34} y_3\big (x_3^2+ y_3^2\big )+d_{35} \zeta y_3\nonumber \\{} & {} \quad +\frac{1}{4} d_{28} y_1^2 y_3. \end{aligned}$$

(47)

Equilibrium points of Eq. (47) are sought, and their stability is analyzed by evaluating the eigenvalues of the corresponding Jacobian matrix. The real amplitudes are then evaluated as:

$$\begin{aligned} r_k=\sqrt{x_k^2+y_k^2} \quad \text {with } k=1,2,3, \end{aligned}$$

(48)

whereas the motion of the system is reconstituted with Eqs. (36) and (41).

4.2 Case 2: ${\varOmega }\simeq \omega _3$

For the specified case, the differences with respect to case 1 are highlighted. In particular, the following scaling is adopted for the defined forcing terms:

$$\begin{aligned} \begin{aligned} c_{f,1}&=\epsilon {\tilde{c}}_{f,1},&c_{f,2}&=\epsilon {\tilde{c}}_{f,2},&c_{f,3}&=\epsilon ^3 {\tilde{c}}_{f,3}. \end{aligned} \end{aligned}$$

(49)

The external detuning here is defined so that:

$$\begin{aligned} \begin{aligned} {\varOmega }&=\omega _3+\epsilon ^2\sigma , \end{aligned} \end{aligned}$$

(50)

while the internal detunings are those given in Eq. (31). The perturbation equations are the same as in the previous case, namely Eqs. (32)–(34), where the forcing terms is now:

$$\begin{aligned} \begin{aligned} {\textbf{F}}_1&\mathrel {\mathop :}=\,f_0\begin{pmatrix}c_{f,1}\\ c_{f,2}\\ 0\end{pmatrix} ,&{\textbf{F}}_3&\mathrel {\mathop :}=\,f_0\begin{pmatrix}0\\ 0\\ c_{f,3}\end{pmatrix}. \end{aligned} \end{aligned}$$

(51)

4.2.1 Linear-order problem

The solution of the linear-order problem is:

$$\begin{aligned} \begin{aligned} \begin{pmatrix} {\textbf{q}}_1 \\ {\textbf{p}}_1 \end{pmatrix}&= \sum _{k=1}^{3}A_k(t_1,t_2) \begin{pmatrix} {\textbf{z}}_k \\ i\omega _k{\textbf{z}}_k \end{pmatrix}e^{i\omega _k t_0} \\&\quad +f_0\sum _{j=1}^{3}\begin{pmatrix} \varvec{{\varLambda }}_j \\ i{\varOmega }\varvec{{\varLambda }}_j \end{pmatrix}e^{i{\varOmega } t_0}+{\textit{cc}}, \end{aligned} \end{aligned}$$

(52)

where the components of the vectors $\varvec{{\varLambda }}_j$ are:

$$\begin{aligned} \varvec{{\varLambda }}_1\mathrel {\mathop :}=\,\begin{pmatrix} \frac{1}{2}\frac{\,c_{f,1}}{\omega _1^2-{\varOmega }^2 }\\ 0\\ 0 \end{pmatrix},\; \varvec{{\varLambda }}_2\mathrel {\mathop :}=\,\begin{pmatrix} 0\\ \frac{1}{2}\frac{\,c_{f,2}}{\omega _2^2-{\varOmega }^2 }\\ 0 \end{pmatrix},\;\varvec{{\varLambda }}_3\mathrel {\mathop :}=\,{\varvec{0}}.\nonumber \\ \end{aligned}$$

(53)

4.2.2 Quadratic-order problem

By substituting expressions (52) into Eq. (33), the second-order amplitude modulation equations reduce to:

$$\begin{aligned} \begin{aligned} \partial _1 A_1&=i d_{11} f_0 {\bar{A}}_2 e^{i \left( -\rho _2+\rho _3+\sigma \right) t_2}+i d_9 A_2 {\bar{A}}_1 e^{i \rho _2 t_2},\\ \partial _1 A_2&=i d_{15} f_0 {\bar{A}}_1 e^{i \left( -\rho _2+\rho _3+\sigma \right) t_2}+i d_{12} A_1^2 e^{-i \rho _2 t_2},\\ \partial _1 A_3&=0, \end{aligned} \nonumber \\ \end{aligned}$$

(54)

and the particular solution of the quadratic-order problem Eq. (33) is:

$$\begin{aligned} \begin{aligned} \begin{pmatrix} {\textbf{q}}_2\\ {\textbf{p}}_2 \end{pmatrix}&=f_0 \begin{pmatrix}{\textbf{w}}_{11}\\ -i\omega _2{\textbf{w}}_{11}\end{pmatrix} {\bar{A}}_1 e^{i (\rho _3 +i \sigma )t_2 +2 i t_0 \omega _1}\\&\quad +f_0 \begin{pmatrix}{\textbf{w}}_{15}\\ -i\omega _1{\textbf{w}}_{15}\end{pmatrix} {\bar{A}}_2 e^{-i( \rho _2 + \rho _3+ \sigma ) t_2+i t_0 \omega _1}\\&\quad +A_2 {\bar{A}}_1 \begin{pmatrix}{\textbf{w}}_{7}\\ -i\omega _1{\textbf{w}}_{7}\end{pmatrix} e^{i \rho _2 t_2+i t_0 \omega _1}\\&\quad +A_3 {\bar{A}}_1 \begin{pmatrix}{\textbf{w}}_{9}\\ -i\omega _2{\textbf{w}}_{9}\end{pmatrix} e^{i \rho _3 t_2+2 i t_0 \omega _1}\\&\quad +A_1 A_2 \begin{pmatrix}{\textbf{w}}_{1}\\ -i\omega _3{\textbf{w}}_{1}\end{pmatrix} e^{i \rho _2 t_2+3 i t_0 \omega _1} \\ {}&\quad +{\hbox {NRT}}+{\textit{cc}}. \end{aligned}\nonumber \\ \end{aligned}$$

(55)

Vectors ${\textbf{w}}_j$ appearing in Eq. (55) are not explicitly written in this specific case for the sake of brevity.

4.2.3 Cubic-order problem

By substituting expressions (52) and (55) into Eq. (34), the amplitude modulation equations at the third order are derived, namely:

$$\begin{aligned} \partial _2 A_1= & {} i d_8 f_0 {\bar{A}}_1^2 e^{i t_2 \left( \rho _3+\sigma \right) }+i d_5 A_1 f_0 {\bar{A}}_3 e^{i \sigma t_2}\nonumber \\{} & {} +i d_1 A_1^2 {\bar{A}}_1+id_2 A_2 A_1 {\bar{A}}_2+i d_3 A_3 A_1 {\bar{A}}_3\nonumber \\{} & {} +i d_{10} A_2^2 f_0 e^{-i t_2 \left( -2 \rho _2+\rho _3+\sigma \right) }\nonumber \\{} & {} +i d_4 A_3 A_1 f_0 e^{-i \sigma t_2}+i d_6 A_1 f_0^2+d_7 \zeta A_1 ,\nonumber \\ \partial _2 A_2= & {} i d_{14} A_1 f_0 {\bar{A}}_2 e^{i t_2 \left( -2 \rho _2+\rho _3+\sigma \right) } \nonumber \\{} & {} +i d_{19} A_2 f_0 {\bar{A}}_3 e^{i \sigma t_2} +i d_{16} A_2^2 {\bar{A}}_2\nonumber \\{} & {} +i d_{13} A_1 A_2 {\bar{A}}_1+i d_{17} A_3 A_2 {\bar{A}}_3\nonumber \\{} & {} +i d_{18} A_3 A_2 f_0 e^{-i \sigma t_2}+i d_{20} A_2 f_0^2+ d_{21} \zeta A_2,\nonumber \\ \partial _2 A_3= & {} i d_{31} f_0^2 {\bar{A}}_3 e^{2 i \sigma t_2}+i d_{23} A_1 f_0 {\bar{A}}_1 e^{i \sigma t_2}\nonumber \\{} & {} +i d_{25}A_2 f_0 {\bar{A}}_2 e^{i \sigma t_2} +i d_{28} A_3 f_0 {\bar{A}}_3 e^{i \sigma t_2}\nonumber \\{} & {} +i d_{22} A_1 A_3 {\bar{A}}_1+i d_{24} A_2 A_3 {\bar{A}}_2\nonumber \\{} & {} +i d_{26} A_3^2 {\bar{A}}_3+i d_{27} A_3^2 f_0 e^{-i \sigma t_2}\nonumber \\{} & {} +i d_{29} A_3 f_0^2+d_{30} A_3 \zeta +i d_{32} f_0^3 e^{i \sigma t_2}.\nonumber \\ \end{aligned}$$

(56)

Reconstitution is made as in Eq. (44) and then, making use of Eq. (45), with the following definition of phases:

$$\begin{aligned} \begin{aligned} \gamma _1=&\frac{1}{3}(\sigma +\rho _3)t,\\ \gamma _2=&\left( \frac{2}{3}\sigma -\rho _2+\frac{2}{3}\rho _3\right) t,\\ \gamma _3=&\sigma t, \end{aligned} \end{aligned}$$

(57)

the set of real ordinary differential equations is obtained:

$$\begin{aligned} {\dot{x}}_1= & {} \zeta d_7 x_1+\left( \frac{\rho _3 }{3}+\frac{\sigma }{3}\right) y_1\nonumber \\{} & {} +2 d_8 f_0 x_1 y_1-d_4 f_0 x_3 y_1-d_5 f_0 x_3 y_1\nonumber \\{} & {} -2 d_{10} f_0 x_2 y_2-d_4 f_0 x_1 y_3+d_5 f_0 x_1 y_3\nonumber \\{} & {} -d_6 f_0^2 y_1+d_{11} f_0 y_2-d_1 x_1^2 y_1-d_2 x_2^2 y_1\nonumber \\{} & {} -d_3 x_3^2 y_1 +d_9 x_2 y_1-d_9 x_1 y_2-d_1 y_1^3\nonumber \\{} & {} -d_2 y_2^2 y_1-d_3 y_3^2 y_1,\nonumber \\ {\dot{y}}_1= & {} -\left( \frac{\rho _3 }{3}+\frac{\sigma }{3}\right) x_1+\zeta d_7 y_1+d_8 f_0 x_1^2+d_6 f_0^2 x_1\nonumber \\{} & {} +d_4 f_0 x_3 x_1+d_5 f_0 x_3 x_1+d_{10} f_0 x_2^2+d_{11} f_0 x_2\nonumber \\{} & {} -d_8 f_0 y_1^2-d_{10} f_0 y_2^2-d_4 f_0 y_1 y_3+d_5 f_0 y_1 y_3\nonumber \\{} & {} +d_1 x_1 y_1^2+d_2 x_1 y_2^2+d_3 x_1 y_3^2+d_1 x_1^3\nonumber \\{} & {} +d_2 x_2^2 x_1 +d_3 x_3^2 x_1+d_9 x_2 x_1+d_9 y_1 y_2,\nonumber \\ {\dot{x}}_2= & {} \zeta d_{21} x_2+\left( \frac{2 (\rho _3+\sigma )}{3}-\rho _2\right) y_2+d_{14} f_0 x_1 y_2\nonumber \\{} & {} -d_{18} f_0 x_3 y_2-d_{19} f_0 x_3 y_2-d_{14} f_0 x_2 y_1\nonumber \\{} & {} -d_{18} f_0 x_2 y_3+d_{19} f_0 x_2 y_3-d_{20} f_0^2 y_2\nonumber \\{} & {} +d_{15} f_0 y_1 +d_{21} \zeta x_2-d_{13} x_1^2 y_2\nonumber \\{} & {} -d_{16} x_2^2 y_2-d_{17} x_3^2 y_2-2 d_{12} x_1 y_1\nonumber \\{} & {} -d_{16} y_2^3-d_{13} y_1^2 y_2-d_{17} y_3^2 y_2,\nonumber \\ {\dot{y}}_2= & {} -\left( \frac{2 (\rho _3 +\sigma )}{3}x_2-\rho _2\right) x_2+\zeta d_{21} y_2\nonumber \\{} & {} +d_{20} f_0^2 x_2+d_{14} f_0 x_1 x_2+d_{18} f_0 x_3 x_2\nonumber \\{} & {} +d_{19} f_0 x_3 x_2 +d_{15} f_0 x_1+d_{14} f_0 y_1 y_2\nonumber \\{} & {} -d_{18} f_0 y_2 y_3+d_{19} f_0 y_2 y_3 +d_{13} x_2 y_1^2\nonumber \\{} & {} +d_{16} x_2 y_2^2 +d_{17} x_2 y_3^2+d_{16} x_2^3 +d_{13} x_1^2 x_2\nonumber \\{} & {} +d_{17} x_3^2 x_2+d_{12} x_1^2,\nonumber \\ {\dot{x}}_3= & {} \zeta d_{30} x_3+\sigma y_3-2 d_{27} f_0 x_3 y_3-d_{29} f_0^2 y_3\nonumber \\{} & {} +d_{31} f_0^2 y_3+d_{30} \zeta x_3-d_{22} x_1^2 y_3-d_{24} x_2^2 y_3\nonumber \\{} & {} -d_{26} x_3^2 y_3-d_{26} y_3^3-d_{22} y_1^2 y_3-d_{24} y_2^2 y_3,\nonumber \\ {\dot{y}}_3= & {} -\sigma x_3+\zeta d_{30} y_3+d_{29} f_0^2 x_3+d_{31} f_0^2 x_3\nonumber \\{} & {} +d_{23} f_0 x_1^2+d_{25} f_0 x_2^2+d_{27} f_0 x_3^2+d_{28} f_0 x_3^2\nonumber \\{} & {} +d_{23} f_0 y_1^2+d_{25} f_0 y_2^2-d_{27} f_0 y_3^2+d_{28} f_0 y_3^2\nonumber \\{} & {} +d_{32} f_0^3+d_{22} x_3 y_1^2+d_{24} x_3 y_2^2\nonumber \\{} & {} +d_{26}x_3y_3^2+d_{26} x_3^3+d_{22}x_1^2x_3+d_{24}x_2^2x_3. \end{aligned}$$

(58)

The numerical values of the coefficients appearing in Eq. (58) are explicitly given in Appendix E for the numerical application defined in the next section, whereas their analytic expressions are omitted for the sake of brevity.

Still, equilibrium points and relevant stability conditions are evaluated, and the real amplitudes $r_k=\sqrt{x_k^2+y_k^2}$ analyzed ($k=1,2,3$).

5 Numerical results

The following parameters are assumed for the pipe under analysis: mean radius of the cross-section $R=0.1$ m, thickness $h=4$ mm, Young modulus $E=1.65\cdot 10^8$ Pa, modal damping factor $\zeta =1\%$ for all the modes, while the length is varied in the range $l\in [1,3]$ m. The first three natural frequencies, evaluated from the eigenvalue problem Eqs. (15)–(23), are shown in solid lines in Fig. 4 as functions of l (and slenderness ratio $\eta =l/R$). They are superimposed (and in good agreement) to those (dots) obtained by a FEM model implemented in a commercial software [26], where the pipe is realized by a mesh of curved shells with four nodes each. (Convergence analysis of the FEM model is omitted for brevity.) The relevant modal shapes are shown in Fig. 5, still in good agreement with those obtained by the F.E.M. model.

Accordingly, the two cases described in Section 4 are chosen to be numerically characterized by the following parameters:

• Case 1: $l=1.246$ m in which $\omega _1=54.0$ rad/s, $\omega _2\simeq 2\omega _1$, $\omega _3=2.8\omega _1$, $f_0=60$ N/m, ${\varOmega }\simeq \omega _2$.

• Case 2: $l=1.344$ m in which $\omega _1=46.6$ rad/s, $\omega _2=2.3\omega _1$, $\omega _3\simeq 3\omega _1$, $f_0=130$ N/m, ${\varOmega }\simeq \omega _3$.

Fig. 4

Frequency vs length (or slenderness ratio $\eta =l/R$) of the first global mode, $\omega _1$, and the first two local modes, $\omega _2,\omega _3$. Solid lines: analytical solution; dotted lines: FEM solution

Therefore, for both the aforementioned cases, it is chosen to have almost perfect internal resonance between the global mode (frequency $\omega _1$) and the local one which is in 1:1 resonance with the external force, namely $\omega _2$ for case 1 and $\omega _3$ for case 2. Furthermore, the next closest frequency ($\omega _4$) is much larger than $\omega _3$, this justifying the choice of the reduced basis of three modes in the Galerkin projection. Anyway, a convergence analysis of the reduced system in terms of number o(Fig. 5)f involved modes is performed as well. More specifically, numerical integration of the system projected on the first ten modes, i.e., adding further four global and three local modes, is carried out (details of the formulation are omitted).

Fig. 5

Shape of the first global mode, which involves v (a) and $\vartheta$ (b), and two local modes, which involve $a_p$ (c) and $a_w$ (d). Solid lines: analytical solution; dotted lines: FEM solution

Fig. 6

Frequency response curves for $l=1.246$ m, $\omega _3=2.8\omega _1$, ${\varOmega }=\omega _2+\epsilon ^2\sigma$ and $\omega _2=2\omega _1$ (dark blue lines), $\omega _2=2.01\omega _1$ (light blue lines), $\omega _2=1.99\omega _1$ (cyan lines): a $r_1$ vs ${\varOmega }/\omega _1$; b $r_2$ vs ${\varOmega }/\omega _1$; c $r_3$ vs ${\varOmega }/\omega _1$. (Color figure online)

5.1 Case 1: ${\varOmega }\simeq \omega _2$

In this case, the external force produces a primary resonance on the second mode (the first local), the latter being in internal resonance with the other two modes (the first global and second local).

The frequency response curves, shown in Fig. 6, are directly expressed in terms of $r_k$, $k=1,2,3$, and are represented versus the external frequency, normalized with respect to the first modal frequency: ${\varOmega }/\omega _1$; the stable branches of the solution are represented by the solid lines, while the unstable branches by dashed lines. Moreover, they are reproduced for different values of the internal detuning $\rho _2$, in order to analyze in more detail the effect of the internal resonance: $\omega _2=2\omega _1$ (dark blue lines), $\omega _2=2.01\omega _1$ (light blue lines), $\omega _2=1.99\omega _1$ (cyan lines). For the three internal detuning values, the second amplitude $r_2$ always exhibits the typical behavior of a monomodal solution which becomes unstable in between two bifurcation points (${\varOmega }/\omega _1\simeq 1.97,2.02$), where the parametric resonance with the first mode takes place (see Fig. 6b). Accordingly, the amplitudes $r_1,r_3$ are zero outside the range in which the parametric resonance is activated, whereas the solution becomes tri-modal inside (see Fig. 6a, c). The effect of the internal detuning $\rho _2$ is to slightly distort the curves as well as slightly shift them toward lower values of ${\varOmega }/\omega _1$ as $\rho _2$ is increased; however, it can be concluded that $\rho _2$ qualitatively leaves the phenomena essentially unchanged.

Fig. 7

Frequency response curves for $l=1.246$ m, $\omega _2=2\omega _1$, $\omega _3=2.8\omega _1$, ${\varOmega }=\omega _2+\epsilon ^2\sigma$: a $\max (q_1)$ vs ${\varOmega }/\omega _1$; b $\max (q_2)$ vs ${\varOmega }/\omega _1$; c $\max (q_3)$ vs ${\varOmega }/\omega _1$. Solid line: perturbation method; dotted line: numerical integration

To validate the results derived via the perturbation solution, a comparison of the reconstituted solution in terms of peak values of the modal amplitudes $q_1,q_2,q_3$ is made with the outcomes of numerical integration of Eq. (25) carried out via a Runge–Kutta routine in Mathematica [27]. The comparison between approaches is conduced only in the case $\omega _2=2\omega _1$, and it is illustrated in Fig. 7, where the blue lines indicate the perturbation solution, while the black dots denote the numerical results. It can be observed that the stable branches of the solution are very well captured for what concerns $q_1$ (see Fig. 7a) and $q_2$ (see Fig. 7b). However, the accuracy reached for $q_3$, which by the way assumes much lower values than $q_1$ and $q_2$, is slightly inferior (see Fig. 7c), perhaps due to the internal detuning $\rho _3$ which is quite large, although the behavior is still qualitatively quite well-captured.

Fig. 8

Time histories of the modal coordinates for $l=1.246$ m, $\omega _2=2\omega _1$, $\omega _3=2.8\omega _1$ and ${\varOmega }/\omega _1=1.99$: a $q_1$ vs t; b $q_2$ vs t; c $q_3$ vs t. Blue line: perturbation method; black line: numerical integration. (Color figure online)

Fig. 9

Frequency response curves for $l=1.246$ m, $\omega _2=2\omega _1$, $\omega _3=2.8\omega _1$ and ${\varOmega }=\omega _2+\epsilon ^2\sigma$: a $\max (v(l))$ vs ${\varOmega }/\omega _1$; b $\max (\vartheta (l))$ vs ${\varOmega }/\omega _1$; c $\max (a_p(l/4))$ vs ${\varOmega }/\omega _1$; d $\max (a_w(l/4))$ vs ${\varOmega }/\omega _1$. Solid line: perturbation method; dotted line: numerical integration of the 3-d.o.f. system; crosses: numerical integration of the 10-d.o.f. system

The results are also compared in terms of time histories of modal coordinates, evaluated at ${\varOmega }/\omega _1=1.99$. Those are reported in Fig. 8, where the blue lines denote the perturbations solution, while the numerical results are represented by the black lines. Specifically, as illustrated in Fig. 8a, $q_1$ is very well captured by the perturbation solution that completely overlaps the numerical solution. Similarly, $q_2$ is very well captured by the perturbation solution that overlaps the numerical solution except for a negligible difference (less than $2\%$) in correspondence of the peaks (see Fig. 8b). On the other hand, as for the frequency plots, the time history for $q_3$ highlights a slight loss of accuracy (see Fig. 8c). For that, the fitting may be improved by considering higher-order terms in the perturbation solution; however, as it is deduced by Fig. 9, the error in $q_3$ does not significantly affect the response in terms of global ($v,\vartheta$) and local ($a_p,a_w$) displacement variables of the beam-like structure. In particular, in Fig. 9, the peak response is evaluated at the beam tip $s=l$ for the displacement v (see Fig. 9a) and the cross-section rotation $\vartheta$ (see Fig. 9b), and at $s=l/4$ for flattening $a_p$ (see Fig.  9c) and warping $a_p$ (see Fig. 9d) amplitudes. The numerical response of v and $\vartheta$, strictly related to $q_1$ (see Eq. (24)), exhibits a very good agreement with the perturbation solution. Moreover, the response of the local variables $a_p$ (see Fig. 9c) and $a_w$ (see Fig. 9d) is strongly influenced by $q_2$, and the agreement between the perturbation solution and the numerical result is very good as well. This reveals that the contribution of the third mode is small, though not negligible since it turns out to have a significant role in the determination of the position of the bifurcation points. Furthermore, the grey crosses, indicating the outcomes given by integration of the ten d.o.f. system, provided for convergence analysis, show good qualitative agreement, with a small quantitative deviation in terms of amplitudes of limit cycles close to the right bifurcation point. The latter aspect confirms the validity of the three-mode reduction proposed here.

However, as a major result, Fig. 9 proves the energy exchange from the directly excited local to the global response of the pipe, due to the internal resonance.

5.2 Case 2: $\omega _3\simeq 3\omega _1$, ${\varOmega }\simeq \omega _3$

In this case, the external force produces a primary resonance on the third mode (the second local), the latter being in internal resonance with the other two modes (the first global and first local).

The frequency response curves are shown in Fig. 10, directly expressed in terms of $r_k$, $k=1,2,3$. From this figure, it is clear that only $r_3$ is involved in the response, being the contribution of $r_1,r_2$ vanishing.

Fig. 10

Frequency response curves for $l=1.344$ m, $\omega _2=2.3\omega _1$, $\omega _3=3\omega _1$ and ${\varOmega }=\omega _3+\epsilon ^2\sigma$: a $r_1$ vs ${\varOmega }/\omega _1$; b $r_2$ vs ${\varOmega }/\omega _1$; c $r_3$ vs ${\varOmega }/\omega _1$

Therefore, in the considered case, even though internal resonances are present, the following two circumstances concurrently happen: (1) a de facto nonlinear orthogonality among modes occurs [28] in the selected range of frequencies, which induces the coefficients responsible for the modal interaction in the amplitude modulation equations (AMEs), even not zero, not to provoke coupling; (2) the nonlinear terms are not able to (independently) trigger the 1:3 and 2:3 subharmonic resonances on modes 1 and 2, respectively. As a consequence, the first global and local modes, besides the contribute induced by the external force, only passively participate to the motion.

Fig. 11

Frequency response curves for $l=1.344$ m, $\omega _2=2.3\omega _1$, $\omega _3=3\omega _1$ and ${\varOmega }=\omega _3+\epsilon ^2\sigma$: a $\max (q_1)$ vs ${\varOmega }/\omega _1$; b $\max (q_2)$ vs ${\varOmega }/\omega _1$; c $\max (q_3)$ vs ${\varOmega }/\omega _1$. Solid line: perturbation method; dotted line: numerical integration

This occurrence is confirmed by the frequency response curves in terms of reconstructed modal coordinates $q_1,q_2,q_3$, shown in Fig. 11. There, the solution obtained by the perturbation method, shown in blue solid lines, is superimposed to numerical solutions (dots) obtained by numerical integration of the Galerkin equations. On the one hand, as expected, the response has prevailing component on the amplitude $q_3$, that is, directly activated by the external excitation. It exhibits a hardening behavior characterized by the presence of multi-valued solutions and unstable branch (see Fig. 11c). On the other hand, the response of $q_1,\,q_2$ (see Fig. 11a, b respectively) is mainly governed by the non-resonant terms ensuing at the first and second order (see Eqs. (52) and (55)). It is observed that though $q_1, q_3$ are very well captured, the perturbation solution slightly loses accuracy in terms of $q_2$ around ${\varOmega }/\omega _1\simeq 3.04$ (see Fig. 11b).

As done for case 1, the response is also compared in terms of time histories of the modal coordinates evaluated at ${\varOmega }/\omega _1=3.04$, and the result is illustrated in Fig. 12. As expected, the time histories of $q_1,\,q_3$ predicted by the perturbation solution completely overlap the numerical curves (see Fig. 12a, c), while $q_2$ is affected by a slight loss of accuracy in correspondence of the peaks (see Fig. 12b).

Fig. 12

Time histories of the modal coordinates for $l=1.344$ m, $\omega _2=2.3\omega _1$, $\omega _3=3\omega _1$ and ${\varOmega }/ \omega _1=3.04$: a $q_1$ vs t; b $q_2$ vs t; c $q_3$ vs t. Blue line: perturbation method; black line: numerical integration. (Color figure online)

Fig. 13

Frequency response curves for $l=1.344$ m, $\omega _2=2.3\omega _1$, $\omega _3=3\omega _1$ and ${\varOmega }=\omega _3+\epsilon ^2\sigma$: a $\max (v(l))$ vs ${\varOmega }/\omega _1$; b $\max (\vartheta (l))$ vs ${\varOmega }/\omega _1$; c $\max (a_p(l/4))$ vs ${\varOmega }/\omega _1$; d $\max (a_w(l/4))$ vs ${\varOmega }/\omega _1$. Solid line: perturbation method; dotted line: numerical integration of the 3-d.o.f. system; crosses: numerical integration of the 10-d.o.f. system

Finally, the global and local variables response curves are reconstituted and compared to the numerical solution. As done previously, the maximum value of the response of v and $\vartheta$ are evaluated at the beam tip $s=l$, and the curves are represented in Fig. 13a, b, respectively, whereas the response of $a_p$ and $a_w$ is evaluated at $s=l/4$, and the curves are shown in Fig. 13c, d, respectively. The response of the global variables is led by $q_1$, whereas the local variables mainly follow $q_3$, having $q_2$ a lower contribution in qualitatively determining the overall response, though it has a significant role in quantitative terms. It can be finally observed that no exchange of energy from the local to the global modes of the pipe occurs in this case. This is also confirmed by the outcomes of the 10 d.o.f. system, indicated by grey crosses; quantitative differences with the 3 d.o.f. system occur only on the passive mode amplitudes, which actually give a very small contribution to the overall response of the pipe, still confirming the validity of the three-mode reduction.

6 Conclusions

The nonlinear dynamic response of a pipe under external harmonic load is addressed in the paper. The pipe is modeled as a beam-like structure, taking into account the change in shape of the cross sections by means of the introduction of specific (local) variables. Specifically, the change in shape provides a further contribution to the system, which is competing with those given by elastic and inertial terms, which typically interact in cantilevers. The load, acting on half cap of the pipe, has nonzero direct component in the equation ruling local variables, and it is assumed resonant with one of the local modes. Moreover, 1:2 and 1:3 internal resonances between global and local modes are considered as well.

After a Galerkin projection, the response of the pipe is addressed for two different load cases, respectively, i.e., external resonance with the first or second local mode, via perturbation methods. Specific scaling and implementations of the MSM are carried out for the two cases.

The obtained solutions, which are in general good agreement with numerical integration, show possible exchange of energy from the local to the global motions. On the one hand, if the external force is resonant with the first local mode, the nonlinear terms are able to trigger the internal resonances and induce tri-modal solutions. On the other hand, if the load is resonant with the second local mode, the internal resonances are not activated due to a de facto nonlinear orthogonality among modes, and the response mostly remains bounded in the local behavior.

Appendices

The nonlinear integral-partial differential equations of motion

The nonlinear IPDEs of motion are:

$$\begin{aligned}{} & {} \left[ c_{1} \left( v'-\vartheta -\left( \frac{\vartheta ^2}{2}-\vartheta v'\right) \vartheta +\frac{1}{6}(\vartheta ^3-3\vartheta ^2v')\right) \right. \nonumber \\{} & {} \left. \quad -\frac{1}{2} c_{1} a_{w} \vartheta \right] '-\Bigl [\frac{c_{1} (v'-\vartheta )\vartheta ^2}{2} -\vartheta \Bigl (c_{1} (v'-\vartheta )\vartheta \nonumber \\{} & {} \quad -\int _{s}^{l}\!\!(m_{1}\int _{0}^{\xi }\Bigl (\frac{\vartheta ^2}{2}-\vartheta v'\Bigr )^{\bullet \bullet }\textrm{d}\zeta )\textrm{d}\xi \Bigr )\Bigr ]'\nonumber \\{} & {} \quad +f_0\cos ({\varOmega } t)-m_{1} \ddot{v}=0,\nonumber \\{} & {} \Bigl [c_{2} \vartheta +c_{3} a_{p} \vartheta +c_{4} a_{p}^2 \vartheta -\frac{1}{2} c_{1} a_{w} \Bigl (v'-\vartheta \Bigr )\Bigr ]'\nonumber \\{} & {} \quad +\Bigl [c_{1} \Bigl (v'-\vartheta -\Bigl (\frac{\vartheta ^2}{2}-\vartheta v'\Bigr )\vartheta \nonumber \\{} & {} \quad +\frac{1}{6}(\vartheta ^3-3\vartheta ^2v')\Bigr ) -\frac{1}{2} c_{1} a_{w} \vartheta \Bigr ]\nonumber \\{} & {} \quad +(\vartheta -v')\Bigl [c_{1}(v'-\vartheta )\vartheta \nonumber \\{} & {} \quad -\int _{s}^{l}\!\!(m_{1}\int _{0}^{\xi }\Bigl (\frac{\vartheta ^2}{2}-\vartheta v'\Bigr )^{\bullet \bullet }\textrm{d}\zeta )\textrm{d}\xi \Bigr ]\nonumber \\{} & {} \quad +c-\Bigl (m_{2} \ddot{\vartheta }+m_{3} {\dot{a}}_p {\dot{\vartheta }}+m_{3} a_p \ddot{\vartheta }\nonumber \\{} & {} \quad +m_{4} {\dot{a}}_p a_p {\dot{\vartheta }}+m_{5} a_p^2 \ddot{\vartheta }\Bigr )=0, \nonumber \\{} & {} \left[ \frac{1}{4} c_{1} a_{p}'+c_{10} a_{w}\right. \nonumber \\{} & {} \left. \quad +c_{12} a_{p}^2 a_{w}+c_{11} a_{w}^3\right] '\nonumber \\{} & {} \quad -\Bigl [c_{5} a_{p}+c_{4} a_{p} \vartheta ^2+c_{6} \vartheta ^2 +c_{8} a_{p} a_{w} a_{p}'\Bigr ]\nonumber \\{} & {} \quad -\frac{4f_0}{3\pi }\cos ({\varOmega } t)\nonumber \\{} & {} \quad -\Bigl (m_{4} \ddot{a}_p-\frac{5}{8} m_{6} a_p {\dot{\vartheta }}^2+m_{7} {\dot{\vartheta }}^2\Bigr )=0, \nonumber \\{} & {} \Bigl [c_{17} a_{w}'+c_{9} a_{p} a_{w}^2\Bigr ]'-\Bigl [c_{13} a_{w}+c_{10} a_{p}'+c_{7} a_{p}^2 a_{w}\nonumber \\{} & {} \quad +c_{12} a_{p}^2a_{p}' +c_ {15} a_{w}^2 a_{p}'+\frac{1}{2} c_ {1} a_{w} \vartheta ^2+c_{14}a_{w}^3\nonumber \\{} & {} \quad -\frac{1}{2} c_{1}(v'-\vartheta ) \vartheta +c_{16} a_{p} a_{w} a_{w}'\Bigr ]\nonumber \\{} & {} \quad -m_{6} \ddot{a}_w-m_{6} a_w {\dot{\vartheta }}^2=0. \end{aligned}$$

(59)

The essential boundary conditions at $s=0$ are:

$$\begin{aligned} v=\vartheta =a_{p}=a_{w}=0, \end{aligned}$$

(60)

and the natural boundary conditions at $s=l$ are:

$$\begin{aligned} \begin{aligned}&c_{1} \Bigl [v'-\vartheta -\Bigl (\frac{\vartheta ^2}{2}-\vartheta v'\Bigr )\vartheta +\frac{1}{6}\Bigl (\vartheta ^3-3\vartheta ^2v'\bigr )\Bigr ]\\&\quad -\frac{1}{2} c_{1} a_{w} \vartheta +\frac{c_{1}(v'-\vartheta )\vartheta ^2}{2}=0,\\&c_{2} \vartheta +c_{3} a_{p} \vartheta +c_{4} a_{p}^2 \vartheta -\frac{1}{2} c_{1} a_{w} (v'-\vartheta )=0, \\&\frac{1}{4} c_{1} a_{p}'+c_{10} a_{w}+c_{12} a_{p}^2 a_{w}+c_{11} a_{w}^3=0, \\&c_{17} a_{w}'+c_{9} a_{p} a_{w}^2=0. \end{aligned}\nonumber \\ \end{aligned}$$

(61)

Nonlinear terms

The column vector ${\mathcal {N}}$ collects the quadratic and cubic nonlinear terms as expressed in Eq. (27). Each term appearing in the latter equation is explicitly defined by the following nonlinear functions.

The quadratic functions are:

$$\begin{aligned}{} & {} {\textbf{N}}_{2,1}({\textbf{x}},{\textbf{y}})\nonumber \\= & {} \left( \begin{aligned}&c_{4,5} x_1 y_2+c_{4,7} x_1 y_3 \\&c_{5,11} x_3 y_3+c_{5,3} x_1 y_1+c_{5,6} x_2 y_2+c_{5,8} x_2 y_3 \\&c_{6,11} x_3 y_3+c_{6,3} x_1 y_1+c_{6,6} x_2 y_2+c_{6,8} x_2 y_3 \end{aligned} \right) \nonumber \\ \end{aligned}$$

(62)

$$\begin{aligned}{} & {} {\textbf{N}}_{2,2}({\textbf{x}},{\textbf{y}})\nonumber \\{} & {} = \left( \begin{aligned}&c_{4,18} x_1 y_2+c_{4,19} x_1 y_3 \\&c_{5,13} x_1 y_1 \\&c_{6,13} x_1 y_1 \end{aligned} \right) \end{aligned}$$

(63)

$$\begin{aligned}{} & {} {\textbf{N}}_{2,3}({\textbf{x}},{\textbf{y}})\nonumber \\{} & {} = \left( \begin{aligned}&c_{4,13} x_2 y_1+c_{4,17} x_3 y_1 \\&0 \\&0 \end{aligned} \right) \end{aligned}$$

(64)

The cubic functions are:

$$\begin{aligned}{} & {} {\textbf{N}}_{3,1}({\textbf{x}},{\textbf{y}},{\textbf{z}})\nonumber \\{} & {} = \left( \begin{aligned}&c_{4,1} x_1 y_1 z_1+c_{4,3} x_1 y_2 z_2+c_{4,4} x_1 y_2 z_3 \\&\quad +c_{4,6} \ x_1 y_3 z_3\\&c_{5,10} x_3 y_3 z_3+c_{5,1} x_1 y_1 z_2+c_{5,2} x_1 y_1 z_3 \\&\quad +c_{5,4} \ x_2 y_2 z_2+c_{5,5} x_2 y_2 z_3 \\&\quad +c_{5,7} x_2 y_3 z_3\\&c_{6,10} x_3 y_3 z_3+c_{6,1} x_1 y_1 z_2+c_{6,2} x_1 y_1 z_3 \\&\quad +c_{6,4} \ x_2 y_2 z_2+c_{6,5} x_2 y_2 z_3 \\&\quad +c_{6,7} x_2 y_3 z_3 \end{aligned} \right) \nonumber \\ \end{aligned}$$

(65)

$$\begin{aligned}{} & {} {\textbf{N}}_{3,2}({\textbf{x}},{\textbf{y}},{\textbf{z}})\nonumber \\{} & {} = \left( \begin{aligned}&c_{4,11} x_2 y_1 z_2+c_{4,12} x_2 y_1 z_3 \\&\quad +c_{4,15} x_3 y_1 \ z_2 +c_{4,16} x_3 y_1 z_3 \\&\quad +c_{4,8} x_1 y_1 z_1 \\&c_{5,12} x_3 y_1 z_1+c_{5,9} x_2 y_1 z_1 \\&c_{6,12} x_3 y_1 z_1+c_{6,9} x_2 y_1 z_1 \end{aligned} \right) \end{aligned}$$

(66)

$$\begin{aligned}{} & {} {\textbf{N}}_{3,3}({\textbf{x}},{\textbf{y}},{\textbf{z}})\nonumber \\{} & {} = \left( \begin{aligned}&c_{4,10} x_2 y_3 z_1+c_{4,14} x_3 y_3 z_1 \\ {}&\quad +c_{4,2} x_1 y_1 \ z_1+c_{4,9} x_2 y_2 z_1 \\&0 \\&0 \end{aligned} \right) \end{aligned}$$

(67)

where ${\textbf{x}},{\textbf{y}},{\textbf{z}}$ are generic vectors with components $x_j,y_j,z_j$ ($j=1,2,3$), respectively, and the coefficients are defined as:

$$\begin{aligned} c_{4,1}&=\int _0^l\frac{2}{3} c_{1} \phi _{\vartheta ,1}^2 \left( -5 \phi _{\vartheta ,1} \phi _{v,1}'+3 \phi _{v,1}'^2+2 \phi _{\vartheta ,1}^2\right) \textrm{d}s \nonumber \\ c_{4,2}&=m_1\int _0^l\left[ \int _0^s\left( \phi _{\vartheta ,1}^2-2 \phi _{\vartheta ,1} \phi _{v,1}'\right) \textrm{d}\xi \right] ^2\textrm{d}s \nonumber \\ c_{4,3}&=\int _0^l\left( c_{4} \phi _{p,2}^2 \phi _{\vartheta ,1}^2+\frac{1}{2} c_{1} \phi _{w,2}^2 \phi _{\vartheta ,1}^2\right) \textrm{d}s \nonumber \\ c_{4,4}&=\int _0^l\left( 2 c_{4} \phi _{p,2} \phi _{p,3} \phi _{\vartheta ,1}^2+c_{1} \phi _{w,2}\phi _{w,3} \phi _{\vartheta ,1}^2\right) \textrm{d}s \nonumber \\ c_{4,5}&=\int _0^l\left( c_{3} \phi _{p,2} \phi _{\vartheta ,1}'^2+c_{1} \phi _{w,2}\phi _{\vartheta ,1}' \left( \phi _{\vartheta ,1}-\phi _{v,1}'\right) \right) \textrm{d}s \end{aligned}$$

(68)

$$\begin{aligned} c_{4,6}&=\int _0^l\left( c_{4} \phi _{p,3}^2 \phi _{\vartheta ,1}'^2+\frac{1}{2} c_{1} \phi _{w,3}^2 \phi _{\vartheta ,1}'^2\right) \textrm{d}s \nonumber \\ c_{4,7}&=\int _0^l\left( c_{3} \phi _{p,3} \phi _{\vartheta ,1}'^2+c_{1} \phi _{w,3} \phi _{\vartheta ,1}' \left( \phi _{\vartheta ,1}-\phi _{v,1}'\right) \right) \textrm{d}s \nonumber \\ c_{4,8}&=m_1\int _0^l\left[ \int _0^s\left( \phi _{\vartheta ,1}^2-2 \phi _{\vartheta ,1} \phi _{v,1}'\right) \textrm{d}\xi \right] ^2\textrm{d}s \nonumber \\ c_{4,9}&=\int _0^l\left( m_{5} \phi _{p,2}^2 \phi _{\vartheta ,1}^2+m_{6} \phi _{w,2}^2 \phi _{\vartheta ,1}^2\right) \textrm{d}s \nonumber \\ c_{4,10}&=\int _0^l\left( 2 m_{5} \phi _{p,2} \phi _{p,3} \phi _{\vartheta ,1}^2+2 m_{6} \phi _{w,2} \phi _{w,3} \phi _{\vartheta ,1}^2\right) \textrm{d}s \end{aligned}$$

(69)

$$\begin{aligned} c_{4,11}&=\int _0^l\left( m_{4} \phi _{p,2}^2 \phi _{\vartheta ,1}^2+m_{1} \phi _{w,2}^2 \phi _{\vartheta ,1}^2\right) \textrm{d}s \nonumber \\ c_{4,12}&=\int _0^l\left( m_{4} \phi _{p,2} \phi _{p,3} \phi _{\vartheta ,1}^2+m_{1} \phi _{w,2} \phi _{w,3} \phi _{\vartheta ,1}^2\right) \textrm{d}s \nonumber \\ c_{4,13}&=\int _0^l\left( m_{3} \phi _{p,2} \phi _{\vartheta ,1}^2\right) \textrm{d}s \nonumber \\ c_{4,14}&=\int _0^l\left( m_{5} \phi _{p,3}^2 \phi _{\vartheta ,1}^2+m_{6} \phi _{w,3}^2 \phi _{\vartheta ,1}^2\right) \textrm{d}s \nonumber \\ c_{4,15}&=\int _0^l\left( m_{4} \phi _{p,2} \phi _{p,3} \phi _{\vartheta ,1}^2+m_{1} \phi _{w,2} \phi _{w,3} \phi _{\vartheta ,1}^2\right) \textrm{d}s \end{aligned}$$

(70)

$$\begin{aligned} c_{4,16}&=\int _0^l\left( m_{4} \phi _{p,3}^2 \phi _{\vartheta ,1}^2+m_{1} \phi _{w,3}^2 \phi _{\vartheta ,1}^2\right) \textrm{d}s \nonumber \\ c_{4,17}&=\int _0^l\left( m_{3} \phi _{p,3} \phi _{\vartheta ,1}^2\right) \textrm{d}s \nonumber \\ c_{4,18}&=\int _0^l\left( m_{3} \phi _{p,2} \phi _{\vartheta ,1}^2\right) \textrm{d}s \nonumber \\ c_{4,19}&=\int _0^l\left( m_{3} \phi _{p,3} \phi _{\vartheta ,1}^2\right) \textrm{d}s \end{aligned}$$

(71)

$$\begin{aligned} c_{5,1}&=\int _0^l\left( c_{4} \phi _{p,2}^2 \phi _{\vartheta ,1}'^2+\frac{1}{2} c_{1} \phi _{w,2}^2 \phi _{\vartheta ,1}'^2\right) \textrm{d}s\nonumber \\ c_{5,2}&=\int _0^l\left( c_{4} \phi _{p,2} \phi _{p,3} \phi _{\vartheta ,1}'^2+\frac{1}{2} c_{1} \phi _{w,2} \phi _{w,3} \phi _{\vartheta ,1}'^2\right) \textrm{d}s\nonumber \\ c_{5,3}&=\int _0^l\left( c_{6} \phi _{p,2} \phi _{\vartheta ,1}'^2+\frac{1}{2} c_{1} \phi _{w,2} \phi _{\vartheta ,1}' \left( \phi _{\vartheta ,1}-\phi _{v,1}'\right) \right) \textrm{d}s\nonumber \\ c_{5,4}&=\int _0^l\Big (c_{11} \phi _{w,2}^3 \phi '_{p,2}+c_{15} \phi _{w,2}^3 \phi '_{p,2}\nonumber \\&\quad +c_{8} \phi _{p,2}^2 \phi _{w,2} \phi '_{p,2}+2 c_{12} \phi _{p,2}^2 \phi _{w,2} \phi '_{p,2}\nonumber \\&\quad +2 c_{9} \phi _{p,2} \phi _{w,2}^2 \phi '_{w,2}+c_{16} \phi _{p,2} \phi _{w,2}^2 \phi '_{w,2}\nonumber \\&\quad +2 c_{7} \phi _{p,2}^2 \phi _{w,2}^2+c_{14} \phi _{w,2}^4\Big )\textrm{d}s \nonumber \\ c_{5,5}&=\int _0^l\Big ( c_{8} (\phi _{p,2} \phi _{p,3} \phi _{w,2} \phi '_{p,2}+\phi _{p,2}^2 \phi _{w,3} \phi '_{p,2}\nonumber \\&\quad +\phi _{p,2}^2 \phi _{w,2} \phi '_{p,3}\Big )+c_{12} \Big (4 \phi _{p,2} \phi _{p,3} \phi _{w,2} \phi '_{p,2}\nonumber \\&\quad +\phi _{p,2}^2 \phi _{w,3} \phi '_{p,2}+\phi _{p,2}^2 \phi _{w,2} \phi '_{p,3}\Big )\nonumber \\&\quad +c_{15} \Big (2 \phi _{w,2}^2 \phi _{w,3} \phi '_{p,2}+\phi _{w,2}^3 \phi '_{p,3}\Big )\nonumber \\&\quad +3 c_{11} \phi _{w,2}^2 \phi _{w,3} \phi '_{p,2}+c_{16} \Big (\phi _{p,2} \phi _{w,2} \phi _{w,3} \phi '_{w,2}\nonumber \\&\quad +\phi _{p,2} \phi _{w,2}^2 \phi '_{w,3}+\phi _{p,3} \phi _{w,2}^2 \phi '_{w,2}\Big )\nonumber \\&\quad +c_{9} \Big (4 \phi _{p,2} \phi _{w,2} \phi _{w,3} \phi '_{w,2}+\phi _{p,2} \phi _{w,2}^2 \phi '_{w,3}\nonumber \\&\quad +\phi _{p,3} \phi _{w,2}^2 \phi '_{w,2}\Big )+c_{7} \Big (3 \phi _{p,2} \phi _{p,3} \phi _{w,2}^2\nonumber \\&\quad +3 \phi _{p,2}^2 \phi _{w,2} \phi _{w,3}\Big )+3 c_{14} \phi _{w,2}^3 \phi _{w,3})\textrm{d}s \end{aligned}$$

(72)

$$\begin{aligned} c_{5,7}&=\int _0^l\Big ( c_{12} (2 \phi _{p,3}^2 \phi _{w,2} \phi '_{p,2}+2 \phi _{p,2} \phi _{p,3} \phi _{w,3} \phi '_{p,2}\nonumber \\&\quad +2 \phi _{p,2} \phi _{p,3} \phi _{w,2} \phi '_{p,3}\Big )+c_{8} \Big (\phi _{p,2} \phi _{p,3} \phi _{w,3} \phi '_{p,2}\nonumber \\&\quad +\phi _{p,2} \phi _{p,3} \phi _{w,2} \phi '_{p,3}+\phi _{p,2}^2 \phi _{w,3} \phi '_{p,3}\Big )\nonumber \\&+c_{15} \Big (\phi _{w,2} \phi _{w,3}^2 \phi '_{p,2}+2 \phi _{w,2}^2 \phi _{w,3} \phi '_{p,3}\Big )\nonumber \\&\quad +3 c_{11} \phi _{w,2} \phi _{w,3}^2 \phi '_{p,2}+c_{16} \Big (\phi _{p,2} \phi _{w,2} \phi _{w,3} \phi '_{w,3}\nonumber \\&\quad +\phi _{p,3} \phi _{w,2} \phi _{w,3} \phi '_{w,2}+\phi _{p,3} \phi _{w,2}^2 \phi '_{w,3}\Big )\nonumber \\&\quad +c_{9} \Big (2 \phi _{p,2} \phi _{w,3}^2 \phi '_{w,2}+2 \phi _{p,2} \phi _{w,2} \phi _{w,3} \phi '_{w,3}\nonumber \\&\quad +2 \phi _{p,3} \phi _{w,2} \phi _{w,3} \phi '_{w,2} \Big )+c_{7} \Big (4 \phi _{p,2} \phi _{p,3} \phi _{w,2} \phi _{w,3}\nonumber \\&\quad +\phi _{p,2}^2 \phi _{w,3}^2+\phi _{p,3}^2 \phi _{w,2}^2\Big )+3 c_{14} \phi _{w,2}^2 \phi _{w,3}^2\Big )\textrm{d}s \nonumber \\ c_{5,9}&=\int _0^l\Big (-\frac{1}{8} m_{6} \phi _{\vartheta ,1}^2 \Big (5 \phi _{p,2}^2+8 \ \phi _{w,2}^2\Big )\Big )\textrm{d}s \nonumber \\ c_{5,10}&=\int _0^l\Big ( c_{12} \Big (\phi _{p,3}^2 \phi _{w,3} \phi '_{p,2}+\phi _{p,3}^2 \phi _{w,2} \phi '_{p,3}\Big )\nonumber \\&\quad +c_{11} \phi _{w,3}^3 \phi '_{p,2}+c_{8} \phi _{p,2} \phi _{p,3} \phi _{w,3} \phi '_{p,3}\nonumber \\&\quad +c_{9} \Big (\phi _{p,2} \phi _{w,3}^2 \phi '_{w,3}+\phi _{p,3} \phi _{w,3}^2 \phi '_{w,2}\nonumber \\&\quad +c_{7} \Big (\phi _{p,2} \phi _{p,3} \phi _{w,3}^2+\phi _{p,3}^2 \phi _{w,2} \phi _{w,3}\Big )\nonumber \\&\quad +c_{15} \phi _{w,2} \phi _{w,3}^2 \phi '_{p,3}+c_{16} \phi _{p,3} \phi _{w,2} \phi _{w,3} \phi '_{w,3}\nonumber \\&\quad +c_{14} \phi _{w,2} \phi _{w,3}^3\Big )\textrm{d}s\nonumber \\ c_{5,12}&=\int _0^l\Big (-\frac{1}{8} m_{6} \phi _{\vartheta ,1}^2 \Big (5 \phi _{p,2} \phi _{p,3}+8 \phi _{w,2} \phi _{w,3}\Big )\Big )\textrm{d}s \nonumber \\ c_{5,13}&=\int _0^l\Big (m_{7} \phi _{p,2} \phi _{\vartheta ,1}^2\Big )\textrm{d}s \end{aligned}$$

(73)

$$\begin{aligned} c_{6,1}&=\int _0^l\Big (c_{4} \phi _{p,2} \phi _{p,3} \phi _{\vartheta ,1}^2+\frac{1}{2} c_{1} \phi _{w,2} \phi _{w,3} \phi _{\vartheta ,1}^2\Big )\textrm{d}s \nonumber \\ c_{6,2}&=\int _0^l\Big (c_{4} \phi _{p,3}^2 \phi _{\vartheta ,1}^2+\frac{1}{2} c_{1} \phi _{w,3}^2 \phi _{\vartheta ,1}^2\Big )\textrm{d}s \nonumber \\ c_{6,3}&=\int _0^l\Big (c_{6} \phi _{p,3} \phi _{\vartheta ,1}'^2+\frac{1}{2} c_{1} \phi _{w,3} \ \phi _{\vartheta ,1}' \Big (\phi _{\vartheta ,1}-\phi _{v,1}'\Big )\Big )\textrm{d}s \nonumber \\ c_{6,4}&=\int _0^l\Big (c_{12} (\phi _{p,2}^2 \phi _{w,3} \phi '_{p,2}+\phi _{p,2}^2 \phi _{w,2} \phi '_{p,3}\Big )\nonumber \\&\quad +c_{8} \phi _{p,2} \phi _{p,3} \phi _{w,2} \phi '_{p,2}+c_{15} \phi _{w,2}^2 \phi _{w,3} \phi '_{p,2}\nonumber \\&\quad +c_{9} \Big (\phi _{p,2} \phi _{w,2}^2 \phi _{w,3}'+\phi _{p,3} \phi _{w,2}^2 \phi _{w,2}'\Big )\nonumber \\&\quad +c_{7} \Big (\phi _{p,2} \phi _{p,3} \phi _{w,2}^2+\phi _{p,2}^2 \phi _{w,2} \phi _{w,3}\Big )\nonumber \\&\quad +c_{16} \phi _{p,2} \phi _{w,2} \phi _{w,3} \phi _{w,2}'\nonumber \\&\quad +c_{11} \phi _{w,2}^3 \phi '_{p,3}+c_{14} \phi _{w,2}^3 \phi _{w,3}\Big )\textrm{d}s \end{aligned}$$

(74)

$$\begin{aligned} c_{6,5}&=\int _0^l\Big (c_{8} \Big (\phi _{p,3}^2 \phi _{w,2} \phi '_{p,2}+\phi _{p,2} \phi _{p,3} \phi _{w,3} \phi '_{p,2}\nonumber \\&\quad +\phi _{p,2} \phi _{p,3} \phi _{w,2} \phi '_{p,3}\Big )+c_{12} \Big (2 \phi _{p,2} \phi _{p,3} \phi _{w,3} \phi '_{p,2}\nonumber \\&\quad +2 \phi _{p,2} \phi _{p,3} \phi _{w,2} \phi '_{p,3}+2 \phi _{p,2}^2 \phi _{w,3} \phi '_{p,3}\Big )\nonumber \\&\quad +c_{15} \Big (2 \phi _{w,2} \phi _{w,3}^2 \phi '_{p,2}+\phi _{w,2}^2 \phi _{w,3} \phi '_{p,3}\Big )\nonumber \\&\quad +c_{16} \Big (\phi _{p,2} \phi _{w,3}^2 \phi _{w,2}'+\phi _{p,2} \phi _{w,2} \phi _{w,3} \phi _{w,3}'\nonumber \\&\quad +\phi _{p,3} \phi _{w,2} \phi _{w,3} \phi _{w,2}'\Big )+c_{9} \Big (2 \phi _{p,2} \phi _{w,2} \phi _{w,3} \phi _{w,3}'\nonumber \\&\quad +2 \phi _{p,3} \phi _{w,2} \phi _{w,3} \phi _{w,2}'+2 \phi _{p,3} \phi _{w,2}^2 \phi _{w,3}'\Big )\nonumber \\&\quad +c_{7} \Big (4 \phi _{p,2} \phi _{p,3} \phi _{w,2} \phi _{w,3}+\phi _{p,2}^2 \phi _{w,3}^2+\phi _{p,3}^2 \phi _{w,2}^2\Big )\nonumber \\&\quad +3 c_{11} \phi _{w,2}^2 \phi _{w,3} \phi '_{p,3}+3 c_{14} \phi _{w,2}^2 \phi _{w,3}^2\Big )\textrm{d}s\nonumber \\ c_{6,7}&=\int _0^l\Big ( c_{8} \Big (\phi _{p,3}^2 \phi _{w,3} \phi '_{p,2}+\phi _{p,2} \phi _{p,3} \phi _{w,3} \phi '_{p,3}\nonumber \\&\quad +\phi _{p,3}^2 \phi _{w,2} \phi '_{p,3}\Big )+c_{12} \Big (\phi _{p,3}^2 \phi _{w,3} \phi '_{p,2}\nonumber \\&\quad +4 \phi _{p,2} \phi _{p,3} \phi _{w,3} \phi '_{p,3}+\phi _{p,3}^2 \phi _{w,2} \phi '_{p,3} )\nonumber \\&\quad +c_{15} \Big (\phi _{w,3}^3 \phi '_{p,2}+2 \phi _{w,2} \phi _{w,3}^2 \phi '_{p,3}\Big )\nonumber \\&\quad +c_{16} \Big (\phi _{p,2} \phi _{w,3}^2 \phi _{w,3}'+\phi _{p,3} \phi _{w,3}^2 \phi _{w,2}'\nonumber \\&\quad +\phi _{p,3} \phi _{w,2} \phi _{w,3} \phi _{w,3}'\Big )+c_{9} \Big (\phi _{p,2} \phi _{w,3}^2 \phi _{w,3}'\nonumber \\&\quad +\phi _{p,3} \phi _{w,3}^2 \phi _{w,2}'+4 \phi _{p,3} \phi _{w,2} \phi _{w,3} \phi _{w,3}'\Big )\nonumber \\&\quad +c_{7} \Big (3 \phi _{p,2} \phi _{p,3} \phi _{w,3}^2+3 \phi _{p,3}^2 \phi _{w,2} \phi _{w,3}\Big )\nonumber \\&\quad +3 c_{11} \phi _{w,2} \phi _{w,3}^2 \phi '_{p,3}+3 c_{14} \phi _{w,2} \phi _{w,3}^3\Big )\textrm{d}s \nonumber \\ c_{6,9}&=\int _0^l\Big (-\frac{1}{8} m_{6} \phi _{\vartheta ,1}^2 (5 \phi _{p,2} \phi _{p,3}+8 \phi _{w,2} \phi _{w,3})\Big )\textrm{d}s \nonumber \\ c_{6,10}&=\int _0^l\Big (c_{11} \phi _{w,3}^3 \phi '_{p,3}+c_{15} \phi _{w,3}^3 \phi '_{p,3}\nonumber \\&\quad +c_{8} \phi _{p,3}^2 \phi _{w,3} \phi '_{p,3}+2 c_{12} \phi _{p,3}^2 \phi _{w,3} \phi '_{p,3}\nonumber \\&\quad +2 c_{9} \phi _{p,3} \phi _{w,3}^2 \phi _{w,3}'+c_{16} \phi _{p,3} \phi _{w,3}^2 \phi _{w,3}'\nonumber \\&\quad +2 c_{7} \phi _{p,3}^2 \phi _{w,3}^2+c_{14} \phi _{w,3}^4\Big )\textrm{d}s\nonumber \\ c_{6,12}&=\int _0^l\Big (-\frac{1}{8} m_{6} \phi _{\vartheta ,1}^2 \Big (5 \phi _{p,3}^2+8 \ \phi _{w,3}^2\Big )\Big )\textrm{d}s \nonumber \\ c_{6,13}&=\int _0^l\Big (m_{7} \phi _{p,3} \phi _{\vartheta ,1}^2\Big )\textrm{d}s. \end{aligned}$$

(75)

Coefficients of the perturbation equations

1.1 Case 1

The coefficients appearing in the modulation equations for the case 1 (Eqs. (40) and (43)) are defined in what follows. At the second order (Eq. (40)), they are:

$$\begin{aligned} \begin{aligned} d_1&=-\frac{1}{2\omega _1}{\textbf{z}}_1^T\left[ {\textbf{N}}_{2,1}(\bar{{\textbf{z}}}_1,{\textbf{z}}_2)+{\textbf{N}}_{2,2}(-i\omega _1\bar{{\textbf{z}}}_1,i\omega _2{\textbf{z}}_2) \right. \\&\quad +\left. {\textbf{N}}_{2,3}({\textbf{z}}_2,-\omega _1^2\bar{{\textbf{z}}}_1)\right] \\ d_2&=-\frac{1}{2\omega _1}{\textbf{z}}_1^T\left[ {\textbf{N}}_{2,1}(\bar{{\textbf{z}}}_1,\varvec{{\varLambda }}_3)\right. \\&\quad \left. +{\textbf{N}}_{2,2}((-i\omega _1)\bar{{\textbf{z}}}_1,i{\varOmega }\varvec{{\varLambda }}_3) + {\textbf{N}}_{2,3}(\varvec{{\varLambda }}_3,-\omega _1^2\bar{{\textbf{z}}}_1)\right] \\ d_3&=-\frac{1}{2\omega _1}{\textbf{z}}_1^T\left[ {\textbf{N}}_{2,1}(\bar{\varvec{{\varLambda }}}_1,{\textbf{z}}_3)\right. \\&\quad \left. +{\textbf{N}}_{2,2}(-i{\varOmega }\bar{\varvec{{\varLambda }}}_1,i\omega _3{\textbf{z}}_3) + {\textbf{N}}_{2,3}({\textbf{z}}_3,-{\varOmega }^2\bar{\varvec{{\varLambda }}}_1)\right] \\ d_4&=-\frac{1}{2\omega _2}{\textbf{z}}_2^T\left[ {\textbf{N}}_{2,1}({\textbf{z}}_1,{\textbf{z}}_1)+{\textbf{N}}_{2,2}(i\omega _1{\textbf{z}}_1,i\omega _1{\textbf{z}}_1) \right. \\&\quad +\left. {\textbf{N}}_{2,3}({\textbf{z}}_1,-\omega _1^2{\textbf{z}}_1)\right] \\ d_5&=-\frac{1}{2\omega _3}{\textbf{z}}_3^T\left[ {\textbf{N}}_{2,1}({\textbf{z}}_1,\varvec{{\varLambda }}_1)+{\textbf{N}}_{2,1}(\varvec{{\varLambda }}_1,{\textbf{z}}_1) \right. \\&\quad +\left. {\textbf{N}}_{2,2}(i\omega _1{\textbf{z}}_1,i\omega \varvec{{\varLambda }}_1)+{\textbf{N}}_{2,2}(i\omega \varvec{{\varLambda }}_1,i\omega _1{\textbf{z}}_1)\right] , \end{aligned}\nonumber \\ \end{aligned}$$

(76)

while those appearing in the cubic-order modulation equations (Eq. (43)) are:

$$\begin{aligned} d_6&=-\frac{1}{2\omega _1}{\textbf{z}}_1^T\Big [{\textbf{N}}_{3,1}\left( z_1,z_1,{\bar{z}}_1\right) +{\textbf{N}}_{3,1}\left( {\bar{z}}_1,z_1,z_1\right) \nonumber \\&\quad + {\textbf{N}}_{3,1}\left( z_1,{\bar{z}}_1,z_1\right) +{\textbf{N}}_{3,2}\left( z_1,i \omega _1 z_1,-i \omega _1 {\bar{z}}_1\right) \nonumber \\&\quad + {\textbf{N}}_{3,2}\left( {\bar{z}}_1,i \omega _1 z_1,i \omega _1 z_1\right) \nonumber \\&\quad +{\textbf{N}}_{3,2}\left( z_1,-i \omega _1 {\bar{z}}_1,i \omega _1 z_1\right) \nonumber \\&\quad + {\textbf{N}}_{3,3}\Big (z_1,z_1,-\omega _1^2 {\bar{z}}_1\Big )+{\textbf{N}}_{3,3}\Big ({\bar{z}}_1,z_1,-\omega _1^2 z_1\Big )\nonumber \\&\quad + {\textbf{N}}_{3,3}\Big (z_1,{\bar{z}}_1,-\omega _1^2 z_1\Big )\Big ]+QOT\nonumber \\ d_7&=-\frac{1}{2\omega _1}{\textbf{z}}_1^T\Big [{\textbf{N}}_{3,1}\left( z_1,z_2,{\bar{z}}_2\right) +{\textbf{N}}_{3,1}\left( z_1,{\bar{z}}_2,z_2\right) \nonumber \\&\quad +{\textbf{N}}_{3,3}\left( z_2,{\bar{z}}_2,-\omega _1^2 z_1\right) \nonumber \\&\quad +{\textbf{N}}_{3,3}\left( {\bar{z}}_2,z_2,-\omega _1^2 z_1\right) \Big ] +QOT\nonumber \\ d_8&=-\frac{1}{2\omega _1}{\textbf{z}}_1^T\Big [ {\textbf{N}}_{3,1}\left( z_1,z_2,\bar{{\varLambda } }_3\right) \nonumber \\\&\quad +{\textbf{N}}_{3,2}\left( z_2,i \omega _1 z_1,-i {\varOmega } {\bar{{\varLambda }}}_3\right) \nonumber \\&\quad + {\textbf{N}}_{3,2}\left( {\bar{{\varLambda }}}_3,i \omega _1 z_1,i \omega _2 z_2\right) \nonumber \\&\quad +{\textbf{N}}_{3,3}\left( z_2,{\bar{{\varLambda }}}_3,-\omega _1^2 z_1\right) \Big ]\ +QOT\nonumber \\ d_9&=-\frac{1}{2\omega _1}{\textbf{z}}_1^T\Big [ {\textbf{N}}_{3,1}\left( z_1,{\bar{z}}_2,{\varLambda } _3\right) \nonumber \\&\quad +{\textbf{N}}_{3,2}\left( {\bar{z}}_2,i \omega _1 z_1,i {\varOmega } {\varLambda } _3\right) \nonumber \\&\quad + {\textbf{N}}_{3,2}\left( {\varLambda } _3,i \omega _1 z_1,-i \omega _2 {\bar{z}}_2\right) \nonumber \\&\quad +{\textbf{N}}_{3,3}\left( {\bar{z}}_2,{\varLambda } _3,-\omega _1^2 z_1\right) \Big ] +QOT\nonumber \\ d_{10}&=-\frac{1}{2\omega _1}{\textbf{z}}_1^T\Big [ {\textbf{N}}_{3,1}\left( z_1,z_3,{\bar{z}}_3\right) +{\textbf{N}}_{3,1}\left( z_1,{\bar{z}}_3,z_3\right) \nonumber \\&\quad + {\textbf{N}}_{3,2}\left( z_3,i \omega _1 z_1,-i \omega _3 {\bar{z}}_3\right) \nonumber \\&\quad +{\textbf{N}}_{3,2}\left( {\bar{z}}_3,i \omega _1 z_1,i \omega _3 z_3\right) + {\textbf{N}}_{3,3}\left( z_3,{\bar{z}}_3,-\omega _1^2 z_1\right) \nonumber \\&\quad +{\textbf{N}}_{3,3}\left( {\bar{z}}_3,z_3,-\omega _1^2 z_1\right) \Big ] +QOT\nonumber \\ d_{11}&=-\frac{1}{2}{\textbf{z}}_1^T\Big [ {\textbf{C}}{\textbf{z}}_1\Big ]\end{aligned}$$

(77)

$$\begin{aligned} d_{12}&=-\frac{1}{2\omega _1}{\textbf{z}}_1^T\Big [{\textbf{N}}_{3,1}\left( z_1,{\varLambda } _1,{\bar{{\varLambda }}}_1\right) \nonumber \\&\quad +{\textbf{N}}_{3,1}\left( z_1,\bar{{\varLambda } }_1,{\varLambda } _1\right) +{\textbf{N}}_{3,1}\left( {\varLambda } _1,z_1,\bar{{\varLambda } }_1\right) \nonumber \\&\quad +{\textbf{N}}_{3,1}\left( {\varLambda } _1,\bar{{\varLambda } }_1,z_1\right) + {\textbf{N}}_{3,1}\left( {\bar{{\varLambda }}}_1,z_1,{\varLambda } _1\right) \nonumber \\&\quad +{\textbf{N}}_{3,1}\left( {\bar{{\varLambda }}}_1,{\varLambda } _1,z_1\right) \nonumber \\&\quad + {\textbf{N}}_{3,2}\left( z_1,i {\varOmega } {\varLambda } _1,-i {\varOmega } {\bar{{\varLambda }}}_1\right) \nonumber \\&\quad + {\textbf{N}}_{3,2}\left( z_1,-i {\varOmega } {\bar{{\varLambda }}}_1,i {\varOmega } {\varLambda } _1\right) \nonumber \\&\quad + {\textbf{N}}_{3,2}\left( {\varLambda } _1,i \omega _1 z_1,-i {\varOmega } {\bar{{\varLambda }}}_1\right) \nonumber \\&\quad +{\textbf{N}}_{3,2}\left( {\varLambda } _1,-i {\varOmega } {\bar{{\varLambda }}}_1,i \omega _1 z_1\right) \nonumber \\&\quad + {\textbf{N}}_{3,2}\left( {\bar{{\varLambda }}}_1,i \omega _1 z_1,i {\varOmega } {\varLambda } _1\right) \nonumber \\&\quad +{\textbf{N}}_{3,2}\left( {\bar{{\varLambda }}}_1,i {\varOmega } {\varLambda } _1,i \omega _1 z_1\right) \nonumber \\&\quad + {\textbf{N}}_{3,3}\left( z_1,{\varLambda } _1,-{\varOmega } ^2 \bar{{\varLambda } }_1\right) \nonumber \\&\quad +{\textbf{N}}_{3,3}\left( z_1,{\bar{{\varLambda }}}_1,-{\varOmega } ^2 {\varLambda } _1\right) \nonumber \\&\quad + {\textbf{N}}_{3,3}\left( {\varLambda } _1,z_1,-{\varOmega } ^2 \bar{{\varLambda } }_1\right) \nonumber \\&\quad +{\textbf{N}}_{3,3}\left( {\varLambda } _1,{\bar{{\varLambda }}}_1,-\omega _1^2 z_1\right) \nonumber \\&\quad + {\textbf{N}}_{3,3}\left( {\bar{{\varLambda }}}_1,z_1,-{\varOmega } ^2 {\varLambda } _1\right) \nonumber \\&\quad +{\textbf{N}}_{3,3}\left( {\bar{{\varLambda }}}_1,{\varLambda } _1,-\omega _1^2 z_1\right) \Big ] +QOT \end{aligned}$$

(78)

$$\begin{aligned} d_{13}&=-\frac{1}{2\omega _1}{\textbf{z}}_1^T\Big [{\textbf{N}}_{3,1}\left( {\varLambda } _1,z_2,{\bar{z}}_3\right) \nonumber \\&\quad +{\textbf{N}}_{3,2}\left( z_2,i {\varOmega } {\varLambda } _1,-i \omega _3 {\bar{z}}_3\right) \nonumber \\&\quad + {\textbf{N}}_{3,2}\left( {\bar{z}}_3,i {\varOmega } {\varLambda } _1,i \omega _2 z_2\right) \nonumber \\&\quad +{\textbf{N}}_{3,3}\left( z_2,{\bar{z}}_3,-{\varOmega } ^2 {\varLambda } _1\right) \Big ]+QOT \nonumber \\ d_{14}&=-\frac{1}{2\omega _1}{\textbf{z}}_1^T\Big [ {\textbf{N}}_{3,1}\left( {\varLambda } _1,{\bar{z}}_3,{\varLambda } _3\right) \nonumber \\&\quad +{\textbf{N}}_{3,1}\left( {\varLambda } _1,{\varLambda } _3,{\bar{z}}_3\right) + {\textbf{N}}_{3,2}\left( {\bar{z}}_3,i {\varOmega } {\varLambda } _1,i {\varOmega } {\varLambda } _3\right) \nonumber \\&\quad + {\textbf{N}}_{3,2}\left( {\varLambda } _3,i {\varOmega } {\varLambda } _1,-i \omega _3 {\bar{z}}_3\right) \nonumber \\&\quad + {\textbf{N}}_{3,3}\left( {\bar{z}}_3,{\varLambda } _3,-{\varOmega } ^2 {\varLambda } _1\right) \nonumber \\&\quad +{\textbf{N}}_{3,3}\left( {\varLambda } _3,{\bar{z}}_3,-{\varOmega } ^2 {\varLambda } _1\right) \Big ] +QOT \end{aligned}$$

(79)

$$\begin{aligned} d_{15}&=-\frac{1}{2\omega _2}{\textbf{z}}_2^T\Big [{\textbf{N}}_{3,1}\left( z_1,{\bar{z}}_1,z_2\right) +{\textbf{N}}_{3,1}\left( {\bar{z}}_1,z_1,z_2\right) \nonumber \\&\quad + {\textbf{N}}_{3,2}\left( z_2,i \omega _1 z_1,-i \omega _1 {\bar{z}}_1\right) \nonumber \\&\quad +{\textbf{N}}_{3,2}\left( z_2,-i \omega _1 {\bar{z}}_1,i \omega _1 z_1\right) \Big ]+QOT\nonumber \\ d_{16}&=-\frac{1}{2\omega _2}{\textbf{z}}_2^T\Big [ {\textbf{N}}_{3,1}\left( z_1,{\bar{z}}_1,{\varLambda } _3\right) +{\textbf{N}}_{3,1}\left( {\bar{z}}_1,z_1,{\varLambda } _3\right) \nonumber \\&\quad +{\textbf{N}}_{3,2}\left( {\varLambda } _3,i \omega _1 z_1,-i \omega _1 {\bar{z}}_1\right) \nonumber \\&\quad +{\textbf{N}}_{3,2}\left( {\varLambda } _3,-i \omega _1 {\bar{z}}_1,i \omega _1 z_1\right) \Big ]+QOT \nonumber \\ d_{17}&=-\frac{1}{2\omega _2}{\textbf{z}}_2^T\Big [ {\textbf{N}}_{3,1}\left( z_1,\bar{{\varLambda } }_1,z_3\right) +{\textbf{N}}_{3,1}\left( \bar{{\varLambda } }_1,z_1,z_3\right) \nonumber \\&\quad + {\textbf{N}}_{3,2}\left( z_3,i \omega _1 z_1,i {\varOmega } \bar{{\varLambda } }_1\right) \nonumber \\&\quad +{\textbf{N}}_{3,2}\left( z_3,i {\varOmega } {\bar{{\varLambda }}}_1,i \omega _1 z_1\right) \Big ]+QOT\nonumber \\ d_{18}&=-\frac{1}{2\omega _2}{\textbf{z}}_2^T\Big [ {\textbf{N}}_{3,1}\left( z_2,z_2,{\bar{z}}_2\right) +{\textbf{N}}_{3,1}\left( z_2,{\bar{z}}_2,z_2\right) \nonumber \\&\quad +{\textbf{N}}_{3,1}\left( {\bar{z}}_2,z_2,z_2\right) \Big ]+QOT \nonumber \\ d_{19}&=-\frac{1}{2\omega _2}{\textbf{z}}_2^T\Big [ {\textbf{N}}_{3,1}\left( z_2,z_2,\bar{{\varLambda } }_3\right) +{\textbf{N}}_{3,1}\left( z_2,{\bar{{\varLambda }}}_3,z_2\right) \nonumber \\&\quad + {\textbf{N}}_{3,1}\left( {\bar{{\varLambda }}}_3,z_2,z_2\right) \Big ]+QOT \nonumber \\ d_{20}&=-\frac{1}{2\omega _2}{\textbf{z}}_2^T\Big [ {\textbf{N}}_{3,1}\left( z_2,{\bar{z}}_2,{\varLambda } _3\right) \nonumber \\&\quad + {\textbf{N}}_{3,1}\left( {\bar{z}}_2,z_2,{\varLambda } _3\right) \Big ]+QOT \end{aligned}$$

(80)

$$\begin{aligned} d_{21}&=-\frac{1}{2\omega _2}{\textbf{z}}_2^T\Big [ {\textbf{N}}_{3,1}\left( z_2,z_3,{\bar{z}}_3\right) \nonumber \\&\quad +{\textbf{N}}_{3,1}\left( z_2,{\bar{z}}_3,z_3\right) \Big ]+QOT \nonumber \\ d_{22}&=-\frac{1}{2}{\textbf{z}}_2^T\Big [ {\textbf{C}}{\textbf{z}}_2\Big ] \nonumber \\ d_{23}&=-\frac{1}{2\omega _2}{\textbf{z}}_2^T\Big [ {\textbf{N}}_{3,1}\left( {\varLambda } _1,\bar{{\varLambda } }_1,z_2\right) \nonumber \\&\quad +{\textbf{N}}_{3,1}\left( {\bar{{\varLambda }}}_1,{\varLambda } _1,z_2\right) \nonumber \\&\quad + {\textbf{N}}_{3,2}\left( z_2,i {\varOmega } {\varLambda } _1,-i {\varOmega } {\bar{{\varLambda }}}_1\right) \nonumber \\&\quad +{\textbf{N}}_{3,2}\left( z_2,-i {\varOmega } {\bar{{\varLambda }}}_1,i {\varOmega } {\varLambda } _1\right) \Big ]+QOT \nonumber \\ d_{24}&=-\frac{1}{2\omega _2}{\textbf{z}}_2^T {\textbf{N}}_{3,1}\left( {\bar{z}}_2,{\varLambda } _3,{\varLambda } _3\right) \nonumber \\&\quad +QOT \nonumber \\ d_{25}&=-\frac{1}{2\omega _2}{\textbf{z}}_2^T\Big [{\textbf{N}}_{3,1}\left( z_3,{\bar{z}}_3,{\varLambda } _3\right) +{\textbf{N}}_{3,1}\left( z_3,{\varLambda } _3,{\bar{z}}_3\right) \nonumber \\&\quad {\textbf{N}}_{3,1}\left( {\bar{z}}_3,z_3,{\varLambda } _3\right) +{\textbf{N}}_{3,1}\left( {\bar{z}}_3,{\varLambda } _3,z_3\right) \nonumber \\&\quad + {\textbf{N}}_{3,1}\left( {\varLambda } _3,z_3,{\bar{z}}_3\right) +{\textbf{N}}_{3,1}\left( {\varLambda } _3,{\bar{z}}_3,z_3\right) \Big ]\nonumber \\&\quad +QOT \end{aligned}$$

(81)

$$\begin{aligned} d_{26}&=-\frac{1}{2\omega _2}{\textbf{z}}_2^T\Big [{\textbf{N}}_{3,1}\left( {\varLambda } _1,{\varLambda } _1,{\bar{{\varLambda }}}_3\right) \nonumber \\&\quad +{\textbf{N}}_{3,1}\left( {\varLambda } _1,{\bar{{\varLambda }}}_1,{\bar{{\varLambda }}}_3\right) \nonumber \\&\quad + {\textbf{N}}_{3,1}\left( {\bar{{\varLambda }}}_1,{\varLambda } _1,\bar{{\varLambda } }_3\right) +{\textbf{N}}_{3,1}\left( {\varLambda } _3,{\varLambda } _3,\bar{{\varLambda } }_3\right) \nonumber \\&\quad + {\textbf{N}}_{3,1}\left( {\varLambda } _3,{\bar{{\varLambda }}}_3,{\varLambda } _3\right) +{\textbf{N}}_{3,1}\left( {\bar{{\varLambda }}}_3,{\varLambda } _3,{\varLambda } _3\right) \nonumber \\&\quad + {\textbf{N}}_{3,2}\left( {\bar{{\varLambda }}}_3,i {\varOmega } {\varLambda } _1,i {\varOmega } {\varLambda } _1\right) \nonumber \\&\quad +{\textbf{N}}_{3,2}\left( {\bar{{\varLambda }}}_3,i {\varOmega } {\varLambda } _1,-i {\varOmega } {\bar{{\varLambda }}}_1\right) \nonumber \\&\quad + {\textbf{N}}_{3,2}\left( {\bar{{\varLambda }}}_3,-i {\varOmega } {\bar{{\varLambda }}}_1,i {\varOmega } {\varLambda } _1\right) \Big ]+QOT\nonumber \\ d_{27}&=-\frac{1}{2\omega _2}{\textbf{z}}_2^T\Big [ -\frac{c_{f,2}}{2}{\textbf{z}}_2\Big ] +QOT \end{aligned}$$

(82)

$$\begin{aligned} d_{28}&=-\frac{1}{2\omega _3}{\textbf{z}}_3^T\Big [ {\textbf{N}}_{3,1}\left( z_1,{\bar{z}}_1,z_3\right) \nonumber \\&\quad +{\textbf{N}}_{3,1}\left( {\bar{z}}_1,z_1,z_3\right) + {\textbf{N}}_{3,2}\left( z_3,i \omega _1 z_1,-i \omega _1 {\bar{z}}_1\right) \nonumber \\&\quad +{\textbf{N}}_{3,2}\left( z_3,-i \omega _1 {\bar{z}}_1,i \omega _1 z_1\right) \Big ]+QOT \nonumber \\ d_{29}&=-\frac{1}{2\omega _3}{\textbf{z}}_3^T\Big [{\textbf{N}}_{3,1}\left( {\bar{z}}_1,{\varLambda } _1,z_2\right) +{\textbf{N}}_{3,1}\left( {\varLambda } _1,{\bar{z}}_1,z_2\right) \nonumber \\&\quad + {\textbf{N}}_{3,2}\left( z_2,-i \omega _1 {\bar{z}}_1,i {\varOmega } {\varLambda } _1\right) \nonumber \\&\quad +{\textbf{N}}_{3,2}\left( z_2,i {\varOmega } {\varLambda } _1,-i \omega _1 {\bar{z}}_1\right) \Big ]+QOT \nonumber \\ d_{30}&=-\frac{1}{2\omega _3}{\textbf{z}}_3^T\Big [ {\textbf{N}}_{3,1}\left( {\bar{z}}_1,{\varLambda } _1,{\varLambda } _3\right) \nonumber \\&\quad +{\textbf{N}}_{3,1}\left( {\varLambda } _1,{\bar{z}}_1,{\varLambda } _3\right) \nonumber \\&\quad + {\textbf{N}}_{3,2}\left( {\varLambda } _3,-i \omega _1 {\bar{z}}_1,i {\varOmega } {\varLambda } _1\right) \nonumber \\&\quad +{\textbf{N}}_{3,2}\left( {\varLambda } _3,i {\varOmega } {\varLambda } _1,-i \omega _1 {\bar{z}}_1\right) \Big ]+QOT \nonumber \\ d_{31}&=-\frac{1}{2\omega _3}{\textbf{z}}_3^T\Big [{\textbf{N}}_{3,1}\left( z_2,{\bar{z}}_2,z_3\right) +{\textbf{N}}_{3,1}\left( {\bar{z}}_2,z_2,z_3\right) \Big ]\nonumber \\&\quad +QOT \nonumber \\ d_{32}&=-\frac{1}{2\omega _3}{\textbf{z}}_3^T\Big [ {\textbf{N}}_{3,1}\left( z_2,z_3,\bar{{\varLambda } }_3\right) \nonumber \\&\quad +{\textbf{N}}_{3,1}\left( z_2,\bar{{\varLambda } }_3,z_3\right) \Big ]+QOT \nonumber \\ d_{33}&=-\frac{1}{2\omega _3}{\textbf{z}}_3^T\Big [ {\textbf{N}}_{3,1}\left( {\bar{z}}_2,z_3,{\varLambda } _3\right) \nonumber \\&\quad +{\textbf{N}}_{3,1}\left( {\bar{z}}_2,{\varLambda } _3,z_3\right) \Big ]+QOT \nonumber \\ d_{34}&=-\frac{1}{2\omega _3}{\textbf{z}}_3^T\Big [ {\textbf{N}}_{3,1}\left( z_3,z_3,{\bar{z}}_3\right) +{\textbf{N}}_{3,1}\left( z_3,{\bar{z}}_3,z_3\right) \nonumber \\&\quad + {\textbf{N}}_{3,1}\left( {\bar{z}}_3,z_3,z_3\right) \Big ]+QOT \nonumber \\ d_{35}&=-\frac{1}{2}{\textbf{z}}_3^T\Big [{\textbf{C}}{\textbf{z}}_ 3\Big ] \nonumber \\ d_{36}&=-\frac{1}{2\omega _3}{\textbf{z}}_3^T\Big [{\textbf{N}}_{3,1}\left( {\varLambda } _1,{\bar{{\varLambda }}}_1,z_3\right) \nonumber \\&\quad +{\textbf{N}}_{3,1}\left( \bar{{\varLambda } }_1,{\varLambda } _1,z_3\right) \nonumber \\&\quad +{\textbf{N}}_{3,1}\left( z_3,{\varLambda } _3,\bar{{\varLambda } }_3\right) +{\textbf{N}}_{3,1}\left( z_3,{\bar{{\varLambda }}}_3,{\varLambda } _3\right) \nonumber \\&\quad + {\textbf{N}}_{3,1}\left( {\varLambda } _3,z_3,\bar{{\varLambda } }_3\right) +{\textbf{N}}_{3,1}\left( {\varLambda } _3,\bar{{\varLambda } }_3,z_3\right) \nonumber \\&\quad + {\textbf{N}}_{3,1}\left( {\bar{{\varLambda }}}_3,z_3,{\varLambda } _3\right) +{\textbf{N}}_{3,1}\left( {\bar{{\varLambda }}}_3,{\varLambda } _3,z_3\right) \Big ]\nonumber \\&\quad +QOT \end{aligned}$$

(83)

being QOT the nonlinear terms deriving from the quadratic-order operators, when combining the linear solution with the second-order solution (see Eq. (33)); they are not reported here for sake of brevity.

Terms of the particular solution

The column vectors appearing in the particular solution at the second order (Eq. (41)) for the case 1 assume the following expressions:

$$\begin{aligned} \begin{aligned} {\textbf{w}}_1&=\frac{1}{4\omega _1^2}\left[ {\textbf{N}}_{2,1}\left( {\bar{z}}_1,z_2\right) +{\textbf{N}}_{2,2}\left( -i \omega _1 {\bar{z}}_1,i \omega _2 z_2\right) \right. \\&\left. \quad +\, {\textbf{N}}_{2,3}\left( z_2,-\omega _1^2 {\bar{z}}_1\right) \right] \\ {\textbf{w}}_2&=\frac{1}{4\omega _1^2}\left[ {\textbf{N}}_{2,1}\left( {\bar{z}}_1,{\varLambda } _3\right) +{\textbf{N}}_{2,2}\left( -i \omega _1 {\bar{z}}_1,i {\varOmega } {\varLambda } _3\right) \right. \\&\left. \quad +\, {\textbf{N}}_{2,3}\left( {\varLambda } _3,-\omega _1^2 {\bar{z}}_1\right) \right] \\ {\textbf{w}}_3&=\frac{1}{4\omega _1^2}\left[ {\textbf{N}}_{2,1}\left( \bar{{\varLambda } }_1,z_3\right) +{\textbf{N}}_{2,2}\left( -i {\varOmega } {\bar{{\varLambda }}}_1,i \omega _3 z_3\right) \right. \\&\left. \quad +\, {\textbf{N}}_{2,3}\left( z_3,-{\varOmega } ^2 {\bar{{\varLambda }}}_1\right) \right] \\ {\textbf{w}}_4&=\frac{1}{4\omega _2^2}\left[ {\textbf{N}}_{2,1}\left( z_1,z_1\right) +{\textbf{N}}_{2,2}\left( i \omega _1 z_1,i \omega _1 z_1\right) \right. \\&\left. \quad +\,{\textbf{N}}_{2,3}\left( z_1,-\omega _1^2 z_1\right) \right] \\ {\textbf{w}}_5&=\frac{1}{4\omega _2^2}\left[ {\textbf{N}}_{2,1}\left( {\bar{z}}_1,{\varLambda } _3\right) +{\textbf{N}}_{2,2}\left( -i \omega _1 {\bar{z}}_1,i {\varOmega } {\varLambda } _3\right) \right. \\&\left. \quad +\, {\textbf{N}}_{2,3}\left( {\varLambda } _3,-\omega _1^2 {\bar{z}}_1\right) \right] . \end{aligned}\nonumber \\ \end{aligned}$$

(84)

Numerical values of the coefficients of the AME

1.1 Case 1

The numerical values of the coefficients appearing in the amplitude modulation equation for case 1 (Eq. (47)) are given as follows, with reference to the case study of Sect. 5.1:

$$\begin{aligned} \begin{aligned}&d_{1}=-46.310,{} & {} d_{2}=0.054,{} & {} d_{3}=0.219,\\&d_{4}=-11.575,{} & {} d_{5}=0.079,{} & {} d_{6}=-153.600,\\&d_{7}=62.955,{} & {} d_{8}=-0.076,{} & {} d_{9}=-0.076,\\&d_{10}=911.067,{} & {} d_{11}=54.290,{} & {} d_{12}=-0.0006,\\&d_{13}=-0.285,{} & {} d_{14}=0.0003,{} & {} d_{15}=33.054,\\&d_{16}=-0.040,{} & {} d_{17}=-0.150,{} & {} d_{18}=138.980,\\&d_{19}=0.119,{} & {} d_{20}=0.238,{} & {} d_{21}=1867.850,\\&d_{22}=108.610,{} & {} d_{23}=0.0002,{} & {} d_{24}=0.0002,\\&d_{25}=2.053,{} & {} d_{26}=2.037\times 10^{-7},{} & {} d_{27}=0.035,\\&d_{28}=303.689,{} & {} d_{29}=-0.096,{} & {} d_{30}=0.0001,\\&d_{31}=1245.230,{} & {} d_{32}=1.369,{} & {} d_{33}=1.369,\\&d_{34}=5608.680,{} & {} d_{35}=150.160,{} & {} d_{36}=0.002. \end{aligned}\nonumber \\ \end{aligned}$$

(85)

1.2 Case 2

The numerical values of the coefficients appearing in the amplitude modulation equation for case 2 (Eq. (56)) are given as follows, with reference to the case study of Sect. 5.2:

$$\begin{aligned} \begin{aligned}&d_1=-123.535,{} & {} d_2=53.770,{} & {} d_3=730.977,\\&d_4=0.546,{} & {} d_5=0.546,{} & {} d_6=-0.0004,\\&d_7=-46.849,{} & {} d_8=0.376,{} & {} d_9=-38.139,\\&d_{10}=-0.105,{} & {} d_{11}=0.050,{} & {} d_{12}=-8.447,\\&d_{13}=27.977,{} & {} d_{14}=-0.101,{} & {} d_{15}=0.019,\\&d_{16}=111.205,{} & {} d_{17}=1506.890,{} & {} d_{18}=-1.015,\\&d_{19}=-1.0153,{} & {} d_{20}=0.0008,{} & {} d_{21}=-108.246,\\&d_{22}=243.659,{} & {} d_{23}=0.182,{} & {} d_{24}=1004.590,\\&d_{25}=-0.677,{} & {} d_{26}=4563.160,{} & {} d_{27}=-2.947,\\&d_{28}=-5.894,{} & {} d_{29}=0.004,{} & {} d_{30}=-140.550,\\&d_{31}=0.002,{} & {} d_{32}=-1.6848\times 10^{-6},{} & {} d_{33}=0.0003. \end{aligned}\nonumber \\ \end{aligned}$$

(86)