Control of vibration nonlinearity and quality factor for a carbon nanotube mass sensor

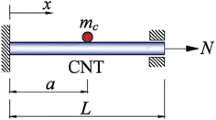
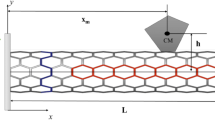
Abstract

Carbon nanotube (CNT) resonant sensors are small in size and have high sensitivity. However, the CNT resonators are susceptible to nonlinear effect. The existing methods to avoid the nonlinearity would decrease the quality factor of the resonator. Here, a novel method for reducing nonlinear effect and increasing quality factor for a CNT resonant mass sensor is proposed. Based on the circuit model and mechanics model of the CNT resonant mass sensor with two feedback loops, the nonlinear vibration equation of the CNT resonant mass sensor is deduced which includes the non-local effect and the feedback control effects. Using this equation, the amplitude–frequency characteristics of the CNT and its variation with size parameters and feedback gain are studied. A method of simulating the nonlinear effect and quality factor of the sensor through the VAR module of ADS is proposed, which provides a reference for simulating nonlinear effect of field effect transistor sensors by using computer-aided design tools. Results show that by tuning feedback gain, the nonlinear effect of the CNT resonant mass sensor could be reduced and its quality factor could be increased. Using the feedback control strategy provided in this paper, the CNT sensor can be in a linear vibration state with high quality factor in a low-vacuum environment by only adjusting the feedback modulation gain, avoiding the expensive and complex ultra-low-temperature system.

Appendices

Appendix 1

The static displacement and modal function of the CNT vibration are solved as follows:

The CNT has an initial deformation under the action of bias voltage and molecular force [4], and the forced vibration occurs on this basis. The average displacement of the CNT under static deformation is:

$$ \overline{{w_{0} }} = \frac{{16L^{4} {\text{BV}}_{g} }}{{\pi^{6} {\text{EIR}}}} $$

(27)

When a concentrated mass (adsorbed particles) is attached to an arbitrary position (x = d) at the CNT, the CNT resonator can be considered to consist of two parts (w₁ (0 ≤ x ≤ d) and w₂ (d ≤ x ≤ L)). The mode function can be given by:

$$ \phi (x) = \left\{ {\begin{array}{*{20}c} {\phi_{1} (x) = C_{1} {\text{ch}}\uplambda _{2} x + C_{2} {\text{sh}}\uplambda _{2} x + C_{3} \cos\uplambda _{1} x + C_{4} \sin\uplambda _{1} x} \\ {\phi_{2} (x) = C_{5} {\text{ch}}\uplambda _{2} x + C_{6} {\text{sh}}\uplambda _{2} x + C_{7} \cos\uplambda _{1} x + C_{8} \sin\uplambda _{1} x} \\ \end{array} } \right.\begin{array}{*{20}c} {(0 \le x \le d)} \\ {(d \le x \le L)} \\ \end{array} $$

(28)

where the constants C₁, C₂, C₃, C₄, C₅, C₆, C₇, and C₈ are determined by boundary conditions and continuity conditions [4, 23].

The CNT is fixed at both ends. The boundary conditions are:

$$ \left\{ \begin{gathered} \phi_{1} (0) = \phi_{2} (L) = 0 \hfill \\ \phi_{1}^{\prime } (0) = \phi_{2}^{\prime } (L) = 0 \hfill \\ \end{gathered} \right. $$

(29)

When the mass and position of the adsorbed particles are given, the continuity conditions are:

$$ \left\{ \begin{gathered} \phi_{1} (d) = \phi_{2} (d) \hfill \\ \begin{array}{*{20}l} {\phi_{1}^{\prime } (d) = \phi_{2}^{\prime } (d)} \hfill \\ {\begin{array}{*{20}l} {\phi_{1}^{\prime \prime } (d) = \phi_{2}^{\prime \prime } (d)} \hfill \\ {EI\left. {\frac{{\partial^{3}\Delta w_{1} \left( {x,t} \right)}}{{\partial x^{3} }}} \right|_{x = d} - EI\left. {\frac{{\partial^{3}\Delta w_{2} \left( {x,t} \right)}}{{\partial x^{3} }}} \right|_{x = d} = m\frac{{\partial^{2}\Delta w_{1} \left( {d,t} \right)}}{{\partial t^{2} }}} \hfill \\ \end{array} } \hfill \\ \end{array} \hfill \\ \end{gathered} \right. $$

(30)

Substituting these conditions into Eq. (28) yields:

$$ \left[ G \right]\left[ C \right] = \left[ 0 \right] $$

(31)

where

$$\left[G\right]=\left[\begin{array}{cccccccc}1& 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& {a}_{9}& {a}_{8}& {a}_{6}& {a}_{7}\\ 0& {\lambda }_{2}& 0& {\lambda }_{1}& 0& 0& 0& 0\\ 0& 0& 0& 0& {\lambda }_{2}{a}_{8}& {\lambda }_{2}{a}_{9}& -{\lambda }_{1}{a}_{7}& {\lambda }_{1}{a}_{6}\\ {a}_{4}& {a}_{5}& {a}_{3}& {a}_{1}& -{a}_{4}& - {a}_{5}& -{a}_{3}& -{a}_{1}\\ {\lambda }_{2}{a}_{5}& {\lambda }_{2}{a}_{4}& -{\lambda }_{1}{a}_{1}& {\lambda }_{1}{a}_{3}& -{\lambda }_{2}{a}_{5}& -{\lambda }_{2}{a}_{4}& {\lambda }_{1}{a}_{1}& -{\lambda }_{1}{a}_{3}\\ {{\lambda }_{2}}^{2}{a}_{4}& {{\lambda }_{2}}^{2}{a}_{5}& -{{\lambda }_{1}}^{2}{a}_{3}& -{{\lambda }_{1}}^{2}{a}_{1}& -{{\lambda }_{2}}^{2}{a}_{4}& -{{\lambda }_{2}}^{2}{a}_{5}& {{\lambda }_{1}}^{2}{a}_{3}& {{\lambda }_{1}}^{2}{a}_{1}\\ \begin{array}{c}{{\lambda }_{2}}^{3}{a}_{5}\\ +{a}_{10}{a}_{4}\end{array}& \begin{array}{c}{{\lambda }_{2}}^{3}{a}_{4}\\ +{a}_{10}{a}_{5}\end{array}& \begin{array}{c}{{\lambda }_{1}}^{3}{a}_{1}\\ +{a}_{10}{a}_{3}\end{array}& \begin{array}{c}-{{\lambda }_{1}}^{3}{a}_{3}\\ +{a}_{10}{a}_{1}\end{array}& -{{\lambda }_{2}}^{3}{a}_{5}& -{{\lambda }_{2}}^{3}{a}_{4}& -{{\lambda }_{1}}^{3}{a}_{1}& {{\lambda }_{1}}^{3}{a}_{3}\end{array}\right]$$

(32)

$$\left[C\right]={\left[\begin{array}{cccccccc}{C}_{1}& {C}_{2}& {C}_{3}& {C}_{4}& {C}_{5}& {C}_{6}& {C}_{7}& {C}_{8}\end{array}\right]}^{T}$$

where ${a}_{1}=\mathrm{sin}{\lambda }_{1}d , {a}_{2}=\mathrm{sin}{\lambda }_{2}d , {a}_{3}=\mathrm{cos}{\lambda }_{1}d , {a}_{4}=\mathrm{ch}{\lambda }_{2}d, {a}_{5}=\mathrm{sh}{\lambda }_{2}d ,{a}_{6}=\mathrm{cos}{\lambda }_{1}L , {a}_{7}=\mathrm{sin}{\lambda }_{1}L , {a}_{8}=\mathrm{sh}{\lambda }_{2}L ,{a}_{9}=\mathrm{ch}{\lambda }_{2}L ,{a}_{10}=m{\left(2\pi f\right)}^{2} /EI$

$$ \left\{ {\begin{array}{*{20}c} {\lambda_{1} = \sqrt {\sqrt {\alpha^{4} /4 + \beta^{4} } - \alpha^{2} /2} } \\ {\lambda_{2} = \sqrt {\sqrt {\alpha^{4} /4 + \beta^{4} } + \alpha^{2} /2} } \\ {\upalpha ^{2} = \frac{N}{{{\text{EI}}}} - \frac{\rho A}{{{\text{EI}}}}\left( {e_{0} a} \right)^{2} \left( {2\pi f} \right)^{2} } \\ {\beta^{4} = \left( {2\pi f} \right)^{2} \frac{\rho A}{{{\text{EI}}}} + \frac{1}{{{\text{EI}}}}\frac{{H_{v} \sqrt {2r} }}{{8(h - \overline{{w_{0} }} - r)^{3} }}} \\ \end{array} } \right. $$

(33)

Equation (31) has a nonzero solution if and only if the coefficient determinant equals zero, that is:

$$\left|G\right|=0$$

(34)

Using Eq. (34), the natural frequencies of the carbon nanotube resonator can be obtained. Substituting the natural frequencies into Eq. (31), constants C₁, C₂, C₃, C₄, C₅, C₆, C₇, and C₈ can be determined. Substituting them into Eq. (28), the mode function can be given.

Appendix 2

ADS is a special software for microwave RF circuit and system design developed by Aglient, with powerful circuit simulation function. The nonlinear capacitance C_s in the equivalent circuit changes with the excitation frequency, so the S1P_Eqn to S6P_Eqn module for S-parameter simulation is used to simulate it. For single-port- or multi-port-based components, the S1P_Eqn to S6P_Eqn blocks can be used to simulate frequency-dependent impedance components such as resistors, capacitors, and inductors. It has up to six ports, and the impedance between each port and each port can be defined. The S1P_Eqn single port has ± two interfaces, and the + interface is often used as an input terminal. S1P_Eqn defines the impedance element through the equivalent impedance, which can realize the definition of a single impedance element or a composite element after combining several impedance elements. To define a component with impedance a + b j, simply make S[X,Y] = a + b j or S[X,Y] = (a,b). The capacitive reactance introduced by the nonlinear capacitor C_s in this study is:

$$ Z_{{\text{s}}} = \frac{1}{{2\pi fC_{{\text{s}}} {\text{j}}}} $$

(35)

Let S[1, 1] = Z_s in the S1P_Eqn module, as shown in Fig. 

Fig. 13

Z_s is defined in the S1P_Eqn module

13. The VAR module is used to define Z_s and establish the relationship between Z_s and signal frequency.

In the forced vibration amplitude–frequency relationship formula (13), the relationship between the amplitude z and f can be expressed as an explicit function:

$$ z\left( f \right) = \frac{{\varepsilon A_{4} }}{{2f_{0}^{2} \sqrt {\left( {\frac{{f - f_{0} }}{{f_{0} }} + \frac{{3\varepsilon A_{3} }}{{8mf_{0}^{2} }}} \right)^{2} + \left( \frac{1}{2Q} \right)^{2} } }} $$

(36)

The functional relationship between Z_s and f is transformed into the language in ADS, as shown in Fig. 10 and Fig. 13, thus completing the establishment of the nonlinear capacitance C_s that varies with the signal frequency f. After the S-parameter simulation, the relationship between the S21 parameter of the sensor and the excitation frequency f can be obtained.

Appendix 3

In order to prove that the latter terms can be ignored in the Taylor expansion formula of electrostatic force (Eq. (6)) in this paper, the following proofs are made:

The electrostatic force can be expressed as:

$$ f_{K} = - \left( {f_{K1}\Delta w^{3} + f_{K2}\Delta w^{4} + f_{K3}\Delta w^{5} + ...} \right) $$

(37)

where $f_{K1} { = }\frac{{ - \varepsilon \varepsilon_{0} \varepsilon_{r} r\left( {{\text{KV}}_{K} /h} \right)^{2} }}{{h^{2} \overline{{w_{0} }} }}$,$f_{K2} { = }\frac{{ - 3\varepsilon \varepsilon_{0} \varepsilon_{r} r\left( {{\text{KV}}_{K} /h} \right)^{2} }}{{2h^{3} \overline{{w_{0} }} }}$, and $f_{K3} { = }\frac{{ - 2\varepsilon \varepsilon_{0} \varepsilon_{r} r\left( {{\text{KV}}_{K} /h} \right)^{2} }}{{h^{4} \overline{{w_{0} }} }}$.

In order to calculate f_K, the dimensions and control parameters of the CNT need to be acquired. As shown in Table

Table 4 Size and control parameters of the CNT required to calculate the f_K

4, according to the conclusions drawn in Fig. 3, a certain size and control parameters when the vibration can achieve stable hysteresis are selected.

Taking $\overline{{\Delta w}}$ as the average amplitude in the vibration process of the CNT, then under the parameters shown in Table 4, $\overline{{\Delta w}} { = 5}\;{\text{nm}}$.

After calculation, $f_{K1}\Delta w^{3} { = }$ 1.82 × 10^–12 N, $f_{K2}\Delta w^{4} { = }$ 1.92 × 10^–13 N, $f_{K3}\Delta w^{5} { = }$ 1.72 × 10^–14 N can be obtained. If only the first term of the expansion is considered when using Eq. (7), the calculation error of f_K is about 9.5%, and the resulting analysis error of K is about 3.0%. According to Fig. 4, it can be obtained that when the K fluctuates by 3.0%, the influence on the analysis of the nonlinear state is negligible. Therefore, when using this model to analyze the nonlinear control parameters, it is sufficient to only consider the first term in the expansion of the electrostatic force exerted by the top plate on the CNT.