Geometrical nonlinearities in a curved cantilever beam: a condensation model and inertia-induced nonlinear features

Abstract

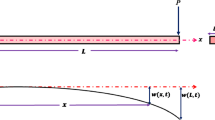
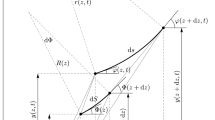
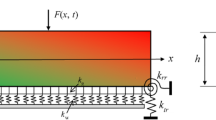
Subjected to high level forcing, flexible and curved beams exhibit pronounced geometrical nonlinearities. In particular, intrinsic nonlinearities of cantilevers are different from their counterparts with end-constrained boundaries and the combination of the enhanced nonlinear-inertia effects with initial curvature creates harsh demand on the modeling, numerical simulation and understanding of associated physical phenomena. This paper investigates the salient nonlinear features in a curved cantilever beam, with particular attention paid to the inertia-induced effects through both linear and nonlinear analyses. An inextensible condensation model, with the consideration of the initial curvature, is proposed based on a geometrically exact model for an Euler–Bernoulli cantilever beam. The free boundary of the cantilever gives rise to more significant longitudinal motion, which increases the inertia effects in the beam vibration which is in turn enhanced by the initial curvature. Specific techniques are proposed to numerically implement the developed model with increased accuracy and robustness. Numerical simulations are then conducted to validate the proposed model through comparisons with the finite element method, examine the assumptions underpinning the model and explore the salient physical features, in particular the inertia-induced effects in both linear and nonlinear cases. Results show a decrease in the natural frequencies due to the initial curvature effect, a transition of the first mode from hardening to softening caused by enhanced curvature-induced inertia effect, and a pronounced asymmetry of the higher order modes with respect to frequencies.

Appendices

Appendix 1

The generalized-α method

The generalized-α method is applied to offer intuitive time history of the system responses. In the main text, Eq. (19) requires the treatment of different system response terms, especially displacement x, as well as its derivatives representing velocity ${\dot{\mathbf{x}}}$ and acceleration ${\ddot{\mathbf{x}}}$. The interrelation among them can be cast into the following general form [54]:

$$ \begin{gathered} {\dot{\mathbf{x}}}_{i + 1} = {\dot{\mathbf{x}}}_{i} + \left( {1 - \gamma } \right)\Delta t{\ddot{\mathbf{x}}}_{i} + \gamma \Delta t{\ddot{\mathbf{x}}}_{i + 1} \hfill \\ {\mathbf{x}}_{i + 1} = {\mathbf{x}}_{i} + \Delta t{\dot{\mathbf{x}}}_{i} + \Delta t^{2} \left( {\frac{1}{2} - \beta } \right){\ddot{\mathbf{x}}}_{i} + \Delta t^{2} \beta {\ddot{\mathbf{x}}}_{i + 1} \hfill \\ \end{gathered} $$

(46)

The governing equation of motion, Eq. (19), is built on semi-point scheme in the time discretization. The semi-point values of these quantities write

$$ \begin{gathered} {\mathbf{x}}_{{i + 1 - \alpha_{f} }} = \left( {1 - \alpha_{f} } \right){\mathbf{x}}_{i + 1} + \alpha_{f} {\mathbf{x}}_{i} \hfill \\ {\dot{\mathbf{x}}}_{{i + 1 - \alpha_{f} }} = \left( {1 - \alpha_{f} } \right){\dot{\mathbf{x}}}_{i + 1} + \alpha_{f} {\dot{\mathbf{x}}}_{i} \hfill \\ {\ddot{\mathbf{x}}}_{{i + 1 - \alpha_{m} }} = \left( {1 - \alpha_{m} } \right){\ddot{\mathbf{x}}}_{i + 1} + \alpha_{m} {\ddot{\mathbf{x}}}_{i} \hfill \\ t_{{i + 1 - \alpha_{f} }} = \left( {1 - \alpha_{f} } \right)t_{i + 1} + \alpha_{f} t_{i} \hfill \\ \end{gathered} $$

(47)

A residual vector is formulated from Eq. (19) as

$$ {\mathbf{r}}\left( {\mathbf{x}} \right) = {\mathbf{M}}\ddot{\mathbf{x}} + {C\dot{\mathbf{x}}} + {\mathbf{Kx}} + {\mathbf{f}}_{nl} \left( {{\mathbf{x}},{\dot{\mathbf{x}}},{\ddot{\mathbf{x}}}} \right) - {\mathbf{f}}_{ext} = {\mathbf{0}} $$

(48)

Discretized version of the above equation in terms of $({\mathbf{x}}_{{i + 1 - \alpha_{f} }} ,{\dot{\mathbf{x}}}_{{i + 1 - \alpha_{f} }} ,{\ddot{\mathbf{x}}}_{{i + 1 - \alpha_{m} }} )$ writes

$$ {\mathbf{r}}\left( {{\mathbf{x}}_{{i + 1 - \alpha_{f} }} ,{\dot{\mathbf{x}}}_{{i + 1 - \alpha_{f} }} ,{\ddot{\mathbf{x}}}_{{i + 1 - \alpha_{m} }} } \right) = {\mathbf{0}} $$

(49)

Let us denote $({\mathbf{x}}_{{i + 1 - \alpha_{f} }}^{k} ,{\dot{\mathbf{x}}}_{{i + 1 - \alpha_{f} }}^{k} ,{\ddot{\mathbf{x}}}_{{i + 1 - \alpha_{m} }}^{k} )$ as the approximate value of $({\mathbf{x}}_{{i + 1 - \alpha_{f} }} ,{\dot{\mathbf{x}}}_{{i + 1 - \alpha_{f} }} ,{\ddot{\mathbf{x}}}_{{i + 1 - \alpha_{m} }} )$ resulting from the iteration k. In the vicinity of the prediction value, the residual equation can be replaced with sufficient accuracy through the following linear expression:

$$ {\mathbf{r}}^{k + 1} \approx {\mathbf{r}}^{k} + {\mathbf{S}}^{k} \Delta {\mathbf{x}}_{{i + 1 - \alpha_{f} }}^{k} = {\mathbf{r}}^{k} + {\mathbf{S}}_{T}^{k} \Delta {\mathbf{x}}_{i + 1}^{k} = {\mathbf{0}} $$

(50)

in which the Jacobian (also called iteration) matrix writes:

$$ {\mathbf{S}}_{T}^{k} = \left( {1 - \alpha_{f} } \right)\left. {\frac{{\partial {\mathbf{r}}}}{{\partial {\mathbf{x}}}}} \right|_{{{\mathbf{x}}_{{i + 1 - \alpha_{f} }}^{k} }} $$

(51)

whose expression is detailed as

$$ {\mathbf{S}}_{T} \left( {\mathbf{x}} \right) = \left( {1 - \alpha_{f} } \right)\left( {{\mathbf{M}}\frac{{\partial {\ddot{\mathbf{x}}}}}{{\partial {\mathbf{x}}}} + {\mathbf{C}}\frac{{\partial {\dot{\mathbf{x}}}}}{{\partial {\mathbf{x}}}} + {\mathbf{K}} + \frac{{\partial {\mathbf{f}}_{nl} }}{{\partial {\mathbf{x}}}} + \frac{{\partial {\mathbf{f}}_{nl} }}{{\partial {\dot{\mathbf{x}}}}}\frac{{\partial {\dot{\mathbf{x}}}}}{{\partial {\mathbf{x}}}} + \frac{{\partial {\mathbf{f}}_{nl} }}{{\partial {\ddot{\mathbf{x}}}}}\frac{{\partial {\ddot{\mathbf{x}}}}}{{\partial {\mathbf{x}}}}} \right) $$

(52)

The integration relationship, Eq.(46), can be written as

$$ \frac{{\partial {\ddot{\mathbf{x}}}_{{i + 1 - \alpha_{m} }} }}{{\partial {\mathbf{x}}_{{i + 1 - \alpha_{f} }} }} = \frac{{1 - \alpha_{m} }}{{\left( {1 - \alpha_{f} } \right)\beta \Delta t^{2} }}{\mathbf{I}},\quad \frac{{\partial {\dot{\mathbf{x}}}_{{i + 1 - \alpha_{f} }} }}{{\partial {\mathbf{x}}_{{i + 1 - \alpha_{f} }} }} = \frac{\gamma }{\beta \Delta t}{\mathbf{I}} $$

(53)

Combining Eqs. (52) and (53) yields the expression of the iteration matrix as:

$$ \begin{gathered} {\mathbf{S}}_{T} \left( {\mathbf{x}} \right) = \frac{{1 - \alpha_{m} }}{{\beta \Delta t^{2} }}{\mathbf{M}} + \frac{{\gamma \left( {1 - \alpha_{f} } \right)}}{\beta \Delta t}{\mathbf{C}} + \left( {1 - \alpha_{f} } \right){\mathbf{K}} \hfill \\ \quad + \left( {1 - \alpha_{f} } \right)\frac{{\partial {\mathbf{f}}_{nl} }}{{\partial {\mathbf{x}}}} + \frac{{\gamma \left( {1 - \alpha_{f} } \right)}}{\beta \Delta t}\frac{{\partial {\mathbf{f}}_{nl} }}{{\partial {\dot{\mathbf{x}}}}} + \frac{{1 - \alpha_{m} }}{{\beta \Delta t^{2} }}\frac{{\partial {\mathbf{f}}_{nl} }}{{\partial {\ddot{\mathbf{x}}}}} \hfill \\ \end{gathered} $$

(54)

The nonlinear equation (50) is then solved using an iteration scheme using Newton–Raphson method. Substituting Eqs. (46 and 47) into Eq. (50) gives

$$ {\mathbf{S}}_{T}^{k} \Delta {\mathbf{x}}_{i + 1}^{k} = - {\mathbf{r}}^{k} $$

(55)

with

$$ \begin{gathered} {\mathbf{r}}^{k} = \beta \Delta t^{2} {\mathbf{S}}_{L} {\ddot{\mathbf{x}}}_{i + 1}^{k} + {\mathbf{f}}_{nl,i + 1}^{k} - {\mathbf{p}}_{i + 1} \hfill \\ {\mathbf{S}}_{L} = \frac{{1 - \alpha_{m} }}{{\beta \Delta t^{2} }}{\mathbf{M}} + \frac{{\gamma \left( {1 - \alpha_{f} } \right)}}{\beta \Delta t}{\mathbf{C}} + \left( {1 - \alpha_{f} } \right){\mathbf{K}} \hfill \\ {\mathbf{p}}_{i + 1} = \left( {1 - \alpha_{f} } \right){\mathbf{f}}_{ext,i + 1} + \alpha_{f} {\mathbf{f}}_{ext,i} - \left( {{\mathbf{a}}_{1} {\mathbf{x}}_{i} + {\mathbf{a}}_{2} {\dot{\mathbf{x}}}_{i} + {\mathbf{a}}_{3} {\ddot{\mathbf{x}}}_{i} } \right) \hfill \\ {\mathbf{a}}_{1} = {\mathbf{K}} \hfill \\ {\mathbf{a}}_{2} = {\mathbf{C}} + \left( {1 - \alpha_{f} } \right)\Delta t{\mathbf{K}} \hfill \\ {\mathbf{a}}_{3} = \alpha_{m} {\mathbf{M}} + \left( {1 - \alpha_{f} } \right)\left( {1 - \gamma } \right)\Delta t{\mathbf{C}} + \Delta t^{2} \left( {1 - \alpha_{f} } \right)\left( {\frac{1}{2} - \beta } \right){\mathbf{K}} \hfill \\ \end{gathered} $$

(56)

The velocity and acceleration are found from

$$ \Delta {\ddot{\mathbf{x}}}_{i + 1}^{k} = \frac{1}{{\beta \Delta t^{2} }}\Delta {\mathbf{x}}_{i + 1}^{k} ,\quad \Delta {\dot{\mathbf{x}}}_{i + 1}^{k} = \frac{\gamma }{\beta \Delta t}\Delta {\mathbf{x}}_{i + 1}^{k} $$

(57)

When $k = 0$, the initial prediction to initialize the process is ${\ddot{\mathbf{x}}}_{i + 1}^{0} = {\ddot{\mathbf{x}}}_{i}$ as the first-order approximation, which would need more correction steps.

To simplify the process and reduce the computation burden, an alternative prediction formulation with third-order precision, i.e.,${\ddot{\mathbf{x}}}_{i + 1}^{0} = 4{\ddot{\mathbf{x}}}_{i} - 6{\ddot{\mathbf{x}}}_{i - 1} + 4{\ddot{\mathbf{x}}}_{i - 2} - {\ddot{\mathbf{x}}}_{i - 3}$, is proposed by using the four latest points. Stepwise correction continues until $||{\mathbf{r}}({\mathbf{x}}_{i + 1}^{k} )|| \le \varepsilon$, where ε is a predefined tolerance value.

The above calculation scheme is combined with the generalized-α method [54]. The parameters are chosen as follows

$$ \begin{gathered} \alpha_{m} = \frac{{2\rho_{\infty } - 1}}{{\rho_{\infty } + 1}},\quad \alpha_{f} = \frac{{\rho_{\infty } }}{{\rho_{\infty } + 1}},\quad \rho_{\infty } \in \left[ {0,\;1} \right] \hfill \\ \gamma = \frac{1}{2} - \alpha_{m} + \alpha_{f} ,\quad \beta = \frac{1}{4}\left( {1 - \alpha_{m} + \alpha_{f} } \right)^{2} \hfill \\ \end{gathered} $$

(58)

The dissipation parameter $\rho_{\infty }$ is set to 0.8 in the present study.

Appendix 2

Efficiency and robustness enhanced by OS technique

The OS technique discussed in Sect. 3.2 is expected to improve the efficiency and the robustness of the generalized-α method by separating a full complex problem into several sub-problems. To demonstrate this, the generalized-α methods with and without the OS technique are compared using a beam vibration problem.

Examine the straight cantilever beam (used in Sect. 4) excited by a harmonic force at its free end. The excitation force has an amplitude 0.5 N at 3.85 Hz, which is arbitrarily chosen around the first natural frequency of the beam. The computation duration is 70 s, which is long enough to get stable response in the system. The sampling frequency is $f_{s} = 400\;{\text{Hz}}$. Figure 

Fig. 12

a Time responses obtained by the generalized-α method with and without OS technique, b close-up view taken in the stable region for a period. Note the two curves coincide perfectly, so it is difficult to visually differentiate them

12a illustrates the overall time response signals obtained by using the two methods. The two curves coincide completely during the entire time duration, as better shown in the close-up view (Fig. 12b). The residual values (as defined by Eq. (56) in Appendix 1) are calculated for both methods and shown in Fig. 

Fig. 13

a Residual and b minimum iteration in each time point obtained by the generalized-α method with and without OS technique. Note in Figure 13 b, the method using OS needs only one iteration to reach the convergence

13a. It follows that OS technique yields very small residuals, which are smaller than the ones without OS for nearly every single time point, demonstrating the accuracy of the proposed OS technique. Figure 13b shows the minimum iteration number required to achieve converged result with a residual value capped at $10^{ - 6}$. It can be seen that, by embedding the OS technique into the generalized-α method, it takes only one iteration to reach converged result, while more iterations are required without OS technique. This happens even within the stable region. Moreover, it was also noticed that generalized-α method without OS technique may not always yield converged solution for some frequencies, while the one with OS technique always does. The above comparison shows the high efficiency and the robustness of the generalized-α method after embedding the proposed OS technique.