Zeno-free event-triggered fixed-time control of two-time-scale systems by Chang transformation and backstepping design

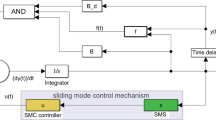
Abstract

This paper investigates fixed-time stabilization of linear two-time-scale systems. The existing fixed-time control techniques are no longer applicable due to the inherent ill-conditioned numerical issues, which is induced by the time-scale separation of two-time-scale systems when carrying out stability analysis. Alternative challenge is that the considered systems are not fully actuated, such that some full rank conditions regarded to the control matrix do not hold anymore. All of these pose difficulties to the fixed-time controller design and stability analysis. To handle these issues, appropriate state transformations are proposed to decouple the system into slow and fast subsystems with approximate strict feedback structure. Then, by the backstepping method, a continuous-time controller is designed to achieve fixed-time stabilization. Furthermore, a Zeno-free event-triggered strategy is proposed to reduce the control updates and then a practical stability result of two-time-scale systems is obtained. A numerical simulation is presented to illustrate the effectiveness of the results.

7 Appendix

1.1 7.1 Technical Lemmas

Lemma 3

[7] For any $x_i\in \mathbb {R}$, $i=1, \ldots , n$, and $\alpha \ge 1$, $0<\beta \le 1$,

$$\begin{aligned} \begin{array}{l} \big (\sum \limits _{i = 1}^n {\left| {{x_i}} \right| }\big )^\alpha \ge \sum \limits _{i = 1}^n {\left| {{x_i}} \right| ^\alpha } \ge n^{1-\alpha }\big (\sum \limits _{i = 1}^n {\left| {{x_i}} \right| }\big )^\alpha ,\\ \big (\sum \limits _{i = 1}^n {\left| {{x_i}} \right| }\big )^\beta \le \sum \limits _{i = 1}^n {\left| {{x_i}} \right| ^\beta } \le n^{1-\beta }\big (\sum \limits _{i = 1}^n {\left| {{x_i}} \right| }\big )^\beta . \end{array} \end{aligned}$$

Lemma 4

[25] For any $x\in \mathbb {R}$, $y\in \mathbb {R}$ and $a>0$, $b>0$,

$$\begin{aligned} \left| x^ay^b \right|\le & {} \varsigma (x,y)\left| x \right| ^{a+b}+\frac{b}{a+b}\\{} & {} \times \Big (\frac{a}{(a+b)\varsigma (x,y)}\Big )^{\frac{a}{b}}\left| y \right| ^{a+b}, \end{aligned}$$

where $\varsigma (x,y)>0$.

Lemma 5

For any $e=(e_1,e_2,\ldots ,e_n)$, $x=(x_1,x_2, \ldots ,x_n)$, where $e_i, x_i \in \mathbb {R}$, $i=1,\ldots ,n$;

$$\begin{aligned}&sig (x^T)^{\alpha _1}{} sig (x\!+\!e)^\beta \\&\quad \ge (1-2^{1-\beta }\varsigma )sig (x^T)^{\alpha _1}{} sig (x)^\beta \\&\qquad -\!\frac{2^{1-\beta }\beta \alpha _1^{\frac{\alpha _1}{\beta }}}{(\alpha _1\!+\!\beta )^{\frac{\alpha _1}{\beta }+1}{\varsigma }^{\frac{\alpha _1}{\beta }}}{} sig (e^T)^{\alpha _1}{} sig (e)^\beta ,\\&sig (x^T)^{\alpha _1}{} sig (x\!+\!e)^\alpha \\&\quad \ge (2^{1-\alpha }-\varsigma )sig (x^T)^{\alpha _1}{} sig (x)^\alpha \\&\qquad -\!\frac{\alpha \alpha _1^{\frac{\alpha _1}{\alpha }}}{(\alpha _1\!+\!\alpha )^{\frac{\alpha _1}{\alpha }+1}{\varsigma }^{\frac{\alpha _1}{\alpha }}}{} sig (e^T)^{\alpha _1}{} sig (e)^\alpha , \end{aligned}$$

where $0<\beta \le 1$, $\alpha \ge 1$, $\alpha _1>0$, $\varsigma >0$.

Proof

With a similar proof as in [14], it can be obtained that, $\forall a,b\in \mathbb {R}$,

$$\begin{aligned} \text {sig}(a)^{\alpha _1}\cdot \text {sig}(a+b)^\beta&\ge \left| a\right| ^{\alpha _1}(\left| a\right| ^\beta -2^{1-\beta }\left| b\right| ^\beta ), \end{aligned}$$

(46)

$$\begin{aligned} \text {sig}(a)^{\alpha _1}\cdot \text {sig}(a+b)^\alpha&\ge \left| a\right| ^{\alpha _1}(2^{1-\alpha }\left| a\right| ^\alpha -\left| b\right| ^\alpha ). \end{aligned}$$

(47)

Thus, from (46), it has, for $\varsigma >0$ and $0<\beta \le 1$,

$$\begin{aligned}&\text {sig}(x^T)^{\alpha _1}\text {sig}(x\!+\!e)^\beta \\&\quad \ge \sum \limits _{i = 1}^n {\left| x_i \right| ^{\alpha _1}(\left| x_i \right| ^\beta -2^{1-\beta }\left| e_i \right| ^\beta )}\\&\quad \ge (1-2^{1-\beta }\varsigma )\text {sig}(x^T)^{\alpha _1}\text {sig}(x)^\beta \\&\quad -\!\frac{2^{1-\beta }\beta \alpha _1^{\frac{\alpha _1}{\beta }}}{(\alpha _1\!+\!\beta )^{\frac{\alpha _1}{\beta }+1}{\varsigma }^{\frac{\alpha _1}{\beta }}}\text {sig}(e^T)^{\alpha _1}\text {sig}(e)^\beta . \end{aligned}$$

Similarly, from (47), for $\alpha \ge 1$ and $\varsigma >0$,

$$\begin{aligned}&\text {sig}(x^T)^{\alpha _1}\text {sig}(x\!+\!e)^\alpha \\&\quad \ge (2^{1-\alpha }-\varsigma )\text {sig}(x^T)^{\alpha _1}\text {sig}(x)^\alpha \\&\qquad -\!\frac{\alpha \alpha _1^{\frac{\alpha _1}{\alpha }}}{(\alpha _1\!+\!\alpha )^{\frac{\alpha _1}{\alpha }+1}{\varsigma }^{\frac{\alpha _1}{\alpha }}}\text {sig}(e^T)^{\alpha _1}\text {sig}(e)^\alpha . \end{aligned}$$

$\square$

1.2 7.2 Proof of Theorem 1

Proof

Let $T>0$, $\varepsilon \in (0,{\bar{\varepsilon }})$, where ${\bar{\varepsilon }}>0$ is specified in the following. Recall $V_c(\xi _c)=\sum _{i = 1}^{k_s}V_{s,i}(\bar{x}_{s})+\varepsilon \sum _{j = 1}^{k_f}V_{f,j}(\bar{z}_{f})$,where $\xi _c\!:=\!(\bar{x}_{s},\bar{z}_{f})$. From (13), (14), (17), and (18), there exist two class ${\mathcal {K}}_{\infty }$ functions ${\underline{\alpha }}(\Vert \xi _c\Vert )$, ${\overline{\alpha }}(\Vert \xi _c\Vert )$, such that for any $\xi _c\in \mathbb {R}^{n_x+n_z}$,

$$\begin{aligned} {\underline{\alpha }}(\Vert \xi _c\Vert )\le V_c(\xi _c)\le {\overline{\alpha }}(\Vert \xi _c\Vert ). \end{aligned}$$

(48)

From (31), (36) and Lemma 2, for $\Vert \xi _c\Vert \ge \nu _1$,

$$\begin{aligned} \left\langle \nabla V_c(\xi _c),f(\xi _c)\right\rangle \!\le&\! -\!\sum _{i= 1}^{k_s}(\frac{b}{2}\Vert \bar{x}_{s,i}\Vert ^2\!+\!\frac{b}{2}\Vert \bar{x}_{s,i}\Vert ^{2-2\sigma }) \nonumber \\&\! -\!\sum _{j = 1}^{k_f}(\frac{b}{2}\Vert {\tilde{z}}_{f,j}\Vert ^2\!+\!\frac{c}{2}\Vert {\tilde{z}}_{f,j}\Vert ^{2-2\sigma }). \end{aligned}$$

(49)

From (14), (18) and Lemma 3,

$$\begin{aligned} (V_c(\xi _c))^{\frac{2}{2-\sigma }}\le&(\sum _{i = 1}^{k_s}b_{s,i}\text {sig}({{\bar{x}}}_{s,i}^T)^{1-\sigma }{{\bar{x}}}_{s,i}\nonumber \\&+\sum _{j = 1}^{k_f}\varepsilon b_{f,j}\text {sig}({{\bar{z}}}_{f,j}^T)^{1-\sigma }{{\bar{z}}}_{f,j})^{\frac{2}{2-\sigma }}\nonumber \\ \!\le&2\sum _{i= 1}^{k_s}\Vert \bar{x}_{s,i}\Vert ^2+\!2\sum _{j = 1}^{k_f}\Vert {\tilde{z}}_{f,j}\Vert ^2,\nonumber \\ (V_c(\xi _c))^{\frac{2-2\sigma }{2-\sigma }}\!\le&(\sum _{i = 1}^{k_s}b_{s,i}\text {sig}({{\bar{x}}}_{s,i}^T)^{1-\sigma }{{\bar{x}}}_{s,i}\nonumber \\&+\sum _{j = 1}^{k_f}\varepsilon b_{f,j}\text {sig}({{\bar{z}}}_{f,j}^T)^{1-\sigma }{{\bar{z}}}_{f,j})^{\frac{2-2\sigma }{2-\sigma }} \end{aligned}$$

(50)

$$\begin{aligned} \le&2(n_x\!+\!n_z)^{\frac{-\sigma }{2-\sigma }}\sum _{i= 1}^{k_s}\Vert \bar{x}_{s,i}\Vert ^{2-\sigma }\nonumber \\&+2(n_x\!+\!n_z)^{\frac{-\sigma }{2-\sigma }}\sum _{j = 1}^{k_f}\Vert {\tilde{z}}_{f,j}\Vert ^{2-\sigma }\nonumber \\ \!\le&4\sum _{i=1}^{k_s}\Vert \bar{x}_{s,i}\Vert ^{2\!-\!\sigma }+\!4\sum _{j=1}^{k_f}\Vert {\tilde{z}}_{f,j}\Vert ^{2\!-\!\sigma }. \end{aligned}$$

(51)

Thus, for all $\Vert \xi _c\Vert \ge \nu _1$,

$$\begin{aligned} \left\langle \nabla V_c(\xi _c),f(\xi _c)\right\rangle&\!\le \!-\!\frac{b}{4}(V_c(\xi _c))^{\frac{2}{2-\sigma }}\!-\!\frac{c}{8}(V_c(\xi _c))^{\frac{2-2\sigma }{2-\sigma }}. \end{aligned}$$

(52)

From Lemma 4.1 of [7], there exists a function $\sigma _{T_1,\varepsilon }\in {\mathcal {K}}{\mathcal {L}}$ defined similar as $\beta _{T,\varepsilon }$ in Definition 1 with $T_1:=(\frac{2}{b}+\frac{4}{c})\frac{\sigma -2}{\sigma }$, such that, for any solution $\xi _c$,

$$\begin{aligned} V_c(\xi _c)\le&\max \big \{\sigma _{T_1,\varepsilon }({\overline{\alpha }}^{-1}(\Vert \xi _c(0)\Vert ),t),2\nu _1^{2-\sigma }\big \}\nonumber \\ \le&\sigma _{T_1,\varepsilon }({\overline{\alpha }}^{-1}(\Vert \xi _c(0)\Vert ),t)+2\nu _1^{2-\sigma }. \end{aligned}$$

(53)

Supposed that $[0,T_M)$ is the maximally defined interval of the solution of the closed-loop TTSS (1) and (36), where $0<T_M\le \infty$. From (53), the solution of the closed-loop TTSS (1) and (36) would not escape in finite time and thus $T_M=\infty$.

When ${{\varvec{k}}_{{\varvec{m}}}:=\textbf{max}\{{\varvec{k}}_{{\varvec{s}}},{\varvec{k}}_{{\varvec{f}}}\}=\textbf{1}}$, it has $\nu _1=0$. From (9), (13), (17) and (38), there exist a function $\beta _{T,\varepsilon }\in {\mathcal {K}}{\mathcal {L}}$ defined similar as $\beta _{T,\varepsilon }$ in Definition 1 with ${T}\ge 2T_1$, and a function $\gamma (\varepsilon )\in {\mathcal {K}}$ independent of $T,\varepsilon$, such that, for any solution (x, z) and $t\ge 0$, (3) holds with $\gamma (\varepsilon )=0$.

When ${{\varvec{k}}_{{\varvec{m}}}>\textbf{1}}$, it has $0<\nu _1\le \nu$ being $O(\varepsilon ^{-\frac{1}{(k_m-1)\sigma }})$. Then, for all $\varepsilon \in (0,{\bar{\varepsilon }}]$, $\sigma \in (0,{\bar{\sigma }}]$ and any solution $\xi _c$,

$$\begin{aligned} V_c(\xi _c) \le&\sigma _{T_1,\varepsilon }({\overline{\alpha }}^{-1}(\Vert \xi _c(0)\Vert ),t)+2\nu ^{2-\sigma }. \end{aligned}$$

Since $V_c(\xi _c)=\sum _{i = 1}^{k_s}V_{s,i}(\bar{x}_{s})+\varepsilon \sum _{j = 1}^{k_f}V_{f,j}(\bar{z}_{f})$, the ultimate bound of $\sum _{j = 1}^{k_f}V_{f,j}(\bar{z}_{f})$ depends on $\varepsilon$. It cannot yet find a function $\gamma \in {\mathcal {K}}$ independent of $\varepsilon$ such that (3) holds.

Let $V_f(\xi _c):=\varepsilon \sum _{j = 1}^{k_f}V_{f,j}(\bar{z}_{f})$ for any $\xi _c \in \mathbb {R}^{n_x+n_z}$. With a similar proof of (52), it can be obtained that, for all $\varepsilon \in (0,{\bar{\varepsilon }}]$, $\sigma \in (0,{\bar{\sigma }}]$ and $\Vert \xi _c\Vert \ge \nu$,

$$\begin{aligned}&\left\langle \nabla V_f(\xi _c),F(\xi _c)\right\rangle \\&\quad \le -\frac{b}{4}(V_f(\xi _c))^{\frac{2}{2-\sigma }}\!-\!\frac{c}{8}(V_f(\xi _c))^{\frac{2-2\sigma }{2-\sigma }}\\&\qquad + \sum _{i= 1}^{k_s}(\frac{b}{2}\Vert \bar{x}_{s,i}\Vert ^2\!+\!\frac{b}{2}\Vert \bar{x}_{s,i}\Vert ^{2-2\sigma }). \end{aligned}$$

Since $V_c(\xi _c) \le \sigma _{T_1,\varepsilon }({\overline{\alpha }}^{-1}(\Vert \xi _c(0)\Vert ),t)+2\nu ^{2-\sigma }$, there exist two functions $\gamma _1$, $\gamma _2\in {\mathcal {K}}$, for all $\varepsilon \in (0,{\bar{\varepsilon }}]$, $\sigma \in (0,{\bar{\sigma }}]$ and $\Vert \xi _c\Vert \ge \nu$,

$$\begin{aligned}&\left\langle \nabla V_f(\xi _c),F(\xi _c)\right\rangle \\&\quad \le -\frac{b}{4}(V_f(\xi _c))^{\frac{2}{2-\sigma }}\!-\!\frac{c}{8}(V_f(\xi _c))^{\frac{2-2\sigma }{2-\sigma }}\\&\qquad +\!\gamma _1(\sigma _{T_1,\varepsilon }({\overline{\alpha }}^{-1}(\Vert \xi _c(0)\Vert ),t)) \!+\! \gamma _2(\nu ). \end{aligned}$$

Then, there exist a function ${\bar{\sigma }}_{T_1,\varepsilon }\in {\mathcal {K}}{\mathcal {L}}$ defined similar as $\beta _{T,\varepsilon }$ in Definition 1, and two functions $\gamma _3, \gamma _4\in {\mathcal {K}}$ independent of $T_1, \varepsilon$, so that for $t\le T_1$,

$$\begin{aligned} \Vert \bar{z}_f(t)\Vert ^2\le \max&\{ {\bar{\sigma }}_{T_1,\varepsilon }({\overline{\alpha }}^{-1}(\Vert \xi _c(0)\Vert ),t),\\&\gamma _3(\sigma _{T_1,\varepsilon }({\overline{\alpha }}^{-1}(\Vert \xi _c(0)\Vert ),0))\!+\!\gamma _4(\nu )\}. \end{aligned}$$

For $t\ge T_1$, it has $V_c(\xi _c) \le 2\nu ^{2-\sigma }$. Thus, for $t\ge T_1$,

$$\begin{aligned}&\left\langle \nabla V_f(\xi _c),F(\xi _c)\right\rangle \\&\quad \le \!-\!\frac{b}{4}(V_f(\xi _c))^{\frac{2}{2\!-\!\sigma }}\!-\!\frac{c}{8}(V_f(\xi _c))^{\frac{2\!-\!2\sigma }{2\!-\!\sigma }} \!+\! \gamma _2(\nu ). \end{aligned}$$

Similarly, for $t\ge T_1$,

$$\begin{aligned} \Vert \bar{z}_f(t)\Vert ^2\!\le \! \max \{{\bar{\sigma }}_{T_1,\varepsilon }(V_f(\xi _c(T_1)),t-T_1), \gamma _4(\nu )\}. \end{aligned}$$

Thus, there exists a function ${\hat{\sigma }}_{2T_1,\varepsilon }\in {\mathcal {K}}{\mathcal {L}}$ defined similar as $\beta _{T,\varepsilon }$ in Definition 1, such that, $\forall (t,j)\in \text {dom} \chi$,

$$\begin{aligned} \Vert \bar{z}_f(t)\Vert ^2 \le {\hat{\sigma }}_{2T_1,\varepsilon }(\Vert \xi _c(0)\Vert ,t)+2\gamma _4(\nu ). \end{aligned}$$

Then, there exist two functions $\gamma _5, \gamma _6\in {\mathcal {K}}$ such that for any $0<\varepsilon \le {\bar{\varepsilon }}$, and any $(t,j)\in \text {dom} \chi$,

$$\begin{aligned} \Vert \xi _c(t)\Vert ^2 \le&\gamma _5(\sigma _{T_1,\varepsilon }({\overline{\alpha }}_U^{-1}(\Vert \chi (0,0)\Vert ),t))\nonumber \\&+\!{\hat{\sigma }}_{2T_1,\varepsilon }(\Vert \chi (0,0)\Vert ,t)\!+\!\gamma _5(\nu ). \end{aligned}$$

(54)

Since $2T_1<T$, there exist a function $\beta _{T,\varepsilon }\in {\mathcal {K}}{\mathcal {L}}$ defined in Definition 1, and a function $\gamma \in {\mathcal {K}}$ independent of $T,\varepsilon$, such that (3) is ensured for any $t\ge 0$.

$\square$

1.3 7.3 Proof of Theorem 2

Proof

Denote $U(\chi ):=\sum _{i = 1}^{k_s}V_{s,i}(\bar{x}_{s})+\sum _{j = 1}^{k_f}V_{f,j} (\bar{z}_{f})+ \varphi ^T\varphi$, where $\chi :=(x, z, {\hat{x}}, {\hat{z}}, \varphi )$. Then, there exist functions ${\underline{\alpha }}_1, {\overline{\alpha }}_1\in {\mathcal {K}}_{\infty }$ such that, $\forall \chi \in \mathbb {X}$,

$$\begin{aligned} {\underline{\alpha }}_1(\Vert (\xi ,\varphi )\Vert )\le U(\chi )\le {\overline{\alpha }}_1(\Vert (\xi ,\varphi )\Vert ). \end{aligned}$$

(55)

Let $\chi \in C$. Following similar steps as in the Proof of Theorem 1 to obtain (49), it has

$$\begin{aligned}&\left\langle \nabla U(\chi ),F(\chi )\right\rangle \nonumber \\ \le&-\sum _{i = 1}^{k_s}(b\Vert \bar{x}_{s,i}\Vert ^2\!+\!c\Vert \bar{x}_{s,i}\Vert ^{2-2\sigma } ) \nonumber \\&-\sum _{j = 1}^{k_f}(b\Vert \bar{z}_{f,j}\Vert ^2\!+\!c\Vert \bar{z}_{f,j}\Vert ^{2-2\sigma }) \nonumber \\&-a\sum _{i = 1}^{k_s}V_{s,i}(\bar{x}_{s})-\frac{a}{\varepsilon }\sum _{j = 1}^{k_f}V_{f,j}(\bar{z}_{f}) \nonumber \\&-2(\omega _1\Vert \varphi \Vert ^2 \!+\! \omega _2(\Vert \varphi \Vert ^2)^{\frac{2}{2-\sigma }} \!+\! 2^{\frac{\sigma }{2-\sigma }} \omega _3(\Vert \varphi \Vert ^2)^{\frac{2-2\sigma }{2-\sigma }})\nonumber \\&+ \text {sig}{({{\bar{x}}_{s,k_s}^T})^{2-l_{s,k_s+1}}} {\tilde{B}}_s(u-{\alpha }_{s,k_s}({\tilde{x}}_s))\nonumber \\&+ \text {sig}{({{\bar{z}}_{f,k_f}^T})^{2-l_{f,k_f+1}}} {\tilde{B}}_f(u-{\alpha }_{f,j}({\tilde{z}}_f))\nonumber \\&+\sum _{i = 1}^{k_s}\text {sig}{({{\bar{x}}_{s,i}^T})^{2\!-\!l_{s,i+1} }}(O(\varepsilon ){\tilde{x}}_{s}\!+\!O(\varepsilon )u)\nonumber \\&+\sum _{i = 1}^{k_s}\sum _{p = 1}^{i }\frac{\partial V_{s,i}}{\partial {\tilde{x}}_{s,p}}(O(\varepsilon ){\tilde{x}}_{s}\!+\!O(\varepsilon )u)\nonumber \\&+\sum _{j = 1}^{k_f}\text {sig}{({{\bar{z}}_{f,j}^T})^{2\!-\!l_{z,j+1} }}(O(\varepsilon ){\tilde{z}}_{f}\!+\!O(\varepsilon )u)\nonumber \\&+\sum _{j = 1}^{k_f }\sum _{p = 1}^{j }\frac{\partial V_{f,j}}{\partial {\tilde{z}}_{f,p}}(O(\varepsilon ){\tilde{z}}_{f}\!+\!O(\varepsilon )u). \end{aligned}$$

(56)

From Lemma 5 and (44), with the similar proof of (37), there exists ${\bar{\varepsilon }}_1>0$, such that for $\varepsilon \le {\bar{\varepsilon }}_1$ and $\Vert \xi _c\Vert \ge \nu _1$,

$$\begin{aligned}&f_{\varepsilon }({\tilde{x}}_{s},{\tilde{z}}_{f},u)\!+\!\text {sig}{({{\bar{x}}_{s,k_s}^T})^{2-l_{s,k_s+1}}} {\tilde{B}}_s(u\!-\!{\alpha }_{s,k_s}({\tilde{x}}_s))\nonumber \\&\qquad + \text {sig}{({{\bar{z}}_{f,k_f}^T})^{2-l_{f,k_f+1}}} {\tilde{B}}_f(u\!-\!{\alpha }_{f,j}({\tilde{z}}_f))\nonumber \\&\quad =f_{\varepsilon }({\tilde{x}}_{s},{\tilde{z}}_{f},u)\!+\!\text {sig}({{\bar{x}}_{s,k_s}^T})^{2-l_{s,k_s+1}}\check{\beta }_{s,k_s}({\check{x}},{\check{z}})\nonumber \\&(\text {sig}(g_{s,k_s}({\check{x}}_{s})+e_{s,1})^{l_{s,k_s+1}}-\text {sig}({{\bar{x}}_{s,k_s}})^{l_{s,k_s+1}}) \nonumber \\&\qquad +c \text {sig}({{\bar{x}}_{s,k_s}^T})^{2-l_{s,k_s+1}} (\text {sig}(g_{f,k_f}({\check{z}}_f)+e_{s,1})^{l_{s,k_s}-\sigma } \nonumber \\&\qquad - \text {sig}({{\bar{x}}_{s,k_s}})^{l_{s,k_s+1}}) \nonumber \\&\qquad +\text {sig}({{\bar{x}}_{s,k_s}^T})^{2-l_{s,k_s+1}}(e_{s,2}\text {sig}(g_{s,k_s}(\hat{x}_{s}))^{l_{s,k_s+1}}) \nonumber \\&\qquad +\!\text {sig}({{\bar{z}}_{f,k_f}^T})^{2\!-\!l_{f,k_f\!+\!1}}\check{\beta }_{f,k_f}({\check{x}},{\check{z}})(\text {sig}(g_{f,k_f}(\hat{z}_f)\!\nonumber \\&\qquad +\!e_{f,1})^{l_{f,k_f\!+\!1}}-\text {sig}({{\bar{z}}_{f,k_f}})^{l_{f,k_f+1}}) \nonumber \\&\qquad +c \text {sig}({{\bar{z}}_{f,k_f}^T})^{2-l_{f,k_f+1}} (\text {sig}(g_{f,k_f}(\hat{z}_f)+e_{f,1})^{l_{f,k_f}-\sigma } \nonumber \\&\qquad +\text {sig}({{\bar{z}}_{f,k_f}^T})^{2-l_{f,k_f+1}}(e_{f,2}\text {sig}(g_{f,k_f}(\hat{z}_f))^{l_{f,k_f+1}}) \nonumber \\&\quad \le \sum _{i = 1}^{k_s}\frac{b}{4}\Vert \bar{x}_{s,i}\Vert ^2+\frac{c}{4}\Vert \bar{x}_{s,i}\Vert ^{2-2\sigma } \nonumber \\&\qquad +\sum _{j = 1}^{k_f}\frac{b}{4}\Vert \bar{z}_{f,j}\Vert ^2+\frac{c}{4}\Vert \bar{z}_{f,j}\Vert ^{2-2\sigma } \nonumber \\&\qquad + \!\varpi _1(\Vert e_{s,1}\Vert ^2 \!+\! \Vert e_{f,1}\Vert ^2) \!+\! \varpi _2(\Vert e_{s,1}\Vert ^{2\!-\!2\sigma } \!+\! \Vert e_{f,1}\Vert ^{2c \!-\!2\sigma })\nonumber \\&\qquad + \varpi _3(\Vert e_{s,2}\Vert ^2\Vert \hat{x}_{s,k_s}\Vert ^2+\Vert e_{f,2}\Vert ^2\Vert \hat{z}_{f,k_f}\Vert ^2)\nonumber \\&\quad \le \sum _{i = 1}^{k_s}\frac{b}{2}\Vert \bar{x}_{s,i}\Vert ^2+\frac{c}{2}\Vert \bar{x}_{s,i}\Vert ^{2-2\sigma }+\varpi _5\varphi _s^2 \nonumber \\&\qquad +\sum _{j = 1}^{k_f}\frac{b}{2}\Vert \bar{z}_{f,j}\Vert ^2+\frac{c}{2}\Vert \bar{z}_{f,j}\Vert ^{2-2\sigma } + \varpi _5\varphi _f^2+\nu . \end{aligned}$$

(57)

where $\nu _1=0$ when $k_m:=\max \{k_s,k_f\}=1$, otherwise $\nu _1>0$ being $O(\varepsilon ^{-\frac{1}{(k_m-1)\sigma }})$.

Thus, from (56) and the definition of $\varpi _i$, $i=1,2,3,4$, a, b, c, for $\varepsilon <{\bar{\varepsilon }}$ and $\chi \in \mathbb {X}$ with $\Vert \xi _c\Vert \ge \max \{\nu _1,\frac{8\nu }{b}\}$,

$$\begin{aligned} \left\langle \nabla U(\chi ),F(\chi )\right\rangle \!\le&-\frac{b}{4}U^{\frac{2}{2-\sigma }}\!-\!\frac{c}{8}U^{\frac{2-2\sigma }{2-\sigma }}. \end{aligned}$$

(58)

Then, the existence of a uniform semiglobal average dwell-time will be proved to exclude the Zeno behavior.

From (44), the time between two continuous triggering event due to D is always longer than the time it needs for ${\bar{f}}_e=\varpi _1(\Vert e_{s,1}\Vert ^2\!+\!\Vert e_{f,1}\Vert ^2)\!+\!\varpi _2(\Vert e_{s,1}\Vert ^{2-2\sigma }\!+\!\Vert e_{f,1}\Vert ^{2-2\sigma }) \!+\!\varpi _3(\Vert e_{s,2}\Vert ^{\frac{2}{l_{s,k_s+1}}}\Vert g_{s,k_s}(\hat{x}_{s})\Vert ^2\!+\!\Vert e_{f,2}\Vert ^{\frac{2}{l_{f,k_f+1}}}\Vert g_{f,k_f}(\hat{z}_f)\Vert ^2)$ to grow from 0 to $\nu _s$. Denote $\Delta >0$ with $||\chi (0,0)||\le \Delta$. Since $\check{\beta }_{s,k_s}$ is smooth positive function, from (10) and (58), $\dot{e}_{s,1}$ and $\dot{e}_{s,2}$ are bounded. Thus, there is a constant $\delta _{\varepsilon }(\Delta )>0$, such that $D^+({\bar{f}}_e)\le \delta _{\varepsilon }(\Delta )$, where $D^+(\cdot )$ denotes the upper right-hand Dini derivative. Hence, for any (s, i), $(t,k)\in \text {dom}\chi$ with $s+i\le t+k$,

$$\begin{aligned} k-i \le \frac{(t-s)}{\tau _{\varepsilon }(\Delta )}+1, \end{aligned}$$

(59)

where $\tau _{\varepsilon }(\Delta ):= \frac{\nu _1}{\delta _{\varepsilon }(\Delta )}>0$. Thus, the Zeno behavior is excluded. Similarly, it can also be obtained that the solution of the system (42) would not escape in finite time and exists in $[0,\infty )$.

Let $U_f(\chi ):= \varphi ^T\varphi +\varepsilon \sum _{j = 1}^{k_f}V_{f,j}(\bar{z}_{f})$. With the similar proof of (54), for any $\varepsilon \in (0,{\bar{\varepsilon }}]$, there exist $\gamma , {\bar{\gamma }}\in {\mathcal {K}}$, $\beta _{T,\varepsilon }\in {\mathcal {K}}{\mathcal {L}}$ defined similar as $\beta _{T,\varepsilon }$ in Definition 1, such that, for any solution $\chi$ to (42), any $(t,j)\in \text {dom} \chi$,

$$\begin{aligned}{} & {} \Vert (x(t,j),z(t,j))\Vert \\{} & {} \quad \le \beta _{T,\varepsilon }(\Vert \chi (0,0)\Vert ,t)+\gamma (\varepsilon )+{\bar{\gamma }}(\nu ). \end{aligned}$$

The proof is completed. $\square$