Skip to main content

Advertisement

SpringerLink
Log in

Bifurcation and chaos for a novel model of trigonal centrifugal governor with non-smooth control

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

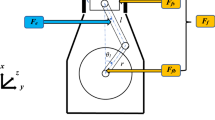
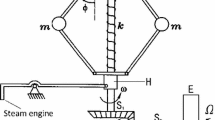
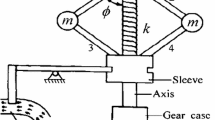
The traditional Watt’s centrifugal governors with a flywheel ball cause research challenges in both model design and analytical approach. The development of the new model and the new control scheme for the centrifugal governor system, however, has received little attention. The three-dimensional differential equations of motion for trigonal centrifugal governor (TCG) model are presented with the aid of Euler–Lagrange’s equation and the theorem of angular momentum. A novel TCG system with new-style nonlinearities of quotient (*/*) function, radical (the square root \(\sqrt{*}\)) function, and non-smooth control strategy (|*|) is proposed. To display the complex relationship of parameter dependence relationship, the mechanical properties of nonlinear restoring force surfaces and non-smooth torque surfaces are plotted. Then, various dynamical behaviors for the autonomous system are examined, including the equilibrium bifurcation, potential energy, Hamilton energy, equilibrium stability, and phase portraits. Additionally, the numerical simulation of chaotic phase portraits are used to validate the theoretical chaotic criteria, and the three-dimensional Melnikov’s method is newly defined and employed to obtain the analytical chaotic thresholds for the non-autonomous TCG system. Last but not least, an experimental setup is established to verify the theoretical analysis and numerical findings. Thus, a wide range of mechanical engineering and control system applications could use the new proposed TCG system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25

Similar content being viewed by others

Data availability

These datasets generated during the current study are available from the corresponding authors on reasonable request.

References

  1. Chen, Z.H., Yuan, X.H., Ji, B., Wang, P.T., Tian, H.: Design of a fractional order PID controller for hydraulic turbine regulating system using chaotic non-dominated sorting genetic algorithm II. Energy Convers. Manag. 84, 390–404 (2014)

    Article  Google Scholar 

  2. Carlucci, A.P., Chiara, F.F., Laforgia, D.: Analysis of the relation between injection parameter variation and block vibration of an internal combustion diesel engine. J. Sound Vib. 295, 141–164 (2006)

    Article  Google Scholar 

  3. Badami, M., Mura, M.: Preliminary design and controlling strategies of a small-scale wood waste Rankine cycle (RC) with a reciprocating steam engine (SE). Energy 34, 1315–1324 (2009)

    Article  Google Scholar 

  4. Najafi, G., Ghobadian, B., Tavakoli, T., Yusaf, T.F., Faizollahnejad, M.: Performance and exhaust emissions of a gasoline engine with ethanol blended gasoline fuels using artificial neural network. Appl. Energy 86, 630–639 (2009)

    Article  Google Scholar 

  5. Priest, M., Taylor, C.M.: Automobile engine tribology-approaching the surface. Wear 241, 193–203 (2000)

    Article  Google Scholar 

  6. Maxwell, J.C.: On governors. Proc. R. Soc. Lond. 16, 220–283 (1868)

    MATH  Google Scholar 

  7. Vyshnegradskii, I.A.: Direct action controllers. Izv. S. Peterb. Tekhnol. Inst. 1, 21–62 (1877)

    Google Scholar 

  8. Pontryagin, L.S.: Ordinary Differential Equations. Addison-Wesley, London (1962)

    MATH  Google Scholar 

  9. Manychkin, N., Sakharov, M., Tarabarin, V.: The Models of Centrifugal Governors in the Collection of Bauman Moscow State Technical University. Springer, Netherlands (2010)

    Book  Google Scholar 

  10. Liu, Y.Y., Barabasi, A.L.: Control principles of complex systems. Rev. Mod. Phys. 88, 035006 (2016)

    Article  Google Scholar 

  11. Moroz, I.M., Holmes, P.: Double Hopf bifurcation and quasi-periodic flow in a model for baroclinic instability. J. Atmos. Sci. 41, 3147–3160 (1984)

    Article  Google Scholar 

  12. Denny, M.: Watt steam governor stability. Eur. J. Phys. 23, 339–351 (2002)

    Article  MathSciNet  Google Scholar 

  13. Sotomayor, J., Mello, L.F., Braga, D.C.: Stability and Hopf bifurcation in an hexagonal governor system. Nonlinear Anal. Real World Appl. 9, 889–898 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  14. Luo, S.H., Li, J.Y., Li, S.B., Hu, J.J.: Dynamical analysis of fractional-order centrifugal flywheel governor system and its accelerated adaptive stabilization with the optimality. Int. J. Electr. Power Energy Syst. 118, 105792 (2020)

    Article  Google Scholar 

  15. Deng, S.N., Ji, J.C., Wen, G.L., Xu, H.D.: Delay-induced novel dynamics in a hexagonal centrifugal governor system. Int. J. Nonlinear Mech. 121, 103465 (2020)

    Article  Google Scholar 

  16. Alidousti, J., Eskandari, Z.: Dynamical behavior and poincare section of fractional-order centrifugal governor system. Math. Comp. Simul. 182, 791–806 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  17. Zhang, J.G., Mello, L.F., Chu, Y.D., Li, X.F., An, X.L.: Hopf bifurcation in an hexagonal governor system with a spring. Commun. Nonlinear Sci. Numer. Simul. 15, 778–786 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  18. Wen, G.L., Xu, H.D., Lv, Z.Y., Zhang, S.J., Wu, X., Liu, J., Yin, S.: Anti-controlling Hopf bifurcation in a type of centrifugal governor system. Nonlinear Dyn. 81, 811–812 (2015)

    Article  MATH  Google Scholar 

  19. Zhu, Q., Ishitobi, M., Nagano, S.: Condition of chaotic vibration in a centrifugal governor. J. Sound Vib. 268, 627–631 (2003)

    Article  Google Scholar 

  20. Ge, Z.M., Lee, C.I.: Anticontrol and synchronization of chaos for an autonomous rotational machine system with a hexagonal centrifugal governor. J. Sound Vib. 282, 635–648 (2005)

    Article  Google Scholar 

  21. Chu, Y.D., Zhang, J.G., Li, X.F., Chang, Y.X., Luo, G.W.: Chaos and chaos synchronization for a non-autonomous rotational machine systems. Nonlinear Anal. Real World Appl. 9, 1378–1393 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  22. Aghababa, M.P., Aghababa, H.P.: Finite-time stabilization of non-autonomous uncertain chaotic centrifugal flywheel governor systems with input nonlinearities. J. Vib. Control 20, 436–446 (2014)

    Article  MathSciNet  Google Scholar 

  23. Rao, X.B., Chu, Y.D., Xu, L., Chang, Y.X., Zhang, J.G.: Fractal structures in centrifugal flywheel governor system. Commun. Nonlinear Sci. Numer. Simul. 50, 330–339 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  24. Luo, S.H., Hou, Z.W., Zhang, T.: Performance enhanced design of chaos controller for the mechanical centrifugal flywheel governor system via adaptive dynamic surface control. AIP Adv. 6, 1881–1888 (2016)

    Article  Google Scholar 

  25. Yan, B., He, S.H., Sun, K.H., Wang, S.J.: Complexity and multistability in the centrifugal flywheel governor system with stochastic noise. IEEE Access 8, 30092–30103 (2020)

    Article  Google Scholar 

  26. Lin, X.B.: Using Melnikov’s method to solve Silnikov’s problems. Proc. R. Soc. A 116, 295–325 (1990)

    MATH  Google Scholar 

  27. Du, Z.D., Zhang, W.N.: Melnikov method for homoclinic bifurcation in nonlinear impact oscillators. Comp. Math. Appl. 50, 445–458 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  28. Chacon, R.: Melnikov method approach to control of homoclinic/heteroclinic chaos by weak harmonic excitations. Philos. Trans. R. Soc. A 364, 2335–2351 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  29. Awrejcewicz, J., Holicke, M.: Analytical prediction of chaos in rotated Froude pendulum. Nonlinear Dyn. 47, 3–24 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  30. Yin, J.L., Zhao, L., Tian, L.: Melnikov’s criteria and chaos analysis in the nonlinear Schordinger equation with Kerr law nonlinearity. Abst. Appl. Anal. 6, 1–12 (2014)

    Google Scholar 

  31. Dong, Y.Y., Han, Y.W., Zhang, Z.J.: On the analysis of nonlinear dynamic behavior of an isolation system with irrational restoring force and fractional damping. Acta Mech. 230, 2563–2579 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  32. Timoshenko, S.P., Young, D.H., Weaver, W.: Vibration Problems in Engineering. Wiley, NewYork (1990)

    Google Scholar 

  33. Helrich, C.S.: Analytical Mechanics. Springer, Switzerland (2017)

    Book  MATH  Google Scholar 

  34. Guckenheimer, J., Holmes, P.J.: Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Field. Springer, New York (1983)

    Book  MATH  Google Scholar 

  35. Golubitsky, M., Schaeffer, D.G.: Singularities and Groups in Bifurcation Theory. Springer, New York (1984)

    MATH  Google Scholar 

  36. Lorenz, E.N.: Deterministic nonperiodic flow. J. Atoms. 20, 130–141 (1963)

    Article  MathSciNet  MATH  Google Scholar 

  37. Duffing, G.: Erzwungene Schwingungen bei Veränderlicher Eigenfrequenz. F. Vieweg U. Sohn, Braunschweig (1918)

  38. Melnikov, V.K.: On the stability of the center for time periodic perturbations. Trans. Moscow Math. Soc. 12, 3–52 (1963)

    MathSciNet  Google Scholar 

  39. Wiggins, S.: Introduction to Applied Nonlinear Dynamical Systems and Chaos. Springer, NewYork (2003)

    MATH  Google Scholar 

  40. Zhang, Y., Ding, C.S., Wang, J., Cao, J.Y.: High-energy orbit sliding mode control for nonlinear energy harvesting. Nonlinear Dyn. 105, 191–211 (2021)

    Article  Google Scholar 

  41. Heinrich, M., Dahms, T., Flunkert, V., Teitsworth, S.W., Scholl, E.: Symmetry-breaking transitions in networks of nonlinear circuit elements. New J. Phys. 12, 113030 (2010)

    Article  MATH  Google Scholar 

  42. Chay, T.R.: Chaos in a three-variable model of an excitable cell. Physica D 16, 233–242 (1985)

    Article  MATH  Google Scholar 

  43. Qian, H.: Open-system nonequilibrium steady state: statistical thermodynamics, fluctuations, and chemical oscillations. J. Phys. Chem. B 110, 15063–15074 (2006)

    Article  Google Scholar 

  44. Agyemang, I., Freedman, H.I.: An environmental model for the interactions of industry with two competing agricultural resources. Math. Comp. Model. 49, 1618–1643 (2009)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Funding

This work was supported by the State Key Laboratory of Robotics and System (HIT) (Grant no. SKLRS-2022-KF-19).

Author information

Authors and Affiliations

  1. School of Civil Engineering, Henan University of Science and Technology, Luoyang, 471023, China

    Yanwei Han

  2. School of Astronautics, Nanjing University of Aeronautics and Astronautics, Nanjing, 210016, China

    Zijian Zhang

Authors
  1. Yanwei Han
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zijian Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yanwei Han.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Han, Y., Zhang, Z. Bifurcation and chaos for a novel model of trigonal centrifugal governor with non-smooth control. Nonlinear Dyn 111, 5249–5268 (2023). https://doi.org/10.1007/s11071-022-08115-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-022-08115-w

Keywords

Search

Navigation