Hidden attractors in Chua circuit: mathematical theory meets physical experiments

Abstract

After the discovery in early 1960s by E. Lorenz and Y. Ueda of the first example of a chaotic attractor in numerical simulation of a real physical process, a new scientific direction of analysis of chaotic behavior in dynamical systems arose. Despite the key role of this first discovery, later on a number of works have appeared supposing that chaotic attractors of the considered dynamical models are rather artificial, computer-induced objects, i.e., they are generated not due to the physical nature of the process, but only by errors arising from the application of approximate numerical methods and finite-precision computations. Further justification for the possibility of a real existence of chaos in the study of a physical system developed in two directions. Within the first direction, effective analytic-numerical methods were invented providing the so-called computer-assisted proof of the existence of a chaotic attractor. In the framework of the second direction, attempts were made to detect chaotic behavior directly in a physical experiment, by designing a proper experimental setup. The first remarkable result in this direction is the experiment of L. Chua, in which he designed a simple RLC circuit (Chua circuit) containing a nonlinear element (Chua diode), and managed to demonstrate the real evidence of chaotic behavior in this circuit on the screen of oscilloscope. The mathematical model of the Chua circuit (further, Chua system) is also known to be the first example of a system in which the existence of a chaotic hidden attractor was discovered and the bifurcation scenario of its birth was described. Despite the nontriviality of this discovery and cogency of the procedure for hidden attractor localization, the question of detecting this type of attractor in a physical experiment remained open. This article aims to give an exhaustive answer to this question, demonstrating both a detailed formulation of a radiophysical experiment on the localization of a hidden attractor in the Chua circuit, as well as a thorough description of the relationship between a physical experiment, mathematical modeling, and computer simulation.

1 Introduction

The Chua circuit is one of the reference models of nonlinear dynamics [1, 2]. This model was developed by Leon Chua as the first example of a radiophysical generator where dynamical chaos can be observed in a physical experiment [3]. One of the design goals of this generator was to verify, whether chaotic dynamics exists in reality, or it is the result of computational errors in numerical modeling. In a physical experiment, where the electronic circuit starts with zero initial conditions (initial voltages across the capacitors and the current through the coil), corresponding to the zero equilibrium state, only self-excited attractors could be observed with instability of the zero equilibrium state. Hundreds of such different self-excited attractors have been found in the Chua circuit [4]. Thus, the conjectures were put forward that only self-excited chaotic attractors can exist in the circuit [2] (see also discussions in [5, 6]).

In 2009, as a farther development of effective analytical-numerical methods for the study of oscillations [7], the idea of constructing a hidden chaotic Chua attractor was first proposed by Nikolay Kuznetsov [6, 8,9,10] and, in 2011, the first hidden chaotic attractor in the classical Chua circuit [11,12,13] was discovered. This hidden attractor has a very “thin” basin of attraction, which is not connected with equilibria, and coexists with a stable zero equilibrium, thus being “hidden” for a while for standard physics experiments and mathematical modeling of the circuit with random initial data. In recent years, the discovery of hidden Chua attractors led to the emergence of the theory of hidden oscillations [6, 14, 15], which represents the genesis of the modern era of Andronov’s theory of oscillations and has attracted attention from the world’s scientific community (see, e.g., [16] and references within).¹

In this work, using the Chua circuit as an example, we demonstrate the features of circuit simulation and the possibility of observing hidden attractors in a radiophysical experiment, and also compare the results obtained with mathematical modeling. For this, a special electronic circuit has been developed, which complements the Chua circuit, allowing to adjust the initial conditions. To analyze the dynamics of the Chua circuit, we consider the following models: a model at the radiophysical level (radiophysical implementation and block diagram of the Chua circuit), a model at the level of radiophysical mathematical relations (radiophysical mathematical model of the Chua circuit) and the classical (idealized) mathematical model of the Chua circuit in the phase space of dimensionless variables.

The work is structured as follows. In Sect. 2, we present the Chua circuit diagram, its derivation, and the relations between the schematic and mathematical models. We pay special attention to the definition and role of the initial conditions in the schematic model. In Sect. 3, we present the results of numerical modeling of a mathematical model for two different configurations of the structure of the phase space with hidden attractors and also consider the current–voltage characteristic (further on, I–V curve) of the model to determine the possibility of realizing such parameters in a physical experiment. Then we carry out a bifurcation analysis of the mathematical model depending on the parameters characterizing the I–V curve, determine the regions and characteristic I–V curve for the existence of hidden attractors and also describe the bifurcation scenarios of the birth of hidden attractors and their transformation into self-excited ones. In Sect. 4, we present the results of an experiment in which the initial conditions are changed, which allow us to visualize hidden attractors in practice. In Sect. 5, using the harmonic balance method, the initial conditions for the visualization of hidden attractors are analytically determined and the results of numerical and physical experiments are compared.

2 Schematic diagram and mathematical model of the Chua circuit

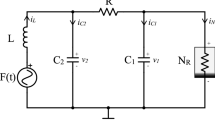
The Chua circuit (see Fig. 1a) was proposed in 1983 by Leon Chua [1, 17] as the simplest electrical circuit that demonstrates the regimes of chaotic oscillations.

Fig. 1

Simplified scheme of the Chua circuit

The circuit consists of an inductor L, capacitors C1 and C2, a linear resistor R, and a nonlinear element with negative conductivity $-G$, commonly called the Chua diode.

To describe and analyze the dynamics in physical processes various mathematical models and their properties can be used. The dynamics obeys physical laws, which in our case can be described by a mathematical model in the form of ODEs $\dot{u} = \frac{\textrm{d}u}{\textrm{d}t} = g(u,p)$, where u is the vector of system states, p is the vector of parameters, and t is the time (from zero to infinity). This model may have equilibria $u_{\textrm{e}}(p)$ : $g(u_{\textrm{e}}(p),p)=0$, or one can always supplement the model by additional variable $v = t$ and equation $\dot{v}=1$, so the new model has no equilibria. Following this way for the Chua circuit in Fig. 1 we derive corresponding mathematical model from Kirchhoff’s laws:

$$\begin{aligned} \begin{array}{l l l} I_{G} = I_{C1} + I_R,\\ I_{R} = I_{C2} + I_L,\\ U_{L} = U_{2},\\ \end{array} \end{aligned}$$

(1)

where $I_{C1} = C1 \,\dot{U_1}$, $I_{C2} = C2 \,\dot{U_2}$, $I_R = (U_1 - U_2)/R$, $I_G = - G(U_1) \, U_1$. In a real physical experiment, one should take into account the parasitic resistance of the inductor L, which physically corresponds to the resistor $R_L$ connected in series to the inductor (Fig. 1b). The voltage of such a resistor is $U_{R_{L}} = R_L I_L$, which is added to $U_L$. The current flowing through the inductor is described by the following relationship: $U_L = L \dot{I_L}$. Taking into account all the presented relations, we obtain the following system of equations describing the circuit in Fig. 1b:

$$\begin{aligned} \begin{array}{l l l} C1 \dot{U_1} = -(U_1 - U_2)/R + I_G(U_1),\\ C2 \dot{U_2} = (U_1 - U_2)/R - I_L,\\ L \dot{I_L} = U_2 - R_L I_L. \end{array} \end{aligned}$$

(2)

For $R_L = 0$, system (2) describes the circuit without taking into account the parasitic resistance of the inductor L (see Fig. 1a).

Fig. 2

a The Chua circuit implemented with op-amps, b experimental I–V curve of the Chua diode

The Chua diode is an element with a piecewise linear I–V curve $I_G (U_1)$ having 3 segments with a negative slope. Such an element can be implemented in various ways. The classical one is the configuration of two operational amplifiers (op-amps), which was used in the first implementation [18] of the original circuit designed by Chua in [19, see Fig. P4.12]. Other realizations with op-amps as well as semiconductor diodes and transistors [20, 21] are possible. In [22], the implementation of the Chua diode as an integrated device with adjustable I–V curve is presented. In [23, 24], one can find detailed descriptions for physical realizations of the Chua circuit via standard off-the-shelf electronic components.

In this work, we compare the results of mathematical modeling and experiment and show the effects associated with the emergence of hidden attractors. For that, we consider the simplest implementation, which makes it easy to control the I–V curve. The Chua diode with an adjustable I–V curve is most easily implemented using op-amps. Figure 2a shows a diagram of the Chua circuit, in which the diode (highlighted by a rectangle in the diagram) is realized using circuits based on op-amps DA1.1 and DA1.2. The Chua diode contains two negative conducting elements. The first element is assembled with the op-amp DA1.1 and has a negative small-signal conductance equal to $G_1 = - (\frac{R4 + R3}{R4} - 1) / R1$, where the ratio $K_1 = \frac{R4 + R3}{R4} > 1$ defines the gain of DA1.1. Similarly, the second element is assembled with the op-amp DA1.2 and has a negative small-signal conductance equal to $G_2 = - (\frac{R6 + R5}{R6} - 1) / R2$, where the ratio $K_2 = \frac{R6 + R5}{R6} > 1$ defines the gain of DA1.2. Without loss of generality, we assume that $K_1$ is larger than $K_2$. Thus, each of these sub-circuits represents a piecewise linear element with a negative small-signal resistance, and, in parallel, these two elements form the I–V curve of the entire Chua diode.

The principle of operation for a negative small-signal resistance at a DC operating point implemented with an op-amp can be described as follows: the input voltage is linearly amplified with the gain of the op-amp; however, the small-signal resistance of the entire circuit is negative. When the op-amp’s output voltage becomes equal to the saturation voltage, the op-amp switches to saturation mode and the circuit’s small-signal resistance becomes positive. Thus, a configuration of two op-amps in parallel makes it possible to implement a piecewise linear I–V curve by setting proper values of gains. In the range of input voltages $[-U_{\textrm{DA1}}, U_{\textrm{DA1}}]$ both op-amps DA1.1 and DA1.2 operate in amplification mode with total negative conductance $G_1 + G_2$. When the input voltage is increased and reaches intervals $[-U_ {\textrm{DA2}},-U_ {\textrm{DA1}}) \bigcup (U_{\textrm{DA1}}, U_{\textrm{DA2}}]$, the op-amp DA1.1 switches to the saturation mode and thus the total negative conductance is determined by the negative conductance introduced by the DA1.2 op-amp circuit and the positive conductance introduced by the DA1.1 op-amp circuit. The total conductivity is equal to $1/R1 + G_2$, while the slope angles of the I–V curve are changed. With a further increase in the input voltage beyond the interval $[-U_{\textrm{DA2}}, U_{\textrm{DA2}}]$, both op-amps operate in the saturation mode and their total conductance becomes positive, equal to $1/R1 + 1/R2$. Figure 2b shows the I–V curve of the Chua diode, obtained in a physical experiment; it has three linear sections. The parameters of experimental model are selected in such a way that the bounded phase trajectories (in the limit) do not reach the second break points $-U_{\textrm{DA2}}$, $U_{\textrm{DA2}}$, since the mathematical model of the Chua circuit takes into account only the first break points $-U_{\textrm{DA1}}$, $U_{\textrm{DA1}}$. The tilt angles of different sections of the I–V curve can be varied by changing the values of R1–R6. The breakpoints of the I–V curve determine the voltages $U_{\textrm{DA1}}$ and $U_{\textrm{DA2}}$ as follows:

$$\begin{aligned} \begin{array}{ll} \pm U_{\textrm{DA1}} = \pm E \frac{R4}{R3 + R4} = \pm E/K_1,\\ \pm U_{\textrm{DA2}} = \pm E \frac{R6}{R5 + R6} = \pm E/K_2, \end{array} \end{aligned}$$

(3)

where E is the DC supply voltage of the circuit. Thus, in general terms, the small-signal conductance $G(U_1)$ at the DC operating point $U_1$ of the I–V curve of the Chua diode shown in Fig. 2a is described by the following

$$\begin{aligned} G(U_1) = \left\{ \begin{array}{l l l} G_1+G_2, &{} |U_1| \le U_{\textrm{DA1}}\\ \frac{1}{R1} + G_2, &{} \begin{array} {ll} U_{\textrm{DA1}}<U_1\le U_{\textrm{DA2}}, \\ -U_{\textrm{DA2}}\le U_1<-U_{\textrm{DA1}} \end{array}\\ \frac{1}{R1} + \frac{1}{R2}, &{} |U_1| > U_{\textrm{DA2}}. \end{array} \right. \end{aligned}$$

(4)

Introducing new dimensionless normalized dynamical variables: $x = U_1/U_{\textrm{DA1}}$, $y = U_2/U_{\textrm{DA1}}$, $z = - I_L R/U_{\textrm{DA1}}$, the piecewise linear function describing the I–V curve of the Chua diode can be written as follows:

$$\begin{aligned} f(x) = \left\{ \begin{array}{ll} R[G_1+G_2]x, &{} |x| \le 1\\ R[\frac{1}{R1} + G_2]x - \frac{R K_1}{R_1}, &{} 1< x \le \tfrac{U_{DA2}}{U_{DA1}},\\ R[\frac{1}{R1} + G_2]x + \frac{R K_1}{R_1}, &{} - \tfrac{U_{DA2}}{U_{DA1}} \le x< -1,\\ R[\tfrac{1}{R1} + \tfrac{1}{R2}]x - [\frac{R K_1}{R_1}+\frac{R K_1}{R_2}], &{} x > \tfrac{U_{DA2}}{U_{DA1}},\\ R[\tfrac{1}{R1} + \tfrac{1}{R2}]x + [\frac{R K_1}{R_1}+\frac{R K_1}{R_2}], &{} x < -\tfrac{U_{DA2}}{U_{DA1}}. \end{array} \right. \end{aligned}$$

(5)

Figure 3 shows the I–V curve corresponding to function (5), which depicts all five different linear segments. For a rigorous in-depth analysis of the two op-amp circuits (connected in parallel) inside the rectangle in Fig. 2a, the reader is referred to Chapter 4 of [19], and [25].

Fig. 3

Complete theoretical I–V curve of the Chua diode, taking into account all 4 break points (3). The I–V curve is odd-symmetric. The innermost breakpoints are located at $|x| = 1$; the outermost breakpoints are located at $|x| = \tfrac{U_{\textrm{DA2}}}{U_{\textrm{DA1}}}$

After performing the following renormalization of time: $\tau \rightarrow \frac{1}{C2 R} t$, and taking into account (19), we obtain the following system of equations in dimensionless form:

$$\begin{aligned} \begin{array}{l l l} \dot{x} = -\alpha (x-y)-\alpha f(x),\\ \dot{y} = z-(y-x),\\ \dot{z} = -\beta y - \gamma z,\\ \end{array} \end{aligned}$$

(6)

where $\alpha = C2/C1$, $\beta = C2 R^2/L$, $\gamma = C2 R R_L/L$.

Fig. 4

The Chua circuit diagram with the on/off switch $K_1$

Multistability is a fairly common phenomenon that arises not only in radiophysical systems, but also in various abstract problems of mathematics (see, e.g., the 16th Hilbert problem [26]) and engineering problems (see, e.g., [6, 14, 27,28,29,30,31,32,33,34]). Prediction and investigation of coexisting regimes, especially if they are hidden, is a rather difficult task that is important for various engineering applications (see, e.g., phase-locked loops [35,36,37,38,39]). One of the most important questions in the study of multistable systems, especially with hidden attractors, is the choice of the initial conditions to reveal all possible limiting regimes. This problem is much easier to solve in numerical simulation; setting the initial conditions is an obligatory part for the initial value problem (IVP). However, even numerically, the search for attractors with small basins of attraction in the phase space (rare attractors) and hidden attractors may be an essentially nontrivial problem and require additional research methods [6].

In a physical experiment, it is rather difficult to control the choice of the initial conditions. If we talk about a radiophysical experiment with the Chua circuit then the initial conditions are the starting voltages on the capacitors C1 and C2, as well as the current in the inductor $I_L$ at the moment of starting the setup. Traditionally, without additional sub-circuits, the initial conditions are determined by the voltages across the capacitors and the current in the inductor at the moment the circuit is switched on and at this moment are zero. This corresponds to the situation when the circuit switched off at the moment when the power supply is turned off. Figure 4 shows a diagram of the Chua circuit, in which the switch $K_1$ can be used to open and close the circuit. When the switch $K_1$ is open, the capacitors are discharged; the current in the inductor is zero. Thus, when the circuit is closed, the system starts from zero initial conditions. In a real physical experiments, the closed circuit is usually triggered by supplying power E to the op-amps (see Fig. 2). Usually in the literature, only closed circuit is considered (see Fig. 1, [2, 17]), which leads to the fact that the question of initial conditions for starting the circuit is ignored.

For the mathematical modeling we use the Chua circuit model in form (6), and the I–V curve of the Chua diode is considered as a piecewise linear function of the following form:

$$\begin{aligned} f(x) = m_1 x + \tfrac{1}{2} (m_0 - m_1)(|x + 1| - |x - 1|), \end{aligned}$$

(7)

with the following expressions for the slope coefficients [according to (5)]:

$$\begin{aligned} m_0 = R\big (-\tfrac{R3}{R4R1}-\tfrac{R5}{R6R2}\big ), \ m_1 = R\big (\tfrac{1}{R1}-\tfrac{R5}{R6R2}\big ).\nonumber \\ \end{aligned}$$

(8)

In this form, the system of differential equations for the Chua circuit was first proposed and is most often used in literature. Note that piecewise linear function (7) does not fully match I–V curve (5). Function (7) does not have the second pair of symmetric break points, since the third linear segment corresponds to the saturation mode of op-amps, which in a physical experiment does not allow the values of quantities corresponding to the variables of system (6) to escape to infinity. However, the main dynamics of system (6) evolves on the basis of the first break points of the I–V curve; the phase trajectories do not enter the region of the phase space $|x| > \frac{U_{\textrm{DA2}}}{U_{\textrm{DA1}}}$, which leads to the fact that the mathematical model and the experimental circuit are in good agreement.

Within the framework of this paper, we reproduce in a real physical experiment the results of numerical simulation and demonstrate various bifurcations of the birth of hidden attractors in the Chua circuit.

3 Mathematical modeling of dynamical regimes and bifurcations in the Chua circuit

For the bifurcation analysis, the equilibria play an important role. If the mathematical model has a known periodic orbit (limit cycle) $u(t,u_0)=u(t+T,u_0)$, i.e., the initial data $u_0$ and the period T are known in advance, then it is possible to construct a mathematical model represented the discrete dynamics of the original system on the Poincaré section, which has an equilibrium state corresponding to the periodic orbit. In this regard, following [40, p. 81], [41, p. 10–11], [42, p. 58–59], for the chosen mathematical model, a local bifurcation is a qualitative restructuring of the model’s behavior in an arbitrarily small neighborhood of the equilibrium state during a process that continuously depending on a parameter when the parameter passes through the critical (bifurcation) value; the bifurcations that cannot be detected by considering an arbitrarily small neighborhood of equilibria are called global bifurcations. Also in this classification, one can separate out a class of bifurcations in small vicinity of unstable manifolds of equilibrium states (e.g., the birth of homoclinic or heteroclinic orbits and self-excited chaotic attractors). For the analysis of local bifurcations, various analytical methods are well developed (see, e.g., [40, 42,43,44]), while the analysis of global bifurcations is often a challenging task. For example, the identification of global bifurcations associated with the birth or destruction of hidden attractors is the key task in the analysis of the boundaries of global stability regions (the case of attraction of all system’s trajectories to the stationary set consisting of the equilibrium points) in the parameter space. The parts of the global stability boundary in the space of parameters associated with global bifurcations and the birth of hidden oscillations are called hidden parts of the global stability boundary [6, 14,15,16, 45], while the loss of global stability through local bifurcations in vicinity of the stationary set corresponds to trivial parts. The difficulties of studying global bifurcations and hidden attractors can be demonstrated by Hilbert’s 16th problem [40, 41, 46]).

Chua system (6)–(7) has five control parameters $\alpha$, $\beta$, $\gamma$, $m_0$, and $m_1$. It is shown in [5] that for fixed $\alpha = 8.4$, $\beta = 12$, $\gamma = -\,0.005$ on the parameter plane $(m_0, m_1)$, there are two regions corresponding to the existence of two configuration of hidden attractors.² The parameters $\alpha$, $\beta$ and $\gamma$ in the Chua system are determined by the elements of the oscillatory sub-circuit, while the parameters $m_0$ and $m_1$ are set by the I–V curve of the active nonlinear element. Thus, depending on the I–V curve of the Chua diode, hidden attractors can be realized in the system.

Model (6) may have one or three equilibria depending on the relations between the parameters. There is always the equilibrium state ($u^0 =(x^0,y^0,z^0)= (0, 0, 0)$), and for some values of the parameters,³ two additional symmetric equilibria with coordinates:

$$\begin{aligned} u_{S}^{1,2} = (\pm \, u_x, \pm \, u_y, \mp \, u_z), \end{aligned}$$

(9)

where

$$\begin{aligned} u_x= & {} u_y + u_z, \quad u_y = \tfrac{\gamma (m_0 - m_1)}{\gamma m_1 +\beta m_1 + \beta }, \\ u_z= & {} \tfrac{\beta (m_0 - m_1)}{\gamma m_1 +\beta m_1 + \beta }, \end{aligned}$$

can arise.

Fig. 5

Phase portraits and attractors of the Chua system with parameters $\alpha = 8.4$, $\beta = 12$, $\gamma = 0$, $m_0 = -0.12$, and $m_1 = -1.15$ (see a); with parameters $\alpha = 8.41$, $\beta = 12.23$, $\gamma = 0.0435$, $m_0 = -1.366$, and $m_1 = -0.17$ (see d). For the attractors, 2D cross sections of their basins of attraction for $\alpha = 8.4$, $\beta = 12$, $\gamma = 0$, $m_0 = -0.12$, $m_1 = -1.15$ with $z_0 = 0.001$ (see b), and with $z_0 = 6.868$ (see c); for $\alpha = 8.41$, $\beta = 12.23$, $\gamma = 0.0435$, $m_0 = -1.366$, $m_1 = -0.17$ with $z_0 = 0.001$ (see e), and $z_0 = 1.443$ (see f)

Consider examples of hidden attractors with different configurations. Figure 5 shows examples of hidden attractors for two points of the parameter plane corresponding to two different regions with hidden attractors.⁴ Figure 5a–c shows illustrations for the first region, for parameters $\alpha = 8.4$, $\beta = 12$, $\gamma = 0$, $m_0 = -0.12$, and $m_1 = -1.15$. In this case, two symmetric coexisting chaotic attractors are observed in the system. At the origin there is a stable focus with eigenvalues $\lambda _1 = -\,8.348114$, $\lambda _{2,3} = -\,0.021943 \pm i 3.259625$, and there are also two symmetric unstable equilibria with coordinates ($\pm \, 6.8667, 0, \mp \, 6.8667$) and eigenvalues $\lambda _1 = 2.236517$, $\lambda _{2,3} = -\,0.988258 \pm i 2.404965$. Trajectories from the vicinity of these two saddle-foci tend either to the stable zero equilibrium or to infinity. Figure 5a shows the structure of the phase space; different colors indicate trajectories starting from different initial conditions: gray and black lines indicate the trajectories tending to hidden attractors; red and pink colors indicate the trajectories starting from a neighborhood of symmetric equilibria. In Fig. 5b and c, the two-dimensional planes of initial conditions for vicinities of equilibrium points are shown (here we consider the Poincaré cross section by plane $z = 0$). The regime of divergency⁵ is marked by blue color, the basin of attraction⁶ of the stable zero equilibrium is marked by maroon color. The basins of attraction of chaotic⁷ attractors are denoted by gray color. The projections of the equilibrium points in the plane are identified by white dots. Figure 5b shows a two-dimensional plane of initial conditions for fixed $z_0 = 0.001$ in the vicinity of the zero equilibrium $u^0$ (stable focus). Figure 5b shows the structure of the basins of attraction for two coexisting regimes. There is a rather large basin of attraction surrounding the stable zero equilibrium (maroon color), and a large area of divergency. The zero stable equilibrium point is located in the center of the basin of attraction; consequently, choosing initial conditions from a neighborhood of zero equilibrium, the corresponding trajectory may not leave beyond its basin of attraction. Between these two areas we have an area of chaotic oscillations, which represents the basins of attraction of chaotic attractors. Between the areas of divergency and attraction area of chaotic attractor one can find a thick area, which corresponds to the stable zero equilibrium basin attraction. In Fig. 5c is shown a vicinity of one of the symmetric points $z_0 = u_{z} = -6.8665$ (saddle-focus). The basin of attraction for the stable zero equilibrium $u^0$ at the center is combined with the another part of the basin of attraction for the stable zero equilibrium point $u^0$ on the boundary of the area of divergency, and a projection of saddle equilibrium $u_{S}^1$ is located on the boundary between the basin of attraction for the stable zero equilibrium point and the area of divergency. Consequently, a chaotic attractors are hidden because if we choose initial states near one of the equilibrium points, then we cannot reach the chaotic attractors.

Figure 5d–f shows the results of a similar study of hidden attractors for the second region of the parameter space with $\alpha = 8.41$, $\beta = 12.23$ $\gamma = 0.0435$, $m_0 = -1.366$, and $m_1 = -0.17$. For the second region, the zero equilibrium is a saddle-focus with two-dimensional stable and one-dimensional unstable manifolds (corresponding eigenvalues are $\lambda _1 = 4.12175$ and $\lambda _{2,3} = -1.043595 \pm i 2.857504$), and symmetric equilibria $(\mp 1.4471, \mp 0.005129, \pm 1.442)$, which are stable foci with eigenvalues $\lambda _1 = -7.968363$ and $\lambda _{2,3} = -0.027719 \pm i 3.271839$. In Fig. 5d from the vicinity of the unstable equilibrium state (maroon color), the phase trajectories arrive at one of the symmetric stable foci. Also, a pair of symmetric chaotic attractors coexists in the phase space. With this choice of parameters, a stable hidden limit cycle of a large amplitude is also observed in the phase space, within which all other discussed coexisting limiting regimes are located.

Figure 5e and f shows the structure of basins of attraction for different cross sections of the phase space, including the basins of attraction of coexisting attractors in the vicinity of the stable focus $u_S^1$ and in the vicinity of the zero saddle equilibrium, respectively. The projections of equilibrium points are marked in the plane by black dots. We shaded the basins of attraction of different symmetric chaotic attractors by the gray colors (light and dark). The basin of attraction of the external limit cycle is marked in the plane by the light green color. We use the pink and red colors to denote the basins of attraction of the two symmetric equilibria $u_{S}^1$ and $u_{S}^2$, respectively. Firstly, we consider a plane of initial conditions and the basins of attraction of different attractors in the vicinity of the saddle equilibrium point (Fig. 5e). We can see that the phase trajectories starting from the vicinity of the saddle point can reach only one of the stable symmetric equilibria. The zero equilibrium point $u^0$ is located on a boundary between the attracting areas of symmetric stable equilibria. The basins of attraction are symmetric to each other, and the boundary between these areas (a curve between the basins of attraction of different stable equilibria near zero) represents the cross section of stable two-dimensional manifold of the zero saddle-focus. Consequently, if we choose initial conditions in the vicinity of any equilibrium point, we reach one of the stable equilibrium points and, thus, all of oscillatory attractors are hidden attractors. Then, we consider a vicinity of the stable equilibrium (Fig. 5f). There one can see a large basin of attraction surrounds one of the symmetric stable equilibrium points. Also, there are the basin of attraction of another symmetric stable equilibrium point, and the symmetric basins of attraction of two symmetric chaotic attractors. For these chaotic attractors, the complex structure of their basins of attraction is represented by the area of attractions in the form of bands, which are spiraled together, and their boundaries have self-similar patterns, i.e., fractal structures. Also, there is a basin of attraction of the external stable limit cycle, which surrounds all other discussed basins of attraction.

As mentioned above, in our physical experiment we change the initial conditions of only two dynamic variables x and y corresponding to the voltages $U_1$ and $U_2$ on the capacitors of the oscillatory circuit, respectively. We do not change the initial state of the third variable z corresponding to the current in the inductor $I_L$. Inductor current fluctuates in small vicinity of zero. Thus, it is not possible to distinguish and reveal hidden attractors for the first region of parameters, since we do not able to set the value of the variable z to a nonzero value when closing the circuit and to investigate the neighborhood of a nonzero equilibrium state. Also, for this configuration of hidden attractors, the implementation of the regime with trajectories escaping to infinity has its own specifics. The property of a trajectory tending to infinity indicates that this trajectory falls into a region in the phase space where there is no global contraction of the phase volume, and in some sense the system becomes nondissipative having an unlimited growth of the dynamical variable. In a physical experiment, it is impossible to observe the escape of a trajectory to infinity due to the peculiarities of the operation of the op-amps: if the voltage at the output of the op-amp becomes higher than the supply voltage, then the op-amp goes into the saturation mode. In this case, in the experiment, one do not observe self-oscillations, the voltages on the capacitors are constant and equal to the supply voltage of the op-amps. This difference is a consequence of the difference between nonlinear I–V curve (5) and its approximation (7). The third condition in (5) defines an additional break in the I–V curve (which, however, is outside the dynamics we are considering for the second configuration of attractors). For the first configuration of attractors, this feature leads to the fact that instead of the ”escape-to-infinity” regime, a stable equilibrium corresponding to the supply voltage of the circuit is observed.

For the second region in the parameter space and corresponding second configuration of attractors, the situation is different: it is fundamentally important to investigate the neighborhood of the zero equilibrium, and the neighborhoods of symmetric equilibria do not play a special role. It is also worth noting that such a configuration is richer in terms of multistability: it assumes possibility to observe five attractors, three of which are hidden. This configuration of attractors previously demonstrated in [5, 50,51,52] is quite robust to parameter changes (see works [5, 51], where the corresponding structure of the parameter space is analyzed). In [5, 50], the implementation of hidden attractors for the case of negative values of the parameter $\gamma$ is demonstrated, while in Fig. 5d an example of the existence of hidden attractors for positive values of the parameter $\gamma$ is shown.

Further in this work, we consider the parameters of the radiophysical model corresponding to the second region of the parameter space. To this end, we numerically investigate the bifurcation scenario of the birth and transition from hidden to self-excited attractors and the configuration of the I–V curve only for such a choice of parameters.

In the work [5], the regions of existence of hidden attractors in a two-parameter space ($m_0$, $m_1$) are shown and scenarios of their occurrence are described. In particular, for the region of parameters interesting to us, it is shown that the external large-amplitude limit cycle appears as a result of the supercritical Andronov–Hopf bifurcation of the zero equilibrium (see, e.g., [45, 53]).

Let us turn to one-parameter bifurcation analysis depending on the parameter $m_1$. In Fig. 6a, a bifurcation diagram built using the numerical package XPPAUT [54] is presented where with different colors we depict stable (red) and unstable (black) equilibrium points and maximum values of stable (green) and unstable (blue) limit cycles in projection into dynamical variable x (the package determines all variables). We started from stable equilibrium at $m_1 = 0$ and continuation of equilibrium point firstly was implemented with detection of the Andronov–Hopf bifurcation point. Then we started from the Andronov–Hopf bifurcation point and construct a cycle which was born near equilibrium point with standard XPPAUT command. Remark that XPPAUT allow to continue this cycle on parameter (the path in the parameter space is determined automatically) and also find and construct another cycle which was born as a result of saddle-node bifurcation. The line of cycles was constructed in one iteration. From the period-doubling bifurcation (point PD) it is possible to construct additional stable cycle, but the second round of iteration is needed for that, which was missed to avoid difficultization of the figure. In Fig. 6b and c, two bifurcation trees obtained with direct integration are shown. They were constructed with Poincaré cross section by plane $z=0$, and Fig. 6b and c demonstrate the projection of the tree into dynamical variable x. For parameter intervals where the equilibrium point is stable we depict x-projection position of the equilibrium point. All the diagrams are built for the parameters: $\alpha = 8.41$, $\beta = 12.23$, $\gamma = 0.0435$, and $m_0 = -1.366$.

To visualize self-excited attractors we should check the behavior of trajectories in vicinities of unstable equilibria. For Chua system (6), we should check trajectories from vicinity of saddle-focus at zero. Remark that the system is linear near zero equilibrium, there are two-dimensional stable and one-dimensional unstable manifolds, and the Jacobian matrix near zero equilibrium is independent of the parameter $m_1$. We verified the set of initial conditions, chosen randomly in the cube of phase space with a side $10^{-3}$ surrounding the zero saddle equilibrium, and we obtained the same bifurcation tree. By red and pink in Fig. 6b, we depict bifurcation trees constructed for the initial conditions fixed in the vicinity of the saddle zero equilibrium: $x_0 = 0.001$, $y_0 = 0.001$, and $z_0 = 0.001$ for the red tree; $x_0 = -0.001$, $y_0 = -0.001$, and $z_0 = -0.001$ for the pink one.

Fig. 6

Bifurcation diagram (a); bifurcation trees (b, c). Parameters $\alpha = 8.41$, $\beta = 12.23$, $\gamma = 0.0435$, and $m_0 = -1.366$. LP is the saddle-node bifurcation; HB is the Andronov–Hopf bifurcation; PD is the period-doubling bifurcation

Figure 6c shows a family of bifurcation trees built with inheritance of the initial conditions.⁸ The starting initial conditions for the tree shown in black (see Fig. 6a) are chosen on the hidden attractor at $m_1 = -0.12$ ($x_0 = 0.55$, $y_0 = -0.36$, $z_0 = 0.00$). From this point we scan a parameter interval in two directions, defined by increasing, or decreasing parameter $m_1$, and apply inheritance of the initial conditions. For the gray tree, the starting point is chosen on the symmetric hidden attractor.

Thus, as the parameter $m_1$ increases, the following bifurcation transitions can be observed. At $m_1 = -0.4$, the system has two coexisting symmetric saddle equilibria (saddle-foci with two-dimensional unstable manifold); the system also contains a saddle-focus with a one-dimensional unstable manifold. At $m_1 \approx -0.2447$, saddle-foci with two-dimensional unstable manifold undergo the Andronov–Hopf bifurcation (HB) and become stable. This bifurcation is subcritical, and a saddle limit cycle is born. The cycle has a relatively large amplitude because system (6) is piecewise linear and the equilibrium is a center at the Andronov–Hopf bifurcation point. With further increasing of the parameter $m_1$ at $m_1 \approx -0.1031$, as a result of a saddle-node bifurcation (see point LP in Fig. 6a), the saddle cycle is merged with another stable limit cycle (one pair of cycles is shown in Fig. 6a; the other pair is obtained due to the presence of symmetry in the system), which coexists with stable equilibria. Such a configuration is typical for the subcritical Andronov–Hopf bifurcation and can be associated with the co-dimension-2 Bautin bifurcation [42]. The limit cycles are located in such a way that from the vicinity of the equilibria, including the saddle-focus with one-dimensional unstable manifold, a phase trajectory is attracted to one of these equilibria; thus, these stable limit cycles are hidden. As the parameter $m_1$ decreases, the stable limit cycles undergo a period doubling bifurcation (at $m_1 \approx -0.1441$ labeled with PD in Fig. 6a). The bifurcation trees (Fig. 6c) show a cascade of period doubling bifurcations forming coexisting hidden chaotic attractors. At $m_1 \approx -0.186$, chaotic attractors are collapses as a result of the crisis [55, 56] and the trajectories tend to equilibria. For $m_1 < -0.2447$, equilibrium points become unstable and trajectories from the vicinity of the zero unstable equilibrium begin to reach the chaotic attractor. At the same time, it is clearly seen on the bifurcation tree (Fig. 6b, c) that symmetric chaotic attractors have already merged into one chaotic attractor; however, this attractor is already self-excited. Such bifurcations⁹ form a structure of bifurcation tree with gap between hidden and self-excited attractors, where stable equilibrium states are dominant. To guarantee the absence of other hidden attractors one may carry out a detailed analysis of the structure for basins of attraction in the same way as in Fig. 5b, c, e, and f.

Thus, with the considered change in the parameters and for the given range, hidden attractors arise as a result of a saddle-node bifurcation of the production of two pairs of cycles, and undergo a crisis, which leads to their collapse. Subsequently, they transform into a merged self-excited attractor through the subcritical Andronov–Hopf bifurcation. In Fig. 6c, the interval of the parameter $m_1$, corresponding to the existence of hidden attractors, is marked in purple. Remark that in our experiments the attractors are revealed by the standard integration (fourth-order Runge–Kutta method), and the obtained results are in a good agreement with physical experiments. At the same time, more accurate numerical methods (see, e.g., [58, 59]) may help to reveal other attractors and repellers in the mathematical model, which we do not observe in the physical model due to the presence of noise.

Fig. 7

Graphs of the function f(x) (7), which is an approximation of the I–V curve of the Chua diode. The I–V curve configurations in which hidden attractors can be observed are marked in purple

Let us move on to consider the features of the nonlinear function that characterizes the Chua diode. As mentioned earlier, the nonlinear I–V curve is a piecewise linear function, different sections of which have different tilt angles, which in the experiment are controlled by resistors connected to op-amps within the Chua diode. For mathematical modeling, the I–V curve of this element is approximated by piecewise linear function (7), in which the tilt angles of various linear sections are controlled by the parameters $m_0$ and $m_1$ [17]. When changing only the parameter $m_1$, the central part of the I–V curve in the range $(-1, 1)$ remains unchanged, and the angle of the side branches changes. Varying the parameter $m_0$ leads to a change in the angle of the central part of the curve within the range $(-1, 1)$. Figure 7 shows the graphs of the nonlinear function f(x) for the critical values of the parameter $m_1$ which correspond to the existence of hidden attractors: the black line for $m_1 = -0.1031$ corresponds to the saddle-node bifurcation point, which resulted in appearing of a hidden attractor; the red line for $m_1 = -0.186$ corresponds to the crisis point of the hidden chaotic attractor. Thus, in this graph, we can distinguish the regions corresponding to different dynamics of the system and different types of attractors. The purple areas correspond to the existence of three hidden attractors.

In general case, numerical analysis of dynamics via direct integration or by using Poincaré sections suffers from the accuracy of determining stationary points, the corresponding periodic trajectories, their periods, and initial data (which can fill an unbounded domain of the phase space, e.g., as in example (36)), numerical integration of irregular and unstable trajectories (e.g., for the Lorenz system, the shadowing theory gives a rather short time interval of reliable integration for the standard numerical procedure and parameters of tolerances [49, 60]), as well as identifying chaotic behavior by finite-time local Lyapunov exponents (which can change their signs as the time interval of integration is increasing [49]). Also, there are classes of systems for which the application of the analysis of dynamics on a Poincaré section to reveal and analyze hidden attractors may not be straightforward. These are, for example, multidimensional ODEs and difference systems (where the choice of Poincaré sections may not be obvious); systems with fractional derivative operators (which do not have periodic solutions at all [61]); systems with a cylindrical phase space that can have a global attractor without equilibria [62] and systems without equilibria and with local attractors in Euclidean space; as well as discontinuous systems (where the birth of attractors may be essentially determined by the behavior of the system on the discontinuity surface, see, e.g., [63,64,65,66]) and systems with uncountable and unbounded set of equilibrium states (see, e.g., [67]).

4 Experimental observation of dynamical regimes in the Chua circuit

Now let us turn to the experimental study and visualization of the hidden attractors. As it is mentioned above, we are able to implement the changing of two initial conditions $x_0$ and $y_0$ related to capacitor voltages C1 and C2 at the moment the circuit is turn on. The circuit implementation for changing the third initial condition corresponding to the inductor current is more difficult and is not included in this work. As one can see from the structure of the basins of attraction, for checking the regime discussed above, it is enough to vary one initial condition. Hence, we keep the voltage on the second capacitor C2 satisfying the zero initial condition.

Fig. 8

a Schematic diagram of the experimental Chua circuit with switches for changing initial conditions; b the photograph of the experimental laboratory model and the IJBC journal cover with hidden Chua attractors [5]. The classical Chua circuit is marked with a blue rectangle

Figure 8a shows the schematic diagram of the Chua circuit with an additional block that allows us to control the initial conditions. Figure 8b presents a photograph of the experimental setup. To control the operation of the circuit and set the initial conditions, electronic keys (multiplexors) DD1 and DD2 are added to the circuit. With a zero signal at the input (In), the key 01 of the multiplexor DD1 connects the capacitor C1 to point 1, and the key 11 connects the capacitor C2 to point 2. Keys 01, 11 of the multiplexor DD2 are connected to the inputs of the op-amps DA1.1, DA1.2, respectively, as shown for the Chua circuit in Fig. 2. When a high logic level is applied to the input (In), the keys 01 and 11 of the multiplexor DD1 open, and keys 00 and 10 close, connecting the capacitors C1 and C2 to the sliding contacts of potentiometers R7 and R8, respectively. At the same time, keys 01 and 11 of the multiplexor DD2 also open, turning off the negative resistance block for the duration of the pulse. In Table 1, we summarize states of electronic keys DD1, DD2 depending on the control input parameter (In).

Table 1 States of electronic keys DD1, DD2 depending on the control input parameter In

We can change the voltage at the sliding contacts of potentiometers R7 and R8 during the experiment by adjusting manually the initial voltages of the capacitors. Thus, when rectangular pulses of duration $T_{\textrm{imp}}$ with a repetition period T are applied to the input (In), throughout the pulse, the capacitors charge to some initial values, and at the end of the pulse, the circuit is switched to the normal operation of the generator with the fixed/specified initial conditions. During the experiment, we apply a pulse signal to the input (In) and changed the voltage at the sliding contacts of potentiometers R7 and R8, thereby controlling the initial conditions. Using a two-channel oscilloscope operating in the X–Y mode, we observe transient processes in the circuit, stable and unstable limit cycles and equilibrium points. The period T and the duration of the pulses $T_{\textrm{imp}}$ are selected so that the charging time of the capacitors is less than $(T-T_{\textrm{imp}})$. A similar technique is used to study transient processes and basins of attraction of multistable systems in [68]. Op-amps DA2.1, DA2.2 and DA3.1 are voltage buffers, or so-called decoupling amplifiers, which are needed to ensure measuring circuits, do not affect the operation of the main circuit. Here, for the experimental setup we use op-amps AD822 (see, e.g., [69]).

Table 2 Comparison of the parameters for physical and mathematical models

To detect hidden oscillations, the nominal values for the experimental scheme are carefully calculated so that they corresponded to the values of the model parameters. The nominal values of the oscillatory circuit are fixed as follows:

$$\begin{aligned} \begin{array}{l} C1 = {311}\, {\hbox {nF}}, \textit{C2} = {37}\, {\hbox {nF}}, \textit{L} = {15.79}\,{\hbox {mH}},\\ \textit{R} = {788}\,\Omega , R_L = {2.8}\,\Omega . \end{array} \end{aligned}$$

(10)

For these nominal values, the dimensionless parameters of the model $\alpha$, $\beta$, and $\gamma$ are as follows: $\alpha = \frac{C2}{C1} \approx 8.4054$, $\beta = \frac{C2 R^2}{L} \approx 12.2301$, and $\gamma = \frac{C2 R R_L}{L} \approx 0.0435$. The slopes of the linear pieces and the break points of the I–V curve are determined by potentiometers R1–R6: $R1 = {8520}\,\Omega$, $R2 = {123}\,\Omega$, $R3 = {12.02}\,{\hbox {k}}\Omega$, $R4 = {1008}\,\Omega$, $R5 = {1003}\,\Omega$, $R6 = {24.41}\,{\hbox {k}}\Omega$. Thus, in the experiment, the amplification coefficients are: $K_1 = 12.9246$, $K_2 = 1.0411$, consequently, and $U_{\textrm{DA1}} = {1.1606}\,{\hbox {V}}$, $U_{\textrm{DA2}} = {14.408}\,{\hbox {V}}$. The slope of the central piece of the I–V curve inside the interval from $-U_{\textrm{DA1}}$ to $U_{\textrm{DA1}}$ equals $G_1 + G_2 = -0.001\, 734 {\hbox {S}}$. For the next intervals, from $-U_{\textrm{DA2}}$ to $-U_{\textrm{DA1}}$ and from $U_{\textrm{DA1}}$ to $U_{\textrm{DA2}}$, the slope is $1/R1 + G_2 = -0.000\, 2167\, {\hbox {S}}$. Then, the parameters $m_0 \approx -1.3661$ and $m_1 \approx -0.1708$, and it corresponds to the regime, when three hidden attractors coexist (a limit cycle and two symmetric chaotic attractors) together with two symmetric stable foci. In Table 2, the relation between parameters of the mathematical and the physical models is presented.

Fig. 9

Photographs of an oscilloscope screen, visualizing hidden chaotic attractors in a radiophysical experiment: The shining dot is the initial condition, a the stable equilibrium point; b the symmetric hidden chaotic attractor; c the stable equilibrium point; d the symmetric hidden chaotic attractor; e, f the external limit cycle. In all 6 photographs, the abscissa is $U_1$ and the ordinate is $U_2$. The coordinate scales are 0.2 volts for X-axis and 0.1 volts for Y-axis of the square grid in (a)–(e); and 0.5 volts for X-axis and 0.2 volts for Y-axis, respectively, in (f)

Using the experimental setup shown in Fig. 8b, a study of hidden attractors is carried out. In Fig. 9, the examples of phase portraits in the projection onto the ($U_1$, $U_2$)-plane are shown in the oscilloscope screen. The experimental setup parameters are fixed in accordance with the above description. The presented phase portraits are obtained for the same parameter values, only the initial condition of the variable $U_1$ is changed, while the initial condition for $U_2$ is set equal to zero. The initial condition for the current $I_L$ can also be set to zero. From the vicinity of the zero saddle-focus equilibrium point, the trajectory converges to one of the symmetric stable foci (see the example in Fig. 9a). With a smooth detuning from the zero saddle-focus, the stable equilibrium mode is replaced by a chaotic attractor; Fig. 9b shows an example of one such attractor. Further changing of the initial condition from zero leads to the basin of attraction of the second symmetric stable equilibrium state (see Fig. 9c). Next, we again observe a hidden chaotic attractor (Fig. 9d), a symmetric partner of the previous one (Fig. 9b). Thus, an accurate selection of the initial conditions allows one to discover two symmetric hidden chaotic attractors. The alternation of domains of stable equilibrium and hidden attractors is in a good agreement with the results of the numerical modeling (see the structure of the basins of attraction in Fig. 5e). The oscilloscope photographs clearly show that there is a switch between the mode on the hidden attractor and the mode corresponding to the stable equilibrium. This feature is related to the fact that the basins of attraction of the obtained hidden attractors are rather small and border on the basins of attraction of the stable foci. Therefore, as a result of the noise influence, we can see a switching from one mode to another. Further moving from zero equilibrium leads to transition to the stable limit cycle of a large amplitude. Figure 9e shows this limit cycle on a scale corresponding to the previous experimental phase portraits, similar to that in Fig. 5c.

In the experiment, by smoothly changing (selecting) the initial conditions, one can find a saddle limit cycle. In Fig. 9e and f, the initial conditions are chosen near an unstable limit cycle; the trajectory first moves to the unstable limit cycle, performs several oscillations in its vicinity and then tends to the stable limit cycle of a larger amplitude. Note that the invariant two-dimensional cylinder-shaped stable and unstable manifolds of cycles may play an essential role in partitioning the phase space into basins of attraction (see, e.g., [70,71,72]).

Fig. 10

Visualization of the saddle limit cycle in numerical (a) and physical experiments (b)

A comparative analysis of the unstable cycle in the numerical and physical experiments is carried out. Figure 10 shows the time series and two-dimensional projections of motion of a representative point in the phase space, when choosing initial conditions on the unstable limit cycle. Figure 10a shows the results of numerical calculations, and Fig. 10b shows the data obtained in the physical experiment. In numerical experiment an initial condition on a saddle limit cycle can be obtained by bifurcation analysis packages which then allow to follow the saddle cycle transformation during the change of bifurcation parameter. For our configuration of attractors we cannot find this cycle in depending on the parameter $m_1$. That is why we found another bifurcation rout in the parameter space leading to occurrence of the saddle cycle (see details in [5]). Then the transformation of saddle cycle along the route is traced to construct the cycle for the desired value of $m_1$, and we get the following initial condition for the saddle cycle visualization in Fig. 10a: $x_0 = -2.321$, $y_0 = -0.787$, $z_0 = 3.129$. The experimental time series (see Fig. 10b) is constructed for the reference points, the sampling step is $2.5 \, \upmu$s, respectively, the length of the presented time series is 11.255 m s. Obtaining the model, we renormalize the dynamical variables according to the renormalization factor 1.16, i.e., close to unity; therefore, the amplitudes of oscillations of the numerical model and the experimental implementation are in a good agreement. However, the time in model (6) is dimensionless and is normalized to the constant $R \, C2$. In the numerical simulations, the oscillation period for the unstable cycle is $T_{\textrm{UC}}^{\textrm{num}} = 2.406$. To convert this period to the dimensional form, it is necessary to multiply it by the normalization constant: $T_{\textrm{UC}}^{\textrm{num}} = 2.406*311 *10^{-9}*788 = {0.59}$ m s. According to the experimental time series, the oscillation period for the unstable limit cycle is 218 samples, which corresponds to $T_{\textrm{UC}}^{\exp } = {0.55}$ m s. This is close enough to the values obtained numerically. Table 3 shows a comparison of the parameters of mathematical model (6) and the data obtained in the physical experiment.

An important and interesting feature of comparing the numerical and experimental implementations is the characteristic of the oscillation time on the unstable limit cycle. It is clearly seen that in the numerical experiment, the trajectory makes 11 oscillations in the vicinity of the unstable limit cycle, after that it escapes the vicinity of the cycle. Meanwhile, only 8 oscillations are visible in the physical experiment. This metric can be used as an estimation of the noise in the physical model. In mathematical modeling, the role of noise is played by the numerical errors of the calculation scheme. To construct the trajectory, the fourth-order Runge–Kutta method with a constant integration step equal to $10^{-3}$ is used. In a physical experiment, the noise voltage consists of several parts: noise of the op-amps, in which the spectral density of the noise voltage at the output is $25 {\hbox {nV}}{/}\sqrt{{\hbox {Hz}}}$; the capacitor’s noise is $0.3 \, {\hbox {mV}}$; external noise and ripple. Also, in the case of absence of voltages at the inputs of op-amps, the output voltage differs from zero, which introduces additional small constant voltages that affect the overall operation of the circuit.

The correspondence between the mathematical model and the experimental laboratory model has some limitations. In a physical experiment, noise is always presented. There are noises, which are mentioned above, associated with fluctuations of voltages and currents. However, one should also not forget about measurement errors. When developing layouts, researchers rely on nominal electrical values of elements, which can vary within 10%. This error is static and can be eliminated by measuring the real electrical values. Within this work, all electrical values are measured using a multimeter; the capacitance of the capacitors and the inductance of the coil are measured using an LCR-meter of the HM8118 type (see, e.g., [73]). However, there is also a dynamical error associated with the error of the measuring device. This error is significantly less than the static one and is 1% of the nominal value for the multimeter, and 0.1% for the HM8118 meter. For the nominal values we measured, the ranges of the maximum and minimum values of the parameters are calculated taking into account the dynamical error, and they are presented in Table 2. It can be seen that the values of the parameters of mathematical model (6) are inside the relevant intervals indicated in this table.

5 Methods to search for hidden attractors and study of multistability

5.1 The hysteresis loop method

Changing the parameters of the mathematical model and carrying out a parametric bifurcation analysis allow one to obtain some bifurcation mechanisms for the birth of attractors. In the physical experiment, this procedure corresponds to a smooth change of some parameters using a mechanical knob. Changing the parameters in the experiment gives some overall view of its dynamics and characteristic modes. The procedure for scanning the parameter space and detecting the boundaries of regions of different modes in the experiment corresponds to the numerical construction of a chart of dynamical modes with inherited initial conditions, discussed in Sect. 3. Changing the scanning direction makes it possible for some situations to localize the multistability regions in the parameter space. For example, in a simple case of multistability, which arises as a result of the subcritical Andronov–Hopf bifurcation, hysteresis curves can be obtained experimentally. If we take the value of a parameter before the Andronov–Hopf bifurcation point, self-oscillations cannot be excited; in the experiment, a stable equilibrium state is observed in the phase space. After the loss of stability, the trajectory jumps to a limit cycle, which is a result of the subcritical Andronov–Hopf bifurcation. Having found this cycle, if we now smoothly change the parameter in the opposite direction, the state remains on the cycle even when the equilibrium has already become stable again. Thus, we can find the value of the parameter at which a pair of limit cycles (stable and saddle) is born, coexisting with a stable equilibrium state. Such a loop is commonly referred to as a hysteresis curve (see, e.g., [74, p. 643]).

A similar situation can be observed in our case. Figure 11 shows the bifurcation diagram and trees of this type for the considered mathematical model of Chua circuit (6)–(7), which are some analog of the hysteresis curve. Scanning the parameter $m_1$ interval with decreasing (Fig. 11b), we reach the Andronov–Hopf bifurcation point, where the equilibrium state becomes unstable and the trajectories go to symmetric self-excited chaotic attractors. With further decreasing $m_1$ symmetric self-excited attractors are merged into one self-excited attractor. If we now start from the region of small values of $m_1$, where the merged self-excited chaotic attractor exists, and will increase parameter $m_1$ (Fig. 11c), then we can find an interval, where chaotic attractor dived into symmetric pair and then becomes hidden and coexisting with symmetric stable equilibrium states.

Fig. 11

Bifurcation diagram (a) and trees (b, c) for parameters $\alpha = 8.4$, $\beta = 12.2$, $\gamma = 0.0$, $m_0 = -1.16$. LP is a saddle-node bifurcation; HB is an Andronov–Hopf bifurcation; PD is a period-doubling bifurcation

The hysteresis curve provides some overall view into the types of dynamical behavior of the system. However, not in all cases it is possible to detect the full variety of modes in this way. The limitation of the physical characteristics of device in the experiment may not allow going beyond the hysteresis curve and identifying its boundaries; thus, a coexisting attractor may be missed. Also, such configurations of bifurcation diagrams are possible in which the access to hidden attractor by changing the scanning direction of the parameter interval is impossible. A similar situation is possible in the Chua system with the parameters discussed in Sect. 3 (see Fig. 6). In contrast to the case shown in Fig. 11, when the parameter $m_1$ decreases, the hidden attractor does not transform into a self-excited one: before the bifurcation threshold of the loss of stability of symmetric equilibrium states, the hidden attractor collapses as a result of the crisis. Thus, in this case, scanning the parameter interval does not allow detecting hidden attractors even in numerical experiments with direct integration. It is necessary to choose special initial conditions leading to the hidden attractor (i.e., in its basin of attraction).

In a physical experiment, the situation is even more complicated since the parameters $m_0$ and $m_1$ are determined by seven resistors, some of which defines the values of both parameters. In a simplified form, the dependence of $m_0$ and $m_1$ on the values of electrical resistance of resistors is given by Eq. (8). Accordingly, using resistors R3 and R4, we can independently change the coefficient $m_0$. Moreover, a change in $m_1$ necessarily entails a change in $m_0$. Thus, to select the parameters we need to search for suitable nominal electrical values in a multi-parameter space. The question of accessibility and usability of the entire plane ($m_0$, $m_1$) from a physical point of view requires additional attention.

5.2 The advanced harmonic balance method

Now we compare the described results of our experiments with the analytical results of applying the harmonic balance method to the mathematical model of Chua circuit (6).

The harmonic balance method (HBM, or describing function method) [75, 76] is an approximate method to search for periodic oscillations in nonlinear systems.

Consider a 3-dimensional system in the Lurie form [6]

$$\begin{aligned} \dot{u} = P \, u + q \,\psi (\sigma ), \quad \sigma = r^*\,u, \end{aligned}$$

(11)

where for Chua system (6)–(7) we have $u = \left( x, y, z \right) ^*$ and

$$\begin{aligned} \begin{aligned}&P \!=\! \left( \! \begin{array}{ccc} -\alpha (m_1+1) &{} \alpha &{} 0 \\ 1 &{} -1 &{} 1 \\ 0 &{} -\beta &{} -\gamma \\ \end{array} \!\right) \!\!, \quad q \!=\! \left( \!\begin{array}{c} -\alpha \\ 0\\ 0 \\ \end{array}\!\right) \!,&r \!=\! \left( \!\begin{array}{c} 1 \\ 0\\ 0 \\ \end{array}\!\right) ,\\&\psi (\sigma ) \!=\! (m_0 \! - \! m_1) \, \textrm{sat}(\sigma )\\&\qquad \qquad \quad \!=\! \tfrac{1}{2} (m_0 \!-\! m_1) \big (|x\!+\!1| \!-\! |x\!-\!1|\big ). \end{aligned}\nonumber \\ \end{aligned}$$

(12)

Here operator $^*$ denotes transposition operation. For our case $\psi (-\sigma )=-\psi (\sigma )$, the HBM searches for a $2\pi /\omega _0$-periodic solution $u(t) = u(t + 2\pi /\omega _0)$ such that $\sigma (t) \!=\! r^* \, u(t) \! \approx \! a_0 + a_1 \cos \omega _0 t$, where $a_0$ is a shift and $a_1 > 0$ is an amplitude. If the matrix P is non-singular, i.e.,

$$\begin{aligned} \det P = -\alpha \big ((\beta +\gamma ) m_1+\beta \big ) \ne 0, \end{aligned}$$

and does not have purely imaginary eigenvalues, then we can define the frequency $\omega _0 > 0$ and coefficient of harmonic linearization k such that

$$\begin{aligned} \textrm{Im}\, W_{P}( i \, \omega _0) = 0, \qquad k = - \big (\textrm{Re}\, W_{P}(i \, \omega _0) \big )^{-1}, \end{aligned}$$

(13)

otherwise $\omega _0$ is known and $k=0$. Here, $W_{P}(s) = r^* \big (P - s \, I\big )^{-1} q$ denotes a transfer function of system (11), i.e., a complex-valued function, which is the ratio between the Laplace transforms of the output signal $\sigma (t)$ and of the input signal $\xi (t)$ for the initial state $u(0) = 0$ [77].

Then, we rewrite system (11) as follows:

$$\begin{aligned} \dot{u} = P_0 \, u + q \, \varphi (r^* \,u), \end{aligned}$$

(14)

where $\varphi (\sigma )=\psi (\sigma )-k\sigma$, and the matrix $P_0 = P + k \,q \, r^*$ has a pair of pure-imaginary eigenvalues $\pm i\omega _0 \ne 0$. The transfer function for system (14) is as follows: $W_{P_0}(s) = r^* \big (P_0 - s \, I\big )^{-1} q$. Following the HBM, the values $a_{0,1}$ are defined by equations:

$$\begin{aligned} \begin{aligned} \frac{2\pi a_0}{\omega _0} + W_{P_0}(0) \int _0^{\tfrac{2\pi }{\omega _0}}\!\!\! \varphi (a_0 + a_1 \cos (\omega _0 \tau )) {\textrm{d}}\tau&= 0,\\ \varPhi (a_0,a_1)\!=\!\!\! \int _0^{\tfrac{2\pi }{\omega _0}} \!\!\! \varphi (a_0 \!+\! a_1 \cos (\omega _0 \tau ))\!\cos (\omega _0 \tau ) {\textrm{d}}\tau&= 0, \end{aligned} \end{aligned}$$

(15)

where $\varPhi (a_0,a_1)$ is called a describing function [77]. If $a_0 = 0$, i.e., there is no shift assumed, the first equation in (15) becomes trivial, since $\varphi (\cdot )$ is odd.

The HBM can be rigorously justified, when a small parameter $\varepsilon > 0$ is introduced in the system, i.e., when the nonlinearity $\varphi (\sigma )$ in (14) is changed by $\varepsilon \varphi (\sigma )$:

$$\begin{aligned} \dot{u} = P_0 \, u + \varepsilon \, q \, \varphi (r^* \, u). \end{aligned}$$

(16)

There is always a nonsingular linear transformation $u = S v$, defined by matrix S, such that

$$\begin{aligned} \begin{aligned}&J \!=\! S^{-1} P_0 S = \left( \! \begin{array}{ccc} 0 &{} -\omega _0 &{} 0 \\ \omega _0 &{} 0 &{} 0 \\ 0 &{} 0 &{} -d \\ \end{array} \!\right) \!, b\!=\! S^{-1}q \!=\! \left( \! \begin{array}{c} b_1 \\ b_2 \\ b_3 \\ \end{array} \!\right) , \\&c^* = r^* \, S = \left( \begin{array}{ccc} 1 &{} 0 &{} -h \\ \end{array} \right) . \end{aligned} \end{aligned}$$

(17)

Thus, due to invariance of transfer functions with respect to linear transformations, for system (16) we have

$$\begin{aligned} W_{P_0}(s)= & {} c^* \big (J - s \, I\big )^{-1} b\nonumber \\= & {} \dfrac{-b_1 s + b_2 \omega _0}{s^2 + \omega _0^2}+\frac{b_3 h}{s+d}. \end{aligned}$$

(18)

Developing the ideas from [46, 78] we get

Theorem 1

If $d>0$ and there exist $a_0$ and $a_1 > 0$ satisfying (15) such that

$$\begin{aligned} b_1\frac{\partial \varPhi (a_0, a)}{\partial a}\bigg |_{a=a_1} < 0, \end{aligned}$$

(19)

then, for sufficiently small $\varepsilon > 0$, system (16) has a stable periodic solution in the form

$$\begin{aligned} S\big (v_{01} + a_1 \cos (\omega _0 t), v_{02} + a_1 \sin (\omega _0 t), v_{03}\big )^* + O(\varepsilon )\nonumber \\ \end{aligned}$$

(20)

with the period $T = \frac{2 \pi }{\omega _0} + O(\varepsilon )$ and

$$\begin{aligned} v_{01}= & {} \varkappa \,\frac{b_2}{\omega _0}, v_{02} = -\varkappa \,\frac{b_1}{\omega _0},\\ v_{03}= & {} -\varkappa \,\frac{b_3}{d}, \varkappa = a_0\,W_{P_0}^{-1}(0). \end{aligned}$$

For the opposite sign in (19), periodic solution (20) is of a saddle type.

For $\omega _0$ and $a_{0,1}$ defined by (13) and (15) the advanced HBM predicts the existence of periodic solutions in system (11), and these predicted periodic solutions can be visualized by Theorem 1 as

$$\begin{aligned} u^\textrm{HBM}(t) \approx S(v_{01} + a_1 \cos (\omega _0 t), v_{02} + a_1 \sin (\omega _0 t), v_{03})^*. \end{aligned}$$

Trajectories with initial data given by Theorem 1

$$\begin{aligned} u^\textrm{HBM}(0) \approx S(v_{01} + a_1, v_{02}, v_{03})^* \end{aligned}$$

(21)

can be used for a numerical search of attractors in system (11). However, a rigorous application of Theorem 1 requires the fulfillment of condition (19) for the visualization of a stable periodic orbit from initial point (21) in system (16) with a sufficiently small $\varepsilon =\varepsilon _0$. Then, the transformation of this initial stable periodic orbit in the phase space while increasing $\varepsilon$ from $\varepsilon _0$ up to 1 can be considered in a continuation procedure. For that on each step of the continuation procedure, the initial point for a trajectory to be integrated is chosen as the last point of the trajectory integrated on the previous step. If, while changing from $\varepsilon _0$ to 1, there is no loss of stability bifurcation and the considered trajectory approaches an attractor, then at the end of the procedure an attractor of initial system (11) is localized.

Now let us apply the advanced HBM to study the Chua model. For the transfer function of (12), we have $W_P(s) = \frac{Y(s)}{X(s)}$, where $Y(s) = \alpha (s^2 + (\gamma + 1) s + \beta + \gamma )$ and $X(s) = s^3 + ((m_1 + 1) \alpha + \gamma + 1) \,s^2 + (((m_1 + 1)\gamma + m_1) \alpha + \beta + \gamma ) \, s + \alpha (m_1 (\beta + \gamma ) + \beta )$. Here $W_P (0) = \frac{\beta +\gamma }{(\beta +\gamma ) m_1+\beta }$. By (13) for $\omega _0 > 0$ we have

$$\begin{aligned} \omega _0^2= & {} \tfrac{-(\gamma ^2+\alpha -2\beta +1)}{2}\\{} & {} \pm \tfrac{\sqrt{\gamma ^4 - 2(\alpha +2\beta +1)\gamma ^2 -8\beta \gamma +(\alpha +1)^2 - 4\beta }}{2}. \end{aligned}$$

From (18) with $P_0 = P + k \,q \, r^*$, we get

$$\begin{aligned} \begin{aligned}&k = \tfrac{-\alpha (m_1+m_1\gamma +\gamma )+\omega _0^2-\gamma -\beta }{\alpha (1+\gamma )},\; d = \tfrac{\alpha +\omega _0^2-\beta +1+\gamma +\gamma ^2}{1+\gamma }, \\&h = \tfrac{\alpha (\gamma +\beta -(1+\gamma )d+d^2)}{\omega _0^2+d^2}, b_1 = \tfrac{\alpha (\gamma +\beta -\omega _0^2-(1+\gamma )d)}{\omega _0^2+d^2}, \\&b_2\!= \!\tfrac{\alpha \big ((1+\gamma -d)\omega _0^2+(\gamma +\beta )d\big )}{\omega _0(\omega _0^2+d^2)},\; b_3\!=\!1, W_{P_0}\!(0)\!= \!\tfrac{ b_2}{\omega _0}\!+\!\tfrac{h}{d}. \end{aligned} \end{aligned}$$

(22)

From (17), we get the matrix $S = \{s_{ij}\}_{i,j=1}^{3}$ with

$$\begin{aligned}&s_{11}=1, \qquad s_{12}=0, \qquad s_{13}=-h, \\&s_{21}=m_1+1+k, \ s_{22}=-\frac{\omega _0}{\alpha },\\&s_{23}=-\tfrac{h(\alpha (m_1+1+k)-d)}{\alpha }, \\&s_{31}=\tfrac{\alpha (m_1+k)-\omega _0^2}{\alpha }, \ s_{32} = -\tfrac{\alpha (\beta +\gamma )(m_1+k)+\alpha \beta -\gamma \omega _0^2}{\alpha \omega _0}, \\&s_{33} = h\tfrac{\alpha (m_1+k)(d-1)+d(1+\alpha -d)}{\alpha }. \end{aligned}$$

Computation of the integrals in (15) gives the following:

• if ($-1 < a_0 + a_1 \le 1$ and $a_0 \le -1$) or ($a_0 + a_1 \le 1$ and $a_0 > -1$ and $a_0 - a_1 < -1$), then

  $$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} (m_0 - m_1)&{} \bigg ( -\tfrac{\pi }{2} (1 - a_0) + (1 + a_0) \arcsin \tfrac{1 + a_0}{a_1} \\ &{} +\sqrt{a_1^2-(1 + a_0)^2}\bigg ) = -\tfrac{\pi a_0}{W_P(0)}, \end{aligned} \\ \begin{aligned} (m_0 - m_1)&{} \bigg ( a_1 \big (\tfrac{\pi }{2} + \arcsin \tfrac{1+a_0}{a_1}\big ) \\ &{} + (1 + a_0) \sqrt{1-\tfrac{(1 + a_0)^2}{a_1^2}} \bigg ) = \pi a_1 k, \end{aligned} \\ \begin{aligned} \frac{\partial \varPhi (a_0, a_1)}{\partial a_1} &{} = \tfrac{1}{\omega _0}\bigg [ (m_0 - m_1) \bigg ( \tfrac{\pi }{2} + \arcsin \tfrac{1+a_0}{a_1} \\ &{}\quad s-\tfrac{1+a_0}{a_1}\sqrt{1-\tfrac{(1 + a_0)^2}{a_1^2}} \bigg ) - \pi k\bigg ]. \end{aligned} \end{array}\right. }\nonumber \\ \end{aligned}$$

  (23)

• if ($a_0 - a_1 < 1$ or $a_0 \le 1$) and $a_0 - a_1 \ge - 1$ and ($a_0 > 1$ or $a_0 + a_1 > 1$), then

  $$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} (m_0 - m_1)&{}\bigg ( \tfrac{\pi }{2} (1 + a_0) - (1 - a_0)\arcsin \tfrac{1-a_0}{a_1}\\ &{} -\sqrt{a_1^2-(1 - a_0)^2} \bigg ) = -\tfrac{\pi a_0}{W_P(0)}, \end{aligned} \\ \begin{aligned} (m_0 - m_1)&{}\bigg ( a_1 \big (\tfrac{\pi }{2} + \arcsin \tfrac{1-a_0}{a_1}\big ) \\ &{} + (1 - a_0) \sqrt{1-\tfrac{(1 - a_0)^2}{a_1^2}}\bigg ) = \pi a_1 k, \end{aligned} \\ \begin{aligned} \frac{\partial \varPhi (a_0, a_1)}{\partial a_1} &{}= \tfrac{1}{\omega _0}\bigg [ (m_0 - m_1) \bigg ( \tfrac{\pi }{2} + \arcsin \tfrac{1-a_0}{a_1} \\ &{}\quad -\tfrac{1 - a_0}{a_1}\sqrt{1-\tfrac{(1 - a_0)^2}{a_1^2}} \bigg ) - \pi k\bigg ]. \end{aligned} \end{array}\right. }\nonumber \\ \end{aligned}$$

  (24)

• if ($a_0 - a_1 < -1$ and ($a_0 > 1$ or $a_0+a_1>1$)) or ($a_0 \le -1$ and $a_0 + a_1 > 1$), then

  $$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} (m_0 &{} - m_1)\bigg ( (1 + a_0)\arcsin \tfrac{1+a_0}{a_1} - (1 - a_0)\arcsin \tfrac{1-a_0}{a_1} \\ &{} +\sqrt{a_1^2-(1 + a_0)^2} -\sqrt{a_1^2-(1 - a_0)^2} \bigg ) = -\tfrac{\pi a_0}{W_P(0)}, \end{aligned} \\ \begin{aligned} &{}(m_0 - m_1)\bigg ( a_1 \big (\arcsin \tfrac{1-a_0}{a_1} + \arcsin \tfrac{1+a_0}{a_1}\big ) \\ &{} + (1 \!-\! a_0) \sqrt{1\!-\!\tfrac{(1 - a_0)^2}{a_1^2}} + (1 \!+\! a_0) \sqrt{1\!-\!\tfrac{(1 + a_0)^2}{a_1^2}} \bigg ) = \pi a_1 k, \end{aligned} \\ \begin{aligned} \frac{\partial \varPhi (a_0, a_1)}{\partial a_1} = \tfrac{1}{\omega _0}\bigg [ (m_0 - m_1) \bigg (\arcsin \tfrac{1-a_0}{a_1} + \arcsin \tfrac{1+a_0}{a_1} \\ -\tfrac{1+a_0}{a_1}\sqrt{1-\tfrac{(1 + a_0)^2}{a_1^2}} -\tfrac{1 - a_0}{a_1}\sqrt{1-\tfrac{(1 - a_0)^2}{a_1^2}} \bigg ) \!-\! \pi k\bigg ]. \end{aligned} \end{array}\right. }\nonumber \\ \end{aligned}$$

  (25)

Case 1. For Chua system (6)–(7) with the parameters

$$\begin{aligned}{} & {} \alpha = 8.4,\ \beta = 12, \gamma = 0,\ m_0 = -0.12,\nonumber \\{} & {} m_1 = -1.15 \end{aligned}$$

(26)

the advanced HBM [see (13), (15), (23)–(25)] predicts the existence of 8 periodic orbits, 2 of which are symmetric and another 6 have shifts with respect to zero equilibrium $F_0$ (see Fig. 12a):

k	$\omega _0$	$a_0$	$a_1$	Thm. 1, Eq. (19)
0.9686	3.2367	$\pm \, 0.0446$	1.2237	Unstable
		0	1.1587	Unstable
0.2123	2.0306	$\pm \, 3.2148$	4.6062	unstable
		$\pm \, 2.935$	4.7771	Stable
		0	6.1492	Stable

For $\omega _0 = 2.0306$, $a_0 = 0$, $a_1 = 6.1492$ (and $T = 3.0941, d=1.5235$), the trajectory with initial data given by (21)

$$\begin{aligned} x(0) = 6.1492, \ y(0) = 0.3832, \ z(0) = -8.7846 \end{aligned}$$

(27)

tends to a stable periodic orbit for $\varepsilon = 0.1$. The continuation procedure (with $\varepsilon _0=0.1$, increment of $\varepsilon$ by 0.3, and integration on time interval [0, 150]) leads to localization of the hidden chaotic Chua attractor $\mathcal {A}_+^\textrm{hid}$ in Fig. 12c [46, 50]. However, in this case, the basins of attraction of $\mathcal {A}_\pm ^\textrm{hid}$ contain the initial point given by (21); thus, the attractors can be visualized directly from this point without the continuation procedure (see Fig. 12b). To localize the symmetric attractor $\mathcal {A}_-^\textrm{hid}$ one can use symmetry of system (6)–(7).

The trajectories with initial point (21) (i.e., $(1.1791, 1.0018, -1.7036)$ and $(1.3915, 0.2871, -3.3656)$) on two predicted stable nonsymmetric periodic orbits for $\varepsilon = 0.1$ tend to the symmetric stable periodic orbit instead of visualizing additional attractors. This shows the significance of smallness of the parameter $\varepsilon$ in Theorem 1 and the difference in the initial data for (20) and (21).

Three predicted unstable periodic orbits in vicinity of stable zero equilibrium may be considered as another justification of the Chua conjecture stating that the birth of the hidden attractor in the Chua system is connected with the subcritical Andronov–Hopf bifurcation [5].

Case 2. For Chua system (6)–(7) with

$$\begin{aligned} \begin{gathered} \alpha = 8.41, \quad \beta = 12.23, \quad \gamma = 0.0435, \\ m_0 = -1.366, \quad m_1 = -0.17, \end{gathered} \end{aligned}$$

(28)

the advanced HBM predicts the existence of 6 periodic orbits, 2 of which are symmetric and another 4 have shifts with respect to zero equilibrium $F_0$ (see Fig. 13a):

k	$\omega _0$	$a_0$	$a_1$	Thm. 1, Eq. (19)
$-\, 0.0746$	3.2392	$\pm \, 1.4214$	0.5447	Unstable
		0	20.3926	Stable
$-\, 0.7511$	2.1344	$\pm \, 0.7813$	1.0797	Unstable
		0	1.9329	Unstable

The trajectory with initial point

$$\begin{aligned} x(0) \!=\! 20.3926, \,\, y(0) \!=\! 15.4037, \,\, z(0) \!=\! -30.4309\nonumber \\ \end{aligned}$$

(29)

on predicted stable periodic orbit ($T = 1.9397, d = 7.396$) visualizes a stable stable periodic orbit in system (16) for $\varepsilon \in (0,1]$. For $\varepsilon = 1$ this periodic orbit represents a hidden attractor $\mathcal {A}^\textrm{hid}_\textrm{limCyc}$.

Trajectories with the initial point on predicted unstable periodic orbit tend to two symmetric hidden chaotic attractors $\mathcal {A}_{\pm }^\textrm{hid}$ (from the initial points $(1.9329, 0.1525, -2.8275)$ and $(-0.8767, 0.4064, 0.6035)$, see Fig. 13a) and to stable symmetric equilibria $S_\pm$.

Case 3. For Chua system (6)–(7) with

$$\begin{aligned} \alpha= & {} 8.4,\ \beta = 12.2,\ \gamma = 0,\nonumber \\ m_0= & {} -1.16,\ m_1 = -0.14, \end{aligned}$$

(30)

the situation is similar to the previous case, and the advanced HBM and predicts the existence of 6 periodic orbits, 2 of which are symmetric and another 4 have shifts with respect to zero equilibrium $F_0$. The disposition of these periodic orbit is similar to Fig. 13a:

k	$\omega _0$	$a_0$	$a_1$	Thm. 1, Eq. (19)
$-0.0451$	3.2626	$\pm \, 1.18$	0.2194	Unstable
		0	28.7658	Stable
$- \, 0.7939$	2.0869	$\pm \, 0.6374$	0.8	Unstable
		0	1.5061	Unstable

The trajectory with initial point

$$\begin{aligned} x(0)= & {} 28.7658, \,\, y(0) = 23.4401, \nonumber \\ z(0)= & {} -41.7789 \end{aligned}$$

(31)

on predicted stable periodic orbit ($T = 1.9258, d = 7.8448$) visualizes a stable stable periodic orbit for $\varepsilon \in (0,1]$, which is a hidden attractor $\mathcal {A}^\textrm{hid}_\textrm{limCyc}$ for $\varepsilon = 1$.

Trajectories with initial points on predicted unstable periodic orbits tend to two symmetric hidden chaotic attractors $\mathcal {A}_{\pm }^\textrm{hid}$ (from the initial points $(1.5061, 0.0995, -2.1874)$ and $(-0.9607, 0.1787, 0.8615)$) and to stable symmetric equilibria $S_\pm$.

Fig. 12

Initial point $(x(0),y(0),z(0)) = (6.1492, 0.3832, -8.7846)$ (black) on the approximate stable periodic orbit (blue), predicted by HBM, could be used for localization of two hidden chaotic attractors $\mathcal {A}_{\pm }^\textrm{hid}$ (cyan, green) in Chua system (6) with parameters $\alpha = 8.4$, $\beta = 12$, $m_0 = -0.12$, $m_1 = -1.15$

Fig. 13

Initial points on the approximate unstable periodic orbits, predicted by HBM, are used for localization of three hidden attractors ($\mathcal {A}^\textrm{hid}_\textrm{limCyc}$ and $\mathcal {A}^\textrm{hid}_{\pm }$) in Chua system (6) with $\alpha = 8.41$, $\beta = 12.23$, $\gamma = 0.0435$, $m_0 = -1.366$, $m_1 = -0.17$. The prediction of unstable periodic orbits could be considered as separation of attractors’ basins of attraction

Along with the HBM presented in this work and rigorously justified for small parameters $\varepsilon$ (see Theorem 1) there are other known attempts [79, 80] to apply the classical HBM to Chua system (6) represented in the form of a jerk system¹⁰ [81]:

$$\begin{aligned} \dddot{u} = F(u, \dot{u}, \ddot{u}). \end{aligned}$$

(32)

Following [79, 80], system (6)–(7) could be represented in form (32) with respect to x-variable, i.e.,

$$\begin{aligned}{} & {} \dddot{x} + ((m_1 + 1) \alpha + \gamma + 1) \,\ddot{x} + \nonumber \\{} & {} \quad + (((m_1 + 1)\gamma + m_1) \alpha + \beta + \gamma ) \, \dot{x} \nonumber \\{} & {} \quad + \alpha (m_1 (\beta + \gamma ) + \beta ) x \nonumber \\{} & {} \quad = \alpha \big (\ddot{\psi }(x) + (\gamma + 1) \dot{\psi }(x) + (\beta + \gamma ) \psi (x)\big ). \end{aligned}$$

(33)

Here, one faces the following issue: function $\psi (x)$ in the Chua system is only continuous and not smooth enough to consider the expression in the right-hand side of (33).

To avoid this issue, we can rewrite the Chua system in form (32) with respect to z-variable, i.e.,

$$\begin{aligned}{} & {} \dddot{z} + \big ((m_1+1) \alpha + \gamma + 1\big ) \,\ddot{z} + \nonumber \\{} & {} \quad + \big (((m_1+1)\gamma + m_1) \alpha + \beta + \gamma \big ) \, \dot{z}\nonumber \\{} & {} \quad + \alpha (m_1 (\beta + \gamma ) + \beta ) \, z = \nonumber \\{} & {} \quad = - \alpha \beta \, \psi \left( \tfrac{1}{\beta } \ddot{z} + \tfrac{1 + \gamma }{\beta } \dot{z} + \tfrac{\beta + \gamma }{\beta } z\right) . \end{aligned}$$

(34)

For system (34), the application of the classical HBM [77, p. 450] yields approximate periodic solutions similar to Figs. 12a and 13a, which have the form $z(t) \approx a_0 + a_1 \cos (\omega _0 t)$ and initial data $z(0) = a_0 + a_1$, $\dot{z}(0) = 0$, and $\ddot{z}(0) = - a_1\omega _0^2$ (but without the additional information about their stability in contrast to Theorem 1).

Fig. 14

Stabilization of the unstable periodic orbit (red) in Chua system (11) using the Pyragas method: a the unstable periodic orbit (red) and its approximation via HBM (dark red, dashed) surrounds 2 hidden chaotic attractors (blue and navy blue); b stabilization of the unstable periodic orbit from the initial point $(-2.321, -0.787, 3.129)$ along the time interval [0, 300]; c evolution of the Pyragas control

Fig. 15

Stabilization of unstable periodic orbits (red) in Chua system (11) using the Pyragas method: a 2 symmetric unstable periodic orbits (red) embedded in 2 hidden chaotic attractors (blue and navy blue) and their approximation via HBM (dark red, dashed); b stabilization of the unstable periodic orbit from the orbit approximated by HBM along the time interval [0, 700]; c evolution of the Pyragas control

Visualization and tracking of unstable unstable periodic trajectories, predicted by HBM, due to their instability requires the use of special computational methods (e.g., as in XPPAUT). Here we discuss the possibilities of the Pyragas method for searching and visualizing unstable periodic trajectories (see, e.g., [14, 82,83,84,85]). The main idea is to construct a control force proportional to the difference between the current state of system (11) and the state delayed by some time in the past:

$$\begin{aligned} \dot{u} = P u + q \, \psi (r^* u) + g \, p \, \big [r^*u(t) - r^*u(t - \tau )\big ],\nonumber \\ \end{aligned}$$

(35)

where p is a real vector, $g > 0$ is a feedback gain. If there is a cycle with period T in initial system (11), then for initial condition on this cycle and $\tau = T$ the control is equal zero: $g \, p \, \big [r^*u(t) - r^*u(t - \tau )\big ] \equiv 0$. The coefficient g is chosen so that for initial data not on the cycle the control force the state of the system to tend to the cycle. To tune the parameters g and $\tau$ for the search and stabilization of cycles, one can use various adaptive procedures [86,87,88]. For Chua system (11) using (35) with $p^* = \left( 1, 0, 0\right)$, $r^* = \left( 1, 0, 0\right)$, $g = 2.5$ and applying the Pyragas method on time interval [0, 300], starting stabilization from initial point $u_0 = (-2.321, -0.787, 3.129)$ chosen previously in the above numerical experiment (see Sect. 4) we have stabilized an unstable periodic orbit $u^\mathrm{upo_1}(t,u_0)$ with period $T \approx 2.4077$ (see Fig. 14), which corresponds to and is in good agreement with the unstable periodic orbit in this physical experiment (see Fig. 10), as well as with the approximate periodic orbit predicted by HMB (see Case 2 and Fig. 13b in Sect. 5.2). The approximate solution from HBM can be used as the initial data for (35). So, for Chua system (11) using same system (35) under control with $g = 2.5$ and applying the Pyragas method on time interval [0, 700], starting stabilization from the orbit approximated by HBM (see Sect. 4) we have stabilized two symmetric unstable periodic orbits $u^\mathrm{upo_2}(t,u_0)$ with period $T \approx 1.9566$ embedded into chaotic hidden Chua attractors (see Fig. 15).

Moreover, the Pyragas method and some other powerful methods (see, e.g., [59, 89]) allow one to reveal more various periodic orbits embedded into chaotic Chua attractors, which have not been detected above by the HBM. However, in some cases, the use of the HBM makes it possible to accurately identify all periodic orbits in a system. For example, for the system [90, 91]

$$\begin{aligned} \ddot{x} + x - b\dot{x}\cos (x) = 0 \end{aligned}$$

(36)

with $b \ne 0$ this method predicts an infinite number of periodic orbits in the form $x^\textrm{HBM}(t) \!=\! a^i_0 \sin (t)$, where $\{a^i_0\}_{i=1}^\infty$ are zeros of the Bessel function: $J_1(a^i_0) \!=\! \tfrac{1}{\pi }\int _0^\pi \cos (\tau \!-\! a^i_0 \sin \tau ) {\textrm{d}}\tau \!=\! 0$. True periodic orbits of this system can be visualized from the obtained initial data. For this system approximations of the nonlinearity $\dot{x} \cos (x)$ by its expansion in the Taylor series leads one to the case of the 16th Hilbert problem on the maximum number of coexisting periodic attractors and repellers and their disposition in two-dimensional polynomial systems (which was formulated in 1900 [26] and is still unsolved even for quadratic polynomials [40, 46, 92, 93]). Remark that for this system the similar straightforward application of the XPPAUT package, as above for the Chua system, does not provide initial data for the visualization of all hidden periodic attractors.

Table 3 Comparison of the parameters for mathematical and physical models for saddle limit cycles

6 Conclusion

In this work, a comparative analysis of three Chua’s models is carried out, i.e., (1) a mathematical model; (2) a schematic circuit model made of ideal circuit elements; and (3) a physical model of the Chua circuit in the form of a laboratory model made of an interconnection of electronic devices. The developed laboratory model of the experimental setup has an additional sub-circuit included in the classical Chua circuit, which makes it possible to implement the changing of the initial conditions.

In the frame of this work, mathematical modeling of the dynamics of the Chua system is carried out. Bifurcation mechanisms of the appearance of hidden attractors are shown. These mechanisms are associated with some local bifurcation: the subcritical Andronov–Hopf bifurcation, as well as the global saddle-node bifurcation of limit cycles and their development. We also demonstrate that the transition between self-excited and hidden attractors can occur via global bifurcations (e.g., crisis of attractor).

An experimental study of the system dynamics is carried out. The experiment shows the possibility of accessing hidden attractors and visualizing of saddle limit cycles. It is shown that in physical experiments where the electronic circuit is triggered by the inclusion of a nonlinear resistor (the Chua diode) in the circuit at zero initial conditions (a starting voltage across the capacitors and the current through the coil), corresponding to zero equilibrium state, only self-excited attractors can be observed. Changing the initial conditions in the experiment allows one to find out hidden attractors. Using this experimental technique for changing initial conditions it is possible to visualize a special class of orbits, i.e., unstable or saddle limit cycles that are rather difficult to detect in a physical experiment. Visualization of such objects is difficult task because we need to find initial conditions on an unstable object. The presence of an accurate mathematical model makes it possible to carry out a numerical bifurcation analysis with the help of which one can trace the bifurcations of not only stable limit cycles, but also the saddle ones, and also visualize them in the phase space. In the experiment, for such visualization one requires special supplements, but even with additional techniques, the trajectories leave such unstable objects much faster and such objects are more difficult to visualize due to the influence of noise. In numerical simulation, the role of noise is played by errors of numerical methods. In this work, it is shown that the noise in the physical experiment is more intense than in the numerical simulations.

Thus, in this work, we used a fairly simple radiophysical generator as an example to show that the detection of coexisting regimes, especially those located far from equilibrium states and having small basins of attraction not connected with equilibria (hidden attractors), may need system modification and development of additional special methods. As demonstrated in this paper the approach based on the existing methods of bifurcation theory and the numerical packages is effective in studying possible scenarios for the birth of attractors and for the analysis of already discovered attractors (as it happened historically with hidden Chua attractors). However, when solving problems of multistability or global stability, where it is necessary to find all nontrivial attractors or to establish their absence, the key problem of this approach is inability to guarantee the absence of other attractors in the phase space than those found. This is well demonstrated by the famous 16th Hilbert problem on the maximum number of limit cycles of polynomial systems on the plane, where this approach made it possible to construct various non-trivial examples with coexisting limit cycles and obtain a lower estimate of the maximum number of cycles depending on the degree of polynomials on the right side; however, revealing all limit cycles and determining their maximum possible number in the general case remains an unsolved problem. Here analytical methods made it possible to prove that there is only a finite number of limit cycles. If there exist undiscovered limit cycles for some of these examples in the gap between the lower and upper bounds for the maximum number of limit cycles, they will belong to the class of hidden oscillations, since self-excited limit cycles are detected trivially in numerical experiments. Similarly, determining of the exact boundary of global stability in the parameter space, implying the absence of nontrivial attractors in the phase space for given parameters of dissipative system, is difficult, because one needs to analyze hidden parts of the global stability boundary associated with global bifurcations and the birth of hidden attractors. At the same time, conservative (internal) estimates of the boundary of global stability can be obtained using various analytical criteria. The above remains an open question for the Chua system, as well: What is the maximum number of coexisting attractors that can be exhibited in the Chua system and how many of the coexisting attractors can be hidden?

Some additional results on the hidden attractors in the Chua circuits can be found, e.g., in [57, 94,95,96,97,98,99,100,101,102,103,104,105].