Skip to main content
SpringerLink
Log in

New solitary wave solutions of a generalized BBM equation with distributed delays

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

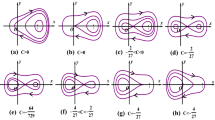
Solitary wave solutions for a generalized Benjamin–Bona–Mahony equation with distributed delay and dissipative perturbation are considered in this paper. The corresponding traveling wave equation is transformed into a four-dimensional dynamical system, which is regarded as a singularly perturbed system for small time delay. The four-dimensional dynamical system is reduced to a near-Hamiltonian planar system via geometric singular perturbation method. The existence of solitary wave solutions with a single crest or trough is established by proving the persistence of homoclinic orbits of the near-Hamiltonian system. More importantly, a new type of solitary wave solution with coexisting crest and trough, which corresponds to a large concave homoclinic orbit, is observed theoretically by using Melnikov’s method. The selection principle for wave speed of the solitary wave is presented which can be utilized directly to determine the limit wave speed. Numerical simulations are in complete agreement with the theoretical predictions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Data availibility

Data sharing not applicable to this article as no datasets were generated or analysed during the current study.

References

  1. Korteweg, D.J., de Vries, G.: On the change of form of long waves advancing in a rectangular canal and on a new type of long stationary waves. Philos. Mag. 39(240), 422–443 (1895)

    Article  MATH  Google Scholar 

  2. Benjamin, T.B., Bona, J.L., Mahony, J.J.: Model equations for long waves in nonlinear dispersive systems. Philos. Trans. Royal Soc. London Ser. A Math. Phys. Sci. 272, 47–78 (1972)

    MATH  Google Scholar 

  3. Belobo, D.B., Das, T.: Solitary and Jacobi elliptic wave solutions of the generalized Benjamin-Bona-Mahony equation. Commun. Nonlinear Sci. Numer. Simul. 48, 270–277 (2017)

    Article  MATH  Google Scholar 

  4. Hubert, M.B., Kudryashov, N.A., Justin, M., et al.: Exact traveling soliton solutions for the generalized Benjamin-Bona-Mahony equation. Eur. Phys. J. Plus 133(3), 108 (2018)

    Article  Google Scholar 

  5. Biswas, A.: 1-soliton solution of Benjamin-Bona-Mahony equation with dual-power law nonlinearity. Commun. Nonlinear Sci. Numer. Simul. 15(10), 2744–2746 (2010)

    Article  MATH  Google Scholar 

  6. Yang, X.L., Tang, J.S., Qiao, Z.: Traveling wave solutions of the generalized BBM equation. Pacific J. Appl. Math. 1, 99–112 (2008)

    Google Scholar 

  7. Wazwaz, A.M.: New travelling wave solutions of different physical structures to generalized BBM equation. Phys. Lett. A 355, 358–362 (2006)

    Article  Google Scholar 

  8. Liu, X., Tian, L., Wu, Y.: Exact solutions of the generalized Benjamin-Bona-Mahony equation. Math. Prob. Eng. 796398 (2010)

  9. Zhao, Z.: Solitary waves of the generalized KdV equation with distributed delays. J. Math. Anal. Appl. 344, 32–41 (2008)

    Article  MATH  Google Scholar 

  10. Li, X., Du, Z., Ji, S.: Existence results of solitary wave solutions for a delayed Camassa-Holm-KP equation. Commun. Pure Appl. Anal. 18(6), 3367–3387 (2019)

    Article  MATH  Google Scholar 

  11. Wei, J., Zhou, J., Tian, L.: Existence and asymptotic behavior of traveling wave solution for Korteweg-de Vries-Burgers equation with distributed delay. J. Appl. Anal. Comput. 9(3), 840–852 (2019)

    MATH  Google Scholar 

  12. Du, Z., Qiao, Q.: The dynamics of traveling waves for a nonlinear Belousov-Zhabotinskii system. J. Differ. Equ. 269(9), 7214–7230 (2020)

    Article  MATH  Google Scholar 

  13. Zhu, K., Wu, Y., Shen, J.: New solitary wave solutions in a perturbed generalized BBM equation. Nonlinear Dyn. 97(4), 2413–2423 (2019)

    Article  MATH  Google Scholar 

  14. Zhu, K., Shen, J.: Smooth travelling wave solutions in a generalized Degasperis-Procesi equation. Commun. Nonlinear Sci. Numer. Simul. 98, 105763 (2021)

    Article  MATH  Google Scholar 

  15. Zhang, L., Han, M., Zhang, M., Khalique, C.M.: A new type of solitary wave solution of the mKdV equation under singular perturbations. Int. J. Bifurc. Chaos 30(11), 1–14 (2020)

    Article  MATH  Google Scholar 

  16. Zhang, L., Wang, J., Shchepakina, E., Sobolev, V.: New type of solitary wave solution with coexisting crest and trough for a perturbed wave equation. Nonlinear Dyn. 106(4), 3479–3493 (2021)

    Article  Google Scholar 

  17. Mansour, M.B.A.: Traveling waves for a dissipative modified KdV equation. J. Egypt. Math. Soc. 20(2), 134–138 (2012)

    Article  MATH  Google Scholar 

  18. Sun, X., Huang, W., Cai, J.: Coexistence of the solitary and periodic waves in convecting shallow water fluid. Nonlinear Anal. Real 53, 103067 (2020)

    Article  MATH  Google Scholar 

  19. Wang, J., Yuen, M., Zhang, L.: Persistence of solitary wave solutions to a singularly perturbed generalized mKdV equation. Appl. Math. Lett. 124, 107668 (2022)

    Article  MATH  Google Scholar 

  20. Han, M.: Bifurcation Theory of Limit Cycles. Science press, Beijing (2013)

  21. Fenichel, N.: Geometric singular perturbation theory for ordinary differential equations. J. Differ. Equ. 31, 53–98 (1979)

    Article  MATH  Google Scholar 

  22. Li, J., Zhang, L.: Bifurcations of Traveling Wave Solutions in Generalized Pochhammer-Chree Equation. Chaos Soliton Fract. 14, 581–593 (2002)

    Article  MATH  Google Scholar 

  23. Yan, W., Liu, Z., Liang, Y.: Existence of solitary waves and periodic waves to a perturbed generalized KdV equation. Math. Model. Anal. 19(4), 537–555 (2014)

    Article  MATH  Google Scholar 

  24. Li, M., Wang, B., Xu, T., Wang, L.: Quantitative Analysis on the Bifurcations and Exact Travelling Wave Solutions of a Generalized Fourth-Order Dispersive Nonlinear Schrödinger Equation in Heisenberg Spin Chain. Chaos Soliton Fract. 145, 110767 (2021)

    Article  MATH  Google Scholar 

  25. Perko, L.: Differential Equations and Dynamical Systems, 3rd edn. Springer-Verlag, New York (2000)

    MATH  Google Scholar 

  26. Luo, D., Han, M., Zhu, D.: Uniqueness of limit cycles bifurcating from a singular closed orbit (I) (in Chinese). Acta Math. Sin. 35(3), 407–417 (1992)

    MATH  Google Scholar 

  27. Li, G., Ma, X., Li, Z., Li, Y.: Optimal trajectory planning strategy for underactuated overhead crane with pendulum-sloshing dynamics and full-state constraints. Nonlinear Dyn. 109, 815–835 (2022)

    Article  Google Scholar 

  28. Weidman, P., Turner, M.R.: Experiments on the synchronous sloshing in suspended containers described by shallow-water theory. J. Fluids Struct. 66, 331–349 (2016)

    Article  Google Scholar 

Download references

Funding

This work is partially supported by the National Natural Science Foundation of China No. 12172199 and No. 12011530062.

Author information

Authors and Affiliations

  1. College of Mathematics and Systems Science, Shandong University of Science and Technology, Qingdao, 266590, Shandong, China

    Jundong Wang, Lijun Zhang & Jibin Li

  2. Qingdao University of Science and Technology, Gaomi, 261500, Shandong, China

    Jundong Wang

  3. International Institute for Symmetry Analysis and Mathematical Modelling, Department of Mathematical Sciences, North-West University, Mafikeng Campus, Mmabatho, South Africa

    Lijun Zhang

Authors
  1. Jundong Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Lijun Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jibin Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

LZ Validation, Methodology, Formal analysis, Writing - review. JW software, Formal analysis, Writing - original draft & editing. JL validation, Methodology.

Corresponding author

Correspondence to Lijun Zhang.

Ethics declarations

Competing interest

Authors declare that no conflict of interest exists.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, J., Zhang, L. & Li, J. New solitary wave solutions of a generalized BBM equation with distributed delays. Nonlinear Dyn 111, 4631–4643 (2023). https://doi.org/10.1007/s11071-022-08043-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-022-08043-9

Keywords

Search

Navigation