Propagation characteristics of an elastic bar coupled with a discrete snap-through element

Abstract

Wave propagation characteristics of an elastic bar coupled at one end with a single degree of freedom, bi-stable, essentially nonlinear snap-through element are considered. The free end of the bar is subjected to sinusoidal excitations. A novel approach based on multiple time scales and harmonic balance method has been proposed to analytically investigate the reflected wave from the nonlinear interface and the dynamic response of the snap-through element. A unified approach to the non-dimensional representation of the governing equations of motion, boundary conditions and system parameters, which is consistent across all the externally applied excitation frequencies and excitation amplitudes, has been developed. Through Taylor series expansion of the non-autonomous forcing functions arising in the governing differential equations and natural boundary condition about an initial stable configuration of the system and the proposed asymptotic method, approximate closed-form analytical solutions have been derived for sufficiently small amplitudes of the excitation pulse. Numerical results obtained through a finite difference algorithm validate the asymptotic model for the same small amplitudes of the excitation pulse. A stability analysis has been subsequently performed for the discrete snap-through element by using the extended Floquet theory for sufficiently large amplitudes of the excitation pulse by approximating the displacement at the nonlinear interface as a sinusoidal function of time, and the Mathieu plot of the excitation frequency vs the excitation amplitude showing the stable and unstable regions for the motion of the snap-through element has been generated. The expressions derived here give the most comprehensive and consistent description of the wave propagation characteristics and the motion of the snap-through element, which can be directly used in finite difference analysis over a wide range of parameter values of the excitation pulse.

1 Introduction

Wave propagation in an elastic continuum is a subject of interest in many fields of engineering [1] and has been explored for several decades from a theoretical, computational and experimental perspective. In this context, a one/two-dimensional elastic continuum is more colloquially called a waveguide since they minimize energy loss by restricting the wave propagation in a specific direction/plane. These one-dimensional elastic waveguides can be dispersion free, such as an elastic bar propagating longitudinal waves, or can exhibit dispersion, such as flexural waves in Euler–Bernoulli or Timoshenko beams. However, in practical engineering structures, such waveguides invariably interact with structural components whose spatial scales are much smaller than the elastic continuum and the wavelength of the wave phenomena that they encounter. Such structural components can be modelled as discrete elements by considering point masses, stiffness and damping. The wave propagation characteristics when elastic waveguides interact with linear discrete elements are well known [2]. The present work primarily dwells on the effect of weakly/essentially nonlinear discrete elements on the wave propagation characteristics in non-dispersive elastic waveguides. Since, in general, closed-form analytical solutions are seldom available for wave propagation problems in nonlinear dynamical systems, in this paper, we propose a systematic approach based on classical perturbation techniques like the method of multiple scales (MMS) to find the solutions. The analytical solutions are validated by numerical results obtained computationally.

This paper focuses on the propagation characteristics in an elastic bar coupled with a discrete nonlinear end attachment. In general discrete nonlinear end attachments can be mathematically modelled as the Duffing oscillator with a stiffness nonlinearity or a Van der Pol oscillator with nonlinear damping [3] or a geometrically nonlinear snap-through truss. The general governing differential equation of motion of such nonlinear end attachments can be given by:

$$\begin{aligned} \frac{d^2 x(t)}{dt^2}+f \left( x(t),{\dot{x}}(t),t \right) =0 \end{aligned}$$

(1)

There are quite a few known methods to solve nonlinear equations of the form (1). Some of them are eigen/modal analysis, perturbation techniques, harmonic balance method and method of averaging [4]. Analysis of dynamical systems comprising of nonlinear oscillators can be found in the existing literature dating back as early as the 80s. In 1982, Nayfeh [5] investigated the response of single degree of freedom systems with quadratic and cubic nonlinearities to a sub-harmonic excitation. In this paper, one can get a general idea of how to apply the multiple time scales analysis and harmonic balance method to solve a nonlinear equation. In the context of more recent works, Young Sup Lee et al. in [6] studied the dynamics of a two degree of freedom system comprising of a grounded linear oscillator coupled to a light mass through an essentially nonlinear stiffness. This seemingly simple system showed a very complicated dynamical behaviour due to the essential nonlinearity of the coupling stiffness even though the nonlinear attachment was chosen to be very light, compared to the main linear oscillator. In the context of energy harvesting using nonlinear oscillators, A. F. Vakakis [7] studied the effect of inducing passive nonlinear energy sinks in linear vibrating systems. He considered a system composed of strongly coupled, grounded damped linear oscillators with a strongly nonlinear end attachment and derived a set of modulation equations using an averaging method and showed that nonlinear attachments if designed properly, can act as passive energy sinks of spurious vibrations. Vakakis et al. in [8] studied the dynamics of linear discrete systems connected to local essentially nonlinear end attachments and observed that if the system parameters are chosen properly and if the external excitation is sufficiently strong, irreversible, passive transfer of energy occurs from the chain to the attachment. Another evidence of a strongly nonlinear oscillator acting as a passive energy sink can be found in the work of Manevitch et al. [9], where the model considered was a semi-infinite chain of coupled linear, grounded oscillators, weakly coupled to a strongly nonlinear oscillator at its free end. An important finding of this work was that energy pumping can occur even when there is no damping in the system. In another work [10] on proving the vibration isolating capabilities of a single degree of freedom nonlinear oscillator with high-static–low-dynamic stiffness, A. Carrella and co-workers considered a lumped mass model supported by three springs to the base and compared the force and displacement transmissibility by finding closed-form solutions, considering a harmonic force on the mass and a harmonic motion of the base in each case separately. Even in the cases of asymmetrical loading conditions, besides energy harvesting, the effectiveness of a nonlinear oscillator with high-static–low-dynamic-stiffness as a vibration isolator compared to a linear oscillator has been proved in [11] by A. Abolfathi et. al. Very recently, in a series of papers, Karlicic et al. [12,13,14,15] employed the incremental harmonic balance (IHB) method in the context of nonlinear piezoelectric energy harvesting. Also, a recent paper [16] by MQ Niu and LQ Chen studies the optimization of a quasi-zero stiffness isolator via oblique beams.

Evidence of the use of a geometrically and essentially nonlinear snap-through truss to effectively absorb vibrations of the linear oscillator can also be found in the existing literature. Avramov and Mikhlin [17] used the nonlinear normal mode (NNM) approach to investigate the phenomenon of elastic oscillations absorption by a snap-through truss by considering a single degree of freedom linear oscillator to represent an elastic continuum and a nonlinear absorber with three equilibrium positions (snap-through truss) attached to the linear oscillator. Considering the same system as in [17], the authors in [18] studied the forced oscillations of the snap-through truss close to its stable equilibrium position by the classical multiple scales method. In their next work on snap-through truss [19], Avramov and Mikhlin investigated the possibility of absorption of the forced oscillations underwent by a linear elastic system using a snap-through truss. They used a combination of the nonlinear normal vibrations modes method, the Rauscher approach and the asymptotic analysis to study the forced oscillations of the essentially nonlinear two degree of freedom system. More work on snap-through motions of a system can be found in [20] where the authors have studied the nonlinear normal mode (NNM) of the snap-through motions of a shallow arch. The stability of the snap-through motions was studied by using the Ince algebraization and the method of Hill determinants. In the context of studying the dynamics of a single degree of freedom linear oscillator subjected to harmonic forcing and coupled to a geometrically nonlinear light end attachment by complexification-averaging method, there is a work done in a recent paper [21] by Yang Liu et. al. Very recently there have been a couple of works [22, 23], based on modal interactions, by A. Mojahed and co-workers on the effectiveness of a geometrically nonlinear oscillator in absorbing vibrations, mitigating shocks and transferring energy in a targeted manner.

The analysis of a dynamical system comprising of an elastic continuum with discrete nonlinearity has been a subject of interest in mechanics for quite some time now. Nayfeh and Asfar [24] investigated the response of a bar constrained by a nonlinear spring with cubic stiffness nonlinearity to harmonic excitation. By using the method of multiple time scales, they found closed-form analytical solutions for the response of the bar in the different cases of resonance. Their work did not address the analysis of a bar coupled to a nonlinear oscillator, but it presented a systematic procedure based on conventional perturbation methods for finding the vibration response of an elastic continuum with a discrete nonlinearity. Considering the similar model as in [24], Lee et al. in [25] checked the validity of the asymptotic solution obtained by Nayfeh from the method of multiple time scales by using the finite difference method to find a numerical solution to the problem and then comparing it with the asymptotic solution. One more reference work in this context by Özkaya et al. [26] deals with the nonlinear vibrations of a beam-mass system by using the perturbation method of multiple time scales to find the approximate analytical solutions. As an example of a work on an elastic continuum interacting with an essentially nonlinear end attachment, we can take into account the paper by Avramov and Gendelman [27] which focuses on the interaction of an elastic beam subjected to a transverse periodic force, with an essentially nonlinear oscillator attached to the midpoint of the beam (the antinode for the first mode of beam vibration). It was concluded from this work that the nonlinear absorber could be used effectively for absorbing the vibrations of the continuous, forced system. In the same context, Mikhlin and Reshetnikova [28] studied the dynamical interaction of an elastic system and an essentially nonlinear absorber by approximating the continuous elastic system by a linear oscillator with a relatively big mass and considering an essentially nonlinear oscillator with a relatively small mass to be linearly coupled to the bigger mass. They analysed the nonlinear normal modes of vibration to find that a stable vibration absorption mode exists in a large region of the system parameters. A paper by Krack et. al [29] also studies the nonlinear modal interactions in the presence of a friction-joint coupling between two Euler–Bernoulli beams in order to find the efficacy of friction damping in the presence of such interactions.

As we can see, the effectiveness of a nonlinear oscillator as an irreversible, passive, nonlinear energy sink and standard procedures to find analytical solutions for the class of free/forced vibration problems involving an elastic continuum with discrete nonlinearity can be found extensively in the existing literature. In the context of wave propagation in an elastic continuum with a discrete nonlinear end attachment, Gendelman and Manevitch [30] considered rectangular wave propagation in an ideal elastic string attached to a strongly nonlinear oscillator through a linear spring, subjected to an external excitation in the form of a rectangular pulse applied to the string at infinity. Considering the oscillator mass to be negligible and the stiffness of the coupling linear spring to be very large, the approximate analytical solutions were derived for the response of the nonlinear oscillator. The conclusions drawn from this work were that this kind of system can be successfully described by a combination of asymptotic methods and that energy pumping is possible from the elastic continuum to the nonlinear oscillator. We can find more evidence of the use of asymptotic analysis for studying the wave propagation behaviour in strongly/essentially nonlinear dynamical systems, composed of discrete particles forming a dimer chain, in a recent work of Z. Ahsan and K. R. Jayaprakash [31]. The paper uses the same multiple time scales analysis to study the evolution of solitary waves and primary pulses in granular dimers with and without velocity proportional foundation damping. In two more works [32, 33], Jayaprakash et al. studied the travelling waves in one-dimensional nonlinear trimer granular lattice by employing numerical methods and the recently developed analytical procedure based on the singular, multi-scale perturbation analysis. In another work on nonlinear trimer model [34], V. Kislovsky et al. studied, both analytically and numerically, the resonant mechanism governing the inter-state transitions of locally excited regimes in a chain of three coupled anharmonic oscillators subject to localized excitation. In the context of elastic, solitary wave scattering at softening-hardening interfaces in strongly nonlinear metamaterials, there is a paper by F. Fraternali et al. [35] which studies the wave propagation characteristics in the medium under impact loading.

Based on the literature survey presented so far, it can be said that the phenomenon of harmonic wave propagation in an un-approximated elastic bar coupled to a discrete nonlinear oscillator had not been dealt with previously in detail. So, there is a dearth of literature when it comes to finding a closed-form analytical solution for this kind of a wave propagation problem. The problem approached in [30] was somewhat similar to the work presented in this paper. But the results were based on some obvious approximations which render them invalid in a more generalized case. Moreover, the nonlinearity did not arise due to the geometry/configuration of the system and also the problem was not an essentially nonlinear one. Also, the work did not give closed-form solutions for the reflected pulse and did not attempt to solve the problem by using conventional perturbation techniques. It was mostly aimed at proving the effectiveness of the nonlinear oscillator as an energy sink and at finding the conditions favourable for maximum energy pumping from the elastic continuum to the nonlinear oscillator. The works covered in [31,32,33] use the conventional perturbation analysis to address the wave propagation phenomenon in nonlinear granular dimer/ trimer chains, but not in an un-approximated elastic continuum with a discrete nonlinear end attachment. On the contrary, this paper mostly aims at using classical perturbation techniques (multiple time scales) and the harmonic balance method to find closed-form solutions to the reflected pulse in an un-approximated elastic bar/rod at the nonlinear interface and the dynamic response of the essentially nonlinear oscillator at different levels of approximation.

Fig. 1

Schematic of an elastic bar coupled with a snap-through truss

The problem studied in this paper considers an elastic bar coupled to a snap-through truss/oscillator at one end. The free end of the bar is subjected to a sinusoidal displacement function. Examples of previous research works focusing on the analysis of systems comprising of a snap-through truss have been presented in this section. A snap-through truss can be mathematically modelled as a single degree of freedom spring-mass oscillator with three equilibrium positions arising due to its geometric configuration and motion. Usually, the phase plane plot of such an oscillator shows homoclinic orbits with two centres as the two stable equilibrium points and one saddle as the unstable equilibrium point in the middle. When we couple such a snap-through element with an elastic bar by means of linear springs and constrain the motion of the snap-through element in a direction perpendicular to the longitudinal axis of the bar, we get an essentially nonlinear system with the nonlinearity arising due to the geometric configuration. It cannot be solved by conventional analytical methods without a basic assumption which is small amplitudes of the excitation pulse. With this necessary assumption and our proposed asymptotic methodology, approximate closed-form analytical solutions have been obtained for the response of the bar as well as the snap-through oscillator. The asymptotic results have been compared to numerical simulations of the actual system, obtained computationally by using an iterative finite difference scheme and it has been shown that they match significantly. It has also been shown in this paper that if the bar displacement at the nonlinear interface is approximated by a generalized sinusoidal function of time which is the superposition of the incident and reflected waves, we can perform a Floquet analysis for the snap-through oscillator in the case of sufficiently large amplitudes of the excitation pulse. The stability/Floquet analysis generates a Mathieu plot of excitation frequency vs approximated excitation amplitude showing the stable and unstable regions for the dynamic response of the snap-through oscillator. The stability diagram can be useful while determining important system excitation parameters such as amplitude and frequency for which the dynamic response of the oscillator becomes unstable/divergent and the oscillator exhibits a snap-through motion.

2 Problem formulation

2.1 The model

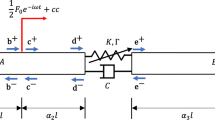
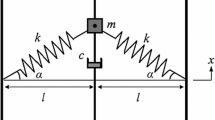
Let us consider a homogeneous, isotropic, elastic bar of mass ${\tilde{M}}$, length ${\tilde{L}}$ and cross-sectional area A, which is free at one end and coupled to a snap-through oscillator of mass m through a linear spring of stiffness constant k as shown in Fig. 1. The snap-through oscillator is connected to a rigid support through another linear spring of stiffness constant k. The motion of the snap-through oscillator is constrained to take place in the vertical direction only. The force–deflection relationship of the linear springs is given by $F=k\delta$, where $\delta$ is the deflection in the springs and F is the restoring force. The natural un-deflected length of the springs is L as shown in the initial configuration. For the purpose of keeping the calculations simple, we have assumed that both the springs have the same stiffness coefficient (k) and same natural length (L).

The free end of the bar is subjected to a sinusoidal excitation of the form $Q(t)={\bar{A}}\sin (\Omega t)$. The excitation is a displacement function, not a force, and it is assumed to be imposed on the free end of the bar. But, since the bar is a linear and non-dispersive medium, to reduce the complexities in algebraic calculations associated with constant phase terms, we shall consider the incident wave in our analysis and calculations when it strikes the nonlinear interface at $x=0$ and consider the time for analysis to be starting from that instant. This means that a simple pre-calculated phase shift is performed on the incident wave. All the subsequent mathematical calculations shall be done including this phase manipulation in the expressions and in the end while illustrating the results graphically, we shall add this phase shift back into our analytical solutions. While deriving the equations of motion and boundary conditions from the Lagrangian of the system initially, it will be assumed that the displacement at the left end of the bar be specified as per our problem definition. The initial displacements have been taken to be zero from their corresponding positions as shown in the schematic of the model in Fig. 1. u(x, t) and v(t) are the generalized displacement functions of the bar and the snap-through oscillator, respectively, where x is the longitudinal spatial coordinate along the bar and t is time.

2.2 Equations of motion and boundary conditions

The diagram is shown for the stable equilibrium configuration of the snap-through oscillator whose vertical coordinate from the base (dashed line) is given by $L\sin {\phi }$. The coordinate $x=0$ is taken at that point where the oscillator is attached to the bar. The equations of motion are derived by using the Variational principle from the Lagrangian of the system. The total kinetic energy of the system is given by

$$\begin{aligned} T= \int _{-{\tilde{L}}}^{0} \frac{1}{2}\rho A\left( \frac{\partial u}{\partial t}\right) ^2 \,dx +\frac{1}{2}m\left( \frac{dv}{dt}\right) ^2 \end{aligned}$$

(2)

The total potential energy is given by

$$\begin{aligned} U= & {} \int _{-{\tilde{L}}}^{0} \frac{1}{2}AE\left( \frac{\partial u}{\partial x}\right) ^2 \,dx\nonumber \\{} & {} +\frac{1}{2}k\left( \sqrt{(L\cos {\phi }-u(0,t))^2+v^2}-L\right) ^2\nonumber \\{} & {} +\frac{1}{2}k\left( \sqrt{L^2\cos ^2{\phi }+v^2}-L\right) ^2 \end{aligned}$$

(3)

The Lagrangian is given by $La=T-U$ and from the Hamilton’s principle $\int _{t_1}^{t_2}\delta La\,dt=0$. Performing the integration and keeping in mind that $\delta u(-{\tilde{L}})=0$ since the displacement is specified at the left end of the bar, we get the equations of motion and boundary conditions as

$$\begin{aligned}{} & {} AE\frac{\partial ^2 u}{\partial x^2}-\rho A\frac{\partial ^2 u}{\partial t^2}=0 \end{aligned}$$

(4)

$$\begin{aligned}{} & {} m\ddot{v}+kv\left( 2-\frac{L}{\sqrt{(L\cos {\phi }-u(0,t))^2+v^2}}\right. \nonumber \\{} & {} \quad \left. -\frac{L}{\sqrt{L^2\cos ^2{\phi }+v^2}}\right) =0 \end{aligned}$$

(5)

$$\begin{aligned}{} & {} AE\frac{\partial u}{\partial x} (0,t)=k\left( 1-\frac{L}{\sqrt{(L\cos {\phi }-u(0,t))^2+v^2}}\right) \nonumber \\{} & {} \quad \quad \quad \left( L\cos {\phi }-u(0,t)\right) \end{aligned}$$

(6)

The excitation pulse in dimensional form, which is also the essential boundary condition at the left end of the bar, is

$$\begin{aligned} Q(t)={\bar{A}}\sin {\Omega t}=u(-{\tilde{L}},t) \end{aligned}$$

(7)

The characteristic length of non-dimensionalization is chosen to be $L_{ch}={\tilde{L}}/l=L$, which is also the natural length of the springs in the initial configuration. We define l as our length ratio or the non-dimensional length of the bar. The characteristic mass is taken as $M_{ch}={\tilde{M}}/l=M=\rho AL$ The non-dimensional parameters are then obtained as

$$\begin{aligned} \tau= & {} \frac{ct}{L}, \omega =\frac{L\Omega }{c} \\ l= & {} \frac{{\tilde{L}}}{L}, \quad z=\frac{v}{L}, \quad w=\frac{u}{L}, \quad y=\frac{x}{L}, \\ A_{m}= & {} \frac{{\bar{A}}}{L}, \quad P(\tau )=\frac{Q(t)}{L} \\ \alpha= & {} \frac{kL}{EA}, r=\frac{m}{M} \end{aligned}$$

The parameters are, respectively, the non-dimensional time, the non-dimensional excitation frequency, length ratio or the non-dimensional length of the bar, the non-dimensional displacement of the oscillator, the non-dimensional displacement of the bar, the non-dimensional longitudinal spatial coordinate, the non-dimensional amplitude of the excitation pulse, the excitation pulse in non-dimensional form, the non-dimensional linear stiffness parameter and the mass ratio. $c=\sqrt{E/\rho }$ is the longitudinal wave speed in the bar and E and $\rho$ are the modulus of elasticity and the material density of the bar, respectively.

This gives the non-dimensional equations of motion and boundary conditions as

$$\begin{aligned}{} & {} \frac{\partial ^2 w}{\partial y^2}-\frac{\partial ^2 w}{\partial \tau ^2}=0 \end{aligned}$$

(8)

$$\begin{aligned}{} & {} rz^{\prime \prime }+\alpha z\left( 2-\frac{1}{\sqrt{(\cos {\phi }-w(0,\tau ))^2+z^2}}\right. \nonumber \\{} & {} \quad \left. -\frac{1}{\sqrt{\cos ^2{\phi }+z^2 }}\right) =0 \end{aligned}$$

(9)

$$\begin{aligned}{} & {} \frac{\partial w}{\partial y}(0,\tau )=\alpha \left( 1-\frac{1}{\sqrt{(\cos {\phi }-w(0,\tau ))^2+z^2 }}\right) \nonumber \\{} & {} \quad \left( \cos {\phi }-w(0,\tau ))\right) \end{aligned}$$

(10)

where prime denotes differentiation with respect to $\tau$. The non-dimensional excitation pulse, which is also the essential non-dimensionalized boundary condition at the left end of the bar, is given by

$$\begin{aligned} P(\tau )=A_{m}\sin {\omega \tau }=w(-l,\tau ) \end{aligned}$$

(11)

2.3 Phase-plane behaviour of the uncoupled oscillator

A qualitative study of the independent dynamic behaviour of the snap-through oscillator, uncoupled from the elastic bar, can be performed by plotting the phase plane trajectories from its governing equation of motion. Uncoupling the oscillator from the bar reduces its governing equation of motion to

$$\begin{aligned} rz^{\prime \prime }+\alpha z\left( 2-\frac{2}{\sqrt{\cos ^2{\phi }+z^2 }}\right) =0 \end{aligned}$$

(12)

The essentially nonlinear system described in (12) has two stable centres at $z=\pm \sin {\phi }$ and one unstable saddle at $z=0$. A phase plane diagram of the system will show two sets of homoclinic orbits corresponding to different initial values for $z(\tau )$ and $z^{\prime }(\tau )$, separated by the saddle in the middle. The values of the non-dimensional parameters chosen for plotting the phase portrait shown below are $\alpha =0.5$, $r=1$, $\sin {\phi }=0.5$.

Fig. 2

Phase plane plot (non-dimensional displacement z vs non-dimensional velocity $z^{\prime }$) of the uncoupled snap-through oscillator showing the trajectories for different sets of initial conditions. The arrows denote the vector field at a point that is the direction of motion or velocity of the oscillator at that point in the phase plane. The open circle marks the starting point and the open square marks the endpoint of a trajectory

As we can see from Fig. 2, the phase plane diagram shows two sets of homoclinic orbits around two stable centres at $z=\pm \sin \phi =\pm 0.5$ separated by an unstable saddle in the middle at $z=0$. For large initial values of the displacement z, the motion of the oscillator follows the larger periodic orbits around the saddle at $z=0$. This seemingly rich dynamic behaviour observed from the qualitative analysis of the uncoupled oscillator motion tempts us to investigate a more interesting system comprising of the oscillator coupled to an elastic bar, which is our chosen model.

3 Dynamic response analysis of the system

3.1 Assumptions and Taylor series approximation

Equations (9) and (10) have non-autonomous forcing terms. So, we perform a Taylor series expansion of these time-dependent functions about a stable fixed point. The assumptions made are:

• The amplitude of the excitation pulse applied to the free end of the bar is sufficiently small ($O(\epsilon )$), $\epsilon \ll 1$ and since the bar is a linear, non-dispersive medium, this implies that the displacement at a point in the bar is sufficiently small. ($w(y,\tau )=O(\epsilon )$)

• For sufficiently small amplitudes of the excitation pulse, the displacement of the endpoint of the bar connected to the snap-through oscillator is very close to zero and the snap-through oscillator remains very close to its initial stable equilibrium position $\sin {\phi }$. ($z=\sin {\phi }+\eta$ and $w(0,\tau )=0+\psi$, where $\eta$ and $\psi$ are of $O(\epsilon )$).

Here, $\epsilon$ is the small asymptotic parameter in terms of which we will later perform the asymptotic expansion of the displacements. It is important to note that the second assumption made is not an independent one and comes as a result of the first assumption. Equations (9) and (10) have two time-dependent variables which are $z(\tau )$ and $w(0,\tau )$ and can be re-written as

$$\begin{aligned} rz^{\prime \prime }+\alpha f(z(\tau ),w(0,\tau ))=0 \end{aligned}$$

(13)

$$\begin{aligned} \frac{\partial w}{\partial y}(0,\tau )=\alpha g(z(\tau ),w(0,\tau )) \end{aligned}$$

(14)

A function of two time-dependent variables x and y can be expanded in Taylor series about a fixed point ($x_{0},y_{0}$) for small perturbations around the fixed point. Here, the fixed points are taken as $z^{\star }=\sin {\phi }$ and $w_{0}^{\star }(0,\tau )=0$. The new variables are formulated as

$$\begin{aligned} z(\tau )=z^{\star }+\eta (\tau ) ,\ w(0,\tau )=w_{0}^{\star }(0,\tau )+\psi (\tau ) \end{aligned}$$

(15)

Substituting equation (15) into equations (13) and (14) gives

$$\begin{aligned} r\eta ^{\prime \prime }+\alpha f(z^{\star }+\eta (\tau ),w_{0}^{\star }+\psi (\tau ))=0 \end{aligned}$$

(16)

$$\begin{aligned} \frac{\partial w}{\partial y}(0,\tau )=\alpha g(z^{\star }+\eta (\tau ),w_{0}^{\star }+\psi (\tau )) \end{aligned}$$

(17)

After performing the Taylor series expansion and retaining up to quadratic terms, equations (16) and (17) are obtained as

$$\begin{aligned}&r\eta ^{\prime \prime }+\alpha \bigg (2\sin ^2{\phi } \eta -\sin {\phi }\cos {\phi }\psi +3\sin {\phi }\cos ^2 {\phi }\eta ^2\nonumber \\&\quad +\cos {\phi }(3\sin ^2{\phi }-1)\eta \psi \nonumber \\&\quad +\frac{1}{2}\sin {\phi }\left( 1-3\cos ^2{\phi }\right) \psi ^2\bigg )=0 \end{aligned}$$

(18)

$$\begin{aligned}&\frac{\partial w}{\partial y}(0,\tau )=\alpha \bigg (\sin {\phi }\cos {\phi }\eta -\cos ^2{\phi }\psi \nonumber \\&\quad +\frac{1}{2}\bigg (\cos {\phi }\left( 1-3\sin ^2{\phi }\right) \eta ^2 \nonumber \\&\quad +2\sin {\phi }\left( 3\cos ^2{\phi }-1\right) \eta \psi \nonumber \\&\quad +3\cos {\phi }\left( 1+\cos ^2{\phi }\right) \psi ^2\bigg )\Bigg ) \end{aligned}$$

(19)

According to our previous assumptions, a re-scaling is done which is $\eta (\tau )=\epsilon \xi (\tau )$,$w(y,\tau )=\epsilon d(y,\tau )$ and $A_{m}=\epsilon \hat{A_{m}}$, where $\xi (\tau )$, $d(y,\tau )$ and $\hat{A_{m}}$ are of O(1). $w(y,\tau )=\epsilon d(y,\tau )$ and after putting $y=0$ in this equation we get

$$\begin{aligned} w(0,\tau )=\epsilon d(0,\tau ) \end{aligned}$$

(20)

In (15) it was assumed that $w(0,\tau )=w_{0}^{\star }+\psi (\tau )$ and substituting this in (20) leads to

$$\begin{aligned} w_{0}^{\star }+\psi (\tau )=\epsilon d(0,\tau ) \end{aligned}$$

(21)

We took $w_{0}^{\star }=0$ and substituting this in (21), we get

$$\begin{aligned} \psi (\tau )=\epsilon d(0,\tau ) \end{aligned}$$

(22)

After substituting (22) and $\eta (\tau )=\epsilon \xi (\tau )$ and $w(y,\tau )=\epsilon d(y,\tau )$ in equations (8), (18) and (19), the re-scaled equations are obtained as

$$\begin{aligned}{} & {} \frac{\partial ^2 d}{\partial y^2}-\frac{\partial ^2 d}{\partial \tau ^2}=0 \end{aligned}$$

(23)

$$\begin{aligned}{} & {} r\xi ^{\prime \prime }+ \alpha \bigg (2\sin ^2{\phi } \xi -\sin {\phi }\cos {\phi } d(0,\tau )\nonumber \\{} & {} \quad +3\sin {\phi }\cos ^2 {\phi }\epsilon \xi ^2\nonumber \\{} & {} \quad + \cos {\phi } \left( 3\sin ^2 {\phi }-1\right) \epsilon \xi d(0,\tau )\nonumber \\{} & {} \quad +\frac{1}{2}\sin {\phi } \left( 1-3\cos ^2{\phi }\right) \epsilon d^2(0,\tau )\bigg )=0 \end{aligned}$$

(24)

$$\begin{aligned}{} & {} \frac{\partial d}{\partial y}(0,\tau ) = \alpha \Bigg (\sin {\phi }\cos {\phi }\xi -\cos ^2{\phi }d(0,\tau )\nonumber \\{} & {} \quad \quad +\frac{1}{2} \bigg (\cos {\phi }(1-3\sin ^2{\phi })\epsilon \xi ^2 \nonumber \\{} & {} \quad \quad + 2\sin {\phi }\left( 1-3\cos ^2{\phi }\right) \epsilon \xi d(0,\tau )\nonumber \\{} & {} \quad \quad +3\cos {\phi }\left( 1+3\cos ^2{\phi }\right) \epsilon d^2(0,\tau )\bigg )\Bigg ) \end{aligned}$$

(25)

3.2 Asymptotic expansion

An asymptotic expansion is performed for $d(y,\tau )$ and $\xi (\tau )$ in terms of the chosen small parameter $\epsilon$ ($\epsilon \ll 1$):

$$\begin{aligned} d(y,\tau )=d_{0} (y,\tau )+\epsilon d_{1} (y,\tau )+O(\epsilon ^2 ) \end{aligned}$$

(26)

$$\begin{aligned} \xi (\tau )=\xi _{0}(\tau )+\epsilon \xi _{1}(\tau )+O(\epsilon ^2 ) \end{aligned}$$

(27)

The method of multiple time scales is used for the expansion to re-scale the time derivatives and two time scales are considered as given below. The displacements and their spatial and temporal derivatives are obtained as

$$\begin{aligned}{} & {} T_{0}=\tau , \ T_{1}=\epsilon \tau \end{aligned}$$

(28)

$$\begin{aligned}{} & {} d(y,\tau )=d_{0}(y,T_{0},T_{1})\nonumber \\{} & {} \quad +\epsilon d_{1}(y,T_{0},T_{1})+O(\epsilon ^2) \end{aligned}$$

(29)

$$\begin{aligned}{} & {} \xi (\tau )=\xi _{0}(T_{0},T_{1})+\epsilon \xi _{1}(T_{0},T_{1})+O(\epsilon ^2) \end{aligned}$$

(30)

$$\begin{aligned}{} & {} \frac{d\xi }{d\tau }=\xi ^{\prime }=(D_{0}+\epsilon D_{1}+\epsilon ^2 D_{2})\xi \end{aligned}$$

(31)

$$\begin{aligned}{} & {} \frac{d^2\xi }{d\tau ^2}=\xi ^{\prime \prime }=(D_{0}^2\nonumber \\{} & {} \quad +2\epsilon D_{0}D_{1}+2\epsilon ^2 D_{0}D_{2}+\epsilon ^2 D_{1}^2)\xi \end{aligned}$$

(32)

$$\begin{aligned}{} & {} \frac{\partial ^2 d}{\partial \tau ^2}=\left( D_{0}^2+2\epsilon D_{0}D_{1}+2\epsilon ^2 D_{0} D_{2}+\epsilon ^2 D_{1}^2 \right) d\nonumber \\ \end{aligned}$$

(33)

$$\begin{aligned}{} & {} \frac{\partial d}{\partial y}(0,\tau )=d_{0_{,y}}(0,T_{0},T_{1})\nonumber \\{} & {} \quad +\epsilon d_{1_{,y}} (0,T_{0},T_{1})+O(\epsilon ^2) \end{aligned}$$

(34)

where $D_{n}=d/dT_{n}$ (partial derivative)

The slow time scale $T_{1}$ can be neglected in the analysis henceforth because the excitation pulse is not a function of $T_{1}$. Therefore, $d_{0}$ and $\xi _{0}$ would not be functions of $T_{1}$. This can be easily proved by assuming a term containing the exponent $e^{i\omega (T_1+y)}$ in the expression for $d_0$ and then satisfying the equations at the first level of approximation (O(1)) to see that the term eventually goes to zero. After substituting equations (28)–(34) into equations (23), (24) and (25), the equations at O(1) & $O(\epsilon )$ approximation are obtained as

$$\begin{aligned}{} & {} \begin{aligned} O(1):\quad&\quad \frac{\partial ^2 d_0}{\partial y^2}-D_{0}^2 d_{0} = 0\\ rD_{0}^2 \xi _{0} +&2\alpha \sin ^2{\phi }\xi _{0} = \alpha \sin {\phi }\cos {\phi }d_{0}(0,T_{0})\\ \frac{\partial d_0}{\partial y}(0,T_{0})&= \alpha \left( \xi _{0}\sin {\phi }\cos {\phi }-\cos ^2{\phi }d_{0}(0,T_{0})\right) \end{aligned} \end{aligned}$$

(35)

$$\begin{aligned}{} & {} \begin{aligned} O(\epsilon ): \quad&\quad \frac{\partial ^2 d_1}{\partial y^2}-D_{0}^2 d_{1} = 0\\ rD_{0}^2 \xi _{1} +&2\alpha \sin ^2{\phi }\xi _{1} = \alpha \sin {\phi }\cos {\phi }d_{1}(0,T_{0})\\&\quad -3\alpha \sin {\phi }\cos ^2{\phi }\xi _0^2\\&\quad - \alpha \cos {\phi }\big (3\sin ^2{\phi }-1\big )\xi _{0}d_{0}(0,T_0 )\\&\quad -\frac{1}{2}\sin {\phi }\big (1-3\cos ^2{\phi }\big )d_{0}^2(0,T_{0})\\ \frac{\partial d_1}{\partial y}(0,T_{0}) \\&\quad = \alpha \Bigg (\xi _{1}\sin {\phi }\cos {\phi }-\cos ^2{\phi }d_{1}(0,T_{0})\\&\qquad +\frac{1}{2}\bigg (\cos {\phi }(1-3\sin ^2{\phi })\xi _{0}^2\\&\qquad + 2\sin {\phi }(3\cos ^2{\phi }-1)\xi _{0}d_{0}(0,T_{0})\\&\qquad +3\cos {\phi }(1+\cos ^2{\phi })d_{0}^2(0,T_{0})\bigg )\Bigg ) \end{aligned} \end{aligned}$$

(36)

On observing the left-hand sides of the second equations of both (35) and (36), the linearized natural frequency of the snap-through oscillator at different levels of approximation is defined as $\omega _0=\sqrt{2\alpha \sin ^2\phi /r}$.

3.3 Analytical closed-form solution

3.3.1 Non-resonant case, $\omega \ne \omega _0\ne \omega _0/2$

O(1) solution

Equations at the O(1) level of approximation (35) can be easily solved for $\xi _{0}$ and $d_{0}$ following standard procedures of solving the governing differential equations and satisfying the boundary conditions by using the harmonic balance method. To express the solutions in a compact form, we define few new variables, D, K, $\phi _R$ and $c_{R}$.

$$\begin{aligned} D= & {} -\frac{i}{2}\hat{A_{m}}\left( 1+e^{i\omega \phi _{R}}\right) , \ \phi _R=\frac{1}{\omega }arg(c_{R}),\nonumber \\ \ c_{R}= & {} \frac{a+ib}{-a+ib} \end{aligned}$$

(37)

where $a= \alpha ^2\sin ^2{\phi }\cos ^2{\phi } - \alpha r \omega ^2\cos ^2{\phi }$, $b = r\omega ^3 - 2\alpha \omega \sin ^2 \phi$

$$\begin{aligned} K=\frac{\alpha \sin \phi \cos \phi D}{r\left( \omega _{0}^2-\omega ^2\right) } \end{aligned}$$

(38)

We have performed a non-dimensional phase shift of $\omega {\tilde{L}}/L$ on the incident wave propagated in the bar as discussed in 2.1 while formulating the model for simplicity in the algebraic calculations. Taking this into account, the closed-form analytical solutions at O(1) approximation are obtained as

$$\begin{aligned}{} & {} d_{0}(y,T_{0})=\hat{A_m}e^{i\omega \left( T_{0}-y\right) }+c_{R}\hat{A_m}e^{i\omega \left( T_{0}+y\right) } \end{aligned}$$

(39)

$$\begin{aligned}{} & {} \xi _{0}(T_{0})=Ke^{i\omega T_{0}}+cc \end{aligned}$$

(40)

$$\begin{aligned}{} & {} d_{0}(0,T_{0})=De^{i\omega T_{0}}+cc \end{aligned}$$

(41)

cc denotes the complex conjugate of its preceding expressions. We have already defined the linearized non-dimensional natural frequency of the snap-through oscillator from the second of the equations of (35) or (36) as $\omega _{0}$ ($\omega _{0}=\sqrt{2\alpha \sin ^2{\phi }/r}$). The frequency of the excitation pulse has already been taken as $\omega$. We define $c_R$ to be the coefficient of reflection and $\phi _R$ to be the phase angle difference between the incident and reflected wave at the O(1) level of approximation for the non-resonant case.

The first expression in (39) can be defined as the incident pulse $d_I (y,T_0)$ and the second expression in (39) can be defined as the reflected pulse $d_R (y,T_0)$ at O(1) approximation from the nonlinear interface whose superposition gives the displacement in the bar. The bar displacement $d_0(y,T_0)$ in real time is obtained by taking the imaginary part of the expression in (39). Similarly, the incident pulse and the reflected pulse in real time are obtained by taking the imaginary parts of the first and second expressions in (39), respectively. We take the imaginary part of the expression to write the bar displacement, i.e. the incident pulse and reflected pulse in real time because our chosen excitation pulse is a sinusoidal displacement function imposed on the free end of the bar. Since the boundary condition we choose at the left end of the bar is a sinusoidal displacement function of time and the bar is a non-dispersive medium, the incident wave propagated is known to be a sinusoidal function of real time and space with the same frequency and wavenumber as the excitation pulse from D’Alembart’s principle [1]. This also results in the reflected wave in the bar from the nonlinear interface to be a sinusoidal function of real time and space with a coefficient of reflection which we have defined as $c_R$. For the ease of calculating the quadratic and coupled terms like $\xi _0^2 (T_0)$, $d_0^2 (0,T_0)$ and $\xi _0(T_0)d_0(0,T_0)$ in the $O(\epsilon )$ equations (27) and for simplicity in performing the harmonic balance method, we prefer to express the O(1) solutions in exponential form.

To solve the equations at $O(\epsilon )$ approximation, we investigate the second equation of (36). The right-hand side of this equation involves quadratic and coupled terms which can be calculated by using the O(1) solutions. They are found to be of the form:

$$\begin{aligned} \xi _{0}^2=\left( K^2e^{2i\omega T_{0}}+K{\bar{K}}\right) +cc \end{aligned}$$

(42)

$$\begin{aligned} d_{0}^2(0,T_{0})=\left( D^2e^{2i\omega T_{0}}+D{\bar{D}}\right) +cc \end{aligned}$$

(43)

$$\begin{aligned} \xi _{0}d_0(0,T_{0})=\left( KDe^{2i\omega T_{0}}+{\bar{K}}D\right) +cc \end{aligned}$$

(44)

So, we can say that $\xi _1$ will contain these combinations of frequencies. Thus, it is reasonable to assume that $d_1(y,T_{0})$ will also contain the second harmonic of $\omega$ along with the zero-frequency component. Keeping this in mind, we assume a form for $d_1(y,T_0)$

$$\begin{aligned} d_1(y,T_0)=\left( D_1e^{2i\omega (T_0+y)}+D_2\right) +cc \end{aligned}$$

(45)

$D_1$ and $D_2$ are the unknown coefficients to be found later by using the harmonic balance method. The wavenumber and frequency will be equal to each other in the non-dimensional form in the expression for wave displacement in the bar at $O(\epsilon )$ level of approximation ($d_1(y,T_0 )$) since it has to satisfy the non-dimensional plane wave equation, the first equation of (36). So the non-dimensional wave speed is unity. We are not assuming any term containing the harmonic $\omega _0$, i.e. our previously defined non-dimensional linearized natural frequency of the snap-through oscillator, in the expression for $d_1(y,T_0 )$. The reason is that from the analysis and solution of O(1) equations (35) by employing the harmonic balance method, we can conclude that the coefficients of these harmonics eventually have to be zero to avoid any secularity in the solution. We shall show how the harmonic balance method has been used in more detail in the following subsection.

The harmonic balance method and $O(\epsilon )$ solution

Solving for $\xi _1$ from the second equation of (36) by standard procedures of solving a second-order in-homogeneous ordinary differential equation with given initial conditions gives

$$\begin{aligned} \begin{aligned}&\xi _1=\frac{1}{r}\Bigg (\bigg (\frac{\alpha \sin \phi \cos \phi D_1-3\alpha \sin \phi \cos ^2\phi K^2-\alpha \cos \phi (3\sin ^2\phi -1)KD - \frac{1}{2}\sin \phi (1-3\cos ^2\phi ) D^2}{\omega _0^2-4\omega ^2}\bigg )e^{2i\omega T_0}\\&+ \frac{1}{\omega _0^2}\bigg (\alpha \sin \phi \cos \phi D_2-3\alpha \sin \phi \cos ^2 \phi K{\bar{K}}-\alpha \cos \phi (3\sin ^2\phi -1){\bar{K}}D\\&-\frac{1}{2}\sin \phi (1-3\cos ^2\phi )D{\bar{D}}\bigg )\Bigg ) \\&\quad + E_1 e^{i\omega _0 T_0} + cc \end{aligned} \end{aligned}$$

(46)

where $E_1$ is an unknown to be determined. From the third equation of (36), we can write

$$\begin{aligned} \begin{aligned} \xi _1&=\frac{1}{\sin \phi \cos \phi }\Bigg (\frac{1}{\alpha }\frac{\partial d_1}{\partial y}(0,T_0)+\cos ^2\phi d_1(0,T_0)\\&\quad -\frac{\cos \phi }{2}(1-3\sin ^2\phi ) \xi _0^2\\&\quad -\sin \phi (3\cos ^2\phi -1)\xi _0 d_0 (0,T_0)\\&\quad -\frac{3}{2} \cos \phi (1+\cos ^2\phi )d_0^2 (0,T_0)\Bigg ) \end{aligned} \end{aligned}$$

(47)

Substituting equations (46), (45) and equations (42), (43), (44) in equation (47) gives

$$\begin{aligned} \begin{aligned}&\bigg (\frac{\alpha \sin \phi \cos \phi D_1-3\alpha \sin \phi \cos ^2\phi K^2-\alpha \cos \phi (3\sin ^2\phi -1)KD - \frac{1}{2}\sin \phi (1-3\cos ^2\phi ) D^2}{r(\omega _0^2-4\omega ^2)}\bigg )e^{2i\omega T_0}\\&\quad + \frac{1}{\omega _0^2 r}\bigg (\alpha \sin \phi \cos \phi D_2-3\alpha \sin \phi \cos ^2\phi K{\bar{K}} -\alpha \cos \phi (3\sin ^2\phi -1){\bar{K}}D -\frac{1}{2}\sin \phi (1-3\cos ^2\phi )D{\bar{D}}\bigg )\\&\quad + E_1 e^{i\omega _0 T_0}=\Bigg (\frac{1}{\sin \phi \cos \phi }\bigg (\frac{2i\omega }{\alpha }+\cos ^2\phi \bigg )D_1\\&\quad -\frac{1}{2\sin \phi }(1-3\sin ^2\phi )K^2-\frac{1}{\cos \phi }(3\cos ^2\phi -1)KD - \frac{3}{2\sin \phi }(1+\cos ^2\phi )D^2\Bigg )e^{2i\omega T_0}\\&\quad +\Bigg (\cot \phi D_2-\frac{1}{2\sin \phi }(1-3\sin ^2\phi )K{\bar{K}} -\frac{1}{\cos \phi }(3\cos ^2\phi -1){\bar{K}}D-\frac{3}{2\sin \phi }(1+\cos ^2\phi )D{\bar{D}}\Bigg ) \end{aligned} \end{aligned}$$

(48)

Equating the coefficients of $e^{2i\omega T_0}$ and $e^{0}$ on both sides of equation (48) gives the unknowns $D_1$ and $D_2$ as

$$\begin{aligned} D_1&=\Big (\frac{\alpha \sin \phi \cos \phi }{r(\omega _0^2-4\omega ^2)} -\frac{\frac{2i\omega }{\alpha }+\cos ^2\phi }{\sin \phi \cos \phi }\Big )^{-1}\nonumber \\&\quad \Bigg (\frac{1}{r(\omega _0^2-4\omega ^2)}\Big (3\alpha \sin \phi \cos ^2\phi K^2\nonumber \\&\quad +\alpha \cos \phi (3\sin ^2\phi -1)KD\nonumber \\ {}&\quad +\frac{\sin \phi }{2}(1-3\cos ^2\phi )D^2\Big )\nonumber \\&\quad -\frac{1}{2\sin \phi }(1-3\sin ^2\phi )K^2\nonumber \\&\quad -\frac{1}{\cos \phi }(3\cos ^2\phi -1)KD\nonumber \\&\quad -\frac{3}{2\sin \phi }(1+\cos ^2\phi )D^2\Bigg ) \end{aligned}$$

(49)

$$\begin{aligned} D_2&=\Big (\frac{\alpha \sin \phi \cos \phi }{r\omega _0^2} \nonumber \\&\quad -\cot {\phi }\Big )^{-1}\Bigg (\frac{1}{r\omega _0^2}\Big (3\alpha \sin \phi \cos ^2\phi K{\bar{K}}\nonumber \\&\quad +\alpha \cos \phi (3\sin ^2\phi -1){\bar{K}}D\nonumber \\&\quad +\frac{1}{2}\sin \phi (1-3\cos ^2\phi )D{\bar{D}}\Big )\nonumber \\&\quad -\frac{1}{2\sin \phi }(1-3\sin ^2\phi )K{\bar{K}}\nonumber \\&\quad -\frac{1}{\cos \phi }(3\cos ^2\phi -1){\bar{K}}D\nonumber \\&\quad -\frac{3}{2\sin \phi }(1+\cos ^2\phi )D{\bar{D}}\Bigg ) \end{aligned}$$

(50)

Equating the coefficients of $e^{i\omega _0 T_0}$ on both sides of equation (48) gives $E_1=0$. Once we find out $D_1$ and $D_2$ explicitly in terms of the known system and excitation parameters, we can derive $\xi _1$ by substituting in equation (46) or (47).

Thus, we have used conventional perturbation techniques like the multiple time scales analysis, and the harmonic balance method to find the approximate analytical closed-form solutions to the system response for cases of sufficiently small amplitudes of the excitation pulse and for any chosen excitation frequency.

Numerical validation of analytical results

A numericalsimulation is performed to solve the essentially nonlinear system described in (8), (9), (10) and the non-dimensional essential boundary condition defined at the left end of the bar (11) using a finite difference centred in time, centred in space (CTCS) explicit scheme [36] for sufficiently small amplitudes of the excitation pulse. The dynamic responses are obtained for the incident and reflected pulse in the bar and the snap-through oscillator. Both the time-domain and frequency-domain responses are obtained for the incident and reflected waves in the bar and the oscillator motion. The incident pulse is already known to be a sinusoidal function of real time and space with the same amplitude and frequency as the excitation pulse from the essential boundary condition at the left end of the bar, even before starting the analysis. So, we show the reflected wave in the bar from the nonlinear interface and the oscillator motion as our obtained propagation characteristics and dynamic response of the system. A suitable numerical value is chosen for the non-dimensional excitation frequency $\omega =\omega _{exc}$.

The analytical solutions obtained before have been compared to the numerical results obtained computationally in Fig. 3. The non-dimensional parameters for both the analytical and numerical calculation have been taken as

$$\begin{aligned} \alpha= & {} 0.5, r=1, \hat{A_m}=1, l=300, \sin {\phi }=0.5,\\ \omega _0= & {} \sqrt{2\alpha \sin ^2{\phi }/r}=0.5,\\ \omega _{exc}= & {} 0.6\omega _0=0.3, \epsilon =0.01 \end{aligned}$$

On the FFT plots, the frequencies are represented in cycles per non-dimensional time along the x coordinate, denoted by the non-dimensional quantity, $\omega /2\pi$. $\omega _0/2\pi =0.08$ cycles per non-dimensional time, $\omega _{exc}/2\pi =0.048$ cycles per non-dimensional time. The sufficiently small amplitude of the excitation pulse considered for numerical simulation is $A_m=\epsilon \hat{A_m}=0.01$. The ratio l, i.e. the non-dimensional length of the bar, has been taken to be 300 to make the total space and time window larger. Since in the non-dimensional form, the longitudinal wave speed in the bar is unity, the time window becomes sufficiently large, i.e. 600, the time required for one complete traverse of the reflected wave along the bar from the nonlinear boundary to the other end. This also helps to get a steady response free from the very few transients that will initially arise due to discretization issues.

Fig. 3

Time-domain response and frequency-domain response of the reflected wave in the bar and the snap-through oscillator for the non-resonant case. $w_R(y,\tau )$ and $w_R(y,\omega )$ denote the non-dimensional reflected wave in the bar from the nonlinear interface in the time and frequency domains, respectively, whereas $\eta (\tau )$ and $\eta (\omega )$ denote the non-dimensional displacement of the oscillator measured with respect to its initial configuration $z=\sin \phi$ in the time and frequency domains, respectively. y, $\tau$ and $\omega$ are the non-dimensional longitudinal spatial coordinate along the bar, the non-dimensional time and the non-dimensional frequency, respectively

The displacement of the snap-through oscillator $z(\tau )$ is measured with respect to its initial position $z=\sin {\phi }$ while obtaining both the analytical and numerical solutions and from the notation introduced in the second of the assumptions in section 3.1, $z(\tau )=\sin {\phi }+\eta (\tau )$. Hence, $z(\tau )$ has been replaced by $\eta (\tau )$ while expressing the dynamic response of the snap-through oscillator in the time domain and $z(\omega )$ by $\eta (\omega )$ in the frequency/spectral domain. In 2.1 while introducing the model and applied excitation, a phase/spatial shift was performed on the incident wave in the bar to simplify the tedious algebra involved with the subsequent analytical calculations. It is notable to mention that while showing the results graphically, that phase has been added back into the solutions to represent the actual physical model without any spatial/temporal approximation. The same operation will be performed while showing the results graphically for the next two cases discussed.

3.3.2 Primary resonance, $\omega =\omega _0$

O(1) solution

For the case of primary resonance, $\omega =\omega _0$ and hence $d_0(y,T_0)$ is assumed to be

$$\begin{aligned} d_0(y,T_0)=\hat{A_m} e^{i\omega _0(T_0-y)}+\hat{A_R} e^{i\omega _0(T_0+y)} \end{aligned}$$

(51)

where $\hat{A_R}$ is unknown at this stage. The first term in the right-hand side of equation (51) is the incident wave and the second term is the reflected wave. The displacements in real time are obtained by taking the imaginary parts of the corresponding expressions. Substituting (51) in the second equation of (35), we get

$$\begin{aligned} r D_0^2 \xi _0+2\alpha \sin ^2\phi \xi _0=\alpha \sin \phi \cos \phi (\hat{A_m}+\hat{A_R})e^{i\omega _0T_0} \nonumber \\ \end{aligned}$$

(52)

Solving $\xi _0$ from (52) by standard methods of solving an inhomogeneous ordinary differential equation with given initial conditions gives

$$\begin{aligned} \xi _0=E_0 e^{i\omega _0 T_0}-\frac{i\alpha \sin \phi \cos \phi T_0}{2\omega _0 r}(\hat{A_m}+\hat{A_R})e^{i\omega _0 T_0} \nonumber \\ \end{aligned}$$

(53)

where $E_0$ is an unknown to be determined. The oscillator response in real time is obtained by taking the imaginary part of the r.h.s of (53). From the third equation of (35), we have

$$\begin{aligned} \xi _0=\frac{1}{\sin \phi \cos \phi }\left( \frac{1}{\alpha }\frac{\partial d_0}{\partial y}(0,T_0)+\cos ^2\phi d_0(0,T_0)\right) \nonumber \\ \end{aligned}$$

(54)

Substituting equations (51) and (53) in equation (54), we get

$$\begin{aligned}{} & {} E_0 e^{i\omega _0 T_0}-\frac{i\alpha \sin \phi \cos \phi T_0}{2\omega _0 r}(\hat{A_m}+\hat{A_R})e^{i\omega _0 T_0}\nonumber \\{} & {} \quad =\Bigg (\hat{A_m}\bigg (1-\frac{i\omega _0}{\alpha \sin \phi \cos \phi }\bigg )\nonumber \\{} & {} \quad +\hat{A_R}\bigg (1+\frac{i\omega _0}{\alpha \sin \phi \cos \phi }\bigg )\Bigg )e^{i\omega _0 T_0} \end{aligned}$$

(55)

contains a secular term which increases linearly with time $T_0$. So for a stable solution, we need to have

$$\begin{aligned} \hat{A_m}+\hat{A_R}=0 \end{aligned}$$

(56)

$$\begin{aligned} \implies \hat{A_R}=-\hat{A_m} \end{aligned}$$

(57)

Defining a new variable $c_R=\hat{A_R}/\hat{A_m}$ as the coefficient of reflection at the nonlinear interface at the O(1) level of approximation, for the case of primary resonance, $c_R=-1$.

Substituting equation (56) in equation 55 and equating the coefficients of $e^{i\omega _0 T_0}$ on both sides gives

$$\begin{aligned} E_0=-\frac{2i\omega _0 \hat{A_m}}{\alpha \sin \phi \cos \phi } \end{aligned}$$

(58)

After substituting equation (58)in equation (53) gives

$$\begin{aligned} \xi _0=-\frac{2i\omega _0 \hat{A_m}}{\alpha \sin \phi \cos \phi }e^{i\omega _0 T_0} \end{aligned}$$

(59)

The solution for $d_0 (y,T_0)$ is obtained from (51) as

$$\begin{aligned} d_0(y,T_0,T_1)=\hat{A_m} e^{i\omega _0(T_0-y)}-\hat{A_m} e^{i\omega _0(T_0+y)} \end{aligned}$$

(60)

The responses in real time are obtained by taking the imaginary parts of the corresponding expressions.

Note that after substituting $y=0$ in (60), we get

$$\begin{aligned} d_0 (0,T_0)=0 \end{aligned}$$

(61)

In complex conjugate form, the responses can be written in real time as

$$\begin{aligned} \xi _0=Ke^{i\omega _0 T_0}+cc \end{aligned}$$

(62)

where $K=-\frac{\omega _0 \hat{A_m}}{\alpha \sin \phi \cos \phi }$ and cc denotes the complex conjugate of its preceding terms. This physically means that the nonlinear interface will act as a fixed end and any excitation pulse incident upon this end will reflect with a phase shift of $\pi$ at O(1) approximation.

$O(\epsilon )$ solution

Substituting the result obtained in (61) in the equations at the $O(\epsilon )$ level of approximation (36) reduces them to

$$\begin{aligned} \begin{aligned}&O(\epsilon ): \quad \frac{\partial ^2 d_1}{\partial y^2}-D_{0}^2 d_{1} = 0\\&\quad rD_{0}^2 \xi _{1} + 2\alpha \sin ^2{\phi }\xi _{1} = \alpha \sin {\phi }\cos {\phi }d_{1}(0,T_{0})\\&-3\alpha \sin {\phi }\cos ^2 {\phi }\xi _0^2\\&\quad \frac{\partial d_1}{\partial y}(0,T_0) = \alpha \Big (\xi _1\sin \phi \cos \phi -\cos ^2\phi d_1(0,T_0)\\&+\frac{1}{2}\cos \phi (1-3\sin ^2\phi )\xi _0^2\Big ) \end{aligned} \end{aligned}$$

(63)

On investigating the second equation of (63), it can be seen that the right-hand side of this equation involves a quadratic term $\xi _0^2$, which can be calculated by using the O(1) solution and appears in the form:

$$\begin{aligned} \xi _{0}^2=\left( K^2e^{2i\omega _0 T_{0}}+K{\bar{K}}\right) +cc \end{aligned}$$

(64)

So, we can say that $\xi _1$ will contain the same frequency. Thus, it is reasonable to assume that $d_1(y,T_{0})$ will also contain the second harmonic of $\omega _0$ along with the zero-frequency component. Keeping this in mind, we assume a form for $d_1(y,T_0)$

$$\begin{aligned} d_1(y,T_0)=\left( R_1e^{2i\omega _0 (T_0+y)}+R_2\right) +cc \end{aligned}$$

(65)

$R_1$ and $R_2$ are the unknown coefficients to be found. The wavenumber and frequency will be equal to each other in the non-dimensional form in the expression for wave displacement in the bar at $O(\epsilon )$ level of approximation ($d_1(y,T_0 )$) since it has to satisfy the non-dimensional plane wave equation, the first equation of (63). So the non-dimensional wave speed is unity. We are not assuming any term containing the harmonic $\omega _0$, i.e. our previously defined non-dimensional linearized natural frequency of the snap-through oscillator, in the expression for $d_1(y,T_0)$. The reason is that from the analysis and solution of O(1) equations in the previous section, we can conclude that the coefficients of these harmonics eventually have to be zero to avoid any secularity in the solution. Solving for $\xi _1$ from the second equation of (63) gives by standard procedures of solving a second-order in-homogeneous ordinary differential equation with given initial conditions

$$\begin{aligned} \xi _1{} & {} =\frac{1}{r(\omega _0^2-4\omega ^2)}\Big (\alpha \sin \phi \cos \phi R_1\nonumber \\{} & {} \quad -3\alpha \sin \phi \cos ^2\phi K^2\Big ) e^{2i\omega _0 T_0}\nonumber \\{} & {} \quad +\frac{1}{\omega _0^2 r}\Big (\alpha \sin \phi \cos \phi R_2-3\alpha \sin \phi \cos ^2 \phi K{\bar{K}}\Big )\nonumber \\{} & {} \quad + E_1 e^{i\omega _0 T_0} + cc \end{aligned}$$

(66)

where $E_1$ is an unknown to be determined. From the third equation of (63), we can write

$$\begin{aligned} \begin{aligned} \xi _1&=\frac{1}{\sin \phi \cos \phi }\bigg (\frac{1}{\alpha }\frac{\partial d_1}{\partial y}(0,T_0)+\cos ^2\phi d_1(0,T_0)\\&\quad -\frac{\cos \phi }{2}(1-3\sin ^2\phi ) \xi _0^2\bigg ) \end{aligned} \end{aligned}$$

(67)

Substituting equations (66), (65) and (64) in equation (67) gives

$$\begin{aligned} \begin{aligned}&\frac{1}{r(\omega _0^2-4\omega ^2)}\Bigg (\alpha \sin \phi \cos \phi R_1\\&-3\alpha \sin \phi \cos ^2\phi K^2\Bigg )e^{2i\omega _0 T_0}\\&\quad +\frac{1}{\omega _0^2 r}\Bigg (\alpha \sin \phi \cos \phi R_2-3\alpha \sin \phi \cos ^2 \phi K{\bar{K}}\Bigg )\\&\quad + E_1 e^{i\omega _0 T_0}=\Bigg (\frac{1}{\sin \phi \cos \phi }\bigg (\frac{2i\omega }{\alpha }+\cos ^2\phi \bigg )R_1\\&\quad -\frac{1}{2\sin \phi }(1-3\sin ^2\phi )K^2\Bigg )e^{2i\omega _0 T_0}\\&\quad +\Bigg (\cot \phi R_2-\frac{1}{2sin\phi }(1-3\sin ^2\phi )K{\bar{K}}\Bigg ) \end{aligned} \end{aligned}$$

(68)

Equating the coefficients of $e^{2i\omega _0 T_0}$ and $e^{0}$ on both sides of equation (68) gives the unknown coefficients $R_1$ and $R_2$ as

$$\begin{aligned} R_1&=\Big (\frac{\alpha \sin \phi \cos \phi }{-3r\omega _0^2} -\frac{2i\omega _0+\alpha \cos ^2\phi }{\alpha \sin \phi \cos \phi }\Big )^{-1}\nonumber \\&\Bigg (\frac{-\alpha \sin \phi \cos ^2\phi }{r\omega _0^2}-\frac{(1-3\sin ^2\phi )}{2\sin \phi }\Bigg )K^2 \end{aligned}$$

(69)

$$\begin{aligned} R_2&=\Big (\frac{\alpha \sin \phi \cos \phi }{r\omega _0^2} -\cot {\phi }\Big )^{-1}\Bigg (\frac{3\alpha \sin \phi \cos ^2\phi }{r\omega _0^2}\nonumber \\&-\frac{(1-3\sin ^2\phi )}{2\sin \phi }\Bigg )K{\bar{K}} \end{aligned}$$

(70)

Equating the coefficients of $e^{i\omega _0 T_0}$ on both sides of equation (68) gives $E_1=0$. Now that we have found $E_1$, $R_1$ and $R_2$ explicitly in terms of the known system and excitation parameters, we can derive $\xi _1$ by substituting either in equation (66) or (67).

Numerical validation of analytical results

The analytical solutions obtained are compared to the numerical results obtained computationally as done for the non-resonant case. The non-dimensional parameters are taken as:

$$\begin{aligned} \alpha= & {} 0.5, r=1, \hat{A_m}=1, l=300, \sin {\phi }=0.5,\\ \omega _0= & {} \sqrt{2\alpha \sin ^2{\phi }/r}=0.5,\\ \omega _{exc}= & {} \omega _0=0.5, \epsilon =0.01 \end{aligned}$$

On the FFT plots, the frequencies will be represented in cycles per non-dimensional time along the x coordinate, denoted by the non-dimensional quantity $\omega /2\pi$. $\omega _0/2\pi =0.08$ cycles per non-dimensional time, $\omega _{exc}/2\pi =\omega _0/2\pi =0.08$ cycles per non-dimensional time. The sufficiently small amplitude of the excitation pulse considered for numerical simulation is $A_m=\epsilon \hat{A_m}=0.01$. The ratio l, i.e. the non-dimensional length of the bar, has been taken to be 300 to make the total space and time window larger. Since in the non-dimensional form, the longitudinal wave speed in the bar is unity, the time window for one complete traverse of the reflected wave along the bar becomes sufficiently large, i.e. 600 and this helps to get a more steady response free from the very few transients that will initially arise due to discretization issues.

We have taken the point of reference for measuring the displacement of the snap-through oscillator $z(\tau )$ at $z=\sin {\phi }$ which is its initial position, as done previously for the non-resonant case while obtaining both the analytical and numerical solutions. Hence, $z(\tau )$ has been replaced by $\eta (\tau )$ while expressing the dynamic response of the snap-through oscillator in the time domain and $z(\omega )$ by $\eta (\omega )$ in the frequency/spectral domain.

The displacement at the endpoint of the bar is plotted specifically for the case of primary resonance to highlight an interesting phenomenon. It has been shown in the analytical results before that for this particular excitation frequency ($\omega =\omega _0$), the displacement at the endpoint of the bar connected to the snap-through oscillator ($d_0(0,T_0)$) that is the superposition of incident and reflected waves at that point goes to 0 at the O(1) level of approximation. At the next $O(\epsilon )$ level of approximation, the displacement in the bar at the nonlinear interface ($d_1(0,T_0)$) is composed of one component with the frequency ($2\omega$) and one zero-frequency component. The calculated analytical solutions are compared to numerical results as done so far for all dynamic responses.

As we can see in Fig. 5, our derived approximated analytical result is in quite good agreement with the numerical solution of the actual system. The motion when plotted shows a behaviour physically consistent with the expectations from our analytical solution, that is a jump from its initial zero value and then oscillations with very small amplitudes about a new dropped/offsetted mean position. The small vertical drop in the initial zero mean position is caused due to the presence of the zero-frequency component and the very small oscillations about the new mean position is attributed to the component with the second harmonic of the excitation frequency ($2\omega$) present at the $O(\epsilon )$ level of approximation. This is further validated by our numerical results obtained computationally. The essential nonlinearity in our system physically manifests itself in this unique behaviour of the nonlinear interface for small amplitudes of excitation pulse at primary resonance. This behaviour is qualitatively quite similar to a soliton-like wave phenomenon.

3.3.3 Secondary resonance, $\omega =\omega _0/2$

O(1) and $O(\epsilon )$ solutions

The solution and analysis for the O(1) equations remain the same as for the non-resonant case with $\omega$ replaced by $\omega _0/2$. The solutions are given as

$$\begin{aligned} d_{0}(y,T_{0})= & {} \hat{A_m}e^{i\frac{\omega _0}{2}\left( T_{0}-y\right) }+c_{R}\hat{A_m}e^{i\frac{\omega _0}{2}\left( T_{0}+y\right) } \end{aligned}$$

(71)

$$\begin{aligned} \xi _{0}(T_{0})= & {} Ke^{i\frac{\omega _0}{2} T_{0}}+cc \end{aligned}$$

(72)

$$\begin{aligned} d_{0}(0,T_{0})= & {} De^{i\frac{\omega _0}{2} T_{0}}+cc \end{aligned}$$

(73)

The first term in (71) is defined as the incident wave, $d_I(y,T_0)$ and the second term the reflected wave, $d_R(y,T_0)$ from the nonlinear interface whose superposition gives the bar displacement at O(1) approximation. cc denotes the complex conjugate of its preceding expressions. For the case of secondary resonance ($\omega =\omega _0/2$), the quadratic and coupled terms in the r.h.s of the second equation of (36) are of the form

$$\begin{aligned} \xi _{0}^2=\left( K^2e^{i\omega _0 T_{0}}+K{\bar{K}}\right) +cc \end{aligned}$$

(74)

$$\begin{aligned} d_{0}^2(0,T_{0})=\left( D^2e^{i\omega _0 T_{0}}+D{\bar{D}}\right) +cc \end{aligned}$$

(75)

$$\begin{aligned} \xi _{0}d_0(0,T_{0})=\left( KDe^{i\omega _0 T_{0}}+{\bar{K}}D\right) +cc \end{aligned}$$

(76)

Recalling our analysis for the non-resonant and primary resonant case, $d_1(y,T_{0})$ is assumed to be of the form

$$\begin{aligned} d_1(y,T_0)=\left( S_1e^{i\omega _0(T_0+y)}+S_2\right) +cc \end{aligned}$$

(77)

$S_1$ and $S_2$ are the unknown coefficients to be found. The non-dimensional wave speed is unity. For the case of secondary resonance, the second equation of (36) becomes after substituting equations (74)–(77)

$$\begin{aligned} \begin{aligned}&rD_{0}^2 \xi _{1} + 2\alpha \sin ^2{\phi }\xi _{1}\\&\quad =\bigg (\alpha \sin \phi \cos \phi S_1 -3\alpha \sin \phi \cos ^2\phi K^2\\&\qquad -\alpha \cos \phi (3\sin ^2\phi -1)KD \\&\qquad -\frac{1}{2}\sin \phi (1-3\cos ^2\phi D^2)\bigg )e^{i\omega _0 T_0}\\&\qquad +\bigg (\alpha \sin \phi \cos \phi S_2-3\alpha \sin \phi \cos ^2 \phi K{\bar{K}}\\&\qquad -\alpha \cos \phi (3\sin ^2\phi -1){\bar{K}}D\\&\qquad -\frac{1}{2}\sin \phi (1-3\cos ^2\phi )D{\bar{D}}\bigg ) \end{aligned} \end{aligned}$$

(78)

Solving for $\xi _1$ from (78) gives by standard procedures of solving a second-order in-homogeneous ordinary differential equation with given initial conditions

$$\begin{aligned} \xi _1{} & {} =-\frac{i T_0}{2\omega _0 r}\bigg (\alpha \sin \phi \cos \phi S_1 -3\alpha \sin \phi \cos ^2\phi K^2\nonumber \\{} & {} \quad -\alpha \cos \phi (3\sin ^2\phi -1)KD\nonumber \\{} & {} \quad -\frac{1}{2}\sin \phi (1-3\cos ^2\phi )D^2\bigg )e^{i\omega _0 T_0}\nonumber \\{} & {} \quad + \frac{1}{\omega _0^2 r}\bigg (\alpha \sin \phi \cos \phi S_2-3\alpha \sin \phi \cos ^2 \phi K{\bar{K}}\nonumber \\{} & {} \quad -\alpha \cos \phi (3\sin ^2\phi -1){\bar{K}}D\nonumber \\{} & {} \quad -\frac{1}{2}\sin \phi (1-3\cos ^2\phi )D{\bar{D}}\bigg )+ E_1 e^{i\omega _0 T_0} + cc\nonumber \\ \end{aligned}$$

(79)

where $E_1$ is an unknown to be determined. From the third equation of (36), we can write

$$\begin{aligned} \begin{aligned} \xi _1&=\frac{1}{\sin \phi \cos \phi }\Bigg (\frac{1}{\alpha }\frac{\partial d_1}{\partial y}(0,T_0)+\cos ^2\phi d_1(0,T_0)\\&\quad -\frac{\cos \phi }{2}(1-3\sin ^2\phi ) \xi _0^2\\&\quad -\sin \phi (3\cos ^2\phi -1)\xi _0 d_0 (0,T_0)\\&\quad -\frac{3}{2} \cos \phi (1+\cos ^2\phi )d_0^2 (0,T_0)\Bigg ) \end{aligned} \end{aligned}$$

(80)

Substituting equations (74)–(77) in equation (80) gives

$$\begin{aligned} \begin{aligned}&-\frac{i T_0}{2\omega _0 r}\bigg (\alpha \sin \phi \cos \phi S_1 -3\alpha \sin \phi \cos ^2\phi K^2\\&\quad -\alpha \cos \phi (3\sin ^2\phi -1)KD \\&\quad -\frac{1}{2}\sin \phi (1-3\cos ^2\phi )D^2\bigg )e^{i\omega _0 T_0}\\&\quad + \frac{1}{\omega _0^2 r}\bigg (\alpha \sin \phi \cos \phi S_2-3\alpha \sin \phi \cos ^2 \phi K{\bar{K}}\\&\quad -\alpha \cos \phi (3\sin ^2\phi -1){\bar{K}}D \\&\quad -\frac{1}{2}\sin \phi (1-3\cos ^2\phi )D{\bar{D}}\bigg )\\&\quad + E_1 e^{i\omega _0 T_0}=\Bigg (\frac{1}{\sin \phi \cos \phi }\bigg (\frac{2i\omega }{\alpha }+\cos ^2\phi \bigg )S_1\\&\quad -\frac{1}{2\sin \phi }(1-3\sin ^2\phi )K^2\\&\quad -\frac{1}{\cos \phi }(3\cos ^2\phi -1)KD\\&\quad - \frac{3}{2\sin \phi }(1+\cos ^2\phi )D^2\Bigg )e^{i\omega _0 T_0}\\&\quad +\Bigg (\cot \phi S_2-\frac{1}{2sin\phi }(1-3\sin ^2\phi )K{\bar{K}}\\&\quad -\frac{1}{\cos \phi }(3\cos ^2\phi -1){\bar{K}}D\\&\quad -\frac{3}{2\sin \phi }(1+cos^2\phi )D{\bar{D}}\Bigg ) \end{aligned} \end{aligned}$$

(81)

Equating the coefficients of $e^{i\omega _0 T_0}$ and $e^{0}$ or 1 on both sides of (81) gives

$$\begin{aligned}&-\frac{i T_0}{2\omega _0 r}\bigg (\alpha \sin \phi \cos \phi S_1 -3\alpha \sin \phi \cos ^2\phi K^2\nonumber \\&\qquad -\alpha \cos \phi (3\sin ^2\phi -1)KD \nonumber \\&\qquad -\frac{1}{2}\sin \phi (1-3\cos ^2\phi )D^2\bigg )\nonumber \\&\qquad +E_1=\frac{1}{\sin \phi \cos \phi }\bigg (\frac{2i\omega }{\alpha }+\cos ^2\phi \bigg )S_1\nonumber \\&\qquad -\frac{1}{2\sin \phi }(1-3\sin ^2\phi )K^2\nonumber \\&\qquad -\frac{1}{\cos \phi }(3\cos ^2\phi -1)KD\nonumber \\&\qquad -\frac{3}{2\sin \phi }(1+\cos ^2\phi )D^2 \end{aligned}$$

(82)

$$\begin{aligned}&\frac{1}{\omega _0^2 r}\bigg (\alpha \sin \phi \cos \phi S_2-3\alpha \sin \phi \cos ^2 \phi K{\bar{K}}\nonumber \\&\qquad -\alpha \cos \phi (3\sin ^2\phi -1){\bar{K}}D \nonumber \\&\qquad -\frac{1}{2}\sin \phi (1-3\cos ^2\phi )D{\bar{D}}\bigg )\nonumber \\&\quad =\cot \phi S_2-\frac{1}{2sin\phi }(1-3\sin ^2\phi )K{\bar{K}}\nonumber \\&\qquad -\frac{1}{\cos \phi }(3\cos ^2\phi -1){\bar{K}}D\nonumber \\&\qquad -\frac{3}{2\sin \phi }(1+cos^2\phi )D{\bar{D}} \end{aligned}$$

(83)

From (79), we can notice that the solution to $\xi _1$ contains a secular term which increases linearly with time $T_0$. So, for a stable solution of $\xi _1$, we need to have

$$\begin{aligned}{} & {} \alpha \sin \phi \cos \phi S_1 -3\alpha \sin \phi \cos ^2\phi K^2\nonumber \\{} & {} \quad -\alpha \cos \phi (3\sin ^2\phi -1)KD\nonumber \\{} & {} \quad -\frac{1}{2}\sin \phi (1-3\cos ^2\phi )D^2=0 \end{aligned}$$

(84)

$$\begin{aligned}{} & {} \implies S_1 = 3\cos \phi K^2+\left( \frac{3\sin ^2\phi -1}{\sin \phi }\right) KD\nonumber \\{} & {} \quad +\left( \frac{1-3\cos ^2\phi }{2\alpha \cos \phi }\right) D^2 \end{aligned}$$

(85)

Solving for $S_2$ from equation (83) gives

$$\begin{aligned} \begin{aligned} S_2&=\bigg (\alpha \sin \phi \cos \phi -r\omega _0^2\cot {\phi }\bigg )^{-1}\\&\quad \Bigg (\bigg (3\alpha \sin \phi \cos ^2\phi -\frac{r\omega _0^2(1-3\sin ^2\phi )}{2\sin \phi }\bigg )K{\bar{K}}\\&\quad +\bigg (\alpha \cos \phi (3\sin ^2\phi -1)\\&\quad -\frac{r\omega _0^2(3\cos ^2\phi -1)}{\cos \phi }\bigg ){\bar{K}}D\\&\quad +\bigg (\frac{1}{2}\sin \phi (1-3\cos ^2\phi )\\&\quad -\frac{3r\omega _0^2}{2\sin \phi }(1+cos^2\phi )\bigg )D{\bar{D}}\Bigg ) \end{aligned} \end{aligned}$$

(86)

Substituting equation (84) in (82) and replacing $\omega$ by $\omega _0/2$ gives

$$\begin{aligned} \begin{aligned}&E_1=\frac{1}{\sin \phi \cos \phi }\bigg (\frac{i\omega _0}{\alpha }+\cos ^2\phi \bigg )S_1\\&\quad -\frac{1}{2\sin \phi }(1-3\sin ^2\phi )K^2\\&\quad -\frac{1}{\cos \phi }(3\cos ^2\phi -1)KD\\&\quad -\frac{3}{2\sin \phi }(1+\cos ^2\phi )D^2 \end{aligned} \end{aligned}$$

(87)

Substituting the expression for $S_1$ as obtained in (85) in (87), we can derive $E_1$. Now that we have found the unknown coefficients $S_1$, $S_2$ and $E_1$, we can easily derive $\xi _1$ from either (79) or (80).

Fig. 4

Time-domain response and frequency-domain response of the reflected wave in the bar and the snap-through oscillator for primary resonance. $w_R(y,\tau )$ and $w_R(y,\omega )$ denote the non-dimensional reflected wave in the bar from the nonlinear interface in the time and frequency domains, respectively, whereas $\eta (\tau )$ and $\eta (\omega )$ denote the non-dimensional displacement of the oscillator measured with respect to its initial configuration $z=\sin \phi$ in the time and frequency domains, respectively. y, $\tau$ and $\omega$ are the non-dimensional longitudinal spatial coordinate along the bar, the non-dimensional time and the non-dimensional frequency, respectively

Numerical validation of analytical results

The analytical solutions obtained are compared to the numerical results obtained computationally as done in the previous two cases with the same non-dimensional parameters, which are:

$$\begin{aligned}{} & {} \alpha =0.5, r=1, \hat{A_m}=1, l=300, \sin {\phi }=0.5, \omega _0\\{} & {} \quad =\sqrt{2\alpha \sin ^2{\phi }/r}=0.5, \omega _{exc}=\omega _0/2=0.25, \epsilon =0.01 \end{aligned}$$

On the FFT plots, the frequencies will be represented in cycles per non-dimensional time along the x coordinate, denoted by the non-dimensional quantity, $\omega /2\pi$. $\omega _0/2\pi =0.08$ cycles per non-dimensional time, $\omega _{exc}/2\pi =\omega _0/4\pi =0.04$ cycles per non-dimensional time. The sufficiently small amplitude of the excitation pulse considered for numerical simulation is $A_m=\epsilon \hat{A_m}=0.01$. The ratio l, i.e. the non-dimensional length of the bar, has been taken to be 300 to make the total space and time window larger. Since in the non-dimensional form, the longitudinal wave speed in the bar is unity, the time window becomes sufficiently large, i.e. 600 and this helps to get a steadier response free from the very few transients that will initially arise due to discretization issues.

We have taken the point of reference for measuring the displacement of the snap-through oscillator $z(\tau )$ at $z=\sin \phi$ which is its initial position, as done for the non-resonant case and primary resonance while obtaining both the analytical and numerical solutions. Hence, $z(\tau )$ has been replaced by $\eta (\tau )$ while expressing the dynamic response of the snap-through oscillator in the time domain and $z(\omega )$ by $\eta (\omega )$ in the frequency/ spectral domain.

3.4 Discussion

We can see from the comparison of our analytical and numerical results for the three cases studied, that the analytical solution for the time-domain response of the reflected pulse matches quite well with the numerical solution obtained from the finite difference scheme for a long duration of time. The frequency-domain response obtained analytically also matches closely with the numerical frequency-domain response.

There are very few initial transients arising in the numerical solution, at $\tau =300$ in the time series plots, which might be due to discretization issues, but they die out very soon and the numerical response evolves in a steady manifold along with the analytical response with the same amplitude and frequency. The dominant harmonic in the dynamic response is the excitation frequency $\omega _{exc}$ and the nonlinearity in the system generates a second harmonic of $\omega _{exc}$, i.e. $2\omega _{exc}$, but of much lower intensity and a zero-frequency component with a considerably large intensity for certain excitation frequencies such as the case of primary resonance. The numerical results also validate our second assumption made in 3.1 while finding the solution analytically that for sufficiently small amplitudes of the excitation pulse, the bar displacement at the nonlinear interface and the displacement of the oscillator from its stable equilibrium position $z=\sin \phi$ will also be sufficiently small.

Fig. 5

The displacement at the point in the bar connected to the snap-through oscillator plotted in the time domain for primary resonance. $w(y,\tau )$ is the non-dimensional displacement at any point in the bar. y and $\tau$ are the non-dimensional longitudinal spatial coordinate along the bar and the non-dimensional time, respectively

3.4.1 Non-resonant case, $\omega \ne \omega _0\ne \omega _0/2$:

For our chosen values of the system parameters $\alpha$, r and $\sin \phi$, the linearized natural frequency is $\omega _0=0.5$ and we have chosen the excitation frequency to be $\omega _{exc}=0.6\omega _0=0.3$. The analytical solution derived for the reflected wave matches significantly with the numerical solution in the time-series plot Fig. 3a. The sharp peak at $\omega _{exc}/2\pi =0.048$ in the FFT plot of the reflected wave Fig. 3b represents the dominant frequency present in the reflected pulse. This is the excitation frequency itself and the same harmonic contained in the incident pulse in the bar. There is a small peak at $(2\omega _{exc})/2\pi =\omega /\pi =0.096$ which is the second harmonic of $\omega$ arising due to the nonlinearity in the system. The oscillator response obtained analytically also matches significantly with the same obtained numerically as can be seen from both the time-domain Fig. 3c and frequency-domain plots Fig. 3d and is found to contain the same frequency as in the reflected wave with peaks occurring at $\omega _{exc}/2\pi$ and $(2\omega _{exc})/2\pi =\omega /\pi$ in the FFT plot. As for the reflected pulse, the effect of the excitation frequency ($\omega _{exc}$) is the most pronounced in the oscillator response with the effect of the second harmonic ($2\omega _{exc}$) being much weaker.

3.4.2 Primary resonance, $\omega =\omega _0$:

The dynamic response of the system shows the same characteristics as for the non-resonant case. We keep our chosen system parameters the same as for the non-resonant case and obtain the linearized natural frequency as $\omega _0=0.5$ and the excitation frequency as $\omega _{exc}=\omega _0=0.5$. The analytical solution derived for the reflected wave and the oscillator matches significantly with the numerical solutions in both the time-domain Figs. 4a, and c and in the frequency-domain Fig. 4(b), 4(d). The sharp peak at $\omega /2\pi =0.08$ in the FFT plot of the reflected wave Fig. 4b represents the dominant frequency present in the reflected pulse. This is the excitation frequency itself and the same harmonic contained in the incident pulse in the bar and for primary resonance the same as the linearized natural frequency $\omega _0$. There is a very small peak at $(2\omega _{exc})/2\pi =\omega _{exc}/\pi =0.16$ which is the second harmonic of $\omega _{exc}$ arising due to the nonlinearity in the system. The effect of the second harmonic ($2\omega _{exc}$) is much much weaker when compared to the fundamental harmonic ($\omega _{exc}$). Along with these two harmonics, the reflected wave also has a pronounced zero-frequency or dc component as can be seen from both the analytical and numerical results. This is quite expected from our analysis and assumed forms while deriving the theoretical solutions which is further validated by the numerical results. On investigating the oscillator response, it can be seen from both the time-domain Fig. 4c and frequency-domain plots Fig. 4d that it contains the same frequencies as in the reflected wave with peaks occurring at $\omega _{exc}/2\pi$ and $(2\omega _{exc})/2\pi =\omega /\pi$ and 0 in the FFT plot. Similar to the reflected pulse, the effects of the excitation frequency ($\omega _{exc}$) and the zero-frequency components are the most pronounced in the oscillator response with the effects of the second harmonic ($2\omega _{exc}$) being much weaker. The displacement at the nonlinear interface in the bar ($w(y,\tau )$ at $y=0$) 5 shows interesting behaviour. The motion at this point in the bar shows a jump from its initial zero value and then oscillates with very small amplitudes about a new dropped/offsetted mean position.

Fig. 6

Time-domain response and frequency-domain response of the reflected wave in the bar and the snap-through oscillator for secondary resonance. $w_R(y,\tau )$ and $w_R(y,\omega )$ denote the non-dimensional reflected wave in the bar from the nonlinear interface in the time and frequency domains, respectively, whereas $\eta (\tau )$ and $\eta (\omega )$ denote the non-dimensional displacement of the oscillator measured with respect to its initial configuration $z=\sin \phi$ in the time and frequency domains, respectively. y, $\tau$ and $\omega$ are the non-dimensional longitudinal spatial coordinate along the bar, the non-dimensional time and the non-dimensional frequency, respectively

3.4.3 Secondary resonance, $\omega =\omega _0/2$:

Since we have kept the system parameters the same, $\omega _0=0.5$. The system’s dynamic response characteristics remain qualitatively the same as the for the two cases studied previously, with the excitation frequency ($\omega _{exc}=\omega _0/2=0.25$) as the fundamental harmonic and the second harmonic ($2\omega _{exc}=2\omega _0/2=\omega _0=0.5$) being present in the reflected wave and the oscillator motion. The effect of the second harmonic is much weaker when compared to the fundamental harmonic. The essential nonlinearity in the system for sufficiently small excitation amplitudes manifests itself as the weaker second harmonic of the excitation frequency in the dynamic response. The numerical results match quite well with the analytical solutions in both the time domain and the frequency domain. The sharp peak at $\omega _{exc}/2\pi =0.04$ in the FFT plots Fig 6b, d represents the dominant/fundamental harmonic in the response and the small peak at $2\omega _{exc}/2\pi =0.08$ represents the effect of the essential nonlinearity with a much weaker intensity for sufficiently small excitation amplitudes. There is also the presence of a small zero-frequency or dc component in both the reflected wave and oscillator response.

Summing up the results obtained for the three different cases studied both analytically and numerically, it can be concluded that even though the attachment to the elastic bar is essentially nonlinear, for sufficiently small amplitudes of the excitation pulse and for any chosen excitation frequency, the dominant harmonic in the dynamic response of the system will be the excitation frequency ($\omega _{exc}$) itself and sometimes the zero-frequency component depending upon the excitation frequency. The effect of the nonlinearity will be manifested as the presence of the much weaker component containing the second harmonic of the excitation frequency ($2\omega _{exc}$) and sometimes a dominant zero-frequency component.

4 Stability Analysis of the snap-through oscillator

4.1 Floquet analysis

To implement the extended Floquet theory [37] for stability analysis, we will investigate the exact non-dimensional governing differential equation of the snap-through oscillator (9) independently. If we consider this equation, we have one unknown at this stage which is the displacement of the endpoint of the bar ($w(0,\tau )$). The displacement at the endpoint is the superposition of the reflected and incident wave at that point. So far in our analysis, we have seen that if the incident pulse is a sinusoidal one with frequency $\omega$, the reflected pulse will also be a sinusoidal one with $\omega$ as the dominant harmonic. The displacement of the end-point of the bar will also be a sinusoidal function of time with the excitation frequency $\omega$ as the dominant harmonic and there will be a phase difference between the incident wave and the reflected wave at the nonlinear interface depending upon the excitation frequency. So, at this stage, we make an approximation for the bar endpoint displacement. We consider it to be a simple sinusoidal function of time with a certain amplitude and composed of a single frequency which we call the excitation frequency $\omega$. So our assumed form for the bar endpoint displacement is

$$\begin{aligned} w(0,\tau )=D\sin {\omega \tau } \end{aligned}$$

(88)

D is unknown and can be sufficiently large, i.e. of O(1). The excitation frequency $\omega$ can have any chosen value. Equation (9), when written in functional form is

$$\begin{aligned} rz^{\prime \prime }+\alpha f(z(\tau ),w(0,\tau ),\tau )=0 \end{aligned}$$

(89)

In section 3.1 while finding the dynamic response analysis, we have taken $w(0,\tau )$ to be very close to zero $(O(\epsilon ))$ because the amplitude of the excitation pulse, i.e. $A_m$ has been considered to be of $O(\epsilon )$. But, here we do the analysis for a more generalized case, where $A_m$ and hence $w(0,\tau )$ and hence D can be of O(1). Since we have taken an approximation for $w(0,\tau )$ in (88), equation (89) reduces to

$$\begin{aligned} rz^{\prime \prime }+\alpha f\left( z(\tau ),\tau \right) =0 \end{aligned}$$

(90)

We shall linearize the function f about a time-periodic reference motion of $z(\tau )$ which is the point $z=\sin \phi$, which is also one of the stable centres of the oscillator in the absence of its interaction with the elastic bar as discussed in 2.3. So we perform a power series expansion by taking

$$\begin{aligned} z(\tau )=\sin \phi +\eta (\tau ) \end{aligned}$$

(91)

Retaining up to linear terms, we get the simplified equation as

$$\begin{aligned} \begin{aligned}&r\eta ^{\prime \prime }+\alpha \Bigg (\bigg (\sin \phi -\frac{\sin \phi }{\sqrt{(\cos \phi -D\sin \omega \tau )^2+\sin ^2\phi }}\bigg )\\&\quad +\bigg (1+\sin ^2\phi \\&\quad - \frac{1}{\sqrt{(\cos \phi -D\sin \omega \tau )^2+\sin ^2\phi }}\\&\quad +\frac{\sin ^2\phi }{((\cos \phi -D\sin \omega \tau )^2+\sin ^2\phi )^{\frac{3}{2}}}\bigg )\eta \Bigg )=0 \end{aligned} \end{aligned}$$

(92)

To bring (92) to a standard form, we do a re-scaling which is $\tau _1=\omega \tau$. With this re-scaling in (92), we get the simplified equation as

$$\begin{aligned} \begin{aligned}&\ddot{\eta }+\Bigg (\frac{\alpha }{r\omega ^2}(1+\sin ^2\phi )\\&\qquad +\frac{\alpha }{r\omega ^2}\bigg (\frac{\sin ^2\phi }{((\cos \phi -D\sin \tau _1)^2+\sin ^2\phi )^{\frac{3}{2}}}\bigg )\\&\qquad -\frac{1}{\sqrt{(\cos \phi -D\sin \tau _1)^2+\sin ^2\phi }}\Bigg )\eta \\&\quad =\frac{\alpha }{r\omega ^2}\Bigg (\frac{\sin \phi }{\sqrt{(\cos \phi -D\sin \tau _1)^2+\sin ^2\phi }}-\sin \phi \Bigg ) \end{aligned} \end{aligned}$$

(93)

where double dot represents differentiation with respect to $\tau _1$. Equation (93) is in the standard form of a non-autonomous, in-homogeneous Mathieu equation given by

$$\begin{aligned} \ddot{\eta }+\left( \delta +\epsilon f_1(\tau _1)\right) \eta =\epsilon g_1(\tau _1) \end{aligned}$$

(94)

where the new terms are defined as

$$\begin{aligned}{} & {} \delta =\frac{\alpha }{r\omega ^2}\left( 1+\sin ^2\phi \right) , \quad \epsilon =\frac{\alpha }{r\omega ^2} \end{aligned}$$

(95)

$$\begin{aligned}{} & {} f_1(\tau _1)= \left( \frac{\sin ^2\phi }{((\cos \phi -D\sin \tau _1)^2+\sin ^2\phi )^{\frac{3}{2}}}\right. \nonumber \\{} & {} \left. \quad -\frac{1}{\sqrt{(\cos \phi -D\sin \tau _1)^2+\sin ^2\phi }}\right) \end{aligned}$$

(96)

$$\begin{aligned}{} & {} g_1(\tau _1)=\left( \frac{\sin \phi }{\sqrt{(\cos \phi -D\sin \tau _1)^2+\sin ^2\phi }}-\sin \phi \right) \nonumber \\ \end{aligned}$$

(97)

The functions $f_1$ and $g_1$ are both periodic functions of the re-scaled time $\tau _1$ with a period of $2\pi$. Equation (94) is a standard in-homogeneous Mathieu equation. We vary D and $\omega$ and examine the stability of this equation numerically by using the extended Floquet theory [37] as in finding out the Floquet multipliers in each case and imposing the conditions that $|max(\lambda _1,\lambda _2)|=1$ and $\lambda _1\ne \lambda _2\ne \pm 1$, where $\lambda _1$ and $\lambda _2$ are the Floquet multipliers of the homogeneous system by taking the right-hand side of (94) to be zero.

4.2 Results and discussion of Floquet analysis

For the purpose of numerical simulation, a tolerance of $\pm 0.001$ is taken. The numerical parameters are taken as

$$\begin{aligned} \alpha =0.5, \quad r=1, \quad \sin \phi =0.5 \end{aligned}$$

(98)

The time period for the Floquet analysis, as done conventionally, has been taken as one complete period of the functions $f_1(\tau _1)$ and $g_1(\tau _1)$, which is $2\pi$. The frequency $\omega$ has been taken to be starting at values greater than zero (0.1) to ensure that the parameter $\epsilon$ does not tend to infinity during the Floquet analysis.

Fig. 7

Mathieu plot showing the stable and unstable regions for the dynamic response of the snap-through oscillator for sufficiently large amplitudes of the excitation pulse

The un-shaded portions in Fig. 7 represent the values of D and $\omega$ for which the solution of the inhomogeneous equation (94) becomes unbounded or unstable. The shaded regions represent the set of values of D and $\omega$ for which the solution of (94) remains bounded or stable. So, we can see that if the displacement of the end-point of the bar is approximated by a simple sinusoidal function of time with an amplitude, which can be sufficiently large, and any chosen excitation frequency, then we can perform stability analysis for the essentially nonlinear governing differential equation of the snap-through oscillator (90). The stability analysis more commonly known as the Floquet analysis generates a Mathieu plot of the approximated excitation amplitude D and excitation frequency $\omega$ showing the stable and unstable regions for the linearized dynamic response of the snap-through oscillator.

To confirm the validity of our stability analysis, we perform numerical integration of our approximated, linearized equation of motion for the snap-through oscillator (92) by using the ODE45 solver in MATLAB for 200-time units. The system parameters are taken the same, as were considered previously for the Floquet analysis. We show two results corresponding to two sets of values of the excitation parameters D and $\omega$. One set of values is chosen from the stable shaded region of the Mathieu plot Fig. 7 and the other set of values is chosen from the unstable un-shaded region. The value of the parameter D is chosen to be sufficiently large, i.e. of O(1) magnitude to focus on the case of sufficiently large excitation amplitude.

Fig. 8

Unbounded and bounded dynamic response of the snap-through oscillator in the linearized regime corresponding to one unstable and one stable point in the Mathieu plot. $\eta (\tau )$ is the non-dimensional displacement of the snap-through oscillator measured from its initial position $z=\sin \phi$ and $\tau$ is the non-dimensional time

The numerical results validate the stability analysis performed for the equation of motion of the snap-through oscillator (92) for sufficiently large bar endpoint displacements arising due to sufficiently large amplitudes of the excitation pulse. The shaded regions in the Mathieu plot correspond to the values of the excitation parameters for which the oscillator motion is periodic and bounded. Physically, this means that for those values of the excitation amplitude and frequency, the un-approximated oscillator (90) motion will follow periodic orbits around one of its stable equilibrium points at $z=\sin \phi$ or $\eta =0$ which is one centre. The un-shaded regions in the Mathieu plot correspond to those values of the excitation parameters for which the oscillator motion in the linearized regime is unbounded in time. Physically, this explosion of the linearized response means that for these sets of values of the excitation parameter, the un-approximated oscillator response (90) undergoes a snap-through from one of its stable equilibrium points to the other stable equilibrium point which is the other centre at $z=-\sin \phi$ or $\eta =-2\sin \phi$ and in doing so it crosses the unstable equilibrium point which is a saddle in the middle at $z=0$ or $\eta =-\sin \phi$.

Recalling that we have defined our natural frequency for the oscillator motion for the linearized systems at different levels of approximation described in (35) and (36) to be $\omega _0=\sqrt{2\alpha \sin ^2\phi /r}$, one more interesting observation from the Mathieu plot is that the first unstable region that is the first prominent white band originates near $\omega =\omega _0=0.5$ at sufficiently small values of the excitation amplitude for our chosen values of the system parameters. This is the primary resonant frequency for the linearized systems described in (35)–(36) at different levels of approximation of the perturbation analysis of our actual nonlinear model. So, we can conclude that the actual un-approximated and essentially nonlinear oscillator (90) response will start showing a snap-through or divergent motion for the first time for excitation frequencies starting close to the linearized primary resonant frequency obtained from the asymptotic analysis of the actual system (35)–(36) and gradually increasing in a nonlinear fashion with the excitation amplitude along the first white band. We shall show in the next section that this behaviour eventually materializes into a harmonic motion which becomes bounded after showing some initial diverging transients when we attach the oscillator to the elastic bar and increase the small nonlinear parameter $\epsilon$ to sufficiently large values for the case of primary resonance. We shall support this statement both by analytical results and numerical solutions. The next prominent unstable/white band starts from $\omega =2\omega _0=1$ for our chosen system parameters and evolves nonlinearly with the excitation amplitude and excitation frequency up to sufficiently large values of the excitation amplitude. So, the Floquet analysis enables us to predict important excitation parameters such as the excitation amplitude, including the case of sufficiently large excitation amplitude, and excitation frequency in terms of the known system parameters for which the linearized dynamic response of the oscillator starts to become unstable that is the un-approximated oscillator dynamics (90) starts exhibiting a snap-through motion.

4.3 A few observations upon increasing the nonlinear parameter $\epsilon$

4.3.1 Non-resonant case

All the other numerical parameters are kept the same from the non-resonant case, except for the small nonlinear parameter $\epsilon$, which is increased directly from 0.01 to 0.07 and then to a sufficiently large value of 0.2 in small steps. As done before, the point of reference for measuring the displacement of the oscillator $z(\tau )$ is taken to be at $z=\sin \phi$ which was its initial position or configuration. The analytical solutions obtained are compared to the numerical results obtained computationally as done previously for the non-resonant case with the same values of the non-dimensional parameters (except for $\epsilon$), which are:

$$\begin{aligned}{} & {} \alpha =0.5, r=1, \hat{A_m}=1, l=300, \sin {\phi }=0.5,\\{} & {} \quad \omega _0=\sqrt{2\alpha \sin ^2{\phi }/r}=0.5, \omega _{exc}=0.6\omega _0=0.3, \\{} & {} \quad \epsilon =0.07, 0.08, 0.09, 0.1 \end{aligned}$$

The actual amplitude of the excitation pulse considered for numerical simulation is given by $A_m=\epsilon \hat{A_m}$ for each of the three cases. The ratio l, i.e. the non-dimensional length of the bar has been taken to be 300 to make the total space and time window larger. Since in the non-dimensional form, the longitudinal wave speed in the bar is unity, the time window becomes sufficiently large, i.e. 600 and this helps to get a steadier response free from the very few transients that will initially arise due to discretization issues. We resort to only plotting the oscillator response in the time domain to observe a few interesting nonlinear phenomena such as stability and bifurcation analysis.

Fig. 9

Time-domain response of the snap-through oscillator for non-resonant case for $\epsilon =0.07,0.08,0.09,0.1$. $\eta (\tau )$ denotes the non-dimensional displacement of the oscillator measured with respect to its initial configuration $z=\sin \phi$ in the time domain. $\tau$ is the non-dimensional time

Now, we increase $\epsilon$ beyond 0.1 and check the cases for $\epsilon =0.14, 0.15, 0.17, 0.2$, keeping all the other numerical parameters same as done just before in this subsection. We again resort to plotting only the oscillator response in the time domain to observe some rich nonlinear effects. The non-dimensional length l of the bar is taken to be same as before which is 300. The non-dimensional parameters used for plotting the results are

$$\begin{aligned}{} & {} \alpha =0.5, r=1, \hat{A_m}=1, \sin {\phi }=0.5,\\{} & {} \quad \omega _0=\sqrt{2\alpha \sin ^2{\phi }/r}=0.5,\\{} & {} \quad \omega _{exc}=0.6\omega _0=0.3, A_m=\epsilon \hat{A_m} \\{} & {} \quad \epsilon =0.14, 0.15, 0.17, 0.2 \end{aligned}$$

Fig. 10

Time-domain response of the snap-through oscillator for non-resonant case for $\epsilon =0.14,0.15,0.17,0.2$. $\eta (\tau )$ denotes the non-dimensional displacement of the oscillator measured with respect to its initial configuration $z=\sin \phi$ in the time domain. $\tau$ is the non-dimensional time

As we can see that for increasing $\epsilon$ from 0.07 to a larger value of 0.2, the numerical solution deviates from the analytical solution in the time domain both in terms of amplitude and phase shift. The observation is quite valid from the perspective of our theoretical framework which considers the nonlinear effects only after truncating them to quadratic terms. But, the numerical solution is still bounded as in it does not become divergent in time. For increasing $\epsilon$ from a very small value of 0.01 up to a value of around 0.07, the response for the oscillator, obtained both analytically and numerically, remains periodic around its initial stable configuration $\eta =0$, and the solutions are both qualitatively and quantitatively similar. For $\epsilon =0.08$, we see an interesting phenomenon of a snap-through in the numerical solution, where the oscillator suddenly sees the other stable centre at $\eta =-2\sin \phi =-1$ for the first time, performs one complete motion about the larger periodic orbit centred at the saddle at $\eta =-\sin \phi =-0.5$ (see 2.3), and then again comes back to perform oscillations around its initial stable centre at $\eta =0$. Beyond this value of $\epsilon$ corresponding to considerably higher excitation amplitudes, where the analytical solution cannot be trusted because of Taylor series approximations, the numerical solution shows an interesting combined motion comprising of steady vibrations around its initial centre at $\eta =0$ and steady vibrations around the other stable centre at $\eta =-2\sin \phi =-1$. This incorporation of two fixed points in the picture can be useful for studying bifurcation analysis. On continuously increasing $\epsilon$ further, this complex combined motion of the oscillator observed numerically slowly begins to transform to sustained motions about the larger periodic orbits centred around the saddle at $\eta =-0.5$, which finally becomes a stable periodic motion around the same saddle at around $\epsilon =0.2$. This shift of stability and birth of a new periodic solution about the saddle can be useful for studying interesting nonlinear effects such Hopf bifurcation and saddle-node bifurcation by varying the parameter $\epsilon$ at will and running our proposed numerical scheme on a computer. Physically, this interesting phenomenon means that the displacement of the bar at the nonlinear interface acts as a type of forced excitation for the oscillator in addition to the initial condition we have already imposed on the oscillator by keeping it initially at $\eta =0$. So, the oscillator due to the complex combined effects of self-excitation and forced excitation, continuously undergoes a switching between two periodic orbits, one centred around $\eta =0$, which is its initial stable centre and the other centred around $\eta =-2\sin \phi =-1$, which is its other stable centre until settling down to a larger periodic orbit around the saddle at $\eta =-\sin \phi =-0.5$. Had we kept the oscillator at its other stable centre at $\eta =-2\sin \phi =-1$ at the beginning of our analysis, it would have undergone continuous switching of energy between periodic orbits around this centre and periodic orbits around the its other stable centre at $\eta =0$ for increasing values of $\epsilon$ before ultimately settling down to a stable periodic motion around the saddle at around the same value of $\epsilon =0.2$ because of the symmetricity in its phase portrait (see 2.3). Such sustained modal energy exchange for the non-resonant case will find very useful practical applications in circumnavigation of ships, submarines, and for launching satellites to their specific orbits. We also notice another important thing from running our finite difference algorithm computationally which is that by adjusting the mesh size for both time and space, the analytical and numerical solutions show a tendency of overlapping and converging towards a steady harmonic behaviour. This can be further validated by conducting experiments in a laboratory under restrained settings with a suitable prototype of our chosen model/system where we can observe what really can happen for such a system.

4.3.2 Primary resonance

All the other numerical parameters are kept the same and the bar end point displacements are plotted for $\epsilon =0.06$ and $\epsilon =0.1$. Since we are studying primary resonance, $\omega =\omega _0=0.5$ or 0.08 cycles per non-dimensional time.

Fig. 11

The displacement at the point in the bar connected to the snap-through oscillator plotted in the time domain for primary resonance for $\epsilon =0.06$ and $\epsilon =0.1$, respectively

For increasing $\epsilon$ in the case of primary resonance, the behaviour of the oscillator response is more or less qualitatively similar to that for the non-resonant case, observed just before in the previous section (see 4.3.1). The oscillator for the smaller value of $\epsilon =0.06$ exhibits periodic motions corresponding to one of the homoclinic orbits around its initial stable configuration $z=\sin \phi$ or $\eta =0$ (see 2.3), and for the larger value of $\epsilon =0.1$, it exhibits periodic motions corresponding to one of the orbits around the unstable saddle at $z=0$ or $\eta =-\sin \phi =-0.5$ (see 2.3). Since the information about the reflected wave is contained in the bar displacement at the nonlinear interface, we resort to only plotting the bar end point displacement for the end connected to our snap-through oscillator. For $\epsilon =0.06$, the truncated analytical solution for the bar endpoint displacement, which cannot be trusted wholly, shows a snap from its initial stable equilibrium position at 0 to another stable equilibrium position and then oscillates with very small amplitudes around this new mean position with a stable manifold. The exact numerical solution for this value of $\epsilon$ starts from 0, shows a vertical jump and then oscillates about a new dropped/offsetted mean position with considerably larger amplitudes corresponding to one of the homoclinic orbits of the discrete snap-through oscillator around $z=\sin \phi$ or $\eta =0$. For $\epsilon =0.1$, the truncated analytical solution of the bar displacement at the nonlinear interface shows a similar snap-through behaviour and the exact numerical solution shows oscillations about its initial zero mean position corresponding to periodic motions of the oscillator around the unstable saddle at $z=0$ or $\eta =-\sin \phi$. But, besides these, in the numerical solution for primary resonance for both the values of $\epsilon$, we observe a slowly modulated response or a seemingly rich dynamic behaviour with a few initial transients for the bar endpoint displacement as is desirous for such a nonlinear model. This case of primary resonance will find useful real-world applications like increasing jet fuel efficiency by proper design of aircraft wings. The advantage of using the method of multiple scales (MMS) is quite conspicuous in this case of primary resonance, because we can already get to see the transients or slow modulations expected for such nonlinear systems in the numerical solution presented by the displacement response (plotted in red) against the steady analytical solution (plotted in blue) in Fig. 11. A notable thing is that MMS reduces to a very simple/classical perturbation approach in our system because of the chosen harmonic excitation/ displacement boundary condition at the free end of the bar in real time $T_0$ or t and this reduces the tedious algebraic calculations to some extent. In conclusion, from our observations, it can be said that using MMS in this case suppresses the mixed secular terms and leads to bounded analytical solutions, and therefore, it is possible to study a steady harmonic motion analytically for smaller values of the nonlinear parameter $\epsilon$, and also the transient/slow modulated response numerically by running our explicit finite difference algorithm for larger values of $\epsilon$.

5 Conclusion

The wave propagation characteristics, namely the reflected pulse and the oscillator motion of an elastic bar coupled to a single degree of freedom snap-through oscillator, are considered. A key feature of this problem is the underlying geometric and essential nonlinearity leading to excitation amplitude and excitation frequency-dependent dynamic response even for linear material properties of the constitutive elements. A physics-based analytical approach leading to closed-form expressions of the reflected wave in the elastic bar and the dynamic response of the snap-through oscillator was presented. The route to this analytical derivation has three key steps. Firstly, the non-dimensional boundary conditions and equations of motion are derived exactly from the Lagrangian of the system. Secondly, a Taylor series approximation is done for the non-autonomous terms in the equations and boundary conditions for sufficiently small amplitudes of the excitation pulse and the method of multiple time scales is used to expand the time-dependent variables asymptotically. Finally, the method of harmonic balance is used to find the dynamic responses at different levels of approximation. The analytical solutions obtained suggest a nonlinear dependence of the response on the system and excitation parameters.

The stability/Floquet analysis performed for the snap-through oscillator for sufficiently large amplitudes of the excitation pulse comes helpful while predicting the excitation parameters which can cause the oscillator to undergo a snap-through motion.

Key novel features of this paper include:

• A generalized asymptotic methodology based on the classical perturbation theory and wave propagation analysis, for deriving the wave propagation characteristics of an elastic bar coupled to any discrete nonlinear end attachment.

• The explicit employment of ordinary differential equations governing the motion of the snap-through element and the harmonic balance method for satisfying the natural boundary condition of the bar into the dynamic response analysis of the system.

• The expressions derived here give the most comprehensive and consistent description of the propagation characteristics of the bar and the motion of the snap-through element which can be directly used in the context of finite difference analysis over a wide range of values of the excitation frequency, including the different possible cases of resonance up to a second order of asymptotic approximation, and sufficiently small values of the excitation amplitude.

• The use of the extended Floquet theory after re-scaling the governing equation of motion of the snap-through oscillator to a standard inhomogeneous Mathieu equation and distinguishing the excitation parameter values for stable and unstable dynamic response of the snap-through oscillator in the chosen linearized regime.

• The Floquet analysis performed here can be done over a wide range of excitation and system parameters and so it is possible to explore the response characteristics of the system by tuning both the excitation and system parameters.

The analytical expressions have been validated with the numerical results from a finite difference algorithm. Results obtained from the analytical expressions derived for the reflected wave and the oscillator motion are graphically illustrated in both the time domain and the frequency domain. The numerical results match significantly with the analytical solution in both the time and frequency domains for a sufficiently large length of the bar and hence a sufficiently large time window. The closed-form expressions derived here provide excellent opportunities to use them for optimization of the excitation and system parameters for an elastic bar coupled to a discrete nonlinear end attachment to obtain desirable wave propagation characteristics and dynamic response in a computationally efficient and physically appealing manner. The explicit finite difference algorithm when run computationally enables us to vary the nonlinear parameter $\epsilon$ at will and study interesting nonlinear phenomena such as modal energy exchange, response stability, sustained resonance capture, Hopf and saddle-node bifurcation.

Application domains of this work will include industrial sectors which exploit elastic waveguides with end attachments for energy harvesting, vibration isolation and vibration suppression. Specific examples include, but are not limited to, energy absorbent machine parts, nonlinear viscous damping models and nonlinear filters, aircraft wings, vehicle suspension systems, periodic molecular chains of bi-stable constituents, flexible mechanical and acoustic meta-materials, satellites that exhibit gyroscopic motion, heart monitoring devices, circumnavigation of ships and submarines, and lastly to study interesting wave phenomenon such as a solitary wave packet or soliton. Although the system is geometrically nonlinear arising due to its underlying configuration, the material behaviours of the constituent elements of the system have been assumed to be linear. The amplitude of the excitation pulse has been assumed to be sufficiently small while deriving the propagation characteristics and dynamic response analytically. Future works in this direction should focus on nonlinear material behaviour to encompass a wide range of materials available to manufacture waveguides with end attachments, and sufficiently large excitation amplitudes to consider a wider range of external excitation present in the surroundings.