Hysteretic behaviour of uniaxially thermoformed auxetic foams under 3-point bending low-frequency vibration

Abstract

The work describes experiments and models related to auxetic (negative Poisson’s ratio) foams subjected to low-frequency and variable amplitude 3-point bending loading. A custom 3-point bending vibration test rig is designed and used to perform the dynamic test of auxetic PU foam beams within low-frequency range (1–20 Hz) and 5 different displacement amplitudes. The auxetic foams tested in this work are manufactured using a simplified and relatively low-cost uniaxially thermoforming compression technique, which leads to the production of foams with transverse isotropic characteristics. Auxetic foam beam samples with two different cutting orientations and different thermoforming compression ratios r_c (20–80%) are tested and compared, also with the use of theoretical Euler–Bernoulli-based and finite element models. The dynamic modulus of the foams increases with r_c, ranging between 0.5 and 5 MPa, while the dynamic loss factor is marginally affected by the compression ratio, with overall values between 0.2 and 0.3. The auxetic PU foam has a noticeable amplitude-dependent stiffness and loss factors, while the dynamic modulus increases but slightly decreases with the frequency. The dynamic modulus is also 20–40% larger than the quasi-static one, while the dynamic and static loss factors are quite close. A modified Bouc–Wen model is also further developed to capture the amplitude and frequency-dependent properties of the conventional and auxetic foams with different volumetric compression ratios. The model shows a good agreement with the experimental results.

1 Introduction

Open-cell polymeric foams are widely used in applications ranging from packaging, cushioning and protective clothing, due to the significant energy absorption caused by their elastic-plateau-densification microstructure mechanism under compressive loading [1]. Since the seminal work of Roderic Lakes in 1987 [2], auxetic (i.e. negative Poisson’s ratio) open-cell polyurethane (PU) foams have been developed and evaluated by many research groups [3]. Due to the counter-intuitive auxetic deformation and the properties of the PU material, auxetic foams show interesting mechanical properties, such as indentation resistance [4], synclastic behaviour [5], compliant shear [6, 7], improved impact [8, 9] and vibration [10] energy absorption. Auxetic foams therefore possess a significant potential for applications like apparel/personal protective equipment [8, 11, 12], cushioning [13, 14], noise reduction [15, 16], smart materials and sensors [17, 18].

Auxetic PU open-cell foams can be manufactured following various methodologies, such as via chemical solvents [19] and compressed CO₂ [20]. Auxetic closed-cell foams with stiffnesses close to 10 MPa can also be produced via steam processing [21, 22]. Traditional auxetic open-cell foams are, however, made from converting conventional foams into an auxetic version, through procedures involving triaxial volumetric compression, annealing via heating, cooling and relaxation [2, 3, 23, 24]. The volumetric compression is used to create the typical re-entrant cell structures inside the foam, while the heating and cooling are used to thermoform the compressed foam via phase transition of the PU material [23]. Some of the authors of this work have recently simplified the complex triaxially thermoforming manufacturing process into a uniaxial one via the use of an open mould. This production procedure provides a relatively low manufacturing cost and excellent auxetic performance [9, 25, 26], which makes it suitable for scaling-up manufacturing purposes.

The dynamic behaviour of auxetic PU foams has been first evaluated by Chen and Lakes [15, 27], and then further studied by Scarpa et al. [28, 29] and Bianchi et al. [10], showing an enhanced damping performance provided by negative Poisson’s ratio foams. The aforementioned research works mainly focus on the dynamic performance of auxetic foams between 60 and 3 kHz, covering noise and machinery vibration isolation applications. However, for applications related to human body, such as cushioning, personal protective equipment and apparel, the frequencies of interest are significantly smaller. Typical fundamental resonances of coupled driver/car seats are between 1.5 Hz and 5 Hz [30], and both static and dynamic indentation characteristics of foams are important to dictate the comfort of the individual using the foam product [31]. Tremors of patients affected by multiple sclerosis tend to cover the 3–4 Hz range in the case of titubation (i.e. nodding head tremor), a feature that could be of interest for the design of protective linings of headsets and helmets. In that sense, Darling has shown that the highest magnitudes of vertical dynamic displacement in impacted NFL helmets are well below the 20–30 Hz [32]. The dynamic deformations of auxetic foams described in open literature are, however, relatively simple, mainly consisting in one-dimensional (single compressional P) waves, both in terms of structural dynamics excitations [10], or acoustic within impedance tubes [16, 33,34,35]. Single dynamic compression/tensile loading is, however, quite different from operational deformations occurring in applications, such as human body support [14], personal protective equipment and apparel [36]. In those applications, the foams could be subjected to compression and bending, with more complicated deformations mechanisms arising. The focus of this work is indeed to evaluate the dynamic properties of the uniaxially thermoformed auxetic foams within a low-frequency range (1–20 Hz), using a 3-point bending vibration rig designed for this purpose.

Open-cell conventional and auxetic PU foams exhibit good damping performance with noticeable hysteresis under dynamic loading [25, 37]. The damping of the PU foams is mainly caused by the viscoelasticity of the PU material and the pneumatic damping effect associated with the porosity and permeability. Patten et al. [38] and Bianchi and Scarpa [10] have previously developed dynamic models for conventional and auxetic PU foams considering only the effect of the pneumatic damping. The pneumatic force of the porous material is proportional to the strain rate, according the Darcy’s law [39]; the pneumatic force is therefore less dominant within the low-frequency range considered in this work. White et al. [37], Deng et al. [40] and Singh et al. [41,42,43] have also developed dynamic models of open-cell PU foams considering the viscoelasticity and nonlinearity, ignoring the pneumatic damping effect. Batt et al. [44, 45] developed a dynamic viscoelastic model of Arcel closed-cell foams without considering pneumatic damping effects. In these works, the PU foams are all subjected to compression and are assumed to behave under linear viscoelastic and nonlinear elastic regimes, using either polynomial [37, 42] or hyperbolic [10, 38] functions to describe the nonlinear stiffness. In the above models however, the nonlinear hysteretic loops of the PU foams under compression are different from the amplitude-dependent hysteretic ones acquired in the 3-point bending tests of this work. The bending-derived hysteretic loops here exhibit decreasing secant stiffness when the amplitude increases, although they maintain an approximately linear behaviour for a constant amplitude and variable frequency. Therefore, the previously used pneumatic damping and viscoelastic models adopted for the vibration of open-cell foams are not suitable to describe the auxetic foams under 3-point bend low-frequency vibration.

The Bouc–Wen (BW) model is a widely used and powerful phenomenological model to describe the different types of hysteresis, such as in the case of magnetorheological [46, 47] and piezoelectric [48, 49] and elastomeric [50, 51] materials. The BW model can describe well the different types of generalized force–displacement hysteretic loops. However, the classical BW model is invariant with the various input frequencies [48, 52]. Various efforts have been performed to modify the BW formulation to capture frequency-dependent properties. For example, Yang et al. introduced fractional derivatives [47]; Zhu et al. proposed a generalized BW model with a frequency factor [48]; Kang et al. have proposed two fractional operators in a modified BW version [49]; and Shao et al. have used a second-order discrete system for the dynamic linear part [53]. All these variations proposed to the original formulation of the BW can cater for frequency-dependent behaviours, but also make the updated models more complicated, by using parameters and components without evident physical meaning. In this work, an exponential relationship between the stiffness parameter of the BW model and the frequency is applied to describe the frequency-dependent stiffness of the PU foams. This exponential relation is inspired by Nagy’s theory that links the strain-rate dependence of open-cell foams under compression, and their quasi-static behaviour [54]. Linearly frequency-dependent relationships of the other parameters of the BW model are used; as it will be demonstrated, this combined approach can capture the mild frequency-dependent stiffness and damping behaviour of the auxetic foams within low-frequency ranges. Besides, the 6 parameters of the classical BW model can be reduced to 5 by performing a normalization to remove the redundant term [49, 52].

The paper is structured as follows. Section 2 summarizes the manufacturing of the open-cell auxetic foams used in this work. Section 3 describes the mechanical tests (quasi-static cyclic and dynamic 3-point bending) and the related rigs developed. The continuous beam transverse vibration model and the concentrated parameter BW model are detailed in Sect. 4. Section 5 shows the results related to the tests and modelling, discussing the effect of amplitude, frequency and manufacturing compression ratio of the auxetic foams. Conclusions are drawn in Sect. 6.

2 The uniaxially thermoformed auxetic foam

The auxetic foams are obtained directly by converting the conventional PU foam (SM Upholstery Ltd, with a density of 27.4 kg/m³ and a pore linear density of 1102–1378/m) into an auxetic version. The manufacturing procedure mainly includes three steps: compression, heating and cooling. The pristine foam is cut into seven blocks with 120 × 120 × 160 mm size and it is then compressed in an open mould (Fig. 1a) along the height direction. The final dimensions are 128, 112, 96, 80, 64, 48 and 32 mm, respectively, corresponding to a compression ratios r_c of 20%, 30%, 40%, 50%, 60%, 70% and 80%. The r_c is defined as the ratio of the foam block heights after and before compression. The compressed foam block and the mould are then placed in an oven (Carbolite PF laboratory oven), heated from ambient temperature up to 145 °C at a rate of 5 °C/min, and then kept constant. A thermocouple is inserted into the middle of the foam block to monitor the inner temperature, and the heating procedure is terminated after the inner temperature reaches ~ 135 °C for 30 min; this temperature is higher than the glass transition temperature of the hard segment component of the polyurethane (114 °C [55, 56]). The compressed foam and the mould are then removed from the oven and cooled at temperature (~ 15 °C). The compressed foam block is released from the open mould after a full cooling down. The dimensions of the compressed foam block show no large changes within one week after release from the mould; this indicates the presence of a stable thermoformed material.

Fig. 1

Manufacturing procedure of the uniaxially thermoformed auxetic foam (a); illustration of the cutting orientations of the foam specimens in the foam block (b); 3D models of the pristine (c) and auxetic foam with r_c = 60% (d) by μ-CT scan

The converted auxetic foams are anisotropic, with significant difference in terms of mechanics along the thermoforming directions d₁ and transverse directions d₂ and d₃, due to the specific uniaxial thermoforming manufacturing procedure adopted [9, 25, 26]. Therefore, two types of specimens are cut from the thermoformed foam blocks with different r_c values for the 3-point bending tests, all with same size of 120 × 20 × 10 mm (Fig. 1b). The T1 specimen is loaded along d₁, while the T2 specimen is subjected to loading along d₃. The mass of the pristine and auxetic foam specimens with the different r_c values (from 20 to 70%) are 0.719; 0.895; 0.992; 1.160; 1.360; 1.712; 2.359 and 3.667 g, respectively.

The 3D models of the pristine and of the r_c = 60% auxetic foams (Fig. 1c and d) have been acquired using a μ-CT scan with a resolution of 4.991 μm from Zeiss Xradia 160 kVp Versa 510 (Carl Zeiss Microscopy GmbH, Germany). The images are processed using the Avizo 2019 software (Thermo Fisher Scientific, France). The cell structures of the pristine foam (Fig. 1c) are mainly in polyhedron shape, with average dimensions around 500 μm. The ribs of the pristine foam are mainly straight. The pores and cells of the pristine foam are also slightly elongated along the d₁ direction, because d₁ corresponds to the reactor foam rising direction [57, 58]. In comparison, the cells structures of the auxetic foam are more tortuous and denser. Most of the ribs of the negative Poisson’s ratio foam are curved due to the uniaxial compression, resulting in the typical re-entrant cell structure of “classical” auxetic structures/materials [3]. The microstructures of the auxetic foams show an evident anisotropy, with more ribs oriented within the transverse plane and lower numbers of ribs along the thermoforming direction d₁. The images observed along d₁ show a reticulated structure partially like the pristine foams, but with the presence of kinks in the ribs, while the microstructural configuration along d₂ and d₃ is more elongated and compressed.

The auxetic foam shows a more evident auxeticity along the thermoforming compression direction d₁ when loaded along the d₂ and d₃ directions. Under tensile loading along the d₂ direction, the Poisson’s ratio ${\nu }_{21}$ for auxetic foams with r_c ranging from 50 to 80% varies between − 0.2 and  − 1.0. Under compression, ${\nu }_{21}$ clusters around − 1 for r_c ranging between 40 and 70%. The Poisson’s ratio ${\nu }_{23}$ is, however, always positive (values between 0 and 0.8) when the foams are compressed or tensioned along d₂. When loaded along the thermoforming direction d₁, the Poisson’s ratio ${\nu }_{12}$ and ${\nu }_{13}$ are all close to 0. More detailed results about the mechanics and deformations of the thermoformed auxetic foams are provided in [9, 25, 26].

3 Test rigs

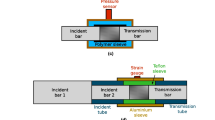
The 3-point static and low-frequency bending test rig for the auxetic foams is shown in Fig. 2. The quasi-static and dynamic tests share the same supporting and loading structures. The foam specimen is constrained at the two ends by two rigid supporting structures and loaded in the middle by a middle holder. The end supports and middle holder are designed to have round contact tips with a diameter of 3 mm, which allow the free rotating movement of the foam beam specimen under transverse loading. The gap between the top and bottom tips of the supports and middle holder of the 10 mm beam specimen depth is constant at 9 mm for the pristine and auxetic foams with r_c ranging 20–70%. This value of the gap can allow to be holding the beam specimen tight enough to provide a stable support, without applying large constrains that affect the free rotation movements of the beam. The gap value for the auxetic foam specimen with r_c = 80% is 9.4 mm; this foam is significantly stiffer than the others, and a same 9 mm holding gap would result in stronger constraint. The support span is constant as 100 mm. The span/depth ratio of the beam specimen is 10, within the limit of Euler beam theory [59, 60]. The mass of the middle holder is 68.4 g.

Fig. 2

Three-point bending quasi-static (a) and dynamic (b) c test rigs

The quasi-static test is performed using a Shimadzu AGS-10kNX machine with a load cell of 100 N. The loading rate is 3 mm/min, sufficiently slow for quasi-static testing [25, 61]. Each specimen is tested three times with amplitudes of 1 mm, 3 mm and 5 mm, respectively. Two loops of cyclic compression and tension loading are performed at each amplitude value, and only the stable and converged second loop is used for comparison.

The dynamic test is conducted using a vertically installed long-stroke low-frequency shaker (APS 113) connected to a power amplifier (APS 125). An aluminium frame supports the structures and the sensors. The measured fundamental resonance of the frame is larger than 100 Hz, safely above the maximum frequency range of 20 Hz used during the tests. The piezoelectric force (PCB 208C01, range 44.48 N) and laser (OMRON ZX2-LD100, resolution 5 μm) sensors are applied to measure the dynamic force and displacement, respectively. The force and displacement signals are recorded using a National Instruments data acquisition hardware (NI 9234) and MATLAB with DAQ extension.

Sinusoidal vibrations with different frequencies and amplitudes are used in this dynamic test. Each foam specimen is tested with 32 different frequencies, ranging between 1 and 20 Hz (Table 1) and with 5 different amplitudes (1, 2, 3, 4, 5 mm) at each frequency. The frequencies used for pristine and auxetic foams with r_c ranging 20–70% are slightly different from the ones of the r_c = 80% auxetic foam, because the r_c = 80% auxetic foam is stiffer and with a larger resonance frequency compared with the other foams. Moreover, more frequencies need to be used to excite the beams close to resonance and obtain a better-quality frequency response function (FRF). A feedback controlling system is applied to control the displacement amplitude at each frequency. In each case, the force and displacement signals are recorded for a period of 10 s, with a sampling frequency of 2560 Hz. A low-pass filter up to 100 Hz has been applied to remove the noise at high frequency.

Table 1 Frequencies of the sinusoidal signals used for the different specimens

4 Theoretical model

4.1 Simplification of the beam transverse vibration model

The 3-point bending vibration model of the foam beam under dynamic excitations can be represented in Fig. 3. The beam has simple supports at the two ends and a concentrated mass in the middle. The Euler–Bernoulli (EB) beam is used in this work by neglecting the shear deformation of the beam itself and the presence of geometric nonlinearity. Detailed discussions about the validity of the use of the EB model in this work are provided in Appendix A.1. The differential equation of this dynamic system based on Euler–Bernoulli beam theory [62,63,64,65] is:

$$ EI\frac{{\partial^{4} y}}{{\partial x^{4} }} + \left[ {\rho A + M\delta \left( {x - l} \right)} \right]\frac{{\partial^{2} y}}{{\partial t^{2} }} = F\left( t \right)\delta \left( {x - l} \right) $$

(1)

Fig. 3

The 3-point bending vibration model of the beam with a concentrated mass in the middle

The $\delta (x-l)$ is the Dirac $\delta$-function, used to introduce the concentrated mass $M$ and force $f(t)$. The characteristic function of the beam vibration model in Fig. 3 can be obtained as in (2), after the processing described in Appendix A.2.

$$ \psi \left( l \right)\left\{ {\omega^{2} M\left[ {\tan \left( {k\frac{L}{2}} \right) - \tanh \left( {k\frac{L}{2}} \right)} \right] - 4k^{3} EI} \right\} = 0 $$

(2)

For the symmetric mode shape, $\psi (l)\ne 0$, therefore the second term in (2) should be equal to 0 and the corresponding mode frequencies can be calculated. For the antisymmetric mode shapes, $\psi \left(l\right)=0$ and ${\psi }^{^{\prime}}\left(l\right)\ne 0$, the concentrated middle mass has no effect and the mode shape and frequency should be the same as the transverse vibration of the continuous beam without middle mass, because the rotary inertia of the concentrated central mass is neglected and only the transverse inertia is considered. Therefore, the natural frequencies of the antisymmetric mode shapes [62, 65] can be calculated as

$$ \omega_{i} = k_{i}^{2} \sqrt {\frac{EI}{{\rho A}}} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} k_{i} = \frac{\pi }{l},\frac{2\pi }{l},\frac{3\pi }{l}... $$

(3)

We can then substitute the typical parameters of the auxetic foam specimens into (2) and (3): L = 0.1 m, beam width b = 20 mm, beam thickness h = 10 mm, E = 1 MPa, $\rho$=76.92 kg/m³, Poisson’s ratio $\nu$=-0.3, M = 68.43 g. The resulting first 3 resonance frequencies are as 5.41 Hz, 206.8 Hz and 324.0 Hz (Table 2). The mode frequencies of the beam model in Fig. 3 are also calculated using finite elements (FE) with ANSYS 15.0; the model consists of 50 BEAM188 and one MASS21 elements (the concentrated mass without rotary inertia). The mode frequencies and shapes obtained from FE are listed in Table 2 and Fig. 4, one can observe a proximity of the FE results with the theoretical ones. The first and third mode are symmetric mode shapes, while the second one is antisymmetric. The first resonance frequency is close to the one measured within the tests, and within the upper frequency bound of 20 Hz used in the experiments; the second resonance frequency is far beyond that upper bound value. Those values are justified by the very soft and light foam specimen used in this work (the mass of the sample is always smaller than 3 g, compared against the 68.4 g of the middle mass). The middle nodal point in the second and third modes is stationary (second mode) or relatively very small (third mode), so the concentrated force at that location will excite the first mode only. Therefore, the second- and third-order mode vibration of the beam sample has very small effect and can be ignored in this work. Consequently, the continuous beam transverse vibration model can be simplified as a single-degree-of-freedom (SDOF) vibration system with concentrated parameters when the vibration of the beam is close to the fundamental resonance of the system.

Table 2 Comparison between resonance frequencies of different models

Fig. 4

The first (a), second (b) and third (c) mode shapes of the beam with concentrated middle mass calculated via FE

The stiffness and mass of the concentrated parameter SDOF system can be obtained via Energy methods, which are equivalent to the Rayleigh–Ritz method when only the first order mode is considered [63, 65]. The Galerkin method can also be applied to this problem and would lead to the same results provided by the Rayleigh–Ritz one, when only the first mode shape is considered [63, 65, 66]. Firstly, the deformation shape of the beam (Fig. 3) during vibration can be simplified to be the same as the static deformation function of a Euler beam (4) [67], where x represents the position in the coordinate in Fig. 3 and y(x) is the transverse displacement at position x under the central force F. Equation (10) is piecewise with a separating point at the middle of the beam; the deforming shape of the beam is symmetrical with respect to the vertical middle line. In some cases, those deformation shapes are simplified as a sinusoidal function [63, 65], which is same of the transverse vibration of a beam, but without the presence of the middle mass. As we will see in later paragraphs, those two types of simplification lead to similar results. It should also be noticed that the exact deforming function should be (a.6), which gives quite similar result to the one provided by (4), but with more complex computations involved.

$$ y\left( x \right) = \left\{ {\begin{array}{*{20}l} { - \frac{{Fx\left( {4x^{2} - 3L^{2} } \right)}}{48EI}} \hfill & {\left( {0 \le x \le \frac{L}{2}} \right)} \hfill \\ {\frac{{F\left( {x - L} \right)\left( {L^{2} - 8Lx + 4x^{2} } \right)}}{48EI}} \hfill & {\left( {\frac{L}{2} < x \le L} \right)} \hfill \\ \end{array} } \right. $$

(4)

The stiffness ${K}_{l}$ of the concentrated parameter SDOF model can be obtained from Eq. (4) by substituting x = L/2. The expression of ${K}_{l}$ is exactly the same as the static transverse stiffness of the simply supported Euler beam loaded in the centre (4). The foam beam tested in this work has a nonlinear hysteretic modulus E, which leads to a nonlinear stiffness ${K}_{l}$, without affecting the format of expression (5).

$$ K_{l} = \frac{48EI}{{L^{3} }} $$

(5)

The kinetic energy of the system can be written as:

$$ T = \frac{1}{2}\int_{0}^{L} {\rho_{l} A\dot{y}^{2} dx + \frac{1}{2}\int_{0}^{L} {\rho_{l} I\left( {\frac{{\partial \dot{y}}}{\partial x}} \right)^{2} dx} } + \frac{{M\dot{y}_{l}^{2} }}{2} $$

(6)

The kinetic energy (6) includes 3 parts [63]. The first term describes the kinetic energy associated with the vertical translation; the second is about the rotational energy of the cross sections; while the third is referred to the part associated with the concentrated middle mass. The ${\rho }_{l}$ term refers to the density per length of the beam specimen. ${\dot{y}}_{l}$ is the velocity of the middle mass. Substituting (4) into (6), the kinetic energy of the system results in:

$$ T\left( {y_{l} } \right) = \left( {\frac{{17m_{f} }}{70} + \frac{{12\rho_{l} I}}{5L} + \frac{M}{2}} \right)\dot{y}_{l}^{2} \approx \frac{1}{2} \cdot \left( {M + \frac{{17m_{f} }}{35}} \right) \cdot \dot{y}_{l}^{2} $$

(7)

In the Euler beam theory, the shear deformation is neglected, and the rotatory inertia and related energy are also neglected. Therefore, the kinetic energy can be further simplified as in (7). The term ${m}_{f}$ represents the mass of the beam specimen. From (7), the mass ${M}_{l}$ of the concentrated parameter SDOF model can be written as (8):

$$ M_{l} = M + \frac{17}{{35}}m_{f} $$

(8)

The ${M}_{l}$ is the combination of concentrated middle mass M and the mass of beam specimen ${m}_{f}$. When the shape function of the beam during vibration is simplified as a sinusoidal one instead of the (4) used in this work, the coefficient 17/35 in (8) is replaced by 0.5, with a 3% of difference. Substituting now the parameters of the dynamic system used in Table 2 into (5) and (8), the resonance frequency of the concentrated parameter SDOF vibration model is $\sqrt{{K}_{l}/{M}_{l}}$ and equal to 5.40 Hz; this value is extremely close to the 5.41 Hz of the first resonance frequency of the continuous beam model. This indicates that the concentrated parameter model can well describe the dynamic behaviour of the 3-point bending beam vibration model, within the frequency range used in this work.

It should be also noticed that the equivalent mass ${m}_{f}$ of the beam would be nonlinear if the beam has a nonlinear stiffness, because the deforming shape will be affected by the nonlinear stiffness Itself. Therefore, the equivalent SDOF system of the foam beam with concentrated middle mass should have a nonlinear stiffness ${K}_{l}$ and a nonlinear mass ${M}_{l}$, because of the nonlinear hysteretic modulus of the polyurethane foam material. However, the mass of the middle holder is 68.4 g, much larger than the < 3 g mass of the foam beam (the equivalent mass of the beam in the SDOF is around half of the total mass ${m}_{f}$, lower than 1.5 g). The equivalent mass of the foam beam therefore only accounts for less than 2% of the total concentrated mass in the SDOF model. Thus, the effect of the nonlinearity of the equivalent mass in the SDOF can be neglected.

Also, the dynamic Euler beam model used here does not consider the auxeticity of the material. Negative Poisson’s ratio is, however, used to represent the beam in the FE simulations. Auxetic structures can show special local deformations with stronger resistance under indentation [4] and synclastic behaviour under bending [5]. In this work, the auxetic foam beam samples are under 3-point bending, without large local deformations from indentation. The auxetic beam shows slight synclastic deformation under bending, but it is not very evident because of the small width of the beam itself (20 mm). The purpose of the dynamic 3-point bending tests here is to study the frequency-dependent nonlinear hysteretic properties of the auxetic foams, which are mainly driven by the deformations of the cell architectures inside the foam and the viscoelasticity of the polyurethane material. As mentioned above, those dynamic properties under bending are important for applications like human body support [14], cushions and personal protective equipment and apparel [36].

4.2 Modified normalized Bouc–Wen model for the concentrated parameter vibration system

The mechanical performance of the auxetic PU foams under 3-point bending vibration is quite different from the one predicted by a simple linear spring and viscous dashpot; it shows hysteresis, nonlinearity and frequency dependency. Therefore, a more sophisticated model needs to be applied to replace the linear spring (5) in the concentrated parameter SDOF vibration model. The Bouc–Wen model (BW) is a widely used method to describe the amplitude-dependent hysteresis of magnetorheological [46, 47], piezoelectric [48, 49] and elastomeric [50] materials, so it is considered a suitable choice for this work. The equivalent mass parameter ${M}_{l}$ in Eq. (8) is the same for the BW approach, because the BW model mainly modifies the stiffness and damping performance of the dynamic system, without effects on the equivalent mass of the beam specimen; this is true when ones assumes the vibration deforming shape of the beam is like Eq. (4). Thus, the concentrated parameter SDOF vibration system with the BW model is represented in Fig. 5.

Fig. 5

The single-degree-of-freedom vibration model with concentrated parameters and Bouc–Wen model

The vibration differential equation of the system is written as:

$$ \left( {M + \frac{17}{{35}}m_{f} } \right)\ddot{y} + F_{f} \left[ {y\left( t \right),z\left( t \right),t} \right] = F\left( t \right) $$

(9)

The displacement $y(t)$ in (9) corresponds to the displacement of the middle point of the beam ${y}_{l}$ in (7). The dynamic force from the foam specimen in (9) can be written following the classical BW approach [52] as:

$$ \left\{ {\begin{array}{*{20}l} {F_{f} \left[ {y\left( t \right),z\left( t \right),t} \right] = \alpha k_{{BW}} y\left( t \right) + \left( {1 - \alpha } \right)k_{{BW}} z\left( t \right)} \hfill \\ {\dot{z}\left( t \right) = A\dot{y}\left( t \right) - \gamma \left| {\dot{y}\left( t \right)} \right|z\left( t \right)\left| {z\left( t \right)} \right|^{{n - 1}} - \beta \dot{y}\left( t \right)\left| {z\left( t \right)} \right|^{n} } \hfill \\ \end{array} } \right. $$

(10)

In (10), ${k}_{BW}$ is the elastic stiffness of the system; $\alpha$ is the ratio between the final tangent and the elastic stiffnesses and $0<\alpha <1$. The force ${F}_{f}(y\left(t\right),z\left(t\right),t)$ in (10) contains two components: the linear elastic component $\alpha {k}_{BW}y(t)$ and the hysteresis component $(1-\alpha ){k}_{BW}y(t)$; the latter component depends on the past history of the stresses and the strains. The parameters $\beta$, $\gamma$ and $n$ control the shape of the hysteresis cycles, while A determines the slope of the hysteresis at z = 0 and the parameter $n$ governs the discontinuity of the transition between the elastic and post-elastic branches of the hysteretic loop [68, 69].

The aforementioned parameters ($\alpha$, ${k}_{BW}$, A, $\gamma$, $\beta$, n) of the classical BW model are redundant [49, 52, 70]. Therefore, a nondimensionalization needs to be performed to remove the redundant parameters [71]. The hysteresis displacement $z(t)$ can be written as

$$ z\left( t \right) = \xi \tilde{z}\left( t \right) $$

(11)

where $\xi >0$ and can be any constant. Substituting (11) into (10), the modified BW model can be written as

$$ \left\{ {\begin{array}{*{20}l} {F_{f} \left[ {y\left( t \right),z\left( t \right),t} \right] = \alpha k_{{BW}} y\left( t \right) + \left( {1 - \alpha } \right)k_{{BW}} \xi \tilde{z}\left( t \right)} \hfill \\ {\dot{\tilde{z}}\left( t \right) = \frac{A}{\xi }\dot{y}\left( t \right) - \gamma \xi ^{{n - 1}} \left| {\dot{y}\left( t \right)} \right|\tilde{z}\left( t \right)\left| {\tilde{z}\left( t \right)} \right|^{{n - 1}} - \beta \xi ^{{n - 1}} \dot{y}\left( t \right)\left| {\tilde{z}\left( t \right)} \right|^{n} } \hfill \\ \end{array} } \right. $$

(12)

With:

$$ \xi = \sqrt[n]{{\frac{A}{\gamma + \beta }}} $$

(13)

which is the largest value of the variable z according to [69, 71], equations (12) can be written as

$$ \left\{ {\begin{array}{*{20}l}F_{f} \left[ {y\left( t \right),\tilde{z}\left( t \right),t} \right] = \tilde{k}_{y} y\left( t \right) + \tilde{k}_{z} \tilde{z}\left( t \right) \hfill \\ \dot{\tilde{z}}\left( t \right) = \tilde{\rho }\left[ {\dot{y}\left( t \right) - \tilde{\sigma }\left| {\dot{y}\left( t \right)} \right|\tilde{z}\left( t \right)\left| {\tilde{z}\left( t \right)} \right|^{{\tilde{n} - 1}} - \left( {\tilde{\sigma } - 1} \right)\dot{y}\left( t \right)\left| {\tilde{z}\left( t \right)} \right|^{{\tilde{n}}} } \right] \hfill \\ \end{array} } \right. $$

(14)

The number of parameters of the normalized BW model has been reduced from 6 in (10) to 5 in (14). The relationship between the parameters of the normalized BW model and the classical BW model is as follows:

$$ \left\{ {\begin{array}{*{20}l} \tilde{k}_{y} = \alpha k_{BW} \hfill \\ \tilde{k}_{z} = \left( {1 - \alpha } \right)\xi k_{BW} \hfill \\ \tilde{\rho } = \frac{A}{\xi } \hfill \\ \tilde{\sigma } = \frac{\gamma }{\gamma + \beta } \hfill \\ \tilde{n} = n \hfill \\ \end{array} } \right. $$

(15)

The parameter $\widetilde{\rho }$ represents the inverse of the apparent yield point of the nonlinear component of the BW model, and $\widetilde{\sigma }$ describes the ratio of the slope of the hysteresis loop at the velocity direction changing point versus the slope of the linear region [71]. The stiffness of the hysteretic loop is mainly determined by the values of ${\widetilde{k}}_{y}$ and ${\widetilde{k}}_{z}$, while the shape of the loop is driven by the five parameters together.

The classical BW model is not frequency-dependent [47, 53, 72] and is therefore unable to capture the noticeable effect of the frequency over the stiffness and damping of the PU foams. According to Nagy’s theory, the modulus of open-cell PU foams under compression has a linear dependence to the strain rate on log–log scale; the latter assumption is valid within the low strain rate range of quasi-static and low-speed dynamic and impact tests [54] as described in Eq. (16). The ${\sigma }_{0}(\varepsilon )$ is the reference stress at the corresponding reference strain rate ${\dot{\varepsilon }}_{0}$, while ${a}_{N}$ and ${b}_{N}$ are coefficients. Nagy’s model can be applied to the modified BW model to capture the frequency-dependent stiffness of the PU foams within a low frequencies range.

$$ \sigma \left( \varepsilon \right) = \sigma_{0} \left( \varepsilon \right)\left( {\frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{0} }}} \right)^{{a_{N} + b_{N} \varepsilon }} $$

(16)

To obtain the variation of the parameters of the normalized BW model versus the frequency, the parameters of the normalized BW model of different PU foams with 5 amplitudes are inversely identified at each frequency between 2 and 10 Hz. The identification is performed using a Levenberg–Marquardt optimization method, which will be introduced in detail in following section. It is found that the stiffness ${\widetilde{k}}_{y}$ is almost linear to the frequency on log–log scale, similarly to Nagy’s model. Therefore, the frequency-dependent stiffness ${\widetilde{k}}_{y}$ can be expressed as the first item in Eq. (17) by revising the Nagy’s model (16), considering the strain rate is proportional to the frequency. The term ${\widetilde{k}}_{y0}$ represents the stiffness parameter for the quasi-static tests, $f$ is the frequency in vibration test, ${A}_{mp}$ is the displacement amplitude, $a$ and $b$ are coefficients. It is also observed that the parameter $\widetilde{n}$ does not change significantly with the frequency, thus it is assumed to be constant. As for the other parameters ${\widetilde{k}}_{z}$, $\widetilde{\rho }$ and $\widetilde{\sigma }$, they are almost linearly proportional to the frequency; therefore, they can be written as items 2–4 in Eq. (17). The ${\widetilde{k}}_{y0}$, ${\widetilde{k}}_{z0}$, ${\widetilde{\rho }}_{0}$, ${\widetilde{\sigma }}_{0}$ and ${\widetilde{n}}_{0}$ are the parameters of the normalized BW model for the quasi-static tests, while $a$, $b$, $c$, $d$, $p$, $q$, $r$ and $s$ are all coefficients describing the frequency dependency of the normalized BW model. Equation (17) can be applied to PU foams under 3-point bending low-frequency vibration.

$$\left\{ {\begin{array}{*{20}l} \tilde{k}_{y} = \tilde{k}_{y0} \left( f \right)^{{a + bA_{mp} }} \hfill \\ \tilde{k}_{z} = \tilde{k}_{z0} \left( {cf + d} \right) \hfill \\ \tilde{\rho } = \tilde{\rho }_{0} \left( {pf + q} \right) \hfill \\ \tilde{\sigma } = \tilde{\sigma }_{0} \left( {rf + s} \right) \hfill \\ \tilde{n} = \tilde{n}_{0} \hfill \\ \end{array} } \right. $$

(17)

4.3 Parameter identification

Each auxetic foam specimen has been tested using different frequencies and amplitudes. The results from the quasi-static and dynamic tests need to be considered together during the parameter identification, so that the nonlinearity and frequency dependency of the auxetic foams can be captured by the inversely fitted BW model. The displacement and force signals in the time domain can be obtained directly from the tests (Fig. 2). The force signal measured by the dynamic force sensor includes two components: the inertial force of the middle holder $(M+17/35{m}_{f})\ddot{y}(t)$ and the force of the foam beam ${F}_{f}(y\left(t\right),z\left(t\right),t)$, as shown in (9). The acceleration and the inertial force can be derived from the measured displacement signal in the time domain. Therefore, the dynamic actual force ${F}_{f}$ provided by the foam beam can be obtained by excluding the inertial force term from the measured total dynamic force using (9). During the quasi-static tests, the force and displacement signals are the ones obtained directly from the machine, without considering inertial effects.

The error function used for the identification of the parameters in each foam specimen is written as:

$$ \chi^{2} \left( {\mathbf{p}} \right) = \sum\limits_{i = 1}^{{N_{1} }} {\sum\limits_{j = 1}^{{N_{2} }} {\left\{ {\frac{1}{{N_{3} A_{{{\text{mp}} ,j}} }}\sum\limits_{k = 1}^{{N_{3} }} {\left[ {F_{f - ij,k} - F_{f} \left( {y_{ij,k} ,{\tilde{\mathbf{p}}}} \right)} \right]^{2} } } \right\}} } $$

(18)

In (18), ${F}_{f-ij,k}$ and ${y}_{ij,k}$ are the measured dynamic (or quasi-static) actual force and displacement of the foam beam at frequency ${f}_{i}$, amplitude ${A}_{mp,j}$ and time ${t}_{k}$. The term ${F}_{f}({y}_{ij,k},\boldsymbol{ }\widetilde{\mathbf{p}})$ is referred to the calculated dynamic and quasi-static actual force from the BW model (14) for the same test case. The data related to 5 different amplitudes at specific frequencies (2 Hz, 4 Hz, 6 Hz, 8 Hz, 10 Hz for pristine and r_c = 20–70% auxetic foams; 2 Hz, 4 Hz, 6 Hz, 8 Hz, 10 Hz, 12 Hz for the r_c = 80% auxetic foam) are used for the data fitting. The results of quasi-static tests are also included in the error function (18) for parameter identification, and 3 different amplitudes in quasi-static tests are involved. The large amplitude vibration at the highest frequencies is beyond the optimal operational conditions of the shaker, leading to noisy hysteretic loops. The maximum frequency used in most samples is therefore 10 Hz, which increases to 12 Hz for the r_c = 80% auxetic foam case, because its higher stiffness is less sensitive to the instabilities of the shaker. The vector $\widetilde{\mathbf{p}}$ contains the 13 parameters (${\widetilde{k}}_{y0}$, ${\widetilde{k}}_{z0}$, ${\widetilde{\rho }}_{0}$, ${\widetilde{\sigma }}_{0}$, ${\widetilde{n}}_{0}$, $a$, $b$, $c$, $d$, $p$, $q$, $r$ and $s$) of the modified normalized BW model in (14) and (17). For each test case (frequency ${f}_{i}$ and amplitude ${A}_{mp,j}$), only data related to one period time ${T}_{i}$ (i.e. one hysteretic loop) are used for the parameter identification. Since the sampling frequency is constant, the higher frequency ${f}_{i}$ leads to a smaller period time ${T}_{i}$, thus less data points obtained within one cycle. Larger amplitudes can also lead to a larger absolute fitting error. Therefore, the fitting error in each test case is divided by the number of data points ${N}_{3}$ and the amplitude of the displacement ${A}_{mp,j}$, which acts as a weight factor. In this way, results from different test cases can play a similar role in the error function.

The Runge–Kutta method (RK4) is used to solve the differential equation in the BW model (14). During the dynamic tests, the displacement signal in the time domain is almost a pure sinusoid, so the sine function can be used to fit the displacement signal and then used for the calculation using a RK4 method. However, the displacement signal in time domain during the quasi-static tests is triangular wave. Therefore, Fourier series (19) with order $G$ of 20 have been used to describe the triangular wave. When calculating the actual force ${F}_{f}({y}_{ij,k},\boldsymbol{ }\widetilde{\mathbf{p}})$, two cycles of data points are used, and the initial value of $\widetilde{z}(t)$ at ${t}_{1}$ is 0. The calculated actual force will converge quickly in the second loop, so calculated data from that loop only are used to compute the fitting error function (18).

$$ y\left( t \right) = \frac{{8A_{mp} }}{{\pi^{2} }}\sum\limits_{g = 0}^{G - 1} {\frac{{\left( { - 1} \right)^{g + 1} }}{{\left( {2g + 1} \right)^{2} }}\sin \left( {\left( {2g + 1} \right)\omega_{0} t} \right)} $$

(19)

The Levenberg–Marquardt (LM) Method is used to minimize the error function (18), so that the material parameters $\widetilde{\mathbf{p}}$ can be extracted. Because the LM method can easily lead to identify local minima, the initial $\widetilde{\mathbf{p}}$ vector provided for the start of the optimization is very important. In this work, a grid search method is applied to provide a proper initial value for the LM optimization. The parameters $\widetilde{\mathbf{p}}$ of the normalized BW model can be calculated using the parameters $\mathbf{p}$ of the classical BW model from (15). The parameters $\mathbf{p}$ have a clear physical meaning and can provide a rough estimate based on data in open literature [47, 70, 72, 73]. As for the coefficients of frequency dependency in (17), the initial values for the optimization can be obtained by identifying the 5 parameters of the normalized BW model (14) at each frequency, and then fitting the curves of the parameters versus frequency. The LM optimization is therefore carried by assigning different initial values for each parameter of $\widetilde{\mathbf{p}}$ uniformly within their possible range, and that obtains 1456 different combinations of initial values of $\widetilde{\mathbf{p}}$. Although some combinations of initial values can only result in local minima with limited fitting accuracy, a large portion (~ 79%) of the different initial values can lead to the same optimization results with the best fitting accuracy. These results indicate that the parameter identification approach used in this work is reliable.

The parameters of the normalized modified BW model for the different pristine and auxetic foam specimens are listed in Appendix Tables 3 and 4. The mean absolute percentage error (MAPE) that describes the fitting accuracy of the BW model is calculated using:

$$ MAPE = \frac{1}{{N_{1} N_{2} N_{3} }}\sum\limits_{i}^{{N_{1} }} {\sum\limits_{j}^{{N_{2} }} {\sum\limits_{k}^{{N_{3} }} {\frac{{\left| {X_{ij,k} - \tilde{X}_{ij,k} } \right|}}{{X_{ij,k} }}} } } $$

(20)

In (20), ${X}_{ij,k}$ and ${\widetilde{X}}_{ij,k}$ are the measured and calculated results; those terms can represent either the quasi-static and dynamic actual force of the foam beam ${F}_{f}$ in (14), or the frequency response function (FRF) of the dynamic system in (9). The MAPE values of the actual force ${F}_{f}$ of different foams are all around ~ 95%, compared with the ~ 98% of the FRF. The calculation of FRF also involves the inertial force, which is much larger than the actual force of the foam beam, so the fitting error of actual force has less effect on the result of FRF. The 95% fitting accuracy of actual force is good enough to describe the mechanical behaviour of the foams in different loading cases using the modified BW model. The model in this work shares the same parameters in different loading cases, i.e. frequency and amplitude, which means 13 parameters are needed for each foam.

The parameters of the normalized BW model have special physical meaning corresponding to the slope and shape of the hysteretic loops [71]. However, it is difficult to use them directly to describe the stiffness and damping properties of the auxetic foams. Therefore, the phenomenological frequency and amplitude-dependent stiffness and loss factor are applied for this purpose. The phenomenological stiffness will be calculated from the tested hysteretic loops of dynamic actual force by using the slope of the line passing through the tensile and compressive peaks of the loops [72, 74], as shown in Fig. 6. Because the nonlinearity of the loops at each amplitude is not severe, the linearized secant stiffness ${K}_{ij}$ can well represent the stiffness properties of the auxetic foams at frequency ${f}_{i}$ and amplitude ${A}_{mp,j}$. Besides, the corresponding dynamic modulus ${E}_{ij}$ can be calculated using ${K}_{ij}$ from (5), which corresponds to the modulus along the d₂ direction of the auxetic foam material based on the beam bending theory. The dynamic loss factor ${\eta }_{ij}$ of the hysteretic loop for the different testing cases can be calculated using (21), where $\Delta W$ represents the energy dissipated per cycle, $U$ indicates the stored energy [75, 76].

$$ \eta = \frac{\Delta W}{{2\pi U}} $$

(21)

Fig. 6

Calculation of the linearized secant stiffness by hysteretic loops

5 Results and discussion

5.1 Quasi-static tests

The experimental and theoretical hysteretic loops of r_c = 60% auxetic foam acquired during the quasi-static 3-point bending test under cyclic compressive-tensile loading with different amplitudes along the d₁ and d₃ directions are shown in Fig. 7a and b. The loops obtained from the identified BW model always coincide well with the experimental results related to the different test cases especially at smaller displacements. This means that the modified BW model in this paper can capture well the quasi-static mechanical properties of the different foams. The inclination angle of the loop clearly decreases with the increase in amplitude of displacement, indicating a decrease of stiffness. The shape of the loops also changes noticeably with the amplitude. With a 1 mm amplitude, the hysteretic loop is narrow, with less energy dissipated. As the amplitude increases, the hysteretic curves during unloading become more convex, enlarging the loop area and the energy dissipation. The shapes of the loops with a bending force along d₁ and d₃ are also quite similar. However, the force obtained from loading along d₃ is larger than that along d₁ (0.27 N at 5 mm along d₁ compared with the 0.35 N along d₃), which means a larger stiffness is present under loading along d₃ than d₁. The effects of the amplitude on the hysteretic loops of other auxetic foams are all similar with those shown in Fig. 7a and b, so they are not repeated here.

Fig. 7

Quasi-static tests results: hysteretic loops of the r_c = 60% auxetic foam loaded along the d₁ (a) and d₃ (b) directions with different amplitudes; hysteretic loops of the auxetic foams with different r_c loaded along d₁ (c) and d₃ (d). The Exp and Mdl in the legend represent the experiment and the model, respectively

The experimental and theoretical hysteretic loops of the different auxetic and conventional foams loaded along d₁ and d₃ with amplitude of 3 mm are shown in Fig. 7c and d. The inclination angles of the loops increase noticeably with the thermoforming compression ratio r_c, denoting an increasing stiffness. The shapes of the loops of the different auxetic foams are all quite similar. The stiffness loaded along d₃ is always larger than the corresponding one along d₁.

The quasi-static secant modulus ${E}_{c}$ and loss factor ${\eta }_{c}$ can be obtained from the hysteretic loops by using equations (5), (21) and Fig. 6 [72, 74]. The experimental and theoretical curves of ${E}_{c}$ versus the compression ratio r_c loaded along d₁ and d₃ are shown in Fig. 8a and b, with extremely good agreement between test and model results. The ${E}_{c}$ increases gently with r_c till 60% and then rise sharply at high r_c. The ${E}_{c}$ always rises with the increase in amplitude, with significantly larger ${E}_{c}$ values (0.93 MPa for r_c = 50% auxetic foam loaded along d₁) for the 1 mm amplitude case, and closer values (0.66 MPa and 0.57 MPa correspondingly) for the 3 mm and 5 mm amplitudes. The ${E}_{c}$ obtained under bending load along d₁ is noticeably smaller than the one loaded along d₃ (${E}_{c}$=1.27 MPa, 0.87 MPa, 0.72 MPa for r_c = 50% auxetic foam loaded along d₃ with amplitudes of 1 mm, 3 mm, 5 mm). The ${E}_{c}$ corresponds to the modulus of the auxetic foam material along d₂, which should be the same in tests with a bending load along d₁ or d₃, if the material was isotropic—according to beam bending theory. However, the auxetic foams are strongly anisotropic due to the uniaxially thermoforming compression process, and are significantly softer along d₁ and stiffer along d₂ and d₃ [25]. The modulus obtained for the auxetic foams under bending deformation along d₁ and d₃ shows indeed a difference around 30%. The bending moduli of the auxetic foams along d₂ in Fig. 8 and the effect of r_c are quite close to the results obtained in previous papers [25, 26, 77] of the same type auxetic foam under the cyclic quasi-static compression/tension loading along d₂. For example, the modulus at 10% strain of auxetic foams with different r_c under quasi-static cyclic tensile loading along d₂ varies between 0.5 and 2 MPa, and mostly clusters around 0.5 MPa [25, 26], which is close to the value of the bending modulus corresponding to the 5 mm amplitude. In comparison, the modulus at 1% strain of the different auxetic foams under quasi-static cyclic compressive-tensile loading along d₂ mainly ranges between 0.5 and 3 MPa, and concentrates around 1 MPa [77], close to the bending modulus at 1 mm amplitude. This difference can also be justified by the fact that the bending modulus is derived from a Euler–Bernoulli beam formulation that neglects the shear deformation. Other aspects that may affect the estimation here proposed are the local deformation of the micro cells of the porous foam at the supporting and loading positions, as well as the effect of the boundary conditions.

Fig. 8

Static modulus (a) (b) and loss factor (c) (d) versus compression ratio r_c loaded along d₁ and d₃, respectively

The experimental and theoretical curves of static loss factor ${\eta }_{c}$ versus the compression ratio r_c loaded along d₁ and d₃ are shown in Fig. 8c and d. The ${\eta }_{c}$ of the different auxetic foams tested with amplitude of 3 mm and 5 mm all cluster between 0.2 and 0.25, showing no significant effect provided by the compression ratio. In comparison, the ${\eta }_{c}$ of 1 mm amplitude is evidently smaller (ranging between 0.1 and 0.2) and fluctuate more noticeably with r_c. The experimental and theoretical results show good agreement, with slightly larger deviations at large amplitudes (5 mm). The bending loss factors in this work are noticeably larger than the ones of the same auxetic foams obtained from quasi-static cyclic tension or compression tests of 10% strain along d₂, which mainly vary between 0.1 and 0.2 [25, 26] (note that the loss factors in [25] needs to be multiplied by 4 due to the different loss factor formulations used). Apart from the different deformation mechanisms under bending (including shear and local deformations, partially under tension and compression), the friction at the end supports and the middle holder can also possibly affect the experimental bending loss factors.

5.2 Dynamic test results

The force and displacement in time and frequency domain of the r_c = 60% auxetic foam loaded along d₃ with amplitude of 3 mm at 12 Hz are shown in Fig. 9a. Both the force and displacement signals are purely sinusoidal, without components at other frequencies. A phase lag around $\pi$ is present between the force and the displacement signals, because 12 Hz is above the resonance frequency of this dynamic system. At larger amplitudes and other frequencies, the force signal may contain noticeable multi-frequency components, showing the presence of slight nonlinearity. However, the displacement signal has always a pure and clean sinusoid for the different specimens tested.

Fig. 9

Vibration signals in time and frequency domain of the r_c = 60% auxetic foam loaded along d₃ with amplitude of 3 mm at 12 Hz; hysteresis loops of total dynamic force (inertial force included) for r_c = 80% auxetic foam loaded along d₃ with amplitude of 3 mm at different frequencies

The hysteretic loops of the total dynamic force (inertial force included) for the r_c = 80% auxetic foam flexed along d₃ with an amplitude of 3 mm at different frequencies are shown in Fig. 9b. The inclination angle of the loops decreases gradually from positive at low frequency to negative at high frequency, passing through the 0 degree at ~ 11 Hz; this corresponds to the resonance frequency of this dynamic system. The actual force ${F}_{f}$ provided by the foam beam during vibration is overwhelmed by the large inertial force provided by the middle holder; this makes it difficult to ascertain the mechanical properties of the foams from the hysteretic loops related to the total dynamic force, as in Fig. 9b. Therefore, as mentioned in Sect. 4.3, the inertial force of the middle holder $(M+17/35{m}_{f})\ddot{y}(t)$ is eliminated from the total dynamic force using Eq. (9) to obtain the dynamic actual force ${F}_{f}$ of the foam beams. The dynamic secant modulus ${E}_{d}$ can be calculated by using the slope of the line passing through the tensile and compressive peaks of the hysteretic loops of the actual force [72, 74], using formula (5) and Fig. 6. The dynamic loss factor ${\eta }_{d}$ can be obtained by (21) from the hysteretic loops of actual force.

5.2.1 Effect of the amplitude

The experimental and theoretical hysteretic loops of the actual force ${F}_{f}$ (inertial force excluded) for the r_c = 60% auxetic foam loaded along d₁ and d₃ with different amplitudes at 7 Hz are shown in Fig. 10a, b. The loops obtained from the identified BW model always coincide well with the experimental results for the different test cases. The inclination angle of the loops decreases with increase in amplitude, showing a more evident convex loop shape, which indicates a smaller stiffness and greater damping at large amplitude; this is similar to the quasi-static test results in Fig. 8. The shape of the loops with a bending load along d₁ and d₃ are quite similar, having larger forces along d₃ (0.37 N loaded along d₁ and 0.54 N along d₃ at 5 mm).

Fig. 10

Hysteretic loops of the actual force (inertial force excluded) for the r_c = 60% auxetic foam loaded along d₁ (a) and d₃ (b) with different amplitudes at 7 Hz; FRF of the r_c = 60% auxetic foam loaded along d₁ (a) and d₃ (b) with different amplitudes. The Exp and Mdl in the legend represent the experiment and the model, respectively

The experimental and theoretical FRF curves for the r_c = 60% auxetic foam loaded along d₁ and d₃ with different amplitudes are shown in Fig. 10c, d. The model shows a good agreement with the experimental data, especially at medium amplitudes. At large amplitudes (5 mm), the deviation between test and model is more noticeable but still acceptable, because the shape of the hysteretic loop at large amplitudes is more complex and shows a stronger nonlinearity. The resonance frequency of the FRFs clearly decrease with the increase in amplitude (from 6.3 to 5 Hz loaded along d₁, from 7.5 to 6 Hz loaded along d₃ as amplitude increases from 1 to 5 mm). This is caused by the softening of the foams with the amplitude, as also observed from the quasi-static tests (see Fig. 7a, b). The value of the peak of the FRF loaded along d₁ increases monotonously with the amplitude, compared with the first decrease and then gradually increases when loaded along d₃. The different performances of the FRFs along d₁ and d₃ are mainly affected by the combined effect of the different stiffness and damping along the two directions. The effect of the displacement amplitude on the hysteretic loops and FRFs of other auxetic foams for the different volumetric compression cases and frequencies is similar to the one shown in Fig. 10, so they are not repeated here for sake of simplicity.

The experimental and theoretical dynamic moduli ${E}_{d}$ of the different auxetic foams versus the amplitude loaded along the d₁ and d₃ directions at 8 Hz are shown in Fig. 11a and b. The moduli from the BW model overlap remarkably well with the experimental results. The ${E}_{d}$ of the different auxetic foam all decreases gently with amplitude. The modulus of the auxetic foam with r_c = 70% and 80% is always noticeably greater than the one of the other foams. And the ${E}_{d}$ loaded along d₃ is mostly around 30%-50% larger than the corresponding one loaded along d₁. For example, the dynamic modulus has values of 1.39 MPa, 1.08 MPa, 0.96 MPa for the r_c = 50% auxetic foam loaded along d₁ with amplitudes of 1 mm, 3 mm, 5 mm at 8 Hz. The same type of foam has, however, dynamic moduli with values of 1.92 MPa, 1.56 MPa, 1.36 MPa when loaded along d₃. On average, the dynamic modulus ${E}_{d}$ is around 20–40% larger than the quasi-static modulus ${E}_{c}$ described in Sect. 5.1.

Fig. 11

Dynamic modulus and loss factors versus amplitude of different foams loaded along d₁ (a) (c) and d₃ (b) (d) directions, respectively, at 8 Hz

The experimental and theoretical dynamic loss factors ${\eta }_{d}$ of the different auxetic foams versus amplitude loaded along the d₁ and d₃ directions at 8 Hz are shown in Fig. 11c and d. The values of ${\eta }_{d}$ for the different auxetic foams mostly cluster between 0.2 and 0.3, compared with the larger ${\eta }_{d}$ value of the r_c = 80% auxetic foam. The ${\eta }_{d}$ loaded along d₁ rises first when the amplitude is enlarged from 1 to 2 mm, and then slightly decreases or maintains an almost unchanged value with the increase in amplitude. The loss factors obtained with a bending load along d₃ show a more noticeable increase versus the amplitude compared with d₁, following a similar large rise at small amplitudes and then a slight increase at large amplitude values. The dynamic loss factor ${\eta }_{d}$ of the different auxetic foams are quite similar to the quasi-static ${\eta }_{c}$ ones, and mostly are within the range of 0.2–0.3. The curves of ${\eta }_{d}$ versus the amplitude calculated by the BW model for the different auxetic foams agree well with the experimental data. However, the deviation between experimental and the theoretical ${\eta }_{d}$ values is larger than the deviation of ${E}_{d}$, especially at large amplitudes (5 mm), which has also been observed in the FRF results (Fig. 10). Considering, however, that the loss factors of the different auxetic foams are mostly distributed between 0.2 and 0.3, with no significant change, this slightly larger discrepancy between tests and models of the ${\eta }_{d}$ values does not invalidate the use of this BW model.

5.2.2 Effect of the frequency

The experimental and theoretical hysteretic loops of the actual force ${F}_{f}$ (inertial force excluded) for the r_c = 80% auxetic foam loaded along d₁and d₃ at different frequencies with an amplitude of 3 mm are shown in Fig. 12. The hysteretic loops at different frequencies have quite similar shapes. The inclination angle of the loops also slightly rises with the increase in frequency, indicating a marginal enhanced stiffness by frequency. The effect of the frequency is quite similar in specimens under bending load along d₁ and d₃. The hysteretic loops calculated using the BW model agree well with the experimental ones at different frequencies; this indicates that the modified BW model developed in this work can satisfactorily capture the frequency-dependent properties of the auxetic foams at low frequencies. The effect of frequency on the hysteretic loops of the other auxetic foams is quite similar to the one shown in Fig. 12, so they are not provided for brevity.

Fig. 12

Hysteretic loops of the actual force (inertial force excluded) for the r_c = 80% auxetic foam loaded along d₁ (a) and d₃ (b) at different frequencies with an amplitude of 3 mm. Also in this case, the Exp and Mdl in the legends represent the experiment and the model, respectively

The experimental and theoretical modulus $E$ (including quasi-static and dynamic moduli ${E}_{c}$ and ${E}_{d}$) of the different foam beams versus frequency when loaded along the d₁ and d₃ directions with amplitude of 3 mm are shown in Fig. 13a and b. The quasi-static test loading rate is 3 mm/min, and the corresponding frequency ranges between 0.0025 Hz and 0.0125 Hz when amplitude decreases from 5 to 1 mm. The $E$ of the different auxetic foams increases ~ 20 to 40% from quasi-static test to 2 Hz dynamic test and then rises ~ 10% when the frequency rise from 2 to 10 Hz (for example: from 0.80 MPa of quasi-static test to 0.97 MPa at 2 Hz and 1.09 MPa at 10 Hz loaded along d₁; from 1.11 MPa of quasi-static test to 1.36 MPa at 2 Hz and 1.56 MPa at 10 Hz loaded along d₃, for the r_c = 60% auxetic foam). The effect of the frequency on the dynamic modulus is monotonic and almost linear in log–log scale within the low-frequency range considered in this work, which coincides well with the theory from Nagy et al.[54]. The curves of ${E}_{d}$ versus the frequency for different auxetic foams calculated using the modified BW model show a very good agreement with the experimental results, which means that the introduction of frequency-dependent stiffness coefficients ${k}_{y}$ and ${k}_{z}$ to the classical BW model in Eq. (17) is able to capture the frequency hardening effect provided by the PU foams.

Fig. 13

Modulus and loss factors of different foams versus frequency loaded along d₁ (a) (c) and d₃ (b) (d) directions, respectively, with amplitude of 3 mm

The experimental and theoretical loss factors $\eta$ (including quasi-static and dynamic loss factor ${\eta }_{c}$ and ${\eta }_{d}$) of the different foams versus frequency when loaded along the d₁ and d₃ directions with amplitude of 3 mm are shown in Fig. 13c and d. The $\eta$ of the different auxetic foams increase noticeably for ~ 20 to 40% from quasi-static test to dynamic test at 2 Hz, and then decrease slowly for ~ 10 to 20% with the increase in frequency till 10 Hz. The theoretical results of $\eta$ from the modified BW model provide good agreement with the tested results, denoting that the modified BW model can properly capture the frequency dependency of the loss factor. The presence of a single peak of loss factor–frequency curves of the open-cell PU foams at low-frequency ranges has also been observed by other researchers [78,79,80]. The peak is caused by the pneumatic damping effect of the air flow trapped inside the porous soft material, according to Gent’s model [78]. In this work, the exact resonance frequency of loss factor cannot be captured because not enough data points at extremely low-frequency ranges between quasi-static test and 2 Hz are available. However, the single peak phenomenon of the curve can be observed.

5.2.3 Effect of the manufacturing compression ratio

The experimental and theoretical hysteretic loops of the actual force ${F}_{f}$ (inertial force excluded) for different auxetic foams loaded along d₁ and d₃ with 3 mm amplitude at 8 Hz are shown in Fig. 14a and b. The loops calculated by the BW model coincide well with the experimental results for all different auxetic foams. The inclination angle of the loop increases evidently with the compression ratio r_c, indicating an increase of stiffness, especially for the auxetic foams with r_c = 70% and 80%. The loops of the pristine and auxetic foams with r_c ranging between 20 and 60% all cluster together, showing small differences in terms of stiffness. The force of the loops loaded along d₃ is always larger than the one along d₁ for the auxetic foams with the same value of r_c. The shape of the hysteretic loops of the different auxetic foams in the dynamic tests are quite similar to those obtained during the quasi-static experiments (Fig. 8). One small difference is about the quasi-static loops having sharper tips, compared with the smooth ends observed in the dynamic experiments. This is because the quasi-static tests uses triangular displacement waveforms with extremely slow loading rate (frequency ranging between 0.0025 and 0.0125 Hz), while the dynamic tests use a sinusoidal displacement wave and fast loading rates.

Fig. 14

Hysteretic loops of the actual force (inertial force excluded) for different auxetic foams loaded along d₁ (a) and d₃ (b) with 3 mm amplitude at 8 Hz; FRF of different auxetic foams loaded along d₁ (a) and d₃ (b) with 3 mm amplitude

The experimental and theoretical FRFs of the different foams loaded along d₁ and d₃ with 3 mm amplitude are shown in Fig. 14c and d. The model shows an extremely good agreement with the experimental data. It is evident that the resonance frequency increases with the increase in compression ratio while the peak of the FRF decreases significantly with r_c, because of the enhanced stiffness.

The experimental and theoretical dynamic moduli ${E}_{d}$ of the auxetic foam versus the manufacturing compression ratio r_c loaded along the d₁ and d₃ directions at 8 Hz are shown in Fig. 15a and b. The curves of ${E}_{d}$ calculated by BW model at different amplitudes always overlap well with the experimental ones. The values of the dynamic moduli obtained via experiments at small amplitudes are always higher than those at large amplitude, similarly to what discussed in Sect. 5.2.1. The ${E}_{d}$ increases slowly with the compression ratios when r_c ranges between 0 and 0.6, and then rise sharply when r_c reaches 0.7 and 0.8. For example, when tested with amplitude of 3 mm, the dynamic modulus for the pristine foam loaded along d₁ is 0.78 MPa and then increases to 0.86 MPa, 1.07 MPa and 2.24 MPa when r_c goes from 0.4, 0.6 to 0.8; the corresponding values when the foam has the bending load along d₃ are 1.11 MPa, 1.57 MPa and 4.42 MPa. For the majority of the auxetic foams, the values of ${E}_{d}$ derived when the bending force is applied to the d₃ direction is ~ 30 to 50% larger than along d₁; the same modulus is, however, almost 100% enhanced when r_c = 80%. The variation of the dynamic modulus ${E}_{d}$ versus r_c is quite similar to the one observed for the quasi-static modulus ${E}_{c}$ in Fig. 8, although the dynamic modulus is again 20–40% larger than the corresponding static value.

Fig. 15

Dynamic modulus and loss factors of the pristine and auxetic foams versus the manufacturing compression ratio r_c loaded along d₁ (a) (c) and d₃ (b) (d) directions, respectively, at 8 Hz

The experimental and theoretical dynamic loss factors ${\eta }_{d}$ of the auxetic foams versus r_c when the foams are loaded along the d₁ and d₃ directions at 8 Hz are shown in Fig. 15c and d. The ${\eta }_{d}$ fluctuates with r_c and mostly clusters within the range 0.2–0.3, showing no evident effect provided by the volumetric compression ratio. The dynamic loss factor for r_c = 80% is noticeably larger than in the case of other foams. The experimental ${\eta }_{d}$ value at small amplitudes (1 mm) is lower than those with larger amplitudes, especially for beam specimens with a bending load along the d₃ direction. The results of the dynamic loss factor ${\eta }_{d}$ versus r_c are quite close to those observed in the quasi-static test (Fig. 8). The ${\eta }_{d}$ values of the different auxetic foams calculated using the BW model show a good agreement with the experimental data at small amplitudes, however, exhibit some discrepancies at larger amplitudes (5 mm). Overall, the deviation between experimental and model loss factors is more noticeable than in the case of the dynamic modulus results, as already discussed in Sect. 5.2.1.

6 Conclusions

A custom 3-point bending vibration test rig has been designed and used to perform dynamic tests on auxetic PU foam beams at low-frequency ranges (1–20 Hz). A feedback controlling system is applied and 5 different displacement amplitudes (1–5 mm) are used at each frequency. A modified normalized Bouc–Wen model has also been developed to capture the amplitude and frequency-dependent properties of the conventional and auxetic foams, and shows good agreement with the results from the tests. The auxetic foam evaluated in this work is manufactured following a simplified and relatively low-cost uniaxially thermoforming compression process, which leads to the production of foams with transverse isotropic characteristics. In this work, auxetic foam beam samples made following two different cutting orientations and different thermoforming compression ratios r_c (20–80%) are considered. The dynamic bending modulus of the foams is extracted from a Euler–Bernoulli-based formulation of a beam subjected to vibration and central mass, all representing the realistic conditions existing in the 3-point bending rig. The dynamic modulus ${E}_{d}$ increases with r_c, and ranges between 0.5 and 5 MPa, while the dynamic loss factor ${\eta }_{d}$ changes little with the compression ratio used for the production of the foams, and mostly clusters between 0.2 and 0.3. The auxetic PU foam has a noticeable amplitude-dependent behaviour, with decreasing ${E}_{d}$ and increasing ${\eta }_{d}$ versus the enlarged displacement amplitude. The auxetic foam also shows an evident frequency-dependent performance; the modulus ${E}_{d}$ rises gently with increasing frequency while ${\eta }_{d}$ rises first and then reduces with frequency. The dynamic modulus ${E}_{d}$ and loss factor ${\eta }_{d}$ are 20–40% larger than the quasi-static tested ones. The testing and modelling analysis of the bending behaviour of auxetic foams within low-frequency ranges can benefit a better understanding of the mechanics of these and other porous materials for applications in areas such as apparel, cushioning and personal protective equipment, in which the reduction of low-frequency vibration is important.

Appendix

1.1 A.1 Validation of the use of the Euler–Bernoulli beam model without geometric nonlinearity

The Euler–Bernoulli (EB) beam used in this work neglects the shear deformation of the beam and the geometric nonlinearity. It has been verified that the nonlinearity, hysteresis and frequency dependency observed in these dynamic tests are mainly originated by the deformation of the cell structures inside the auxetic foam and the viscoelasticity of the Polyurethane material.

1.1.1 Shear effect

The Timoshenko beam model can include the effect of shear deformation in beams with small span to depth ratios. The beam used in this work has a support span of 100 mm and thickness of 10 mm; therefore, the span to depth ratio is 10. A direct comparison between Euler and Timoshenko beams with different span to depth is done by Ghannadiasl et al. by using theoretical modelling [59], and Gaur et al. by using finite elements [60]. The two models provide very close results, with a ~ 2% difference of stiffness, when the span to depth ratio reaches 10 and the beam is simply supported at two ends. We therefore conclude that the span to depth ratio of the foam beam used in our work is sufficiently large to neglect the effect of the shear deformation.

1.1.2 Geometric nonlinearity

A finite element model of the foam beam has been developed using the ANSYS code composed of 50 Timoshenko beam elements (BEAM188) with support span L = 100 mm, beam width b = 20 mm, beam thickness h = 10 mm, modulus E = 1 MPa, density ρ = 76.92 kg/m³ and Poisson’s ratio $\nu$=-0.3. The maximum displacement in the middle of the beam is 5 mm. The calculation was carried out with the geometric nonlinearity option on and off, separately. The stiffness of the beam including the geometric nonlinearity is 79.51 N/m, compared with the 78.72 N/m of the beam without. The difference is less than 1%; therefore, one can conclude that the effect of the geometric nonlinearity is small enough for neglect.

1.2 A.2 Continuous beam transverse vibration model

The differential equation representing the dynamic system based on the Euler–Bernoulli beam theory is Eq. (1). The boundary conditions (BCs) are:

$$\begin{aligned}y\left( {0,t} \right) = 0;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} EI\frac{{\partial^{2} y\left( {0,t} \right)}}{{\partial x^{2} }} = 0;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \\y\left( {2l,t} \right) = 0;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} EI\frac{{\partial^{2} y\left( {2l,t} \right)}}{{\partial x^{2} }} = 0; \end{aligned}$$

(a.1)

The BCs in (a.1) imply that no transverse displacement and moment occur at the two simply supported ends of the beam. The typical solution of Eq. (1) can be written as (a.2), where $\psi (x)$ represents the vibration deforming shape of the beam.

$$ y\left( {x,t} \right) = \psi \left( x \right)e^{j\omega t} $$

(a.2)

Substitute (a.2) into Eq. (1) and (a.1), and then perform the Laplace transform of (1), one obtains:

$$ \overline{\psi }\left( s \right) = L\left[ {\psi \left( x \right)} \right] = \frac{1}{{s^{4} - k^{4} }}\left[ {s^{2} \psi^{\prime}\left( 0 \right) + \psi^{\prime\prime\prime}\left( 0 \right) + \frac{{\omega^{2} M\psi \left( l \right)}}{EI}e^{ - ls} } \right] $$

(a.3)

where:

$$ k^{4} = \frac{{\rho A\omega^{2} }}{EI} $$

(a.4)

The inverse Laplace transform of (a.3) leads to:

$$\begin{gathered} \psi \left( x \right) = L^{ - 1} \left[ {\overline{\psi }\left( s \right)} \right] = \frac{{\psi^{\prime}\left( 0 \right)}}{2k}\left[ {\sinh \left( {kx} \right) + \sin \left( {kx} \right)} \right] + \frac{{\psi^{\prime\prime\prime}\left( 0 \right)}}{{2k^{3} }}\left[ {\sinh \left( {kx} \right) - \sin \left( {kx} \right)} \right] \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + \frac{{\omega^{2} M\psi \left( l \right)}}{{2k^{3} EI}}\left\{ {\sinh \left[ {k\left( {x - l} \right)} \right] - \sin \left[ {k\left( {x - l} \right)} \right]} \right\}u\left( {x - l} \right) \hfill \\ \end{gathered}$$

(a.5)

In (a.5), $u(x-l)$ represents the unit step function. The constants $\psi \prime \left( 0 \right)$ and $\psi^{\prime \prime \prime } \left( 0 \right)$ in (a.5) can be determined by substituting (a.3) into the two boundary conditions of (a.1) at $x=2l$. The resulting beam deforming function $\psi (x)$ is:

$$ \psi \left( x \right) = \frac{{\omega^{2} M\psi \left( l \right)}}{{4k^{3} EI}}\left\{ {\left[ {\frac{{\sin \left( {kx} \right)}}{{\cos \left( {kl} \right)}} - \frac{{\sinh \left( {kx} \right)}}{{\cosh \left( {kl} \right)}}} \right] + 2u\left( {x - l} \right)\left[ {\sinh \left( {k\left( {x - l} \right)} \right) - \sin \left( {k\left( {x - l} \right)} \right)} \right]} \right\} $$

(a.6)

Substituting $x=l$ in (a.6), the characteristic function of the beam vibration model in Fig. 3 can be obtained as Eq. (2).

1.3 A.3 Inversely fitted parameters of the normalized modified Bouc–Wen model for different auxetic foams

See Tables 3, 4.

Table 3 Inversely fitted parameters of the normalized modified Bouc–Wen model for different auxetic foams. Part I: basic parameters of the normalized BW model

Table 4 Inversely fitted parameters of the normalized modified Bouc–Wen model for different auxetic foams. Part II: coefficients for frequency-dependent property