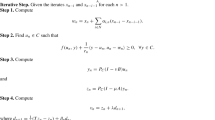Abstract
Accurate and real-time orbit computational methods are highly required in space tasks of the space vehicles. A decoupling method and a quasi-linearization method are proposed to efficiently and accurately solve relative orbit transfer problems. The orbit transfer problem is transformed into a group of orbit propagation problems that are much easier to solve. A novel local variational iteration method is provided for orbit propagation. Relative orbit transfer problems based on the Tschauner–Hempel model are solved by using the decoupling method without initial guess and iteration. The proposed quasi-linear local variational iteration method, which combines the quadratic convergence of quasi-linearization and the high computational performance of the local variational iteration method, is successfully applied to solve two types of strongly nonlinear relative orbit transfer problems. Comparisons are made with the Newton’s shooting and finite-difference-based solver. The QLVIM can derive far more accurate solutions while consuming much less computing time. Simulations also manifest that the proposed method covers longer solvable time span; i.e., it shows better convergency. The initial guess of the QLVIM is easier to obtain. Rather than a refined initial guess of the initial velocity, the proposed method only needs a rough trajectory connecting the boundary positions. It is also very convenient to extend the proposed methods to other engineering boundary value problems.





Similar content being viewed by others
Availability of data and material
The datasets generated during the current study are available from the corresponding author on reasonable request.
Code availability
The codes generated during the current study are available from the corresponding author on reasonable request.
References
Sengupta, P., Sharma, R., Vadali, S.R.: Periodic relative motion near a keplerian elliptic orbit with nonlinear differential gravity. J. Guid. Control. Dyn. 29(5), 1110–1121 (2015). https://doi.org/10.2514/1.18344
Herman, A.L., Conway, B.A.: Direct optimization using collocation based on high-order Gauss-Lobatto quadrature rules. J. Guid. Control. Dyn. 19(3), 592–599 (1996). https://doi.org/10.2514/3.21662
Fox, K.: Numerical integration of the equations of motion of celestial mechanics. Celest. Mech. 33(2), 127–142 (1984). https://doi.org/10.1007/BF01234151
Andrew, A.L., Roberts, S.M., Shipman, J.S.: Two-point boundary value problems: shooting methods. Technometrics 17(2), 277 (1975). https://doi.org/10.2307/1268370
Ha, S.N.: A nonlinear shooting method for two-point boundary value problems. Comput. Math. Appl. 42(10–11), 1411–1420 (2001). https://doi.org/10.1016/S0898-1221(01)00250-4
Faragó, I., Filipov, S.M.: The linearization methods as a basis to derive the relaxation and the shooting methods (2020). https://arxiv.org/abs/2003.03104
Morrison, D.D., Riley, J.D., Zancanaro, J.F.: Multiple shooting method for two-point boundary value problems. Eng. Comput. 20(1), 31–37 (1962). https://doi.org/10.1145/355580.369128
Peng, K., Peng, R., Huang, Z., Zhang, B.N.: Implicit shooting method to solve optimal Lunar soft landing trajectory. Acta Aeronauticaet Astronautica Sinica 40(7), 322641–322641 (2019). https://doi.org/10.7527/S1000-6893.2018.22641
Reinhardt, H.J.: Analysis of approximation methods for differential and integral equations. Math. Comput. 50(182), 641 (1985). https://doi.org/10.2307/2008633
Dong, L., Alotaibi, A., Mohiuddine, S.A., Atluri, S.N.: Computational methods in engineering: a variety of primal & mixed methods, with global & local interpolations, for well-posed or Ill-posed BCs. Comput. Model. Eng. Sci. 99(1), 1–85 (2014). https://doi.org/10.3970/cmes.2014.099.001
Dai, H.H., Yue, X.K., Yuan, J.P.: A time domain collocation method for obtaining the third superharmonic solutions to the Duffing oscillator. Nonlinear Dyn 73, 593–609 (2013). https://doi.org/10.1007/s11071-013-0813-z
Shiralashetti, S.C., Deshi, A.B.: An efficient Haar wavelet collocation method for the numerical solution of multi-term fractional differential equations. Nonlinear Dyn 83, 293–303 (2016). https://doi.org/10.1007/s11071-015-2326-4
Chen, Q.F., Zhang, Y.D., Liao, S.Y., Wan, F.L.: Newton–kantorovich/pseudospectral solution to perturbed astrodynamic two-point boundary-value problems. J. Guid. Control. Dyn. 36(2), 485–498 (2013). https://doi.org/10.2514/1.56590
Elgohary, T.A., Junkins, J.L., Atluri, S.N.: An RBF-Collocation algorithm for orbit propagation. In: AAS/AIAA: Space Flight Mechanics Meeting, pp. 1021–1033 (2015)
Bai, X.L., Junkins, J.L.: Modified Chebyshev-Picard Iteration methods for solution of boundary value problems. J. Astronaut. Sci. 58(4), 615–642 (2011). https://doi.org/10.1007/BF03321534
Wang, X.C., Yue, X.K., Dai, H.H., Atluri, S.N.: Feedback-accelerated picard iteration for orbit propagation and Lambert’s problem. J. Guid. Control. Dyn. 40(10), 2442–2451 (2017). https://doi.org/10.2514/1.G002638
Pan, X., Pan, B.: Practical homotopy methods for finding the best minimum-fuel transfer in the circular restricted three-body problem. IEEE Access 8, 47845–47862 (2020). https://doi.org/10.1109/ACCESS.2020.2978246
Na, T.Y.: An initial value method for the solution of a class of nonlinear equations in fluid mechanics. J. Basic Eng. 92(3), 503–508 (1970). https://doi.org/10.1115/1.3425046
Gooding, R.H.: A procedure for the solution of lambert’s orbital boundary-value problem. Celest. Mech. Dyn. Astron. 48(2), 145–165 (1990)
Battin. R.H.: An introduction to the mathematics and methods of astrodynamics. Revised edition. American Institute of Aeronautics and Astronautics, USA (1999). https://doi.org/10.2514/4.861543
Nelson, S.L., Zarchan, P.: Alternative approach to the solution of lambert’s problem. J. Guid. Control. Dyn. 15(4), 1003–1009 (2015). https://doi.org/10.2514/3.20935
Na, T.Y.: Computational methods in engineering boundary value problems. Academic Press Inc, USA (1979)
Wang, X.C., Atluri, S.N.: A novel class of highly efficient and accurate time-integrators in nonlinear computational mechanics. Comput. Mech. 59(5), 861–876 (2017). https://doi.org/10.1007/s00466-017-1377-4
Lee, E.S.: Quasilinearization and invariant imbedding with applications to chemical engineering and adaptive control. Academic Press Inc., USA (1968)
Li, H.Y., Luo, Y.Z., Zhang, J., Tang, G.J.: Optimal multi-objective linearized impulsive rendezvous under uncertainty. Acta Astronaut. 66(3–4), 439–445 (2010). https://doi.org/10.1016/j.actaastro.2009.06.019
Li, P., Zhu, Z.H.: Model predictive control for spacecraft rendezvous in elliptical orbit. Acta Astronaut. 146(MAY), 339–348 (2018). https://doi.org/10.1016/j.actaastro.2018.03.025
Baresi, N., Dell’Elce, L., Cardoso dos Santos, J., et al.: Long-term evolution of mid-altitude quasi-satellite orbits. Nonlinear Dyn 99, 2743–2763 (2020). https://doi.org/10.1007/s11071-019-05344-4
Xu, G.Y., Wang, D.W.: Nonlinear dynamic equations of satellite relative motion around an oblate earth. J. Guid. Control. Dyn. 31(5), 1521–1524 (2012). https://doi.org/10.2514/1.33616
Franzini, G., Innocenti, M.: Relative motion dynamics with arbitrary perturbations in the local-vertical local-horizon reference frame. J. Astronaut. Sci. 67, 98–112 (2020). https://doi.org/10.1007/s40295-019-00185-0
Wang, X.C., Xu, Q.Y., Atluri, S.N.: Combination of the variational iteration method and numerical algorithms for nonlinear problems. Appl. Math. Model. 79, 243–259 (2020). https://doi.org/10.1016/j.apm.2019.10.034
Inalhan, G., Tillerson, M., How, J.P.: Relative dynamics and control of spacecraft formations in eccentric orbits. J. Guid. Control. Dyn. 25(1), 48–59 (2002). https://doi.org/10.2514/2.4874
Xu, G.Y., Poh, E.K., Wang, D.W., Wu, B.L.: Periodic and quasi-periodic satellite relative orbits at critical inclination. In: IEEE: Aerospace Conference (2009). https://doi.org/10.1109/AERO.2009.4839336
MSIS-E-90 Atmosphere Model, https://ccmc.gsfc.nasa.gov/modelweb/models/msis_vitmo.php
Funding
This work is supported by the Fundamental Research Funds for the Central Universities (3102019HTQD014), National Natural Science Foundation of China (11972026, U2013206) and Innovation Foundation for Doctor Dissertation of Northwestern Polytechnical University (CX2022005).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The authors have no relevant financial or nonfinancial interests to disclose.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A
See Table
In Sect. 2.3, \({\tilde{\varvec{R}}}\) is a row rearranging matrix that moves the (\(dM + m\))th row of unit matrix to the(\(mD + d\))th row, where \(d = 1,2,...,D,{\kern 1pt}\)\(m = 1,2,...,M\), D is the dimension of governing system, M is the number of collocation nodes. The details of \({{\varvec{\Phi}}}(t)\), \({\dot{\varvec{\Phi }}}(t)\), \(\int_{{t_{0} }}^{t} {{{\varvec{\Phi}}}(\tau )} d\tau\) are listed in Table 9.
Appendix B
The motion of the chief satellite \(S_{0}\) can be described by a set of equations as
Appendix C
The variables \(r,\dot{r},h,\omega_{x} ,\omega_{z} ,i,\theta\) are related to the reference orbit and described by:
The variables with subscripts \(J_{2}\) and \(a\) are related to the zonal harmonic perturbations and atmospheric drag, respectively. Due to limited space, more details are not shown here. Readers interested may consult the reference [29].
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Feng, H., Yue, X., Wang, X. et al. Decoupling and quasi-linearization methods for boundary value problems in relative orbital mechanics. Nonlinear Dyn 111, 199–215 (2023). https://doi.org/10.1007/s11071-022-07845-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-022-07845-1