Energy-based swing-up control for a two-link underactuated robot with flexible first joint

Abstract

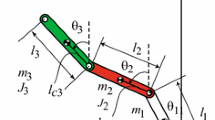
This paper concerns the swing-up control of a two-link robot moving in a vertical plane, which has a single actuator at the second joint and a linear torsional spring at the first joint. First, we present a necessary and sufficient condition such that the robot is linearly controllable at the upright equilibrium point (UEP, where two links are both upright). Second, we prove without any assumption that the robot is at an equilibrium point provided that its actuated joint angle is constant under a constant torque. Third, for the robot with its torsional stiffness of the spring being not greater than a value determined by the coefficients of its gravitational terms, we propose an energy-based swing-up controller without singular points. We conduct a global motion analysis for the robot under the proposed controller. For the case that the total mechanical energy of the robot converges to its desired value, we present the phase portrait of the closed-loop solution. For the case that the convergence is not achieved, we show that the closed-loop solution approaches an equilibrium point belonging to a set of equilibrium points, and give a sufficient condition to check its instability. From the motion analysis, we present a sufficient condition such that the robot can be swung-up close to the UEP under the proposed swing-up controller. Finally, we verify our theoretical results through a numerical simulation.

Appendix A: Proof of Lemma 3

Proof

Notice that (49) holds if and only if

$$\begin{aligned} {k_D} + \left( {E - E_r} \right) {M_p}\left( {{q_2}} \right) \ne 0 , \end{aligned}$$

(A1)

where $M_p(q_2)$ is defined in (52). Since ${M_p}(q_2) > 0$ and $E \ge P(q_1,q_2)$, we have $\left( {{E_r} - P\left( {{q_1},{q_2}} \right) } \right) {M_p}\left( {{q_2}} \right) \ge \left( E_r - E \right) M_p \left( {{q_2}} \right)$. Thus, a sufficient condition for (A1) is

$$\begin{aligned}&{k_D} > \mathop {\max }\limits _{{q_1},{q_2}} \eta ({q_1},{q_2}); \; \eta ({q_1},{q_2})\nonumber \\&\quad = \left( {{E_r} - P\left( {{q_1},{q_2}} \right) } \right) {M_p}\left( {{q_2}} \right) . \end{aligned}$$

(A2)

Next, we show that (A2) is also a necessary condition for (A1). In the case $\mathop {\max }\limits _{{q_1},{q_2}} \eta ({q_1},{q_2}) \ge k_D>0$, we can always find a state $[q_1, q_2,\dot{q}_1, \dot{q}_2]^\mathrm {T}$ for which (A1) does not hold. Letting $[\zeta _1, \zeta _2]^\mathrm {T}$ be a value of $[q_1,q_2]^\mathrm {T}$ which maximizes $\eta ({q_1},{q_2})$ and taking $\zeta _d=[\zeta _{1d}, \zeta _{2d}]^\mathrm {T}$ as

$$\begin{aligned} \zeta _d= & {} M{({\zeta _1},{\zeta _2})^{ - 1/2}}\left[ {\begin{array}{*{20}{c}} {\sqrt{2{d_0}} }\\ 0 \end{array}} \right] ,\nonumber \\ {d_0}= & {} \frac{{\eta ({\zeta _1},{\zeta _2}) - {k_D}}}{{{M_p}({\zeta _2})}} \ge 0 \end{aligned}$$

(A3)

yields

$$\begin{aligned}&{k_D} + \left( {\frac{1}{2}{\zeta _d^\mathrm {T}} M({\zeta _1},{\zeta _2}){\zeta _d} + P({\zeta _1},{\zeta _2}) - {E_r}} \right) \nonumber \\&\quad {M_p}({\zeta _2}) = 0. \end{aligned}$$

(A4)

Therefore, for the state $[q_1, q_2,\dot{q}_1, \dot{q}_2]^\mathrm {T} = [\zeta _1, \zeta _2, \zeta _{1d},\zeta _{2d}]^\mathrm {T}$, (A1) does not hold.

$$\begin{aligned}&\frac{1}{2}{k_1}q_1^2 < {\beta _1} + {\beta _2} - {\beta _1}\cos {q_1} - {\beta _2}\cos \left( {{q_1} + {q_2}} \right) \nonumber \\&\quad {\le } 2\left( {{\beta _1} + {\beta _2}} \right) . \end{aligned}$$

(A5)

Thus, we have

$$\begin{aligned} {\left| {{q_1}} \right| < 2\sqrt{\frac{{{\beta _1} + {\beta _2}}}{{{k_1}}}} = \frac{2}{{\sqrt{\gamma }}}. } \end{aligned}$$

(A6)

Since $\eta ({q_1},{q_2})$ is periodic in $q_2$ with period $2\pi$, by using (A6) we know (A2) holds if and only if (51) holds.

Now, suppose that (49) holds. We have $\dot{V} \le 0$ and V is bounded under controller (50). According to LaSalle’s invariance principle [9] (p. 128), we obtain (53). Then, substituting $E \equiv {E^*}$ and $q_2 \equiv {q_2^*}$ into (3) proves (54). The detailed proof process is omitted here since the process is similar to the analysis in [16]. This completes the proof of Lemma 3. $\square$