Nonlinear forced vibration of hybrid fiber/graphene nanoplatelets/polymer composite sandwich cylindrical shells with hexagon honeycomb core

Abstract

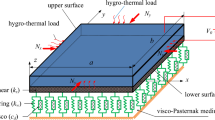
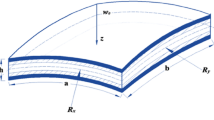
This paper aims to investigate the nonlinear forced vibration characteristics of hybrid fiber/graphene nanoplatelets/polymer composite sandwich cylindrical shells with hexagon honeycomb core (HHC) in a hygrothermal environment. Firstly, an analytical model for such shells is proposed, where the equivalent material parameters of skins are determined based on the law of the mixture and homogenization approach, and the improved Gibson's technique is adopted to estimate the equivalent material properties of HHC. Furthermore, the first-order shear deformation theory together with von Kármán geometric nonlinearity terms and Hamilton’s principle is utilized to obtain the nonlinear governing equations that consider the effect of hygrothermal and mechanical loads, which are further discretized into a series of ordinary differential equations via the Galerkin approach. Subsequently, the static condensation technique and the multiple scale method are utilized to solve the nonlinear forced vibration responses, including primary, super- and sub-harmonic resonances. The results obtained by the present model are compared to the ones from the literature to prove the effectiveness of the proposed model. Also, the influences of key parameters on the nonlinear dynamic performance of the structure are evaluated, with some critical conclusions related to reducing the nonlinear resonance amplitude and resonance region of the structure being summarized.

Appendices

Appendix A

The parameter values of $H_{ij} \left( {i = 1, \, 2, \ldots ,5; \, j = 1, \, 2, \ldots 11} \right),S_{xy} \left( {x = u, \, v, \, w, \, \varphi , \, \theta ; \, y = u, \, v, \, \varphi , \, \theta } \right)$, H_non2 and H_non3 in Eqs. (26), (27), (28), (29) and (30) are stated as:

$$ H_{11} = \int_{0}^{2\pi } {\int_{0}^{L} {\left\{ {A_{11} \frac{{\partial q_{u} }}{\partial \varphi }\frac{{\partial q_{u} }}{\partial \varphi } + A_{66} \frac{1}{{R^{2} }}\frac{{\partial q_{u} }}{\partial \theta }\frac{{\partial q_{u} }}{\partial \theta } + A_{16} \frac{1}{R}\left( {\frac{{\partial q_{u} }}{\partial \varphi }\frac{{\partial q_{u} }}{\partial \theta } + \frac{{\partial q_{u} }}{\partial \theta }\frac{{\partial q_{u} }}{\partial \varphi }} \right)} \right\}} } Rd\varphi {\text{d}}\theta $$

(A1)

$$ H_{12} = \int_{0}^{2\pi } {\int_{0}^{L} {\left\{ {A_{12} \frac{1}{R}\frac{{\partial q_{u} }}{\partial \varphi }\frac{{\partial q_{v} }}{\partial \theta } + A_{16} \frac{{\partial q_{u} }}{\partial \varphi }\frac{{\partial q_{v} }}{\partial \varphi } + A_{26} \frac{1}{{R^{2} }}\frac{{\partial q_{u} }}{\partial \theta }\frac{{\partial q_{v} }}{\partial \theta } + A_{66} \frac{1}{R}\frac{{\partial q_{u} }}{\partial \theta }\frac{{\partial q_{v} }}{\partial \varphi }} \right\}} } Rd\varphi {\text{d}}\theta $$

(A2)

$$ H_{13} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ {A_{12} \frac{1}{R}\frac{{\partial q_{u} }}{\partial \varphi }q_{w} + A_{26} \frac{1}{{R^{2} }}\frac{{\partial q_{u} }}{\partial \theta }q_{w} } \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A3)

$$ H_{14} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ {B_{11} \frac{{\partial q_{u} }}{\partial \theta }\frac{{\partial q_{\varphi } }}{\partial \varphi } + B_{16} \frac{1}{R}\frac{{\partial q_{u} }}{\partial \varphi }\frac{{\partial q_{\varphi } }}{\partial \theta } + B_{16} \frac{1}{R}\frac{{\partial q_{u} }}{\partial \theta }\frac{{\partial q_{\varphi } }}{\partial \varphi } + B_{66} \frac{1}{{R^{2} }}\frac{{\partial q_{u} }}{\partial \theta }\frac{{\partial q_{\varphi } }}{\partial \theta }} \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A4)

$$ H_{15} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ {B_{12} \frac{1}{R}\frac{{\partial q_{u} }}{\partial \varphi }\frac{{\partial q_{\theta } }}{\partial \theta } + B_{16} \frac{{\partial q_{u} }}{\partial \varphi }\frac{{\partial q_{\theta } }}{\partial \varphi } + B_{26} \frac{1}{{R^{2} }}\frac{{\partial q_{u} }}{\partial \theta }\frac{{\partial q_{\theta } }}{\partial \theta } + B_{66} \frac{1}{R}\frac{{\partial q_{u} }}{\partial \theta }\frac{{\partial q_{\theta } }}{\partial \varphi }} \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A5)

$$ H_{16} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ \begin{gathered} A_{11} \frac{{\partial q_{u} }}{\partial \varphi }\left( {\frac{{\partial q_{w} }}{\partial \varphi }} \right)^{2} + 2A_{66} \frac{1}{{R^{2} }}\frac{{\partial q_{u} }}{\partial \varphi }\frac{{\partial q_{w} }}{\partial \varphi }\frac{{\partial q_{w} }}{\partial \theta } + A_{16} \frac{1}{{R^{2} }}\frac{{\partial q_{u} }}{\partial \theta }\left( {\frac{{\partial q_{w} }}{\partial \theta }} \right)^{2} \hfill \\ + 2A_{16} \frac{1}{R}\frac{{\partial q_{u} }}{\partial \varphi }\frac{{\partial q_{w} }}{\partial \varphi }\frac{{\partial q_{w} }}{\partial \theta } + A_{12} \frac{1}{{R^{2} }}\frac{{\partial q_{u} }}{\partial \varphi }\left( {\frac{{\partial q_{w} }}{\partial \theta }} \right)^{2} + A_{26} \frac{1}{{R^{3} }}\frac{{\partial q_{u} }}{\partial \theta }\left( {\frac{{\partial q_{w} }}{\partial \theta }} \right)^{2} \hfill \\ \end{gathered} \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A6)

$$ H_{21} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ {A_{12} \frac{1}{R}\frac{{\partial q_{v} }}{\partial \theta }\frac{{\partial q_{u} }}{\partial \varphi } + A_{16} \frac{{\partial q_{v} }}{\partial \varphi }\frac{{\partial q_{u} }}{\partial \varphi } + A_{26} \frac{1}{{R^{2} }}\frac{{\partial q_{v} }}{\partial \theta }\frac{{\partial q_{u} }}{\partial \theta } + A_{66} \frac{1}{R}\frac{{\partial q_{v} }}{\partial \varphi }\frac{{\partial q_{u} }}{\partial \theta }} \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A7)

$$ H_{22} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ {A_{22} \frac{1}{{R^{2} }}\frac{{\partial q_{v} }}{\partial \theta }\frac{{\partial q_{v} }}{\partial \theta } + A_{26} \frac{1}{R}\left( {\frac{{\partial q_{v} }}{\partial \varphi }\frac{{\partial q_{v} }}{\partial \theta } + \frac{{\partial q_{v} }}{\partial \theta }\frac{{\partial q_{v} }}{\partial \varphi }} \right) + A_{66} \frac{{\partial q_{v} }}{\partial \varphi }\frac{{\partial q_{v} }}{\partial \varphi } + s_{{\text{r}}} A_{44} \frac{1}{{R^{2} }}q_{v} q_{v} } \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A8)

$$ H_{23} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ {A_{22} \frac{1}{{R^{2} }}\frac{{\partial q_{v} }}{\partial \theta }q_{w} + A_{26} \frac{1}{R}\frac{{\partial q_{v} }}{\partial \varphi }Q_{w} - s_{{\text{r}}} A_{44} \frac{1}{{R^{2} }}q_{v} \frac{{\partial q_{w} }}{\partial \theta } - s_{{\text{r}}} A_{45} \frac{1}{R}q_{v} \frac{{\partial q_{w} }}{\partial \varphi }} \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A9)

$$ H_{24} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ \begin{gathered} B_{12} \frac{1}{R}\frac{{\partial q_{v} }}{\partial \theta }\frac{{\partial q_{\varphi } }}{\partial \varphi } + B_{16} \frac{{\partial q_{v} }}{\partial \varphi }\frac{{\partial q_{\varphi } }}{\partial \varphi } + B_{26} \frac{1}{{R^{2} }}\frac{{\partial q_{v} }}{\partial \theta }\frac{{\partial q_{\varphi } }}{\partial \theta } \hfill \\ + B_{66} \frac{1}{R}\frac{{\partial q_{v} }}{\partial \varphi }\frac{{\partial q_{\varphi } }}{\partial \theta } - s_{{\text{r}}} A_{45} \frac{1}{R}Q_{v} Q_{\varphi } \hfill \\ \end{gathered} \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A10)

$$ H_{25} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ {B_{22} \frac{1}{{R^{2} }}\frac{{\partial q_{v} }}{\partial \theta }\frac{{\partial q_{\theta } }}{\partial \theta } + B_{26} \frac{1}{R}\left( {\frac{{\partial q_{v} }}{\partial \theta }\frac{{\partial q_{\theta } }}{\partial \varphi } + \frac{{\partial q_{v} }}{\partial \varphi }\frac{{\partial q_{\theta } }}{\partial \theta }} \right) + B_{66} \frac{{\partial q_{v} }}{\partial \varphi }\frac{{\partial q_{\theta } }}{\partial \varphi } - s_{{\text{r}}} A_{44} \frac{1}{R}q_{v} q_{\theta } } \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A11)

$$ H_{26} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ \begin{gathered} A_{12} \frac{1}{R}\frac{{\partial q_{v} }}{\partial \theta }\left( {\frac{{\partial q_{w} }}{\partial \varphi }} \right)^{2} + 2A_{66} \frac{1}{R}\frac{{\partial q_{v} }}{\partial \varphi }\frac{{\partial q_{w} }}{\partial \varphi }\frac{{\partial q_{w} }}{\partial \theta } + A_{22} \frac{1}{{R^{3} }}\frac{{\partial q_{v} }}{\partial \theta }\left( {\frac{{\partial q_{w} }}{\partial \theta }} \right)^{2} \hfill \\ + A_{16} \frac{{\partial q_{v} }}{\partial \varphi }\left( {\frac{{\partial q_{w} }}{\partial \varphi }} \right)^{2} + 2A_{26} \frac{1}{{R^{2} }}\frac{{\partial q_{v} }}{\partial \theta }\frac{{\partial q_{w} }}{\partial \varphi }\frac{{\partial q_{w} }}{\partial \theta } + A_{26} \frac{1}{{R^{2} }}\frac{{\partial q_{v} }}{\partial \theta }\left( {\frac{{\partial q_{w} }}{\partial \theta }} \right)^{2} \hfill \\ \end{gathered} \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A12)

$$ H_{31} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ {A_{12} \frac{1}{R}q_{w} \frac{{\partial q_{u} }}{\partial \varphi } + A_{26} \frac{1}{{R^{2} }}q_{w} \frac{{\partial q_{u} }}{\partial \theta }} \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A13)

$$ H_{32} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ {A_{22} \frac{1}{{R^{2} }}q_{w} \frac{{\partial q_{v} }}{\partial \theta } + A_{26} \frac{1}{R}q_{w} \frac{{\partial q_{v} }}{\partial \varphi } - \kappa_{{\text{s}}} A_{44} \frac{1}{{R^{2} }}\frac{{\partial q_{w} }}{\partial \theta }q_{v} - s_{{\text{r}}} A_{45} \frac{1}{R}\frac{{\partial q_{w} }}{\partial \varphi }q_{v} } \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A14)

$$ H_{33} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ \begin{array}{l} A_{22} \frac{1}{{R^{2} }}q_{w} q_{w} + s_{{\text{r}}} A_{44} \frac{1}{{R^{2} }}\frac{{\partial q_{w} }}{\partial \theta }\frac{{\partial q_{w} }}{\partial \theta } + s_{{\text{r}}} A_{45} \frac{1}{R}\left( {\frac{{\partial q_{w} }}{\partial \varphi }\frac{{\partial q_{w} }}{\partial \theta } + \frac{{\partial q_{w} }}{\partial \theta }\frac{{\partial q_{w} }}{\partial \varphi }} \right) \hfill \\ \quad + s_{{\text{r}}} A_{55} \frac{{\partial q_{w} }}{\partial \varphi }\frac{{\partial q_{w} }}{\partial \varphi } - \left[ {\left( {a_{1} + a^{\prime}_{1} } \right)\vartriangle T + \left( {b_{1} + b^{\prime}_{1} } \right)\vartriangle C} \right]\frac{{\partial q_{w} }}{\partial \varphi }\frac{{\partial q_{w} }}{\partial \varphi } \hfill \\ \quad - \left[ {\left( {a_{2} + a^{\prime}_{2} } \right)\vartriangle T + \left( {b_{2} + b^{\prime}_{2} } \right)\vartriangle C} \right]\frac{{\partial q_{w} }}{R\partial \theta }\frac{{\partial q_{w} }}{R\partial \theta } \hfill \\ \quad - \left[ {\left( {a_{12} + a^{\prime}_{12} } \right)\vartriangle T + \left( {b_{12} + b^{\prime}_{12} } \right)\vartriangle C} \right]\frac{{\partial q_{w} }}{\partial \varphi }\frac{{\partial q_{w} }}{R\partial \theta } \hfill \\ \end{array} \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A16)

$$ H_{34} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ {B_{12} \frac{1}{R}q_{w} q_{\varphi } + B_{26} \frac{1}{{R^{2} }}q_{w} \frac{{\partial q_{\varphi } }}{\partial \theta } + \kappa_{{\text{s}}} A_{45} \frac{1}{R}\frac{{\partial q_{w} }}{\partial \theta }q_{\varphi } + s_{{\text{r}}} A_{55} \frac{{\partial q_{w} }}{\partial \varphi }q_{\varphi } } \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A17)

$$ H_{35} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ {B_{22} \frac{1}{{R^{2} }}Q_{w} \frac{{\partial Q_{\theta } }}{\partial \theta } + B_{26} \frac{1}{R}Q_{w} \frac{{\partial Q_{\theta } }}{\partial \varphi } + s_{{\text{r}}} A_{44} \frac{1}{R}\frac{{\partial Q_{w} }}{\partial \theta }Q_{\theta } + s_{{\text{r}}} A_{45} \frac{1}{R}\frac{{\partial Q_{w} }}{\partial \varphi }Q_{\theta } } \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A18)

$$ H_{36} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ \begin{array}{l} 2A_{11} \left( {\frac{{\partial q_{w} }}{\partial \varphi }} \right)^{2} \frac{{\partial q_{u} }}{\partial \varphi } + 4A_{66} \frac{1}{{R^{2} }}\frac{{\partial q_{w} }}{\partial \varphi }\frac{{\partial q_{w} }}{\partial \theta }\frac{{\partial q_{u} }}{\partial \varphi } + 2A_{16} \frac{1}{{R^{2} }}\left( {\frac{{\partial q_{w} }}{\partial \theta }} \right)^{2} \frac{{\partial q_{u} }}{\partial \theta } \hfill \\ \quad + 4A_{16} \frac{1}{R}\frac{{\partial q_{w} }}{\partial \varphi }\frac{{\partial q_{w} }}{\partial \theta }\frac{{\partial q_{u} }}{\partial \varphi } + 2A_{12} \frac{1}{{R^{2} }}\left( {\frac{{\partial q_{w} }}{\partial \theta }} \right)^{2} \frac{{\partial q_{u} }}{\partial \varphi } + 2A_{26} \frac{1}{{R^{3} }}\left( {\frac{{\partial q_{w} }}{\partial \theta }} \right)^{2} \frac{{\partial q_{u} }}{\partial \theta } \hfill \\ \end{array} \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A19)

$$ H_{37} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ \begin{array}{l} 2A_{12} \frac{1}{R}\left( {\frac{{\partial q_{w} }}{\partial \varphi }} \right)^{2} \frac{{\partial q_{v} }}{\partial \theta } + 4A_{66} \frac{1}{R}\frac{{\partial q_{w} }}{\partial \varphi }\frac{{\partial q_{w} }}{\partial \theta }\frac{{\partial q_{v} }}{\partial \varphi } + 2A_{22} \left( {\frac{{\partial q_{w} }}{\partial \theta }} \right)^{2} \frac{1}{{R^{3} }}\frac{{\partial q_{v} }}{\partial \theta } \hfill \\ \quad + 2A_{16} \left( {\frac{{\partial q_{w} }}{\partial \varphi }} \right)^{2} \frac{{\partial q_{v} }}{\partial \varphi } + 4A_{26} \frac{1}{{R^{2} }}\frac{{\partial q_{w} }}{\partial \varphi }\frac{{\partial q_{w} }}{\partial \theta }\frac{{\partial q_{v} }}{\partial \theta } + 2A_{26} \frac{1}{{R^{2} }}\left( {\frac{{\partial q_{w} }}{\partial \theta }} \right)^{2} \frac{{\partial q_{v} }}{\partial \theta } \hfill \\ \end{array} \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A20)

$$ H_{non2} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ {A_{12} \frac{1}{R}q_{w} \left( {\frac{{\partial q_{w} }}{\partial \varphi }} \right)^{2} + 2A_{26} \frac{1}{{R^{2} }}q_{w} \frac{{\partial q_{w} }}{\partial \varphi }\frac{{\partial q_{w} }}{\partial \theta } + A_{22} \frac{1}{{R^{3} }}q_{w} \left( {\frac{{\partial q_{w} }}{\partial \theta }} \right)^{2} } \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A21)

$$ H_{38} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ \begin{gathered} 2B_{11} \left( {\frac{{\partial q_{w} }}{\partial \varphi }} \right)^{2} \frac{{\partial q_{\varphi } }}{\partial \varphi } + 4B_{66} \frac{1}{{R^{2} }}\frac{{\partial q_{w} }}{\partial \varphi }\frac{{\partial q_{w} }}{\partial \theta }\frac{{\partial q_{\varphi } }}{\partial \theta } + 4B_{16} \frac{1}{R}\frac{{\partial q_{w} }}{\partial \varphi }\frac{{\partial q_{w} }}{\partial \theta }\frac{{\partial q_{\varphi } }}{\partial \varphi } \hfill \\ \quad + 2B_{16} \frac{1}{R}\left( {\frac{{\partial q_{w} }}{\partial \varphi }} \right)^{2} \frac{{\partial q_{\varphi } }}{\partial \theta } + 2B_{11} \frac{1}{{R^{2} }}\left( {\frac{{\partial q_{w} }}{\partial \theta }} \right)^{2} \frac{{\partial q_{\varphi } }}{\partial \varphi } + 4B_{26} \frac{1}{{R^{2} }}\frac{{\partial q_{w} }}{\partial \varphi }\frac{{\partial q_{w} }}{\partial \theta }\frac{{\partial q_{\varphi } }}{\partial \theta } \hfill \\ \quad + B_{26} \frac{1}{{R^{3} }}\left( {\frac{{\partial q_{w} }}{\partial \theta }} \right)^{2} \frac{{\partial q_{\varphi } }}{\partial \theta } \hfill \\ \end{gathered} \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A22)

$$ H_{39} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ \begin{array}{l} 2B_{12} \frac{1}{R}\left( {\frac{{\partial q_{w} }}{\partial \varphi }} \right)^{2} \frac{{\partial q_{\theta } }}{\partial \theta } + 4B_{66} \frac{1}{{R^{2} }}\frac{{\partial q_{w} }}{\partial \varphi }\frac{{\partial q_{w} }}{\partial \theta }\frac{{\partial q_{\theta } }}{\partial \theta } + B_{16} \left( {\frac{{\partial q_{w} }}{\partial \varphi }} \right)^{2} \frac{{\partial q_{\theta } }}{\partial \varphi } \hfill \\ \quad + 4B_{26} \frac{1}{{R^{2} }}\frac{{\partial q_{w} }}{\partial \varphi }\frac{{\partial q_{w} }}{\partial \theta }\frac{{\partial q_{\theta } }}{\partial \theta } + 2B_{22} \frac{1}{{R^{3} }}\left( {\frac{{\partial q_{w} }}{\partial \theta }} \right)^{2} \frac{{\partial q_{\theta } }}{\partial \theta } + B_{26} \frac{1}{{R^{2} }}\left( {\frac{{\partial q_{w} }}{\partial \varphi }} \right)^{2} \frac{{\partial q_{\theta } }}{\partial \varphi } \hfill \\ \end{array} \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A23)

$$ H_{{{\text{non3}}}} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ \begin{array}{l} A_{11} \left( {\frac{{\partial q_{w} }}{\partial \varphi }} \right)^{4} + 2A_{12} \frac{1}{{R^{2} }}\left( {\frac{{\partial q_{w} }}{\partial \varphi }} \right)^{2} \left( {\frac{{\partial q_{w} }}{\partial \theta }} \right)^{2} + 2A_{16} \frac{1}{R}\left( {\frac{{\partial q_{w} }}{\partial \varphi }} \right)^{3} \frac{{\partial q_{w} }}{\partial \theta } \hfill \\ \quad + A_{22} \frac{1}{{R^{4} }}\left( {\frac{{\partial q_{w} }}{\partial \varphi }} \right)^{4} + 2A_{26} \frac{1}{{R^{3} }}\frac{{\partial q_{w} }}{\partial \varphi }\left( {\frac{{\partial q_{w} }}{\partial \theta }} \right)^{3} + 4A_{66} \frac{1}{{R^{2} }}\left( {\frac{{\partial q_{w} }}{\partial \varphi }} \right)^{2} \left( {\frac{{\partial q_{w} }}{\partial \theta }} \right)^{2} \hfill \\ \end{array} \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A24)

$$ H_{41} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ {B_{11} \frac{{\partial q_{\varphi } }}{\partial \varphi }\frac{{\partial q_{u} }}{\partial \theta } + B_{16} \frac{1}{R}\frac{{\partial q_{\varphi } }}{\partial \theta }\frac{{\partial q_{u} }}{\partial \varphi } + B_{16} \frac{1}{R}\frac{{\partial q_{\varphi } }}{\partial \varphi }\frac{{\partial q_{u} }}{\partial \theta } + B_{66} \frac{1}{{R^{2} }}\frac{{\partial q_{\varphi } }}{\partial \theta }\frac{{\partial q_{u} }}{\partial \theta }} \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A25)

$$ H_{42} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ \begin{array}{l} B_{12} \frac{1}{R}\frac{{\partial q_{\varphi } }}{\partial \varphi }\frac{{\partial q_{v} }}{\partial \theta } + B_{16} \frac{{\partial q_{\varphi } }}{\partial \varphi }\frac{{\partial q_{v} }}{\partial \varphi } + B_{26} \frac{1}{{R^{2} }}\frac{{\partial q_{\varphi } }}{\partial \theta }\frac{{\partial q_{v} }}{\partial \theta } \hfill \\ \quad + B_{66} \frac{1}{R}\frac{{\partial q_{\varphi } }}{\partial \theta }\frac{{\partial q_{v} }}{\partial \varphi } - s_{{\text{r}}} A_{45} \frac{1}{R}q_{\varphi } q_{v} \hfill \\ \end{array} \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A26)

$$ H_{43} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ {B_{12} \frac{1}{R}q_{\varphi } q_{w} + B_{26} \frac{1}{{R^{2} }}\frac{{\partial q_{\varphi } }}{\partial \theta }q_{w} + s_{{\text{r}}} A_{45} \frac{1}{R}q_{\varphi } \frac{{\partial q_{w} }}{\partial \theta } + s_{{\text{r}}} A_{55} q_{\varphi } \frac{{\partial q_{w} }}{\partial \varphi }} \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A27)

$$ H_{44} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ {D_{11} \frac{{\partial q_{\varphi } }}{\partial \varphi }\frac{{\partial q_{\varphi } }}{\partial \varphi } + D_{16} \frac{1}{R}\left( {\frac{{\partial q_{\varphi } }}{\partial \varphi }\frac{{\partial q_{\varphi } }}{\partial \theta } + \frac{{\partial q_{\varphi } }}{\partial \theta }\frac{{\partial q_{\varphi } }}{\partial \varphi }} \right) + D_{66} \frac{1}{{R^{2} }}\frac{{\partial q_{\varphi } }}{\partial \theta }\frac{{\partial q_{\varphi } }}{\partial \theta } + s_{{\text{r}}} A_{55} q_{\varphi } q_{\varphi } } \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A28)

$$ H_{45} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ \begin{gathered} D_{12} \frac{1}{R}\frac{{\partial q_{\varphi } }}{\partial \varphi }\frac{{\partial q_{\theta } }}{\partial \theta } + D_{16} \frac{1}{R}\frac{{\partial q_{\varphi } }}{\partial \varphi }\frac{{\partial q_{\theta } }}{\partial \varphi } + D_{26} \frac{1}{{R^{2} }}\frac{{\partial q_{\varphi } }}{\partial \theta }\frac{{\partial q_{\theta } }}{\partial \theta } + D_{66} \frac{1}{R}\frac{{\partial q_{\varphi } }}{\partial \theta }\frac{{\partial q_{\theta } }}{\partial \varphi } \hfill \\ \quad + s_{{\text{r}}} A_{45} Q_{\varphi } Q_{\theta } \hfill \\ \end{gathered} \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A29)

$$ H_{46} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ \begin{gathered} B_{11} \frac{{\partial q_{\varphi } }}{\partial \varphi }\left( {\frac{{\partial q_{w} }}{\partial \varphi }} \right)^{2} + 2B_{66} \frac{1}{{R^{2} }}\frac{{\partial q_{\varphi } }}{\partial \theta }\frac{{\partial q_{w} }}{\partial \varphi }\frac{{\partial q_{w} }}{\partial \theta } + 2B_{16} \frac{1}{R}\frac{{\partial q_{\varphi } }}{\partial \varphi }\frac{{\partial q_{w} }}{\partial \varphi }\frac{{\partial q_{w} }}{\partial \theta } \hfill \\ \quad + B_{16} \frac{1}{R}\frac{{\partial q_{\varphi } }}{\partial \theta }\left( {\frac{{\partial q_{w} }}{\partial \varphi }} \right)^{2} + B_{11} \frac{1}{{R^{2} }}\frac{{\partial q_{\varphi } }}{\partial \varphi }\left( {\frac{{\partial q_{w} }}{\partial \theta }} \right)^{2} + 2B_{26} \frac{1}{{R^{2} }}\frac{{\partial q_{\varphi } }}{\partial \theta }\frac{{\partial q_{w} }}{\partial \varphi }\frac{{\partial q_{w} }}{\partial \theta } \hfill \\ \quad + B_{26} \frac{1}{{R^{3} }}\frac{{\partial q_{\varphi } }}{\partial \theta }\left( {\frac{{\partial q_{w} }}{\partial \theta }} \right)^{2} \hfill \\ \end{gathered} \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A30)

$$ H_{51} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ {B_{12} \frac{1}{R}\frac{{\partial q_{\theta } }}{\partial \theta }\frac{{\partial q_{u} }}{\partial \varphi } + B_{16} \frac{{\partial q_{\theta } }}{\partial \varphi }\frac{{\partial q_{u} }}{\partial \varphi } + B_{26} \frac{1}{{R^{2} }}\frac{{\partial q_{\theta } }}{\partial \theta }\frac{{\partial q_{u} }}{\partial \theta } + B_{66} \frac{1}{R}\frac{{\partial q_{\theta } }}{\partial \varphi }\frac{{\partial q_{u} }}{\partial \theta }} \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A31)

$$ H_{52} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ {B_{22} \frac{1}{{R^{2} }}\frac{{\partial q_{\theta } }}{\partial \theta }\frac{{\partial q_{v} }}{\partial \theta } + B_{26} \frac{1}{R}\left( {\frac{{\partial q_{\theta } }}{\partial \varphi }\frac{{\partial q_{v} }}{\partial \theta } + \frac{{\partial q_{\theta } }}{\partial \theta }\frac{{\partial q_{v} }}{\partial \varphi }} \right) + B_{66} \frac{{\partial q_{\theta } }}{\partial \varphi }\frac{{\partial q_{v} }}{\partial \varphi } - s_{{\text{r}}} A_{44} \frac{1}{R}q_{\theta } q_{v} } \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A32)

$$ H_{53} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ {B_{22} \frac{1}{{R^{2} }}\frac{{\partial q_{\theta } }}{\partial \theta }q_{w} + B_{26} \frac{1}{R}\frac{{\partial q_{\theta } }}{\partial \varphi }q_{w} + s_{{\text{r}}} A_{44} \frac{1}{R}q_{\theta } \frac{{\partial q_{w} }}{\partial \theta } + s_{{\text{r}}} A_{45} \frac{1}{R}q_{\theta } \frac{{\partial q_{w} }}{\partial \varphi }} \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A33)

$$ H_{54} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ \begin{gathered} D_{12} \frac{1}{R}\frac{{\partial q_{\theta } }}{\partial \theta }\frac{{\partial q_{\varphi } }}{\partial \varphi } + D_{16} \frac{1}{R}\frac{{\partial q_{\theta } }}{\partial \varphi }\frac{{\partial q_{\varphi } }}{\partial \varphi } + D_{26} \frac{1}{{R^{2} }}\frac{{\partial q_{\theta } }}{\partial \theta }\frac{{\partial q_{\varphi } }}{\partial \theta } + D_{66} \frac{1}{R}\frac{{\partial q_{\theta } }}{\partial \varphi }\frac{{\partial q_{\varphi } }}{\partial \theta } \hfill \\ \quad + s_{{\text{r}}} A_{45} Q_{\theta } Q_{\varphi } \hfill \\ \end{gathered} \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A34)

$$ H_{55} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ \begin{gathered} D_{22} \frac{1}{{R^{2} }}\frac{{\partial q_{\theta } }}{\partial \theta }\frac{{\partial q_{\theta } }}{\partial \theta } + D_{26} \frac{1}{R}\left( {\frac{{\partial q_{\theta } }}{\partial \varphi }\frac{{\partial q_{\theta } }}{\partial \theta } + \frac{{\partial q_{\theta } }}{\partial \theta }\frac{{\partial q_{\theta } }}{\partial \varphi }} \right) + D_{66} \frac{{\partial q_{\theta } }}{\partial \varphi }\frac{{\partial q_{\theta } }}{\partial \varphi } \hfill \\ \quad + s_{{\text{r}}} A_{44} Q_{\theta } Q_{\theta } \hfill \\ \end{gathered} \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A35)

$$ H_{56} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {\left\{ \begin{gathered} B_{12} \frac{1}{R}\frac{{\partial q_{\theta } }}{\partial \theta }\left( {\frac{{\partial q_{w} }}{\partial \varphi }} \right)^{2} + 2B_{66} \frac{1}{{R^{2} }}\frac{{\partial q_{\theta } }}{\partial \theta }\frac{{\partial q_{w} }}{\partial \varphi }\frac{{\partial q_{w} }}{\partial \theta } + B_{16} \frac{1}{2}\frac{{\partial q_{\theta } }}{\partial \varphi }\left( {\frac{{\partial q_{w} }}{\partial \varphi }} \right)^{2} \hfill \\ \quad + 2B_{26} \frac{1}{{R^{2} }}\frac{{\partial q_{\theta } }}{\partial \theta }\frac{{\partial q_{w} }}{\partial \varphi }\frac{{\partial q_{w} }}{\partial \theta } + B_{22} \frac{1}{{R^{3} }}\frac{{\partial q_{\theta } }}{\partial \theta }\left( {\frac{{\partial q_{w} }}{\partial \theta }} \right)^{2} + B_{26} \frac{1}{{2R^{2} }}\frac{{\partial q_{\theta } }}{\partial \varphi }\left( {\frac{{\partial q_{w} }}{\partial \varphi }} \right)^{2} \hfill \\ \end{gathered} \right\}} } R{\text{d}}\varphi {\text{d}}\theta $$

(A36)

$$ S_{u} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {I_{0} q_{u} } } q_{u} R{\text{d}}\varphi {\text{d}}\theta ,\quad S_{v} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {I_{0} q_{v} } } q_{v} R{\text{d}}\varphi {\text{d}}\theta ,\quad S_{w} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {I_{0} q_{w} } } q_{w} R{\text{d}}\varphi {\text{d}}\theta $$

(A37)

$$ S_{\varphi } = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {I_{2} q_{\varphi } } } q_{\varphi } R{\text{d}}\varphi {\text{d}}\theta ,\quad S_{\theta } = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {I_{2} q_{\theta } } } q_{\theta } R{\text{d}}\varphi {\text{d}}\theta $$

(A38)

$$ S_{u\varphi } = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {2I_{1} q_{u} } } q_{\varphi } R{\text{d}}\varphi {\text{d}}\theta ,\quad S_{u\theta } = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {2I_{1} q_{u} } } q_{\theta } R{\text{d}}\varphi {\text{d}}\theta $$

(A39)

$$ S_{\varphi u} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {2I_{1} q_{\varphi } q_{u} } } R{\text{d}}\varphi {\text{d}}\theta ,\quad S_{\theta u} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {2I_{1} q_{\theta } q_{u} } } R{\text{d}}\varphi {\text{d}}\theta $$

(A40)

$$ S_{c} = \int_{0}^{{2{\uppi }}} {\int_{0}^{L} {I_{0} cq_{w} } } q_{w} R{\text{d}}\varphi {\text{d}}\theta $$

(A41)

Appendix B

The coefficient expressions $d_{i} \left( {i = 0, \, 1, \ldots ,4} \right)$ in Eq. (34) are formulated as:

$$ d_{0} = 2\xi \omega_{mn} $$

(B1)

$$ d_{1} = \frac{{\left( {H_{31} L_{1} + H_{32} L_{2} + H_{33} + H_{34} L_{3} + H_{35} L_{4} } \right)}}{{S_{w} }} $$

(B2)

$$ d_{2} = \frac{{\left( {H_{36} L_{1} + H_{37} L_{2} + H_{{{\text{non2}}}} + H_{38} L_{3} + H_{39} L_{4} } \right)}}{{S_{w} }} = 0 $$

(B3)

$$ d_{3} = \frac{{H_{{{\text{non3}}}} }}{{S_{w} }} $$

(B4)

$$ d_{4} = \frac{{4F_{{0}} \left[ {\left( { - 1} \right)^{m} - 1} \right]\left[ {\left( { - 1} \right)^{n} - 1} \right]}}{{mn{\uppi }^{2} I_{0} }} $$

(B5)

Appendix C

Based on super-harmonic resonance, Eq. (36) can be re-written as:

$$ \ddot{W}_{mn} \left( \tau \right) + \varepsilon d_{0} \dot{W}_{mn} \left( \tau \right) + d_{1} W_{mn} \left( \tau \right) + \varepsilon d_{3} W_{mn}^{3} \left( \tau \right) = d_{4} \cos \left( {\omega_{ * } \tau } \right) $$

(C1)

By substituting Eqs. (54), (38), (39), (40) and (41) into Eq. (C1) and setting the coefficient of each order perturbation parameter to be zero.

$$ \varepsilon^{0} {:}\,D_{0} W_{0} + \omega_{mn}^{2} W_{0} = d_{4} \cos \left( {\frac{1}{3}\omega_{mn} T_{0} + \frac{1}{3}\sigma T_{1} } \right) $$

(C2)

$$ \varepsilon^{1} {:}\,D_{0}^{2} W_{1} + \omega_{mn}^{2} W_{1} = - 2D_{0} D_{1} W_{0} - d_{0} W_{0} - d_{3} W_{0}^{3} $$

(C3)

In the first step, the general solution of Eq. (C2) can be obtained in the form of:

$$ W_{0} = A\left( {T_{1} , \, T_{2} } \right)\exp \left( {i\omega_{mn} T_{0} } \right) + \Lambda \exp \left[ { - i\left( {\omega_{mn} T_{0} + \sigma T_{1} } \right)} \right] + C_{{\text{J}}} $$

(C4)

where

$$ \Lambda = \frac{{d_{4} }}{{2\left( {\omega_{mn}^{2} - \omega_{ * }^{2} } \right)}},\quad \omega_{ * } = \frac{1}{3}\left( {\omega_{mn} + \varepsilon \sigma } \right) $$

(C5)

Then, by taking Eq. (C4) into Eq. (C3), one can obtain:

$$ \begin{aligned} D_{0}^{2} W_{1} + \omega_{mn}^{2} W_{1} & = \left[ { - i2\omega_{mn} \left( {D_{1} A} \right) - i\omega_{mn} d_{0} A - 6d_{3} A^{2} \Lambda - 3d_{3} A^{2} \overline{A} - d_{3} \Lambda^{3} \exp \left( {i\sigma T_{1} } \right)} \right]\exp \left( {i\omega_{mn} T_{0} } \right) \\ & \quad - \Lambda \left[ {id_{0} (\omega_{mn} T_{0} + \sigma T_{1} ) + 3d_{3} A\overline{A}} \right]\exp \left[ {i\frac{1}{3}(\omega_{mn} T_{0} + \sigma T_{1} )} \right] + \cdots + C_{J} \\ \end{aligned} $$

(C6)

Finally, to eliminate secular terms in Eq. (C6), Eq. (55) can be obtained.

Appendix D

Based on sub-harmonic resonance, Eq. (36) can be also re-written as:

$$ \ddot{W}_{mn} \left( \tau \right) + \varepsilon a_{0} \dot{W}_{mn} \left( \tau \right) + a_{1} W_{mn} \left( \tau \right) + \varepsilon a_{3} W_{mn}^{3} \left( \tau \right) = a_{4} \cos \left( {\omega_{ * } \tau } \right) $$

(D1)

By substituting Eqs. (57), (38), (39), (40) and (40) into Eq. (D1) and setting the coefficient of each order perturbation parameter to be zero.

$$ \varepsilon^{0} : \, D_{0} W_{0} + \omega_{0}^{2} W_{0} = d_{4} \cos \left( {3\omega_{mn} T_{0} + \sigma T_{1} } \right) $$

(D2)

$$ \varepsilon^{1} : \, D_{0}^{2} W_{1} + \omega_{mn}^{2} W_{1} = - 2D_{0} D_{1} W_{0} - d_{0} W_{0} - d_{3} W_{0}^{3} $$

(D3)

In the first step, the general solution of Eq. (D2) can be obtained in the form of:

$$ W_{0} = A\left( {T_{1} , \, T_{2} } \right)\exp \left( {{\text{i}}\omega_{mn} T_{0} } \right) + \Lambda \exp \left[ {{\text{ - i}}\left( {\omega_{mn} T_{0} + \sigma T_{1} } \right)} \right] + {\text{C}}_{{\text{J}}} $$

(D4)

where

$$ \Lambda = \frac{{d_{4} }}{{2\left( {\omega_{mn}^{2} - \omega_{ * }^{2} } \right)}},\quad \omega_{ * } = 3\omega_{mn} + \varepsilon \sigma $$

(D5)

Then, by taking Eq. (D4) into Eq. (D3), one can obtain:

$$ \begin{aligned} D_{0}^{2} W_{1} + \omega_{mn}^{2} W_{1} & = \left[ { - i2\omega_{mn} \left( {D_{1} A} \right) - i\omega_{mn} d_{0} A - 6d_{3} \Lambda^{2} A - 3d_{3} A^{2} \overline{A} - 3d_{3} \Lambda \overline{A}^{2} \exp \left( {i\sigma T_{1} } \right)} \right]\exp \left( {i\omega_{mn} T_{0} } \right) \\ & \quad + \cdots + C_{J} \\ \end{aligned} $$

(D6)

Finally, to eliminate secular terms in Eq. (D6), Eq. (58) can be obtained.