1 Introduction

Understanding the tyre-ground contact is probably the most essential prerequisite of developing accurate models for road vehicles since the contact patches, roughly the size of human palms, provide the interface for the energy-transmission between the ground and the vehicle. The importance of tyre dynamics motivated a multitude of studies on tyre modelling.

Depending on the application, one may follow either a more theoretical or a more empirical approach when choosing a tyre model. In his book [1], providing an extensive summary on the subject, Pacejka considers four categories of tyre models. At the experimental end of the scale, there are the models relying purely on experimental data or using similarity methods. The most famous among these models is the widely used magic formula [2] tyre model. While empirical models can be tuned to be highly accurate, they provide little insight into tyre behaviour as they disregard the actual phenomenon of the dynamic force generation in the tyre-ground contact. At the other end of the scale, one finds the sophisticated physics-based tyre models, such as the FTire [3] model or finite-element-based approaches [4, 5]. Provided that the model parameters are accurately identified, these models can also reach a high level of quantitative accuracy. However, due to their complex formulation and/or large number of model parameters, these models are also prone to losing insight to the underlying force-generation phenomenon.

The simpler physical tyre models: the brush and the stretched-string models [1] and the single contact-point creep-force type models [6] are around the middle of the empirical-theoretical spectrum. Their main advantage is that they are built from relatively simple mechanical elements, require only a few parameters and the resulting force in the tyre-ground contact is derived from first principles. Therefore, even though they provide less quantitative accuracy, they are ideal for the qualitative analysis of the tyre behaviour. The insight gained from these models then can be taken into account in the empirical or the more sophisticated mechanical models as well.

An important element of the tyre models is the sliding model taking into account the saturation of the tyre force for larger values of lateral or longitudinal tyre-slip which is essential for characterising tyre behaviour in the nonlinear domain. Even though physics-based tyre models tend to result in piecewise-smooth systems, the recent advances in investigating such dynamical systems [7] enable a rigorous bifurcation analysis providing qualitative insight to these model’s behaviour. In [8], a towed wheel is studied using a single contact-point model leading to a system with codimension-2 discontinuity allowing for the study of the interaction between lateral and longitudinal sliding.

By considering a finite contact domain rather than a single contact point, the brush and stretched string models are also capable of capturing partial sticking-sliding conditions in the tyre ground contact. The deformation of the sticking part(s) of the contact is described by a nonlinear partial differential equation (PDE) for which a travelling wave solution involving distributed time delay can be provided [9, 10]. This formulation might be seen unnecessarily complex in some applications, therefore it is common to use a quasi-steady state approximation of the deformation leading to tyre force and self-aligning moment characteristics. This approach is usually adequate in applications considering vehicles running at a higher speed. However, it fails to capture possible instabilities arising at lower speeds as demonstrated for wheel shimmy[9], the single-track model of a car [10] and the car-trailer combination [11], respectively. Moreover, there is also a marked difference in the nonlinear behaviour of these models. By the bifurcation analysis of a towed wheel using the brush tyre model with time delay and lateral sliding, a bistable parameter domain with a coexisting stable rectilinear motion and large amplitude periodic solution was identified that is missed by the simplified brush/stretched-string type models using quasi-steady-state approximations for the tyre deformation [12].

These results motivated a similar study on the nonlinear dynamics of wheel shimmy using the stretched string model with sliding. Studies investigating the linear stability of a towed wheel’s rectilinear motion revealed that the structure of the stable and unstable parameter domains predicted by the brush and stretched-string models are qualitatively identical. Nevertheless, by considering tyre deformation outside the contact region, the stretched-string models provide more accurate results when compared to measurements [9].

The non-smooth delayed tyre model, as an extension of the stretched-string model and capable of capturing lateral sliding, has been investigated in [13]. It is demonstrated that, similarly to the brush tyre model, the non-smooth delayed stretched-string model captures bistable parameter regions where for the same set of parameters stable straightline motion and a stable limit cycle coexist. However, this study is incomplete in the sense that while finite dimensional piecewise-smooth systems and smooth delay differential equations can be both studied by software packages for bifurcation analysis (e.g. COCO [14], DDEBiftool [15]), the complex nature of the sliding model made the use the collocation-based algorithms for tracing the periodic solutions in the system infeasible. Instead, relying on numerical simulations, only the stable solutions were found.

Although an unstable periodic orbit is ‘invisible’ in experiments or open-loop simulations, it carries valuable information about the resilience of the stable solutions to perturbations as it is attached to the separatrix between the domains of attractions of the stable rectilinear motion and the stable periodic orbit. This means that the amplitude of the unstable limit cycle can serve as an estimation for the tolerable perturbation level that will not lead to a solution that is divergent from a locally stable orbit.

The issue of finding unstable steady-state solutions can be resolved by the technique of control-based continuation (CBC) [16,17,18]. This technique has been originally developed to trace periodic orbits in experiments, but, being compatible with numerical simulations solving initial value problems, it is also capable of identifying periodic solutions in numerical models that are too complex to be handled with the more standard techniques of numerical bifurcation analysis. Although the original version could be used for systems with periodic forcing only, the method can be used to study autonomous systems by considering phase-locked solutions as control target as shown in [19] where the self-excited vibrations of an aerofoil were studied experimentally.

The aim of this study is to provide further insight into the relationship between the nonlinear dynamics of the towed wheel and the dynamically changing sticking-sliding regions in the tyre-road contact in the context of self-excited oscillations in the yaw angle (wheel shimmy). This is achieved by using the physics-based, non-smooth delayed stretched string tyre model, following up the earlier work on this model [13]. The main novelty of the present study is that, using the CBC technique, thus treating the numerical model as a black-box-type system, it circumvents the issue of the complexity of the model formulation that make the use of collocation based techniques infeasible. Thus, the unstable limit cycles of the system can be surveyed allowing for a more thorough study of the nonlinear behaviour compared to previous studies where only stable steady-state oscillations are captured. The successful use of CBC in this problem also highlights the versatility of the method even though CBC was primarily developed with physical experiments in mind.

The assessment of the theoretical results is also complemented by showing experimental results of a towed-wheel running on a treadmill, exhibiting qualitatively similar nonlinear behaviour [12], where the amplitudes of the unstable limit cycles were estimated by identifying the critical initial angular velocity corresponding to the separatrix between the domains of attractions of the stable rectilinear motion and the large amplitude limit cycle of the system.

The rest of the paper is organised as follows. In Sect. 2, the mechanical model of the towed wheel with the non-smooth delayed stretched-string model is introduced. Then, in Sect. 3, the control-based continuation (CBC) technique used to trace the unstable periodic orbits of the system is described. In Sect. 4, the results of the analysis are discussed, while the conclusions are summarised in Sect. 5.

2 Mechanical model

2.1 Equation of motion of the towed wheel

Fig. 1
figure 1

Top panel: The model of the towed wheel, bottom panel: the stretched-string tyre model

Full size image

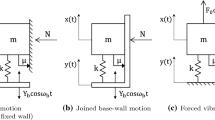
The mechanical model of the towed wheel is shown in Fig. 1. The model consists of a rigid caster, which can rotate about the vertical axis including the centre A of the king pin. A viscous torsional damping of \(b_\mathrm{t}\) is considered in the king pin while we assume that the bearing has negligible torsional stiffness. Two coordinate-systems are considered to describe the state of the model: the ‘global’ coordinate-system (X, Y, Z) fixed to the ground and the ‘local’ coordinate-system (x, y, z) moving together with the tyre-ground contact patch. The orientation of the caster is described by the yaw angle \(\psi \) (deflection angle with respect to the X-axis). The wheel which consists of a rigid wheel-rim and an elastic thread and carcass, can freely rotate in the caster.

The equation of motion of the open-loop (uncontrolled) system can be expressed as

$$\begin{aligned} J_\mathrm{A} \dot{\Omega }(t) + b_\mathrm{t} \Omega (t) = - lF_\mathrm{tyre} + M_\mathrm{tyre}, \end{aligned}$$
(1)

where \(J_\mathrm{A}\) denotes the mass moment of inertia of the system with respect to the vertical axis including the king pin centre A, and with the yaw rate \(\Omega \) defined by

$$\begin{aligned} \dot{\psi }(t) = \Omega (t). \end{aligned}$$
(2)

2.2 The delayed tyre model

The effect of tyre deformation is considered by the force \(F_\mathrm{tyre}\) and the self-aligning torque \(M_\mathrm{tyre}\), which are the result of the distributed force-system acting on the wheel in the contact patch. The delayed tyre model [13] is capable of capturing both the dynamic effects in the tyre-ground contact and the varying sticking and sliding regions as the wheel is oscillating. The contact model, shown in the bottom panel of Fig. 1, is based on the stretched-string tyre model, and the corresponding standard modelling assumptions [1, 9]. This is an in-plane model of the contact patch and its neighbourhood, referred-to as ‘relaxation zones’. The model takes into account the compliance of the tyre tread and the carcass as a stretched string with elastic support. The string is considered to be infinite; thus, oscillations that might travel around the wheel are not taken into account. As it is usually negligible compared to the lateral dynamics, we do not calculate with the longitudinal deformation of the tyre either, i.e. the elastic elements are assumed to have lateral compliance only.

Based on the assumptions above, the lateral tyre force and the self-aligning moment can be calculated by integrating the lateral deformation q(x, t) of the string, yielding to the integral formulae

$$\begin{aligned} F_\mathrm{tyre}= & {} \int _ {-\infty } ^{\infty } k q (x,t) + \int _ {-\infty } ^{\infty } b \frac{\mathrm{d}}{\mathrm{d} t} q (x,t) \; , \end{aligned}$$
(3)
$$\begin{aligned} M_\mathrm{tyre}= & {} \int _ {-\infty } ^{\infty } k x q (x,t)+ \int _ {-\infty } ^{\infty } b x \frac{\mathrm{d}}{\mathrm{d} t} q (x,t) \; . \end{aligned}$$
(4)

where k and b are the distributed lateral stiffness and damping of the tyre [9].

In the tyre-ground contact region (\(x \in [-a, a]\)), if a tyre particle sticks to the ground it is assumed to have zero relative velocity (\(\mathbf {v_\mathrm{P}} = \mathbf {0} \)). From this kinematic constraint, time delayed formulae can be derived for the lateral deformation \(q(x(\tau ),t)\) of the tyre particles in contact.

$$\begin{aligned} \begin{aligned} q(x,t) =&V \tau \sin \psi (t) - (a-l) \sin (\psi (t)-\psi (t-\tau )) \\&+ q (a,t-\tau )\cos (\psi (t)-\psi (t-\tau )), \\ \end{aligned} \end{aligned}$$
(5)

whereas the function \(x(\tau )\) describes the material flow in the contact-patch fixed frame of reference

$$\begin{aligned} \begin{aligned} x(\tau ) =&-V \tau \cos \psi (t) + (a-l) \cos (\psi (t)-\psi (t-\tau )) \\&+ q (a,t-\tau )\sin (\psi (t)-\psi (t-\tau )). \\ \end{aligned} \end{aligned}$$
(6)

In case of the straight-line motion, a position of an arbitrary particle can be given by the formula \(x = a - V \tau \), where the time delay \(\tau \) refers to the time elapsed since the particle entered the sticking region of the contact. Note that in case of the rectilinear motion, the whole contact region is assumed to be sticking.

In Eqs. (5) and (6), the deformation q(a, t) of point L, the leading point of the contact region where the tyre particles come into contact with the ground, also appears as a state variable. By assuming that no ‘kink’ can arise at the leading point L, i.e. the first derivative of the lateral deformation function q(x, t) is continuous at \(x=a\), one can derive an ODE describing the variation of the leading point deformation in time

$$\begin{aligned} \begin{aligned} \dot{q}(a,t) =&V \sin \psi (t) + (a-x)\dot{\psi }(t) \\&+\frac{q(a,t)}{\sigma }\left( q(a,t) \dot{\psi }(t)-V \cos \psi (t) \right) , \\ \end{aligned} \end{aligned}$$
(7)

where \(\sigma \) is the so-called relaxation length while the derivative of the deformation with respect to coordinate x at the leading point is given by

$$\begin{aligned} {q} \prime (a,t) = - \frac{q(a,t)}{\sigma }. \end{aligned}$$
(8)

Outside the contact region, exponentially decaying lateral deformation is assumed which can be given by the formulae

$$\begin{aligned} q(x,t)= & {} q(a,t)e^{\frac{a-x}{\sigma }} \quad \mathrm{for} \quad x \in [a,\infty ), \end{aligned}$$
(9)
$$\begin{aligned} q(x,t)= & {} q(-a,t)e^{\frac{a+x}{\sigma }} \quad \mathrm{for} \quad x \in (-\infty , -a). \end{aligned}$$
(10)

2.3 Sliding model

The lateral sliding of the tyre is one of the most important factors affecting the nonlinear dynamics of the system. While one may neglect the effect of sliding during linear stability analysis assuming small vibrations, it is essential for the bifurcation analysis to capture the saturation in the tyre force as sliding becomes more prominent in the contact region at larger vibration amplitudes. The assumptions made to construct the sliding model build on the studies reported in [13, 20].

The deformation of the stretched string is governed by a PDE of second order in space and first order in time. Unfortunately, this equation is very stiff, as such, obtaining the deformation in the sliding regions by integrating the full PDE is very time-consuming [20]. Therefore, to simplify the algorithm, the material damping of the tyre is neglected (\(b = 0\)) when calculating the deformation in the sliding parts. This reduces the governing equation of the deformation to an ordinary differential equation (ODE) for which analytical solutions are provided. Thus, the material damping of the tyre is considered in Eqs. (3) and (4) by using the time derivative of the tyre deformation derived from the travelling wave solution

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d} t} q (x,t) = V \sin \psi (t) + (l-x) \dot{\psi }(t). \end{aligned}$$
(11)

Clearly, this is a simplification prioritising practical considerations in the simulation rather than the rigorous handling of the sliding model. Nevertheless, the study in [20] investigating the time-delayed stretched string model with material damping considered while establishing the deformation in the sliding regions suggests that this simplification does not lead to a qualitative difference in the nonlinear behaviour.

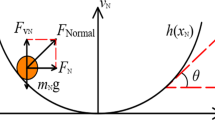
To model sliding, it is common practice to assume a parabolic vertical force distribution in the contact region [1]. This model is a simple way of taking into account the drop of the distributed normal force near the contact boundaries while assuming the maximum in the middle. It is worth mentioning that studies aiming to establish the pressure distribution with experimental techniques [21] or numerical models [22, 23] indicate that the parabolic distribution may not be a very accurate model in all scenarios. Specifically, for larger contact lengths a flatter pressure distribution was found in the middle part of the contact region [21]. Nevertheless, we stick to the parabolic model in this study to keep the formulae as simple as possible. By using Coulomb’s dry friction model, this can be converted into parabolic boundaries for the lateral distributed force system generated by the deforming tyre

$$\begin{aligned} p_{r+} (x)= & {} \frac{3F_z \mu _0}{4a^3}(a^2-x^2), \end{aligned}$$
(12)
$$\begin{aligned} p_{r-} (x)= & {} -\frac{3F_z \mu _0}{4a^3}(a^2-x^2), \end{aligned}$$
(13)

where \(F_z\) is the vertical tyre load while \(\mu _0\) is the friction coefficient for adhesion (see the top panel of Fig. 2). The lateral force distribution corresponding to a given state of deformation is given by the formula

$$\begin{aligned} p(x,t) = k \sigma ^2 q''(x,t) - k (x,t), \end{aligned}$$
(14)

with the primes referring to derivatives with respect to x. Based on the assumptions above, one can infer the necessary condition of rolling that the lateral force distribution should be within the limiting parabolae

$$\begin{aligned} p_{r-}(x)<=p(x,t)<=p_{r+}(x). \end{aligned}$$
(15)

The parts of the contact region where condition (15) is not met are assumed to be sliding. In this case, the kinematic constraint of rolling is dropped. Instead, we assume the lateral force distribution to be equal to the upper or lower sliding limits \(p(x,t) = p_{s+}\) or \(p(x,t) = p_{s-}\), which are considered as similar parabolae to Eqs. (16) and (17).

$$\begin{aligned} p_{s+} (x)= & {} \frac{3F_z \mu }{4a^3}(a^2-x^2), \end{aligned}$$
(16)
$$\begin{aligned} p_{s-} (x)= & {} -\frac{3F_z \mu }{4a^3}(a^2-x^2), \end{aligned}$$
(17)

where \(\mu \) denotes the sliding friction coefficient. With these considerations, the deformation in the sliding regions can be obtained by solving the ODE given by the lateral force formula (14)

$$\begin{aligned} q''_s(x,t)-\frac{1}{\sigma } q_s(x,t) = p_{s \pm }(x) \end{aligned}$$
(18)

with \(p_{s \pm }\) referring to the relevant sliding limit for the lateral distributed force system (either \(p_{s+}\) or \(p_{s-}\)). To solve the ODE above, two boundary- or continuity conditions should be considered for each sliding region. These are overviewed in the next subsection.

2.3.1 Sliding regions and boundary conditions

Fig. 2
figure 2

Top panel: Lateral force-distribution in the tyre-ground contact region and the parabolic limits for sticking (continuous curve) and sliding (dashed curve). Bottom panel: The assumed regions in the vicinity of the contact region. The sticking region is marked by green, the sliding regions by red shading, respectively

Full size image

While the stretched-string model could exhibit an arbitrary combination of sticking/sliding regions, previous studies [20] indicate that to capture the self-excited vibrations of the towed wheel, it is sufficient to consider one sliding region near the leading edge (\(x=a\)) and another one at the rear edge (\(x=-a\)) of the contact region. The appearance of these two sliding regions can be expected for any nonzero deformation since the parabolic sliding limits do not permit any lateral force at the two ends of the contact domain. With these considerations, a simplified sliding model was proposed in [13] which is capable of reducing the computational burden significantly compared to the more general approach presented in [20]. In this study, the sliding model given in [13] is adopted. Nevertheless, the model description is repeated for clarity.

To see the full picture, it is worth considering the two tyre relaxation regions outside the \(x \in [-a,a]\) contact domain when listing the boundary and continuity conditions. Thus, overall, five different regions are assumed in the contact as shown in Fig. 2. In the order which a tyre particle would ‘travel’ through these regions these are

  • Relaxation zone next to the leading edge, \(x \in [a, \infty )\) with the deformation function \(q_{relL}(x,t)\),

  • Sliding region next to the leading edge, \(x \in [x_L, a]\) where the deformation is described by the function \(q_{sL}(x,t)\),

  • Sticking region, \(x \in [x_R, x_L]\) with the deformation function \(q_{r}(x,t)\),

  • Sliding region next to the rear edge, \(x \in [-a, x_R]\) with the deformation function \(q_{sR}(x,t)\),

  • Relaxation zone next to the rear edge, \(x \in (-\infty , -a)\) with the deformation function \(q_{relR}(x,t)\).

Note that, as shown in [13], the Sliding region next to the rear edge may be split into two sub-regions with different sliding directions as indicated in Fig. 2. The occurrence of the two different sliding regions can be explained with the help of the boundary conditions that have to be satisfied according to the assumptions made by means of the delayed tyre model.

The first four conditions express the continuity of the deformation between the neighbouring regions

$$\begin{aligned} q_{relL}(a,t)= & {} q_{sL}(a,t), \end{aligned}$$
(19)
$$\begin{aligned} q_{sL}(x_L,t)= & {} q_{r}(x_L,t), \end{aligned}$$
(20)
$$\begin{aligned} q_{r}(x_R,t)= & {} q_{sR}(x_R,t), \end{aligned}$$
(21)
$$\begin{aligned} q_{sR}(-a,t)= & {} q_{relR}(-a,t). \end{aligned}$$
(22)

Moreover, as mentioned above, we consider decaying deformation outside the contact region, which we can formulate as

$$\begin{aligned} \lim _{x \rightarrow \infty } q_{relL}(x,t) = 0, \end{aligned}$$
(23)

and

$$\begin{aligned} \lim _{x \rightarrow -\infty } q_{relR}(x,t) = 0, \end{aligned}$$
(24)

Studying formula (14) describing the lateral distributed force system, it can be also concluded, that at the boundaries of the five different regions, the derivative \(q'(x,t)\) has to be continuous too since a discontinuity would result in a Dirac-delta-like peak in the second derivative term which would be incompatible with the parabolic limits for the lateral force [13]. These ‘no kink’ conditions are given by

$$\begin{aligned} q'_{relL}(a,t)= & {} q'_{sL}(a,t), \end{aligned}$$
(25)
$$\begin{aligned} q'_{sL}(x_L,t)= & {} q'_{r}(x_L,t), \end{aligned}$$
(26)
$$\begin{aligned} q'_{r}(x_R,t)= & {} q'_{sR}(x_R,t), \end{aligned}$$
(27)
$$\begin{aligned} q'_{sR}(-a,t)= & {} q'_{relR}(-a,t). \end{aligned}$$
(28)

In total, we have 10 boundary and continuity conditions for 4 second-order ODEs which means that the problem is over-constrained. To resolve this issue, the lateral deformation in the two sliding and two relaxation regions are obtained using conditions (19),(20),(21),(22), (23),(24),(25), and (28) while the limits between the rolling region and the two sliding regions (\(x_L\) and \(x_R\)) are handled as unknown parameters [13].

In each timestep in the numerical simulation of the model, the deformation is calculated assuming pure rolling in the contact first, then the limits between the sliding regions where the conditions (26) and (27) mandating the continuity of the first derivative are satisfied too, are found by iteration. It is assumed in general that \(s_R < s_L\). If this is not the case, i.e. the iteration provides limits where \(s_L < s_R\), the sliding regions at the leading and rear edges are merged and the full contact region is considered sliding.

There is another special case, however, related to the sliding region at the rear edge, which is not captured by the model of 5 different regions along the stretched-string. This is due to the fact that sliding at the rear end of the contact is induced by two factors: the travelling wave solution in the rolling region resulting in nonzero lateral force in the end, and the same solution violating the ‘no-kink’ condition at the rear end. If the two effects induce sliding in opposite directions, the rear sliding region is split into two parts with sliding in opposite directions and the deformation is calculated with six different regions.

Splitting the rear sliding region into two subregions also modifies the iteration finding the boundaries of the sliding regions, as, for the rear sliding region, we look for two boundaries: the position \(x_\mathrm{R2}\) where sliding changes direction and the boundary of the rear sliding domain \(x_\mathrm{R}\). The candidate solutions that satisfy the ‘no-kink’ condition at \(x_\mathrm{R}\) lie on a curve in the \((x_\mathrm{R}, x_\mathrm{R2})\) plane. The simulation algorithm selects the point closest to the boundaries in the previous timestep as the new location of the boundaries.

3 Control-based continuation

Fig. 3
figure 3

Block diagram of the control-based continuation method applied to the numerical model of the caster-wheel system. The flowchart of the root-finding algorithm is shown in Fig. 4

Full size image

A standard open-loop simulation of the mechanical model described in Sect. 2 is only capable of tracing the stable steady-state solutions of the system, while the unstable ones remain hidden. In the special case of a 2-dimensional model, one could overcome this issue by reversing the time. This is due to the fact that the variational system corresponding to an unstable periodic orbit in a two-dimensional autonomous system has one unstable and a neutral direction. These can be characterised by the Floquet multipliers \(\nu _1 = 1\) and \(\nu _2 \in \mathcal {R}, \quad |\nu _2 |> 1\) corresponding to the neutral and unstable directions, respectively [24]. This feature is preserved if such a periodic orbit exists in a higher-dimensional system while all other directions are stable \(|\nu _k |< 1, \quad k = 3,4,...\). Reversing the time in the system would reverse the stability of each direction, i.e. if there were any stable directions in the original system, these would become unstable in the reverse-time system. Thus, capturing an unstable limit cycle by simulating the system with reverse time is only possible if there are no extra (stable) directions in the state space. As a result, this approach would not work in case of our infinite dimensional time-delayed model, as even though this would turn the unstable directions in the variational system of an unstable solution stable, all the infinitely many, originally stable, directions would become unstable.

Another approach would be to use a shooting algorithm [24] to find the initial-conditions (including the relevant time-history) that are ‘spot on’ the unstable periodic orbit in an iterative way. This method however can be very inefficient in case of time-delayed systems as the initial function is difficult to find and the domain of convergence of the root-finding algorithm may be very narrow.

In contrast, control-based continuation (CBC) is capable of tracing both stable and unstable periodic solutions in a robust, and more efficient way. The idea of the method is to apply a stabilising and non-invasive control to the system. That is, the control-law has to be selected such that the system converges to a steady-state periodic solution while a root-finding algorithm has to ensure that the steady state control error, i.e. the difference of the target and the realised solutions, thus the steady-state control force imposed on the system is zero. If these conditions are satisfied, the registered steady-state behaviour of the controlled system is identical to the original, uncontrolled system whereas the transient behaviour, as intended, to ensure a stable behaviour even around the originally unstable solutions, is changed. In practice, the condition of non-invasiveness is only ensured to the accuracy determined by the number of harmonic components considered in the solution and the tolerance of the iteration. Nevertheless, we accept these solutions as the limit cycles in the open-loop system.

It is worth pointing out that CBC is a local method in the sense that its aim is to capture a single limit cycle at a time. This is due to the fact that even in a parameter-domain where the original system has multiple steady-state solutions, the control target ensuring non-invasive control is different for each solution. It also needs to be noted that for capturing an unstable limit cycle in the original system, only local stabilisation around this solution is required. Thus, it is not investigated whether other stable or unstable steady-states exist in the controlled system.

In this study, a control-torque is applied to the towed wheel realising a proportional-derivative (PD) control-law using the deflection angle \(\psi \) and the yaw rate \(\Omega \)

$$\begin{aligned} M_\mathrm{ctrl} = k_\mathrm{p} \left( \psi _\mathrm{t} (t) - \psi (t)\right) + k_\mathrm{d} \left( \dot{\psi }_\mathrm{t} (t) - \Omega (t)\right) , \end{aligned}$$
(29)

where \(k_\mathrm{p}\) and \(k_\mathrm{d}\) are the proportional and derivative control gains, whereas \(\psi _\mathrm{t} (t)\) is the control target function. The block diagram of the control approach is presented in Fig. 3. Thus, the governing equations of the closed-loop system can be expressed as

$$\begin{aligned}&J_\mathrm{A} \dot{\Omega }(t) + b_\mathrm{t} \Omega (t) = - lF_\mathrm{tyre} + M_\mathrm{tyre} + M_\mathrm{ctrl}, \end{aligned}$$
(30)
$$\begin{aligned}&\dot{\psi }(t) = \Omega (t), \end{aligned}$$
(31)
$$\begin{aligned}&\begin{aligned} \dot{q}_\mathrm{L} (t) =&V \sin \psi (t) + (a-x)\dot{\psi }(t) \\&+\frac{q_\mathrm{L}(t)}{\sigma }\left( q(a,t) \dot{\psi }(t)-V \cos \psi (t) \right) . \\ \end{aligned} \end{aligned}$$
(32)

In order to find the limit cycle of the open-loop system in an iterative way, the control target has to be considered in a form using a finite number of parameters. In CBC-algorithms, this is typically realised by considering the truncated Fourier series of the target and the registered signals.

The challenge with autonomous systems is that if the limit cycles are related to self-excited oscillations rather than forced vibrations, one has no a priori knowledge about the frequency \(\omega \). One may treat the frequency as a variable among with the amplitudes of the harmonic components; however, this increases the complexity of the root-finding algorithm considerably. An efficient way to overcome this issue is to infer the frequency from the captured solution and use a control target, which is phase-locked to the registered deflection angle [19]. To obtain such a target, we use the instantaneous phase calculated from the deflection angle \(\psi (t)\) and the yaw rate \(\Omega (t)\)

$$\begin{aligned} \phi (t) = \mathrm {arctan} \left( \Omega (t), \omega \psi (t) \right) , \end{aligned}$$
(33)

where the angular frequency \(\omega \) of the vibration is measured (in practice, this can be done, e.g. studying zero-crossings in the captured time profile of the yaw rate \(\Omega (t)\)). Then, the control target is considered in the form

$$\begin{aligned} \psi _\mathrm{t} (t) = A_\mathrm{t}^0 + A_\mathrm{t}^1 \cos \phi (t). \end{aligned}$$
(34)

where \(A_\mathrm{t}^0\) and \( A_\mathrm{t}^1\) are constant coefficients. This leads to a fixed point iteration for the angular frequency \(\omega \), i.e. always the last measured frequency is used in the formula of the instantaneous phase. It is expected though that this iteration generally converges. The higher harmonic Fourier coefficients were omitted from the formula above as they tend to show considerable fluctuation during the simulation of the non-smooth system. As such, they are difficult to capture with good accuracy. Note that the formula in (34) already contains higher harmonic components as the instantaneous phase \(\phi (t)\) is a nonlinear function of the time. Nevertheless, to simplify our formulae, its time derivative is approximated with the angular frequency as \(\phi \approx -\omega t\). Thus, the derivative of the control target reads

$$\begin{aligned} \dot{\psi }_\mathrm{t} (t) = \omega A_\mathrm{t}^1 \sin \phi (t). \end{aligned}$$
(35)

3.1 Root-finding

If the control gains \(k_\mathrm{p}\) and \(k_\mathrm{d}\) are appropriately chosen, the control-law in Eq.  (29) stabilises the system around a periodic solution \(\psi ^*(t)\), which is also considered with the help of the instantaneous phase \(\phi \), the static deflection \(A^{0*}\) and the vibration amplitude \(A^{1*}\)

$$\begin{aligned} \psi ^* (t) \approx A^{0*} + A^{1*} \cos \phi (t). \end{aligned}$$
(36)

Note that there is no general method providing control gains ensuring stabilisability. Nevertheless, the simplicity of the PD control law usually allows for a relatively quick tuning of the control gains by trial and error. A general rule of thumb that one can rely on is that if the control is strong enough to bring the system to a steady state which is within a domain of attraction of a different steady-state solution of the uncontrolled system from where the experiment was started, then usually the control law is strong enough to stabilise the system around an unstable limit cycle.

Let us suppose that the open-loop system has a limit cycle \(\psi _\mathrm{p}(t)\) which is considered in a similar form

$$\begin{aligned} \psi _\mathrm{p} (t) \approx A^{0} + A^{1} \cos \phi (t). \end{aligned}$$
(37)

The task is to find the control target \(\psi _\mathrm{t}(t)\) with coefficients \(A_\mathrm{t}^{0}\) and \(A_\mathrm{t}^{1}\) which result in the system converging to the limit cycle

$$\begin{aligned} \lim _{t \rightarrow \infty } \psi (t) = \psi _\mathrm{t}(t) = \psi _\mathrm{p}(t). \end{aligned}$$
(38)

In the control target, the index \(\kappa \) refers to the number of iteration step.

In the root-finding algorithm, a fixed-point iteration is applied to obtain a steady-state static deflection

$$\begin{aligned} A^{0\kappa +1}_\mathrm{t}:=A^{0 *\kappa }, \end{aligned}$$
(39)

leaving only the vibration amplitude \(\psi _\mathrm{t}^1\) the only unknown parameter. To form a zero problem, the error between the target and measured amplitudes is considered as

$$\begin{aligned} \Phi (A_\mathrm{_t}^1) = A_\mathrm{_t}^1 - A^1(A_\mathrm{_t}^1). \end{aligned}$$
(40)

The zero of this function yields to the amplitude of the limit-cycle in the open-loop system.

As in this case, the non-smooth nature of the system may prohibit the implementation of a derivative-based (e.g. Newton-like) root finding algorithm, a mesh in the target vibration amplitudes is considered such that it includes the suspected amplitude of the limit cycle

$$\begin{aligned} A_{t}^1 - \Delta A = A_{t1}^1< A_{t2}^1< ... < A_{tN}^1 = A_{t}^1 + \Delta A. \end{aligned}$$
(41)

Then, by simulating the system with these control targets, the corresponding amplitude errors are obtained.

$$\begin{aligned} \Phi _k = \Phi (A_{tk}^1), \quad k = 1, ..., N. \end{aligned}$$
(42)

These samples are used to fit a degree M polynomial to the univariate error function (\(\Phi (A_\mathrm{_t}^1) \approx p(q_j,A_\mathrm{_t}^1)\)) where the polynomial coefficients \(q_j\), \(j = 0, .., M\) are fitted using a least mean squares algorithm, and root-finding is performed on this surrogate model. In this study, a uniform mesh in the target amplitude \(A_\mathrm{t}^1\) with 7 nodes and a degree 3 polynomial is used as a surrogate model (\(N = 7, \; M = 3\)).

3.2 Continuation

The algorithm in Sect. 3.1 is capable of finding either a stable or an unstable periodic solution for a given set of parameters. To obtain the bifurcation diagram, one has to trace the branch of limit cycles as one of the system parameters, the bifurcation parameter, is varied. In case of wheel shimmy, the towing speed V is a natural selection as bifurcation parameter, as in practice, shimmy is often triggered by a change in vehicle-speed. Thus, by considering the towing speed as a variable, the zero problem in Eq. (40) will have two arguments

$$\begin{aligned} \Phi (V, A_\mathrm{_t}^1) = A_\mathrm{_t}^1 - A^1(V, A_\mathrm{_t}^1). \end{aligned}$$
(43)

One can take advantage from the fact, that there are no local extrema in the vibration amplitude in the unstable part of the solution-branch. Thus, the branch can be traced by gradually increasing or decreasing the target vibration amplitude \(A^1_\mathrm{t}\) and dealing with the error function \(\Phi \) on Eq. (43) as a univariate function of the towing speed V. In the meantime, the same fixed-point iteration is applied to the static deflection as indicated in Eq. (39). Again, to avoid the inaccuracies that the non-smooth nature of the system may cause in the calculation of derivatives, a uniform mesh with seven nodes (\(N=7\)) in the towing speed interval, where the solution is suspected, is considered.

$$\begin{aligned} V - \Delta V = V_1< V_2< ... < V_N = V + \Delta V. \end{aligned}$$
(44)

Then, by simulating the system with these control targets, the corresponding amplitude errors are obtained.

$$\begin{aligned} \Phi _k = \Phi (V_k, A_{t}^1), \quad k = 1, ..., N. \end{aligned}$$
(45)

Then a third-degree polynomial (\(\Phi (V,A_\mathrm{_t}^1) \approx \hat{p}(\hat{q}_j,V)\) with \(j = 0,...,M\), \(M = 3\)) is fitted to the results and the towing speed corresponding to the periodic orbit of the open-loop system is found by using this surrogate model. If no solution is found within \(V \in [V- \Delta V, V + \Delta V]\), then the interval size may be increased considering a larger \(\Delta V\) to repeat sampling and root finding on a new mesh. The continuation algorithm is illustrated by the flowchart in Fig. 4.

4 Results

4.1 nonlinear dynamics of the numerical studies

In this study, the bifurcation analysis of the towed wheel with the non-smooth delayed tyre model is carried out choosing the towing speed V as bifurcation parameter (see Fig. 5). First, the critical speed corresponding to the linear stability boundary of the rectilinear motion (\(\psi (t) \equiv 0, q(x,t) \equiv 0\)) is established. It is assumed that the linear stability of the equilibrium is unaffected by the sliding effects. Even though this assumption is not rigorously proven, numerical simulations indicate that this consideration does not introduce a significant error into our calculations. It is also worth mentioning that this assumption was proven to be correct for the simpler, but in many ways similar, brush tyre model in [12].

The system parameters used in the numerical study were selected to represent the experimental rig shown in the right panel of Fig. 6. The inertia of the caster-wheel system and lengths of the tyre-ground contact and the caster were measured manually whereas the stiffness, and damping parameters, as well as the tyre relaxation length were identified from measured frequency responses. The friction coefficients were estimated by pulling a rubber-sample on the treadmill and using a mechanical force gauge. Note that the sliding limits are also affected by the vertical tyre load which was tuned such that the numerical model provides realistic vibration amplitudes. It also needs to be noted that this experiment was already used in previous studies. Therefore, we do not repeat all details of the parameter identification procedure which can be found in [13].

As indicated by previous studies on the brush and stretched string models [12, 13], the example presented here is generally representative for the self-excited vibration (wheel shimmy) occurring at different parameter combinations when material damping is considered in the system (i.e. there is a single linearly unstable speed region).

The control gains were selected by trial and error and provided an adequately stabilising control for the continuation algorithm. It is worth mentioning that even though the negative control gain used here may appear counter-intuitive, this is possible for CBC and was also reported in [16].

With the model parameters given in Table 1 one obtains \(V \approx 1.9\) m/s for the critical speed of the caster-wheel system. Below this towing speed the rectilinear motion is linearly stable, while it is unstable for larger speeds. The linearised system has a complex conjugate root-pair at the stability boundary indicating that the nonlinear system undergoes a Hopf bifurcation. However, this bifurcation is degenerate due to the non-smooth nature of the system, i.e. it cannot be described by the Hopf normal form for smooth systems.

Fig. 4
figure 4

Flowchart of the employed continuation algorithm

Full size image

The non-smooth nature of the system also makes it challenging to start the exploration of the periodic solutions at the critical equilibrium (HB). Instead, the stable periodic orbits in the system were traced first with standard, open-loop simulations. This reveals a bistable parameter-range where a stable equilibrium and a stable periodic orbit coexist in the phase-space.

Then, the unstable branch is found by applying CBC and decreasing the target vibration amplitude with the towing speed V being fixed. The topology of the steady-state solutions ensures that this method finds the unstable periodic orbit ‘between’ the stable periodic solution and the equilibrium. From this starting point, the unstable solution branch can be traced by varying the target vibration amplitude and identifying the towing speeds resulting in an amplitude error that is smaller than the given tolerance.

4.2 Nonlinear behaviour observed in the physical experiment

Comparing the bifurcation diagram from the numerical model (see Fig.  5) with the left panel Fig. 6, we find that it is similar to the measured bifurcation diagram from the experimental rig, shown in the right panel for reference.

Fig. 5
figure 5

Bifurcation diagram of the towed wheel showing the steady-state vibration amplitudes of the deflection angle \(\psi \) with respect to the towing speed V. The blue curves correspond to stable, while the red ones to unstable solutions, respectively

Full size image
Fig. 6
figure 6

Left panel: Measured bifurcation diagram indicating the yaw rate amplitudes corresponding to the identified steady-state solutions. The blue markers and curves correspond to the stable, the red ones to the unstable steady state solutions, respectively. Right panel: Experimental rig with a towed wheel on treadmill

Full size image

The experimental rig consists of a wheel with a rubber tyre running on a treadmill. This setup is equivalent to the scenario of the wheel being towed with a constant speed as is the case in the numerical model described in Sect. 2. The caster-wheel system can rotate around the king pin as is the case in the numerical model. The control panel of the treadmill is used to control its speed which is also measured by a sensor sending a signal to the data acquisition device after each full revolution of the treadmill’s rubber belt for a more accurate measurement. In the meantime, the deflection angle of the caster is measured by an angle sensor built on the king pin joint. This signal is also fed to the data acquisition device and processed on a computer asynchronously. Note that this experimental setup was also analysed in [13] and [25] (capturing the stable solutions only), whereas a similar diagram to Fig. 6 indicating the suspected amplitude of the unstable limit cycles is used as a motivating example in [12].

Table 1 Model parameters used in the simulations
Full size table

In the physical experiment, the unstable periodic solution was measured by varying the initial conditions imposing different initial yaw rates on the caster. The boundaries within which the unstable periodic solution is suspected are inferred from the minimal initial angular velocity from where the system converged to the stable periodic orbit and the maximum angular velocity from where the system showed decaying vibrations. One can also observe a slight fluctuation in the stable vibration amplitudes and nonzero amplitude where a rectilinear motion would be expected which can be explained by the noise excitation from the treadmill. This effect made it infeasible to obtain information about the unstable limit cycles at low vibration amplitudes.

4.3 Sticking and sliding regions

Figure 7 shows the typical phase-portraits, time-profiles and sliding regions belonging to periodic orbits from the stable and unstable branches. It can be seen that even though our CBC algorithm is slightly simplified (not taking into account the higher harmonics in the control target) the method can find a periodic orbit that is very close to the control target, i.e. the control is near non-invasive. The bottom panels, portraying the variation of the sticking and sliding regions in time, also point out why the non-smooth time-delayed stretched string model is difficult to handle by more standard techniques of numerical bifurcation analysis: we find alternating uni- and bi-directional sliding regions at the rear end of the contact region. One can also observe that the size of the sliding regions grow with the vibration amplitude until we reach the amplitude where the whole contact region is sliding for some part of the period. Apparently, the critical amplitude where the time-intervals with full sliding appear coincides with the Fold point (where the stability of the solution branch changes). This fact explains the relatively sharp transition from the stable and unstable parts of the solution branch.

Fig. 7
figure 7

Phase portraits, time-profiles and sticking/sliding regions in the tyre–ground contact domain for the periodic orbits S, U1 and U2 (see Fig. 5). The blue curves correspond to the simulated trajectories while the control target is shown in black (where applicable). In the bottom panels, the white regions belong to the sticking, while the grey ones to sliding parts of the tyre–ground contact. The blue, red and green curves correspond to the boundaries of the front and rear sliding regions: \(x_\mathrm{L}\), \(x_\mathrm{R}\) and \(x_\mathrm{R2}\), respectively

Full size image

Unfortunately, the simulation algorithm failed at tracing the unstable solution branch back to the Hopf bifurcation point as the simplified sliding algorithm, which has been optimised to handle the sliding conditions at larger vibration amplitudes, is prone to numerical errors at small amplitudes where the sliding regions are small. This tends to result in misidentifying the boundaries of the sliding regions leading to incorrect solutions. One may overcome this issue by implementing the sliding model without the simplifications [20]. However, since using this model with the iterative CBC algorithm has an enormous computational burden, this was not carried out in this study. It is worth to mention that this part of the branch would also be difficult to trace in a real-life experiment as the random perturbations, that inevitably occur in physical systems, disguise the Hopf bifurcation in the underlying deterministic system. This effect is well known in stochastic dynamical systems and has been previously demonstrated experimentally in [26] for machine-tool vibrations occurring during milling.

5 Conclusions

Using the technique of control-based continuation, both stable and unstable limit cycles of a towed wheel with the non-smooth delayed tyre model were traced. Thus, we obtained a more complete image of the structure of the arising periodic solutions than it is possible with open-loop simulations [13]. From this point of view, one of the most important new finding is that the appearance of a full-sliding interval in the period, as the vibration amplitude grows, is strongly linked to the saddle-node bifurcation of the periodic orbits. The qualitative change in the solution also explains the relatively sharp transition between the unstable and stable part of the branches. This feature of the bifurcation diagram is also observable in the experimental results. This indicates a good qualitative agreement between the mathematical model and the physical system even though, as also concluded in [13], the sliding model presented here with the extent of the sliding regions being governed by the first order continuity of the deformed stretched-string, is too rigid. This results in a sensitivity to even small changes in the control input which was the main reason a polynomial surrogate model is used for the iterations instead of a more direct approach. Moreover, one needs to use unrealistically large friction coefficients or vertical load to find realistic vibration amplitudes. The latter issue could be potentially resolved by considering separate compliances for the tread and carcass by adding additional brush-like elements to the stretched-string [1] or by using more accurate models of the vertical force distribution which are out of scope of this study.

Another interesting result is that the unstable solution branch obtained with the stretched string model seems to emerge in a more shallow angle initially than is the case for the brush tyre model [12]. This means that the rectilinear motion in a physical system may perceived to lose its stability at a significantly lower speed than the deterministic models would indicate due to the random excitation from the road-surface. As such, the road-surface quality can have a significant impact on the measured critical speeds.

Beside the aspects of tyre modelling, the presented study can have another practical use, as it demonstrates that control-based continuation can be performed by applying torque-control on the caster-wheel system. A similar control technique would be feasible in real-life experiments as well, e.g. by using an electric motor to provide the required control-torque at the king pin. Realising the CBC algorithm for physical experiments could potentially lead to further interesting results on wheel shimmy or the dynamics of towed vehicles (trailers, articulated buses), which are described by similar dynamical systems. Moreover, tracing the unstable periodic orbits in these systems could help in the assessment of the ‘robustness’ of the linearly stable motions of these vehicles in bistable parameter regions, thus contributing to the improvement of vehicle safety.