1 Introduction

Time series contain rich information about the system structure and dynamic evolution rules, usually showing nonlinear and non-stationary characteristics. The complexity measurement of time series provides valuable clues to further reveal the dynamic evolution of complex systems, thus attracting many scholars to study.

As a measurement of complexity and determinism, recurrence quantification analysis (RQA) is a milestone method proposed by Webber and Zbilut [31] and has gained much attention in various fields [1, 11, 16]. Based on the internal distribution relationship of recursive points, it transforms time series into a recursive graph to analyze complex systems to obtain quantitative information about the system. However, when converting time series into a recursive graph, there are unstable factors in the embedding dimension and delayed-time estimation, which makes the optimal threshold of RQA difficult to determine. That said, when applying this method, it is difficult to accurately judge the actual recursive state between two points, which results in poor robustness. Thus, the application of this method is limited to a certain extent for time series analysis.

Another suitable tool, entropy, plays a pivotal role in the characterization of nonlinear dynamics. The classical methods include information entropy (IE) [6], permutation entropy (PE) [3], approximate entropy (AE) [22] and sample entropy (SE) [23], etc. IE mainly reflects the quantitative measurement of information on time series. PE is based on the principle of phase space reconstruction, and it measures the relative frequency by counting the occurrences of various alignment patterns in time series. The SE measurement method is an improvement of AE by calculating the logarithm of the probability sum and has no matching process of its own. SE is widely used in time series complexity analysis, and the measurement results are more reliable and robust to the problem of missing data. Based on the SE, Costa proposed multiscale sample entropy (MSE) from a multiscale perspective by means of coarse-graining, measuring the complexity of finite long time series [7]. Research shows that MSE is more comprehensive than SE in revealing the differences between disease and health status. All this kind of entropy can comprehensively reveal the intrinsic dynamics of complex systems in many fields, such as stocks [4, 5], traffic flow [35], meteorology [29, 34], diagnosis system [2, 12,13,14, 28] and biomedicine [21, 27, 30].

However, a large number of test results show existing schemes have large deviations and poor stability when they are used for other types of signals [23]. Say for example, PE is based on the alignment pattern confirmed by the data relationship within time series nearest neighbor value to extract important information features, but it has scale effect to deal with small sample sequences and cannot accurately estimate the complexity of small sample sequences [36]. In addition, time series with noise in the real world irregular jump within a certain range, making it difficult to find the intrinsic patterns contained in the original values of time series [33]. Symbolization can mitigate the impact of noise, reduce data consumption on memory, and accelerate signal processing. Therefore, symbolization is of great practical value for natural signal processing.

Studies show when the symbolization method is selected appropriately, the symbol sequence can effectively retain the dynamic nature of time series and help to uncover the inherent modalities in them, while greatly simplifying the complexity of the analysis [26]. Different symbolic methods are used and have obtained rich research results [8, 9, 32]. Bian et. al. [5] introduced a new two-index entropy by analyzing the maximization of entropy for the case of equal probabilities of basic elements extracted from the system and analysis the complexities of financial markets. Shang et al. [24] adopted a symbolic method to propose topological entropy and geometric entropy, which examines the correlations and complexities of different time series and can effectively distinguish between them.

Interestingly, we propose a complexity measurement method based on time series symbolization combined with the sliding window technique, which is called equiprobable symbolization pattern entropy (EPSPE). Firstly, original time series are implemented with equal probability symbolic procession. Then, the sliding window technique is used to determine the symbolic patterns at different moments and two adjacent patterns are regarded as a pattern pair. Finally, the number of occurrences of each pattern pair is counted and the corresponding probability is calculated to define the entropy. Altogether, we make the following contributions:

  • The symbolic processing of complex jumping data can greatly simplify the complexity of signal analysis while also ensuring the accuracy of the analysis.

  • The pattern pairs and their probabilities are determined by the frequency and direction of different symbolic pattern conversions, which more accurately reflect the degree of interconnection and directionality of the internal primitives of the complex system.

  • We conduct extensive experiments on simulation time series and the natural wind speed time series. Since a finite number of symbolic pattern pairs are used as the events, the method is less affected by the length of time series analysis and is suitable for large data time series analysis. Compared with existing schemes, the robustness and advancement of this method are verified.

The reminder of the paper is organized as follows. In the following section, we introduce some preliminaries. Section 3 presents our design. We provide a complexity analysis experiment based on simulation time series in Sect. 4. Furthermore, the method proposed in this paper is used to analyze the natural wind speed time series signal in Sect. 5. Finally, Sect. 6 concludes this paper.

2 Preliminaries

2.1 Equiprobable symbolization

The method of equiprobable symbolization was first proposed by Lin et al. [19] in 2003 and has been widely applied in the field of data mining. The equiprobable symbolization method refers to the following: assuming that time series meets the Gaussian distribution, the critical points can be determined according to the Gaussian distribution to obtain a number of equal probability regions and then, combined with the segmental aggregation approximation principle for symbolic aggregation representation [20]. Its process is briefly described as follows.

For the time series \({x_i:1\le {i} \le {N}}\), firstly, they are sorted by amplitude. When the number of symbols n is given, \(n-1\) equal probability values are found (denoted as \(t_1,t_2,\cdots , t_{n-1}\)) As a threshold for equiprobable segmentation. According to the rules:

$$\begin{aligned} {s_i} = \left\{ {\begin{array}{*{20}{c}} 0 &{} {x_i} \le {t_1}, \\ 1 &{} {t_1}< {x_i} \le {t_2}, \\ \vdots &{} \vdots \\ {n - 2} &{}{t_{n - 2}} < {x_i} \le {t_{n - 1}},\\ {n - 1} &{}{t_{n - 1}} \le {x_i}. \end{array}} \right. \end{aligned}$$
(1)

The original time series are converted into discrete symbol sequences \(s_i: 1\le {i} \le {N}\).

The equiprobable symbolization has three main benefits. Firstly, after symbolization, the influence of the probability distribution of the original sequence is eliminated. The symbol sequence fully reflects the relationship of the original time series, thus solving the problem that the entropy is affected by the probability distribution. Secondly, the symbolization result is not affected by extreme values, so it can well combat non-stationary mutation interference. Thirdly, a variable resolution in the amplitude domain is realized, that is, more symbols are used in areas with dense amplitude distribution to improve resolution, and fewer symbols are used in the sparse area to reduce redundancy, thus improving the utilization of symbols. At the same time, the variable resolution also breaks through the linear constraints of traditional uniform symbolization.

2.2 Multiscale sample entropy

Generally, for a one-dimensional discrete time series, the calculation process of MSE is as follows.

  1. (a)

    Construct the coarse-grained time series \(y^\tau \) :

    $$\begin{aligned} {y_j}^{\tau }=\frac{1}{\tau }\sum \limits _{(j-1)\tau +1}^{j\tau }{{x_i}}, 1\le j\le N/\tau , \end{aligned}$$
    (2)

    where \(\tau \) is the scale factor and the length of the sequence is \(M=\text {int}(N/\tau )\).

  2. (b)

    Construct a set of m dimensional vectors \({X^m}(i)=\{y_{i+k}^{\tau },0\le k\le m-1\}\), where m is the embedded dimension.

  3. (c)

    For an arbitrary vector \({X^m}(i)\), calculate the distance to all the remaining vectors \({X^m}(j)\),

    $$\begin{aligned} d\left[ {X^m}(i),{X^m}(j) \right] ={\max _{k=0,\cdots ,m-1}}\left( \left| y_{i+k}^{\tau }-y_{j+k}^{\tau } \right| \right) . \end{aligned}$$
    (3)
  4. (d)

    Set a given tolerance r, then count the number \({B^m}(i)\) of \(d\left[ {X^m}(i),{X^m}(j) \right] <r\), \(( i,j=1\sim M-m+1; i\ne j )\) and calculate the ratio to the total number \(C_{i}^{m}(r)\):

    $$\begin{aligned} C_{i}^{m}(r)=\frac{{{B}^{m}}(i)}{M-m+1}. \end{aligned}$$
    (4)
  5. (e)

    Calculate the mean value of \(C_{i}^{m}(r)\) as follows:

    $$\begin{aligned} {{C}^{m}}(r)=\frac{1}{M-m}\sum \limits _{i=1}^{M-m}{C_{i}^{m}(r)}. \end{aligned}$$
    (5)
  6. (f)

    When \(m\rightarrow m+1\), repeat steps b) \(\sim \) e) to obtain \({{C}^{m+1}}(r)\).

When the coarse-grained time series has a finite length, the entropy value SampEn(m, r, M) of the \(\tau \) scale is obtained as described above,

$$\begin{aligned} \text {SampEn}(m,r,M)= - \ln \left[ {\frac{{{C^{m + 1}}(r)}}{{{C^m}(r)}}} \right] . \end{aligned}$$
(6)

We repeat the above steps to calculate the entropies at different scales to obtain the curve of MSE.

The larger the value of MSE, the more complex the time series is. The smaller the value of MSE, the more self-similar the time series is. It is noteworthy that the tolerance limitation of MSE is \(r=0.1 \sim 0.25std(X)\), so the MSE of time series at one scale is not the same as its SE at the same scale, and therefore, MSE can reflect the complexity of the system at multiple scales.

3 Equiprobable symbolization pattern entropy

Symbolization is the conversion of a complex time series into a discrete sequence consisting of a fixed number of numerical values or special symbols. This process allows the efficient and rapid capture of valuable quantitative information from complex systems and can mitigate the effects of noise and reduce the complexity of calculations. In the real world, we often encounter a class of complex signals (e.g., wind field signals), which are typically characterized by a jumping pattern of amplitude rather than the usual gradual variation. In view of the characteristics of this kind of signal, the multi-region amplitude equiprobable segmentation processing can greatly simplify the difficulty of analyzing the signal on the premise of guaranteeing a small loss of precision to the original signal.

Fig. 1
figure 1

Time series symbolic process

Full size image

Considering the intrinsic patterns of signals, this paper proposes equiprobable symbolization pattern entropy(EPSPE), a new complexity measurement method based on equiprobable symbolization combined with sliding window technique. This method symbolizes time series based on the equal probability distribution of jump data and then, uses sliding window technique to obtain a finite number of different symbolization patterns. The pattern pairs are determined by calculating the transition direction of the symbolization patterns and the frequency of the occurrence of pattern pairs determines the probability of a pattern pair. The final implementation is complexity measurement of complex signals. The method is simple to implement, has low computational complexity, strong robustness and is not affected by the length of the time series. The detailed steps are as follows.

  1. (a)

    The original time series \(\left\{ {x_i},i=1,\cdots , n \right\} \) can be Z-standardized using Eq. 7 to obtain a new standardized time series \(\left\{ {y_i},i=1,\cdots , n \right\} \). The processed time series satisfies a Gaussian distribution with a mean of 0 and a variance of 1.

    Obtain \(y_i\) as

    $$\begin{aligned} {y_i}=\frac{ x_i - {\bar{x}} }{\alpha }, \end{aligned}$$
    (7)

    where

    $$\begin{aligned} {\bar{x}}= & {} \frac{1}{n} \sum \limits _{i=1}^n x_i, \end{aligned}$$
    (8)
    $$\begin{aligned} \alpha= & {} \sqrt{\frac{1}{n-1}\sum \limits _{i=1}^{n}{{{({{x}_{i}}-{\bar{x}})}^{2}}}}, \end{aligned}$$
    (9)

    \({\bar{x}}\) is the mean of the original time series and \(\alpha \) is the standard deviation of the original time series.

  2. (b)

    The time series is divided into a number of intervals according to the principle of equal probability, and each interval boundary point is determined. The value falling in each interval is represented by a letter symbol to realize the symbolic conversion of time series. The symbolic sequence S:

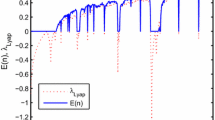
    $$\begin{aligned} S=\left\{ {s_1}{s_2}{s_3}\cdots {s_k}\cdots {s_n} \right\} ,{s_k}\in \left\{ a,b,c,d,\cdots \right\} . \end{aligned}$$
    (10)

    As can be seen in Fig. 1, the symbolized sequences preserve the jump behavior of the original sequence, and these symbols describe the dynamics of the system in the simplest way possible.

  3. (c)

    A sliding window with a fixed length L is set. Starting with the first symbol of the symbolic sequence , slide from left to right to get a set of symbolic sub-segment of length L. If we set L to be 4, we can get \(M:\left\{ chad, haeg, hadg, aege, gbha,\cdots \right\} \), where each sub-segment is a symbolic pattern, thus enabling symbolic pattern characterization of the original time series.

  4. (d)

    The pattern pairs are determined by the conversion relationship between the different symbolization patterns of length L in the symbolization sub-segment set M, where a pattern pair is an event. For example, \(chad\rightarrow haeg\) is a pattern pair. The conversion frequency between the symbolization patterns (the number of occurrences of the event) is counted to calculate probability of transition between symbolic patterns. The total number of events is num, and the number of event i is \(n_i\), then the probability that event i is

    $$\begin{aligned} P(i)={{{n}_{i}}}/{\sum \limits _{i=1}^{Num}{{{n}_{i}}}}. \end{aligned}$$
    (11)
  5. (e)

    The novel entropy E of the time series can be defined as:

    $$\begin{aligned} E=-\sum \limits _{i=1}^{Num}{P(i)\ln }P(i), \end{aligned}$$
    (12)

The advantages of this method are mainly reflected in the following aspects: 1) the symbolic processing of complex hopping data, which can greatly simplify the complexity of signal analysis while guaranteeing analysis accuracy; 2) through the conversion direction and frequency of different symbolic patterns to determine the events and their probabilities, to more accurately reflect the degree of correlation and directionality of the intrinsic patterns from the complex system more effectively; 3) due to the use of limited symbolic patterns, so this method is less affected by the length of the time series analysis, which can be applicable to big data time series analysis. The feasibility and advancement of the method in this paper are verified by testing the classical Logistic signal and the natural wind field signal.

4 Analysis of simulated data

Chaos has captured the fancy of many scholars and researchers. The attractiveness of chaotic dynamics is its ability to generate large movements which appear to be random, with greater frequency than linear models [15]. The simplest chaotic mapping operator, which was brought to the attention of scientists in 1976, is the Logistic map [10]. In order to verify the effectiveness and advancement of this method, the simulation time series of the Logistic mapping system is taken as an example. MSE, IE and EPSPE proposed in this paper are used to analyze Logistic time series with different behaviors.

4.1 Logistic mapping system

The Logistic mapping system is a classical model for generating chaotic time series that enter chaos through doubly-periodic bifurcation. The Logistic mapping system model equations are as follows.

$$\begin{aligned} {x_{n+1}}=\mu {x_n}(1-{x_n}), \end{aligned}$$
(13)

where \({x}_{n}\) is the n-th chaotic number, n denotes the iteration number and \(\mu \) is the main parameter that affects the behavior of the system. Logistic mapping system includes all the properties of chaotic systems, such as self-similarity, ergodicity, semi-random motion, and sensitivity to initial conditions. A detailed explanation about chaotic properties can be found in [25]. On the other hand, the Logistic mapping system can provide more diversity than randomly selected initial solutions [17].

Fig. 2
figure 2

Time series of Logistic system under different parameters

Full size image
Table 1 The behavior of Logistic system under different parameters
Full size table

In this experiment, we set the initial value of the Logistic mapping system as 0.5 and the step size as 0.01. The parameter \(\mu \) is taken as 3.5, 3.6, 3.628, 3.7, 3.74, 3.8, 3.83, 3.9 and 3.99, respectively, so that we can get the Logistic time series of different behaviors with the length of 1500. Due to the large amount of data, only the first 200 data of each time series with different behaviors are plotted in Fig. 2 in order to show the time series characteristics of the different behaviors more clearly. Table 1 gives the behaviors of the Logistic mapping system for different parameters. It can be seen that when the parameter \(\mu \) is 3.5, 3.628, 3.74 and 3.83, the corresponding time series present typical periodical behaviors with fixed number of solutions, which are 4, 6, 5, and 3, respectively. While when the parameter \(\mu \) takes 3.6,3.7,3.8,3.9,3.99, the number of solutions of the system is large and the jumps of the time series are irregular, presenting typical chaotic behaviors, and the degree of chaos increases with increasing parameter.

4.2 Analysis and result

4.2.1 MSE and IE analysis

According to the steps of the MSE algorithm in Sect. 2.2, the values of MSE of the Logistic time series with different behaviors are calculated with the embedding dimension m of 2, as shown in Fig.3. Figure 3a shows the MSE curves of the periodic time series from the Logistic system under different parameters. It can be seen that the curves are messy at multiple scales and cannot measure the complexity difference among the periodic time series. Figure 3b shows the MSE curves of the chaotic time series of the Logistic system under different parameters. When the parameter \(\mu \) = 3.6,3.7,3.8, 3.9 and 3.99, the chaotic intensity of the corresponding time series increases. It can be seen that at different scales, and the entropies of different time series show a decreasing trend. But when \(\mu =\) 3.7 and 3.8, the entropy values of the two corresponding time series cross or even coincide at multiple scales, which indicates that MSE cannot determine the complexity difference of Logistic time series with these two parameters. In addition, the test results of IE are similar to that of MSE, and it is impossible to distinguish among different periodic signals and complex signals, as shown in Fig. 4. In short, existing works like MSE and IE may able to roughly characterize the complexity differences between the chaotic signals, but they cannot identify the complexity differences between the signals with small differences. It has no discriminating ability to measure the complexity of the periodic signals.

Fig. 3
figure 3

MSE of simulation time series with different parameter \(\mu \) through the Logistic map

Full size image
Fig. 4
figure 4

IE of simulated time series under different parameters of \(\mu \) of the Logistic map

Full size image

4.2.2 EPSPE analysis

In accordance with the complexity measurement procedure described in Sect. 3, Logistic time series of different behaviors with a length of 1500 are mapped to symbolic time series. Here, we set the length of the sliding window to 4, which can also be increased according to actual needs. In the following chapters, we will further analyze the influence of sliding window length on entropy. When the number of symbols is small, the distortion of the signal is large, and when the number of symbols is large, the number of possible symbolization patterns will increase sharply, which affects the analysis efficiency. In consideration of the complexity and accuracy of signal analysis, we passed a lot of tests and finally determined that the preferred symbolization level (the number of symbols) is 12. Figure 5 shows the complexity measurement results of Logistic time series with different behaviors when the symbolization level is 12. Different symbol number settings do not change the relative relationship of the entropies of simulation time series, indicating that the method in this paper has good consistency.

Fig. 5
figure 5

EPSPE of simulation time series with different parameter \(\mu \) through the Logistic map

Full size image

When the parameter \(\mu \) is 3.5, 3.628, 3.74 and 3.83, the description in Table 1 is consistent with the complexity measurement trend of the time series given in Fig. 5a. As we know, when the parameter \(\mu \) is taken as 3.6, 3.7, 3.8, 3.9, and 3.99, the corresponding time series are chaotic intensity increasing time series. The corresponding complexity measurement in Fig. 5b also shows a gradual increasing trend and is much larger than the complexity measurement of the periodic signal witch. It can be seen that the complexity measurement based on time series symbolization with sliding window technique can not only distinguish the periodic signals from the chaotic signals, but also has a good sensitivity to the small changes of the periodic and chaotic sequences. In addition, Fig. 5 shows that the analyzed time series length is 1500, it can also analyze time series with large amount of data and completely independent of the data length, thus making the analysis results more reliable and convincing.

4.2.3 The length of sliding window analysis

When measuring the complexity of time series using a complexity measurement based on time series symbolization combined with a sliding window technique, the sliding window length L is a parameter that directly affects the size of the entropy value. Therefore, here we specifically analyze the effect of the sliding window length on the fineness of the entropy value and determine how the length of the sliding window is usually chosen, as shown in Fig. 6.

Fig. 6
figure 6

EPSPE of simulation time series with different sliding window length L

Full size image

The entropy values of the Logistic mapping system under different parameters are shown in Fig. 6 for sliding window lengths of 4, 6, 8, 10, and 12, respectively. When the parameter \(\mu \) is 3.5, 3.628, 3.74, and 3.83, the corresponding time series are periodical time series with fixed number of solutions, and the entropy values is constant and does not change with the sliding window length. The entropy values are identical with the number of solutions. When the parameter \(\mu \) is 3.6, 3.7, 3.8, 3.9 and 3.99, the entropy values of the corresponding chaotic time series increase with the increase in the sliding window length and is much larger than the entropy values of the periodic signals. For chaotic signals, as the sliding window length increases, the range of variation of the entropy values between the signals becomes smaller, i.e., the difference between the signals decreases. For example, when the sliding window is 12 and the parameter \(\mu \) is 3.7, 3.8 and 3.9, the entropy differences between the signals are negligible. This is because, for a fixed number of letter symbols, as the length of the sliding window increases, the number of patterns also increases, which results in an increase in the number of pattern pairs. Therefore, the EPSPEs increase with the increase in the length of the sliding window. Therefore, in order to finely characterize the differences between the complex signals and measure their complexity, the sliding window length is set to 4 in the subsequent analysis in this paper.

4.2.4 The length of time series analysis

In order to analysis the influence of the length of the time series on EPSPE, it is performed on the chaotic time series of the Logistic system with different lengths. Figure 7 shows the three-dimensional diagram of the EPSPE of the chaotic signals at different lengths. First of all, it can be clearly observed that the EPSPE of the time series at different lengths has the same trend in all lengths, i.e., the values of EPSPE increase as the parameter \(\mu \) increases, which indicates that the complexity of the system is increasing. For each parameter, there is an obvious increase in the EPSPE between the time series length of 500 and 1500. When the time series length is greater than 1500, the EPSPE tends to be stable with the increase in the time series length, which shows that the proposed method has good robustness to the time series length. Moreover, in order to describe the complexity of the time series more comprehensively and accurately, it is suggested in this paper that the selected time series length is not less than 1500.

Fig. 7
figure 7

EPSPE of simulation data with different lengths

Full size image

5 Application to natural wind field

In the previous section, it has been demonstrated that it is easy and intuitive to distinguish periodic signals from the chaotic signals. It is possible to distinguish the subtle differences among different chaotic signals. In order to further investigate its ability to analyze complex nonlinear and non-stationary natural signals, this section will discuss the fineness of the proposed method in analyzing complex indoor and outdoor natural wind field signals.

5.1 Acquisition of natural wind field data

The main objective of this experiment is to test the ability of innovative complexity estimation methods to quantify and analyze natural time series signals. For this purpose, a set of outdoor and indoor natural wind field signals with a specific spatial position relationship was collected. Nine two-dimensional ultrasonic anemometers are arranged in a row with an interval of 1m adjacent to each other (as shown in Fig. 8), and the height above the ground is 0.6m. The data collection time is 1 hour, and the sampling frequency is 4Hz. The collected wind speed time series are shown in Fig. 9, and the mean value of each wind speed time series is listed in Table  2.

Fig. 8
figure 8

Deployment of nine two-dimensional ultrasonic anemometers

Full size image
Fig. 9
figure 9

Wind speed time series of nine two-dimensional ultrasonic anemometers

Full size image
Table 2 The means of nine wind speed time series
Full size table

5.2 Complexity analysis of natural wind field data

Using the method proposed in this paper, the experimentally collected wind speed time series are measured for complexity. We quantify to analyze and mine the inherent patterns of the wind speed time series and compare with the results of classical MSE and IE analysis.

5.2.1 MSE and IE analysis

The embedding dimension is set to 2. The MSE of wind speed time series at different spatial positions is calculated according to MSE algorithm in Sect. 2.2, as shown in Fig. 10.

Figure 10 shows the MSE analysis results of the outdoor and indoor wind speed signals at different locations. For the experimental environment where the wind speed time series are collected in this paper, it has been shown that although the gaseous flow field changes continuously with time, the variation of wind speed in a certain region (usually within 10m) is approximately the same [18]. As shown in Fig. 9, for both indoor and outdoor wind time series, the large scale fluctuations of the nine wind speed time series are basically the same, but there are some differences in the small scale fluctuations. The closer the collection locations are, the higher the similarities of the fluctuations are. It can be seen from Fig. 10 that the entropy values of the wind speed time series at different locations shows an increasing trend as the scale increases, i.e., the complexity of the wind speed time series increases as the scale increases. However, the entropy values of the time series at different locations are very close to each other at any scales, and the entropy curves of MSE (Fig. 10) and IE (Fig. 11) are haphazardly intertwined for both indoor and outdoor wind time series. This means that the MSE and IE values are not directly related to the spatial location of the anemometers, and this two works cannot distinguish between indoor and outdoor signals. In addition, the computational complexity of the MSE and IE is large, and there is a limit to the length of the time series.

5.2.2 EPSPE analysis

According to the complexity measurement procedure described in Sect. 3, we set the symbolization level to 12 and the sliding window length to 4. A set of outdoor and indoor natural wind field signals with a specific spatial position relationship are analyzed. The complexity measurement of the wind speed time series collected by nine 2D anemometers is shown in Fig. 12 under the same condition as that used for MSE and IE..

Fig. 10
figure 10

MES of indoor and outdoor wind speed time series

Full size image
Fig. 11
figure 11

IE of indoor and outdoor wind speed time series

Full size image
Fig. 12
figure 12

EPSPE of indoor and outdoor wind speed time series

Full size image

Figure 12 shows the results of the complexity measurement analysis based on the time series symbolization combined with the sliding window technique proposed in this paper. The complexity measurement parameter, entropy, shows a consistent decay trend with the spatial locations of the arranged anemometers for both indoor and outdoor wind time series. The statistical results of the wind rose diagram from the nine acquisition locations show that the main wind direction of the test experiment is northeast. And the energy gradually decreases with the direction of wind flow, i.e., the average wind speed of the wind time series collected by anemometer U9 is the largest and gradually decreases from east to west (with the exception of the U2 position). The research results of reference [18] show that the larger the average wind speed over a small local spatial range (usually less than 10m), the weaker the random fluctuations in the amplitude and frequency of the airflow, i.e., the less complexity the fluctuations are. From the data presented in Fig. 12, it can be seen visually that the large-scale fluctuations of the U9 and U1 time series are almost the same, but the small-scale fluctuations of the U9 time series (maximum average wind speed) are significantly weaker than those of the U1 time series (minimum average wind speed). So the complexity of the U9 time series is smaller than that of the U1 time series. The entropy proposed in this paper reflects the number of symbolic patterns in the time series, and the more symbolic patterns indicate the more complex time series. While the entropy value of the time series from U1 is the largest due to the largest complexity of the fluctuation, and the entropy values of the other positions U3\(\sim \)U9 shows a consistent decaying trend due to the gradually decreasing complexity. Due to the abnormal increase in the average wind speed at U2, the abnormal entropy value is also reasonable. The above analysis shows that the new method proposed in this paper can accurately reflect the similarity and complexity differences of the analyzed signals.

Moreover, it can be observed intuitively and concisely from Fig. 12 that EPSPE value of indoor signals is lower than that of outdoor signals, indicating that the complexity of indoor signals is less than that of outdoor signals, which effectively and intuitively distinguishes indoor and outdoor signals.

In applications, such as wind energy prediction in power systems and wind field zoning in meteorology, similarity and complexity analysis is often performed on wind field signals collected at different spatial locations. Since the natural wind field data are a kind of complex nonlinear and non-stationary time series, there is no effective solution to measure the similarity and complexity of these time series. The method proposed in this paper provides an effective tool to solve this problem.

6 Conclusion

In this paper, a new method for complexity measurement based on time series symbolization combined with the sliding window technique is presented. The standardized time series is firstly processed with equal probability to transform the original time series into a more concise symbolic sequence. Then, a series of symbolic patterns are extracted in combination with the sliding window technique, and the conversion direction and frequency of the symbolic patterns are used as events and the probability of events, thus realizing the complexity estimation of complex signals. Time series analysis of the Logistic mapping system under different parameters shows that the complexity estimation method proposed in this paper can not only intuitively distinguish between periodic and chaotic signals, but also accurately reflect the subtle changes in the periodic and chaotic time series. Finally, the analysis of the complexity measurement of the wind speed time series collected by the regularly arranged anemometers shows that EPSPE can predict the spatial location proximity of the anemometers more accurately. These interesting findings suggest that pattern pairs from EPSPE are potentially valuable characteristics of wind signals, which will have broad applications in researches such as wind power prediction, wind pattern classification, and wind field dynamic analysis.