Combined internal resonances at crossover of slacked micromachined resonators

Abstract

The dynamics of micro-/nanoelectromechanical systems (M/NEMS) curved beams have been thoroughly investigated in the literature, commonly for curved arch beams actuated with electrodes facing their concave surface. Except for few works on slacked carbon nanotubes, the literature lacks a deep understanding of the dynamics of slacked curved resonators, where the electrode is placed in front of the convex beam surface. This paper investigates the dynamics of slacked curved resonators as experiencing combined internal resonances. The curved slacked resonator is excited using an antisymmetric partial electrode while the electrostatic voltage load is driven to elevated excitations, which breaks the symmetry of the system and affects natural frequencies and corresponding mode shapes. The axial load is tuned to monitor the ratios between the natural frequencies of different vibration modes, which induces simultaneous 1:1 and 2:1 internal resonances between the first and second mode with the third. We observe the interaction of hardening and softening bending of the fundamental backbone curves triggering various patterns of the response scenario and the appearance of coexisting regions of irregular dynamics.

1 Introduction

The activation of internal resonances in micro- and nanoelectromechanical systems (M/NEMS) has recently been the focus of a renewed interest in research studies, where they have been observed to develop complex bifurcation structures as driving the device deep into the nonlinear regime [1]. Internal resonance is mainly characterized by the energy leakage to a new vibrational mode rather than the targeted mode where the ratio between the involved modes must be commensurate [2, 3]. Asadi et al.[4] investigate the occurrence of internal resonances in a nonlinear asymmetric microbeam resonator, where the engaged modes experimentally experience asymmetric M-shaped internal resonance curves while exhibiting a vigorous energy exchange until the occurrence of the drop-jump phenomenon. Samanta et al. [5] focus on the complex energy transfer arising at internal resonances in MoS₂ nanomechanical systems and experimentally capture the activation of various internal resonances exhibiting different patterns of the response curves as the drive level is increased. Kirkendall and Kwon [6] detect nested regions of multistability at internal resonance in an electrostatic crystal plate, where the ensuing nonlinear modal interaction can generate topologically distinct dynamics over the parameter space, and the increased complexity related to the internal resonance activation provides a considerable versatility of the device response. Ruzziconi et al. [7] analyze a 2:1 internal resonance experimentally arising in the higher-order modes of a MEMS microbeam, and examine the changes induced in the dynamical response, including a phase shift that can be experienced among the modes, alerting that the internal resonance may affect the occurrence of the ultimate dynamic pull-in threshold.

The inherent nonlinear nature and the low damping of these miniature moveable structures present an ideal platform for activating internal resonances for fundamental analysis [3, 8,9,10] or for exploitation in various potential applications [11,12,13,14,15]. Sarrafan et al. [15] present a proof-of-concept design for a nonlinear rate microsensor, where 2:1 internal resonance is employed for its operation to improve the robustness of the response to design parameter variations. Taheri-Tehrani et al. [16] demonstrate mutual 3:1 subharmonic synchronization in a micromachined silicon disk resonator and suggest applications for the frequency-selective detection of weak signals. Pu et al. [17] investigate synchronization of electrically coupled micromechanical oscillators with 1:3 frequency ratio to design high-performance resonant sensors with better frequency resolution and larger scale factor. Zhang et al. [18] take advantage of internal resonances arising in polyvinylidene fluoride piezoelectric membrane to improve the sensitivity of a resonant mass sensor. Wang et al. [19] observe tunable frequency locking in the internal resonance of two electrostatically coupled microresonators with a frequency ratio 1:3, which is used to achieve enhancement of the frequency stability. Yang and Towfighian [20] intentionally combine internal resonances and magnetic nonlinearity to improve efficiency for energy harvesting, showing via experiments and simulations that the design outperforms the linear system by doubling the frequency bandwidth. As observed in Jeong et al.[21] and successively further investigated in Potekin et al. [22], the internal resonance triggered in atomic force microscopy by the non-smooth nonlinear tip-sample interactions provides stronger sensitivity to material composition, which allows for enhancing simultaneous topography imaging and compositional mapping.

The distinctive features induced by internal resonance activations pave the way for developing novel approaches in different fields [23,24,25,26,27]. Keşkekler et al. [24] activate successive internal resonances in graphene nanodrums by regulating the drive level and show experimental evidence of a nearly two fold increase in nonlinear damping; based on these achievements, they explore the possibility of using modal interactions to controllably tune the nonlinear dissipation. Antonio et al. [25] analyze nonlinear coupling through internal resonance in a MEMS resonator and show that the contributed mode absorbs the frequency and amplitude fluctuation of the targeted mode, i.e., the oscillation frequency stability can be improved by operating the resonator in the internal resonance regime. Chen et al. [26] drive a MEMS oscillator at internal resonance and experimentally observe that the internally coupled mode coherently transfers energy back to the principal mode as the external energy supply is switched off; the coupled mode acts as an energy reservoir, leading to developing novel strategies to engineer the dissipation process.

Notably, curved beams showed considerable potential for activating different types of internal resonances such as 1:1, 2:1, 3:1, and 4:1 [28, 29]. The curvature could be intentionally fabricated (arch resonators) and/or induced by applying compressive stress for buckled beams [28]. Among the main characteristics of curved beams is the high tuning of their natural frequencies as tuning their axial load. More recently, several techniques were investigated to study different methods of axial tuning of arch resonators, such as electrothermal tuning, guided-electrode tuning, or shape optimization. These axially tuned resonators showed great potential for applications [30,31,32,33]. Alcheikh et al. [31] fabricate a highly sensitive and wide-range resonant magnetic microsensor based on the detection of the resonance frequency of an in-plane buckled microbeam operated near the buckling point. Hafiz et al. [32] experimentally demonstrate a reprogrammable logic device based on electrothermal tuning of the resonance frequency of a microelectromechanical arch resonator capable of performing all the fundamental 2-bit logic operations.

The dynamics of initially curved MEMS resonators were deeply investigated in the literature [34,35,36]. The initially curved microbeam comprises inherent quadratic (i.e., due to curvature) and cubic (i.e., due to midplane stretching) nonlinearities, where the dominance of one nonlinearity over the other depends highly on the geometrical properties. Actuating the arch microbeam electrostatically will add an additional quadratic nonlinearity to the system [1, 37]. Classically, MEMS arch resonator is actuated using an electrode facing its concave surface to mainly induce snap-through motion. Ouakad and Sedighi [34] analyze the response of MEMS arches assuming an out-of-plane actuation pattern and show that the static profile can alter from symmetric shape to asymmetric one, depending on the shape and length of the stationary non-parallel electrodes. Najar et al. [35] explore the potential of electrostatic initially curved microbeams to serve as bifurcation gas sensors and investigate the feasibility of exploiting the transition from regular periodic to irregular chaotic response as a detection mechanism. Wang and Ren [29] studied the 3:1 internal resonance between the first two symmetric modes of an electrostatically actuated arch resonator. A multiple scale method was used to investigate the dynamics and the energy transfer between modes as activating the internal resonance. On the other hand, the tuning of the axial load of curved beams leads to monitoring the ratios between different vibration modes. Recently, Hajjaj et al. [10] tune the natural frequencies of MEMS in-plane clamped–clamped arch microbeams up to experience the crossover phenomenon and experimentally demonstrate the induced nonlinear interactions at internal resonances.

Commonly, the MEMS arch resonator actuated using an electrode facing its concave surface leads to higher actuation voltages. Despite extensive research on different types of internal resonances in these MEMS resonators, there is a lack of characterizing them at a slack position, leading to lower actuation voltages and low power consumption. In the present paper, we investigate numerically the effects of assuming slacked configuration while we drive the system by electrodynamic voltage excitations. This configuration is characterized by the suppression of the snap-through instability comparing to classical arches, which is appreciated in a wide range of applications. One should also note that the in-plane slacked arch beam can be easily fabricated using the standard photolithography fabrication processes [32].

Half-electrode configuration is considered. The device is deliberately operated in a relatively elevated bias electrostatic voltage, which visibly breaks the system's symmetry. The microbeam is subjected to compressive axial load, which is conveniently tuned in order to modify the frequency ratios and achieve the simultaneous activation of 1:1 and 2:1 internal resonance between the first three lowest vibration modes. After analyzing the hybridization of modes, we explore the internal resonance activation, showing the evolution of the response dynamics as tuning the stiffness and passing through the crossing zone. The study is focused on the variety of patterns arising in the response of the arched-beam MEMS resonator, where the modes involved in the simultaneous 1:1 and 2:1 internal resonance are differently dominated by hardening and softening bending behavior. As increasing the voltage excitation, we investigate the emergence of regions of irregular motion along the resonant branches. Due to the intrinsic non-symmetry of the system, the device frequency response is examined by referring to different sections of the microbeam, which allows monitoring the contribution of each single mode.

The paper is organized as follows. Section 2 introduces the MEMS arch resonator with slacked configuration and derives the problem formulation. Section 3 presents the tuning of the natural frequency ratios as varying both axial load and electrostatic voltage load. Section 4 explores the evolution of the 1:1 internal resonance between the first and second modes as passing through the veering zone while concurrently activating 2:1 internal resonance with the third mode. Section 5 investigates the response at elevated voltage excitations, showing quasi-periodic and chaotic dynamics. The main conclusions are summarized in Sect. 6.

2 System model

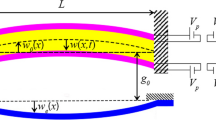
The MEMS device is modeled as a parallel plate capacitor, where the arc microbeam presents an initial curvature $\widehat{C}{}_{i}$ and an initial shape ${\widehat{w}}_{0}(\widehat{x})$ (Fig. 1). The initial shape of the arc microbeam is given by

$$ \hat{w}_{0} \left( {\hat{x}} \right) = \left( {\hat{C}_{i} - R + \sqrt {R^{2} - \left( {\hat{x} - \frac{L}{2}} \right)^{2} } } \right) $$

(1)

Fig. 1

Schematic of the slack curved microbeam electrically actuated with partial electrode configuration

where $\widehat{x}$ denotes the position along the arc length L and R represents the radius of the arc. The arc microbeam is assumed to have a rectangular cross section, $A=bh$, with a moment of inertia, $I=b{h}^{3}/12$, where h and b denote thickness and width, respectively. The stationary electrode faces the arc microbeam convex surface with a transduction gap d, and covers half of the microbeam length, allowing actuating both symmetric modes and the first antisymmetric one. The arc microbeam is actuated electrically via a DC bias voltage V_DC and an AC harmonic voltage of amplitude V_AC and frequency $\widehat{\Omega }$.

The non-dimensional equation of motion governing the transverse vibration of the arc microbeam, w(x,t), is given by [10, 33]

$$ \ddot{w} + \zeta \dot{w} + w^{^{\prime\prime\prime\prime}} = \alpha (w{{^{\prime\prime}}} + w_{0}{{^{\prime\prime}}} ) + \gamma F_{e} $$

(2)

where

$$ \alpha = N_{{{\text{non}}}} + \alpha_{1} \mathop \int \limits_{0}^{1} \left[ {\left( {w^{\prime}} \right)^{2} + 2w^{\prime}w_{0} ^{\prime}} \right]{\text{d}}x $$

(3)

and the electric force term is

$$ F_{e} = \frac{{\left( {V_{{{\text{DC}}}} + V_{{{\text{AC}}}} \cos \left( {{\Omega }t} \right)} \right)^{2} }}{{\left( {1 - w - w_{0} } \right)^{2} }}U\left( {x - 0.5} \right) $$

(4)

where $U\left(x\right)$ is the unit step function defining the lower stationary electrode length and position. The arc microbeam is subjected to the following clamped–clamped boundary conditions

$$ w\left( {0,{ }t} \right) = 0,\quad w\left( {1,{ }t} \right) = 0,\quad w{^{\prime}}\left( {0,{ }t} \right) = 0,\quad w{^{\prime}}\left( {1,{ }t} \right) = 0. $$

(5)

In Eqs. (2)–(5), dots denote derivatives with respect to time t, and primes denote derivatives with respect to space x. The non-dimensional variables in Eqs. (2)–(5) are

$$ x = \frac{{\hat{x}}}{L}\quad w = \frac{{\hat{w}}}{L}\quad w_{0} = \frac{{\hat{w}_{0} }}{d}\quad {\text{C}}_{i} = \frac{{\hat{C}_{i} }}{d}\quad t = \frac{{\hat{t}}}{{T_{s} }} $$

(6)

and the parameters are

$$ \alpha_{1} = 6\frac{{d^{2} }}{{h^{2} }}\quad N_{{{\text{non}}}} = \frac{{L^{2} }}{{{\text{EI}}}}N\quad \zeta = \frac{{L^{4} }}{{{\text{EIT}}_{s} }}\hat{c}\quad \gamma = \frac{{\varepsilon bL^{4} }}{{2{\text{EId}}^{3} }}\quad {\Omega } = T_{s} \hat{\Omega }\quad T_{s} = \sqrt {\rho bhL^{4} /{\text{EI}}} $$

(7)

where E is the effective Young's modulus, ρ is the material density, N is the axial load, $\widehat{c}$ is the viscous damping coefficient, and ε is the permittivity of the gap space medium.

In the literature, inducing axial load in MEMS devices is frequently used to attain large tunability of natural frequencies. In a wide range of applications, such as thermal-conductivity-based gas [30] and pressure sensors [31], and logic memories [32], the axial load was controlled by different transduction mechanisms, mainly electrothermal actuation [30] and sided electrostatic electrode [38]. Here, the non-dimensional axial load, N_non, is kept generic such that any mechanism that can generate axial load could be applied.

By fixing the axial load N_non, we simulate the dynamic response of the arc microbeam by discretizing the equation of motion [Eq. (2)] using Galerkin procedure, where the dynamic transverse vibration of the arc is expressed as

$$ w\left( {x,t} \right) = w_{s} \left( x \right) + \mathop \sum \limits_{i = 0}^{p} u_{i} \left( t \right)\phi_{i} \left( x \right) $$

(8)

where w_s(x) is the static deflection, u_i(t)(i = 0…p) are the non-dimensional modal coordinates, and ${\phi }_{i}(x)$ (i = 0…p) are the mode shapes of the arc microbeam at a fixed axial load N_non. The above yields to the following system of p equations of motion

$$ \mathop \sum \limits_{i = 0}^{p} M_{ik} \left( u \right)\mathop {\ddot{u}_{i}} \left( t \right) + \mathop \sum \limits_{i = 0}^{p} C_{ik} \left( u \right)\dot{u}_{i} \left( t \right) + \mathop \sum \limits_{i = 0}^{p} K_{ik} \left( u \right)u_{i} \left( t \right) = {\text{FC}}_{k} \left( u \right) + {\text{FE}}_{k} \left( t \right){ }\quad \forall \left( {k = 0...p} \right). $$

(9)

In the following sections, five modes are considered for the static and the eigenvalue analysis, while the first three modes are used for the analysis of the nonlinear response dynamics. An arc microbeam made of silicon will be assumed, where its dimensions are given in Table 1.

Table 1 Geometrical and mechanical properties of the silicon arc microbeam

3 Natural frequencies

We analyze the variation of the first three natural frequencies of the arc-shaped MEMS microbeam as increasing the compressive axial load N_non. The frequency trends at no electrostatic voltage (V_DC = 0 V) are reported in Fig. 2a. The first natural frequency (first symmetric) increases when raising the axial load up to nearly settle at about f₁ = 100 kHz at N_non = 250. Concurrently, the second natural frequency (first antisymmetric) decreases up to reach the nearly constant value of f₂ = 73 kHz. As a result, we can observe the crossing phenomenon where both the first and the second natural frequency present the value of f₁ = f₂ = 75 kHz, which occurs at about N_non = 120. As expected, there is an interchange of the order of modes after crossing, while no hybridization between the mode shapes is observed [10].

Fig. 2

Variation of the lowest three natural frequencies with the axial load for a V_DC = 0 V (crossing between f₁ and f₂) and b V_DC = 50 V (veering between f₁ and f₂)

If the electrostatic voltage is induced (V_DC = 50 V), the frequency trends and the corresponding mode shapes visibly modify (Fig. 2b). The crossing between f₁ and f₂ no longer develops, and the scenario turns into veering (avoiding crossing) between the same natural frequencies since systems with repetitive natural frequencies commonly show a very high sensitivity to any introduced perturbation (V_DC bias in this case). As increasing the axial load N_non, the first natural frequency f₁ raises up to become close to f₂, after which its increment develops with lower inclination. The second natural frequency f₂ exhibits an initial decrement until its value becomes close to f₁, after which f₂ increases again over the rest of the range reported in the figure. This veering phenomenon is accompanied by the hybridization of the engaged modes [39]. This aspect is analyzed in Fig. 3, where we report the mode shapes at crossing as V_DC = 0 V (Fig. 3a), and at different sections at veering as V_DC = 50 V (Fig. 3b-d). At crossing, we can recognize the distinct shapes of both the first and the second modes. Instead, a strong hybridization is observed at the veering zone, which leads the modes to become more similar to each other, although not identical. In addition, we can visibly observe the effect of the half-electrode configuration, which, driven at high electrostatic voltage, visibly breaks the symmetry of the modes shapes. A further illustration of the influence of the axial load N_non on the mode contribution around the veering zone is depicted in Fig. 3e.

Fig. 3

Mode shapes of the three lowest natural frequencies of the arc microbeam at a crossing, V_DC = 0 V and at N_non = 0; b–d veering, V_DC = 50 V and N_non = 85, N_non = 105, and N_non = 125, respectively, denoting hybridization of modes and loss of symmetry due to the half-electrode configuration. e Absolute amplitude of the first three normalized mode shapes of the arc microbeam at (from left to right) midpoint, quarter point, and three-quarter point for V_DC = 50 V as varying N_non

Regarding the third natural frequency, its trend initially decreases and successively restarts raising (Fig. 2b), while its mode shape is not clearly affected by the asymmetry of the electrode (Fig. 3e).

In the following sections, we analyze the dynamics as passing through the veering phenomenon, where there is approximately 1:1 internal resonance between the first and second natural frequency. In addition, the third natural frequency is about twice their value, which allows simultaneously establishing 2:1 internal resonance with the previous two frequencies.

4 Internal resonances at crossover: low excitation

We investigate the dynamics of the slack arc microbeam around the crossover zone, focusing on the case where the introduction of the DC bias voltage induces the veering phenomenon. To analyze the evolution of the response scenario, we numerically sweep the excitation frequency around the first and second modes. We initially focus on low electrodynamic voltage excitation and low damping ratio, which allows examining the main aspects of the mode interactions at crossover rising in the response dynamics. In particular, we assume V_DC = 50 V, V_AC = 1.2 V, and ζ = 4.10^–5. We analyze various sections of the dynamic response drawn at different values of axial load, specifically N_non = 85, N_non = 105, and N_non = 125.

We report the frequency response curves representing the maximum amplitude of oscillations and the corresponding modes contribution curves, where the first, second, and third mode components are in black, red, and blue, respectively. Due to the mode hybridization, evaluating the dynamics at different microbeam position is crucial for the comprehensive analysis of the mode interaction as experiencing different types of internal resonances. Thus, the displacement of the arc microbeam is evaluated at the midpoint (x = 0.5), quarter point (x = 0.25), and three-quarter point (x = 0.75). All results are developed via longtime integration combined with shooting technique and local stability analysis based on the Floquet theory [3]. Simulations are conducted via numerical codes developed in Matlab.

We consider the response dynamics as approaching the veering phenomenon, at N_non = 85. The first and second natural frequency occur, respectively, at f₁ = 84.4 kHz and f₂ = 95 kHz, while the third occurs at f₃ = 185 kHz (Fig. 2b). Here, the hybridization of the first and second modes begins (Fig. 3c). At the microbeam midpoint, the contribution of the first and third modes is close to the maximum, while the contribution of the second is deviated by the hybridization from being a node. The frequency response curves at different positions of the arc microbeam with their associate modal contributions are shown in Fig. 4. The frequency response diagram at the midpoint and its corresponding modal contributions are reported in Fig. 4a1 and b1. Around both the first and second resonance frequencies, the resonant and the non-resonant branch are clearly visible. The resonance curves of the hybridized first symmetric mode present bending toward lower frequency values, denoting softening behavior (i.e., the first mode is dominated by the quadratic nonlinearity originated from the electrostatic force and the microbeam curvature), whereas the resonance curves of the hybridized first antisymmetric mode present bending toward higher ones, denoting hardening behavior (i.e., the second mode is dominated by the cubic nonlinearity originated from the midplane stretching). Both modes exhibit a wide extent of the resonant branch, which leads to a considerable range of coexistence with the corresponding non-resonant one. As shown in Fig. 4b1, as sweeping around the second mode, the contributions of mode 1 and mode 2 have about the same amplitude at the microbeam midpoint, while opposite sign; this results in a nearly mode suppression in its corresponding total response in Fig. 4a1 (although not in the other points).

Fig. 4

a1–a3 Frequency response curves at N_non = 85, with V_DC = 50 V, V_AC = 1.2 V, and ζ = 4.10^–5. b1–b3 Corresponding modes contribution response curves, with black, red, and blue denoting first, second, and third mode contribution, respectively. Dynamics at (a1), (b1) midpoint, (a2), (b2) quarter point, and (a3), (b3) three-quarter point

As evidenced at midpoint in Fig. 4b1, the dynamics of the first mode are dominated by their own contribution, while this mode also contributes to the dynamics around the second mode. Similar findings are shown at the three-quarter point. Furthermore, the ratio between the third and second natural frequencies remains around two leading to the activation of the 2:1 internal resonance between the involved modes. This can be confirmed by analyzing the contribution of each mode depicted in Fig. 4b1–b3. In particular, the emergence of a new resonance branch at Ω = 91.5 kHz for all beam positions indicates the main contribution of the third mode into the response due to nonlinear coupling via 2:1 internal resonance.

At N_non = 105, the response scenario rapidly changes. The first and second natural frequencies are very close, as seen from the natural frequency alteration with axial load (Fig. 2b). However, they do not coincide perfectly due to the static deflection induced by the DC bias voltage from the half electrode. Here, there is a strong hybridization of the two modes involved (Fig. 3c and e). While the response around the first resonance frequency continues exhibiting softening bending, the main differences occur at the dynamics around the second resonance frequency, as demonstrated in Fig. 5a1–a3. The extent of the resonant branch strongly decreases, while a band of irregular motion (represented by stars) emerges between the resonant and the non-resonant branches. In particular, at Ω = 92 kHz, the system passes from stable periodic oscillations to irregular ones, after which it returns to the stable periodic non-resonant branch at Ω = 94 kHz. Evidence of a similar emergence of irregular dynamics at crossing was demonstrated experimentally in the case of the classical arc microbeam electrostatically actuated in Hajjaj et al. [10]. Note that the emergence of ranges of irregular motions is frequently observed as driving the system at internal resonance [3]. In addition, as for the previous case at N_non = 85, a hardening branch appears at Ω = 91 kHz, demonstrating the nonlinear coupling due to the 2:1 internal resonance. Despite this weak contribution, it is noticeable at the dynamics of the arc microbeam at all positions.

Fig. 5

a1–a3 Frequency response curves at N_non = 105, with V_DC = 50 V, V_AC = 1.2 V, and ζ = 4.10^–5. b1–b3 Corresponding modes contribution response curves, with black, red, and blue denoting first, second, and third mode contribution, respectively. Dynamics at (a1), (b1) midpoint, (a2), (b2) quarter point, and (a3), (b3) three-quarter point. Stars denote steady-state amplitudes in the regions of irregular motion

At N_non = 125, the interchange of modes via hybridization is almost done. The dynamics at different microbeam position are depicted in Fig. 6. The major oscillation amplitude at midpoint and quarter points is around the second resonance frequency, which corresponds to the hybridized first symmetric mode, showing softening behavior. The dynamics around this mode are more developed than the ones around the hybridized first antisymmetric one, of which we can see the onset. This is characterized by a mix of softening and hardening behavior observed in all the examined microbeam positions, i.e., at the present voltage excitation, it is not clear which nonlinearity will dominate the second mode response. Note that the contribution of the third mode here due to the 2:1 internal resonance is more significant compared to Figs. 4 and 5. The above may be due to the cumulative effect of different aspects, including the increased deflection toward the lower electrode and the modified coupling among the combined internal resonances due to the higher axial load compared to Figs. 4 and 5.

Fig. 6

a1–a3 Frequency response curves at N_non = 125, with V_DC = 50 V, V_AC = 1.2 V, and ζ = 4.10^–5. b1–b3 Corresponding modes contribution response curves, with black, red, and blue denoting first, second, and third mode contribution, respectively. Dynamics at (a1), (b1) midpoint, (a2), (b2) quarter point, and (a3), (b3) three-quarter point

5 Internal resonances at crossover: higher excitation

To better observe the underlying dynamical behavior induced by the crossing phenomenon, we analyze two additional sections of the response dynamics performed, respectively, at N_non = 105 and at N_non = 115, where we consider an increased excitation amplitude V_AC = 14 V, while assuming a higher damping ratio, ζ = 0.02. Higher damping is used to investigate the system response as being operated in air, which is vital in certain applications [28, 40].

At N_non = 105 (Fig. 7), there is a continuation of the resonance branch of the hybridized first mode into the resonance branch of the hybridized second mode, which induces an M-shape response demonstrating the nonlinear coupling among the first and second via 1:1 internal resonance. At midpoint and three-quarter point, the second mode mainly affects the dynamics of the second mode and contributes to the non-resonant branch around the first mode; yet, at these points, the first mode dynamics dominate the response over the entire frequency range, including at the second resonance frequency. Conversely, at the quarter point, the response of the arc microbeam is dominated by the second mode. The 2:1 internal resonance continues to be activated at about Ω = 92 kHz, where it occurs along the M-shape curve of resonant branches. The contribution of the third mode is characterized by a small peak. Unlike Sect. 4, the response does not split into resonant and non-resonant branches due to the high damping assumption.

Fig. 7

a1–a3 Frequency response curves at N_non = 105, with V_DC = 50 V, V_AC = 14 V, and ζ = 0.02. b1–b3 Corresponding modes contribution response curves, with black, red, and blue denoting first, second, and third mode contribution, respectively. Dynamics at (a1), (b1) midpoint, (a2), (b2) quarter point, and (a3), (b3) three-quarter point. Stars denote irregular motion

Furthermore, at Ω = 75.5 kHz, we can observe for a narrow frequency range that the first mode resonant branch evolves into period-2 oscillations, which rapidly lead to a small frequency range of chaotic responses [3]. The time history drawn at Ω = 77.58 kHz is reported in Fig. 8, implying the contribution of two modes in the response leading to a double period, confirmed by the corresponding Poincaré section.

Fig. 8

Time history at the midpoint at N_non = 105 and Ω = 77.58 kHz, with V_DC = 50 V, V_AC = 14 V, ζ = 0.02, a the global motion, b the first mode contribution, c the second mode contribution, and d the third mode contribution. e Corresponding Poincaré section

Along the right-hand side branch of the M-shape curve, at about Ω = 96 kHz, the time histories and the contour arising in Poincaré section (Fig. 9) prove the evolution of the dynamics into a quasi-periodic motion, which might be the consequence of a reversed Hopf bifurcation [3].

Fig. 9

Time history at the midpoint at N_non = 105 and Ω = 96 kHz, with V_DC = 50 V, V_AC = 14 V, ζ = 0.02, a the global motion, b the first mode contribution, c the second mode contribution, and d the third mode contribution. e Corresponding Poincaré section

At N_non = 115 (Fig. 10), the elevated voltage excitation leads to more complex dynamics exhibiting a mix of hardening and softening behaviors. The arch response is governed by a softening bending behavior at midpoint (Fig. 10a1), while it shows a mixture of hardening and softening at quarter and three-quarter points (Fig. 10a2 and a3). Figure 10 suggests the starting of mode separation. It also depicts the widening of the irregular motion bands, especially around the second mode, where there is coexistence with the resonant branch.

Fig. 10

a1–a3 Frequency response curves at N_non = 115, with V_DC = 50 V, V_AC = 14 V, and ζ = 0.02. b1–b3 Corresponding modes contribution response curves, with black, red, and blue denoting first, second, and third mode contribution, respectively. Dynamics at (a1), (b1) midpoint, (a2), (b2) quarter point, and (a3), (b3) three-quarter point. Stars denote irregular motion

6 Conclusions

This study presented a numerical investigation on the combined internal resonances, which may arise at crossover in a slacked micromachined resonator. A partial stationary electrode facing the arc beam convex surface has been used to electrically drive the arc resonator. A nonlinear model has been developed for the slacked arc microbeam taking into account nonlinearities associated with midplane stretching and electrostatic load. After focusing on the hybridization of the first symmetric and antisymmetric modes at crossover, extensive investigations have been conducted, where combined 1:1 and 2:1 internal resonances have been observed among the first three lowest modes. The evolution of the frequency response dynamics has been analyzed passing throughout the veering zone, showing the transition from M-shape resonance curves to more complex behavior. Focus has been placed on the appearance of regions of coexisting periodic and irregular motions. Due to the rich and complex nonlinear dynamics of arch beams, it will be interesting to investigate as part of the future work the activation of combined internal resonances involving different higher-order modes to optimize MEMS performances. Note that in the present paper, we consider only quadratic and cubic terms in the microbeam model formulation; yet there may be an emergence of higher-order nonlinearities at near-cancellation of cubic and quadratic nonlinearities [41, 42], where a thorough investigation should be conducted.

In the present simulations, only viscous damping has been taken into account; however, we have to mention that operating the arc microbeam at the slack configuration squeeze-film damping may also affect the system's dynamics, although investigating its influence is out of the scope of the present paper.

In a nutshell, this work motivates further research to exploit dynamics and particularly internal resonances of slacked curves resonators for practical applications, such as for sensing and frequency stability, thanks to the low actuation voltages compared to the classical actuation of the arch MEMS resonators.