Parametric excitation suppression in a floating cylinder via dynamic vibration absorbers: a comparative analysis

Abstract

Parametric excitation in the pitch/roll degrees of freedom (DoFs) can induce dynamic instability in floating cylinder-type structures such as spar buoys, floating offshore wind or wave energy converters. At certain frequency and amplitude ranges of the input waves, parametric coupling between the heave and pitch/roll DoFs results in undesirable large amplitude rotational motion. One possible remedy to mitigate the existence of parametric resonance is the use of dynamic vibration absorbers. Two prominent types of dynamic vibration absorbers are tuned mass dampers (TMDs) and nonlinear energy sinks (NESs), which have contrasting properties with regard to their amplitude and frequency dependencies when absorbing kinetic energy from oscillating bodies. This paper investigates the suppression of parametric resonance in floating bodies utilizing dynamic vibration absorbers, comparing the performance of TMDs against NESs for a test case considering a floating vertical cylinder. In addition to the type of dynamic vibration absorber utilized, the paper also examines the DoF which it acts on, comparing the benefits between attaching the vibration absorber to the primary (heave) DoF or the secondary (pitch) DoF. The results show that the TMD outperforms the NES and that it is more effective to attach the vibration absorber to the heave DoF when eliminating parametric resonance in the pitch DoF.

1 Introduction

Dynamic instability in floating bodies can occur due to the parametric excitation of the pitch and roll degrees-of-freedom (DoFs). This phenomena was first noted by Froude in the nineteenth century [1], and has since been investigated in applications such as shipping [2,3,4], offshore spar-type structures [5,6,7,8] and wave energy converters [9].

1.1 Suppression of parametric resonance in floating bodies

For most offshore applications, parametric resonance is undesirable. The large amplitude motions occurring due to parametric resonance can have an adverse effect on the performance and safety of offshore structures. For example, container ships lost cargo overboard due to large parametric roll motions [10]. As such, methods for suppression and stabilization of parametric pitch/roll in ships have been investigated, see for example [11,12,13,14] and the references therein.

Considering spar-type structures, Haslum et al. [15] investigate alternative hull shapes to improve the stability of spar platforms in hostile areas. Rho et al. [16] consider the stability of a spar platform with an approximate 2:1 ratio of pitch to heave natural periods, performing experiments and numerical analysis for regular waves. They consider including damping plates and strakes onto the cylindrical spar and find that the use of damping plates to limit the heave motion has the greatest effect of reducing the parametric pitch motion. Yang and Zhou [17, 18] investigate the occurrence of parametric resonance for a spar in irregular waves and means to avoid it. In [17], they consider the effect of hull geometry on the occurrence of parametric resonance in irregular waves. They compare five different spar geometries and conclude those geometries which minimize the heave response also minimize the occurrence of parametric resonance. In [18], some suggestions for designing spar platforms to avoid parametric resonance are presented, such as increasing the damping coefficient, designing the frequency response appropriately and increasing the metacentric height.

A number of studies have investigated suppressing parametric resonance in wave energy converters (WECs). All except for one of these studies, consider parametrically excited pitch/roll motions in spar-type WECs. Nicoll and Wood [19] mitigate the occurrence of parametric resonance in the sway DoF for the SurfPower WEC, which is tethered to the sea floor and acts like an inverted pendulum. Nicoll and Wood show that the parametric sway motion can easily be detuned by adjusting the mooring line tension, which is controllable through the hydraulic pressure in the power take-off (PTO). Considering a two-body heaving WEC with a central spar, the Wavebob, Villegas and van der Schaaf [20] also utilize the PTO system, applying a notch filter to eliminate the coupling between the two bodies at the resonances responsible for the parametric roll. Also considering a Wavebob-type WEC, Beatty et al. [21] investigate the use of fins to prevent parametric pitch and roll by increasing the drag-induced damping in those DoFs. Follow-up work on the same device, by Ortiz [22], investigates an alternative method which utilizes the mooring dynamics to reduce the occurrence of PR. The use of fins was also investigated by Gomes et al. [23] to suppress parametric pitch and roll in the OWC spar buoy, which was previously observed to be prone to parametric resonance [24, 25]. Also considering the OWC spar buoy, Davidson et al. [26, 27] investigated the use of a pressure relief valve in the OWC chamber to decouple the motion of the spar and internal water column, analogous to the notch filter used in [20].

One suppression method which has not been thoroughly examined is the use of dynamic vibration absorbers (DVAs), as detailed in the next section.

1.2 Dynamic vibration absorbers (DVAs)

DVAs consist of a small mass attached to a primary structure through a visco-elastic connection. Establishing a modal coupling between the primary system and the absorber, part of the vibration energy of the primary system is transferred to the absorber and dissipated, resulting in an overall reduction in vibration amplitude. In terms of frequency response, the use of tuned mass dampers (TMDs) enables the suppression of an essentially undamped high resonant peak, by generating two largely damped smaller peaks, thus avoiding large amplitude oscillation of the primary system [28]. The same principle can be used to avoid self-excited oscillations, for instance in wing profiles subject to flutter oscillations [29]. This kind of devices were first proposed for reducing rolling motions in ships [30, 31] by Watt already in 1883. However, their design was formalized in more rigorous terms only few decades later by Ormondroyd and Den Hartog [28, 32]. Nowadays, TMDs are extensively used in engineering practice for a variety of application; between the most famous examples, we cite the one installed in the Taipei 101 skyscraper [33] and the series of TMDs in the Millenium Bridge in London [34]. The main advantages of the TMD are related to its low cost, easy implementation and low maintenance required.

The main limitation of the TMD is related to its narrow operation bandwidth. Indeed, this prevents the TMD to work efficiently in systems undergoing large oscillations at various frequencies or systems with variable natural frequency. This limit motivated the development of alternative DVAs. In particular, the nonlinear energy sink (NES) is analogous to a TMD, but it is connected to the primary system through an essentially nonlinear spring, instead of a linear one. This allows it to resonate virtually at any frequency, enabling broadband energy dissipation [35]. However, an efficient modal coupling between a primary system and an NES is obtained only at a specific amplitude range. In particular, below a specific energy threshold, the NES becomes practically ineffective [36]. Besides many potential applications, its implementation was also proposed for a submerged body oscillating on an elastic support [37], however to the authors’ knowledge, has not been investigated for a floating body.

1.3 Objective and outline of paper

The main objective of this work is to perform a comparative analysis of the TMD and NES vibration absorbers for the suppression of parametric excitation in a floating cylinder. Considering their different range of operation, the TMD and the NES have somehow complementary properties. The TMD works very efficiently only at its natural frequency, but at virtually any vibration amplitude, while the NES works only at specific amplitude ranges, but over a broad frequency band. A floating body may be subject to excitation from waves that span a large frequency and amplitude range, therefore presenting a challenging application for both the TMD and the NES.

In addition to the type of DVA, the comparative analysis also considers the degree of freedom (DoF) in which the DVA acts on. Parametric resonance results from the transfer of energy from a primary DoF to a secondary DoF. For a floating cylinder, the primary DoF is heave, which can parametrically excite the pitch and roll DoFs. Therefore, the study will compare the performance of the DVAs acting on both the primary heave and the secondary pitch DoFs to analyse which configuration is more effective at suppressing the occurrence of parametric resonance. The comparative analysis is performed via numerical simulations of a floating cylinder which is known to be prone to parametric resonance due to the close proximity of the heave natural frequency to twice the pitch natural frequency.

The remainder of the paper is laid out as follows. Section 2 describes the comparative study, providing details on the floating cylinder, the considered DVA configurations, the modelling and simulation of the system, the input wave conditions considered and the metrics used to assess and compare the performance of the different DVA configurations. The results are then presented in Sect. 3, and conclusions are drawn in Sect. 4.

2 The comparative study

The comparative study is performed using a numerical testbed, evaluating the ability of the different DVA configurations to suppress the occurrence of parametric resonance in a floating cylinder. The floating cylinder considered in this study is described in Sect. 2.1. The hydrodynamic model employed to simulate the wave induced motion of the cylinder is then detailed in Sect. 2.2. The attachment of the DVAs to the cylinder and their inclusion in the numerical model is presented in Sect. 2.3, along with a discussion on the selection of the optimal DVA parameters. The methodology for the comparative analysis is then described in Sect. 2.4. Finally, in Sect. 2.5, the simulation details for the numerical testbed are given.

2.1 The floating cylinder

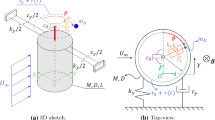
The floating cylinder employed in this study is a widely used test case from the literature considering parametric resonance in spar-type structures. The natural period of the cylinder’s pitch/roll motion is about twice the heave resonant period, which makes the floating cylinder susceptible to parametric resonance. Hong et al. [38] first introduced this case study, performing model-scale tests on the floating cylinder in a wave tank. Numerous authors then investigated various aspects relating to the dynamic instability and parametric excitation of the cylinder using numerical models [8, 39,40,41,42,43,44,45]. A schematic of the cylinder is shown in Fig. 1, and the relevant parameters are listed in Table 1.

Fig. 1

Cylinder schematic with geometrical parameters utilized in the numerical model

2.2 Hydrodynamic modelling

A brief introduction on articulating parametric resonance in hydrodynamic models for floating bodies is first given in Sect. 2.2.1, to provide the reader with a background on the main driver of the nonlinear behaviour herein analysed. The particular model employed in this comparative study is then detailed in Sect. 2.2.2.

2.2.1 Modelling parametric resonance in floating bodies

Parametric resonance is generated by the time-varying changes in the parameters of a system [46]. For floating bodies, this condition is met due to the wave-induced variation in the pitch and roll restoring stiffness. The pitch and roll restoring stiffness parameters are proportional in magnitude to the distance between the centre of buoyancy (CoB) and the centre of mass (CoM). In the presence of waves, the relative motion between the oscillating water surface and floating body continually alters the position of the CoB, thereby inducing time variation in the pitch and roll stiffness parameters.

Table 1 Relevant floating cylinder parameters used in the test case

The mathematical consideration of parametric excitation requires differential equations with time-varying coefficients [47]. Floating structures, like many dynamical systems, can be modelled as a second-order ODE, comprising an inertia term, a resistance/damping term, a restoring term and an excitation term, analogous to a mass-spring-damper system in mechanics or an L-R-C system in electronics [48]. Traditionally, each of these terms consists of a linear time-invariant (LTI) function, allowing computationally efficient frequency domain analysis to be employed when considering the vast range of wave spectra likely to be encountered by the structure in the ocean. The function parameters in each of these terms depend on the geometry of the floating structure’s wetted surface relative to its CoM. The LTI approach considers constant parameters derived from the wetted surface at the floating structure’s equilibrium position, based on the assumption of small amplitude waves and body motion. However, when considering larger amplitude waves and/or body motion, for example if the wave frequency matches the natural frequency of the floating body and its start to resonate, then the LTI approach breaks down [49].

Modelling parametric resonance in floating structures can therefore be achieved employing a time-varying function for the restoring term, which articulates the variation in the pitch and roll restoring stiffness parameters, due to the evolving wetted surface, as the body submergence oscillates in the presence of waves. For simple geometries, the time-varying function for the restoring terms can be derived analytically [50, 51]. Alternatively, system identification techniques can be employed from measured data to derive a suitable function to encapsulate the variation in the restoring parameters [52].

A higher fidelity but more computationally costly approach is the nonlinear Froude–Krylov force (NLFK) method. The Froude–Krylov force is the integral of the static and dynamic pressure fields of the undisturbed wave over the wetted surface of the body, which can be calculated using boundary element methods. Since the Froude–Krylov force considers the undisturbed wave, it excludes the effects of wave diffraction on the body. However, for bodies of small extension compared to the wavelength, diffraction is negligible, and the Froude–Krylov force is a good approximation to the sum of the restoring and excitation forces [48]. The NLFK method, calculates the Froude–Krylov force at each time step based on the instantaneous wetted surface of the body. Therefore, the parameters of the restoring and excitation force terms are continuously recalculated during the simulation and the NLFK method can articulate parametric resonance [53,54,55].

The most high-fidelity, but computationally expensive, method is to employ computational fluid dynamics, or other similar numerical modelling tools, to implement a numerical wave tank (NWT) [56]. The NWT domain is typically discretized spatially into over a million cells/nodes/particles and the Navier–Stokes equations are numerically solved in each of these cells/nodes/particles at each time step to calculate the evolving fluid pressure, velocity and free-surface elevation in the water. The motion of the floating body is calculated by a coupled solver which integrates the fluid pressure over the body surface at each time step.

2.2.2 The hydrodynamic model for the comparative study

The hydrodynamic model follows the validated model from the previous studies of this cylinder in [8, 38, 39, 45], comprising the following coupled equations for heave $x_{3}$ and pitch $x_{5}$

$$\begin{aligned}&F_{I,3}(\ddot{x}_{3})+F_{D,3}\left( \dot{x}_{5}\right) +F_{R,3}\left( x_{3},x_{5},t\right) ={F}_{E,3}\left( t\right) , \end{aligned}$$

(1)

$$\begin{aligned}&F_{I,5}(\ddot{x}_{5})+F_{D,5}\left( \dot{x}_{5}\right) +F_{R,5}\left( x_{3},x_{5},t\right) ={F}_{E,5}\left( t\right) , \end{aligned}$$

(2)

where $F_{I,i}$ is the inertia, ${F}_{R,i}$ is the hydrostatic restoring force, $F_{D,i}$ is the hydrodynamic damping force and ${F}_{E,i}$ is the wave excitation force. In addition to the experimental validation performed in [38], the ability of this hydrodynamic model to correctly predict parametric resonance is also verified in a code-to-code comparison against a NLFK model in [57].

The inertial forces are the product of the acceleration and inertia:

$$\begin{aligned} F_{I,3}= & {} (M+m_{3})\ddot{x}_{3}, \end{aligned}$$

(3)

$$\begin{aligned} F_{I,5}= & {} (I_{5}+m_{5})\ddot{x}_{5}, \end{aligned}$$

(4)

where M is the mass of the cylinder, $m_{3}$ is the hydrodynamic added mass in heave, $I_{5}$ is the moment of inertia in pitch of the cylinder and $m_{5}$ is the hydrodynamic added moment of inertia in pitch.

The hydrostatic restoring terms include time-varying parameters, allowing the occurrence of parametric resonance to be possible in the hydrodynamic model:

$$\begin{aligned}&F_{R,3}\left( x_{3},x_{5},t\right) =\rho gA_{C}\left[ x_{3}-x_{5}^{2} \frac{L_{MS}}{2}\right] , \end{aligned}$$

(5)

$$\begin{aligned}&F_{R,5}\left( x_{3},x_{5},t\right) \nonumber \\&=\rho gA_{C}L_{D}\left[ \overline{GM}x_{5}-\frac{1}{2}x_{3}x_{5}+\frac{1}{2}\eta (t)x_{5}\right] , \end{aligned}$$

(6)

where $\rho$ is the water density, g is the gravitational acceleration, $A_{C}$ is the horizontal cross-sectional area of the cylinder, $L_{MS}$ is distance from the still water level to the centre of mass, $L_{D}$ is the draft, $\overline{GM}$ is the metacentric height and $\eta (t)$ is the wave elevation.

The hydrodynamic damping is identified from the experimental data in [38] and is represented by

$$\begin{aligned}&F_{D,3}\left( \dot{x}_{3}\right) =C_{3}\dot{x}_{3}, \end{aligned}$$

(7)

$$\begin{aligned}&F_{D,5}\left( \dot{x}_{5}\right) =C_{5}\dot{x}_{5}, \end{aligned}$$

(8)

where $C_{i}$ are the experimentally determined damping coefficients.

The excitation force, for an input wave with amplitude A, frequency $\omega$ and phase $\phi$, is given by

$$\begin{aligned} {F}_{E,i}\left( t\right) =H_{E,i}(\omega )A\sin \left( \omega t+\phi +\phi _{E,i}(\omega )\right) , \end{aligned}$$

(9)

where $H_{E,i}(\omega )$ is the excitation force gain and $\phi _{E,i}(\omega )$ the excitation force phase shift. When considering polychromatic waves, the excitation force consists of a linear combination of $N_f$ frequency components.

$$\begin{aligned}&{F}_{E,i}\left( t\right) \nonumber \\&=\sum _{j=1}^{{N_f}}H_{E,i}(\omega _{j})A_{j} \sin \left( \omega _{j}t+\phi _{j}+\phi _{E,i}(\omega _{j})\right) . \end{aligned}$$

(10)

The excitation force gain and amplitude shift are frequency-dependent. Their values for the test case cylinder are calculated using Nemoh [53], which is an open-source linear potential flow boundary element method software. The calculated excitation force coefficients are plotted in Fig. 2 as a function of frequency.

Fig. 2

Excitation force coefficients a $H_{E,3}(\omega )$, b $\phi _{E,3}(\omega )$, c $H_{E,5}(\omega )$ and d $\phi _{E,5}(\omega )$

Table 2 lists the parameter values used in the model.

Table 2 Parameter values

2.3 Dynamic vibration absorbers

Four different DVA configurations are compared: (1) TMD acting in heave, (2) TMD acting in pitch, (3) NES acting in heave and (4) NES acting in pitch.

The attachment of the DVAs and their inclusion into the numerical model is detailed in Sect. 2.3.1 and 2.3.2 for the heave and pitch, respectively, and a schematic is shown in Fig. 3. The optimization of the parameter values for the different DVAs is discussed in Sect. 2.3.3. It is important to note that the addition of the DVA to the cylinder should not alter the original draught of the cylinder. This means that the overall mass of the entire cylinder and DVA system should always remain equal to the original cylinder mass, M:

$$\begin{aligned} M_c+M_a=M \end{aligned}$$

(11)

where $M_a$ is the mass of the absorber and $M_c$ the mass of the rest of the cylinder. Similarly, the addition of the DVA is assumed to not alter the moment of inertia of the cylinder, $I_5$.

Fig. 3

Schematic of the DVA attachment to the cylinder for a the heave DoF and b the pitch DoF

2.3.1 Heave

When acting in the heave DoF, the DVA is attached to the cylinder through a spring and a resistive damper and oscillates along the central axis of the cylinder, as shown in Fig. 3a. The force applied by the DVA on the cylinder is given by:

$$\begin{aligned} F_{\mathrm{a3}}=-b_{\mathrm{a3}}\dot{x}_{\mathrm{a3}}-k_{\mathrm{a3}}x_{\mathrm{a3}}-k_{\mathrm{nl}3}x_{\mathrm{a3}}^3 \end{aligned}$$

(12)

where $x_{\mathrm{a3}}$ is the translational displacement of the DVA mass ($m_{\mathrm{a3}}$) along the cylinder axis from its rest position at the CoM, $b_{\mathrm{a3}}$ is the damping coefficient, $k_{\mathrm{a3}}$ is the linear spring coefficient and $k_{\mathrm{nl}3}$ is the nonlinear spring coefficient. For the TMD, $k_{\mathrm{nl}3}=0$, and for the NES, $k_{\mathrm{la}}=0$. Following the derivation in “Appendix A”, we obtain the following system of equation governing the dynamics of the system:

$$\begin{aligned} \begin{aligned}&({M_c}+M_{\mathrm{a}3})\ddot{x}_3-M_{\mathrm{a}3} x_{\mathrm{a}3}\ddot{x}_5\sin (x_5)\\&\quad -2M_{\mathrm{a}3}\dot{x}_5\sin (x_5)\dot{x}_{\mathrm{a}3}-M_{\mathrm{a}3} x_{\mathrm{a}3}\dot{x}_5^2\cos (x_5)\\&\quad +M_{\mathrm{a}3}\cos (x_5)\ddot{x}_{\mathrm{a}3}=F_3\left( x_3,x_5,\dot{x}_3,\dot{x}_5,\ddot{x}_3,\ddot{x}_5;t\right) \\&\left( I_5+M_{\mathrm{a}3} x_{\mathrm{a}3}^2\right) \ddot{x}_5-M_{\mathrm{a}3} x_{\mathrm{a}3}\ddot{x}_3\sin (x_5)\\&\quad +2M_{\mathrm{a}3} x_{\mathrm{a}3}\dot{x}_5\dot{x}_{\mathrm{a}3}-M_{\mathrm{a}3}g x_{\mathrm{a}3}\sin \left( x_5\right) \\&\quad =F_5\left( x_3,x_5,\dot{x}_3,\dot{x}_5,\ddot{x}_3,\ddot{x}_5;t\right) \\&M_{\mathrm{a}3}\ddot{x}_{\mathrm{a}3}+M_{\mathrm{a}3}\ddot{x}_3\cos (x_5)-M_{\mathrm{a}3}\dot{x}_5^2 x_{\mathrm{a}3} +k_{\mathrm{a3}} x_{\mathrm{a}3}\\&\quad +k_{\mathrm{nl}3} x_{\mathrm{a}3}^3 -M_{\mathrm{a}3} g+M_{\mathrm{a}3}g\cos (x_5)+b_{\mathrm{a3}}\dot{x}_{\mathrm{a3}}=0. \end{aligned} \end{aligned}$$

(13)

$F_3$ and $F_5$ account for all hydrodynamic forces and inertial effects related to the water, as detailed in Sect. 2.2.

2.3.2 Pitch

For the pitch DoF, a rotational DVA is attached to the cylinder at its CoM, as shown in Fig. 3b. Examples of rotational DVAs can be found in applications such as rail [58] and vibration isolation [59]. The attachment of a rotational DVA acting in pitch has the following simplifications and advantages compared to the translational DVAs acting in heave:

• No stroke limit: there is no end stop for a rotating DVA

• No coupling with the heave DoF: while the translation of the heave DVA mass within the cylinder affects the pitch dynamics, the rotation of the pitch DVA within the cylinder does not affect the heave dynamics.

The DVA is coupled to the pitch DoF through the spring-damper torque:

$$\begin{aligned} F_{\mathrm{a5}}=-b_{\mathrm{a5}}(\dot{x}_{\mathrm{a5}}-\dot{x}_5)-k_{\mathrm{a5}}(x_{\mathrm{a5}}-x_5)-k_{\mathrm{nl}5}(x_{\mathrm{a5}}-x_5)^3 \end{aligned}$$

(14)

where $x_{\mathrm{a5}}$ is the rotation of the TMD with respect to the inertial reference frame. The equation of motion for the TMD is therefore given by:

$$\begin{aligned} I_{\mathrm{a5}}\ddot{x}_{\mathrm{a5}}=F_{\mathrm{a5}} \end{aligned}$$

(15)

where $I_{\mathrm{a5}}$ is the DVA mass moment of inertia in the pitch direction. We thus obtain the following system of equation governing the dynamics of the system:

$$\begin{aligned} \begin{aligned}&{(M_c+m_{a5})}\ddot{x}_{3}=F_3\left( x_3,x_5,\dot{x}_3,\dot{x}_5,\ddot{x}_3,\ddot{x}_5;t\right) \\&\quad I_5 \ddot{x}_{5}-b_{\mathrm{a5}}(\dot{x}_{\mathrm{a5}}-\dot{x}_5)-k_{\mathrm{a5}}(x_{\mathrm{a5}}-x_5)\\&\quad -k_{\mathrm{nl}5}(x_{\mathrm{a5}}-x_5)^3 \\&\quad =F_5\left( x_3,x_5,\dot{x}_3,\dot{x}_5,\ddot{x}_3,\ddot{x}_5;t\right) \\&\quad I_{\mathrm{a5}}\ddot{x}_{\mathrm{a5}}+b_{\mathrm{a5}}(\dot{x}_{\mathrm{a5}}-\dot{x}_5)\\&\quad +k_{\mathrm{a5}}(x_{\mathrm{a5}}-x_5) +k_{\mathrm{nl}5}(x_{\mathrm{a5}}-x_5)^3=0\\ \end{aligned} \end{aligned}$$

(16)

2.3.3 Parameter optimization

The performance of DVAs is dependent on the mass, spring and damping properties, thus these parameters must be optimized when assessing a particular DVA configuration. To aid in the optimization and provide a better understanding of the physical meaning of the results obtained, the following non-dimensional parameters are introduced, as listed in Table 3.

Table 3 Non-dimensional parameters for the heave and pitch cases

The optimization procedure involves first setting the DVA’s mass/moment of inertia as a fraction of the cylinder’s mass/moment of inertia, denoted by the mass ratio parameter, $\varepsilon$. For a realistic and viable DVA, the size and mass should ideally be as small as possible to reduce its cost and obtrusiveness on the rest of the system. Therefore, the mass ratio value is an important assessment criteria in the DVA comparison, with smaller $\varepsilon$ values being more favourable. Once the mass ratio is set then the natural frequency ratio, $\gamma _{\mathrm{a}}$, for the TMD or the pseudo-natural frequency ratio, $\kappa _{\mathrm{a}}$, for the NES, and the damping ratio, $\zeta _{\mathrm{a}}$, for both, must be optimized, according to a specific objective, by tuning the damping and spring parameters.

Considering a single DoF primary structure, several studies provide the optimal damping and spring parameters, depending on different objectives that optimize for different metrics, such as: (a) minimizing the maximum displacement of the primary mass [32, 60], (b) minimizing the total displacement of the primary mass over all frequencies [61, 62], (c) minimizing the transient vibration of the system [63, 64], (d) minimizing the relative displacement (i.e. the DVA stroke) [65], (e) minimizing the total kinetic energy of the primary mass over all frequencies [61], or (f) maximizing the power dissipated by the absorber [66]. The different optimization methods are summarized in [66]. Optimal performance of nonlinear energy sinks in multiple-degree-of-freedom systems was studied by, for example, Tripathi et al. [67].

However, for the comparative study in the present paper, the system under consideration has two coupled DoFs, and does not have existing analytical solutions for the optimal parameters. Therefore, herein the optimal parameters will be found through a brute-force approach by sweeping through the parameter value combinations. This approach requires two key components:

• A well-defined metric that encapsulates the objective of the optimization. This is discussed in Sect. 2.4.

• A computationally fast method to simulate the system and calculate the metric for all of the parameter value combinations. This is discussed in Sect. 2.5.

2.4 The comparative analysis

The performance of the DVAs is assessed on their ability to suppress the occurrence of parametric pitch motion in the cylinder for a wide range of wave conditions. The input wave conditions are described in Sect. 2.4.1, and the performance metrics on which the DVA parameters are optimized and the different DVA configuration are compared are discussed in Sect. 2.4.2.

2.4.1 Input wave conditions

Parametric resonance is both frequency- and amplitude-dependent, thus the performance of the DVAs are assessed in a range of input wave frequencies and amplitudes. In addition, the comparative analysis considers the performance of the DVAs in both single-frequency regular waves and multi-frequency wave spectra.

The regular waves encompass 8000 different wave conditions, parameterized by their frequency and amplitude, spanning an array of 80 frequencies and 100 amplitudes. Parametric resonance is expected at twice the pitch natural frequency; therefore, the wave frequencies range from 0.8 to 1.2 times this parametric resonant frequency ($2\omega _5$). The wave amplitudes span 0.001 to 0.5 times the metacentric height of the floating cylinder ($\overline{GM}$).

The irregular waves are derived from the JONSWAP spectra, comprising $N_f = 300$ harmonic components (spanning 0.01 to 3 rad/s) with randomly assigned phases. The irregular waves also encompass 8000 different wave spectra, parameterized by the peak frequency and significant wave amplitude (half the significant wave height). The 80 peak frequencies range from 0.2 to 1.7 times the parametric resonant frequency. The 100 significant wave amplitudes span 0.001 to 5 times the metacentric height of the floating cylinder.

2.4.2 Performance criteria

The performance of the DVAs are assessed on their ability to suppress the occurrence of parametric resonance. Each particular DVA configuration, with a certain mass, spring and damping parameter combination, is simulated over the array of 8000 different wave conditions. The calculated cylinder motion for each wave condition is then analysed to detect the presence or absence of parametric resonance. From these results, the following two performance criteria are considered:

• $u^*$ : the parametric resonance region ratio.

  This criteria refers to the region in the frequency-amplitude space for which parametric resonance occurs compared to the total frequency-amplitude space spanned by the 8000 wave conditions. It is essentially the ratio of simulations for which parametric resonance was present to the total number of simulations. For example, if parametric resonance is present in 4000 of the 8000 simulations, then $u^*=0.5$.

• $A^*$ : the minimum normalized wave amplitude which generates parametric resonance.

  This criteria refers to the wave amplitude (normalized by the cylinder’s metacentric height) with the lowest amplitude across all frequencies for which parametric resonance is present.

These two criteria are used in the optimization of the DVA parameters and as a metric in the overall assessment of the DVA performance. The brute-force parameter optimization procedure, described in Sect. 2.3.3, involves sweeping through the parameter values and identifying where $u^*$ is minimum and $A^*$ is maximum. Some other criteria, which are also important in the overall assessment of the DVA performance but not explicitly used in the optimization of the DVA parameters, are the DVA mass and the maximum DVA displacement. The smaller the size of the DVA, in terms of weight and required displacement, the more attractive it is as a viable solution. Therefore, the DVA mass and maximum DVA displacement should ideally be as small as possible.

2.5 Simulation details

To identify the optimal performance of the four different DVA configurations, many combinations of DVA stiffness, damping and inertia values must be explored, each requiring 8000 simulations. Therefore, it is imperative that the simulations be computationally efficient. For this reason, to perform the optimization of the DVA parameters, we adopted the harmonic balance method (HBM) [68], as described in Sect. 2.5.1. Additionally, although significantly slower to compute than the HBM, direct numerical simulations are also necessary for the optimization and analysis for the following two reasons: 1) to verify the results produced by the HBM, and 2) because for certain conditions the HBM could not converge on a result, thus direct numerical simulations are needed to compute the results for these cases. The details of the direct numerical simulations are presented in Sect. 2.5.2.

2.5.1 Harmonic balance method

The HBM consists of approximating the steady-state solution of the system by a series of harmonic terms. The approximated solution is then substituted into the system of differential equations under study. Subsequently, all harmonic terms are collected, reducing the nonlinear system of differential equations to a nonlinear system of algebraic equations, which can be solved with root finding procedures, such as the Newton–Raphson algorithm. Harmonic terms not included in the trial solution are neglected. In order to solve the system for a given frequency (or amplitude) range, the solution obtained for a specific frequency can be used as trial solution for the following one, significantly reducing the computational time, which, overall, is several order of magnitude faster compared to regular numerical simulations.

In practice, we approximate the solution of the system by

$$\begin{aligned} \begin{aligned}&x_3=c_{31}\cos (\omega t)+s_{31}\sin (\omega t)\\&\quad \quad \; +c_{32}\cos \left( \frac{\omega t}{2}\right) +s_{32}\sin \left( \frac{\omega t}{2}\right) \\&x_5=c_{51}\cos (\omega t)+s_{51}\sin (\omega t)\\&\quad \quad \; +c_{52}\cos \left( \frac{\omega t}{2}\right) +s_{52}\sin \left( \frac{\omega t}{2}\right) \\&x_{\mathrm{a}}=c_{\mathrm{a1}}\cos (\omega t)+s_{\mathrm{a1}}\sin (\omega t)\\&\quad \quad \; +c_{\mathrm{a2}}\cos \left( \frac{\omega t}{2}\right) +s_{\mathrm{a2}}\sin \left( \frac{\omega t}{2}\right) , \end{aligned} \end{aligned}$$

(17)

where $x_\mathrm{a}$ indicates either $x_{\mathrm{a}3}$ or $x_{\text{ a }5}$ for the cases of the absorber acting in heave or in pitch, respectively. This formulation implies that we consider only the frequency of excitation $\omega$ and its half, $\omega /2$, which is the frequency of the parametric excitation if triggered. Then, we plug this approximate solution into the equations of motion of the system [Eqs. (13) or (16)] for the absorber set either in heave or in pitch, respectively). For the case of the absorber in heave, before inserting the approximate solution, trigonometric terms of $x_5$ are expanded in Taylor series up to the fifth order.

Collecting terms with the same trigonometric order, we obtain a 12-dimensional nonlinear system of algebraic equations whose unknowns are $c_{31}$, $s_{31}$, $c_{32}$, $s_{32}$, $c_{51}$, $s_{51}$, $c_{52}$, $s_{52}$, $c_{\mathrm{a1}}$, $s_{\mathrm{a1}}$, $c_{\mathrm{a2}}$ and $s_{\mathrm{a2}}$, in the form

$$\begin{aligned}&f_i\left( c_{31},s_{31},c_{32},s_{32},c_{51}, s_{51},c_{52},s_{52},c_{\mathrm{a1}},s_{\mathrm{a1}}, c_{\mathrm{a2}},\right. \nonumber \\&\left. s_{\mathrm{a2}}; \omega ,A;\mathbf{k}\right) =0,\qquad i=1,...,12, \end{aligned}$$

(18)

where $\mathbf{k}$ is a vector including all system parameters. The algebraic equations $f_i$ are extremely lengthy and can be practically handled only with computer algebra. The solution of this system with the Newton–Raphson method provides an approximation of the steady state solution of the original system.

In order to predict when parametric resonances are triggered, the stability of the obtained solution is investigated. The stability analysis is performed by determining if the real part of at least one of the Floquet exponents is positive. For this purpose, Hill’s method is adopted [69], following the steps outlined in [70, 71]. In practice, if the analysis shows that for certain parameter values the response is unstable, we assume that a parametric resonance is triggered. On the contrary, parametric resonance responses, are not directly investigated with the HBM in this work. This approach is rather standard for the analysis of this kind of dynamical behaviour.

We remark some limitations of the implemented HBM for the system under study. First of all, neglecting higher harmonics and constant terms (harmonics of order zero) might have an effect on the system dynamics, especially at high amplitude [57]. However, for the analysed cases, the considered harmonic components seemed sufficient. Besides, as mentioned above, the procedure does not directly study parametric resonances, information about the existence of parametric resonances is extrapolated by the instability of the regular resonance solution; clearly, a similar approach is not necessarily correct. Furthermore, the procedure studies only periodic solutions, while nonlinear systems, and especially NESs, typically exhibit quasi-periodic motions, relaxation oscillations [72] or even chaotic motions [73], completely overlooked by the HBM adopted. Additionally, the procedure is unable to identify coexisting branches of periodic solutions [57]; it would be possible to implement control schemes to partially analyse if more branches coexist; however, considering the already high computational cost of the analysis, we decided not to implement such techniques. Finally, the HBM is not effective for studying multi-frequency sea spectra and cannot be used for the irregular wave simulations. Therefore, the usage of direct numerical simulations will also play a key role in the analysis where necessary. A code-to-code verification between the HBM and direct numerical simulation is performed in “Appendix B”.

2.5.2 Direct numerical simulations

The direct numerical simulations involve integrating the governing system of equations using the ode45 solver in MATLAB. Each simulation is 10,000 s in length; however, if the pitch angle exceeds 90 degrees, the simulation is aborted. At such extreme angles, the validity of the model is diminished and predictions of the cylinder continuing to oscillate past its horizontal orientation are unrealistic. Thus, for these cases, the simulation is terminated and flagged as a capsizing event due to parametric resonance.

The same method to identify parametric resonance in regular waves as used in [45] is employed here. For normal operating conditions, in single-frequency regular waves, the frequency of the pitch motion and the input waves is the same. However, when parametric resonance occurs, the frequency of the pitch motion becomes half of the input wave frequency. Therefore, the occurrence of parametric resonance in regular waves can be easily identified during post processing by comparing the frequency of the pitch motion to the input wave frequency. If the peak amplitude of the power spectral density (PSD) occurs at a frequency less than 75% of the input wave frequency, then it is clear that parametric resonance has occurred for that input wave condition.

Fig. 4

Frequency/amplitude range of input waves considered for the analysis of the generation of parametric resonances. Regular resonance solutions are generated through the HBM, while parametric resonances through direct numerical simulations. Colours indicate, in a the normalized amplitude of heave oscillations at steady state, while in b the pitch amplitude. White areas mark regions where the system experienced capsizing

For irregular waves a different method must be adopted to identify parametric resonance, as discussed in [45]. For an irregular wave spectrum, there is energy in the wave frequencies below the peak of the spectrum; thus, if there is pitch motion at half the peak frequency of the input waves, it cannot be instantly identified whether this pitch motion response is due to parametric excitation or direct excitation from the spectral wave components at that lower frequency. Similarly, there is energy at wave frequencies above the peak of the spectrum, so once again it cannot be instantly identified whether large pitch motion at low frequencies is due to direct excitation from the wave components at that frequency, or from parametric excitation caused by the wave components at twice that frequency. Therefore, a different metric is applied for the identification of parametric resonance in irregular waves, based on the energy increase in the pitch motion observed during the simulation. The energy in the pitch motion (calculated from the root-mean-square value of $x_5$), measured at the start of the simulation is compared to that at the end of the simulation. Based on the findings in [45], if the energy increase from the start to the end of the simulation is more than double, then the simulation is added to the parametric resonance region. Following [45], the energy is measured over a duration equal to $5T_p$, where $T_p$ is the peak period of the wave spectrum. The energy at the start of the simulation is measured from $5T_p \le t \le 10T_p$, so that the motion of the buoy is not measured from a cold start and the energy at the end of the simulation is measured from $10{,}000\ \text{[ }s]-5T_p \le t \le 10{,}000\ \text{[ }s]$.

3 Results

The results of the comparative study are presented in the section, first considering the regular waves and then the irregular wave spectra. In Sect. 3.1, to create a baseline against which the performance of the different DVA configurations can be compared, the occurrence of parametric resonance for the floating cylinder without any DVA attached is analysed. In Sect. 3.2, the DVA parameters are optimized, considering a fixed mass ratio of $\varepsilon =0.05$. The mass ratio is initially fixed, considering that typically the larger the mass ratio, the better a DVA performs, as also discussed later in Sect. 3.3. The performance of the different DVA configurations are then compared in Sect. 3.2.5. Next, in Sect. 3.3, the effect that varying the mass ratio has on the performance of the DVAs is analysed. Lastly, in Sect. 3.4, the performance of the DVAs in irregular wave spectra are analysed and compared.

Fig. 5

Referring to the system with a TMD acting in heave, for each couple of absorber’s natural frequency ratio $\gamma _{\mathrm{a}}$ and damping ratio $\zeta _{\mathrm{a}}$ ($\varepsilon =0.05$), a illustrates the results for the $u^*$ metric, while b shows the results for the $A^*$ metric. The red and blue dots mark the optimal absorber configuration according to the given criterion

3.1 Regular waves: baseline case with no vibration absorber

The baseline case, which considers the floating cylinder without any DVAs, is simulated using the HBM, and the results are shown in Fig. 4 which illustrates the frequency/amplitude range for which parametric resonances are triggered. The colours indicates the heave/pitch amplitude of the regular wave solutions. The thick black line marks the stability boundary of the regular solution, meaning that inside the boundary the system undergoes parametric resonances. Regular resonance solutions were generated through the HBM, while parametric resonances through direct numerical simulations. We remind that the HBM enables to detect parametric resonances directly from instabilities of regular resonances, without requiring to actually obtain the parametric resonance response. The figure shows that parametric resonances are generated already for a very low wave amplitude ($A^*_0=0.011$) when the wave frequency matches $2\omega _5$. The frequency region for which parametric resonance occurs widens as the wave amplitude increases and overall 36 % of the area in the considered frequency/amplitude range is subject to parametric resonance ($u^*_0=0.36$).

Fig. 6

System response for a TMD acting in heave, tuned according to the optima in Fig. 5a ($\varepsilon =0.05$, $\gamma _{\mathrm{a}}=0.9125$ and $\zeta _{\mathrm{a}}=0.074$). Colours indicate: a normalized heave ($x_3/\overline{GM}$), b pitch ($x_5$) and c normalized absorber relative displacement ($x_{\mathrm{a3}}/\overline{GM}$). The thick black lines mark the boundary of the parametric resonance region

3.2 Regular waves: optimization of vibration absorber parameters

The optimization shall initially consider the mass ratio fixed at $\varepsilon =0.05$. For each DVA configuration, the optimal values for the natural frequency ratios, $\gamma _a$ or $\kappa _a$, and the damping ratio, $\zeta _a$, are determined from the brute-force approach of sweeping through the parameter values.

3.2.1 TMD acting in heave

The first configuration considered is the TMD acting in the heave direction. The result of the optimization is summarized in Fig. 5a, b, which represent the parametric resonance region ratio $u^*$ and the minimal wave amplitude for generating parametric resonance $A^*$, respectively. The optimal conditions obtained with the first criterion are $\gamma _{\mathrm{a}}=0.9125$ ($k_{\text{ a }}=4.44\times 10^5$ N/m) and $\zeta _{\mathrm{a}}=0.074$ ($b_{\text{ a }}=376{,}100$ Ns/m), while for the second criterion, they are $\gamma _{\mathrm{a}}=0.9125$ ($k_{\mathrm{a}}=4.44\times 10^5$ N/m) and $\zeta _{\mathrm{a}}=0.0786$ ($b_{\mathrm{a}}=388{,}000$ Ns/m). Optimal conditions are marked by red and blue dots, respectively, in the figure. The optimal values are very similar in the two cases. The natural frequency ratio is the same, while damping ratio differs by only 6 %. In terms of performance, the TMD operating in heave seems extremely efficient. Utilizing a mass of only 5 %, it is able to reduce the parametric resonance area ratio $u^*$ from 0.36 to 0.015, while $A^*$ is increased from 0.011 to 0.44.

Figure 6 shows the response of the system with the attached TMD optimally tuned according to Fig 5a. In the three subplots, the response of the system in heave, pitch and the relative displacement of the absorber are represented. In Fig. 6a, the two resonant peaks generated by the TMD are clearly recognizable. The unstable area, which generates the parametric resonance, is limited to two small regions existing for high wave amplitudes. Interestingly, the right unstable area does not appear where the heave response is maximal, but on the left of the right peak. This is probably related to the frequency content, which should be as close as possible to $2\omega _5$. The TMD manages to suppress parametric resonance instabilities by significantly reducing the heave oscillation amplitude for $\omega \approx \omega _3$. If the heave response is reduced, the term $\rho gA_CL_Dx_3x_5/2$, which is responsible for the generation of the parametric resonance, is also reduced, suppressing this kind of behaviour. The reduced amplitude of the heave response can be noticed comparing Fig. 6a with 4a. A comparison of Fig. 6b and 4b shows that, apart from changing the stability properties of the response, the amplitude of oscillation in pitch (without considering the parametric resonance) is practically unvaried. This is expected, considering that the absorber operates in heave and it does not directly affect oscillations in pitch direction (except for nonlinear terms, which depends on $x_5$ and are practically negligible if $x_5$ is small). Figure 6c highlights an important technological aspect of the system. Namely, in the considered frequency range, the TMD has a relatively large vertical displacement, which poses a challenging aspect in the practical design of this system. In fact, although the considered mass is relatively small, the space required for its vertical displacement is not negligible. In Fig. 6, the parametric resonance solutions are obtained through direct numerical simulations, differently from the regular resonance solutions which are obtained through the HBM. We notice that large pitch values are exhibited only in the left parametric resonance region, which suggest that the TMD acting in heave might be even more efficient than what is predicted by the HBM.

3.2.2 TMD acting in pitch

The second configuration investigated is the TMD acting in pitch. The result of the optimization is shown in Fig. 7. For the minimal parametric resonance region criterion, the optimal value is $u^*=0.28$, provided by the parameter values: $\gamma _{\mathrm{a}}=0.4427$ ($k_{\mathrm{a}}=8.418\times 10^8$ Nm) and $\zeta _{\mathrm{a}}=0.0487$ ($b_{\mathrm{a}}=1.938\times 10^9$ Nms). Instead, by maximizing the wave amplitude required for generating parametric resonance, the optimal parameter values are $\gamma _{\mathrm{a}}=0.5464$ ($k_{\mathrm{a}}=1.2821\times 10^9$ Nm) and $\zeta _{\mathrm{a}}=0.024$ ($b_{\mathrm{a}}=9.57$ Nms), which provide $A^*=0.086$. The absorber in pitch seems to have performance significantly worse than the absorber in heave. The minimal achievable $u^*$ with the TMD in pitch is 0.28 and the maximal $A^*$ is 0.086, compared against $u^*=0.015$ and $A^*=0.44$ provided by the TMD in heave. Also, the optimal values for the TMD’s natural frequency ratio $\gamma _{\mathrm{a}}$ and damping ratio $\zeta _{\mathrm{a}}$ are significantly different for the two optimization criteria, which was not the case for the TMD in heave. The curvy trend of the optimal region in Fig. 7b cannot be easily interpreted. It suggests that if the natural frequency of the TMD is exactly as the pitch frequency ($\gamma _{\mathrm{a}}=0.5$), absorber damping should be slightly higher than if $\gamma _{\mathrm{a}}$ is slightly lager or smaller than 0.5.

Fig. 7

Referring to the system with a TMD acting in pitch, for each couple of absorber’s natural frequency ratio $\gamma _{\mathrm{a}}$ and damping ratio $\zeta _{\mathrm{a}}$ ($\varepsilon =0.05$), a illustrates the results for the $u^*$ metric, while b shows the results for the $A^*$ metric. The red and blue dots mark the optimal absorber configuration according to the given criterion

Figure 8 illustrates the response of the system with the TMD optimally tuned according to Fig. 7a. Comparing it with Fig. 4, we notice that the improvement of stability is limited to a relative thin strip for $\omega$ slightly smaller than $2\omega _5$. Such performance is probably insufficient to justify the implementation of the TMD in pitch in any engineering system.

Fig. 8

System response with a TMD in pitch, tuned according to the optimization in Fig. 5a ($\varepsilon =0.05$, $\gamma _{\mathrm{a}}=0.4427$ and $\zeta _{\text{ a }}=0.0487$). Colours indicate: a normalized heave ($x_3/\overline{GM}$), b pitch ($x_5$) and c absorber displacement ($x_{\mathrm{a5}}$). The thick black lines mark the boundary of the parametric resonance region. Parametric resonance solutions are obtained through direct numerical simulations. White areas mark points where the system experienced capsizing

3.2.3 NES acting in pitch

The next configuration considered is the NES acting in the pitch DoF. For this case (and for the NES acting in heave), the HBM was ineffective. Often, during the computation, the continuation procedure failed and was unable to converge to any solution. A more in-depth analysis revealed that the failure of the continuation was due to the presence of folds in the frequency response function. The adopted continuation technique consists of discretizing the continuation parameter (usually the wave frequency), finding the solution for the first point by utilizing as initial guess the solution of the linearized problem, then, for each subsequent point, by utilizing the solution of the previous point as initial guess, finding the solution for the new point. This technique is extremely simple and has the advantage of providing the solution on a given grid of values in the desired variables space, for instance the frequency, amplitude space ($\omega ,\,A$). However, the presence of folds makes the branch of solutions turn back, which is something that the algorithm cannot follow. Furthermore, the solution of the system after the fold is not necessarily close the previous point, therefore the initial guess utilized might be unable to converge towards any solution. Therefore, the optimization procedure for the NES cases (pitch and heave) is performed utilizing direct numerical simulation instead of the HBM.

The results of the optimization procedure revealed that the NES acting in pitch is unable to reduce the occurrence of parametric resonance. Sweeping a wide range of $\kappa _{\mathrm{a}}$ and $\zeta _{\mathrm{a}}$ values, spanning many orders of magnitude, the values of $A^*$ and $u^*$ remained unchanged from the baseline values.

3.2.4 NES acting in heave

The results of the optimization for the NES acting in heave is shown in Fig. 9. A very large range of spring and damper coefficient values were swept (note the log-scale on both axes in the contour plots). The results in Fig. 9a have a minimum value of $u^*=0.30$, revealing that the NES is unable to reduce the parametric resonance region much below the baseline value of $u^*=0.36$. In fact for many spring and damper values, the NES in heave actually increases the parametric resonance region. Figure 9b shows that the for $0.1 \le \kappa _{\mathrm{a}} \le 0.2$, the NES is able to increase the normalized minimal wave amplitude generating instability to above $A^*=0.05$, which is an improvement on the baseline value of $A^*=0.011$ but well below the values achieved by the TMD acting in heave.

Fig. 9

Results of the NES acting in heave, for each combination of pseudo-natural frequency ratio $\kappa _{\mathrm{a}}$ and damping ratio $\zeta _{\mathrm{a}}$ ($\varepsilon =0.05$), a illustrates the results for the $u^*$ metric, while b shows the results for the $A^*$ metric

Fig. 10

Example of post process identification of PR: a The pitch displacement time series, b The PSD for the entire time series c The PSD for only the second half of the time series

Further analysing the results raises an interesting question towards the metric used to evaluate the performance of the DVA: whether the DVA should be judged on its ability to suppress parametric resonance when it occurs or on its ability to mitigate the onset of parametric resonance before it occurs. This question arises after noting that in some instances, parametric resonance would appear at the start of the simulation and then be suppressed by the NES, such that the second half of the time simulation shows no unstable motions. An example is shown in Fig. 10a. The PSD for the entire time series is plotted in Fig. 10b, showing a much larger response around half the input wave frequency than at the input wave frequency ($\omega = 1.86\omega _5$). Therefore, the identification algorithm classes this case as a positive occurrence of parametric resonance, and the NES is deemed ineffective. On the other hand, if only the second half of the time series is considered then the corresponding PSD is plotted in the Fig. 10c, which shows a single peak that corresponds with the input wave frequency. The identification algorithm would class this case as being stable and that the NES was effective in suppressing the occurrence of parametric resonance. For many applications, it may not be acceptable to incur any large amplitude, parametrically induced oscillations before they are, i.e. parametric resonance should be mitigated before it occurs. However for the sake of completeness and out of interest a comparison of these parametric resonance suppression results against the original parametric resonance mitigation results are presented.

Reanalysing the results, considering only the second half of the time series is shown in Fig. 11. Here, it can be seen that the values of the $u^*$ and $A^*$ metrics are greatly improved in the region around $\zeta _{\mathrm{a}}\approx 10^0$ for very small spring coefficients, $\kappa _{\mathrm{a}}\le 10^{-4}$. Compared to Fig. 9, the minimum $u^*$ value is improved from to 0.3 to 0.13 and the maximum $A^*$ value increased from 0.085 to 0.21. At such low spring coefficient values, the spring force is basically negligible and the NES is behaving similar to a Lancaster damper (which is a mass damper system without any spring).

Fig. 11

Considering the second half of the pitch displacement time series only, results of the NES acting in heave, for each couple of absorber’s pseudo-natural frequency ratio $\kappa _{\mathrm{a}}$ and damping ratio $\zeta _{\mathrm{a}}$ ($\varepsilon =0.05$), a illustrates the results for the $u^*$ metric, while b shows the results for the $A^*$ metric

Fig. 12

Response of the system tuned according to the Lancaster damper-type NES with parameters at Point 1 on Fig. 11 ($\varepsilon =0.05$, $\kappa _{\text{ a }}=0.0003$ and $\zeta _{\mathrm{a}}=0.56$). Colours indicate: a pitch ($x_5$) and c normalized absorber displacement ($x_{\mathrm{a3}}/\overline{GM}$). The identified region of parametric resonance considering the entire time series is denoted by the red dashed line and considering the second half of the time series by the black dashed line. For reference, the baseline region of parametric resonance, for the case with no DVA, is denoted by the solid grey line. The white area indicates where the pitch angle exceeded 90 degrees and the simulation was aborted

To examine the cause of the improved performance for the Lancaster damper type NES configurations with very low spring coefficients, the simulation results for the parameter values producing the optimal $A^*$ result (marked by Point 1 on Fig. 11) are investigated in detail. Figure 12 plots the response of the system over the considered frequency-amplitude range and compares the difference between the identified regions of parametric resonance considering the entire time series (inside the red dashed line) and considering the second half of the time series (inside the black dashed line). The results show that when considering the second half of the time series only, parametric resonance is identified almost only when the system goes catastrophically unstable and the buoy capsizes (denoted by the white region in the graphs, where the simulation is aborted after the pitch angle exceeds 90 degrees). The region between the red and black dashed curves corresponds to cases where parametric resonance occurs at the start of the simulation but then the NES is able to suppress it.

Fig. 13

Simulation results from Point 1 in Figure 12 ($A/\overline{GM}=0.26$, $\omega /2\omega _5=0.93$) a The normalized heave motion b The pitch motion c the normalized DVA motion d The pitch motion PSD for entire time series e The pitch motion PSD for the second half of the time series

The results in Fig. 12b show that Lancaster damper type NES requires very large displacements in order to suppress the occurrence of parametric resonance, with stroke distances 5 - 25 times $\overline{GM}$. Another interesting result can be observed when comparing the parametric resonance region for the Lancaster damper type NES against the baseline parametric resonance region for the case with no DVA, denoted by solid grey line in Fig. 12. It can be seen that although the NES significantly decreases the region of parametric resonance for frequencies higher than $\omega /2\omega =1$, it actually slightly increases the parametric resonance region for lower frequencies. The reason for the very large displacements and for the shift of the parametric resonance region to lower frequencies is due to centripetal acceleration on the DVA mass, from the pitch motion, forcing the DVA mass to drift away from its equilibrium position at the buoy’s CoM.

Centripetal acceleration on the DVA mass is represented by the term $-m_\mathrm{a3}\dot{x}_5^2 x_\mathrm{a3}$ in Eq. (13), which therefore acts as negative restoring force proportional to the pitch velocity squared. For the cases when the NES spring coefficient is very small (seen on Fig. 11, for $\kappa _a < 10^{-4}$) the centripetal acceleration term dominates the spring restoring force, $k_{nl}x_\mathrm{a3}^3$, and the DVA mass begins to drift from $x_\mathrm{a3}=0$. The effect of the drifting DVA position on suppressing parametric resonance can be gleaned from inspection of the inertia term for the pitch motion in Equation (13); $\left( I_5+m_\mathrm{a3} x_\mathrm{a3}^2\right) \ddot{x}_5$, which shows that the pitch inertia increases with the square of the DVA displacement. An increase in pitch inertia results in a decrease in the pitch natural frequency, which explains why the parametric resonance region is slightly shifted to lower frequencies in Fig. 12. This also explains why the large amplitude DVA displacements found between the red and black dashed lines in Fig. 12b corresponds to cases where parametric resonance occurs at the start of the simulation but then gets suppressed by the second half of the time series. The large amplitude parametric pitch motions result in a large centripetal force which causes the DVA mass to drift far from $x_\mathrm{a3}=0$ and therefore detunes the parametric resonant frequency from the frequency of the input waves. These effects are highlighted in Figs. 13 and 14, which plot the simulation results from Points 1 and 2 on Fig. 12, respectively.

Fig. 14

Simulation results from Point 2 in Fig. 12 ($A/\overline{GM}=0.26$, $\omega /2\omega _5=1.1$) a The normalized heave motion b The pitch motion c the normalized DVA motion d The pitch motion PSD for entire time series e The pitch motion PSD for the second half of the time series

Figure 13 corresponds to Point 1, which is in between the red and black dashed curves in Fig. 12, where parametric resonance is identified when considering the whole pitch displacement time series but not when considering only the second half of the time series. The pitch displacement time series is shown in Fig. 13b, where at the start of the simulation an exponential increase in the pitch displacement oscillation amplitude occurs. The DVA displacement is plotted in Fig. 13c, showing a large displacement from equilibrium occurring when the pitch oscillations increase in amplitude. When the DVA displacement increases, the large parametric resonance pitch motions are seen to be suppressed and the frequency of the pitch oscillations is seen to decrease, highlighting the detuning effect the drifting DVA displacement has on the pitch natural frequency. This can also be seen in the PSD plot in Fig. 13d, corresponding to the Fourier transform of the pitch displacement for the entire time series, which shows a very large broadband region that starts around half the input wave frequency and then decreases to a main peak at a much lower frequency. By comparison, the PSD corresponding to only the second half of the pitch displacement time series, plotted in Fig. 13d, shows a single small amplitude, narrow banded, peak at the input wave frequency, indicating that the occurrence of parametric resonance has been suppressed by the DVA. The simulation results for Point 2, which is out of the parametric resonance region, are shown in Fig. 14, where the PSD for both the entire and the second half of the pitch displacement time series contains only a single peak at the input wave frequency. The effect of the centripetal acceleration causing the DVA mass to drift from its equilibrium can be seen in Fig. 14c.

3.2.5 Regular waves: DVA performance comparison

The performance of the different DVA configurations are directly compared in Fig. 15, which depicts the parametric resonance boundary computed for each of the DVA configurations, as well as for the baseline case with no DVA. Note that for the NES acting in heave, the two different optimal cases are shown: (1) considering the pitch displacement from the full simulation (Fig. 9) and (2) only considering the second half of the simulation (Fig. 12) are shown. The figure summarizes the results presented in the previous subsections, namely:

• the absorber in heave outperforms the absorber in pitch, and

• the TMD outperforms the NES.

Accordingly, the TMD acting in heave is the most effective, almost completely eliminating the parametric resonance region in the area of interest. Conversely, the NES acting in pitch is the least effective, providing no distinguishable reduction in the parametric resonance region. Therefore, coupled with the fact that the NES can only be assessed utilizing the computationally expensive direct numerical simulations, the NES acting in pitch shall be omitted from the further investigations in the following sections.

Fig. 15

Comparison of the stable region provided by the optimal TMD acting in heave (blue lines), the optimal TMD acting in pitch (yellow line), the optimal NES acting in heave when considering the second half of the simulation only (red line), the optimal NES acting in heave when considering the full simulation (green line) and the optimal NES acting in pitch (hidden beneath the black line), with respect to the case of no absorber (black line); $\varepsilon =0.05$

Fig. 16

Minimum parametric resonance region ratio, $u^*$, achievable for the different DVA configurations for varying mass ratio values, $\varepsilon$, normalized against the parametric resonance region ratio for the baseline case with no absorber ($u^*_0=0.36$)

3.3 Regular waves: variation of the mass ratio

Here, the effect of varying the DVA mass is examined. As mentioned in Sect. 2.4.2, the DVA mass is one of the most important parameters since the smaller the DVA mass the more feasible the device. The optimization procedure for the spring and damper parameters is performed utilizing various values of the mass ratio $\varepsilon$, and the results are shown in Fig. 16. The TMD acting in heave (blue line) is seen to completely eliminate the parametric resonance region once the mass ratio exceeds 0.06. By comparison, the NES acting in heave does not completely eliminate the parametric resonance region until the mass ratio approaches 0.2. (Note that the resolution of the considered mass ratios for the NES cases is more sparse than for the TMD cases, since the NES cases require more computational effort using the direct numerical simulations.) For the NES acting in heave, the two different optimal cases that consider the pitch displacement from either the full simulation (green line) or only the second half of the simulation (red line) are shown. When considering the second half of the simulation only, the minimum parametric resonance region for the NES in heave is approximately constant for mass ratio values of less than 0.15 and outperforms the TMD in heave for mass ratio values of less than 0.03. Here, the constant value is equivalent to the white region in Fig. 12 where the buoy capsizes and the simulation is aborted, which means that for mass ratio values less than 0.15 the NES acting in heave cannot stop the buoy from capsizing but so long as the simulation does not abort it can suppress the parametric resonance by the second half of the simulation (albeit with very large stroke displacements).

Fig. 17

a Maximum pitch displacement for the range of considered irregular wave spectra. The parametric resonance region is denoted inside the white dashed line. b The same information as in a but presented using contour lines with a 0.01 rad step size. The parametric resonance region is denoted inside the black dashed line

The TMD acting in pitch is unable to completely eliminate the parametric resonance region for the considered mass ratio values up to 0.2. Here, an important point should be highlighted: practical considerations of the mass ratio reveals that the TMD in pitch is unfeasible. The inertia in pitch is $I_5+m_5=1.85\times 10^{12} kgm$. Considering the design of the DVA in pitch shown in the schematic in Fig. 3, the upper limit for the DVA inertia is physically constrained by the radius of the cylindrical buoy, which is the maximum distance the DVA mass can be located from the centre of rotation. Therefore, the maximum inertia is $I_a=M_{a5}(D/2)^2$, which means that in the extreme upper limit case where the DVA mass equals in the entire mass of the buoy, $M_a=M$, then $I_a=7.4\times 10^{10}$, which equates to a mass ratio value of $\varepsilon =0.04$. So, the analysis performed in Sect. 3.2, which considered a mass ratio of $\varepsilon =0.05$, is infeasible, requiring a DVA mass greater than the entire buoy mass. Therefore, it can be stated that the TMD acting in pitch is significantly inferior to the DVAs acting in heave. As such, the TMD acting in pitch will be omitted from further investigations. Further explanation of the superior performance of the DVA acting in heave compared to pitch is given in the comparative analysis in Sect. 3.5.

3.4 Irregular wave spectra

While the results from the regular waves showed the superior performance of the TMD over the NES, it is possible that the NES may possess some advantages over the TMD for multi-frequency wave spectra due to the intrinsic broadband nature of the NES. In this section the performance for the TMD and the NES acting in heave are compared considering external excitation from irregular wave spectra. A baseline case with no DVA is given in Sect. 3.4.1, and then the performance of the TMD and NES are compared in Sect. 3.4.2.

3.4.1 Baseline case with no vibration absorber

Figure 17a plots the maximum pitch displacement for each sea state and identifies the parametric resonance region within the white dashed line. Figure 17b shows the same information, but uses contour lines (each contour line represents 0.01 rad) in order to better highlight the results. In particular, the synchronous location of the identified parametric resonance region and the area where the density of the contour lines increases, provides confidence in the procedure employed to identify parametric resonance in irregular wave spectra. Regarding the baseline values for the performance criteria, the parametric resonance region ratio¹$u^*_0=0.417$ and the minimal normalized wave amplitude to generate parametric resonance $A^*_0=0.07$.

3.4.2 Comparison of TMD and NES acting in heave

The performance of the DVAs will be optimized and assessed considering $\varepsilon =0.05$, which is the same mass ratio value used for the regular waves in Sect. 3.2. The results for the TMD acting in heave are shown in Fig. 18, revealing the TMD is able to completely eliminate the occurrence of parametric resonance in the area of interest for a relatively wide range of spring and damper values. In comparison, Fig. 19 shows that the NES acting in heave is unable to completely eliminate the occurrence of parametric resonance, thus the TMD has displayed the superior ability to suppress the occurrence of parametric resonance in both regular and irregular waves.

Fig. 18

Results of the TMD acting in heave, for each couple of absorber’s natural frequency ratio $\gamma _{\mathrm{a}}$ and damping ratio $\zeta _{\mathrm{a}}$ ($\varepsilon =0.05$), a illustrates the ratio of unstable area in the frequency/amplitude space, while b indicates the minimal normalize amplitude at which instability occurs

Fig. 19

Results of the NES acting in heave, for each combination of pseudo-natural frequency ratio $\kappa _{\mathrm{a}}$ and damping ratio $\zeta _{\mathrm{a}}$ ($\varepsilon =0.05$), a illustrates the ratio of unstable area in the frequency/amplitude space, while b indicates the minimal normalize amplitude at which instability occurs

Further analysis and comparison of the results is given in Fig. 20, which shows contour plots of the maximum pitch displacement over the range of considered sea states for the optimal DVA parameter combinations. Figure 20a plots the TMD results, using the parameters from point 1 in Fig. 18, where the maximum pitch displacement is almost entirely below 0.03 rads. The maximum pitch displacement values over the entire frequency-amplitude space in Fig. 20a are comparable to the values for the baseline case that fall outside of the parametric resonance region in Fig. 17.

For the NES, two optimal values are considered and shown in Fig. 20b, c, corresponding to points 1 and 2 in Fig. 19, respectively. Similar to the case for the regular waves, the NES has an optimal performance region around $\kappa _a=0.1$ and then another region for very low spring coefficient values, $\kappa _a\le 0.001$, which behaves similar to a Lancaster damper. Although the parametric resonance region ratio value is similar for the two NES configurations, Fig. 20b shows that the Lancaster damper type configuration, increases the region, relative to the baseline case, where the pitch motion is catastrophically unstable and the buoy capsizes.

Fig. 20

Comparison of the maximum pitch displacement over the a TMD acting in heave using the parameters from point 1 in Fig. 18, b NES acting in heave using the parameters from point 1 in Fig. 19 and c NES acting in heave using the parameters from point 2 in Fig. 19. The contour lines represent a 0.01 rad increase in max pitch displacement

Additional comparison between the DVA performances in irregular waves is given in Fig. 21, which shows the maximum DVA displacements for the corresponding simulations in Fig. 20. Here, it can be seen the Lancaster damper type configuration of the NES with a very low spring value, Fig. 21b, requires extremely large, infeasible stroke displacements, similar to the case for the regular waves, whereas the other NES configuration in Fig. 21c requires much smaller stroke displacements. Comparing the maximum DVA displacements for the TMD in Fig. 21a with the results for the regular waves in Fig. 6c shows slightly smaller DVA displacements in the irregular waves; however, the TMD stroke displacement required for the TMD in heave are still quite large.

Fig. 21

Comparison of the maximum DVA stroke displacement. a The TMD acting in heave using the parameters from point 1 in Fig. 18, b the NES acting in heave using the parameters from point 1 in Fig. 19 and c the NES acting in heave using the parameters from point 2 in Fig. 19

3.5 Comparative analysis

The results from the comparative analysis clearly show that DVAs acting in heave outperform the DVAs acting in pitch. This agrees with the findings in [16, 17] that reducing the heave oscillations is the most beneficial means to mitigate parametric resonance in pitch/roll. Parametric resonances are a sort of self-excited oscillations, generated by a harmonically varying stiffness term, which for the system under study is $\rho gA_CL_Dx_3x_5/2$. The DVA acting in heave directly reduces the heave oscillation amplitude $x_3$ acting against forced vibrations, therefore reducing the amplitude of the varying stiffness term. On the contrary, the TMD acting in pitch has practically no effect on heave oscillations, but it increases the damping of pitch oscillations, thus preventing, to some extent, the onset of parametric resonances.

Another significant benefit of applying to the DVA to the heave rather than pitch DoF is that DVA acting in heave would also be able to suppress parametric resonance in the roll DoF. Although this study only considered a 2 DoF system, heave and pitch, parametric resonance is activated in roll by the same means as in pitch, therefore the DVA acting in heave can suppress both parametric resonance in pitch and roll. By comparison, the DVA in pitch would have no effect on the roll DoF; therefore, a second DVA would need to be implemented in roll. Thus, the single DVA acting in heave is much more efficient and practical than requiring two separate DVAs acting in the rotational DoFs. Similarly, although out of the scope of the present paper, the implementation of DVAs acting in both the heave and pitch DoFs at the same time can be considered, in order to investigate if utilizing multiple DVAs can enhance the suppression of parametric resonance enough to justify the added complexity to the system.

The results from the comparative analysis also demonstrate that the TMDs outperformed the NESs. This is probably due to the nature of parametric resonances, which are related to a relatively narrow frequency band, despite waves having a broad frequency content. Therefore, the TMD can work efficiently for the whole frequency range of interest. Indeed, previous studies revealed that the TMD frequency band of operation can be enlarged if its damping and natural frequency are properly tuned [74]. This observation practically eliminates the advantage of the NES, of being able to resonate in a broad frequency range. Additionally, the NES requires a minimum energy threshold in the primary system to be activated, probably limiting its effectiveness. Conversely, the TMD, being a linear device, is not affected by the energy level, at least within the limits of validity of the mechanical model adopted.

TMD displacement poses a practical limit on its feasibility. In the irregular wave spectra, the results in Fig. 21a showed the maximum TMD displacement values approximately increase linearly with the significant wave amplitude, requiring an 8–9 times greater stroke displacement than the significant wave height. For the regular wave case, in Fig. 6c, the TMD displacement is over 10 times greater than the wave amplitude. In a realistic system, it would be necessary to constrain the physical stroke length of the DVA system, resulting in end-stop collisions whose effects should be added to the model and assessed in future work, following methods such as those used for the vibro-impact WEC [75].

An interesting result emerging from the wide sweep of the DVA parameter values was the identification of a Lancaster damper-type system, which is a mass and damper without a spring, being a theoretically good means of suppressing parametric resonance after it occurs (but not at mitigating it before it starts). The Lancaster damper provides a sort of self-detuning mechanism, where the pitch rotations cause a centrifugal force on the DVA mass, which accelerates the DVA mass away from its resting position. The displaced DVA mass alters the mass distributions within the cylinder, thereby changing the moment of inertia which shifts the pitch natural frequency and detunes the parametric resonance. Although this is a theoretically interesting application, the results showed that such a system requires unrealistically large stroke displacements thus is not practically feasible.

4 Conclusion

The ability of different DVA configurations to suppress the occurrence of heave induced parametric pitch motion in a floating cylinder was assessed via simulation using a 2 DoF coupled heave-pitch numerical model. Two prominent DVA methods, the TMD and the NES, were considered, in combination with the DoF in which they acted, either on the heave motion or the pitch motion. The results demonstrated that suppressing parametric resonance in the pitch DoF is far more efficiently achieved by applying a DVA to the heave DoF than applying a DVA to the pitch DoF. In addition, the TMD demonstrated superior performance to the NES in both DoFs and in single frequency regular waves as well as multi-frequency irregular waves. Therefore, the TMD acting in the heave DoF was most effective at suppressing the occurrence of parametric resonance, however the maximum displacement/stroke length required by the TMD acting in heave became quite large as the wave amplitude increased, therefore further work is required to understand its performance in stroke-limited situations involving end-stop collisions.

Appendices

A Derivation of models

In order to obtain the equations of motion of the system in Fig. 3a, we adopt the Lagrangian equation of second kind, at first neglecting the hydrodynamic contribution, which are considered as generalized forces. The kinetic energy of the system (excluding hydrodynamic contribution) is given by

$$\begin{aligned} T=\frac{1}{2}M\dot{x}_3^2+\frac{1}{2}I_5\dot{x}_5^2+\frac{1}{2}m_\mathrm{a3}v_\mathrm{a3}^2, \end{aligned}$$

(19)

where $v_\mathrm{a3}$ is the absolute value of the absorber’s linear velocity. Considering a Cartesian coordinate system, the absorber velocity $\mathbf{v}_\mathrm{a3}$ can be defined as

$$\begin{aligned} \mathbf{v}_\mathrm{a3}=\left[ \begin{array}{l} \dot{{\tilde{x}}}_\mathrm{a3}\sin (x_5)+\left( {\tilde{x}}_\mathrm{a3}+l_0\right) \dot{x}_5\cos (x_5)\\ \dot{x}_3+\dot{{\tilde{x}}}_\mathrm{a3}\cos (x_5)-\left( {\tilde{x}}_\mathrm{a3}+l_0\right) \dot{x}_5\sin (x_5) \end{array}\right] , \end{aligned}$$

(20)

where ${\tilde{x}}_\mathrm{a3}$ is the position of the absorber’s mass when the absorber’s spring is at rest. The absorber’s spring is assumed at rest when the absorber’s mass is at a height $l_0$ above the buoy’s CoM.

Fig. 22

Code-to-code verification of the results for the harmonic balance method (a) and (c) and the direct numerical simulations (b) and (d), for the heave (left) and pitch (right) displacements with no TMD

The square of the velocity of aborber’s mass is then

$$\begin{aligned} v_\mathrm{a3}^2= & {} \dot{x}_3^2+\left( {\tilde{x}}_\mathrm{a3}+l_0\right) ^2\dot{x}_5^2+\dot{{\tilde{x}}}_\mathrm{a3}^2\nonumber \\&+\,\dot{x}_3\left( 2\cos (x_5)\dot{{\tilde{x}}}_\mathrm{a3}-2\sin (x_5)\left( {\tilde{x}}_\mathrm{a3}+l_0\right) \dot{x}_5\right) .\nonumber \\ \end{aligned}$$

(21)

We then define the potential energy function of the system, including the gravitational potential energy of the absorber mass and the elastic potential energy. The gravitational potential energy of the buoy is neglected, since it is compensated by hydrodynamic forces. We have

$$\begin{aligned} U= & {} \frac{1}{2}k_{\mathrm{1}}{\tilde{x}}_\mathrm{a3}^2+\frac{1}{3}k_{\mathrm{2}}{\tilde{x}}_\mathrm{a3}^3 +\frac{1}{4}k_3x_\mathrm{a3}^4\nonumber \\&+m_\mathrm{a3}g\left( x_3+\left( {\tilde{x}}_\mathrm{a3}+l_0\right) \cos (x_5)\right) . \end{aligned}$$

(22)

The spring restoring force function is assumed having a linear, a quadratic and a cubic term, which are designed such that the spring behaves either linearly or as a purely cubic spring around the equilibrium point, as detailed below. The dissipation function is

$$\begin{aligned} D=\frac{1}{2}b_{\mathrm{a3}}\dot{x}_\mathrm{a3}^2. \end{aligned}$$

(23)

We then apply the Lagrange’s equation

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{dt}}\left( \frac{\partial L}{\partial \dot{q}_j}\right) -\frac{\partial L}{\partial q_j}+\frac{\partial D}{\partial \dot{q}_j}=Q_j, \end{aligned}$$

(24)

where $L=T-U$ and $q_j$ is either $x_3$, $x_5$ and ${\tilde{x}}_\mathrm{a3}$, for the three equations of motion, and $Q_j$ accounts for hydrodynamic forces and inertial effects related to the water. We then attain

$$\begin{aligned}&(M+m_\mathrm{a3})\ddot{x}_3-m_\mathrm{a3}\left( {\tilde{x}}_{\mathrm{a3}}+l_0\right) \ddot{x}_5\sin (x_5)\nonumber \\&\quad -\,2m_\mathrm{a3}\dot{x}_5\sin (x_5)\dot{{\tilde{x}}}_\mathrm{a3}-m_\mathrm{a3}\left( {\tilde{x}}_{\mathrm{a3}}+l_0\right) \dot{x}_5^2\cos (x_5)\nonumber \\&\quad +\,m_\mathrm{a3}\cos (x_5)\ddot{{\tilde{x}}}_\mathrm{a3}+m_\mathrm{a3}g\nonumber \\&=F_3\left( x_3,x_5,\dot{x}_3,\dot{x}_5,\ddot{x}_3,\ddot{x}_5;t\right) \end{aligned}$$

(25)

$$\begin{aligned}&\left( I_5+m_\mathrm{a3}\left( {\tilde{x}}_{\mathrm{a3}}+l_0\right) ^2\right) \ddot{x}_5\nonumber \\&-m_\mathrm{a3}\left( {\tilde{x}}_{\mathrm{a3}}+l_0\right) \ddot{x}_3\sin (x_5)+\,2m_\mathrm{a3}\left( {\tilde{x}}_{\mathrm{a3}}+l_0\right) \dot{x}_5\dot{{\tilde{x}}}_\mathrm{a3}\nonumber \\&\quad -\,m_\mathrm{a3}g\left( {\tilde{x}}_{\mathrm{a3}}+l_0\right) \sin \left( x_5\right) \nonumber \\&\quad =F_5\left( x_3,x_5,\dot{x}_3,\dot{x}_5,\ddot{x}_3,\ddot{x}_5;t\right) \end{aligned}$$

(26)

$$\begin{aligned}&m_\mathrm{a3}\ddot{{\tilde{x}}}_\mathrm{a3}+m_\mathrm{a3}\ddot{x}_3\cos (x_5)-m_\mathrm{a3}\dot{x}_5^2\left( {\tilde{x}}_{\mathrm{a3}}+l_0\right) \nonumber \\&\quad +\,k_1 {\tilde{x}}_{\mathrm{a3}}+k_2{\tilde{x}}_{\mathrm{a3}}^2+k_3{\tilde{x}}_{\mathrm{a3}}^3+m_\mathrm{a3}g\cos (x_5)\nonumber \\&\quad +b_{\text{ a }}\dot{{\tilde{x}}}_{\mathrm{a3}}=0. \end{aligned}$$

(27)

We neglect the term $m_\mathrm{a3}g$ in Eq. (25), since it is a negligible static term compensated by hydrostatic forces included in $F_3$.

In order to have the equilibrium position of the absorber’s mass corresponding to the CoM of the buoy—i.e. ${\tilde{x}}_{\mathrm{a3}}=-l_0$—we impose that $l_0$ is such that

$$\begin{aligned} gm_\mathrm{a3}=k_1l_0-k_2l_0^2+k_3l_0^3. \end{aligned}$$

(28)

Equation (28) is obtained by imposing all variables and their derivatives equal to zero in Eq. (27), except ${\tilde{x}}_{\mathrm{a3}}=-l_0$. We then substitute a new variable $x_{\mathrm{a3}}={\tilde{x}}_{\mathrm{a3}}+l_0$ into Eqs. (25)–(27), where $x_{\mathrm{a3}}$ marks the relative displacement of the absorber’s mass starting from the buoy CoM, obtaining

$$\begin{aligned}&(M+m_\mathrm{a3})\ddot{x}_3-m_\mathrm{a3} x_{\mathrm{a3}}\ddot{x}_5\sin (x_5)\nonumber \\&\quad -2m_\mathrm{a3}\dot{x}_5\sin (x_5)\dot{x}_{\mathrm{a3}} -\,m_\mathrm{a3} x_{\mathrm{a3}}\dot{x}_5^2\cos (x_5)\nonumber \\&\quad +m_\mathrm{a3}\cos (x_5)\ddot{x}_{\mathrm{a3}}\nonumber \\&\quad =\,F_3\left( x_3,x_5,\dot{x}_3,\dot{x}_5,\ddot{x}_3,\ddot{x}_5;t\right) \end{aligned}$$

(29)

$$\begin{aligned}&\left( I_5+m_\mathrm{a3} x_{\mathrm{a3}}^2\right) \ddot{x}_5-m_\mathrm{a3} x_{\mathrm{a3}}\ddot{x}_3\sin (x_5)\nonumber \\&\quad +\,2m_\mathrm{a3} x_{\mathrm{a3}}\dot{x}_5\dot{x}_{\mathrm{a3}}-m_\mathrm{a3}g x_{\mathrm{a3}}\sin \left( x_5\right) \nonumber \\&\quad =\,F_5\left( x_3,x_5,\dot{x}_3,\dot{x}_5,\ddot{x}_3,\ddot{x}_5;t\right) \end{aligned}$$

(30)

$$\begin{aligned}&m_\mathrm{a3}\ddot{x}_{\mathrm{a3}}+m_\mathrm{a3}\ddot{x}_3\cos (x_5)-m_\mathrm{a3}\dot{x}_5^2 x_{\mathrm{a3}}\nonumber \\&\quad +\,\left( k_1-2k_2l_0+3k_3l_0^2\right) x_{\mathrm{a3}}+\left( k_2-3k_3l_0\right) x_{\mathrm{a3}}^2\nonumber \\&\quad +k_3 x_{\mathrm{a3}}^3+\,\left( -k_1l_0+k_2l_0^2-k_3l_0^3\right) \nonumber \\&\quad +m_\mathrm{a3}g\cos (x_5)+b_{\mathrm{a}}\dot{x}_{\mathrm{a3}}=0. \end{aligned}$$

(31)

We then choose $k_2=3k_3l_0$, such that the absorber’s spring restoring force has no quadratic component. Then, we call $k_{\mathrm{a3}}=k_1-2k_2l_0+3k_3l_0^2=k_1-3k_3l_0^2$ and $k_{\mathrm{nl}3}=k_3$. Therefore, we can rewrite the equations of motion as

$$\begin{aligned}&(M+m_\mathrm{a3})\ddot{x}_3-m_\mathrm{a3} x_{\mathrm{a3}}\ddot{x}_5\sin (x_5)\nonumber \\&\quad -2m_\mathrm{a3}\dot{x}_5\sin (x_5)\dot{x}_{\mathrm{a3}} -\,m_\mathrm{a3} x_{\mathrm{a3}}\dot{x}_5^2\cos (x_5)\nonumber \\&\quad +m_\mathrm{a3}\cos (x_5)\ddot{x}_{\mathrm{a3}}\nonumber \\&\quad =\,F_3\left( x_3,x_5,\dot{x}_3,\dot{x}_5,\ddot{x}_3,\ddot{x}_5;t\right) \end{aligned}$$

(32)

$$\begin{aligned}&\left( I_5+m_\mathrm{a3} x_{\mathrm{a3}}^2\right) \ddot{x}_5-m_\mathrm{a3} x_{\mathrm{a3}}\ddot{x}_3\sin (x_5)\nonumber \\&\quad +\,2m_\mathrm{a3} x_{\mathrm{a3}}\dot{x}_5\dot{x}_{\mathrm{a3}}-m_\mathrm{a3}g x_{\mathrm{a3}}\sin \left( x_5\right) \nonumber \\&\quad =\,F_5\left( x_3,x_5,\dot{x}_3,\dot{x}_5,\ddot{x}_3,\ddot{x}_5;t\right) \end{aligned}$$

(33)

$$\begin{aligned}&m_\mathrm{a3}\ddot{x}_{\mathrm{a3}}+m_\mathrm{a3}\ddot{x}_3\cos (x_5)-m_\mathrm{a3}\dot{x}_5^2 x_{\mathrm{a3}}+k_{\mathrm{a3}} x_{\mathrm{a3}}\nonumber \\&\quad +\,k_{\mathrm{nl}3} x_{\mathrm{a3}}^3-m_\mathrm{a3} g+m_\mathrm{a3}g\cos (x_5)\nonumber \\&\quad +b_{\mathrm{a3}}\dot{x}_{\mathrm{a3}}=0. \end{aligned}$$

(34)

If the absorber under consideration is a TMD, then we should have $k_2=k_3=0$ and $m_\mathrm{a3} g=k_1l_0$, such that $k_{\mathrm{nl}3}=0$. Conversely, in the case of an NES, we should impose $k_1=3k_3l_0^2$, such that $k_{\mathrm{a3}}=0$.

We notice that realizing a spring which satisfies the requirements of an NES is very challenging. However, the practical realization of such a system is out of the scope of this research.

B Verification of harmonic balance method against direct numerical simulation

The results for the code-to-code verification between the HBM and direct numerical simulations is shown in Fig. 22, which considers the baseline case with no attached DVA presented in Sect. 3.1. The results look qualitatively the same and quantitatively the values for the two performance criteria metrics are also the same. The minimum normalized wave amplitude which generates parametric resonance for the direct numerical simulations is: $A^*=0.011$, and the parametric resonance region ratio is: $u^*=0.36$, which agree with the values obtained by the HBM in Sect. 3.1.