Dynamics and integrability of the swinging Atwood machine generalisations

Abstract

This paper studies the dynamics and integrability of two generalisations of a 3D Swinging Atwood’s Machine with additional Coulomb’s interactions and Hooke’s law of elasticity. The complexity of these systems is presented with the help of Poincaré cross sections, phase-parametric diagrams and Lyapunov exponents spectrums. Amazingly, such systems possess both chaotic and integrable dynamics. For the integrable cases we find additional first integrals and we construct general solutions written in terms of elliptic functions. Moreover, we present bifurcation diagrams for the integrable cases and we find resonance curves, which give families of periodic orbits of the systems. In the absence of the gravity, both models are super-integrable.

1 Introduction

An amazing property of the laws of nature is the fact that analytical formulas can be used to describe simple models that are built to illustrate these properties. Such models are said to be solvable. This property is closely related with conservation laws. In the case of models described by ordinary differential equations

$$\begin{aligned} {\dot{\varvec{x}}}=\varvec{v}(\varvec{x}),\qquad \varvec{x}=(x_1,\ldots ,x_n)\in \mathbb {R}^n, \end{aligned}$$

(1)

the conservation laws are first integrals. A first integral of equations of motion (1) is a non-constant scalar function $F(\varvec{x}):\mathbb {R}^n\rightarrow \mathbb {R}$, which does not change during time evolution of the system, i.e., $F (\varvec{x}(t)) = F (\varvec{x}(0))$ for an arbitrary t. If we are able to find a large enough number of independent first integrals, then the system is called integrable and its solutions can be found. However, the absence of first integrals indicates that the behaviour of our system is complicated or chaotic. If we know only a few first integrals (fewer than the number necessary for integrability), we can reduce the dimension of the system.

For most systems of a physical origin, the best-known examples of first integrals are the energy, linear momentum, and angular momentum of the system. These properties are directly related to conservations of certain physical quantities. Moreover, even in a case of simple models, the universal conservation laws are not sufficient to describe them analytically. For instance, to solve the heavy top problem, it is not enough to know the laws of conservation of energy, and the conservation of the projection of the angular momentum into vertical directions. Additional first integrals exist only for special inertia tensor and the location of the fixed point in the body. Moreover, distinguishing exceptional cases when the heavy top problem is integrable is not at all obvious.

A second system we discuss which is integrable for a certain set of values of parameters is the classical Swinging Atwood’s Machine (SAM). This is an ordinary Atwood’s machine in which one of the weights can swing in a plane. This model, which is the system of two degrees of freedom, was intensively studied by Tufillaro and co-workers, see [1,2,3,4,5,6,7]. They performed a numerical analysis via the Poincaé sections and they showed that for most values of the mass ratio $M/m>1$ SAM is not integrable displaying highly chaotic behavior. However, as they noted, for the mass ratio $M/m=4n^2-1$ where $n\in \mathbb {Z}$, the system behaves less chaotically and motion looks regular. Indeed, after introducing the parabolic coordinates, Tufillaro in [8] showed that Hamilton–Jacobi equation for the classical SAM system for $M/m=3$ is separable and the equations of motion can be solved in terms of elliptic functions, which is quite unusual for systems with two degrees of freedom.

For some time, it was unclear whether SAM system could have other integrable cases. However, after five years of research, thanks to new criterion for the integrability of homogeneous Hamiltonian systems obtained by Yoshida in [9], the non-integrability of the system for $M/m\ne \mu _p$, where $\mu _p=p(p+1)/(p(p+1)-4)$ for every integer $p>2$ was proved [5]. This result was later completed for the case $p=2$ in [10] by Martínez and Simó.

Currently, the SAM is considered to be a paradigm of a simple, mechanical system that exhibits chaotic as well as regular properties. Indeed, one can find numerous web pages and video clips devoted to constructions of real SAM models and reviews of its dynamics. However, it seems that a study of the dynamics and integrability of certain generalisations of the SAM model do not attract sufficient attention. To the best of our knowledge, only two modifications of the classical SAM system exist, both of which were considered in [11,12,13,14]. Both systems, however, manifest complicated and, in fact, not integrable dynamics for all values of the parameters.

The only integrable generalisation of the SAM model that was found was the one from a three-dimensional swinging Atwood’s machine [15]. As in the 2D version, the problem is integrable when the mass ratio $M/m=3$. However, what is particularly interesting is the fact that the additional first integral is a polynomial of the fourth degree with respect to momenta. Unlike the 2D case with quadratic first integrals, integrable Hamiltonian systems with first integrals of higher degree do not necessary possess separable solutions of Hamilton-Jacobi equations. Such systems are absolutely unique and only a few examples are known. This is why in our paper we focus on dynamics and integrability studies of two generalized classes of 3D SAM systems with additional Coulomb’s interactions between two point charges and Hooke’s law of elasticity. We show that, in general, both models are not integrable and chaotic. However, for specific values of parameters, the models admit additional first integrals. We use these first integrals to construct general solutions of equations of motion.

The paper is organised as follows: A description of the systems and their complex dynamics analysis is given in Sects. 2 and  3 respectively. For this purpose, we calculate the Poincaré sections, phase-parametric diagrams and Lyapunov exponents spectrums. Moreover, we present the integrable cases that were found and we construct phase-parametric diagrams of the integrable systems as well as the general solutions of equations of motion. The composition of both models and its integrability is discussed in Sect. 4. Final conclusions are drawn in Sect. 5.

2 Model 1: SAM with Coulomb interactions

2.1 Presentation of the system and its equations of motion

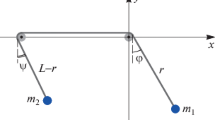
In Fig. 1, the geometry of system under consideration is presented. As in the classical SAM, the model consists of two masses M and m linked by an inextensible string of length l. The mass m is allowed to swing in 3-dimensional space, while the second mass M plays the role of a counterweight and it is constrained to move only along the vertical direction. The constant gravitational field acts on the masses, so their gravitational potential energy is $V_\mathrm {g}=g(m z-M X)$.

We propose the following modification of the classical SAM. Namely, in the centre of the left pulley, we put an electric static point charge Q. The mass m has a charge q, so the Coulomb potential of these two charges is $V_\mathrm {c}=-\gamma / \sqrt{x^2+y^2+z^2}$, where $\gamma$ is proportional to $Q \,q$. We assume that the mass M is electrically neutral.

Fig. 1

Geometry of 3D swinging Atwood’s machine moving in the gravitational and Coulomb potentials. Here M and m are the masses linked by an inextensible string of length l. The mass m swings in 3-dimensional space, while M is constrained to move along the vertical direction. The whole system moves under the influence of the potential (10). The Hamiltonian function corresponding to this model is defined in (9)

The Lagrange function of the system is as follows

$$\begin{aligned} \begin{aligned}&L=T-V,\\&T=\frac{M}{2}\dot{X}^2+\frac{m}{2}\left( \dot{x}^2+\dot{y}^2+\dot{z}^2\right) ,\\&V=g (m z-M X)-\frac{\gamma }{\sqrt{x^2+y^2+z^2}}. \end{aligned} \end{aligned}$$

(2)

The holonomic constraint imposed on the system is

$$\begin{aligned} \sqrt{x^2+y^2+z^2}+X=l. \end{aligned}$$

(3)

Thus, we introduce the spherical coordinates according to the constraint

$$\begin{aligned} x=r \sin \vartheta \cos \varphi ,\;\; y=r\sin \vartheta \sin \varphi , \;\; z=-r \cos \vartheta . \end{aligned}$$

(4)

In these coordinates, the Lagrange function (2) takes the form

$$\begin{aligned} \begin{aligned} L=\left( \frac{m+M}{2}\right) \dot{r}^2+\frac{m}{2}r^2\left( {\dot{\vartheta }}^2+\sin ^2\vartheta {\dot{\varphi }}^2\right) -V(r,\vartheta ), \end{aligned}\nonumber \\ \end{aligned}$$

(5)

where

$$\begin{aligned} V(r,\vartheta )=g r (M-m \cos \vartheta ) -\frac{\gamma }{r}. \end{aligned}$$

(6)

Since $\varphi$ is the cyclic variable, i.e., $\partial L/\partial \varphi =0$, the corresponding generalized momentum

$$\begin{aligned} I=p_\varphi =\frac{\partial L}{\partial {\dot{\varphi }}}=mr^2\sin ^2\vartheta {\dot{\varphi }}=\varPi ={\text {const}}, \end{aligned}$$

(7)

is the first integral of motion. The existence of this first integral corresponds to the axial symmetry of the system. Performing the Legendre transformation

$$\begin{aligned} p_r=\frac{\partial L}{\partial \dot{r}}= (m+M)\dot{r},\quad p_\vartheta =\frac{\partial L}{\partial {\dot{\vartheta }}}=m r^2{\dot{\vartheta }}, \end{aligned}$$

(8)

we obtain the Hamiltonian function

$$\begin{aligned} \begin{aligned}&H_{3D}=\frac{1}{2}\left( \frac{p_r^2}{m+M}+\frac{p_\vartheta ^2}{mr^2}\right) +\frac{\varPi ^2}{2mr^2 \sin ^2\vartheta }+ V(r,\vartheta ). \end{aligned} \end{aligned}$$

(9)

The system has two degrees of freedom and the effective potential reads

$$\begin{aligned} V_{\text {eff}}(r,\vartheta ,\varPi )=\frac{\varPi ^2}{2mr^2 \sin ^2\vartheta }+ V(r,\vartheta ). \end{aligned}$$

(10)

In the case when $\varPi =0$, the pendulum with mass m oscillates on a plane, while for $\varPi \ne 0$, the pendulum can perform spacial oscillations.

Hamilton’s equations of motion generated by Hamiltonian (9) form a system of four first-order ordinary differential equations

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} &{}\dot{r}=\dfrac{p_r}{m+M},\\ &{} \dot{p}_r=\dfrac{p_\vartheta ^2}{mr^3}+\dfrac{\varPi ^2}{mr^3\sin ^2\vartheta }-g (M-m\cos \vartheta )-\dfrac{\gamma }{r^2},\\ &{}{\dot{\vartheta }}=\dfrac{p_\vartheta }{mr^2}, \\ &{}\dot{p}_\vartheta =\dfrac{\varPi ^2\cos \vartheta }{mr^2\sin ^3\vartheta }-g m r\sin \vartheta . \end{aligned} \end{array}\right. } \end{aligned}$$

(11)

The time dependence of cyclic variable $\varphi$ can be determined by

$$\begin{aligned} \varphi (t)-\varphi (t_0)=\int _{t_0}^t\left( \frac{\partial H}{\partial \varPi }\right) \mathrm {d}t. \end{aligned}$$

(12)

2.2 Numerical analysis

2.2.1 Poincaré cross-sections

Fig. 2

Poincaré sections of system (9) made for $M=2,\, m=1,\, g=1,\, \gamma =-0.5, \, \varPi =0$, with gradually increasing energy E. The cross-section plane was specified as $r=1$, with $p_r>0$. The plots indicate the complex dynamics of the system. Each colour corresponds to distinct initial condition

Fig. 3

Poincaré sections of system (9) made for $M=2,\, m=1,\, g=1,\, \gamma =-0.5, \, \varPi =0.25$, with gradually increasing energy E. Cross section plane was specified as $r=1$, with $p_r>0$. The plots present chaotic dynamics of the system. Each colour corresponds to distinct initial condition

We present the complex dynamics of the system under consideration with the help of numerical analysis. Figures 2 and 3 present exemplary Poincaré sections of system (9) with gradually increased values of energy. These plots were constructed for two sets of constant parameters

$$\begin{aligned}&M=2,\;\; m=1,\;\; g=1,\;\; \gamma =-\frac{1}{2},\;\;\varPi =0, \end{aligned}$$

(13)

$$\begin{aligned}&M=2,\;\; m=1,\;\; g=1,\;\; \gamma =-\frac{1}{2},\;\; \varPi =\frac{1}{4}. \end{aligned}$$

(14)

The section plane was specified as $r=1$ and a cross-section is marked on the figure if $p_r>0$. Figure 2 was made for a zero level of the cyclic first integral $\varPi =0$, which implies that mass m moves in the vertical plane. The Poincaré sections visible in Fig. 3 were constructed for a non-zero value of the cyclic first integral, i.e., $\varPi =1/4$, which corresponds to the case that mass m performs spacial oscillations.

Figures 2a and 3a present Poincaré sections for the lowest energies. As is typical in Hamiltonian systems, for energies close to the energy minimum, the patterns are very regular. In the central part, the stable particular periodic solution is visible. It is surrounded by closed loops related to the quasi-periodic motion of the system. They are just intersection of invariant tori. It is noticeable that the amplitude of the oscillations of mass m is very small. We may conclude that for small values of the energy, the system is very close to an integrable one.

The picture becomes more complex when we increase the value of the energy. In Fig. 2b and in Fig. 3b, we can notice that the invariant tori are visibly deformed and some of them decayed into sequences of stable and unstable periodic solutions. For instance, at the prescribed energy levels, the stable particular solutions depicted in the centre of Figs. 2a and 3a have been bifurcated, which led to the emergence of stable periodic solutions enclosed by the remains of the separatrix. Moreover, we observe the first signs of chaotic behaviour of the system visible in the plane as scattered points appearing in the regions where the separatrices where located.

The last pair of Poincaré sections, visible in Figs. 2c and 3c, show highly chaotic stages of the system dynamics. Indeed, almost all invariant tori located in the central parts decayed into the global chaos. For a not integrable Hamiltonian system, these random-looking points correspond to the fact that trajectories can freely wander over larger regions of a phase space. Trajectories (in contrary to those in an integrable system) are no longer confined to surfaces of a set of nested tori, but they begin to move outside the tori. We may conclude that the Hamiltonian (9), for the prescribed values of the parameters, is highly not integrable.

2.2.2 Spectrum of Lyapunov exponents

The Poincaré sections visible in Figs. 2 and 3 show the beauty of coexistence of three types of motion: periodic (finite numbers of points of orbit in the cross-section plane), quasi-periodic, and chaotic (scattered points). However, from these plots, we cannot deduce any information about the strength of chaos. For this purpose, the Lyapunov exponents can be computed. The use of Lyapunov exponents is an essential tool for quantifying chaos in dynamical systems. It measures the exponential divergence of two close trajectories (orbits) in a phase space. According to the chaos theory, for autonomous differential systems, chaos appears when at least one Lyapunov exponent is positive [16, 17].

In this paper, we use the standard algorithm introduced by Benettin et al. [18]. This method is based on the successive integrations of variational equations for n initial conditions together with applications of the Gram-Schmidt orthonormalization procedure, see also [19]. This procedure can be effectively implemented in Mathematica [20]. We adopt a sufficient amount of k steps, so that the convergence of Lyapunov exponents is assured.

Figure 4 presents the Lyapunov exponents spectrum of the system (11) made for constant values of the parameters (14) with the initial conditions

$$\begin{aligned} r_0=1.05,\quad \dot{r}_0={\dot{\vartheta }}_0=0,\quad \text {where}\quad \vartheta _0\in (0,\pi ), \end{aligned}$$

(15)

is the control parameter. Here, $\{\lambda ,\lambda _2,\lambda _3,\lambda _4\}$ denotes the full spectrum, where $\lambda \equiv \lambda _1$ is the largest Lyapunov exponent. Figure 4 presents how the change of the initial swing angle of the pendulum (with zero initial velocities) affects the dynamics of the system. We can observe the coexistence of regular and chaotic behaviour depending on the values of the control parameter. Specifically, regions of the spectrum with positive values of $\lambda$ are responsible for chaotic motion of the system, while regions with $\lambda \approx 0$ indicate regular (non-chaotic) behaviour. First, we can notice that the spectrum obeys the pairing rule, i.e., Lyapunov exponents appear in additive inverse pairs. This is due to the time reversibility of the Hamiltonian vector field (11). Moreover, the existence of the first integral, which is the conservation of the energy $H=E$, implies that one pair of Lyapunov exponents is zero [18, 21,22,23]. Hence, for the Hamiltonian system (11), which is the system of two degrees of freedom, the possible spectrum is $\{\lambda ,0,0,-\lambda \}$. In the case considered, the maximum pick value of $\lambda$ is at point $\vartheta _0\approx 2.9$, where $\lambda \approx 0.05$.

Fig. 4

Lyapunov exponents spectrum of system (11) versus the initial swinging angle $\vartheta _0\in (0,\pi )$ with the initial condition $(r_0=1.05,\,\vartheta _0=\vartheta _0,\,\dot{r}_0={\dot{\vartheta }}_0=0)$. The constant parameters where chosen as: $M=2,\, m=1,\, g=1,\, \gamma =-0.5, \, \varPi =0.25$. Here, $\{\lambda ,\lambda _2,\lambda _3,\lambda _4\}$ denotes the full spectrum, where $\lambda \equiv \lambda _1$ is the largest Lyapunov exponent. The intervals with positive values of $\lambda$ are responsible for the chaotic motion of the system, while the regions with $\lambda \approx 0$ indicate regular (non-chaotic) behaviour

2.2.3 Phase-parametric diagram

Fig. 5

The phase-parametric diagram of system (11) versus the initial swing angle $\vartheta _0$. The diagram is combined together with the maximal Lyapunov exponent $\lambda$, where the colour scale is proportional to the value of $\lambda$. The diagram displays the extreme values of $\vartheta (t)$ when ${\dot{\vartheta }}(t_\star )=0$ with the change of $\vartheta _0$. We can observe the very good agreement of the phase-parametric diagram with $\lambda$. Coexistence of periodic, quasi-periodic and chaotic orbits together with ,,periodic windows” between chaotic layers is visible. Parameters where chosen as: $M=2,\, m=1,\, g=1,\, \gamma =-0.5, \, \varPi =0.25$, with the initial condition $(r_0=1.05,\,\vartheta _0=\vartheta _0,\,\dot{r}_0={\dot{\vartheta }}_0=0)$. The coloured labels correspond to the respective initial conditions for which periodic, quasi-periodic and chaotic orbits are plotted in Fig. 6

Fig. 6

Chaotic, quasi-periodic and periodic phase curves of system (11). Parameters where chosen as: $M=2,\, m=1,\, g=1,\, \gamma =-0.5, \, \varPi =0.25$, with the initial condition $(r_0=1.05,\,\vartheta _0=\vartheta _0,\,\dot{r}_0={\dot{\vartheta }}_0=0)$. The respective values of $\vartheta _0$ were taken from the phase-parametric diagram (see the coloured labels in Fig. 5b). Points of intersections with cross-sectional plane, ${\dot{\vartheta }}(t)=0$, are depicted by small bullets

Fig. 7

Chaotic and regular orbits of system (11) plotted in 3D Euclidean space. The plots indicate the spatial oscillations of the pendulum. The parameters where chosen as: $M=2,\, m=1,\, g=1,\, \gamma =-0.5, \, \varPi =0.25$, with the initial condition $(r_0=1.05,\,\vartheta _0=\vartheta _0,\,\dot{r}_0={\dot{\vartheta }}_0=0)$. The respective values of $\vartheta _0$ were taken from the phase-parametric diagram (see the coloured labels in Fig. 5(b))

The spectrum of Lyapunov exponents visible in Fig. 4 gives us an insight into the system dynamics by specifying the intervals of the control parameter $\vartheta _0$ where the chaotic motion takes place. However, from this figure, we are not able to classify whether the regular patterns with $\lambda \approx 0$ are responsible for periodic or quasi-periodic motion. For this purpose, a phase-parametric diagram is very useful. For Hamiltonian systems, the phase-parametric diagram enables the detection of periodic orbits and their families, routes to chaos and ,,periodic windows” between chaotic layers by plotting a state variable as a function of a certain control parameter [24, 25].

Figure 5 presents the phase-parametric diagram of the system (11) constructed for the same values of the parameters (14) and initial conditions (15) as the Lyapunov exponents spectrum visible in Fig. 4. For the calculated phase-parametric diagram, we display the extreme values of $\vartheta (t)$ versus the initial swing angle $\vartheta _0\in (0,\pi )$. That is, for a given initial condition, we numerically integrate equations of motion (11), and we constituted the diagram by sampling points $\vartheta (t_\star )$ periodically when ${\dot{\vartheta }}(t_\star )=0$. In order to make the analysis more effective, we combine the phase-parametric diagram with the maximal Lyapunov exponent $\lambda$. The colour scale is proportional to value of $\lambda$.

Fig. 8

Poincaré sections of system (9) made for $M=3,\, m=1,\, g=1,\, \gamma =-0.5, \, E=10$. The cross section plane was specified as $r=1$, with $p_r>0$. The plots indicate regular (non-chaotic) behaviour suggesting the integrability of the system. Each colour corresponds to distinct initial condition

At first sight, we observe very good agreement of the phase-parametric diagram with $\lambda$. Moreover, while not being visible via Lyapunov exponents, we can distinguish from the regular regimes periodic and quasi-periodic orbits. This is due to the fact that we plot the amplitudes of $\vartheta (t)$ not its time series as was done for another model in [26]. Thanks to that, we are able to select from the computed phase-parametric diagram the values of the control parameter, $\vartheta _0$, for which the system possesses periodic, quasi-periodic and chaotic behaviours. The exemplary values of $\vartheta _0$ corresponding to these types of motion are marked on the x-axis of Fig. 5b. For better understanding, we also plot these particular orbits with marked points of intersections plane ${\dot{\vartheta }}(t)=0$ in Fig. 6.

Figure 5 shows, moreover, that for the initial range of $\vartheta _0$ the system performs regular, quasi-periodic oscillations up to the point $\vartheta _0\approx 0.125$, where the periodic solution appeared. However, we claim that this periodic solution is unstable because in the right-neighbourhood of this point: at $\vartheta _0\approx 0.13$, to be precise, we observe the chaotic behaviour in terms of the large pick with $\lambda \approx 0.038$. Further, over the range $\vartheta _0\in (0.13,2.02]$, the motion is regular with mostly quasi-periodic orbits. As $\vartheta _0$ is increased, the regular pattern diverges up to the appearance of global chaos, where the orbits’ maxima densely occupy the large admissible region. However, as is evidenced in Fig. 5c, even for very large values of the initial amplitude $\vartheta _0$, we still detect stable solutions localized in the gaps (windows) between completely chaotic regions. Finally, Fig. 7 shows the regular and chaotic orbits of system (11) plotted in 3D Euclidean space. These plots confirm that the motion of the pendulum is spatial. Respective values of $\vartheta _0$ were taken from the phase-parametric diagram (see the coloured labels in Fig. 5b and also Fig. 6).

2.3 Integrability

2.3.1 The separable case

From the Poincaré sections, the phase-parametric diagram and Lyapunov exponents spectrum, we can conclude so far that the system seems to be not integrable. However, numerical analysis was performed for certain fixed values of the parameters. For other values, the dynamics can be completely different and the system can be even integrable. For instance, Fig. 8 presents the Poincaré sections of the system obtained for values of parameters

$$\begin{aligned} M=3,\quad m=1,\quad g=1,\quad \gamma =-0.5, \end{aligned}$$

(16)

at energy level $E=10$. As we can notice, even for such high value of the energy, the dynamics of the system is very regular. Moreover, the Lyapunov exponent spectrum and the phase-parametric diagram (see Figs. 9 and 10) also indicate the presence of an additional first integral, functionally independent with the Hamiltonian. This is because another pair of Lyapunov exponents tends to zero for all values of the initial swing angle $\vartheta \in (0,\pi )$ of the pendulum. Hence, for parameters (16), the numerical analysis excludes chaotic behaviours of the system and, in fact, suggests its integrability. Surprisingly, more detailed numerical analysis (not included) shows that for

$$\begin{aligned} M=3m \quad \text {with}\quad g,\gamma , \varPi \in \mathbb {R}, \end{aligned}$$

(17)

the system seems to be integrable. However, to ensure the integrability, we have to find an additional first integral functionally independent with the Hamiltonian. It seems that for this purpose, the Hamilton–Jacobi theory could be very useful. The main idea of this theory is to introduce an appropriate canonical transformation after which Hamilton’s equations become separable. However, for study the system considered, we perform a separation of variables directly.

Fig. 9

Lyapunov exponents spectrum of system (11) versus the initial swinging angle $\vartheta _0\in (0,\pi )$ with the initial condition $(r_0=1,\,\vartheta _0=\vartheta _0,\,\dot{r}_0={\dot{\vartheta }}_0=0)$. The constant parameters where chosen as: $M=3,\, m=1,\, g=1,\, \gamma =-0.5, \varPi =0.25$. Here, $\{\lambda ,\lambda _2,\lambda _3,\lambda _4\}$ denotes the full spectrum. The plot indicates regular (non-chaotic) behaviour

Fig. 10

The phase-parametric diagram of system (11) versus the initial swing angle $\vartheta _0$. The colour scale is proportional to value of the maximal Lyapunov exponent $\lambda$. The diagram displays the extreme values of $\vartheta (t)$, when ${\dot{\vartheta }}(t_\star )=0$, at a variation of $\vartheta _0$. The constant parameters where chosen as: $M=3,\, m=1,\, g=1,\, \gamma =-0.5, \varPi =0.25$ with the initial condition $(r_0=1,\,\vartheta _0=\vartheta _0,\,\dot{r}_0={\dot{\vartheta }}_0=0)$. We observe periodic and quasi-periodic orbits without any regimes responsible for chaotic behaviour

We consider the case $M=3m$, and (without loss of generality) we set $m=1$. Then, by means of the following canonical change of the variables

$$\begin{aligned} \begin{aligned}&r=\frac{u^2+v^2}{2},\quad \vartheta =2\arctan \left( \frac{u^2-v^2}{2uv}\right) ,\\&p_r=\frac{u p_u+v p_v}{u^2+v^2},\quad p_\vartheta =\dfrac{v p_u-u p_v}{4}, \end{aligned} \end{aligned}$$

(18)

the Hamiltonian (9) reads

$$\begin{aligned} \begin{aligned}&{\widetilde{H}}=\frac{H_u+H_v}{4(u^2+v^2)}+\dfrac{\varPi ^2(u^2+v^2)^2}{8u^2v^2(u^2-v^2)^2},\\&\text {where}\\&H_u = \frac{1}{2}p_u^2 \!+\! 8gu^4\!-\! 4\gamma , \quad H_v = \frac{1}{2}p_v^2 + 8gv^4- 4\gamma . \end{aligned} \end{aligned}$$

(19)

As we can notice, for $\varPi =0$ the system separates. Namely, from equality

$$\begin{aligned} 4(u^2+v^2) {\widetilde{H}}=H_u +H_v, \end{aligned}$$

we separate terms which depend only either on $(u,p_u)$ or $(v,p_v)$. Then, we find that

$$\begin{aligned} F= \frac{v^2H_u-u^2 H_v}{4(u^2+v^2)}, \end{aligned}$$

(20)

is the additional first integral, which is functionally independent with the Hamiltonian (19). Hence, the SAM model with Coulomb’s interactions is integrable at zero level of the cyclic integral, $\varPi =0$.

Performing the inverse change of variables (18) to (20) we get the desired constant of motion written in the polar coordinates. The explicit form of the integrable system becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} H_{2D}=\dfrac{p_r^2}{8}+\dfrac{p_\vartheta ^2}{2r^2}+ g r(3-\cos \vartheta )-\dfrac{\gamma }{r},\\ I_{2D}=r^{-1}\sin \dfrac{\vartheta }{2}p_\vartheta ^2-\dfrac{1}{2}\cos \dfrac{\vartheta }{2}p_rp_\vartheta \\ \quad - gr^2\cos \dfrac{\vartheta }{2}\sin \vartheta -\gamma \sin \dfrac{\vartheta }{2}. \end{array}\right. } \end{aligned}$$

(21)

It is evident that the integrable system (21) is the generalisation of the classical SAM model by the additional term in the potential coming from the Coulomb interaction. We can easily recover the classical SAM by putting $\gamma =0$. Moreover, in the absence of gravitational potential, the system is obviously super-integrable with the additional cyclic first integral, $J=p_\vartheta$.

2.3.2 Bifurcation diagram of the integrable system

In further consideration we put $\varPi =0$ and to simplify analysis, we chose units in such a way that $g=1$.

Let us consider a common level of the first integrals (19)–(20), namely

$$\begin{aligned} {\mathscr {M}}_{h,f} = \left\{ \varvec{x}\in {{\mathscr {M}}}\,|\, {\widetilde{H}}=h, F=f\right\} , \end{aligned}$$

(22)

where $\varvec{x}=(u,v,p_u,p_v)$. It is easy to notice that on the common level (22), the following equalities

$$\begin{aligned} \begin{aligned}&p_u^2=8(\gamma +f+h u^2-2u^4),\\&p_v^2=8(\gamma -f+hv^2-2v^4), \end{aligned} \end{aligned}$$

(23)

are fulfilled. Notice also, that Eq. (23) is invariant under the change

$$\begin{aligned} f\rightarrow -f,\quad u\rightarrow v,\quad p_u\rightarrow p_v. \end{aligned}$$

(24)

Therefore, it is sufficient to consider only positive values of $f\ge 0$ because topological types of level set ${\mathscr {M}}_{h,f}$ for (h, f) and for $(h,-f)$ are the same.

In a generic case, if ${\mathscr {M}}_{h,f}$ is not empty, then it is diffeomorphic to a two dimensional torus. Thus, it is important to know values $(h,f)\in {\mathbb {R}}^2$ such that ${\mathscr {M}}_{h,f}\ne \emptyset$. These values of (h, f) belong to an image of the so-called momentum map

$$\begin{aligned} {\mathbb {R}}^4\ni \varvec{x}\longmapsto {\varvec{\varPhi }}(\varvec{x})=\left( {\widetilde{H}}(\varvec{x}), F(\varvec{x})\right) \in \varSigma \subset {\mathbb {R}}^2, \end{aligned}$$

(25)

A point $\varvec{P}\in {\mathscr {M}}\subset \mathbb {R}^4$ is a critical point of the momentum map if

$$\begin{aligned} {\text {rank}}\mathrm {d}\varvec{\varPhi }(\varvec{P})={\text {rank}}\dfrac{\partial \varvec{\varPhi } }{\partial \varvec{x}}(\varvec{P})<2, \end{aligned}$$

(26)

A set of critical points of the momentum is defined by

$$\begin{aligned} S=\left\{ \varvec{P}\in {\mathscr {M}}\ | \ {\text {rank}}\mathrm {d}\varvec{\varPhi }(\varvec{P})<2\right\} . \end{aligned}$$

(27)

It is an invariant set completely filled with critical trajectories. By condition (27) set S is a union of two disjoint subsets

$$\begin{aligned} \begin{aligned}&S=S_0\cup S_1, \\&S_0=\left\{ \varvec{P}\in {\mathscr {M}}\ | \ {\text {rank}}\mathrm {d}\varvec{\varPhi }(\varvec{P})=0\right\} , \\&S_1=\left\{ \varvec{P}\in {\mathscr {M}}\ | \ {\text {rank}}\mathrm {d}\varvec{\varPhi }(\varvec{P})=1\right\} . \end{aligned} \end{aligned}$$

(28)

In a typical situation, $S_0$ consists of isolated fixed points, while $S_1$ includes families of curves, which are either periodic or asymptotic to unstable equilibria. We refer to such orbits as critical orbits in order to distinguish them from periodic ones that lie in regular level sets with resonant characteristic frequencies.

A bifurcation diagram of an integrable system is defined as a region of possible motions $\varvec{\varPhi }({\mathscr {M}})$ on a plane of first integrals together with the images of the critical sets

$$\begin{aligned} \varSigma =\varSigma _0\cup \varSigma _1,\quad \varSigma _0=\varPhi (S_0),\quad \varSigma _1=\varPhi (S_1), \end{aligned}$$

(29)

depicted on the same plane.

Let us assume that $\varvec{P}\in S_0$. Condition ${\text {rank}}\mathrm {d}\varvec{\varPhi }(\varvec{P})=0$ implies that gradients $\nabla {\widetilde{H}}(\varvec{P})$ and $\nabla F(\varvec{P})$ restricted to ${\mathscr {M}}$ vanish. Hence, one may conclude that $S_0$ coincides with the set of equilibria of the Hamiltonian vector field. Indeed, set $S_0$ is defined by the equations

$$\begin{aligned}&p_u=0,\quad p_v=0,\quad v^2=u^2,\quad \gamma =-2u^4, \end{aligned}$$

(30)

$$\begin{aligned}&p_u=0, \quad p_v=0,\quad v=0,\quad \gamma =-u^4. \end{aligned}$$

(31)

Using the relation (23), we can show that in terms of parameters $(\gamma ,f, h)\in \mathbb {R}^3$ and variables $(u,v)\in \mathbb {R}^2$ image $\varSigma _0$ of set $S_0$ on a plane of first integrals (h, f) consists of two families of distinct fixed points $P_1, P_2$, such that

$$\begin{aligned} \begin{aligned}&P_1:\quad \gamma <0,\quad h=2\sqrt{2 |\gamma |},\quad f=0,\end{aligned} \end{aligned}$$

(32)

with $u^2= v^2=h/4$,

$$\begin{aligned} \begin{aligned}&P_2:\quad \gamma <0,\quad h=4\sqrt{ |\gamma |},\quad f= |\gamma |, \end{aligned} \end{aligned}$$

(33)

with $v=0$ and $u^2=h/4$.

Fig. 11

The three-dimensional bifurcation diagram of the integrable system (19) presenting the region of possible motions $\varvec{\varPhi }({\mathscr {M}})$ depicted in $(\gamma ,h,f)$-space. The diagram is symmetric about f-axis and it consists of four admissible regions separated by bifurcation curves. Each region corresponds to a distinct dynamical behavior of the system. For better understanding, see Fig. 12, which presents projections of the bifurcation diagram to a plane of first integrals (h, f) for $\gamma =\pm 1$

Fig. 12

A projection of a three-dimensional bifurcation diagram (see Fig. 11) restricted to (h, f)-plane with the numbering of domains. Each region corresponds to a distinct dynamical behavior of the system, see Fig. 13, in which exemplary quasi-periodic solutions are plotted. Here, $\sigma _i \in \varSigma _1$ are the critical (bifurcation) curves defined in Eqs. (38)–(39). At these degenerated curves, exceptional families of particular periodic solutions appeared, see Fig. 14

In order to find set $S_1$ of critical periodic orbits $\sigma _i\in \varSigma _1$, we need to specify the conditions when ${\text {rank}}\mathrm {d}\varPhi (P)=1$ for $P\in S_1$. This indicates that gradients $\nabla {\widetilde{H}}(\varvec{P})$ and $\nabla F(\varvec{P})$ are parallel at P. It transpires that the only possible critical periodic solutions contained in $S_1$ are determined by two different families of equations

$$\begin{aligned}&p_v=0, \quad p_u^2=16\left( v^4+2v^2u^2-u^4+\gamma \right) , \end{aligned}$$

(34)

$$\begin{aligned}&p_v=0,\quad v=0. \end{aligned}$$

(35)

Eliminating the momenta by relation (23), we obtain

$$\begin{aligned}&4v^2-h=0,\quad 2v^4-f+\gamma =0, \end{aligned}$$

(36)

$$\begin{aligned}&f=\gamma ,\quad v=0. \end{aligned}$$

(37)

We remark that one can obtain the mirror family of the above equations by a change of variables defined in (24). Taking into account that the coordinates (u, v) and momenta (23) must be real, we can easily determine admissible range of critical (bifurcation) curves $\sigma _i \in \varSigma _1$ on a plane of first integrals (h, f). These curves are parametrized by $\gamma$, such that

$$\begin{aligned} \begin{aligned}&\sigma _{1}^+:\quad f=\frac{h^2}{8}+\gamma ,\quad \text {for}\quad \gamma \ge 0,\quad h\ge 0,\quad \\&\sigma _{1}^-:\quad f=\frac{h^2}{8}+ \gamma ,\quad \text {for}\quad \gamma <0,\quad h>2\sqrt{2 |\gamma |}, \end{aligned} \end{aligned}$$

(38)

where $v^2=h/4$ and $-u_0\le u\le u_0$,

$$\begin{aligned} \begin{aligned}&\sigma _2^+:\quad f=\gamma ,\quad \text {for}\quad \gamma> 0,\quad h\in \mathbb {R},\\&\sigma _2^-:\quad f= \gamma , \quad \text {for}\quad \gamma < 0,\quad h> 4\sqrt{ |\gamma |}, \end{aligned} \end{aligned}$$

(39)

where $v=0$ and $-u_0\le u\le u_0$.

Figure 11 shows the 3-dimensional bifurcation diagram of an integrable system (19) by presenting the region of possible motions $\varvec{\varPhi }({\mathscr {M}})$ depicted in a $(\gamma ,h,f)$-space. For better understanding, we also present in Fig. 12 the projections of Fig. 11 in a plane of first integrals (h, f) for $\gamma =\pm 1$. As expected, according to invariance (24), the bifurcation diagram is symmetric with respect to the f-axis. Moreover, we can notice that $\varvec{\varPhi }({\mathscr {M}})$ consists of four admissible regions separated by bifurcation curves $\pm \sigma _i$. It is worth emphasizing that in each connected component of the level set ${\mathscr {M}}_{h,f}$ has the same topological type. However, if constants h and f pass though the bifurcations lines, then the topological type of ${\mathscr {M}}_{h,f}$ may change and the bifurcation of invariant tori takes place. In order to specify all topological types of ${\mathscr {M}}_{h,f}$ over regions I-IV, the Fomenko theorem of bifurcation for Liouville tori can be adopted, see Chpt. 2, and Chpt. 6 in [27]. A more detailed description of algebraic and geometric aspects of two-dimensional integrable Hamiltonian systems can be found in [28].

Fig. 13

Exemplary quasi-periodic orbits of the system plotted in (x, y)-plane. Here, (h, f) have been taken from Region I, Region II and Region IV of the bifurcation diagram depicted in Fig. 12. In all cases the initial conditions were specified as $u_0=1, v_0=1$, which implies $r_0=1, \vartheta _0=0$

Fig. 14

Exemplary critical periodic orbits of the system plotted in (x, y)-plane. The values of (h, f) lay at the bifurcations curve $\sigma _1$. In all cases the initial conditions were specified as $u_0=1, v_0=\sqrt{h}/2$, which implies: a $r_0=17/32,\ \vartheta _0\approx 2.16$ and (b–c) $r_0=1,\ \vartheta _0=0$

Fig. 15

Exemplary periodic orbits of the system plotted in (x, y)-plane for $f=0$. In all cases the initial conditions were specified as $u_0=1/2,\ v_0=-1/2$, which implies $r_0=1/4$ and $\vartheta _0=0$

For our purpose, let us show that inside the regions separated by the bifurcation lines, the values of h and f correspond to distinct dynamical behaviours of the system. First, from the bifurcation diagram, we specify values of first integrals (h, f), and thus we can find initial conditions for $(u,v,p_u,p_v)$ from the admissible regions where trajectories are confined in ${\mathscr {M}}_{h,f}$. Then, by making the inverse change of variables (18), we find initial conditions for $(r,\vartheta ,p_r,p_\vartheta )$. Figure 13 shows three exemplary solutions of the system plotted in (x, y)-plane with (h, f) taken from admissible regions of the bifurcation diagram. Despite the fact that in all these cases the motion is quasi-periodic, the structures of the orbits and the behaviour of the swinging mass are quite different.

As we have noted previously, at the bifurcation lines, where invariant tori decay and level sets ${\mathscr {M}}_{h,f}$ becomes degenerated, exceptional families of particular periodic solutions may appear. In Fig. 14 we present the periodic orbits of the system corresponding to values of (h, f), which lie at the bifurcation curve $\sigma _1$. As in the ordinary swinging Atwood machine model, we observe characteristic ,,loops” and ,,smile” trajectories. As it transpires, orbits (not presented) lying at the bifurcation curve $\sigma _2$ correspond to singular orbits approaching into the fixed point $(x,y)=(0,0)$.

Fig. 16

Contour plots showing resonance curves plotted in (h, f)-plane. Here, $R_{n:m}=T_{u}/T_{v}$ denotes the rotational number defined in Eq. (65). Each curve corresponds to periodic motion of the system with an appropriate rotational number $R_{n:m}$. For instance, at level $f=0$, there exist a family of periodic orbits with resonant characteristic frequency $R_{1:1}$, see Fig. 15 corresponding to this case. Figures 17, 18 and 19 present small ratio resonance trajectories together with regions of possible motion plotted in (x, y)-plane

Surprisingly, we found a family of periodic but not critical solutions (rank $\mathrm {d}\varPhi (x)=2$), which lie at zero level of f. Figure 15 shows exemplary periodic orbits with various values of h. It will be clear shortly that zero value of f is, in some sense, also exceptional.

2.3.3 Derivation of a general solution

To derive explicit solutions, we perform a time transformation $t\mapsto \tau$ by setting

$$\begin{aligned} \frac{\mathrm {d}t}{\mathrm {d}\tau }=4(u^2+v^2). \end{aligned}$$

(40)

Then, the dynamics of the system at level ${{\widetilde{H}}} =h$ is described by Hamilton’s equations generated by the following Hamiltonian

$$\begin{aligned} {{\mathscr {H}}}= & {} 4(u^2+v^2) ({{\widetilde{H}}} -h)\nonumber \\= & {} H_u - 4hu^2 +H_v - 4hv^2, \end{aligned}$$

(41)

restricted to its zero level. As

$$\begin{aligned} \frac{\mathrm {d}u}{\mathrm {d}\tau } = \dfrac{\partial {{\mathscr {H}}} }{\partial p_{u}} =p_u ,\qquad \frac{\mathrm {d}v}{\mathrm {d}\tau } = \dfrac{\partial {{\mathscr {H}}} }{\partial p_{v}} =p_v, \end{aligned}$$

(42)

from (23), we obtain

$$\begin{aligned} {u'}^2 = 8P_+(u^2) \quad \text {and}\quad {v'}^2 = 8P_-(v^2), \end{aligned}$$

(43)

where prime denotes the derivative with respect to $\tau$ and

$$\begin{aligned} P_\pm (x):=\gamma \pm f+h x-2x^2. \end{aligned}$$

(44)

The right-hand sides of (43) are polynomials of degree four. Thus, their solutions can be expressed in terms of the elliptic functions. An explicit form of these solutions depends of the parameters’ values. In general, we can represent them in terms of the Weierstrass $\wp$-function or in terms of the Jacobi elliptic functions. We choose the latter option because it is simpler and easier for interpretation.

We assume that the motion takes place within Region IV of the bifurcation diagram, i.e., we restrict

$$\begin{aligned} \gamma >0,\quad h\in \mathbb {R},\quad |f|<\gamma . \end{aligned}$$

(45)

In this region we can set

$$\begin{aligned} \begin{aligned} 8 P_+(u^2)=&16(a^2-u^2)(b^2+u^2),\\ 8P_-(v^2)=&16(c^2-v^2)(d^2+v^2), \end{aligned} \end{aligned}$$

(46)

where the real positive parameters (a, b, c, d) are defined in the following way

$$\begin{aligned} \begin{aligned} \gamma +f=&2 a^2b^2,&h=&2(a^2-b^2),\\ \gamma -f=&2 c^2d^2,&h=&2(c^2-d^2). \end{aligned} \end{aligned}$$

(47)

Thus, the motion takes place within the region

$$\begin{aligned} -a \le u\le a, \qquad -c \le v\le c. \end{aligned}$$

(48)

Next, we have to perform inversion of the following integrals

$$\begin{aligned} \tau = \int _{u_\star }^{u(\tau )}\frac{\mathrm {d}x}{\sqrt{8P_+(x^2)}}, \quad \tau = \int _{v_\star }^{v(\tau )}\frac{\mathrm {d}x}{\sqrt{8P_-(x^2)}}. \end{aligned}$$

(49)

Taking into account equalities (46), we can rewrite (49) by

$$\begin{aligned} \begin{aligned} \tau =&\frac{1}{4}\int _{u_\star }^{u(\tau )}\frac{\mathrm {d}x}{\sqrt{(a^2-x^2)(b^2+x^2) }}, \\ \tau =&\frac{1}{4}\int _{v_\star }^{v(\tau )}\frac{\mathrm {d}x}{\sqrt{(c^2-x^2)(d^2+x^2) }}. \end{aligned} \end{aligned}$$

(50)

Both integrals are of the same type. Making a substitution $x=A{\text {cn}}(y,k)$, for appropriate constants A and k, we immediately obtain the desired inversion formulae. This is the standard procedure described in [29]. We fix $u_{\star } = a$ and $v_{\star } = c$, then we obtain

$$\begin{aligned} u(\tau )=a {\text {cn}}(4 \omega _u \tau , k_u), \quad v(\tau )=c {\text {cn}}(4 \omega _v \tau , k_v), \end{aligned}$$

(51)

where

$$\begin{aligned} \begin{aligned} \omega _u=&\sqrt{a^2+b^2},&\quad k_u^2=&\frac{a^2}{a^2+b^2}, \\ \omega _v=&\sqrt{c^2+d^2},&\quad k_v^2=&\frac{c^2}{c^2+d^2}. \end{aligned} \end{aligned}$$

(52)

The function ${\text {cn}}(x,k)$ has period 4K(k) where K(k) is the complete elliptic integral of the first kind. Hence, the function $u(\tau )$ has period $T_u=K(k_u)/\omega _u$, while the function $v(\tau )$ has period $T_v=K_v(k_v)/\omega _v$.

For the case considered, we can find an explicit relation between t and $\tau$. Direct integration of (40) gives

$$\begin{aligned}&t = 4\int _0^{\tau } ( u(s)^2 + v(s)^2) \mathrm {d}s =A \tau \nonumber \\&\quad +\frac{1}{4k_u^2,k_v^2} \left[ a^2 {{\mathscr {E}}}( 4 \omega _u \tau ,k_u) +c^2 {{\mathscr {E}}}( 4 \omega _v \tau ,k_v) \right] , \end{aligned}$$

(53)

where

$$\begin{aligned} A = a^2 \left( 1-\frac{1}{k_u^2} \right) + c^2 \left( 1-\frac{1}{k_v^2} \right) , \end{aligned}$$

(54)

and ${{\mathscr {E}}}( x,k)=\int _0^x {\text {dn}}(s,k) \mathrm {d}s$ denotes the Jacobi epsilon function.

Fig. 17

Exemplary periodic orbits with the region of possible motion depicted in (x, y)-plane. The values of (h, f) were taken from Fig. 16a

Fig. 18

Exemplary periodic orbits with the region of possible motion depicted in (x, y)-plane. The values of (h, f) were taken from Fig. 16b

Fig. 19

Exemplary periodic orbits with the region of possible motion depicted in (x, y)-plane. The values of (h, f) were taken from Fig. 16c

Let us now consider motion of the system restricted to Region II of the bifurcation diagram. Thus, we assume

$$\begin{aligned} h>0,\qquad \gamma<f<\frac{h^2}{8}+\gamma . \end{aligned}$$

(55)

The formula for $p_u$ remains unchanged. However, inside this region, the polynomial $P_-(v^2)$ has four real roots, so we set

$$\begin{aligned} 8P_-(v^2)= 16(c^2-v^2)(v^2-d^2), \qquad c>d>0, \end{aligned}$$

(56)

where c and d are defined by

$$\begin{aligned} f-\gamma =2c^2d^2, \qquad h = 2(c^2+d^2). \end{aligned}$$

(57)

Thus, we have to invert the following integral

$$\begin{aligned} \tau = \frac{1}{4}\int _{v_\star }^{v(\tau )}\frac{\mathrm {d}x}{\sqrt{(x^2-c^2)(d^2-x^2) }}. \end{aligned}$$

(58)

It can be done easily – it is enough to make a substitution $x={\text {dn}}(4\omega \tau , k)$. Fixing $v_\star =c$, we obtain

$$\begin{aligned} v(\tau )=c{\text {dn}}(4\omega _v \tau , k_v), \;\;\omega _v=c, \;\; k_v^2= \frac{c^2-d^2}{c^2}. \end{aligned}$$

(59)

The real period of $v(\tau )$ is $T_v=K(k_v)/2\omega _v$.

If (h, f) belongs to Region I, both polynomials $P_{\pm }(x^2)$ have four real roots. This region consists of two parts. The first one is given by

$$\begin{aligned} |f |<\frac{h^2}{8}+ \gamma , \;\; \gamma <0, \;\; 4\sqrt{|\gamma |}> h>2\sqrt{2 |\gamma |}, \end{aligned}$$

(60)

and the second one by

$$\begin{aligned} |f |<\gamma , \qquad \gamma < 0, \qquad h> 4\sqrt{ |\gamma |}. \end{aligned}$$

(61)

In this case $v(\tau )$ is given by formula (59). To find $u(\tau )$ we set

$$\begin{aligned} 8P_+(u^2)= 16(a^2-u^2)(u^2-b^2), \quad a>b>0. \end{aligned}$$

(62)

Then, a and b are defined by

$$\begin{aligned} f+\gamma =-2a^2b^2, \qquad h = 2(a^2+b^2). \nonumber \\ \end{aligned}$$

(63)

Proceeding like in the previous case, we obtain that

$$\begin{aligned} u(\tau ) = a {\text {dn}}(4 \omega _u \tau ,k_u), \quad \omega _u =a, \quad k_u^2=\frac{a^2-b^2}{a^2}. \end{aligned}$$

(64)

Hence, the real period of $u(\tau )$ is $T_u=K(k_u)/2\omega _u$.

Obtaining solutions $(u(\tau ), v(\tau ))$ and their periods, we are able to construct resonance curves corresponding to periodic solutions lying on regular tori. The ratio of periods of functions $(u(\tau ), v(\tau ))$, defined by

$$\begin{aligned} \left. R_{n:m}=\left\{ (h,f)\in \mathbb {R}^2\, \right| \, \frac{T_u}{T_v}=\frac{n}{m} \right\} , \end{aligned}$$

(65)

is called the rotation number. If $R_{n:m}$ is rational, then the orbit $(u(\tau ), v(\tau ))$ is periodic, otherwise it is quasi-periodic. Hence, we can effectively find families of periodic solutions within the indicated regions by sampling $R_{n:m}$ on the plane of first integrals (h, f). Figure 16 presents the contour plots of such families. We can read from it the initial conditions for which motion of the system is periodic with an appropriate rotational number $R_{n:m}$. For instance, it is now clear that previously mentioned exceptional curves (see Fig. 15) lying at level $f=0$ are, in fact, periodic orbits that lie in regular level sets with a resonant characteristic frequency $R_{1:1}$. Moreover, in Figs. 17, 18 and 19, we present examples of trajectories with regions of possible motion plotted in the Cartesian (x, y)-plane given by numerical computations with initial values related to small ratio resonances. It is worth emphasizing that, within the regions indicated, every initial condition $(u_0,v_0)$, which can be easily translated to $(x_0,y_0)$, corresponds to an orbit with distinct shape but the ratio $R_{n:m}$ is the same for prescribed values of first integrals (h, f). For instance, Fig. 18 presents orbits for $R_{1:2}, R_{1:3}$ and $R_{2:3}$, with two different initial condition each.

2.3.4 3D integrable case with a quartic first integral

In terms of the parabolic-cylinder coordinates (18), the Hamiltonian (9) becomes separable at zero level of first integral (7). So, we put $\varPi =0$ and, in this case, the system admits first integral (20), which is the quadratic polynomial with respect to the momenta. However, Poincaré sections show in Fig. 8b that the system can be also integrable for $\varPi =1/4$. In fact, more detailed analysis (not included) suggests integrability of the system for arbitrary $\varPi \in \mathbb {R}$. So, let us try to confirm integrability by constructing a complementary first integral of a higher degree.

The Hamiltonian (9) is an even function with respect to the momenta, and also equations of motion (11) are invariant by the time reflection $t\rightarrow {\widetilde{t}}=-t$, i.e.,

$$\begin{aligned} \begin{aligned}&(r,\vartheta )\rightarrow ({\widetilde{r}},{\widetilde{\vartheta }})=(r,\vartheta ),\\&(p_r,p_\vartheta )\rightarrow (\widetilde{p_r},\widetilde{p_\vartheta })=-(p_r,p_\vartheta ). \end{aligned} \end{aligned}$$

(66)

Hence, without loss of generality, we can restrict our search for even or odd degree polynomial first integrals. Moreover, as noted and successfully used in papers [15, 30,31,32], to build a complementary first integral, we can apply the so-called order doubling. For this purpose, the quadratic integral $I_{2D}$ (21) can be adopted. We postulate that the additional first integral, quartic in the momenta, is following

$$\begin{aligned} I_{3D}=[I_{2D}+a_1]^2+a_2p_r^2+a_3p_rp_\vartheta +a_4p_\vartheta ^2+a_5, \nonumber \\ \end{aligned}$$

(67)

where $a_i=a_i(r,\vartheta )$ are coefficients to be determined. Calculating the time derivative of $I_{3D}$, and using equations of motion (11), we receive a polynomial with respect to the momenta. Thus, the equation $\dot{I}_{3D}=0$ gives rise a system of first-order, nonlinear partial differential equations for unknown functions $a_i(r,\vartheta )$. The solution of this system gives the final form of the first integral we look for. After, tedious symbolic calculations, it can be written as follows

(68)

where $\varPi ,g,\gamma \in \mathbb {R}$. It is clear that at zero level of cyclic first integral (7), $\varPi =0$, the quartic first integral $I_{3D}$ reduces to a quadratic one $I_{3D}=I_{2D}I_{2D}$, where $I_{2D}$ is defined in (21). The Hamiltonian (68) defines the new three-parameter family of an integrable system, which is the generalisation of the model studied by Elmandouh in [15]. Surprisingly, the addition of the term related to Coulomb interactions $V_c=-\gamma /r$, does not destroy the structure of integrability. Let us summarize the main results of this section by the following theorem.

Theorem 1

If $M=3m$, then the 3D-SAM with static Coulomb interactions governed by Hamiltonian (9) is completely integrable, for arbitrary $g,\gamma ,\varPi \in \mathbb {R}$. The integrable system has for its explicit form defined by (68).

3 Model 2: SAM with harmonic interactions

3.1 Presentation of the system

Fig. 20

Geometry of a 3D swinging Atwood’s machine moving in the gravitational and Hooke’s potentials. The system consists of two masses M, m, two springs $k_1, k_2,$ and two inextensible strings of the same length. The mass m swings in 3-dimensional space, while M is constrained to move along the vertical direction. Spring $k_1$ stretches vertically and at its end we have a massless ring to which the red string is attached. This string is thread on two massless pulleys and at its end, the mass M is hung. Spring $k_2$ connects mass m with spring $k_1$. The whole system moves under the influence of the potential (71) and the corresponding Hamiltonian function is defined in (70)

In Fig. 20 the geometry of the second system under consideration is presented. As in the classical case, the masses M and m are connected to each other by one string. The mass M is constrained to move only along the vertical direction, while the second mass m is allowed to move in 3D space. However, we propose the following modification. We introduce, two springs with spring constants $k_1,k_2\in \mathbb {R}^+$ and one additional string (coloured red). Spring $k_1$ with natural length d is rigidly restrained. It stretches vertically and at its end we have a massless ring to which the red string is attached. This string is thread on two massless pulleys and at its end, the mass M is hung. Spring $k_2$ connects mass m with spring $k_1$. Potential energies coming from Hooke’s interactions between springs $k_1$ and $k_2$ are given by

$$\begin{aligned}&V_{k_1}=\frac{1}{2}k_1\left( l-r-d\right) ^2,\nonumber \\&V_{k_2}=\frac{1}{2}k_2\left[ (r-r \cos \vartheta )^2+r^2\sin ^2\vartheta \right] , \end{aligned}$$

(69)

The Hamiltonian function of the system, written in spherical coordinates $(r,\vartheta ,\varphi )$, is given as follows

$$\begin{aligned} {\begin{matrix}&H_{3D}=\frac{1}{2}\left( \frac{p_r^2}{m+M}+\frac{p_\vartheta ^2}{mr^2}\right) +V(r,\vartheta ), \end{matrix}} \end{aligned}$$

(70)

Fig. 21

Poincaré sections of system (70) made for $M=3,\, m=1,\, g=1,\, s=5, \, k_1=1, \, k_2=0.25, \, E=2$. The section plane was specified as $r=3$, with $p_r>0$. The plots indicate the chaotic dynamics of the system. Each colour corresponds to distinct initial condition

where the effective potential reads

$$\begin{aligned} {\begin{matrix}V(r,\vartheta )&{}=\frac{\varPi ^2}{2mr^2 \sin ^2\vartheta }+g r(M-m \cos \vartheta ) \\ &{}+\frac{1}{2}k_1\left( r-s\right) ^2+k_2r^2(1-\cos \vartheta ). \end{matrix}} \end{aligned}$$

(71)

As for the first model, $\varPi$ represents a value of cyclic integral $J=p_\varphi =\varPi$, associated to cyclic coordinate $\varphi$, while $s=l-d\ge 0$ has been introduced for simplicity. Hamilton’s equations generated by Hamiltonian (70) are as follows

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{r}=\dfrac{p_r}{m+M}, \\ \dot{p}_r=\dfrac{p_\vartheta ^2}{mr^3}+\dfrac{\varPi ^2}{mr^3\sin ^2\vartheta }-g (M-m\cos \vartheta )\\ \quad -k_1(r-s)-2k_2r(1-\cos \vartheta ),\\ {\dot{\vartheta }}=\dfrac{p_\vartheta }{mr^2},\\ \dot{p}_\vartheta =\dfrac{\varPi ^2\cos \vartheta }{mr^2\sin ^3\vartheta }-(g m +k_2r)r\sin \vartheta , \end{array}\right. } \end{aligned}$$

(72)

where cyclic variable $\varphi$ can be determined by relation (12).

3.2 Numerical analysis

Figures 21 and 22 present Poincaré sections of system (72). We observe the beautiful coexistence of periodic, quasi-periodic and chaotic motion. We see, in particular, the magnification of the Poincaré section presenting families of high-order resonance orbits. Hence, the ratio of the masses $M/m=3$ does not imply integrability of the system for arbitrary remaining parameters which was the case in the first model. Here, values of the remaining parameters $\varPi , s,k_1,k_2$ matter.

Moreover, as evidenced in Fig. 23, due to the appearance of the harmonic interactions, the model considered for the mass ratio $M/m<1$ still possesses very complex dynamics. This is particularly visible in the phase-parametric diagram presented in Fig. 24. The diagram shows the extreme values of $\vartheta (t)$ versus an initial swing angle $\vartheta _0\in (0,\pi )$ of the pendulum. The colour scale is proportional to value of the maximal Lyapunov exponent $\lambda$. As we can notice, this figure presents completely different dynamics compared to the classical SAM model for which assumption $M/m>1$ is needed for oscillations, see [4]. We observe the rich structure of high-order resonance periodic solutions coexisting with chaotic orbits in their neighbourhoods. Since a value of the cyclic integral is different from zero (we put $\varPi =1$), the pendulum with mass m performs spacial oscillations. Some of the regular orbits plotted in 3D Euclidean space are depicted in Fig. 25. The initial conditions were taken from the phase-parametric diagram (see the coloured labels in Fig. 24).

Fig. 22

Poincaré section of system (70) made for $M=3,\, m=1,\, g=1,\, s=0, \, k_1=1, \, k_2=1, \, E=6.5,$ and $\varPi =0$. The section plane was specified as $r=1$, with $p_r>0$. The plot and, in particular, its magnification show the beautiful coexistence of periodic, quasi-periodic and chaotic motion. We observe a number of orbits corresponding to high-order resonances. Each colour corresponds to a distinct initial condition

Fig. 23

Poincaré sections of system (70) made for $M=1,\, m=3,\, g=1,\, s=5, \, k_1=2, \, k_2=0.5, \, E=-12$. The section plane was specified as $r=5$, with $p_r>0$. Central region of the section is responsible for highly chaotic stages of the system dynamics. Each colour corresponds to distinct initial condition

Fig. 24

The phase-parametric diagram of system (72) versus the initial swing angle $\vartheta _0$. The diagram is combined together with the maximal Lyapunov exponent $\lambda$, where colour scale is proportional to the value of $\lambda$. Parameters where chosen as $M=1,\, m=3,\, g=1,\, s=5, \, k_1=2, \, k_2=0.5, \, \varPi =1$ with initial condition $(r_0=3.78,\,\vartheta _0=\vartheta _0,\,\dot{r}_0={\dot{\vartheta }}_0=0)$. Here $\vartheta (t_\star )$ denotes extreme values of $\vartheta (t)$ when ${\dot{\vartheta }}(t_\star )=0$ for some $t_\star$. Periodic motion diverges as $\vartheta _0$ increases and finally becomes chaotic. We can also detect the stable “windows” between completely chaotic regions. Coloured labels correspond to the respective initial conditions for which periodic orbits are plotted in Fig. 25

Fig. 25

Regular orbits of system (72) plotted in 3D Euclidean space. The plots confirm spatial oscillations of the pendulum. Parameters where chosen as: $M=1,\, m=3,\, g=1,\, s=5,\, k_1=2,\, k_2=0.5,\, \varPi =-0.5$, with the initial condition $(r_0=3.78,\,\vartheta _0=\vartheta _0,\,\dot{r}_0={\dot{\vartheta }}_0=0)$. Respective values of $\vartheta _0$ were taken from the phase-parametric diagram (see the coloured labels in Fig. 24)

3.3 Integrability

3.3.1 Separable case

Numerical analysis shows the complex and, in fact, highly chaotic behaviour of the system for a wide range values of the parameters. Surprisingly, however, a more detailed analysis (not included) suggests that for

$$\begin{aligned} M=3m,\quad k_1=\frac{4}{3}k_2,\quad s=0,\quad \text {with}\quad \varPi \in \mathbb {R}, \end{aligned}$$

(73)

the dynamics is very regular and it suggests the integrability of the system. So, let us try to ensure its integrability by constructing an additional first integral.

We start by making a canonical change of dependent variables from the polar coordinates into the parabolic-cylinder ones (18). For values of parameters (73) and (without a loss of generality) with $m=1$ and $k_2=3k$, the Hamiltonian (70) transforms to the form

$$\begin{aligned}&{\widetilde{H}}=\frac{H_u+H_v}{4(u^2+v^2)}+\dfrac{\varPi ^2(u^2+v^2)^2}{8u^2v^2(u^2-v^2)^2},\nonumber \\&\text {where}\\&H_u = \frac{1}{2}p_u^2 + 8gu^4+8ku^6 , \nonumber \\&H_v = \frac{1}{2}p_v^2 + 8gv^4+8kv^6.\nonumber \end{aligned}$$

(74)

It is obvious that at zero level of the cyclic integral, i.e., $p_\varphi =\varPi =0$, variables u, v are separated. Hence, we put $\varPi =0$. Now, from equality

$$\begin{aligned} 4(u^2+v^2) {\widetilde{H}}=H_u +H_v, \end{aligned}$$

(75)

we separate terms which depend only either on $(u,p_u)$ or $(v,p_v)$. Then, we find that

$$\begin{aligned} F= \frac{v^2H_u-u^2 H_v}{4(u^2+v^2)}, \end{aligned}$$

(76)

is the additional first integral. Hence, we conclude that a SAM system with additional Hooke’s potential (69) is integrable at zero level of cyclic integral $\varPi =0$.

We perform an inverse change of variables (18) on (76) to obtain a desired constant of motion written in the polar coordinates. The explicit form of the integrable system is as follows

$$\begin{aligned} {\left\{ \begin{array}{ll} H_{2D}=\dfrac{p_r^2}{8}+\dfrac{p_\vartheta ^2}{2r^2}+g r(3-\cos \vartheta )\\ \quad +kr^2\left( 5-3\cos \vartheta \right) ,\\ G_{2D}=r^{-1}\sin \dfrac{\vartheta }{2}p_\vartheta ^2-\dfrac{1}{2}\cos \dfrac{\vartheta }{2}p_rp_\vartheta \\ \quad - g r^2\cos \dfrac{\vartheta }{2}\sin \vartheta -2 k r^3\cos \dfrac{\vartheta }{2}\sin \vartheta . \end{array}\right. } \end{aligned}$$

(77)

System (77) is the new integrable model. It is the generalization of the classical 2D SAM model. This generalisation is given by the appearance of the additional term in the potential which comes from the Hooke interactions between the springs.

3.3.2 Bifurcation diagram of the integrable system

We chose units in such a way that $g=1$. Assuming $\varPi =0$, we consider a common level of first integrals (74) and (76), specifically

$$\begin{aligned} {\mathscr {M}}_{h,f} = \left\{ \varvec{x}\in {\mathbb {R}}^4\,|\, {\widetilde{H}}=2h, F=2f\right\} , \end{aligned}$$

(78)

where $\varvec{x}=(u,v,p_u,p_v)$. Values of (h, f) belong to an image of the momentum map

$$\begin{aligned} {\mathbb {R}}^4\ni \varvec{x}\longmapsto \mathbf {\varvec{\varPhi }}(\varvec{x})=\left( {\widetilde{H}}(\varvec{x}), F(\varvec{x})\right) \in \varSigma \subset {\mathbb {R}}^2, \end{aligned}$$

(79)

From equations ${{\widetilde{H}}}=2h$ and $F=2f$ we find that

$$\begin{aligned} \begin{aligned}&p_u^2 = 16\left( f+hu^2-u^4-k u^6\right) ,\\&p_v^2=16\left( -f+hv^2-v^4-k v^6\right) . \end{aligned} \end{aligned}$$

(80)

Notice, that these equations are invariant under change (24). Hence, we can restrict our consideration for $f\ge 0$. In order to build a bifurcation diagram we processed as in the first model. Let $S=S_0\cup S_1$ be a set of critical points P of the momentum map (79), such that ${\text {rank}}\mathrm {d}\varvec{\varPhi }(\varvec{P})<2$. If ${\text {rank}}\mathrm {d}\varvec{\varPhi }(\varvec{P})=0$, then $S_0$ contains isolated fixed points. Otherwise, if ${\text {rank}}\mathrm {d}\varvec{\varPhi }(\varvec{P})=1$, then $S_1$ consists of families of periodic or asymptotic curves.

It can be easily verified that set $S_0=\emptyset$. Hence, the Hamiltonian vector field governed by Hamiltonian function (74) does not possesses any equilibrium point. To find set $S_1$ of critical periodic orbits, we have to find points P for which gradients $\nabla H(P)$ and $\nabla F(P)$ are linearly dependent. Direct calculations show two distinct families of equations exist, which can define possible critical periodic solutions contained in $S_1$. They have the form

$$\begin{aligned}&p_v=0,\nonumber \\&p_u^2=16\left( k(2v^6-u^6+3 v^4u^2)+v^4-u^4+2u^2v^2\right) ,\nonumber \\&\text {and} \nonumber \\&p_v=0,\quad v=0. \end{aligned}$$

(81)

Then, we eliminate momenta $(p_u,p_v)$ using formulae defined in (80). Hence, we receive

$$\begin{aligned}&3k v^4+2v^2-h=0,\quad kv^6+v^4-hv^2+f=0,\nonumber \\&f=0,\quad v=0. \end{aligned}$$

(82)

We remark a mirror family of the above equations exists according to invariance (24). Taking into account that the coordinates (u, v) and momenta (80) must be real, we can easily find critical curves $\lambda _i\in \varSigma =\varPhi (S_1)$, on a plane of first integrals (h, f). They are as follows

$$\begin{aligned} \begin{aligned}&\lambda _1:\quad f=\frac{-2-9h\,k +2\sqrt{(1+3h\,k)^3}}{27k^2},\\&\quad \text {for}\quad h\ge 0, \end{aligned} \end{aligned}$$

(83)

where $v^2=(-1+\sqrt{1+3h\, k})/3k$ and $-u_0\le u\le u_0$,

$$\begin{aligned} \begin{aligned} \lambda _2:\quad f=0,\quad \text {for}\quad h\ge 0, \end{aligned} \end{aligned}$$

(84)

where $v=0$ and $-u_0\le u\le u_0$.

Figure 26 shows a 3D bifurcation diagram of an integrable system (74) by presenting the region of possible motion depicted in a (k, h, f)-space. For greater detail, see Fig. 28, which presents the projection of the bifurcation diagram to a plane of first integrals (h, f). Due to invariance (24), the bifurcation diagram is symmetric about f-axis. Moreover, we can notice that $\varvec{\varPhi }({\mathscr {M}})$ consists of two admissible regions separated by critical curves $\pm \sigma _i$. At these curves, the bifurcations occur and exceptional families of periodic solutions appeared, see Fig. 28.

3.3.3 Derivation of a general solution

Next, we perform time a transformation $t\mapsto \tau$ by setting

$$\begin{aligned} \frac{\mathrm {d}t}{\mathrm {d}\tau }=4(u^2+v^2). \end{aligned}$$

(85)

Then, from (42) and (80), we obtain

$$\begin{aligned} u'^2 = 16 P_{+}(u^2), \qquad v'^2=16P_-(v^2), \end{aligned}$$

(86)

where

$$\begin{aligned} P_{\pm }(x) =\pm f+h x-x^2-k x^3. \end{aligned}$$

(87)

Direct integrations of these equations lead to hyperelliptic integrals so a change of variable has to be made to reduce them to elliptic integrals. Let us set

$$\begin{aligned} w(\tau ) = \frac{16 f}{u(\tau )^2} + \frac{16}{3h},\qquad \text {with}\qquad fh\ne 0. \end{aligned}$$

(88)

Then, we obtain

$$\begin{aligned} w'^2 = 4 w^3 -g_2 w -g_3. \end{aligned}$$

(89)

The above equation defines the Weierstrass elliptic function $w(\tau )=\wp (\tau , g_2^+,g_3^+)$, with invariants

$$\begin{aligned} g_2^+ =\frac{2^{10}}{3}(3f+h^2), \quad g_3^+= \frac{2^{14}}{3^3}(27k f^2 -9fh - 2 h^3).\nonumber \\ \end{aligned}$$

(90)

Thus, from Eq. (88) we have

$$\begin{aligned} u(\tau )^2 = \frac{16 f}{\wp (\tau , g_2^+,g_3^+) -\frac{16}{3}h}. \end{aligned}$$

(91)

In the similar way, we obtain

$$\begin{aligned} v(\tau )^2 = \frac{-16 f}{\wp (\tau , g_2^-,g_3^-) -\frac{16}{3}h}. \end{aligned}$$

(92)

where

$$\begin{aligned} g_2^- =\frac{2^{10}}{3}(h^2-3f), \quad g_3^-= \frac{2^{14}}{3^3}(27k f^2 +9fh - 2 h^3).\nonumber \\ \end{aligned}$$

(93)

Fig. 26

The three-dimensional bifurcation diagram of an integrable system (74) presenting the region of possible motions $\varvec{\varPhi }({\mathscr {M}})$ depicted in a (k, h, f)-space. The diagram is symmetric about f-axis and it consists of two admissible regions separated by bifurcation curves. Each region corresponds to distinct dynamical behaviour of the system. For better understanding, see Fig. 27 presenting projection of the bifurcation diagram to a plane of first integrals (h, f) for $k= 1$

Fig. 27

A projection of a three-dimensional bifurcation diagram (see Fig. 26) restricted to (h, f)-plane with the numbering of domains. Each region corresponds to distinct dynamical behaviour of the system. Here $\lambda _1$ and $\lambda _2$ are the critical (bifurcation) curves defined in Eqs. (83)–(84). At these degenerated curves, exceptional families of particular periodic solutions appeared, see Fig. 28

Fig. 28

The loop, the teardrop and the heart orbits of the system plotted in (x, y)-plane. In the all cases, the initial conditions were specified as $u_0=1,\ v_0=-1$, which implies $r_0=1$ and $\vartheta _0=0$

As we already have noted, the case with $f=0$ is exceptional because at this level, invariant tori bifurcate. Figure 28b–c presents two different closed trajectories. As its turns out, for a small initial angle $\vartheta _0$, we get the teardrop orbit, while for a sufficiently large $\vartheta _0$ the orbit is called the heart orbit. This unexpected feature was observed in the ordinary SAM system by Tufillaro [6]. In our model, however, we have the additional term in the potential related with the Hooke interactions.

Let us make a deeper insight into the structure of an explicit form of solutions. We put $f=0$. Then, from Eq. (86), we have to perform inversion of the following integral

$$\begin{aligned} \tau = \int _{u_\star }^{u(\tau )}\frac{\mathrm {d}x}{x\sqrt{h-x^2-k x^4}}. \end{aligned}$$

(94)

Direct elementary integration (by substitution) gives

$$\begin{aligned} \tau = \frac{1}{2\sqrt{h}}\ln \left( \frac{Q(u^2)}{u_\star }\right) , \end{aligned}$$

(95)

where

$$\begin{aligned} Q(x):=\frac{2h-x-2\sqrt{h}\sqrt{h-x-k x^2}}{x}. \end{aligned}$$

(96)

After some algebraic manipulation, we find that a general solution of the system for $f=0$ is defined by

$$\begin{aligned} \begin{aligned} u(\tau )^2=\frac{4 h\,u_\star e^{8\sqrt{h}\tau }}{4h\,k+\left( 1+u_\star e^{8\sqrt{h}\tau }\right) ^2}. \end{aligned} \end{aligned}$$

(97)

In analogous way we find that

$$\begin{aligned} v(\tau )^2=\frac{4 h\,v_\star e^{8\sqrt{h}\tau }}{4h\,k+\left( 1+v_\star e^{8\sqrt{h}\tau }\right) ^2}. \end{aligned}$$

(98)

Finally, one can go through to the real-time parametrization by integrating relation (85) which gives

$$\begin{aligned} {\begin{matrix} t&{} = 4\int _0^{\tau } ( u(s)^2 + v(s)^2) \mathrm {d}s \\ &{}=\frac{\arctan \left( \frac{1+u_\star e^{8\sqrt{h}\tau }}{2\sqrt{h\, k}}\right) +\arctan \left( \frac{1+v_\star e^{8\sqrt{h}\tau }}{2\sqrt{h\, k}}\right) }{\sqrt{k}} \end{matrix}} \end{aligned}$$

(99)

Let us now find an equation of orbits in $(r,\vartheta )$-plane. Instead of using explicit formulae for u and v, it seems easier way to eliminate $\mathrm {d}\tau$ from Eq. (86). By separating the variables, the orbit equation becomes

$$\begin{aligned} c=\int \frac{\mathrm {d}u}{u\sqrt{h-u^2-k u^4}}-\int \frac{\mathrm {d}v}{v\sqrt{h-v^2-k v^4}}, \end{aligned}$$

(100)

which can be easily integrated to give

$$\begin{aligned} c=\frac{1}{2\sqrt{h}}\ln \left( \frac{Q(u^2)}{Q(v^2)}\right) . \end{aligned}$$

(101)

Here, c is a constant of the integration. Taking the exponents of both sides, we find the implicit orbit equation in (u, v) variables

$$\begin{aligned} a=\frac{Q(u^2)}{Q(v^2)},\qquad \text {where}\qquad a =e^{2 \sqrt{h}\, c}>0. \end{aligned}$$

(102)

Taking the inverse of transformation (18), namely

$$\begin{aligned} u^2=r-r \sin \frac{\vartheta }{2},\quad v^2=r+r \sin \frac{\vartheta }{2}, \end{aligned}$$

(103)

we get an implicit equation of orbits in the polar coordinates as

$$\begin{aligned} a=\frac{Q(r-r \sin \frac{\vartheta }{2})}{Q(r+r \sin \frac{\vartheta }{2})}. \end{aligned}$$

(104)

Squaring both sides and making additional algebraic manipulations, we finally obtain

$$\begin{aligned} \begin{aligned}&r(\vartheta )=\frac{4h\, a}{b \cos ^2\frac{\vartheta }{2}}\left( \frac{a^2+1}{a^2-1}\sqrt{b\cos ^2\frac{\vartheta }{2}-16h\,k\,a^2}-2a\right) ,\\&\text {where}\ b=(a^2-1)^2+4h\, k(a^2+1). \end{aligned} \nonumber \\ \end{aligned}$$

(105)

Since r must be positive, a restriction for the angle $\vartheta$ is as follows

$$\begin{aligned} - \vartheta _0<\vartheta <\vartheta _0,\qquad \vartheta _0=2\arccos \left( \frac{2a }{a^2+1}\right) . \end{aligned}$$

(106)

Formula (105) explicitly defines the teardrop and the heart orbits equations written in the polar form. Indeed, directly from formulae (105)–(106), we can easily reproduce families of the teardrop-heart orbits visible in Fig. 28b–c. Moreover, we can immediately recover the orbit equation for the classical SAM system given in  [6] by excluding Hooke’s interactions from the system, i.e., by putting $k=0$.

3.3.4 3D integrable case with a quartic first integral

As we have noted at the beginning of this subsection, the numerical analysis suggests the integrability of the Hamiltonian (70) for values of the parameters (73) also at non-zero level of the cyclic first integral $p_\varphi =\varPi \ne 0$. We look for an additional first integral using the order-doubling of $G_{2D}$. We postulate

$$\begin{aligned} G_{3D}\!=\!\left[ G_{2D}\!+\!b_1\right] ^2\!+\!b_2p_r^2\!+\!b_3 p_rp_\vartheta \!+\!b_4p_\vartheta ^2\!+\!b_5,\nonumber \\ \end{aligned}$$

(107)

where $b_i=b_i(r,\vartheta )$ are unknown coefficients. Calculating the Lie derivative of $G_{3D}$, and equating to zero all coefficients of the momenta, we obtain a system of algebraic and partial differential equations. Their solution determines final forms of expressions $b_i(r,\vartheta )$. After some lengthy calculations, one can define an explicit form of an integrable system (70) for values of parameters (73) with $\varPi \in \mathbb {R}$. The integrable system has for its explicit form defined as

$$\begin{aligned} {\left\{ \begin{array}{ll} H_{3D}=\dfrac{p_r^2}{8}+\dfrac{p_\vartheta ^2}{2r^2}+\dfrac{\varPi ^2}{2r^2\sin ^2\vartheta } +g r(3-\cos \vartheta )\\ \quad + kr^2\left( 5-3\cos \vartheta \right) ,\\ G_{3D}=\left[ G_{2D}+\varPi ^2\dfrac{\sin (\vartheta /2)}{r\sin ^2\vartheta }\right] ^2\\ \quad +\varPi ^2\left( \dfrac{p_r^2}{16\sin ^{2}(\vartheta /2)}+2 g r+4kr^2\right) , \end{array}\right. } \end{aligned}$$

(108)

where $G_{2D}$ is defined in (77). It is clear that at a zero level of the cyclic first integral, i.e., $p_\vartheta =\varPi =0$, the complementary quartic first integral $G_{3D}$ reduces to the quadratic one. Moreover, as we can notice the integrable Hamiltonian (108) is the natural generalisation of 2D and 3D classical SAM system by the appearance of additional parameter k coming from Hooke’s interactions.

3.4 Super-integrability

Certain integrable Hamiltonian systems with n degrees of freedom admit more than n first integrals. Such systems are called super-integrable and have very peculiar properties. For example: their phase curves lie in tori of dimension smaller than n; one can give an algebraic procedure for finding explicit forms of their solutions (see e.g. [33]); their equations of motion are separable in a more than one coordinate system (see e.g. [34]).

Unexpectedly, in the absence of the gravity, $g=0$, the 3D integrable system (108) is maximally super-integrable. It possesses an additional, functionally independent, first integral quadratic in the momenta. The explicit form of the super-integrable system is as follows

$$\begin{aligned} {\left\{ \begin{array}{ll} H^s_{3D}=\dfrac{p_r^2}{8}+\dfrac{p_\vartheta ^2}{2r^2}+\dfrac{\varPi ^2}{2r^2\sin ^2\vartheta }+ kr^2\left( 5-3\cos \vartheta \right) , \\ F_{3D}^s=\left( \dfrac{p_r^2}{8}-\dfrac{p_\vartheta ^2}{2r^2}-\dfrac{\varPi ^2}{2r^2\sin ^2\vartheta }\right) \cos \vartheta -\dfrac{\sin \vartheta }{2r}p_rp_\vartheta \\ \quad -kr^2\left( 3-5\cos \vartheta \right) ,\\ G_{3D}^s=\left[ G_{2D}^s+\varPi ^2\dfrac{\sin (\vartheta /2)}{r\sin ^2\vartheta }\right] ^2\\ \quad +\varPi ^2\left( \dfrac{p_r^2}{16\sin ^{2}(\vartheta /2)}+4kr^2\right) , \end{array}\right. }\nonumber \\ \end{aligned}$$

(109)

where

$$\begin{aligned} G_{2D}^s= & {} r^{-1}\sin \dfrac{\vartheta }{2}p_\vartheta ^2-\dfrac{1}{2}\cos \dfrac{\vartheta }{2}p_rp_\vartheta \nonumber \\&-2 k r^3\cos \dfrac{\vartheta }{2}\sin \vartheta . \end{aligned}$$

(110)

This is the new, not trivial, super-integrable mechanical system.

As it is well-known terminology, maximal integrability implies that all bounded trajectories are closed and the motion is periodic. Indeed, Fig. 29 shows the phase-parametric diagram of the super-integrable system. Again, for the calculated diagram, we display the extreme values of $\vartheta (t)$ as a function of the initial swing angle $\vartheta _0\in (0,\pi )$ of the pendulum. We obtain elegant curves corresponding to periodic motion of the system even for large values of $\vartheta _0$. Compared to the integrable system (see Fig. 10), there are no quasi-periodic orbits at all. Since $\varPi \ne 0$, the pendulum with mass m performs spacial oscillations. Some of the particular periodic orbits, plotted in 3D Euclidean space, are visible in Fig. 30. The initial conditions were taken from the phase-parametric diagram. As we can notice, each orbit is closed and we obtain 3D versions of the heart orbit and the loop orbit visible in Fig. 30a and in Fig. 30c.

Fig. 29

The phase-parametric diagram of super-integrable system (109) for $\varPi =1$ at variations of the initial angle $\vartheta _0$. The initial conditions was chosen as $(r_0=1,\,\vartheta _0=\vartheta _0,\,\dot{r}_0= {\dot{\vartheta }}_0=0)$. Here, $\vartheta ({t_\star })$ denotes the extreme values of $\vartheta$ when ${\dot{\vartheta }}(t_\star )=0$ for some $t_\star$. The diagram indicates the periodic orbits of the super-integrable system without any regimes responsible for quasi-periodic motion. See Fig. 30, which shows exemplary periodic orbits plotted in 3D Euclidean space

Fig. 30

Periodic solutions of super-integrable system (109) plotted in 3D Euclidean space for $\varPi =1$. The presented orbits are 3-dimensional generalisations of the heart and the loop orbits visible in Fig. 30a and in Fig. 30c

Let us summarize the results of this section in the following theorem.

4 Composition of the models

Finally, let us now combine both integrable models into one and let us study its integrability. Specifically, we consider the following Hamiltonian

$$\begin{aligned} \begin{aligned} H_{3D}^\star =&\dfrac{p_r^2}{8}+\dfrac{p_\vartheta ^2}{2r^2}+\dfrac{\varPi ^2}{2r^2\sin ^2\vartheta } +g r(3-\cos \vartheta )\\&+kr^2\left( 5-3\cos \vartheta \right) -\dfrac{\gamma }{r}. \end{aligned} \nonumber \\ \end{aligned}$$

(111)

The question of what can be added to an integrable Hamiltonian function without destroying its integrability has a long history. KAM theory says that most of perturbations destroy integrability. However, it does not give any conditions for possible integrable perturbations. As a matter of fact, most modifications of an integrable potential gives rise a non-integrable one, see e.g. [35,36,37,38,39].

Surprisingly enough, the Hamiltonian (111) is integrable and an additional first integral is a quartic polynomial with respect to the momenta. An explicit form of the integrable system is as follows

$$\begin{aligned} \begin{aligned} J_{3D}=&\left[ J_{2D}+\varPi ^2\dfrac{\sin (\vartheta /2)}{r\sin ^2\vartheta }\right] ^2\\&\quad +\varPi ^2\left( \dfrac{p_r^2}{16\sin ^{2}(\vartheta /2)}+2 g r+4kr^2\right) , \end{aligned} \end{aligned}$$

(112)

where

$$\begin{aligned} J_{2D}= & {} r^{-1}\sin \dfrac{\vartheta }{2}p_\vartheta ^2-\dfrac{1}{2}\cos \dfrac{\vartheta }{2}p_rp_\vartheta - g r^2\cos \dfrac{\vartheta }{2}\sin \vartheta \nonumber \\&\quad -\gamma \sin \dfrac{\vartheta }{2}-2 k r^3\cos \dfrac{\vartheta }{2}\sin \vartheta , \end{aligned}$$

(113)

is the first integral of the system at zero level of $p_\varphi =\varPi =0$. This is the new, not trivial, integrable model with physical origin.

5 Conclusions and open problems

This paper has discussed a fundamental problem of dynamical systems which is the distinction of integrable systems from non integrable ones. We focused our theoretical analysis on two generalized classes of 3D SAM system with additional Coulomb’s and Hooke’s interactions. For most values of the parameters, both models exhibit highly complex dynamics, which was presented via the Poincaré sections, the phase-parametric diagrams and the Lyapunov exponents spectrums. However, surprisingly, we have also found integrable cases: for the first model, the ratio of the masses $M/m=3$ was sufficient for integrability, while for the second model, the additional condition for the ratio of the spring constant $k_1/k_2=4/3$ was needed for integrability. We constructed the bifurcation diagrams for the integrable systems and we found explicit forms of general solutions of the equations of motion. These solutions are expressed in terms of the elliptic Jacobi functions. Moreover, we showed that in the absence of the gravitational potential, both models are maximally super-integrable This is an exceptional feature for Hamiltonian systems with more than one degree of freedom.

All in all, the results presented in this manuscript were obtained with powerful tools, whose application seems to be of importance and usefulness to the study of other oscillatory systems. Moreover, the systems considered in this paper can be treated as unique theoretical models of Hamiltonian systems with two degrees of freedom which are chaotic, integrable, and super-integrable for certain values of the parameters. Therefore, such systems provide excellent examples for the teaching of Lagrangian and Hamiltonian mechanics.

Nevertheless, there is a number open problems related to the analysis of these models. For instance, the question of existence of other integrable cases for different values of the parameters remains open. For this purpose the Morales–Ramis theory can be adopted [40, 41]. This theory enables a distinction between values of the parameters for which a considered model is suspected to be integrable. Morales-Ramis theory has already been successfully applied to various, important physical systems, see for instance [11, 42,43,44,45,46,47,48].

As second problem results from a lack of research on the dynamics and integrability the Atwood machine with two swinging masses. This model, which is the system of three degrees of freedom, was preliminary considered in [13]. However, its dynamics and its integrability analysis still does not attract sufficient attention and it is interesting whether this model possesses an additional first integral or even if it integrable for the mass ratio $M/m=3$.

Finally, the physical construction of the models considered is now under way. We plan to obtain experimental results concerning their dynamics and compare these results with numerical and analytical results obtained in this paper. Therefore, our future work arguably will complete the above theoretical results.