1 Introduction

The importance of the vertical component of earthquake isolation is undeniable especially in near-fault areas, based on the database of previous earthquakes [1]. In 1991, Niazi and Bozorgnia showed that the ratio of 2/3 for vertical-to-horizontal peak acceleration ratio V/H for designing structures is not conservative in near-fault areas [2]. This ratio is generally higher in the near-field than the far-field, at low frequencies than high frequencies and on soil than on rock base [3]. In another paper, Papazoglou & Elnashai indicated that a V/H ratio exceeding 1.7 can cause damage to structural elements [4]. Based on evidence, the damage was seen to be due to the increase in axial compression forces in columns and shear walls which is also a threat to human life. In addition, fluctuation in the forces led to flexural or shear failures in those members. Moreover, the vertical component of the earthquake can cause damage to non-structural elements as well [5, 6]. Therefore, it is worth pursuing research on vertical seismic base isolation to decrease transmission of the vertical acceleration to a structure in near-fault areas.

Although most of the successful isolation mechanisms in use are for horizontal seismic excitation, vertical isolation has also been investigated, particularly in the last decade. For instance, the use of a lead-rubber bearing to isolate a structure from the vertical component of earthquakes has been investigated. However, it was shown that it can amplify the acceleration and is not suitable for isolating structures in the vertical direction [7]. Furukawa et al. [8] also have done experimental research on a four-storey building on a base isolator and found out that, although the vertical component of the earthquake is amplified, the damage was not detrimental for vertical ground acceleration below 2 g in base-isolated buildings. Some papers focused on 3D seismic isolation. Liu et al. [9] investigated a three-dimensional isolator for a four-storey building subjected to seismic ground motions. This mechanism includes two separate layers for isolating structures in different directions: a lead-rubber bearing in the horizontal direction and simple linear springs in the vertical direction. The results showed that the mechanism reduced the acceleration response of the building. Another paper proposed vertical seismic base isolation with a variable stiffness using hydraulic cylinders which was shown to be effective in reducing the axial force as well as acceleration [10]. Wei et al. [11] proposed a method of designing a 3D seismic isolator with separate layers for vertical and horizontal isolators and shaking table testing validated this technique.

The numerical investigation conducted by Barbieri et al. [12] employed semi-active control strategies in a two-storey building on a seismic vertical isolation system with changeable stiffness. This did not depend on applying dynamic forces to oppose the earthquake forces. Instead, isolation was achieved by changing the stiffness of the support to half its static state, when either the acceleration or the velocity of the base exceeds a specific value, with results showing that transmissibility of acceleration could be reduced by using an isolator with such stiffness variation. However, this was a specific case study and would require an active control system to change the stiffness.

Turning to a mechanical engineering concept for passive isolators, nonlinear isolator mechanisms with positive and negative stiffness elements have been popular. In 2011, Le and Ahn adopted two inclined bars connected to vertical and horizontal springs to create a Quasi-Zero Stiffness Systems (QZSS) for isolating seats in vehicles from vibrations [13]. Subsequently, experimental investigations were conducted for low-frequency vibration of a Negative Stiffness System (NSS) [14]. This mechanism, which was developed for a vehicle seat suspension, showed good isolation for a wide range of frequencies in comparison with a system without the NSS. Moreover, Le and Nguyen suggested adjusting the parameters of the system in order to maintain optimal performance and isolation in case of changes in the self-weight of the payloads [15]. In another paper, an optimization was performed for four different seat isolation systems with negative stiffness structures to find the ideal design [16]. The optimisation was based on a compromise between the required load-bearing capacity of the mechanism and the bearing flexibility for higher isolation. This is because larger negative stiffness reduces the bearing capacity while isolating the seats from vibration coming from road profiles. Mochida et al. [17] also investigated the use of negative stiffness in reducing transmission of forces in structures and suggested its use for seismic isolation, but the analysis was limited to the static case, and they did not conduct a dynamic analysis. Systems that provide such varying stiffness are called High-Static-Low-Dynamic Stiffness Systems (HSLDSS). If the system is designed to have zero stiffness at the equilibrium state, these are called QZSS.

The benefits of active control using time delay or adaptive active controls have been investigated as well [18,19,20]. Local and global bifurcations for a triple springs QZSS were investigated in [21]. Liu and Yu took advantage of modelling of a QZSS to examine the superharmonic behaviour, while taking into account the damping effects of the vertical and lateral springs as well as the revolution joint [22]. In another paper, they studied the superharmonics of a QZSS and the effects of different parameters on them [23]. It was shown that by decreasing either the nonlinearity of the system or the amplitude of the excitation, these superharmonic resonances became weaker. Increasing the damping ratio also has the same effect on the superharmonic resonances. In addition, these superharmonics did not affect the isolation performance for the high-frequency range which was still better than an equivalent linear isolator.

A QZSS can isolate a system over a wide range of frequencies. Therefore, it has been suggested by many researchers as a candidate for seismic isolation of structures. This is because by reducing the natural frequency of the system to lower than 0.5 Hz, isolation of the vertical acceleration can be improved for the high-frequency range (above 1 Hz). Asai proposed a QZSS with a variable ellipse curve mechanism to reduce the acceleration response of structures and proved the efficiency with a prototype experiment [24]. Liu et al. [25] proposed an isolator including a QZSS and a vertical damper to reduce vertical ground motion in near-fault earthquakes. In a number of papers Zhou and co-authors proposed a 3D base isolator for both vertical and horizontal components of earthquake using a QZSS and lead-rubber bearing base isolator [26,27,28]. Zhu et al. [29] investigated the efficiency of a QZSS isolator through experiments and compared the results with analysis for sine sweep input. Bouna et al. [30] proposed a QZSS for the piers of a multi-span bridge to isolate vibration and compared this system with a linear viscoelastic isolator. Najafijozani et al. [31] innvestigated several 3D adaptive seismic isolator mechanisms for nuclear powerplant equipment. In this study, six adaptive vertical isolators with linear and nonlinear stiffness and damping were compared. The results showed that the system with a nonlinear spring (with hardening behaviour) and linear damping decreases the peak response acceleration more than other cases. In addition, the linear or nonlinear damping did not significantly affect the response.

The studies on vertical isolators to date do not consider theoretical and experimental investigation into the performance of non-QZSS or HSLDSS isolators with friction elements under seismic loading. The purpose of this paper is to address these questions. The results from this study show that by a careful choice of HSLDSS parameters, it is possible to retain some effective stiffness at the static equilibrium position to maintain a relatively stable equilibrium, and achieve good isolation performance that is comparable to a QZSS. A QZSS is more susceptible to disturbance at its equilibrium state due to fluctuations in static loading. The dynamic model used in this study also includes a friction element to provide a more realistic model. Laboratory experiments performed on a small-scale table-top model, using several actual, scaled earthquake signals as input are presented, and the results show reasonable agreement with theoretical predictions. Both theoretical and experimental results show the passive isolator investigated performs very well in reducing transmissibility.

2 Model description

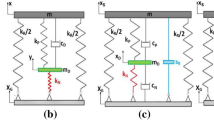
The single-degree-of-freedom (SDoF) system representation of the mechanism is shown in Fig. 1. The aim is to isolate the mass (\(m\)) from base motion. This system comprises two rigid, massless arms (inclined bars in the figure) with length \(l\). The angle between arms and horizontal direction is \(\theta \). One end of each arm is supported by a horizontal spring (stiffness \({k}_{h}\)) and the other end is connected to the mass. The mass is also supported by a vertical spring (stiffness kv) which is parallel to a viscous damper (\(c\)) and a friction element. One end of each spring is connected to the base. The two horizontal springs remain horizontal all the time. The arms are assumed to be able to rotate freely in relation to the mass and the horizontal springs.

Fig. 1
figure 1

SDoF model of the system with the isolator mechanism

Full size image

A QZSS is generally designed to have zero equivalent stiffness at the static equilibrium position \(\theta =0.\) The vertical spring has positive stiffness, and the horizontal springs add negative stiffness to the system if they are in compression when \(\theta =0\). Therefore, in the equilibrium position, the arms are horizontal, and they add the maximum negative stiffness to the system and the equivalent stiffness of the system becomes zero while retaining stability, but at a critical state. It is important to note that the stiffness of the horizontal spring cannot be larger than this value or else the system becomes unstable at \(\theta =0\).

3 Static behaviour of the mechanism

To find the static stiffness of the system, consider a force \(F\) which is applied at point \(\mathrm{A}\) in the vertical direction \(x\) as shown in Fig. 2. The origin of the vertical coordinate \(x\) is set to the unloaded state of point A, \(x=0\), that is the position of the point \(\mathrm{A}\) before applying the static loading and it is assumed that both horizontal and vertical springs are unstretched in this position (Fig. 3a). The initial value for \(\theta \) is \({\theta }_{0}\). For any given force \(F\) the internal force in the inclined bars, horizontal springs and the vertical spring is \({F}_{i}\), \({F}_{h}\), and \({F}_{v}\), respectively. The vertical bearing reactions at the bottom of the arms shown as Rb do not affect the calculations. The equation of equilibrium of point A in the vertical direction gives

$$ F = 2{ }F_{i} \sin \theta + F_{v} . $$
(1)
Fig. 2
figure 2

Diagram of the SDoF system and the isolator mechanism for static loading

Full size image
Fig. 3
figure 3

Diagram of the isolator mechanism for a unloaded position, b static equilibrium position

Full size image

Considering \(b=l\mathrm{cos}\theta \) as the horizontal projected length of each arm and \({b}_{0}\) as the initial value of \(b\) when \(\theta ={\theta }_{0}\), the force in the inclined bars is

$${F}_{i}=\frac{{F}_{h}}{\mathrm{cos}\theta }={k}_{h}\frac{{b}_{0}-b}{\mathrm{cos}\theta }.$$
(2)

From Eqs. (2) and (1)

$$F=2{k}_{h} \left({b}_{0}-b\right)\mathrm{tan}\theta +{F}_{v}.$$
(3)

Based on Eq. (3) and rewriting \(b\) = \(\sqrt{{l}^{2}-{(l\mathrm{sin}{\theta }_{0}+x) }^{2}}\), in which \(x\) is the vertical upward displacement of point A from the unloaded initial state, the force–displacement equation can be written as

$$ F = 2k_{h} { }\left( {l\cos \theta_{0} - \sqrt {l^{2} - \left( {l\sin \theta_{0} + x} \right){ }^{2} } { }} \right) \times \frac{{\left( {l{ }\sin \theta_{0} + x} \right)}}{{\sqrt {l^{2} - \left( {l\sin \theta_{0} + x} \right){ }^{2} } }} + k_{v} { }x. $$
(4)

Consequently, the equivalent vertical stiffness of the mechanism is defined by

$${k}_{e}=\frac{dF}{dx}. $$
(5)

By substituting Eq. (4) into Eq. (5), it follows that

$${k}_{e}=2{k}_{h}\left(\frac{\mathrm{cos}{\theta }_{0}}{{\left(1-{\left(\mathrm{sin}{\theta }_{0}+\left(\frac{x}{l}\right)\right)}^{2}\right)}^{3/2}}-1\right)+{k}_{v} .$$
(6)

The static load F in this case is due to the weight of the mass and, at the equilibrium state, the arms are designed to be horizontal \(({\theta }_{s}={0}^{^\circ })\) hence.

$$F=-mg.$$
(7)

The static displacement \({x}_{s}\) at the equilibrium position is then given by.

$${x}_{s}=-l\mathrm{sin}{\theta }_{0},$$
(8)

where the arms will be horizontal and \({\theta }_{s}={0}^{^\circ }\). This is shown in Fig. 3b.

In this case, the vertical component of the force in the bars is zero. Therefore, \({m\mathrm{g}=k}_{v} l\mathrm{sin}{\theta }_{0}\), with the arms being horizontal in this position giving,

$${k}_{v}=\frac{mg}{l\mathrm{sin}{\theta }_{0}} .$$
(9)

In the QZSS, the equivalent vertical stiffness is zero. Therefore, by setting \({k}_{e}=0\) and substituting Eq. (9) into Eq. (6), the stiffness of the horizontal springs for a QZSS, \({k}_{h,Q}\), is given by

$$k_{h,Q} = \frac{mg}{{2l\sin \theta_{0} \left( {1 - \cos \theta_{0} } \right)}} .$$
(10)

The ratio of horizontal spring stiffness to the vertical one is defined as

$$\lambda =\frac{{k}_{h}}{{k}_{v}}.$$
(11)

By substituting Eqs. (9) and (10) into Eq. (11), for a QZSS

$$\lambda =\frac{1}{2\left(1-\mathrm{cos}{\theta }_{0}\right)} ,$$
(12)

which only depends on \({\theta }_{0}\).

For a HSLDSS, the stiffness of the vertical spring, \({k}_{v}\), is calculated from Eq. (9), which results in \({\theta }_{s}=0.\) The stiffness of the horizontal springs can be any value less than \({k}_{h,Q}\). The ratio of the horizontal spring stiffness in a HSLDSS to that of the QZSS is given by

$$\beta =\frac{{k}_{h}}{{k}_{h,Q}}$$
(13)

in which \(\beta \) can take any value between 0 (linear system) and 1 (QZSS). If \(\beta >1\), \(\theta =0\) is unstable which needs to be avoided.

Figure 4a shows the force–displacement graphs for a linear system, a QZSS (\(\beta \) = 1) and a HSLDSS with different horizontal spring stiffnesses. All the cases have the same vertical spring stiffness of 140 N/m, length of the arms 0.1 m and initial angle \({\theta }_{0}=30^\circ \). As can be seen, the nonlinearity in the system increases with the horizontal spring stiffness. Figure 4b shows the equivalent stiffness of the mentioned systems. It is evident that the equivalent stiffness of the QZSS (\(\beta =1)\) is zero when \(x=-l\mathrm{sin}{\theta }_{0}\) and the arms are horizontal, while, for an HSLDSS, the system retains some stiffness when the arms are horizontal.

Fig. 4
figure 4

a Force–displacement graphs and b equivalent stiffness–displacement graphs, for system with \(l=0.1 \mathrm{m}\), \({k}_{v}=140\mathrm{ N}/\mathrm{m}\) and \({\theta }_{0}=30^\circ .\)

Full size image

4 Dynamic behaviour of the mechanism

4.1 Dynamic model

When deriving the equation of motion for a SDoF system with the isolator, it is considered that the mechanism is designed in order to have horizontal arms (\({\theta }_{s}=0^\circ \)) at the static equilibrium position which is shown in Fig. 5. In this figure, \(z\) is the base excitation and the relative displacement of the mass to that of the base is defined as

Fig. 5
figure 5

Diagram of the SDoF system and the isolator mechanism for dynamic loading

Full size image
$$y=x-z ,$$
(14)

As can be seen, a friction element with maximum force of \({f}_{dv}\) is also considered in parallel to the vertical spring as well as the viscous damping element, c. The damping ratio \(\xi \) is defined in terms of \(c\) as

$$\xi =\frac{c}{2m{\omega }_{n}} ,$$
(15)

in which

$${\omega }_{n}=\sqrt{\frac{{k}_{v}}{m}} .$$
(16)

The resonance frequency, however, is defined in this paper to be

$${\omega }_{r}={\sqrt{\frac{{k}_{e}}{m}} }.$$
(17)

By substituting Eq. (6) into Eq. (16)

$${\omega }_{r}=\sqrt{\frac{2{k}_{h}\left(\frac{\mathrm{cos}{\theta }_{0}}{{\left(1-{\left(\mathrm{sin}{\theta }_{0}+\left(\frac{y}{l}\right)\right)}^{2}\right)}^{3/2}}-1\right)+{k}_{v}}{m}} .$$
(18)

As can be seen, this frequency depends on y and hence depends on the amplitude of the base excitation. Moreover, for the friction element, a continuous Coulomb friction model has been chosen in the numerical modelling in order to avoid computational difficulties caused by force discontinuities in the stick–slip model. This model has been proven to be an accurate approximation for the signum function [32], the friction force being

$$f={f}_{dv}.\mathrm{tanh}\left(\frac{\dot{y}}{{v}_{d}}\right) ,$$
(19)

in which \({f}_{dv}\) and \({v}_{d}\) are the maximum dynamic friction force in the vertical direction and the velocity tolerance which is a real number close to zero [32]. Figure 6 illustrates the relationship between the friction force and velocity (\(\dot{y}\)) given in Eq. (19) for various velocity tolerances (\({v}_{d}\)). As can be seen, a small value of velocity tolerance, \({v}_{d}=0.001\), gives an accurate approximation to a step function, while for higher values (e.g. \({v}_{d}=1\)) it can cause the equation to be less stiff numerically and the behaviour becomes a poorer approximation to the step function as \({v}_{d}\) increases.

Fig. 6
figure 6

Friction force versus velocity for various velocity tolerances

Full size image

The equation of motion for both QZSS and HSLDSS is given by

$$ \begin{aligned} & m\ddot{y} + c\dot{y} + 2k_{h} \left( {l\cos \theta_{0} - \sqrt {l^{2} - \left( {l\sin \theta_{0} + y} \right)^{2} } } \right) \\ & \; \times \frac{{l \sin \theta_{0} + y}}{{\sqrt {l^{2} - \left( {l\sin \theta_{0} + y} \right)^{2} } }} + k_{v} y \\ & \; + f_{dv} .\tanh \left( {\frac{{\dot{y}}}{{v_{d} }}} \right) = - m\ddot{z} - mg. \\ \end{aligned} $$
(20)

4.2 Time harmonic excitation

The major consideration which is used to evaluate the performance of the system under the time harmonic excitation is transmissibility. Transmissibility is defined as the ratio of the maximum response acceleration to the maximum input acceleration. Because the system is nonlinear, the transmissibility is a function of the amplitude of the input. In the examples below, sinusoidal acceleration inputs with a constant amplitude of 0.08 g and various frequencies are employed and the response of the system is calculated by direct integration of the equation of motion [Eq. (20)]. This equation is modelled in MATLAB and solved numerically using an adaptive step size Runge–Kutta scheme (ode45). As there are multiple solutions for frequencies around resonance in some cases, the numerical analysis was done once from low to high frequencies (sweep up) and once from high to low frequencies (sweep down) to capture the two solutions.

Figure 7 indicates the transmissibility of the linear system as well as QZSS and HSLDSS with various stiffness ratios \(\beta \). All the cases have the same vertical spring stiffness \({k}_{v}=\) 140 N/m, length of the arms \(l=0.1\) m, initial angle \({\theta }_{0}=30^\circ \), mass of the payload \(m=0.708\) kg and static equilibrium position \({\theta }_{s}=0.\) The friction force \({f}_{dv}\) and the velocity tolerance \({v}_{d}\) are considered as 0.27 N and 0.001 m/s, respectively. The value of the friction force is that found from experimental results as explained in Sect. 6.5. The damping ratio, \(\xi \), is taken to be 5%. As seen, by increasing \(\beta \) from zero (linear) to 1 (QZSS), the resonance peak and frequency decrease. By decreasing the resonance frequency, the range of frequencies with a transmissibility of less than 1 becomes wider. In other words, the system is able to isolate a wider range of frequencies. Therefore higher \(\beta \) would result in isolation over a wider range of frequencies.

Fig. 7
figure 7

Transmissibility for systems with \(l=0.1 \mathrm{m}\), \({k}_{v}=140\mathrm{ N}/\mathrm{m},\) \({\theta }_{0}=30^\circ \) and different values for \(\beta \)

Full size image

4.3 Earthquake excitations

In this study, eight historical near-fault earthquakes are taken from the PEER ground motion database website [1] to compare the performance of a QZSS with a HSLDSS. Table 1 shows the year and station of occurrence, magnitude (M), distance from the source (Rcl) and the average shear velocity at 30 m depth (VS30) of each signal as well as the characteristics of the vertical component of these earthquakes including peak ground acceleration (PGA), velocity (PGV) and displacement (PGD). All of these earthquakes have a magnitude greater than 6.5 on the Richter scale and are located within 15 km from faults.

Table 1 Near-fault strong vertical ground motions [1]
Full size table

The criteria which are used for evaluating the performance of the mechanisms for earthquake applications are based on the following factors, with lower values indicating better performance:

(a) ratio of the maximum response acceleration to the maximum base acceleration.

(b) ratio of the root-mean-square (RMS) response/base strong motion acceleration. The RMS criterion is calculated for the strong motion duration of the signal as this part includes the majority of energy which is the main cause of damage to structures [33]. To do this, the duration of the strong motion is calculated based on a percentage of cumulative energy [34] given by

$$CE=\int {a}^{2}(t)dt,$$
(21)

in which a is the acceleration time history and \(t\) is time. The part of the signal with CE between 5 and 95% gives the strong ground motion which is used to determine the RMS response.

(c) Maximum non-dimensional force magnification (\({f}_{mag})\), which is defined as.

$${f}_{mag}=\mathrm{max}\left(\frac{\left(\ddot{y} + g\right)}{g}\right).$$
(22)

This shows the magnification of the compressive force in the structural components (columns) from the design force at static equilibrium. Values higher than one, typical when the ground motion is upwards, indicate that the components are overstressed and any negative value would indicate the members undergoing tension.

Figure 8 illustrates the ground acceleration spectra for the mentioned earthquake signals. As seen, most of these earthquakes are rich in frequencies larger than 1 Hz, and a successful vertical isolator should be able to minimise their damaging effects. Comparing the spectrum of input acceleration time history with that of the response provides an indication of the performance of the isolator as the response without an isolator would be the same as the input.

Fig. 8
figure 8

Vertical ground acceleration spectra for 5% damping

Full size image

5 Base isolator performance subjected to earthquakes

In this section, the effect of initial angle \({\theta }_{0}\) and the stiffness of the horizontal springs are considered when designing an isolator for earthquake inputs. There are three criteria considered for this comparison: maximum acceleration, RMS acceleration and force transmitted to the mass. The design parameters of the isolator considered for this purpose are \(m=\) 0.708 \(\mathrm{kg}\) and \(l=\) 0.1 \(\mathrm{m}\). The values of \({k}_{v}\) and \({k}_{h,Q}\) are calculated using Eqs. (9) and (10), respectively, for different values of \({\theta }_{0}=10, 20, 30, 40, 50, 60, 70\) and \(80\) degrees. To consider different combinations of HSLDSS, various horizontal spring stiffness values are considered, including \(\beta =0, 0.1, 0.2, \dots , 1.\) As mentioned before, \(\beta =0\) represent a linear system, while \(\beta =1\) gives the QZSS response. The other values \(0<\beta <1\) represent the HSLDSS. In all cases, the static equilibrium position is when the arms are horizontal and \({\theta }_{s}=0.\) The damping value, c, is taken as 10 N.s/m for all cases. The friction force \({f}_{dv}\) is taken to be 0.27 N, which is estimated from experimental results (explained in Sect. 6.5), and the velocity tolerance \({v}_{d}\) is 0.001.

Figure 9 indicates the resonance frequency of these systems calculated using Eq. (18) at the static equilibrium position in which \(y=-l\mathrm{sin}{\theta }_{0}\). It is expected that the systems with lower frequencies have higher earthquake isolation performance than others for the input signals considered, because the vertical component of earthquakes in most of the cases has higher energy at relatively higher frequencies (more than 1 Hz).

Fig. 9
figure 9

Frequencies for systems with \(l=0.1\ \mathrm{ m}\), \(m=0.708\ \mathrm{ kg}\), \({f}_{dv}=0.27\ \mathrm{ N}\), \({v}_{d}=0.001\) and various \({\theta }_{0}\), \({k}_{v}\) and various \(\beta\)

Full size image

5.1 Maximum acceleration ratio

Figure 10 illustrates the maximum acceleration ratio for various HSLDSS and QZSS subjected to eight earthquakes as a function of \({\theta }_{0}\) and \(\beta \). By increasing \(\beta \), the nonlinearity of the system increases. As can be seen, by increasing the initial angle \({\theta }_{0}\) and \(\beta \), the maximum acceleration ratio decreases. In most cases, the maximum acceleration ratio is less than one which means that the mechanism reduces the peak acceleration. For some combinations subjected to the Chi-Chi earthquake, however, this ratio exceeds 1 (maximum of 1.24).

Fig. 10
figure 10

Maximum acceleration ratio for systems with \(l=0.1\ \mathrm{ m}\), \(m=0.708\ \mathrm{ kg}\),\( {f}_{dv}=0.27\ \mathrm{ N}\), \({v}_{d}=0.001\) and various \({\theta }_{0}\), \({k}_{v}\) and \(\beta \) for different earthquake inputs

Full size image

5.2 RMS ratio of acceleration

Figure 11 shows the RMS ratio of the acceleration for the isolator for various \({\theta }_{0}\) and \(\beta \). By increasing the initial angle, the RMS ratio decreases. This trend is also true for the horizontal spring stiffness ratio. For the mechanism with various initial angle and horizontal stiffness ratios subjected to El Centro 182, El Centro 170, Northridge, Bam and Christchurch inputs, the RMS ratio is less than one and the mechanism reduces the response of the system by 30–70 percent. However, the RMS ratio for some combinations with low initial angle (larger vertical spring stiffness) and low horizontal spring stiffness ratio, the responses of the system to LGPC and Chi-Chi reach 1.15 and 1.27, respectively.

Fig. 11
figure 11

RMS ratio of acceleration for systems with \(l=0.1\ \mathrm{ m}\), \(m=0.708\ \mathrm{ kg }{f}_{dv}=0.27\ \mathrm{ N}\), \({v}_{d}=0.001\) and various \({\theta }_{0}\), \({k}_{v}\) and \(\beta \) for different earthquake inputs

Full size image

5.3 Maximum non-dimensional force magnification

The main purpose of isolating a structure or equipment from the vertical component of earthquakes is to decrease the force magnification from the base to the columns and other structural members. In this section, the maximum non-dimensional force magnification (\({f}_{mag})\) to a rigid mass on the isolator mechanism (QZSS and HSLDSS) subjected to eight ground excitations is calculated and compared.

Figure 12 shows the response of HSLDSS and QZSS to eight earthquake inputs for various \(\beta \) and \({\theta }_{0}\). As seen, by increasing the initial angle \({\theta }_{0}\) and \(\beta \), the non-dimensional force magnification decreases for all earthquake inputs. In other words, if the vertical spring is softer and \(\beta \) is closer to one, the force magnification is lower.

Fig. 12
figure 12

Force magnification ratio of compressive force for systems with \(l=0.1\ \mathrm{ m}\), \(m=0.708\ \mathrm{ kg}\), \({f}_{dv}=0.27\ \mathrm{ N}\), \({v}_{d}=0.001\) and various \({\theta }_{0}\), \({k}_{v}\) and \(\beta \) for different earthquake inputs

Full size image

6 Experimental results for a HSLDSS

In this section, experimental and numerical results for the static and dynamic behaviour of a HSLDSS are compared. The test model has 0.1 m long arms (\(l\)), 0.708 kg (including half of the mass of the arms) mass (\(m\)), 30 degrees initial unloaded angle (\({\theta }_{0}\)), vertical (\({k}_{v}\)) and horizontal (\({k}_{h}\)) spring stiffness of 140 N/m and 280 N/m, respectively (\(\beta \approx 0.5)\). The friction force \({f}_{dv}\), tolerance velocity \({v}_{d}\) and damping ratio were considered as 0.27 N, 0.001 and 5%, respectively, in the numerical model. The friction force for the rig was estimated using the least squared error method based on earthquake results as described in Sect. 6.5.

6.1 Rig description

Figure 13 illustrates the rig. There are two 100-mm long arms (A), two horizontal guides of 8 mm diameter circular cross section (B) and a vertical guide 10 mm diameter circular cross section (C). The guides keep the springs straight. The horizontal guides are supported by two linear ball bearings (D), inlaid in the housing in the side frames to reduce the friction between the surfaces. The carriage (or platform E) is made of plastic and slides on the vertical guide. (F) and (G) are the horizontal and vertical compression springs, respectively. The top frame (H) and arms are made of aluminium (to decrease the weight), while the rest of the parts are of stainless steel.

Fig. 13
figure 13

The rig

Full size image

6.2 Static tests

In order to validate and confirm the static parameters, the static behaviour of the rig was tested using an Instron 5900 series 100 kN machine (Fig. 14a). The tests were done at a speed of 20 mm/min which was found to be sufficient to get consistent readings. The tolerance of measurements is 0.1 mm. Figure 14b shows the experimental and analytical force–displacement results for the static loading. It also includes a third-order polynomial curve fitted to the experimental data (hollow circles), given by the equation shown in the figure. The analytical curve (dash line) shows good agreement with the experiments and verifies the static parameters used in the computer model.

Fig. 14
figure 14

a The rig in the Instron 5900 series 100 kN machine. b Experimental and analytical static results for the systems with \(l=0.1\,\mathrm{ m}\), \(m=0.708\,\mathrm{ kg}\), \({\theta }_{0}=30^\circ \), \({k}_{v}=140\,\mathrm{ N}/\mathrm{m}\), \({f}_{dv}=0.27\,\mathrm{ N}\), \({v}_{d}=0.001\) and \(\beta \approx 0.5\)

Full size image

6.3 Harmonic tests

A series of pure sinusoidal tests were conducted using an APS 113 Electro-series shaker (shown in Fig. 15a) to find the transmissibility of the time harmonic excitation. The purpose of this set of tests is to find the resonance frequency and verify the numerical model. The tests were done using closed-loop acceleration control with an amplitude of 0.08 g once from low to high frequencies (sweep up) and another time from high to low frequencies (sweep down). This is because around resonance, there can be multiple solutions and by sweeping up and down, both solutions are captured.

Fig. 15
figure 15

a The rig on the APS 113 Electro-series shaker, b experimental and analytical transmissibility results for the systems with a = 0.08 g, \(l=0.1\mathrm{ m}\), \(m=0.708\,\mathrm{ kg}\), \({\theta }_{0}=30^\circ \), \({k}_{v}=140\,\mathrm{ N}/\mathrm{m}\),\({f}_{dv}=0.27\mathrm{ N}\), \({v}_{d}=0.001\) and \(\beta \approx 0.5\)

Full size image

Figure 15b indicates the experimental transmissibility results (black circles for sweep up and black stars for sweep down) in comparison with the numerical modelling results (grey stars). These results have a good agreement. The difference between the numerical and experimental curves can be due to the assumption regarding the friction force, which is assumed to be in the vertical direction only and taken as a constant irrespective of the signal, and a relative velocity value used based on all the experimental results.

6.4 Earthquake tests

The same APS 113 Electro-series shaker was used for the earthquake tests using close-loop acceleration control.

Figure 16 illustrates the strong part of the response of the rig subjected to different earthquake inputs in comparison with the numerical results which shows a good agreement qualitatively.

Fig. 16
figure 16

Experimental response acceleration time history in comparison with the numerical cases for various earthquake excitations for the systems with \(l=0.1\,\mathrm{ m}\), \(m=0.708\,\mathrm{ kg}\), \({\theta }_{0}=30^\circ \), \({k}_{v}=140\,\mathrm{ N}/\mathrm{m}\), \({f}_{dv}=0.27\,\mathrm{ N}\), \({v}_{d}=0.001\) and \(\beta \approx 0.5\)

Full size image

Table 2 gives the maximum acceleration for the mass and the base and the ratio of the maximum acceleration with respect to the base for the experimental results compared to the numerical cases. In the table, the numbers before some earthquake names (e.g. 0.5 Bam) show the scale factor used to scale the amplitude of the acceleration time histories. For Bam, Christchurch and LGPC earthquakes, the scale factors are 0.5, 0.3 and 0.5, respectively. The scale factor is 1 for the rest of earthquake inputs. As is evident, both experimental and numerical results show more than 50% reduction in the maximum acceleration. Table 3 shows the RMS input acceleration and the response of the system for the experiments compared to the numerical results. The RMS is calculated for the stronger part of the signals with cumulative energy between 5 and 95%. In all cases, reduction in both the maximum and RMS values is substantial except for the Chi-Chi earthquake, which amplifies the input excitation.

Table 2 Maximum acceleration of experimental and numerical results for the systems with \(l=0.1\,\mathrm{ m}\), \(m=0.708\,\mathrm{ kg}\), \({\theta }_{0}=30^\circ \), \({k}_{v}=140\,\mathrm{ N}/\mathrm{m}\), \({f}_{dv}=0.27\,\mathrm{ N}\), \({v}_{d}=0.001\) and \(\beta \approx 0.5\)
Full size table
Table 3 RMS values of experimental results and numerical results for the systems with \(l=0.1\,\mathrm{ m}\), \(m=0.708\,\mathrm{ kg}\), \({\theta }_{0}=30^\circ \), \({k}_{v}=140\,\mathrm{ N}/\mathrm{m}\), \({f}_{dv}=0.27\,\mathrm{ N}\), \({v}_{d}=0.001\) and \(\beta \approx 0.5\)
Full size table

Figure 17a illustrates the input acceleration spectrum compared to Fig. 17b which shows the response acceleration spectrum. As evident, the mechanism isolates the input excitation substantially for frequencies above 3 Hz. However, the frequencies less than 3 Hz are magnified because of the resonance. The Chi-Chi earthquake is rich in low frequencies close to the natural frequency of the system and, as a result, the response of the system to this signal was magnified to twice the input acceleration. Therefore, the mechanism works well for the inputs with frequency content above 3 Hz as we expect in near-fault earthquakes.

Fig. 17
figure 17

a Input acceleration spectra and b response acceleration spectra for the systems with \(l=0.1\,\mathrm{ m}\), \(m=0.708\,\mathrm{ kg}\), \({\theta }_{0}=30^\circ \), \({k}_{v}=140\,\mathrm{ N}/\mathrm{m}\), \({f}_{dv}=0.27\,\mathrm{ N}\), \({v}_{d}=0.001\) and \(\beta \approx 0.5\)

Full size image

6.5 Friction estimation from earthquake excitations

In this section, the friction force estimation using the least squared error method based on the error between the numerical and the experimental earthquake results is described. In this method, the numerical response for each earthquake input was generated using various values for the maximum friction force. Then the square of the difference between the numerical and experimental acceleration response time histories gives the error. The sum of the squared errors gives a parameter to minimise to estimate the friction force which gives the smallest error. The squared error, which is a function of friction force, is given as

$$ e^{2} \left( {f_{dv} } \right) = \sum \left( {a_{exp} \left( t \right) - a_{num} \left( {t,f_{dv} } \right)} \right)^{2} $$
(23)

in which \({a}_{exp}\) is the experimental response acceleration time history and \({a}_{num}\) is the numerical response acceleration time history.

The estimated maximum friction force is calculated based on three sets of experimental data for eight earthquake inputs. For each different earthquake input there is a different value of the maximum friction force which minimises the squared error. These values are shown in Table 4. The mean of these friction forces is taken and subsequently used in the numerical model. It should also be noted that friction in the horizontal direction and in the hinges is neglected.

Table 4 Friction force for each earthquake measured for the systems with \(l=0.1\,\mathrm{ m}\), \(m=0.708\,\mathrm{ kg}\), \({\theta }_{0}=30^\circ \), \({k}_{v}=140\,\mathrm{ N}/\mathrm{m}\), \({v}_{d}=0.001\) and \(\beta \approx 0.5\)
Full size table

Figure 18 illustrates the squared error as a function of \({f}_{dv}\) for various earthquake inputs. As can be seen, the friction force which makes this squared error minimum is different for each earthquake input. The mean value for these friction forces is 0.27 N, which gives good agreement between experimental and numerical results for both harmonic and earthquake tests.

Fig. 18
figure 18

Squared error vs. friction force for various earthquake inputs set 1 for the systems with\(l=0.1\,\mathrm{ m}\), \(m=0.708\,\mathrm{ kg}\),\({\theta }_{0}=30^\circ \),\({k}_{v}=140\,\mathrm{ N}/\mathrm{m}\), \({v}_{d}=0.001\) and \(\beta \approx 0.5\)

Full size image

It is recognised that the actual friction force may not be in the form assumed in Eq. (19) and may vary between different tests, since it depends on the bearing/contact force which is likely to vary. However, the results show that using an average value based on several tests gives response results which are in close agreement with measured values.

7 Conclusion

In this paper, the static and dynamic behaviour of a High-Static-Low-Dynamic Stiffness System (HSLDSS) isolator under sinusoidal and scaled actual vertical earthquake excitations based on numerical and experimental results was presented.

Numerical results showed that both the HSLDSS and the quasi-zero-stiffness system (QZSS) can significantly reduce transmission of acceleration and magnification of force, with seven of the eight earthquake inputs showing good performance. One exception was the Chi-Chi earthquake signal, which caused some amplification. This observation was also confirmed experimentally, where reduction in transmissibility was consistent for all signals except for the Chi-Chi earthquake. In all other cases, experimental results showed that the HSLDSS with \(\beta \approx 0.5\) maintains good isolation performance and reduces the maximum and the RMS value of the acceleration by at least 50% and 60%, respectively, in most of the cases, compared to 40% for the theoretical results. The Chi-Chi signal had a significantly higher lower-frequency content. However, it is also worth noting that low-frequency excitations tend to have lower amplitudes of acceleration and, for the signals that had relatively higher frequencies, both systems performed well. Numerical results showed that it is possible to isolate the Chi-Chi earthquake by changing the design parameters, increasing the initial angle and selecting different values for the spring stiffnesses.

The effect of friction in the vertical direction was considered in the theoretical model. The friction force was estimated using a least square error method, taking the difference between the experimental and theoretical results as the objective function, based on all the test results. This value was used in comparing the theoretical and experimental results. It is likely that in reality the actual friction force may depend on signal amplitude and characteristics and may not be of the form assumed in Eq. (19), but the general agreement between the theory and experiment shows that the approach used is reasonable.

Since the special case of an HSLDSS, namely a QZSS, which has zero net vertical stiffness at the equilibrium position, the system may become unstable at \(\theta =0\) if the nonlinearity is more than what the system was designed for (because of any mistuning in construction or change in the payload). To avoid this, when using a QZSS, a lock-release-type mechanism or a semi-active control system could be used, to ensure sufficient stiffness is maintained at the equilibrium state when there is no seismic activity. However, the HSLDSS with small net vertical stiffness at the equilibrium position has a satisfactory performance.

The experimental results validate the concept on a small-scale model. Since the resonance frequency of the rig at the static equilibrium position is close to that of a building on the mechanism, the time scaling for the earthquake inputs was not required. However, the amplitude of three of the earthquake acceleration inputs was scaled because of the capacity of the testing equipment.

This study presented proof-of-concept results using a small-scale model. There are a number of issues that would need to be addressed prior to application to a full-scale structure. For practical implementations, multiple isolators would normally be needed and therefore differential movements in structures, rotations and the interaction between horizontal and vertical displacements would need to be considered. In addition, the effect of isolators in more than one direction also needs to be taken into account. Scaling issues would include the mass to be isolated together with the maximum vertical displacement that the design should accommodate: this would affect the length of the arms. There might also be a need to accommodate mistune. Further experimental work to verify the potential use of this concept for practical implementation will need to address the above.