Abstract
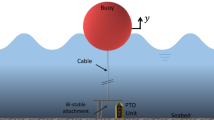
To expand the narrow response bandwidth of linear point wave energy absorbers (PWAs), a few research studies have recently proposed incorporating a bi-stable restoring force in the design of the absorber. Such studies have relied on numerical simulations to demonstrate the improved bandwidth of the bi-stable absorbers. In this work, we aim to understand how the shape of the bi-stable restoring force influences the effective bandwidth of the absorber. To this end, we use perturbation methods to obtain an approximate analytical solution of the nonlinear differential equations governing the complex motion of the absorber under harmonic wave excitations. The approximate solution is validated against a numerical solution obtained via direct integration of the equations of motion. Using a local stability analysis of the equations governing the slow modulation of the amplitude and phase of the response, the loci of the different bifurcation points are determined as function of the wave frequency and amplitude. Those bifurcation points are then used to define an effective bandwidth of the absorber. The influence of the shape of the restoring force on the effective bandwidth is also characterized by generating design maps that can be used to predict the kind of response behavior (small amplitude periodic, large amplitude periodic, or aperiodic) for any given combination of wave amplitude and frequency. Such maps are critical toward designing efficient bi-stable PWAs for known wave conditions.

















Similar content being viewed by others
Data Availability
The data that support the findings of this study will be made available upon reasonable request.
Notes
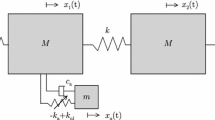
The mathematical representation of the restoring force can change depending on the type of mechanism used to introduce bi-stability. However, generally for a symmetric bi-stable restoring force, the canonical form \(F=k_1 y +k_3 y^3\) can be used to capture the main features of the dynamics without curtailing the generality of the analysis.
References
AlShami, E., Zhang, R., Wang, X.: Point absorber wave energy harvesters: a review of recent developments. Energies 12(1), 47 (2019)
Falnes, J., Hals, J.: Heaving buoys, point absorbers and arrays. Philosoph. Trans. Royal Soc. A Math. Phys. Eng. Sci. 370(1959), 246–277 (2012)
Drew, B., Plummer, A.R., Sahinkaya, M.N.: A review of wave energy converter technology. Proceed. Instit. Mech. Eng. Part A J. Power Energy 223(8), 887–902 (2009)
Younesian, D., Alam, M.-R.: Multi-stable mechanisms for high-efficiency and broadband ocean wave energy harvesting. Appl. Energy 197, 292–302 (2017)
Schubert, B.W., Robertson, W.S., Cazzolato, B.S., Ghayesh, M.H., Sergiienko, N.Y.: Performance enhancement of submerged wave energy device using bistability. Ocean Eng. 213, 107816 (2020)
Daqaq, M. F., Masana, R., Erturk, A., Dane Quinn, D.: On the role of nonlinearities in vibratory energy harvesting: a critical review and discussion. Appl. Mech. Rev. 66(4)
Xi, R., Zhang, H., Zhao, H., Mondal, R., et al.: High-performance and robust bistable point absorber wave energy converter. Ocean Eng. 229, 108767 (2021)
Xiao, X., Xiao, L., Peng, T.: Comparative study on power capture performance of oscillating-body wave energy converters with three novel power take-off systems. Renew. Energy 103, 94–105 (2017)
Zhang, H., Xi, R., Xu, D., Wang, K., Shi, Q., Zhao, H., Wu, B.: Efficiency enhancement of a point wave energy converter with a magnetic bistable mechanism. Energy 181, 1152–1165 (2019)
Zhang, X.-T., Yang, J.-M., Xiao, L.-F.: An oscillating wave energy converter with nonlinear snap-through power-take-off systems in regular waves. China Ocean Eng. 30(4), 565–580 (2016)
Zhang, X., Tian, X., Xiao, L., Li, X., Chen, L.: Application of an adaptive bistable power capture mechanism to a point absorber wave energy converter. Appl. Energy 228, 450–467 (2018)
Zhang, X., Tian, X., Xiao, L., Li, X., Lu, W.: Mechanism and sensitivity for broadband energy harvesting of an adaptive bistable point absorber wave energy converter. Energy 188, 115984 (2019)
Song, Y., Guo, X., Wang, H., Tian, X., Wei, H., Zhang, X.: Performance analysis of an adaptive bistable point absorber wave energy converter under white noise wave excitation. IEEE Trans. Sustain. Energy
Jin, H., Zhang, H., Xu, D., Liu, C., Xu, S.: Analytical investigation on wave attenuation performance of a floating breakwater with nonlinear stiffness. Ocean Eng. 243, 110160 (2022)
Nayfeh, A.H., Mook, D.T., Marshall, L.R.: Nonlinear coupling of pitch and roll modes in ship motions. J. Hydronaut. 7(4), 145–152 (1973)
Li, W., Tang, Y., Liu, L., Liu, S., Cai, R.: Heave-roll-pitch coupled nonlinear internal resonance response of a spar platform considering wave and vortex exciting loads. J. Ocean Univ. China 16(2), 209–222 (2017)
Harne, R.L., Wang, K.: A review of the recent research on vibration energy harvesting via bistable systems. Smart Mater. Struct. 22(2), 023001 (2013)
Hulme, A.: The wave forces acting on a floating hemisphere undergoing forced periodic oscillations. J. Fluid Mech. 121, 443–463 (1982)
Ogilvie, T.F., Tuck, E.O.: A rational strip theory of ship motions: part i. University of Michigan, Technical Report (1969)
Haskind, M.: The exciting forces and wetting of ships in waves
Newman, J.N.: The exciting forces on fixed bodies in waves. J. Ship Res. 6(04), 10–17 (1962)
Nayfeh, A.H.: Perturbation Methods. Wiley (2008)
Wang, L.: Modelling and advanced control of fully coupled wave energy converters subject to constraints: the wave-to-wire approach, Ph.D. thesis, Acta Universitatis Upsaliensis (2017)
Meyers, R.A.: Mathematics of Complexity and Dynamical Systems. Springer (2011)
Kovacic, I., Rand, R., Mohamed Sah, S.: Mathieu’s equation and its generalizations: overview of stability charts and their features. Appl. Mech. Rev. 70(2)
Brunton, S.L., Kutz, J.N.: Data-driven Science and Engineering: Machine Learning, Dynamical Systems, and Control. Cambridge University Press (2019)
Funding
This research was funded by Abu Dhabi Education and Knowledge Council (ADEK) under grant number AARE2019-161: Exploiting Bi-stability to Develop a Novel Broadband Point Wave Energy Absorber.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Eigensystem realization algorithm
Consider the following single-input single-output discrete-time dynamical system:
and a discrete-time scalar input u:
According to linear system theory, the discrete-time impulse response data \(h_{k}^{\delta }\) could be expressed as:
In our analysis, the discrete-time impulse response data are obtained through substituting the radiation damping coefficients \(B(\omega _i)\) into Eq. (3). The next step is to proceed by constructing the generalized Hankel matrix \(\mathbf{H }_{r \times s} (g)\) for \(g=0,1\) which consists of r rows and s columns, generated by stacking time-shifted impulse response data in the following order:
Using Eq. (A.3), we can express the generalized Hankel matrix in Eq. (A.4) in terms of the realized state-space matrices \(\mathbf{A }_r\), \(\mathbf{B }_r\) and \(\mathbf{C }_r\) as:
which could be reduced as:
where
are, respectively, the generalized observability and controllability matrices, with observability and controllability indices of r and s. Upon taking the singular value decomposition (SVD) for the first Hankel matrix \(\mathbf{H }_{r \times s} (0)\), we get the following definition:
where
The diagonal matrix \(\tilde{\Sigma }\) which is constructed from the first \(N \times N\) block of \(\Sigma \) contains the dominant singular values \(\sigma _i\) in the following order \((\sigma _1 \ge \sigma _2 \ge \dots \ge \sigma _N \ge 0)\), while \(\Sigma _t\) contains the small truncated singular values. This truncation step is very vital for reducing the order of the realized state-space model; such that the realized dynamics matrix \(A_r\) has size N. Also, vectors in \(\tilde{\mathbf{U }}\) and \(\tilde{\mathbf{V }}^T\) contain the dominant modes associated with the singular values retained in \(\tilde{\Sigma }\). As a result, the product \(\tilde{\mathbf{U }} \tilde{\Sigma } \tilde{\mathbf{V }}^T\) is considered to be a faithful representation of the original Hankel matrix \(\mathbf{H }\) for the smallest size of \(\tilde{\Sigma }\).
It follows from Eq. (A.6) that
Using the above balanced decomposition of \(\mathbf{H }_{r \times s} (0)\), we can write:
Also from Eq. (A.6), we can express the second Hankel matrix \(\mathbf{H }_{r \times s} (1)\) as:
Using the properties of \(\mathbf{U }\) and \(\mathbf{V }\), we can write:
It follows that the matrix \(\mathbf{A }_r\) could be obtained through:
Let:
where \(\mathbf{E }^T_1\) and \(\mathbf{E }^T_2\) are, respectively, \(1 \times r\) and \(1 \times s\) vectors. We use that along with Equation (A.5) to write the following balanced expression for \(h_k^\delta \):
We use the decomposed expression above to obtain the reduced input and output matrices \(\mathbf{B }_r\) and \(\mathbf{C }_r\) as:
Appendix B: Approximating the convolution integral
To find an approximate analytical representation of the convolution integral, we first use the fact that the output, z(t), of a linear dynamical system can be expressed as a convolution integral between its input u(t), and an impulse response function h(t), in the form
Here, \(\mathbf{z}(t) \in {\mathbb {R}}^q\) is the output vector, \(\mathbf{x}(t) \in {\mathbb {R}}^n\) is the state vector and \(\mathbf{C }_r\) is a \(q \times n \) output matrix governed by the following linear state-space equation
Using the eigensystem realization algorithm (ERA) detailed in Ref. [26], the convolution integral can be expressed in terms of the realized state-space matrices \(\mathbf{A }_r, \mathbf{B }_r\) and \(\mathbf{C }_r\) as:
where the realized state-space matrices are :
and
Note that the numerical values appearing in the realized state-space matrices are general for any spherical buoy of radius, \(\textit{R}\). For more details on the ERA procedure, the interested reader can refer to Appendix A.
The matrix exponential \(e^{\mathbf{A }_rt}\) in Equation (B.3) can be further expressed in the following form
Here, \({\mathcal {L}}^{-1}\) is the inverse Laplace transform, and I is the identity matrix. Substituting Equation (B.4) into Eq. (B.3), we obtain the following analytical expression for h(t):
where \(\mu , \uplambda _1, \uplambda _2\), and \(\uplambda _3\) are constants listed in Table 1, and are valid for any spherical buoy of radius, R.
Appendix C: Parametric terms constants
where:
Rights and permissions
About this article
Cite this article
Khasawneh, M.A., Daqaq, M.F. Response behavior of bi-stable point wave energy absorbers under harmonic wave excitations. Nonlinear Dyn 109, 371–391 (2022). https://doi.org/10.1007/s11071-022-07507-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-022-07507-2