Neural-based formation control of uncertain multi-agent systems with actuator saturation

Abstract

The formation control problem for a group of first-order agents with model uncertainty and actuator saturation is investigated in this manuscript. An algorithm-and-observer-based formation controller is developed to ensure the semi-global boundedness of the formation tracking error with actuator saturation. First, a fully local-error-related cooperative weight tuning procedure is proposed for the adaptive uncertainty estimation of each agent. The effect of actuator saturation on both the cooperative adaptive estimation and the controller design part is then analysed and discussed. A three-layer neural-based observer is further constructed to achieve finite-time uncertainty approximation with actuator saturation. Besides, the reverse effect led by coupled and saturated control inputs is defined and a new control input distribution algorithm is presented to attenuate the potential oscillation in system states. Finally, comparative simulations based on a multiple omnidirectional robot system are conducted to illustrate the performance of the proposed formation controllers and the new algorithm.

1 Introduction

Recently, the cooperative control issue of multi-agent systems has become one popular research area in control engineering and robotics [2, 16, 17, 26, 27, 32]. As an important subbranch of cooperative control [18, 34], the topic of formation control [6, 21, 22, 24, 25, 33, 39] has received massive amount of attention due to its close connection with practical applications such as multi-quadcopter systems [3] and multi-rover systems [30, 36].

While completing different tasks, a cluster of agents can be affected by factors like system uncertainties and external disturbances [23, 35, 38] that influence their performance negatively. Under the subject of adaptive control, disturbance observers [7, 37] and neural networks (NNs) [5, 31] are usually employed for uncertainty estimation to ensure the robustness of the system. In most published results, the implemented NNs are usually two-layer networks like Chebyshev NNs [5], fuzzy wavelet NNs [29] and radial basis function NNs [40].

Although two-layer networks are famous for their simplicity, three-layer NNs are trusted more for the approximation of unknown functions with strong nonlinearities. In [19], the dynamic programming approach was used along with a three-layer NN to achieve optimised reference tracking. To estimate the uncertain nonlinearities and external disturbances in each individual agent, three-layer NNs were tuned based on the formation tracking error to perform formation control for a group of autonomous underwater vehicles [4].

However, the cooperative weight tuning law in [4] is not fully error-related, leading to the potential divergence of weight values. Hence, how to obtain a fully local-error-related cooperative tuning law has become a considerable challenge for multi-agent scenarios.

In the area of control engineering, it is also vital to consider the actuator saturation phenomenon when justifying the applicability of one control scheme. Currently, a convenient way to deal with the saturation effect is to treat it as a bounded disturbance and make corresponding compensation while designing the controller [9, 28]. The three-layer NN was first used in [9] to approximate the effect of saturation phenomenon. However, the network weight in the hidden layer is set to be constant in [9], which leads to a lack of adaptiveness. The estimation accuracy is further improved in [28] by constructing adaptive tuning law for the weight matrix in the hidden layer.

Although the tracking-error-based weight tuning approach in [28] is proved to be effective for both saturated and unsaturated systems, the convergence time of the neural estimation error will increase along with the system’s initial tracking error.

Furthermore, the neural estimation error will not settle before the tracking error converges. Such features expose the drawbacks of employing variables related to the reference tracking error as the weight tuning criterion in systems with actuator saturation. Therefore, it is necessary to develop a finite-time tuning approach that adjusts the neural weights regardless of the reference tracking error.

To ensure that the amplitude of the control input is restricted within the saturation limitation, many researchers choose to implement smooth and bounded functions within the controller design [12, 15, 20]. Currently, plenty of results have been obtained for systems without input coupling effect [1, 12]. An adaptive reaching-law-based sliding mode control approach was developed for formation tracking of electromagnetic systems in [12] to achieve finite-time and chattering-free error convergence. In [1], one compensation term was introduced along with an auxiliary system for a class of discrete-time system to perform adaptive control based on reinforcement learning .

Similarly, saturated functions are also applied in the controller design of coupled systems. For example, a saturation function was added into the controller in [8] to deal with the input saturation problem for a cluster of marine surface vehicles. Additional control terms were introduced in [15] to deal with the input saturation issue of underwater vehicles.

However, obvious oscillations of system states were observed in [8], while chattering phenomenons were recorded for control inputs in [15]. Such observations indicate that the amplitude limitation of control input is not the only concern for systems that have both coupled and saturated actuators. Hence, it is essential to investigate the joint effect of actuator saturation and input coupling effect.

Motivated by the aforementioned gaps and challenges, this paper focuses on the formation control problem for a group of uncertain first-order agents with coupled and saturated actuators. The contributions of this article are:

• 1. In contrast to the partially error-related weight tuning laws in [4, 31], this study proposes a fully local-error-related cooperative weight tuning method for three-layer NN-based function approximators to avoid the divergence of approximation error and further construct an adaptive formation control scheme for multi-agent systems.

• 2. To reduce the convergence time of the error states within the neural-based observer structure proposed in [19], a fractional-order term is employed to ensure that the observation error is bounded within finite time regardless of the reference tracking errors.

• 3. Motivated by [8], this paper derives a framework for investigating the joint effect of input coupling and actuator saturation, and further defines the correlated issue as the reverse effect. A new algorithm is also proposed to attenuate the oscillation in error-related states caused by the reverse effect.

Notation: In this paper, let $\Vert \mathcal {M}\Vert _F$ denote the Frobenius norm of matrix $\mathcal {M}$. If $\mathcal {M}$ is a square matrix, let $\overline{\sigma }(\mathcal {M})$ and $\underline{\sigma }(\mathcal {M})$ denote the maximum eigenvalue and the minimum eigenvalue of $\mathcal {M}$, respectively. $R^+$ denotes the set of positive real numbers. $\otimes$ represents the Kronecker production. $I_n$ stands for an n-dimensional identity matrix throughout this paper.

2 Preliminaries

2.1 System model

Consider a distributed nonlinear multi-agent system consists of N first-order agents, and the dynamics of the ith agent is given as

$$\begin{aligned} \dot{x}_i = f_i(x_i) + g_i (x_i,\mathbf {P}_i) \mathcal {S}_i(u_i) + \bar{w}_i, \ i = 1,2,\dots ,N \end{aligned}$$

(1)

where $x_i\in \mathbb {R}^n$ is the position information of the ith agent, $g_i(x_i,\mathbf {P}_i)\in \mathbb {R}^{n \times n}$ is the nonlinear control gain matrix, $\mathbf {P}_i$ represents the model parameter set, $u_i\in \mathbb {R}^n$ is the control input, $f_i(x_i)\in \mathbb {R}^n$ is the unknown dynamics of the system, $\bar{w}_i\in \mathbb {R}^n$ represents the external disturbance, $\mathcal {S}_i(\cdot )$ is the actuator saturation phenomenon and $\mathcal {S}_i(u_i) \in \mathbb {R}^n$ is the saturated control input. The jth element of $\mathcal {S}_i(u_i)$ is expressed as

$$\begin{aligned} \mathcal {S}_i(u_{i}(j))= \left\{ \begin{aligned}&u_{i}(j)&|u_{i}(j)|\le U_{Mi}\\&\mathrm{sign}(u_{i}(j))U_{Mi}&|u_{i}(j)|>U_{Mi} \end{aligned} \right. \end{aligned}$$

(2)

where $u_{i}(j)$ is the jth element of $u_i$ and $U_{Mi} \in \mathbb {R}^+$ is the saturation limit. Obtaining the value of $g_i(x_i,\mathbf {P}_i)$ is necessary for controller design, but it is hard to obtain the precise value of $\mathbf {P}_i$ with the existence of measurement error. If define $\widehat{\mathbf {P}}_i$ to be our measurement of the parameter set, then the control gain matrix we obtain through calculation is $\widehat{g}_i(x_i, \widehat{\mathbf {P}}_i) \in \mathbb {R}^{n \times n}$, and the parameter estimation error is given as $\widetilde{\mathbf {P}}_i = \mathbf {P}_i - \widehat{\mathbf {P}}_i$. Define $\widetilde{g}_i(x_i, \widetilde{\mathbf {P}}_i) = g_i(x_i,\mathbf {P}_i) - \widehat{g}_i(x_i, \widehat{\mathbf {P}}_i)$ to represent the modelling error of the input coupling matrix, we then have:

$$\begin{aligned} \dot{x}_i = \widehat{g}_i(x_i, \widehat{\mathbf {P}}_i) \mathcal {S}_i(u_i) + E_i \end{aligned}$$

(3)

where $E_i = \widetilde{g}_i(x_i, \widetilde{\mathbf {P}}_i) \mathcal {S}_i(u_i) + \bar{w}_i + f_i(x_i)$ represents the combination of unknown factors. For simplicity, we will use $g_i$ and $\widehat{g}_i$ to represent $g_i(x_i,\mathbf {P}_i)$ and $\widehat{g}_i(x_i, \widehat{\mathbf {P}}_i)$, respectively, unless specially stated.

Then we have the dynamics of the cluster as follows:

$$\begin{aligned} \dot{x} = \widehat{g} \mathcal {S}(u) + E \end{aligned}$$

(4)

where

$$\begin{aligned} x&= [x_1^\mathrm{T},x_2^\mathrm{T},\dots ,x_N^\mathrm{T}]^\mathrm{T} \in \mathbb {R}^{nN}\\ \widehat{g}&= \mathrm{diag}\{ \widehat{g}_1, \widehat{g}_2, \dots , \widehat{g}_N \} \in \mathbb {R}^{nN \times nN}\\ \mathcal {S}(u)&= [ \mathcal {S}^\mathrm{T}_1(u_1), \mathcal {S}^\mathrm{T}_2(u_2) , \dots , \mathcal {S}^\mathrm{T}_N(u_N)]^\mathrm{T} \in \mathbb {R}^{nN} \\ E&= [E_1^\mathrm{T}, E_2^\mathrm{T}, \dots , E_N^\mathrm{T}]^\mathrm{T} \in \mathbb {R}^{nN} \end{aligned}$$

Definition 1

[10] Consider a vector X, we have a correlated continuous Lyapunov function V(X). Then the vector X is said to be semi-globally uniformly ultimately bounded (SGUUB) if V(X) satisfies $V(X)=0$ only when $\Vert X\Vert =0$, and there exists a positive boundary $b_{X}$ and a time $t_X(X(t_0), b_{X})$ such that $\Vert V(X)\Vert \le b_{X}$ for all $t\ge t_X + t_0$ and $X(t_0) \in \varOmega _X^V$, where $t_0$ is the initial time, $X(t_0)$ is the initial value of X and $\varOmega _X^V$ is a compact set of X.

Lemma 1

[10] Consider a vector X that satisfies $X(t_0) \in \varOmega _X^V$ and its correlated continuous Lyapunov function V(X), if we have $\dot{V}(X)<0$ when $\Vert X\Vert > b_{X}$, then $\Vert X\Vert$ is said to be SGUUB within the neighbourhood of $[0,b_X]$.

The position and velocity references of the ith agent are described by $x_{di}\in \mathbb {R}^{n}$ and $\dot{x}_{di}\in \mathbb {R}^{n}$, respectively. The main purpose of the controller design is to ensure the semi-global uniform ultimate boundedness of each uncertain agent’s reference tracking error with the actuator saturation (2), which is illustrated as

$$\begin{aligned}&\lim _{t \rightarrow \infty }\Vert x_i(t)-x_{di}(t) \Vert \le \rho , \ \forall x_i(t_0) \in \varOmega _x, \nonumber \\&\quad \ i=1,2,\dots ,N \end{aligned}$$

(5)

where $\varOmega _x$ is a compact set of $x_i$ and $\rho$ is a small and positive constant.

Assumption 1

The state references $x_{di}$ and $\dot{x}_{di}$ are known and bounded when $t \ge t_0$. The parameter measurement error $\widetilde{\mathbf {P}}_i$ is also bounded.

Assumption 2

There is a known positive constant $\tau _i$ and a finite time $t_s$ for the ith agent such that the following inequality is satisfied when $t \ge t_s$

$$\begin{aligned} | g_i^{-1}(t) (\dot{x}_{di}(t) - f_i(x_i(t)) - \bar{w}_i(t) )| \le \tau _i \mathbf {1}_{n \times 1 } \end{aligned}$$

where $\tau _i < U_{Mi}$ and $\mathbf {1}_{n \times 1 }$ is an n-dimensional column vector whose every entry is 1.

Remark 1

Notice that Assumption 2 is made to ensure that the formation tracking process is feasible to the saturated agents in (1) after a finite amount of time. In an ideal situation where $u_i = g_i^{-1}(t) (\dot{x}_{di}(t) - f_i(x_i(t)) - \bar{w}_i(t) )$, we can have $\dot{x}_i = \dot{x}_{di}$, meaning that the agent can successfully track the velocity reference. However, it is still necessary to have a residual amount of control input to reduce the value of $\Vert x_i(t)-x_{di}(t)\Vert$ when $\Vert x_i(t_0)-x_{di}(t_0)\Vert >\rho$, where $x_i(t_0)$ and $x_{di}(t_0)$ are the initial system state and the initial position reference. Hence, we have $\tau _i < U_{Mi}$ to offer the redundancy in the control input. The time $t_s$ is defined to mark the time when the formation tracking task is feasible to each agent in (4).

2.2 Graph theory

In this paper, the communication topology of the distributed multi-agent system is illustrated by a directed graph $G=\{\mathcal {R},\mathcal {E},\mathcal {A}\}$, where $\mathcal {R}=\{r_{1},r_{2},\dots ,r_{N}\}$ represents the set of nodes, $\mathcal {E}\subseteq {R} \times {R}$ stands for the set of edges and $\mathcal {A}=[a_{ij}]\in \mathbb {R}^{N \times N}$ is the adjacency matrix with nonnegative entries. An edge of the graph G is illustrated as $e_{ij}=(r_i,r_j)$, which stands for an edge points from node $r_i$ to node $r_j$. Self-loops are not considered in this paper and $a_{ji}=1$ if and only if $e_{ij}\in {E}$. We define $\mathrm{deg_{in}}(r_i)=\sum _{j=1}^N a_{ij}$ to be the in-degree of the ith node and the degree matrix of the graph is illustrated as $\mathcal {D}=\mathrm{diag}\{ \mathrm{deg_{in}}(r_i), i=1,2,\dots ,N \}$. The Laplacian matrix of the graph is defined as $L=\mathcal {D}-\mathcal {A}$ [14]. If there always exists a directed path between a pair of distinguished nodes, then the directed graph G is said to be strongly connected. In this paper, the communication topology of the multi-agent system (4) is chosen as a strongly connected directed graph. The following lemma is useful for the stability analysis of the proposed control scheme.

Lemma 2

[14] Define $B \in \mathbb {R}^{n \times n}$ to be a nonnegative diagonal matrix with at least one positive element. If the graph G is strongly connected, then its corresponding Laplacian matrix L satisfies that the matrix $(L+B)$ is an irreducible nonsingular M-matrix. Define

$$\begin{aligned} q=[q_1\ q_2\ \dots \ q_N]^\mathrm{T}=(L+B)^{-1} 1_{N\times 1} \end{aligned}$$

then we obtain that $P=\mathrm{diag}\{{p_i}\}=\mathrm{diag}\{{1/q_{i}}\}$ is a positive definite matrix. If we define $Q=P(L+B)+(L+B)^\mathrm{T} P$, then the matrix Q is symmetric and positive definite.

2.3 Three-layer NN approximation

In this paper, three-layer NNs are implemented to approximate the unknown nonlinear function $E_i$ and act as a part of the adaptive control law. According to the work in [19], an $m\ (m\ge 3)$ layered NN is able to estimate any unknown function with high precision if the input vector of the NN is restricted to its compact set. Define $\varOmega _u$ to be a compact set of $u_i$, then the three-layer NN estimation of $E_i$ is written as

$$\begin{aligned} E_i&= W^\mathrm{T}_i \mathcal {T} (J^\mathrm{T}_i y_i) + \epsilon _i, \ \forall x_i \in \varOmega _x, \ u_i \in \varOmega _u, \\&\ i = 1,2,\dots ,n \end{aligned}$$

where $J_i \in \mathbb {R}^{2n \times \bar{n}}$ and $W_i \in \mathbb {R}^{\bar{n} \times n}$ are the optimal weight matrices, $y_i = [x_i^\mathrm{T}, u_i^\mathrm{T}]^\mathrm{T}\in \mathbb {R}^{2n}$ is the input vector of the NN, $\bar{n}\in \mathbb {R}$ is the number of neurons in the hidden layer, $\epsilon _i \in \mathbb {R}^{n}$ is the network bias and $\mathcal {T}(\cdot )$ is the hyperbolic tangent activation function of the hidden layer. Define $\bar{y}_j$ as the jth element of the vector $J^\mathrm{T}_i y_i$, then the jth element of $\mathcal {T} (J^\mathrm{T}_i y_i)$ has the following expression:

$$\begin{aligned} \mathcal {T}(\bar{y}_j) = \frac{e^{\bar{y}_j} - e^{-\bar{y}_j}}{e^{\bar{y}_j}+e^{-\bar{y}_j}} \end{aligned}$$

The estimation process of a three-layer NN is

$$\begin{aligned} \widehat{E}_i = \widehat{W}^\mathrm{T}_i \mathcal {T}(\widehat{J}^\mathrm{T}_i y_i) \end{aligned}$$

(6)

where $\widehat{J}_i$ and $\widehat{W}_i$ are the estimated weight matrices.

The estimation error of the NN is given as

$$\begin{aligned} \begin{aligned} \widetilde{E}_i&= E_i - \widehat{E}_i = \widetilde{W}^\mathrm{T}_i \mathcal {T}(\widehat{J}^\mathrm{T}_i y_i) + \bar{\epsilon }_i(y_i) \end{aligned} \end{aligned}$$

where $\bar{\epsilon }_i(y_i) = W_i^\mathrm{T} [\mathcal {T} (J_i^\mathrm{T} y_i) - \mathcal {T} (\widehat{J}^\mathrm{T}_i y_i)] + \epsilon _i$ and $\widetilde{W}_i = W_i - \widehat{W}_i$.

Assumption 3

The approximation compact set $\varOmega _u$ includes the neighbourhood of $[-U_{Mi}, U_{Mi}]$ for each individual agent.

Assumption 4

The weight matrices W, J and the estimation error $\epsilon$ are bounded such that there are positive constants $W_M$, $J_M$ and $\epsilon _M$ that satisfy

$$\begin{aligned} \Vert W\Vert _F \le W_M, \ \Vert J\Vert _F\le J_M, \ \Vert \epsilon \Vert \le \epsilon _M \end{aligned}$$

where we have

$$\begin{aligned} \begin{aligned} \epsilon&= [\epsilon _1^\mathrm{T}, \epsilon _2^\mathrm{T}, \dots , \epsilon _N^\mathrm{T}]^\mathrm{T} \in \mathbb {R}^{nN}\\ W&= \mathrm{diag}\{ W_1, W_2, \dots , W_N \} \in \mathbb {R}^{\bar{n}N \times nN} \\ J&= \mathrm{diag}\{ J_1, J_2, \dots , J_N \} \in \mathbb {R}^{2nN \times \bar{n}N} \end{aligned} \end{aligned}$$

Lemma 3

[19] Based on the boundedness of the activation function $\mathcal {T}(\cdot )$, the NN approximation error $\epsilon$ and the optimal weight matrices W and J, there exist positive constants $\mathcal {T}_{Mi}$, $\bar{\epsilon }_{Mi}$, $\mathcal {T}_M$ and $\bar{\epsilon }_M$ such that:

$$\begin{aligned} \begin{aligned}&\Vert \mathcal {T}(\widehat{J}_i^\mathrm{T} y_i)\Vert \le \mathcal {T}_{Mi},&\Vert \bar{\epsilon }_i(y_i)\Vert \le \bar{\epsilon }_{Mi}\\&\Vert \mathcal {T}(\widehat{J}^\mathrm{T} y)\Vert \le \mathcal {T}_M,&\Vert \bar{\epsilon }(y)\Vert \le \bar{\epsilon }_M \end{aligned} \end{aligned}$$

where $\bar{\epsilon }(y) = [\bar{\epsilon }_1^\mathrm{T}(y_1), \bar{\epsilon }_2^\mathrm{T}(y_2), \dots , \bar{\epsilon }_N^\mathrm{T}(y_N)]^\mathrm{T}$.

3 Main results

3.1 Neural-based formation control for unsaturated multi-agent systems

In this subsection, the saturation phenomenon is removed by setting $U_{Mi} = +\infty$. According to the agent dynamics (3), we have

$$\begin{aligned} \delta _{xi} = x_i - x_{di} \end{aligned}$$

(7)

where $\delta _{xi} \in \mathbb {R}^n$ is the position tracking error of the ith agent.

Then we have the global form as follows:

$$\begin{aligned} \begin{aligned}&\delta _{x} = x - x_{d} \end{aligned} \end{aligned}$$

(8)

where

$$\begin{aligned} \delta _x&= [\delta ^\mathrm{T}_{x1},\delta ^\mathrm{T}_{x2},\dots ,\delta ^\mathrm{T}_{xN}]^\mathrm{T} \in \mathbb {R}^{nN}\\ x_d&= [x_{d1}^\mathrm{T},x_{d2}^\mathrm{T}, \dots , x_{dN}^\mathrm{T}]^\mathrm{T} \in \mathbb {R}^{nN} \end{aligned}$$

Define $b_i \in \mathbb {R}^+$ to be the ith diagonal element of B, the local formation tracking error of the ith agent is obtained as

$$\begin{aligned} e_{xi}=\sum \limits _{j=1}^{N}a_{ij}(\delta _{xi}- \delta _{xj}) +b_{i}\delta _{xi} =\sum \limits _{j=1}^{N}l_{ij}\delta _{xj} + b_{i}\delta _{xi} \end{aligned}$$

(9)

where $l_{ij}$ is the element on the ith row and jth column of L. In (9), the practical meaning of $b_i$ is the ith agent’s sensitivity on its own reference tracking error $\delta _{xi}$. Define $e_x = [e^\mathrm{T}_{x1},e^\mathrm{T}_{x2},\dots ,e^\mathrm{T}_{xN}]^\mathrm{T}$, we then have the following global form:

$$\begin{aligned} e_x = (L+B)\otimes I_n \delta _x \end{aligned}$$

(10)

The time derivative of (10) is obtained as

$$\begin{aligned} \dot{e}_x = (L+B) \otimes I_n (\widehat{g}u + E - \dot{x}_d) \end{aligned}$$

(11)

To perform adaptive estimation, the weight tuning law set of a three-layer NN is usually chosen as [4, 31]:

$$\begin{aligned} \begin{aligned} \dot{\widehat{W}}_i&= \varGamma _1 G_W(e_{xi}, \widehat{J}_i, \widehat{W}_i, y_i) - \varGamma _2 \widehat{W}_i \\ \dot{\widehat{J}}_i&= \varGamma _3 G_J(e_{xi}, \widehat{J}_i, \widehat{W}_i, y_i) - \varGamma _4 \widehat{J}_i \end{aligned} \end{aligned}$$

where $\varGamma _i \in \mathbb {R}^+(i\in [1,4])$ are the error-invariant tuning gains, and $G_W$ and $G_J$ represent the related tuning functions that satisfy $\Vert G_W\Vert _F = \Vert G_J\Vert _F = 0$ when $\Vert e_{xi}\Vert =0$ ($G_W$ and $G_J$ will no longer affect $W_i$ when there is no error).

In [4], parameters $\varGamma _2$ and $\varGamma _4$ are set to be static. Although it is reasonable to include terms like $- \varGamma _2 \widehat{W}_i$ and $- \varGamma _4 \widehat{J}_i$ to attenuate the oscillation of neural weights when the value of $\Vert e_{xi}\Vert$ is high, such terms will also lead to contradictions that $\dot{\widehat{W}}_i = - \varGamma _2 \widehat{W}_i$ and $\dot{\widehat{J}}_i = - \varGamma _4 \widehat{J}_i$ when $\Vert e_{xi}\Vert =0$, meaning that a potential divergence of estimation error always exists unless $\Vert W_i\Vert _F=\Vert J_i\Vert _F=0$ or $\varGamma _2=\varGamma _4=0$.

To deal with the estimation error divergence issue, the idea of selecting $\varGamma _2$ and $\varGamma _4$ as time-related exponentially decreasing functions is proposed in [31]. Although such approach is found to be effective, it does introduce the danger that the NN will lose the protection of $- \varGamma _2 \widehat{W}_i$ and $- \varGamma _4 \widehat{J}_i$ after certain period of time, leading to potential chattering or oscillation.

To maintain the protection of $- \varGamma _2 \widehat{W}_i$ and $- \varGamma _4 \widehat{J}_i$ while avoiding the divergence issue, a fully error-related tuning approach was then proposed in [19]. However, this approach is never investigated in a cooperative way for multi-agent systems. Therefore, we propose a set of fully local-error-related tuning laws of $\widehat{W}_i$ and $\widehat{J}_i$ as the following equations, respectively:

$$\begin{aligned} \dot{\widehat{W}}_i&= \eta _1 \mathcal {T}(\widehat{J}^\mathrm{T}_i y_i) e^\mathrm{T}_{xi} - \eta _2 \Vert e_{xi}\Vert \widehat{W}_i \nonumber \\ \dot{\widehat{J}}_i&= \frac{\eta _3}{2 n N} \mathrm{sign}(y_i) e^\mathrm{T}_{xi} \widehat{W}^\mathrm{T}_i(I_{\bar{n}} - \alpha (\widehat{J}^\mathrm{T}_i y_i)) - \eta _4 \Vert e_{xi}\Vert \widehat{J}_i \end{aligned}$$

(12)

where $\alpha (\widehat{J}^\mathrm{T}_i y_i) = \mathrm{diag}\{ \mathcal {T}^2_j(\widehat{J}^\mathrm{T}_i y_i) \}, j\in [1,\bar{n}]$ and $\eta _i \in \mathbb {R}^{+} \ (i=1,2,3,4)$. Then we have $\Vert \dot{\widehat{W}}_i\Vert _F = \Vert \dot{\widehat{J}}_i\Vert _F = 0$ when $\Vert e_{xi}\Vert =0$, while $- \eta _2 \Vert e_{xi}\Vert \widehat{W}_i$ and $- \eta _4 \Vert e_{xi}\Vert \widehat{J}_i$ remain to be the counter parts to reduce the chattering in the network output without triggering the divergence of the NN estimation error. Accordingly, we have the global form as

$$\begin{aligned} \dot{\widehat{W}}&= \eta _1 \mathcal {T}(\widehat{J}^\mathrm{T} y) e_{x}^\mathrm{T} - \eta _2 \varDelta _e \otimes I_{\bar{n}} \widehat{W} \nonumber \\ \dot{\widehat{J}}&= \frac{\eta _3}{2 n N} \mathrm{sign}(y) e_x^\mathrm{T} \widehat{W}^\mathrm{T} (I_{\bar{n}N} - \alpha (\widehat{J}^\mathrm{T} y)) - \eta _4 \varDelta _e \otimes I_{2n} \widehat{J} \end{aligned}$$

(13)

where the following equations are applied:

$$\begin{aligned} \begin{aligned} \widehat{W}&= \mathrm{diag}\{ \widehat{W}_1, \widehat{W}_2, \dots , \widehat{W}_N \} \in \mathbb {R}^{\bar{n}N \times nN}\\ \widehat{J}&= \mathrm{diag}\{ \widehat{J}_1, \widehat{J}_2, \dots , \widehat{J}_N \} \in \mathbb {R}^{2nN \times \bar{n}N}\\ \varDelta _e&= \mathrm{diag}\{ \Vert e_{x1}\Vert , \Vert e_{x2}\Vert ,\dots ,\Vert e_{xN}\Vert \} \in \mathbb {R}^{N \times N} \\ y&= \left[ y_1^\mathrm{T}, y_2^\mathrm{T}, \dots , y_N^\mathrm{T}\right] ^\mathrm{T} \in \mathbb {R}^{2nN \times 1} \end{aligned} \end{aligned}$$

Based on the NN estimation (6) and the weight tuning law set (13), the cooperative formation controller is designed as

$$\begin{aligned} u_i = \widehat{g}_i^{-1} ( \dot{x}_{di} - \widehat{E}_i - k_i e_{xi} ) \end{aligned}$$

(14)

Now we are ready to present the first main result in this paper.

Theorem 1

Consider system (4) without actuator saturation ($U_{Mi} = + \infty$), and Assumptions 1 and 4 hold. By the three-layer NN estimation (6), the weight tuning law set (12), and the formation controller (14), the system states $e_x$, $\delta _x$, $\widetilde{W}$ and $\widetilde{J}$ are SGUUB if the following conditions are met:

• 1. The parameters $\eta _2$, $\eta _3$ and $\eta _4$ in (12) and (13) satisfy $\eta _2>\eta _3/2$ and $\eta _4>\eta _3/2$.

• 2. The compact set conditions of the NN hold such that we have $x_i(t) \in \varOmega _x$ and $u_i(t) \in \varOmega _u$ when $t\ge t_0$.

Proof

If we define $\widetilde{W} = W - \widehat{W}$ and $\widetilde{J}= J - \widehat{J}$, we construct the following Lyapunov function candidate:

$$\begin{aligned} V_1 = \frac{1}{2}e_x^\mathrm{T} \mathcal {P} e_x + \frac{1}{2}\mathrm{tr}\{ \widetilde{W}^\mathrm{T} \widetilde{W}\} +\frac{1}{2}\mathrm{tr}\{ \widetilde{J}^\mathrm{T} \widetilde{J}\} \end{aligned}$$

(15)

where $\mathcal {P}=P \otimes I_n$. By Lemma 2, we have

$$\begin{aligned} \begin{aligned} \dot{V}_1&= e_x^\mathrm{T} \mathcal {P} [(L+B) \otimes I_n] \dot{\delta }_x - \mathrm{tr}\{ \widetilde{W}^\mathrm{T} \dot{\widehat{W}}\} - \mathrm{tr}\{ \widetilde{J}^\mathrm{T} \dot{\widehat{J}}\} \\&= \frac{1}{2} e_x^\mathrm{T} \mathcal {Q} \bar{\epsilon } - \frac{1}{2} e_x^\mathrm{T} \mathcal {Q} K e_x + \eta _4 \mathrm{tr} \{ \widetilde{J}^\mathrm{T} \varDelta _e \otimes I_{2{n}} (J-\widetilde{J}) \} \\&\quad - \mathrm{tr} \bigg \{ \widetilde{J}^\mathrm{T} \frac{\eta _3}{2 n N} \mathrm{sign}(y) e_x^\mathrm{T} \widehat{W}^\mathrm{T} (I_{N\bar{n}} - \alpha (\widehat{J}^\mathrm{T} y)) \bigg \} \\&\quad + \mathrm{tr} \bigg \{ \widetilde{W}^\mathrm{T} \mathcal {T} (\widehat{J}^\mathrm{T} y) e_x^\mathrm{T} \bigg (\frac{1}{2} \mathcal {Q} - \eta _1 \otimes I_{nN} \bigg ) \bigg \} \\&\quad + \eta _2 \mathrm{tr} \{ \widetilde{W}^\mathrm{T} \varDelta _e \otimes I_{\bar{n}} (W-\widetilde{W}) \} \\ \end{aligned} \end{aligned}$$

where we have $K = \mathrm{diag}\{ k_1, k_2, \dots , k_N \} \otimes I_n$ and $\mathcal {Q} = (P(L+B)) \otimes I_n$. With the following inequalities:

$$\begin{aligned} \begin{aligned}&\mathrm{tr} \{ \widetilde{W}^\mathrm{T} (W - \widetilde{W}) \} \le W_M \Vert \widetilde{W}\Vert _F - \Vert \widetilde{W}\Vert _F^2 \\&\quad \mathrm{tr} \{ \widetilde{J}^\mathrm{T} (J - \widetilde{J}) \} \le J_M \Vert \widetilde{J}\Vert _F - \Vert \widetilde{J}\Vert _F^2 \\&\quad \varDelta _e \le \Vert e_x\Vert \otimes I_{N}, \ \bigg \Vert \frac{1}{2 n N} \mathrm{sign}(y) \bigg \Vert \le 1 \end{aligned} \end{aligned}$$

we further obtain that

$$\begin{aligned} \dot{V}_1&\le -\frac{1}{2} \underline{\sigma }(\mathcal {Q} K) \Vert e_x\Vert ^2 + (r_1 \Vert \widetilde{W}\Vert _F + r_2 - \eta _2 \Vert \widetilde{W}\Vert _F^2 \nonumber \\&\quad + r_3 \Vert \widetilde{J}\Vert _F + \eta _3 \Vert \widetilde{W}\Vert _F \Vert \widetilde{J}\Vert _F - \eta _4 \Vert \widetilde{J}\Vert _F^2) \Vert e_x\Vert \end{aligned}$$

(16)

where we have $r_1 = \overline{\sigma }( \mathcal {Q}/2 - \eta _1 \otimes I_{nN}) \mathcal {T}_M+ \eta _2 W_M$, $r_2 = \overline{\sigma }(\mathcal {Q}) \bar{\epsilon }_M/2$ and $r_3 = \eta _3 W_M + \eta _4 J_M$.

With the parameters chosen as $\eta _2 > \eta _3/2$ and $\eta _4 > \eta _3/2$, we can rewrite (16) into the following form:

$$\begin{aligned} \begin{aligned} \dot{V}_1&\le -\frac{1}{2} \underline{\sigma }(\mathcal {Q} K) \Vert e_x\Vert ^2 + r_4 \Vert e_x\Vert \end{aligned} \end{aligned}$$

(17)

where $r_4 = r_3^2/(4\eta _4 - 2\eta _3) + r_1^2/(4\eta _2-2\eta _3)+ r_2$. Hence, $\dot{V}_1$ will remain negative when $e_x$ belongs to the following region:

$$\begin{aligned} \varOmega _e = \bigg \{ e_x \bigg | \Vert e_x\Vert > \frac{2r_4}{\underline{\sigma }(\mathcal {Q} K)} \bigg \} \end{aligned}$$

(18)

By (10), we also have that the reference tracking error is SGUUB within the following neighbourhood:

$$\begin{aligned} \varOmega _{\delta } = \bigg \{ \delta _x \bigg | \Vert \delta _x\Vert \le \frac{2r_4}{\underline{\sigma }(\mathcal {Q} K) \underline{\sigma }(L+B)} \bigg \} \end{aligned}$$

By the Lyapunov theory extension in [13], both $\widetilde{W}$ and $\widetilde{J}$ are SGUUB, which completes the proof. $\square$

Although the cooperative tuning approach (12) can guarantee the semi-global uniform ultimate boundedness of the error states $e_x$ and $\delta _x$, its performance is questionable when there exists the actuator saturation phenomenon (2).

Theoretically, the error-related weight tuning procedure (12) will not settle before $\Vert e_{xi}\Vert$ converges to a neighbourhood around 0. Correspondingly, the settling time for the weight tuning process is expected to be prolonged along with the increment in each agent’s initial local formation tracking error because of the actuator saturation in (2). Hence, further investigation is essential to explore a more suitable way to implement three-layer NNs when the system is saturated.

3.2 Observer-based formation control for uncertain and saturated multi-agent systems

Now we consider the systems with saturated actuators. In most of the previous research works like [8, 12], the only issue regarding saturation is considered as restricting the amplitude of each element in the control input within the saturation limitation $U_{Mi}$. However, such results are far from sufficient for a system that has coupled and saturated control inputs like (3).

For example, consider a two-dimensional first-order system that has two control inputs that are coupled and suppose that the calculated nominal control input is obtained as the two dotted vectors $U_1$ and $U_2$ as shown in Fig. 1, where the circle with the radius of $U_{Mi}$ represents the saturation limitation.

Fig. 1

Saturation’s effect on coupled control input

If the saturation phenomenon is ruled out, we can then obtain the dotted vector $U_c$ as the combined control input, which is expected to bring about a negative speed in the X direction. However, the amplitude of $U_2$ will be reduced to $\bar{U}_2$ if the controller is saturated (as the solid vector shows), which will further lead to a saturated combined control input $\bar{U}_c$ that imposes an opposite result in the X direction. Such circumstances will lead to elevations or fluctuations of the system’s formation tracking error. To have further investigation, we first define the aforementioned behaviour as the reverse effect of coupled actuator saturation phenomenons.

Definition 2

For a saturated system whose control input is coupled and saturated like (3), the control input is said to be affected by the reverse effect of coupled actuator saturation if the following equation stands:

$$\begin{aligned} \mathrm{sign}(g_iu_i) \ne \mathrm{sign}(g_i \mathcal {S}_i(u_i)) \end{aligned}$$

Moreover, as we mentioned in Sect. 3.1, the saturation phenomenon will also delay the cooperative neural tuning procedure (12) because the output of the NN cannot be fully reflected by the control input due to the saturation phenomenon. It is unreasonable to employ a weight tuning process (12) that cannot guarantee the semi-global uniform ultimate boundedness of $\widetilde{W}$ and $\widetilde{J}$ before the convergence of $e_x$ and $\delta _x$. As a result, apart from the aim to make the control input bounded, two more problems correlated with the saturation phenomenon are worthy of further discussion:

Problem 1

How to have a finite-time NN-based estimation of system uncertainties regardless of the reference tracking errors $\delta _{xi}$ and $e_{xi}$?

Problem 2

How to ensure that the coupled controller can provide control inputs with correct combined control direction to attenuate the reverse effect?

Regarding the first problem, we reconstruct the previous three-layer NN into a finite-time observer as follows with the inspiration from [19]:

$$\begin{aligned} \dot{\widehat{x}}_i = \widehat{g}_i u_i + \widehat{E}_i + \gamma _i \mathrm{diag}\{ \mathrm{sign} (\widetilde{x}_i) \} |\widetilde{x}_i|^{\beta _i} \end{aligned}$$

(19)

where $\widetilde{x}_i = x_i - \widehat{x}_i$, $\gamma _i \in \mathbb {R}^{n \times n}$ is a positive definite constant diagonal matrix and $\beta _i$ is a real number that satisfies $\beta _i\in (0.5,1)$.

The weight tuning law set of the NN is chosen as follows:

$$\begin{aligned} \begin{aligned} \dot{\widehat{W}}_i =&\eta _1 \mathcal {T}(\widehat{J}^\mathrm{T}_i y_i) \widetilde{x}^\mathrm{T}_{i} - \eta _2 \Vert \widetilde{x}_{i}\Vert \widehat{W}_i \\ \dot{\widehat{J}}_i =&\frac{\eta _3}{\Vert \mathrm{sign}(y_i)\Vert } \mathrm{sign}(y_i) \widetilde{x}^\mathrm{T}_{i} \widehat{W}^\mathrm{T}_i(I_{\bar{n}} - \alpha (\widehat{J}^\mathrm{T}_i y_i)) \\&\quad - \eta _4 \Vert \widetilde{x}_{i}\Vert \widehat{J}_i \end{aligned} \end{aligned}$$

(20)

Then the error dynamics of the neural-based observer is obtained as

$$\begin{aligned} \dot{\widetilde{x}}_i =\widetilde{E}_i - \gamma _i \mathrm{diag}\{ \mathrm{sign} (\widetilde{x}_i) \} |\widetilde{x}_i|^{\beta _i} + \widehat{g}_i (\mathcal {S}_i(u_i) - u_i) \end{aligned}$$

(21)

The following assumption is made to ensure the boundedness of the initial error in (19):

Assumption 5

The error states $\widetilde{x}_i$, $\widetilde{W}_i$ and $\widetilde{J}_i$ are all bounded such that

$$\begin{aligned} \begin{aligned}&\widetilde{x}^\mathrm{T}_i(t_0) \widetilde{x}_i(t_0) + \mathrm{tr}\{ \widetilde{W}^\mathrm{T}_i(t_0) \widetilde{W}_i(t_0)\} \\&\quad + \mathrm{tr}\{ \widetilde{J}^\mathrm{T}_i(t_0) \widetilde{J}_i(t_0)\} \le \mathcal {V}_e \end{aligned} \end{aligned}$$

where $\mathcal {V}_e$ is a positive constant.

Before we present our result in the observer design, we first recall one useful result:

Lemma 4

[11] For a continuous Lyapunov function V(X) that satisfies:

$$\begin{aligned} \dot{V} \le -\rho _{1}V^{\bar{\rho }}(t) + \rho _2 V^{1/2}(t) \end{aligned}$$

the state X is globally finite-time UUB within the region of $\varOmega _V = \{ X | V(X) ^{\bar{\rho } - 1/2} < \rho _2/\bar{\rho }_1 \}$, where $\bar{\rho }_1 \in (0, \rho _1)$, $\bar{\rho } > 1/2$, $\rho _1, \rho _2>0$. The settling time T is bounded by:

$$\begin{aligned} T \le \frac{V^{1-\bar{\rho }}(t_0)}{(\rho _1 - \bar{\rho _1}) (1 - \bar{\rho }) } \end{aligned}$$

Then we have the next result on the finite-time observer design.

Theorem 2

Consider system (3) with actuator saturation (2), where Assumptions 1, 3, 4 and 5 hold. By the neural-based observer (19), and the weight tuning law set (20), the semi-global uniform ultimate boundedness of $\widetilde{x}_i$, $\widetilde{W}_i$ and $\widetilde{J}_i$ is guaranteed if the following conditions are met:

• 1. The control input satisfies $|u_i|\le U_{Mi} \mathbf {1}_{n \times 1}$.

• 2. The parameters $\eta _2$, $\eta _3$ and $\eta _4$ in (20) satisfy $\eta _2>\eta _3/2$ and $\eta _4>\eta _3/2$.

• 3. The compact set conditions of the NN hold such that we have $x_i(t) \in \varOmega _x$ and $u_i(t) \in \varOmega _u$ when $t\ge t_0$.

Furthermore, the observation error $\widetilde{x}_i$ is semi-globally finite-time UUB.

Proof

Consider a Lyapunov candidate as follows:

$$\begin{aligned} V_2 = \frac{\eta _1}{2} \widetilde{x}_i^\mathrm{T} \widetilde{x}_i + \frac{1}{2} \mathrm{tr}\{ \widetilde{W}_i^\mathrm{T} \widetilde{W}_i \} + \frac{1}{2} \mathrm{tr}\{ \widetilde{J}_i^\mathrm{T} \widetilde{J}_i \} \end{aligned}$$

(22)

With the control input satisfies $|u_i| \le U_{Mi} \mathbf {1}_{n \times 1}$, we have $\mathcal {S}_i(u_i) = u_i$, which further leads to

$$\begin{aligned} \dot{V}_2&= \eta _1 \widetilde{x}_i^\mathrm{T} \dot{\widetilde{x}}_i + \mathrm{tr} \{ \widetilde{W}_i^\mathrm{T} \dot{\widetilde{W}}_i \} + \mathrm{tr} \{ \widetilde{J}_i^\mathrm{T} \dot{\widetilde{J}}_i \} \\&= -\gamma _i \eta _1 \widetilde{x}_i^\mathrm{T} \mathrm{diag}\{ \mathrm{sign} (\widetilde{x}_i) \} |\widetilde{x}_i|^{\beta _i} + \eta _1 \widetilde{x}_i^\mathrm{T} (\widetilde{W}^\mathrm{T}_i \mathcal {T}(\widehat{J}^\mathrm{T}_i y_i) \\&\quad + \bar{\epsilon }_i(y_i)) - \eta _1 \mathrm{tr}\{ \widetilde{W}_i^\mathrm{T} \mathcal {T}(\widehat{J}_i^\mathrm{T} y_i) \widetilde{x}_i^\mathrm{T} \} \\&\quad - \eta _3 \mathrm{tr} \bigg \{ \widetilde{J}_i^\mathrm{T} \frac{\mathrm{sign}(y_i)}{\Vert \mathrm{sign}(y_i)\Vert } \widetilde{x}_i^\mathrm{T} \widehat{W}_i^\mathrm{T} (I_n - \alpha (\widehat{J}_i^\mathrm{T} y_i)) \bigg \} \\&\quad + \eta _4 \mathrm{tr} \{ \widetilde{J}_i^\mathrm{T} \Vert \widetilde{x}_i\Vert \widehat{J}_i \} + \eta _2 \mathrm{tr}\{ \widetilde{W}_i^\mathrm{T} \Vert \widetilde{x}_i\Vert \widehat{W}_i\}\\&\le -\underline{\sigma }(\gamma _i) \eta _1 \Vert \widetilde{x}_i\Vert ^{1+\beta _i} + \eta _3 \Vert \widetilde{J}_i\Vert _F \Vert \widetilde{x}_i \Vert (W_{Mi} + \Vert \widetilde{W}_i\Vert _F) \\&\quad - \eta _2\Vert \widetilde{W}_i\Vert _F^2 \Vert \widetilde{x}_i\Vert - \eta _4\Vert \widetilde{J}_i\Vert _F^2 \Vert \widetilde{x}_i\Vert + \eta _1 \Vert \widetilde{x}_i\Vert \bar{\epsilon }_{Mi} \\&\quad + \eta _4 J_{Mi} \Vert \widetilde{J}_i\Vert _F \Vert \widetilde{x}_i\Vert + \eta _2 W_{Mi} \Vert \widetilde{W}_i\Vert _F \Vert \widetilde{x}_i\Vert \end{aligned}$$

where $\Vert W_i\Vert \le W_{Mi}$ and $\Vert J_i\Vert \le J_{Mi}$ are applied based on Lemma 3.

Similar to the proof of Theorem 1, if we define $r_5 = \eta _2 W_{Mi}$ and $r_6 = \eta _3 W_{Mi} + \eta _4 J_{Mi}$, we obtain

$$\begin{aligned} \begin{aligned} \dot{V}_2&\le -\Vert \widetilde{x}_i\Vert \bigg [ \eta _1(\underline{\sigma }(\gamma _i)\Vert \widetilde{x}_i\Vert ^{\beta _i} - \bar{\epsilon }_{Mi}) - \frac{r_5^2}{2(2\eta _2 - \eta _3)} \\&\quad - \frac{r_6^2}{2(2\eta _4 - \eta _3)} \bigg ] \end{aligned} \end{aligned}$$

Then we have the SGUUB region of $\Vert \widetilde{x}_i\Vert$ as follows:

$$\begin{aligned} \begin{aligned} \Vert \widetilde{x}_i\Vert&\le \bigg [ \frac{1}{2\eta _1 \underline{\sigma }(\gamma _i)} \bigg ( \frac{r_5^2}{(2\eta _2 - \eta _3)} + \frac{r_6^2}{(2\eta _4 - \eta _3)} \\&\quad + 2\eta _1 \bar{\epsilon }_{Mi} \bigg ) \bigg ]^{{1}/{\beta _i}} \end{aligned} \end{aligned}$$

(23)

By the Lyapunov theory extension in [13], both $\widetilde{W}$ and $\widetilde{J}$ are also SGUUB. Alternatively, if we select the Lyapunov candidate as follows:

$$\begin{aligned} V_3 = \frac{1}{2} \widetilde{x}_i^\mathrm{T} \widetilde{x}_i \end{aligned}$$

We can then obtain the time derivative of $V_3$ as

$$\begin{aligned} \begin{aligned} \dot{V}_3&= \widetilde{x}_i^\mathrm{T} \dot{\widetilde{x}}_i\\&= -\gamma _i \widetilde{x}_i^\mathrm{T} \mathrm{diag}\{ \mathrm{sign} (\widetilde{x}_i) \} |\widetilde{x}_i|^{\beta _i} + \widetilde{x}_i^\mathrm{T} (\widetilde{W}^\mathrm{T}_i \mathcal {T}(\widehat{J}^\mathrm{T}_i y_i) \\&\quad + \bar{\epsilon }_i(y_i)) \\&\le -\underline{\sigma }(\gamma _i) \Vert \widetilde{x}_i\Vert ^{\beta _i+1} + \Vert \widetilde{x}_i\Vert \widetilde{w}_M \end{aligned} \end{aligned}$$

where we have that $\widetilde{w}_M$ is a positive constant that satisfies $\Vert \widetilde{W}^\mathrm{T}_i \mathcal {T}(\widehat{J}^\mathrm{T}_i y_i) + \bar{\epsilon }_i(y_i)\Vert \le \widetilde{w}_M$ due to the boundedness of the NN estimation error.

Define $r_7 = \underline{\sigma }(\gamma _i) \sqrt{2^{\beta _i+1}}$ and $r_{8} = \sqrt{2} \widetilde{w}_M$, we have

$$\begin{aligned} \dot{V}_3 \le - r_7 V_3^{(\beta _i+1)/{2}} + r_{8} V_3^{{1}/{2}} \end{aligned}$$

(24)

By Lemma 4, $\widetilde{x}_i$ is finite-time UUB. However, because the input of the NN needs to satisfy $x_i \in \varOmega _x$ and $u_i \in \varOmega _u$, $\widetilde{x}_i$ is considered to be semi-globally finite-time UUB, and the finite-time characteristics of $\Vert \widetilde{x}_i\Vert$ remains until it reaches the following neighbourhood:

$$\begin{aligned} \varOmega _{\widetilde{x}} = \bigg \{ \widetilde{x}_i \bigg | \Vert \widetilde{x}_i\Vert \le \bigg ( \frac{ \widetilde{w}_M}{\underline{\sigma }(\gamma _i)} \bigg )^{{1}/{\beta _i}} \bigg \} \end{aligned}$$

(25)

which completes the proof. $\square$

After constructing the finite-time neural-based observer (19), Problem 1 is solved. Next, we consider Problem 2.

To attenuate the previously defined reverse effect of saturation, we first decompose the previous controller design (14) for our analysis:

$$\begin{aligned} u_i = u_{t,i} + {u}_{d,i} + u_{e,i} \end{aligned}$$

(26)

where $u_{t,i}=\widehat{g}_i^{-1} \dot{x}_{di}$ is the control input to maintain the velocity tracking behaviour, ${u}_{d,i}=-\widehat{g}_i^{-1}\widehat{E}_i$ is the control input to compensate for the estimated system uncertainties, and $u_{e,i}=- k_i\widehat{g}_i^{-1} e_{xi}(k_i\in \mathbb {R}^+)$ is the control input for formation error reduction.

We know that both $u_{t,i}$ and $u_{d,i}$ are consistently needed throughout the formation tracking process. By Assumption 2, we also have

$$\begin{aligned} \lim _{t \rightarrow t_s} | \widehat{g}_i^{-1}(t) (\dot{x}_{di}(t) - \widehat{E}_i)| \le \tau _i \mathbf {1}_{n \times 1 } \end{aligned}$$

which indicates that the combination of $u_{t,i}$ and $u_{d,i}$ is bounded after $t_s$.

By Assumption 5 and Theorem 2, we have a finite time $t_o$ and three positive constants $E_M$, $\bar{E}_M$ and $\widetilde{E}_M$ that satisfy $|E_i| \le E_M \mathbf {1}_{n \times 1}$, $|E_i - \widehat{E}_i| \le \bar{E}_M \mathbf {1}_{n \times 1}$ and $\lim _{t \rightarrow t_o}|E_i(t) - \widehat{E}_i(t)| \le \widetilde{E}_M \mathbf {1}_{n \times 1}$. Based on the boundedness we obtained, we introduce the following smooth projection function [5] $\bar{\mathcal {S}}(\mathcal {V},\tau _M,\psi _M)$ to improve the performance of our controller:

$$\begin{aligned}&\bar{\mathcal {S}}(\mathcal {V}(j),\tau _M,\psi _M)\nonumber \\&\quad = \left\{ \begin{aligned}&\tau _M + \psi _{M} (1 - \mathrm{e}^{(\tau _M-\mathcal {V}(j))/\psi _M} ), \\&\quad \quad \quad \quad \quad \ \mathrm{if}\ \mathcal {V}(j)>\tau _M\\&\mathcal {V}(j), \quad \quad \quad \mathrm{if}\ |\mathcal {V}(j)| \le \tau _M \\&\psi _M (\mathrm{e}^{(\tau _M+\mathcal {V}(j))/\psi _M} -1) -\tau _M, \\&\quad \quad \quad \quad \quad \ \mathrm{if}\ \mathcal {V}(j)<-\tau _M \end{aligned} \right. \end{aligned}$$

(27)

where $\mathcal {V}(j)$ denotes the jth element of the column vector $\mathcal {V}$, $\tau _M$ is a positive constant, and $\psi _M$ denotes a small positive constant. Then we define $u_{m,i}\in \mathbb {R}^{n}$ to be the control input to maintain the velocity tracking behaviour for the ith agent:

$$\begin{aligned} u_{m,i} = \widehat{g}_i^{-1} (\dot{x}_{di} - \bar{\mathcal {S}}(\widehat{E}_i, E_M, \psi _{E}) ) \end{aligned}$$

(28)

where $\psi _E$ is a small positive constant.

To attenuate the reverse effect of the saturation phenomenon, we propose a control input distribution algorithm (CIDA) that generates a positive variable $\xi _i$ to shrink $u_{e,i}$ as shown in Algorithm 1. The CIDA keeps monitoring if the nominal control input $u_\mathrm{nom}^i = u_{m,i} + u_{e,i}$ triggers the reverse effect. If the nominal control input does not exceed the saturation limit, then the controller will run at its maximum effort within the saturation limitation. Otherwise, a series of calculation is performed to generate a shrinking factor $\xi _i \in (0,1]$ for each agent to reduce the scenarios where $\mathrm{sign}(\widehat{g}_i u_i) \ne \mathrm{sign}(\widehat{g}_i \mathcal {S}_i(u_i))$. Based on the discussions about the neural-based observer (19), the weight tuning law set (20), the formation maintaining control input (28), and Algorithm 1, we have the final design as

$$\begin{aligned} \bar{u}_i = \bar{\mathcal {S}}(u_{m,i}, \tau _i, \psi _u) + \xi _i u_{e,i} \end{aligned}$$

(29)

where $\mathcal {S}_i(\bar{u}_i) = \bar{u}_i$ is guaranteed by Algorithm 1.

Fig. 2

Robust controller based on CIDA and neural-based observer

Based on the results of neural-based observer and the CIDA, we obtain a system design as shown in Fig. 2. Now we are ready to present our new saturated formation controller design:

Theorem 3

Consider system (4) with actuator saturation (2), and Assumptions 1-5 hold. By the finite-time neural-based observer (19), the weight tuning law set (20), the formation control law (29), and the CIDA (Algorithm 1), the error states $e_x$ and $\delta _x$ are SGUUB within the following regions, respectively:

$$\begin{aligned} \Vert e_x\Vert \le \frac{\overline{\sigma }(Q) \widetilde{E}_M nN}{\bar{k}\underline{\sigma }(Q)}, \ \Vert \delta _x\Vert \le \frac{\overline{\sigma }(Q) \widetilde{E}_M nN}{\bar{k}\underline{\sigma }(Q)\underline{\sigma }(L+B)} \end{aligned}$$

(30)

if the following conditions are met simultaneously:

• 1. $\eta _2$, $\eta _3$ and $\eta _4$ in (20) satisfy $\eta _2>\eta _3/2$ and $\eta _4>\eta _3/2$

• 2. $k_i$ in (29) satisfies $k_i = \bar{k}>0 (i=1,2,\dots , N)$

• 3. $\psi _u$ in (29) satisfies $\psi _u < \bar{U}_{Mi} - \widetilde{E}_M - \epsilon _{E}$

• 4. The compact set conditions of the NN hold such that we have $x_i(t) \in \varOmega _x$ and $u_i(t) \in \varOmega _u$ when $t\ge t_0$.

Proof

With the implementation of the shrinking factor $\xi _i$ generated by Algorithm 1, it is hard to use Lyapunov functions to directly obtain a result for the stability analysis. Therefore, we need to first illustrate that the value of $\xi _i$ will converge to 1 within finite time for each individual agent. Then we will use the Lyapunov stability theory to prove that $e_x$ is SGUUB.

The formation tracking procedure of the ith agent is divided into the following three stages:

• 1. When $t \le t_f = \mathrm{max}(t_s,t_o)$ and $\xi _i \in [0,1)$.

• 2. When $t > t_f = \mathrm{max}(t_s,t_o)$ and $\xi _i \in [0,1)$.

• 3. When $t > t_f = \mathrm{max}(t_s,t_o)$ and $\xi _i=1$.

To analyse the transformation from one stage to another, we first construct a Lyapunov function regarding the formation tracking error of system (4):

$$\begin{aligned} V_4 = \frac{1}{2} e_x^\mathrm{T} P \otimes I_n e_x \end{aligned}$$

Then the time derivative is obtained as

$$\begin{aligned} \begin{aligned} \dot{V}_4&= e_x^\mathrm{T} P (L+B) \otimes I_n (\widehat{g} \mathcal {S}(\bar{u}) + E - \dot{x}_d) \end{aligned} \end{aligned}$$

where $\bar{u} = [\bar{u}_1^\mathrm{T}, \bar{u}_2^\mathrm{T}, \dots , \bar{u}_N^\mathrm{T}]^\mathrm{T}$. Based on the knowledge of $\mathcal {S}_i(\bar{u}_i) = \bar{u}_i$, we have

$$\begin{aligned} \begin{aligned} \dot{V}_4&= e_x^\mathrm{T} P (L+B) \otimes I_n (\widehat{g}\bar{u} + E - \dot{x}_d) \end{aligned} \end{aligned}$$

(31)

For the first stage, we consider one extreme circumstance that equations $\xi _i = 0$ and $|\widetilde{E}_i| = \bar{E}_M \mathbf {1}_{n \times 1}$ remain true until time $t_f$, when the neural-based observer is settled and the formation tracking task is achievable. With $|\bar{\mathcal {S}}(u_{m,i},\tau _i,\psi _u)| \le |u_{m,i}|$, we obtain the following equation from (31):

$$\begin{aligned} \dot{e}_x = (L+B) \otimes I_n (\bar{E}_M \mathbf {1}_{nN \times 1}) \end{aligned}$$

With $(L \otimes I_n) \bar{E}_M \mathbf {1}_{nN \times 1} = \mathbf {0}_{nN \times 1}$, we have $|\dot{e}_x| \le \overline{\sigma }(B) \bar{E}_M \mathbf {1}_{nN \times 1}$, which further leads to

$$\begin{aligned} |e_x(t_f)| \le |e_x(t_0)| + t_f \overline{\sigma }(B) \bar{E}_M \mathbf {1}_{nN \times 1} \end{aligned}$$

where $t_0$ is the initial time.

After the finite time $t_f$, the system (4) is at the second stage, where (31) is expressed as

$$\begin{aligned} \dot{V}_4 = e_x^\mathrm{T} P (L+B) \otimes I_n ( \widetilde{E} - \bar{k} \xi \otimes I_n e_x) \end{aligned}$$

where

$$\begin{aligned} \xi = \mathrm{diag}\{ \xi _1, \xi _2, \dots , \xi _N \}, \ \widetilde{E} = [\widetilde{E}_1^\mathrm{T}, \widetilde{E}_2^\mathrm{T}, \dots , \widetilde{E}_N^\mathrm{T}]^\mathrm{T} \end{aligned}$$

If we define $\bar{U}_{Mi} = U_{Mi} - \tau _i$ to represent the minimum amplitude of the accessible control input for error reduction, it is reasonable to have $\widetilde{E}_M<\bar{U}_{Mi}$ for every agent when $t \ge t_f$.

Define $\underline{e}_x = \mathrm{min}(|e_x|)$ and $\overline{e}_x= \mathrm{max}(|e_x|)$ to represent channels with the lowest and the highest amplitude in vector $e_x$, respectively. By $\psi _u < \bar{U}_{Mi} - \widetilde{E}_M$, if we define $\widetilde{U}_{Mi} = \bar{U}_{Mi} - \widetilde{E}_M - \psi _u$ to represent the least amount of residual control input for each agent, we are confident to say that the available control input can reduce the amplitude of $\overline{e}_x$ with the speed of

$$\begin{aligned} \frac{d|{\overline{e}}_x|}{dt} \le - \underline{\sigma }(L+B) \widetilde{U}_{Mi} \end{aligned}$$

For other channels, consider the extreme scenario where $\dot{e}_{xi}(j) e_{xi}(j) >0$ when $|e_{xi}(j)| < |\overline{e}_x|$. Because the controller parameter $k_i$ is chosen as $k_i=\bar{k}$ for each individual agent, $|e_{xi}(j)|$ will increase until $|e_{xi}(j)| = |\overline{e}_x|$, leading to

$$\begin{aligned} \left\{ \begin{aligned}&\dot{\dot{e}}_{xi}(j) \le - \underline{\sigma }(L+B) \widetilde{U}_{Mi},&\mathrm{if}\ \overline{e}_x > 0 \\&\dot{\dot{e}}_{xi}(j) \ge \underline{\sigma }(L+B) \widetilde{U}_{Mi},&\mathrm{if}\ \overline{e}_x < 0 \\ \end{aligned} \right. \end{aligned}$$

Thus, the parameter $\xi _i$ is expected to converge to 1 within the finite time of

$$\begin{aligned} t_{\xi } = \frac{|\overline{e}_x(t_0)| + t_f \overline{\sigma }(L+B) \bar{E}_M - \widetilde{U}_{Mi} /\bar{k}}{\underline{\sigma }(L+B) \widetilde{U}_{Mi}} \end{aligned}$$

Finally, every agent will achieve the third stage after the finite time of $t_f + t_{\xi }$ to have the following results:

$$\begin{aligned} \begin{aligned} \dot{V}_4&= e_x^\mathrm{T} P(L+B) \otimes I_n (- \bar{k} e_x + \widetilde{E}) \\&= -\frac{\bar{k}}{2} e_x^\mathrm{T} Q \otimes I_n e_x + \frac{1}{2} e_x^\mathrm{T} Q \otimes I_n \widetilde{E} \\&\le -\frac{\bar{k}}{2} \underline{\sigma }(Q) \Vert e_x\Vert ^2 + \frac{1}{2} \overline{\sigma }(Q) \Vert e_x\Vert \Vert \widetilde{E}\Vert \end{aligned} \end{aligned}$$

(32)

Hence, $\dot{V}_4$ will remain negative unless the following inequalities are satisfied:

$$\begin{aligned} \Vert e_x\Vert \le \frac{\overline{\sigma }(Q) \widetilde{E}_M nN}{\bar{k}\underline{\sigma }(Q)}, \ \Vert \delta _x\Vert \le \frac{\overline{\sigma }(Q) \widetilde{E}_M nN}{\bar{k}\underline{\sigma }(Q)\underline{\sigma }(L+B)} \end{aligned}$$

(33)

Note that the neural-based observer (19) only holds semi-global stability. Hence, by Lemma 1, both $e_x$ and $\delta _x$ are SGUUB, which completes the proof. $\square$

Remark 2

In (20), parameters $\eta _1$ and $\eta _3$ both act as the NN’s sensitivity to the observation error $\widetilde{x}_i$. Hence, if the values of $\eta _1$ and $\eta _3$ are increased, the convergence neighbourhood of $\Vert \widetilde{x}_i\Vert$ (23) will shrink in theory. However, if we set the values of $\eta _1$ and $\eta _3$ to be very high, the NN in (6) will be oversensitive to errors, leading to oscillations in its output. On the other hand, both $\eta _2$ and $\eta _4$ act as the damper to stop the weight matrix from changing rapidly. Hence, increasing the values of $\eta _2$ and $\eta _4$ will decrease the amount of chattering in the network output, but it will also extend the convergence time of the observation error.

Remark 3

The constant matrix $\gamma _i$ in (19) acts as the observer’s sensitivity to term $\mathrm{diag}\{ \mathrm{sign} (\widetilde{x}_i) \} |\widetilde{x}_i|^{\beta _i}$. By both (23) and (25), we see that the convergence region of $\Vert \widetilde{x}_i\Vert$ will shrink if we increase the value of $\underline{\sigma }(\gamma _i)$. The effect of $\beta _i$ is comparatively complex. When $\Vert \widetilde{x}_i\Vert \le 1$, setting $\beta _i$ close to 0.5 will bring faster convergence speed. However, due to the characteristics of the fractional order, choosing $\beta _i$ close to 1 will lead to a faster convergence when $|\widetilde{x}_i|> \mathbf {1}_{n \times 1}$.

Remark 4

The purpose of employing the smooth projection law in (28) is to restrict the effect of $\widehat{E}_i$, which will attenuate chattering in the control input $u_i$ and system state $x_i$ if the states in the neural-based observer are experiencing oscillation. Regarding the proportional parameter $k_i$ in term $u_{e,i}$, a rise in its value will result in a decrease in the ultimate convergence region of both $\delta _x$ and $e_x$ (see (33)).

Remark 5

The purpose of Assumption 5 is to ensure that the initial estimation error of the neural-based observer is bounded. Related parameters are also useful to prove the finite-time convergence of observation error $\widetilde{x}_i$ and the shrinking factor $\xi _i$.

4 Simulation

To justify the performance of the proposed neural-based observer (19), the CIDA (Algorithm 1) and the distributed formation control law (29), simulations and comparisons regarding a multi-robot system are provided.

Consider a multi-robot system that contains 6 omnidirectional robots [7], and the dynamics of the ith robot is given as

$$\begin{aligned} \dot{x}_i = {T}_i(\theta _i, {R}_i) u_i + \bar{w}_i \end{aligned}$$

where $x_i = [p_i^x, p_i^y, \theta _i]^\mathrm{T}$ denotes the state vector that contains the position and orientation information of the robot, $u_i = [u_{i}^1, u_{i}^2, u_{i}^3]^\mathrm{T}$ represents the speed vector of the robot’s motors, $\bar{w}_i$ is the external disturbance vector, and ${T}_i(\theta _i, {R}_i)$ is the control gain matrix with the following expression:

$$\begin{aligned} {T}_i(\theta _i, {R}_i)= \begin{bmatrix} -\mathrm{sin}(\theta _i) &{} -\mathrm{sin}(\pi /3-\theta _i) &{} \mathrm{sin}(\pi /3+\theta _i)\\ \mathrm{cos}(\theta _i) &{} -\mathrm{cos}(\pi /3-\theta _i) &{} -\mathrm{cos}(\pi /3+\theta _i)\\ 1/{R}_i &{} 1/{R}_i &{} 1/{R}_i \end{bmatrix} \end{aligned}$$

where ${R}_i \in \mathbb {R}^+$ is the radius of the robot.

With the existence of measurement error, it is hard for us to get the precise value of ${R}_i$. Hence, the parameter value that is measured and employed in the controller design process is illustrated as $\widehat{R}_i$. The value of $R_i$, $\widehat{R}_i$ and the initial state values are provided in Table 1. The actuator saturation limit is set as $U_{Mi} = 0.25$ by Assumption 2.

Table 1 Model parameters and initial states

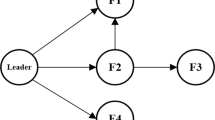
The communication topology is chosen as Fig. 3 and $b_i=2$. The system uncertainties and formation references are chosen as follows, respectively:

$$\begin{aligned} \begin{aligned} \bar{w}_i&= [0.02\mathrm{cos}(0.5t+\pi /2) + 0.03e^{-|p_i^x| - 1}, \\&\quad \ \ 0.03\mathrm{sin}(0.2t) + 0.02\mathrm{tanh}(p_i^y), \\&\quad \ \ 0.04\mathrm{sin}(0.1t+\theta _i)+0.01\mathrm{tanh}(\theta _i)]^\mathrm{T}, \\ x_{di}&= [2\mathrm{cos}(-0.15t+\pi )+2\mathrm{cos}(i\pi /3)-1, \\&\quad \ \ \ 2\mathrm{sin}(i\pi /3) + 2\mathrm{sin}(-0.15t+\pi ),0]^\mathrm{T}, \\&\quad \ \ \ i=1,2,\dots ,6 \end{aligned} \end{aligned}$$

(34)

Fig. 3

A strongly connected topology for the multi-robot system

To justify the effectiveness of our designs, simulations based on the following four controller designs are conducted:

• 1. The cooperatively tuned formation controller design (CTFC) that uses (12) as the weight tuning law. The control input is chosen as $u_i = \bar{\mathcal {S}}(u_{c,i},\bar{\tau }_i,\bar{\psi }_i)$, where $u_{c,i} = \widehat{g}_i^{-1} ( \dot{x}_{di} - \widehat{E}_i - k_i e_{xi} )$, $\bar{\tau }_i = 0.24$ and $\bar{\psi }_i = 0.01$.

• 2. The restricted cooperatively tuned formation controller design (RCTFC) that uses (12) as the weight tuning law. The control input is chosen as $u_i = \bar{\mathcal {S}}(u_{c,i},\bar{\tau }_i,\bar{\psi }_i)$, where $u_{c,i} = u_{m,i} + u_{e,i}$, $E_M = 0.10$, $\bar{\tau }_i = 0.24$ and $\bar{\psi }_i = \psi _{E} = 0.01$.

• 3. The observer-based formation controller design (OBFC) that implements the proposed neural-based observer (19) and the weight tuning law (20). Algorithm 1 is not applied and the controller is chosen as $u_i = \bar{\mathcal {S}}(u_{o,i},\bar{\tau }_i,\bar{\psi }_i)$, where we have $u_{o,i} = u_{e,i} + \bar{\mathcal {S}}(u_{m,i},\tau _i,\psi _i)$, $\bar{\tau }_i = 0.24$, $\tau _i = 0.22$, $E_M = 0.10$ and $\psi _i = \psi _{E} = \bar{\psi }_i = 0.01$.

• 4. The algorithm-and-observer-based formation controller design (AOBFC) that has the neural-based observer (19) tuned by (20). Algorithm 1 is implemented to generate the shrinking factor $\xi _i$ and the controller is designed as (29), where $\tau _i = 0.22$, $E_M = 0.10$ and $\psi _{E} = \psi _u = 0.01$.

Fig. 4

Merits of using the neural-based observer over using the cooperative tuning design

The tuning parameters of the NN are chosen as $\eta _1 = 15$, $\eta _2 = 0.1$, $\eta _3 = 0.1$ and $\eta _4 = 0.06$ in all simulations. Initially, $\widehat{J}_i(0)$ is chosen as a random $6 \times 5$ matrix with elements whose norms are less than 1 and $\widehat{W}_i(0)$ is chosen as a $5 \times 3$ zero matrix. For the designs that employ the neural-based observer (19), the parameters are chosen as $\beta _i = 0.9$ and $\gamma _i = \mathrm{diag}\{ 12,12,18 \}$.

The proportional parameter $k_i$ in $u_{e,i}$ is chosen as $k_i = \bar{k}= 3$ for every agent in each simulation. To compare the performance of different designs, we define the 2-norm calculation of an arbitrary column vector $\mathcal {V}$ as $\bar{\varDelta }(\mathcal {V}) = \sqrt{\mathcal {V}^\mathrm{T} \mathcal {V}}$. To illustrate the merits of using the neural-based observer (Theorem 2) over using the cooperative tuning approach (Theorem 1), we have provided the trends of $\bar{\varDelta }(\widetilde{E})$, $\bar{\varDelta }(e_x)$, $\bar{\varDelta }(\delta _x)$ and $\bar{\varDelta }(u)$ in Fig. 4. The SGUUB region and convergence time of each method are recorded in Table 2.

Table 2 Performance comparison of four control schemes

Although the norm of $e_x$ and $\delta _x$ are both SGUUB for CTFC, we can hardly say that the system error states converged due to the high value of $b_{\widetilde{E}}$ (over 1000). Adding an extra smooth projection function to restrict the amplitudes of the NN output can lead to a success converge for both $e_x$ and $\delta _x$ in RCTFC, but the accuracy of the NN is far from sufficient ($\bar{\varDelta }(\widetilde{E}) \ge 100$). Furthermore, the control input of the RCTFC is also filled with chattering (see $\bar{\varDelta }(u)$ in Fig. 4), which indicates that the cooperative tuning method (12) is not suitable when the actuators are restricted by saturation phenomenon.

Fig. 5

Illustration of the reverse effect and the merits of implementing CIDA

Fig. 6

Evolution of control inputs in AOBFC

On the contrary, $\bar{\varDelta }(\widetilde{E})$ of the neural-based observer (19) in AOBFC is bounded within the region of 0.053 in 4.2 seconds, which proves the validity of the finite-time characteristics claimed in Theorem 2. Besides, the local formation tracking error $e_x$ and the reference tracking error $\delta _x$ are SGUUB within 0.015 and 0.005, respectively. As a result, the existence of Problem 1 and the validity of Theorem 2 are both illustrated. Hence, the neural-based observer design (19) is a method more suitable than the cooperative tuning design (12) for systems with actuator saturation.

To verify the existence of the reverse effect mentioned in Problem 2, the values of each agent’s local formation tracking error $e_{xi}$ in the first 20 seconds are recorded and presented in Fig. 5. It is observed that every agent with the OBFC design experiences oscillation in the value of $e_{\theta }$ and part of the agents have fluctuated trends in $e_x$ (agents 1, 3, 4 and 6) and $e_y$ (agents 2, 5 and 6), which indicates the existence of the reverse effect. In comparison, most of the state fluctuations are attenuated in the AOBFC design. To validate that the CIDA is also capable to restrict the amplitudes of the control input within the saturation limit to satisfy $\mathcal {S}_i(\bar{u}_i) = \bar{u}_i$, the curves of each agent’s control input are shown in Fig. 6.

The evolution of the shrinking factor $\xi _i$ in Algorithm 1 is provided in Fig. 7, where we see that each $\xi _i$ converges to 1 within the finite time of 13.8 seconds, illustrating the validity of Theorem 3. However, the proposed CIDA design cannot completely avoid the state fluctuation led by the reverse effect mentioned in Problem 2 (see agent 3 in Fig. 5). As we stated in the proof of Theorem 3, the factor $\xi _i$ is determined by both the accessible control input amplitude $\bar{U}_{Mi}$ and the maximum error amplitude in $e_{xi}$. Hence, when one channel ($p_i^y$ channel in $e_{x3}$) has a significant amount of error over other channels ($p_i^x$ channel in $e_{x3}$), the channels with small error amplitudes can be overshadowed due to a low value of $\xi _i$, which leads to an increment of $e_x$. This circumstance is eased when the amplitude of different channels in the error vector achieves similar values or the shrinking factor $\xi _i$ rises to higher values (see agent 3 in Figs. 5 ,  7 around 10 seconds).

To monitor the formation tracking behaviour of the system (4), the trajectories of all agents are recorded in Fig. 8. It is observed that the entire system is able to track the desired time-varying circular formation (34) (a circular formation whose centre is moving in a circular trajectory) with the existence of model uncertainty, external disturbances and actuator saturation, which concludes the effectiveness of the proposed formation control scheme (29) and the CIDA (Algorithm 1).

Remark 6

In all simulations, the system uncertainty is chosen as (34), which is a function related to both the system state $x_i$ and the task time t. In practice, the relationship between the actual system state $x_i$ and the task time t should be a continuous but unknown function $x_i=\mathcal {F}(t)$. In theory, we can also express the task time t with system state $x_i$ by an unknown function $t=\mathcal {G}(x_i)$. Hence, both the system uncertainty $\bar{w}_i$ and the overall system uncertainty $E_i$ can be treated as an unknown function that use $x_i$ as the variable, which indicates that the estimation process (6) is valid.

Fig. 7

Shrinking factor $\xi _i$

Fig. 8

Trajectories of the multi-robot system

5 Conclusion

In this paper, we focused on the implementation of three-layer NNs in the formation tracking problem of uncertain and saturated first-order multi-agent systems. First, a fully local-error-related cooperative tuning law for unsaturated agents was proposed to avoid the divergence of estimation error. After introducing the actuator saturation phenomenon along with the input coupling phenomenon into the system dynamics, two correlated problems including the slow convergence of cooperative neural estimation and the reverse effect were discussed. The three-layer NN was further modified into an observer to achieve semi-global finite-time convergence regardless of each agent’s formation tracking error. A control input distribution algorithm was then developed to attenuate the reverse effect caused by coupled and saturated control inputs. Simulation examples are given to show the effectiveness and advantages of the proposed new designs compared with some existing results.