1 Introduction

Waverider Vehicles (WVs) have been regarded as the most promising technology for feasible and affordable hypersonic flight. The flight control design, which is the key technique to ensure safe flight and successful completion of flight missions, has caused worldwide concerns [1,2,3,4,5]. The special dynamics of WVs, including uncertainty, nonlinearity, non-affine property, saturation and coupling, leads to control challenges. The current focus of flight control for WVs is mainly on pursing excellent robustness and accuracy under certain conditions such as actuator saturation/fault and uncertainties/disturbances via fuzzy/neural-based intelligent control [6,7,8], sliding mode control [9], back-stepping control [10,11,12], and fault-tolerant control [13, 14]. However, all of them are unable to guarantee control system with satisfactory transient performance which is crucial to realize hypersonic maneuvering flight for WVs [15, 16].

The prescribed performance control (PPC), firstly proposed by Bechlioulis et al. [17, 18], is a pioneering methodology which is expected to provide an effective tool to ensure desired transient and steady-state performance. The main ideal of PPC is to devise a type of prescribed funnels called performance functions whose shapes can be designed as needed [19,20,21,22]. The developed controllers based on PPC are capable of guaranteeing that tracking errors always evolve within prescribed funnels such that both the transient performance and the stead-state performance are satisfactory. In the existing studies [23, 24], prescribed performance guaranteed tracking controllers were exploited for WVs. Though tracking errors satisfy the desired prescribed performance, those methods [23, 24] require that the models of WVs must have affine formulations, which cannot be directly obtained owing to the nonlinear characteristics. It is for this reason that non-affine-model-based PPC schemes were investigated for WVs in [7, 15, 16]. Furthermore, to reject system uncertainties and disturbances, fuzzy/neural approximations are commonly used methods [7, 15, 16, 23, 24] to enhance the robustness performance. However, too much online learning/computation burden caused by fuzzy/neural approximations undoubtedly harms the real-time performance of control system, which is not conducive to realize hypersonic maneuvering flight for WVs. Besides, to improve the operability and practicability, some researchers proposed improved versions of PPC with finite-time convergence [16, 22] such that the regulation time can be quantitatively designed as needed.

Despite the above developments of PPC, a facing defect is the fragile problem. By fragile problem, we mean that tracking errors may break away from prescribed funnels if actuators are saturated. The flight airspace of WVs is so high that it easily leads to actuator saturation. The actuator saturation will inevitably result in error increasing such that tracking errors show the trend of breaking away from prescribed funnels, yielding the fragile problem. Unfortunately, the existing PPC strategies [3, 8, 16,17,18,19,20,21,22,23,24] did not take into consideration actuator saturation since all of them couldn’t deal with the fragile problem. In view of this, we propose a novel non-fragile tracking controller with readjusting prescribed performance for WVs subject to actuator saturation. The addressed controllers are developed based on non-affine models of WVs. Moreover, there is no need of fuzzy/neural approximation, reducing online learning computation burden. The main contributions are listed as follows.

  1. (1)

    The addressed method avoids the limitations of previous finite-time PPC (FPPC) approaches [23, 24] that they are only suitable for affine dynamic systems. In this article, FPPC is extended into the non-affine model of WVs.

  2. (2)

    The developed controller doesn’t require neural/fuzzy approximation [7, 15, 16, 23] that may cause lots of online learning parameters. As a result, the computation burden of the design is satisfactory.

  3. (3)

    The proposed approach handles the fragile problem of PPC that the existing PPC strategies [8, 16,17,18,19,20,21,22,23,24] cannot deal with actuator saturation. In this article, by proposing a new kind of readjusting prescribed performance, both desired transient performance and steady-state performance are guaranteed for tracking errors in finite time under actuator saturation.

The rest of this paper is structured as follows. Section 2 presents problem statement. Section 3 shows the control design process. Section 4 provides the simulation results, and Sect. 5 gives the conclusions.

2 Problem statement

2.1 Vehicle model

We consider the following nonlinear model of an WV [25] whose map of geometry and force is shown in Fig. 1.

$$\begin{aligned} m\dot{V}= & {} T\cos \left( {\theta - \gamma } \right) - D - g\sin \gamma , \end{aligned}$$
(1)
$$\begin{aligned} \dot{h}= & {} V\sin \gamma , \end{aligned}$$
(2)
$$\begin{aligned} mV\dot{\gamma }= & {} L\mathrm{{ + }}T\sin \left( {\theta - \gamma } \right) - mg\cos \gamma , \end{aligned}$$
(3)
$$\begin{aligned} \dot{\theta }= & {} Q, \end{aligned}$$
(4)
$$\begin{aligned} {I_{yy}}\dot{Q}= & {} M + {\tilde{\psi }_1}{\ddot{\eta }_1} + {\tilde{\psi }_2}{\ddot{\eta }_2}, \end{aligned}$$
(5)
$$\begin{aligned} {k_1}{I_{yy}}{{\ddot{\eta }}_1}= & {} - 2{I_{yy}}{\zeta _1}{\omega _1}{{\dot{\eta }}_1} - {I_{yy}}\omega _1^2{\eta _1} \nonumber \\&+ {I_{yy}}{N_1} - {{\tilde{\psi }}_1}\left( {M + {{\tilde{\psi }}_2}{{\ddot{\eta }}_2}} \right) , \end{aligned}$$
(6)
$$\begin{aligned} {k_2}{I_{yy}}{{\ddot{\eta }}_2}= & {} - 2{I_{yy}}{\zeta _2}{\omega _2}{{\dot{\eta }}_2} - {I_{yy}}\omega _2^2{\eta _2} \nonumber \\&+ {I_{yy}}{N_2} - {{\tilde{\psi }}_2}\left( {M\mathrm{{ + }}{{\tilde{\psi }}_1}{{\ddot{\eta }}_1}} \right) . \end{aligned}$$
(7)

The vehicle model has five rigid-body states, i.e., velocity (\(V \in {\Re _{ > 0}}\)), altitude (\(h \in {\Re _{ > 0}}\)), flight-path angle(\(\gamma \in \Re \)), pitch angle (\(\theta \in \Re \)) and pitch rate (\(Q \in \Re \)), and two flexible states (\({\eta _{\text {1}}} \in \Re \) and \({\eta _{\text {2}}} \in \Re \)). The control inputs (fuel equivalence ratio \(\Phi \in {\Re _{ > 0}}\) and elevator angular deflection \({\delta _e} \in \Re \)) are implied in trust force T, drag force D, lift force L, pitching moment M, and generalized forces \(N_1\) and \(N_2\) [25], given by

$$\begin{aligned} T\approx & {} {\beta _1}\Phi {\alpha ^3} + {\beta _2}{\alpha ^3} + {\beta _3}\Phi {\alpha ^2} + {\beta _4}{\alpha ^2} \\&+ {\beta _5}\Phi \alpha + {\beta _6}\alpha + {\beta _7}\Phi + {\beta _8}, \\ D\approx & {} \frac{1}{2}\exp \left( {\frac{{{h_0} - h}}{{{h_s}}}} \right) {\rho _0}{V^2}SC_D^{{\alpha ^2}}{\alpha ^2} \\&+ \frac{1}{2}\exp \left( {\frac{{{h_0} - h}}{{{h_s}}}} \right) {\rho _0}{V^2}SC_D^{\delta _e^2}\delta _e^2 \\&+ \frac{1}{2}\exp \left( {\frac{{{h_0} - h}}{{{h_s}}}} \right) {\rho _0}{V^2}SC_D^\alpha \alpha \\&+ \frac{1}{2}\exp \left( {\frac{{{h_0} - h}}{{{h_s}}}} \right) {\rho _0}{V^2}SC_D^{{\delta _e}}{\delta _e} \\&+ \frac{1}{2}\exp \left( {\frac{{{h_0} - h}}{{{h_s}}}} \right) {\rho _0}{V^2}SC_D^0, \\ L\approx & {} \frac{1}{2}\exp \left( {\frac{{{h_0} - h}}{{{h_s}}}} \right) {\rho _0}{V^2}SC_L^\alpha \alpha \\&+ \frac{1}{2}\exp \left( {\frac{{{h_0} - h}}{{{h_s}}}} \right) {\rho _0}{V^2}SC_L^{{\delta _e}}{\delta _e} \\&+ \frac{1}{2}\exp \left( {\frac{{{h_0} - h}}{{{h_s}}}} \right) {\rho _0}{V^2}SC_L^0, \\ {N_1}= & {} N_1^{{\alpha ^2}}{\alpha ^2} + N_1^\alpha \alpha + N_1^0, \\ {N_2}= & {} N_2^{{\alpha ^2}}{\alpha ^2} + N_2^\alpha \alpha + N_2^{{\delta _e}}{\delta _e} + N_2^0, \\ M\approx & {} {z_T}T + \frac{1}{2}\exp \left( {\frac{{{h_0} - h}}{{{h_s}}}} \right) {\rho _0}{V^2}S\bar{c}C_{M,\alpha }^{{\alpha ^2}}{\alpha ^2} \\&+ \frac{1}{2}\exp \left( {\frac{{{h_0} - h}}{{{h_s}}}} \right) {\rho _0}{V^2}S\bar{c}C_{M,\alpha }^\alpha \alpha \\&+ \frac{1}{2}\exp \left( {\frac{{{h_0} - h}}{{{h_s}}}} \right) {\rho _0}{V^2}S\bar{c}C_{M,\alpha }^0 \\&+ \frac{1}{2}\exp \left( {\frac{{{h_0} - h}}{{{h_s}}}} \right) {\rho _0}{V^2}S\bar{c}{c_e}{\delta _e}. \end{aligned}$$
Fig. 1
figure 1

Geometry and force map of an WV

Full size image

All the coefficients and variables in the above equations are clearly defined in [25] and also are listed in the Nomenclature (See the Appendix).

2.2 The Fragility of prescribed performance

By prescribed performance we mean that the tracking error \(e(t):{\Re _{ \ge 0}} \rightarrow \Re \) evolves within prescribed funnels \({\rho _L}(t):{\Re _{ \ge 0}} \rightarrow {\Re _{ < 0}}\) and \({\rho _R}(t):{\Re _{ \ge 0}} \rightarrow {\Re _{ > 0}}\) that are also called performance functions, that is, \({\rho _L}(t)< e(t) < {\rho _R}(t)\) holds for all \(t \in {\Re _{ \ge 0}}\) if e(0) satisfies \({\rho _L}(0)< e(0) < {\rho _R}(0)\), as depicted in Fig. 2a. The overshoot of e(t) is no more than \(\max \left\{ { - {\rho _L}(0),{\rho _R}(0)} \right\} \) and the steady-state value of e(t) is less than \(\max \left\{ { - {\rho _L}(\infty ),{\rho _R}(\infty )} \right\} \). Thus, prescribed behaviours including the transient performance (i.e., overshoot and convergence time) and the steady-state performance (i.e., steady-state error) can be guaranteed for e(t).

It is impossible to devise feed-back controllers by directly using the constraint formulation \({\rho _L}(t)< e(t) < {\rho _R}(t)\). In order to facilitate controller design, we introduce the following equivalent form

$$\begin{aligned} e(t) = S_\varepsilon ^e\left( {{\varepsilon _e}(t)} \right) \left( {{\rho _R}(t) - {\rho _L}(t)} \right) \mathrm{{ + }}{\rho _L}(t)\ \end{aligned}$$
(8)

with \(S_\varepsilon ^e\left( {{\varepsilon _e}(t)} \right) = \frac{{{e^{{\varepsilon _e}(t)}}}}{{1 + {e^{{\varepsilon _e}(t)}}}}:\Re \rightarrow \left( {0,1} \right) \). The transformed error \({\varepsilon _e}(t) \in \Re \) is derived from (8) as

$$\begin{aligned} {\varepsilon _e}(t) = \ln \left( {\frac{{e(t) - {\rho _L}(t)}}{{{\rho _R}(t) - e(t)}}} \right) . \end{aligned}$$
(9)

The transformed error \({\varepsilon _e}(t) \in \Re \), instead of the initial tracking error e(t), will be utilized for control feedback. Hereon, we stress the fragile problem of the existing PPC methodologies when there exists actuator saturation. When actuator is saturated, the tracking error e(t) will inevitably increase [26], making e(t) close to (even exceed) the prescribed funnels \({\rho _L}(t)\) and \({\rho _R}(t)\), as shown in Fig. 2b. From (9), we know that \({\varepsilon _e}(t) \rightarrow - \infty \) as \(e(t) \rightarrow {\rho _L}(t)\) and \({\varepsilon _e}(t) \rightarrow + \infty \) as \(e(t) \rightarrow {\rho _R}(t)\). The non-convergence of \({\varepsilon _e}(t)\) will cause control singularity problem.

Fig. 2
figure 2

Prescribed performance; a without actuator saturation, b with actuator saturation

Full size image

2.3 Readjusting prescribed performance

To handle the singularity problem, we propose an alternative PPC approach that is able to adaptively readjust its prescribed funnel, namely the Readjusting Prescribed Performance, given by

$$\begin{aligned} p_\text {lower}^e(t)< e(t) < p_{upper}^e(t),\ \end{aligned}$$
(10)

where \(p_\text {lower}^e(t):{\Re _{ \ge 0}} \rightarrow {\Re _{ < 0}}\) and \(p_\text {upper}^e(t):{\Re _{ \ge 0}} \rightarrow {\Re _{ > 0}}\) are newly developed performance functions

$$\begin{aligned} p_\text {upper}^e(t) = \left\{ \begin{array}{l} {\left( {\frac{{T_{FT}^e - t}}{{T_{FT}^e}}} \right) ^{{l_e}}}\left( {p_0^e - p_{T_{FT}^e}^e} \right) \\ + p_{T_{FT}^e}^e + {p^e}(t),\mathrm{{if }}\ 0 < t \le T_{FT}^e,\\ p_{T_{FT}^e}^e + {p^e}(t),\mathrm{{if }}\ t > T_{FT}^e, \end{array} \right. \ \end{aligned}$$
(11)

with \(p_\text {lower}^e(t) = - p_\text {upper}^e(t)\), \(p_0^e( \in {\Re _{> 0}})> p_{T_{FT}^e}^e( \in {\Re _{ > 0}})\), \(T_{FT}^e \in {\Re _{ > 0}}\), \({p^e}(t) = \kappa _2^etanh\left( {\kappa _1^e{\text {abs}}\left( {u - {u_d}} \right) } \right) \), \(\kappa _1^e \in {\Re _{ > 0}}\) and \(\kappa _2^e \in {\Re _{ > 0}}\), where \({u_d} \in \Re \) is the ideal value of the control input \(u \in \Re \), and \({\text {abs}}\left( {u - {u_d}} \right) \) denotes the saturation of actuator u.

Remark 1

Unlike the exiting performance functions [8, 16,17,18,19,20,21,22,23,24], the newly designed \(p_\text {lower}^e(t)\) and \(p_\text {upper}^e(t)\) contain the readjusting term \({p^e}(t) {=} \kappa _2^etanh\left( {\kappa _1^e{\text {abs}}\left( {u {-} {u_d}} \right) } \right) \) that is capable of adaptively regulating the prescribed funnels (i.e., decrease \(p_\text {lower}^e(t)\) and increase \(p_\text {upper}^e(t)\) when \(u - {u_d} \ne 0\)) according to the saturation \({\text {abs}}\left( {u - {u_d}} \right) \), being expected to avoid the singularity problem.

Remark 2

It is clearly concluded that \(p_\text {lower}^e(t)\) and \(p_\text {upper}^e(t)\) are bounded since \(p_\text {upper}^e(t) \in [p_0^e + \kappa _2^e,p_{T_{FT}^e}^e + \kappa _2^e]\) and \(p_\text {lower}^e(t) = - p_\text {upper}^e(t)\).

2.4 Control objective

Due to the nonlinearity of vehicle model, (1)-(5) can be rewritten as the following non-affine formulation [3, 5].

Velocity subsystem

$$\begin{aligned} {\dot{x}_V} = f_\Phi ^V\left( {{x_V},\Phi } \right) = F_\Phi ^V\left( {{x_V},\Phi } \right) + \iota _\Phi ^V\Phi .\ \end{aligned}$$
(12)

Altitude subsystem

$$\begin{aligned} \dot{x}_h^h= & {} f_\gamma ^h\left( {x_h^h,x_h^\gamma } \right) \nonumber \\= & {} F_\gamma ^h\left( {x_h^h,x_h^\gamma } \right) + \iota _\gamma ^hx_h^\gamma , \nonumber \\ \dot{x}_h^\gamma= & {} f_\theta ^h\left( {x_h^h,x_h^\gamma ,x_h^\theta } \right) \nonumber \\= & {} F_\theta ^h\left( {x_h^h,x_h^\gamma ,x_h^\theta } \right) + \iota _\theta ^hx_h^\theta , \nonumber \\ \dot{x}_h^\theta= & {} f_Q^h\left( {x_h^Q} \right) \nonumber \\= & {} F_Q^h\left( {x_h^Q} \right) + \iota _Q^hx_h^Q, \nonumber \\ \dot{x}_h^Q= & {} f_{{\delta _e}}^h\left( {x_h^h,x_h^\gamma ,x_h^\theta ,x_h^Q,{\delta _e}} \right) \nonumber \\= & {} F_{{\delta _e}}^h\left( {x_h^h,x_h^\gamma ,x_h^\theta ,x_h^Q,{\delta _e}} \right) + \iota _{{\delta _e}}^h{\delta _e}. \end{aligned}$$
(13)

In (12) and (13), \([{x_V},x_h^h,x_h^\gamma ,x_h^\theta ,x_h^Q]{: =} [V,h,\gamma ,\theta ,Q]\) are system states. \(\iota _\Phi ^V > \frac{1}{2}\frac{{\partial f_\Phi ^V\left( {{x_V},\Phi } \right) }}{{\partial \Phi }}\), \(\iota _\gamma ^h > \frac{1}{2}\frac{{\partial f_\gamma ^h\left( {x_h^h,x_h^\gamma } \right) }}{{\partial x_h^\gamma }}\), \(\iota _\theta ^h > \frac{1}{2}\frac{{\partial f_\theta ^h\left( {x_h^h,x_h^\gamma ,x_h^\theta } \right) }}{{\partial x_h^\theta }}\), \(\iota _Q^h > \frac{1}{2}\frac{{\partial f_Q^h\left( {x_h^Q} \right) }}{{\partial x_h^Q}}\) and \(\iota _{{\delta _e}}^h > \frac{1}{2}\frac{{\partial f_{{\delta _e}}^h\left( {x_h^h,x_h^\gamma ,x_h^\theta ,x_h^Q,{\delta _e}} \right) }}{{\partial {\delta _e}}}\) are constants [3, 5]. \(F_\Phi ^V\left( {{x_V},\Phi } \right) = f_\Phi ^V\left( {{x_V},\Phi } \right) - \iota _\Phi ^V\Phi :\Re \times {\Re _{ > 0}} \rightarrow \Re \), \(F_\gamma ^h\left( {x_h^h,x_h^\gamma } \right) = f_\gamma ^h\left( {x_h^h,x_h^\gamma } \right) - \iota _\gamma ^hx_h^\gamma :{\Re ^2} \rightarrow \Re \), \(F_\theta ^h\left( {x_h^h,x_h^\gamma ,x_h^\theta } \right) = f_\theta ^h\left( {x_h^h,x_h^\gamma ,x_h^\theta } \right) - \iota _\theta ^hx_h^\theta :{\Re ^3} \rightarrow \Re \), \(F_Q^h\left( {x_h^Q} \right) = f_Q^h\left( {x_h^Q} \right) - \iota _Q^hx_h^Q:\Re \rightarrow \Re \), and \(F_{{\delta _e}}^h\left( {x_h^h,x_h^\gamma ,x_h^\theta ,x_h^Q,{\delta _e}} \right) = f_{{\delta _e}}^h\left( {x_h^h,x_h^\gamma ,x_h^\theta ,x_h^Q,{\delta _e}} \right) - \iota _{{\delta _e}}^h{\delta _e}:{\Re ^5} \rightarrow \Re \) are unknown but continuous functions. The control inputs \(\Phi \) and \({\delta _e}\) are constrained by

$$\begin{aligned} \Phi = \left\{ \begin{array}{l} {\Phi _{\max }},\text {if}\ {\Phi _d} \in \left( {{\Phi _{\max }}, + \infty } \right) ,\\ {\Phi _d},\text {if}\ {\Phi _d} \in \left[ {{\Phi _{\min }},{\Phi _{\max }}} \right] ,\\ {\Phi _{\min }},\text {if}\ {\Phi _d} \in \left( { - \infty ,{\Phi _{\min }}} \right) , \end{array} \right. \ \end{aligned}$$
(14)
$$\begin{aligned} {\delta _e} = \left\{ \begin{array}{l} {\delta _e}_{\max },\text {if}\ {\delta _e}_d \in \left( {{\delta _e}_{\max }, + \infty } \right) ,\\ {\delta _e}_d,\text {if}\ {\delta _e}_d \in \left[ {{\delta _e}_{\min },{\delta _e}_{\max }} \right] ,\\ {\delta _e}_{\min },\text {if}\ {\delta _e}_d \in \left( { - \infty ,{\delta _e}_{\min }} \right) , \end{array} \right. \ \end{aligned}$$
(15)

with \({\Phi _d}\) and \({\delta _e}_d\) being the ideal values of \(\Phi \in \left[ {{\Phi _{\min }},{\Phi _{\max }}} \right] \) and \({\delta _e} \in \left[ {{\delta _e}_{\min },{\delta _e}_{\max }} \right] \), where \({\Phi _{\max }}{\text {(}} \in {\Re _{> 0}}{\text {)}}> {\Phi _{\min }}{\text {(}} \in {\Re _{ > 0}}{\text {)}}\) and \({\delta _e}_{\max }{\text {(}} \in \Re {\text {)}} > {\delta _e}_{\min }{\text {(}} \in \Re {\text {)}}\) are constants.

Control Objective: Develop control laws for \(\Phi \) and \({\delta _e}\) under constraints (14) and (15) such that \({[{x_V},x_h^h,x_h^\gamma ,x_h^\theta ,x_h^Q]^T} \in {\Re ^5}\) track their reference commands \({[x_V^d,x_h^{h,d},x_h^{\gamma ,d},x_h^{\theta ,d},x_h^{Q,d}]^T} \in {\Re ^5}\), and furthermore the tracking errors \({[{e_V},e_h^h,e_h^\gamma ,e_h^\theta ,e_h^Q]^T} = [{x_V} - x_V^d,x_h^h - x_h^{h,d},x_h^\gamma - x_h^{\gamma ,d},x_h^\theta - x_h^{\theta ,d},x_h^Q - x_h^{Q,d}] \in {\Re ^5}\) satisfy the prescribed behavior (10), i.e., tracking errors converge to steady-sates in finite-time \(T_{FT}^e \in {\Re _{ > 0}}\) whose value can be set as needed, and moreover their steady-state values are within \(( - p_{T_{FT}^e}^e,p_{T_{FT}^e}^e)\).

Assumption 1

[16]. The reference commands \(x_V^d\), \(x_h^{h,d}\), \(x_h^{\gamma ,d}\), \(x_h^{\theta ,d}\), \(x_h^{Q,d}\) and their time derivatives are bounded.

3 Controller design

3.1 Velocity controller

In this subsection, we develop a constrained controller \(\Phi \in [{\Phi _{\min }},{\Phi _{\max }}]\) to let \({x_V} \rightarrow x_V^d\) in finite-time with readjusting prescribed performance.

The velocity tracking error \({e_V}\) should satisfy the following readjusting prescribed performance

$$\begin{aligned} p_\text {lower}^{{e_V}}\left( t \right)< {e_V} < p_\text {upper}^{{e_V}}\left( t \right) ,\ \end{aligned}$$
(16)

with performance functions \(p_\text {lower}^{{e_V}}\left( t \right) = - p_\text {upper}^{{e_V}}\left( t \right) \) and

$$\begin{aligned} p_\text {upper}^{{e_V}}\left( t \right) = \left\{ \begin{array}{l} {\left( {\frac{{T_{FT}^{{e_V}} - t}}{{T_{FT}^{{e_V}}}}} \right) ^{{l_{{e_V}}}}}\left( {p_0^{{e_V}} - p_{T_{FT}^{{e_V}}}^{{e_V}}} \right) \\ + p_{T_{FT}^{{e_V}}}^{{e_V}} + p_\Phi ^{{e_V}}\left( t \right) ,\mathrm{{if }}\ 0 < t \le T_{FT}^{{e_V}},\\ p_{T_{FT}^{{e_V}}}^{{e_V}} + p_\Phi ^{{e_V}}\left( t \right) ,\mathrm{{if }}\ t > T_{FT}^{{e_V}}, \end{array} \right. \ \end{aligned}$$
(17)

where \(p_0^{{e_V}}\left( { \in {\Re _{> 0}}} \right)> p_{T_{FT}^{{e_V}}}^{{e_V}}\left( { \in {\Re _{ > 0}}} \right) \) and \({l_{{e_V}}} \in {\Re _{ > 0}}\) are design parameters, and \(T_{FT}^{{e_V}} \in {\Re _{ > 0}}\) means the convergence time. \(p_\Phi ^{{e_V}}\left( t \right) = \kappa _{\Phi ,2}^{{e_V}}tanh\left( {\kappa _{\Phi ,1}^{{e_V}}{\text {abs}}\left( {\Phi {-} {\Phi _d}} \right) } \right) \) is the readjusting term that correspondingly adjusts the funnels of \(p_\text {lower}^{{e_V}}\left( t \right) \) and \(p_\text {upper}^{{e_V}}\left( t \right) \) to avoid the singularity problem caused by actuator saturation. \(\kappa _{\Phi ,1}^{{e_V}} \in {\Re _{ > 0}}\) and \(\kappa _{\Phi ,2}^{{e_V}} \in {\Re _{ > 0}}\) are two design parameters.

(16) is equivalently expressed as

$$\begin{aligned} {e_V} \!=\! S_\varepsilon ^{{e_V}}\left( {\varepsilon _V^{{e_V}}(t)} \right) \left( {p_\text {upper}^{{e_V}}\left( t \right) \!-\! p_\text {lower}^{{e_V}}\left( t \right) } \!\right) \!+\!p_\text {lower}^{{e_V}}\left( t \right) \nonumber \\ \end{aligned}$$
(18)

with \(S_\varepsilon ^{{e_V}}\left( {\varepsilon _V^{{e_V}}(t)} \right) = \frac{{\varepsilon _V^{{e_V}}(t)}}{{1 + \varepsilon _V^{{e_V}}(t)}}:\Re \rightarrow \left( {0,1} \right) \). The transformed error \(\varepsilon _V^{{e_V}}(t):{\Re _{ \ge 0}} \rightarrow \Re \) is derived from (18) as

$$\begin{aligned} \varepsilon _V^{{e_V}}(t) = \ln \left( {\frac{{{e_V} - p_\text {lower}^{{e_V}}\left( t \right) }}{{p_\text {upper}^{{e_V}}\left( t \right) - {e_V}}}} \right) .\ \end{aligned}$$
(19)

To cope with the actuator saturation, a compensated system is devised as

$$\begin{aligned} {\dot{s}_V} = - {k_{{s_V}}}{d_{\varepsilon _V^{{e_V}}}}\arctan \left( {{s_V}} \right) + \iota _\Phi ^V{d_{\varepsilon _V^{{e_V}}}}\left( {\Phi - {\Phi _d}} \right) ,\ \end{aligned}$$
(20)

with \(d_\varepsilon ^V = \frac{{p_\text {upper}^{{e_V}}(t) - p_\text {lower}^{{e_V}}(t)}}{{\left( {p_\text {upper}^{{e_V}}(t) - {e_V}} \right) \left( {{e_V} - p_\text {lower}^{{e_V}}(t)} \right) }} > 0\), \({s_V} \in \Re \), and \({k_{{s_V}}} \in {\Re _{ > 0}}\) .

The system state of (2) (i.e., \({s_V} \in \Re \)) is used to modify \(\varepsilon _V^{{e_V}}(t)\).

$$\begin{aligned} z_V^{{e_V}} = \varepsilon _V^{{e_V}}(t) - {s_V}.\ \end{aligned}$$
(21)

By employing (12), (18) and (20), the time derivative dynamics of (21) is given by

$$\begin{aligned} \frac{{\dot{z}_V^{{e_V}}}}{{d_\varepsilon ^V}} =&F_\Phi ^V\left( {{x_V},\Phi } \right) - \dot{x}_V^d + {k_{{s_V}}}\arctan \left( {{s_V}} \right) \nonumber \\&\quad + \iota _\Phi ^V{\Phi _d}\mathrm{{ + }}\sum _V^{p,\dot{p}}\ \end{aligned}$$
(22)

with

$$\begin{aligned} \sum _V^{p,\dot{p}}:= & {} \frac{{\dot{p}_\text {lower}^{{e_V}}(t) - \dot{p}_\text {upper}^{{e_V}}(t)}}{{p_\text {upper}^{{e_V}}(t) - p_\text {lower}^{{e_V}}(t)}}S_\varepsilon ^{{e_V}}(\varepsilon _V^{{e_V}})p_\text {upper}^{{e_V}}(t) \\&- \frac{{\dot{p}_\text {lower}^{{e_V}}(t) - \dot{p}_\text {upper}^{{e_V}}(t)}}{{p_\text {upper}^{{e_V}}(t) - p_\text {lower}^{{e_V}}(t)}}S_\varepsilon ^{{e_V}}(\varepsilon _V^{{e_V}})p_\text {lower}^{{e_V}}(t) \\&\mathrm{{ + }}\frac{{\dot{p}_\text {lower}^{{e_V}}(t) - \dot{p}_\text {upper}^{{e_V}}(t)}}{{p_\text {upper}^{{e_V}}(t) - p_\text {lower}^{{e_V}}(t)}}p_\text {lower}^{{e_V}}(t) \\&+ \frac{{\dot{p}_\text {upper}^{{e_V}}(t)p_\text {lower}^{{e_V}}(t) - \dot{p}_\text {lower}^{{e_V}}(t)p_\text {upper}^{{e_V}}(t)}}{{p_\text {upper}^{{e_V}}(t) - p_\text {lower}^{{e_V}}(t)}}\ \end{aligned}$$

where \(\sum _V^{p,\dot{p}}\) is bounded since its arguments are bounded.

The velocity controller is chosen as

$$\begin{aligned} {\Phi _d} = - \frac{{k_V^{{\Phi _d}}}}{{\iota _\Phi ^V}}z_V^{{e_V}} - \frac{{{k_{{s_V}}}}}{{\iota _\Phi ^V}}\arctan \left( {{s_V}} \right) \ \end{aligned}$$
(23)

with \(k_V^{{\Phi _d}} \in {\Re _{ > 0}}\).

Substituting (23) into (22) and invoking (18), it leads to

$$\begin{aligned} \frac{{\dot{z}_V^{{e_V}}}}{{d_\varepsilon ^V}} \le - k_V^{{\Phi _d}}z_V^{{e_V}} - \dot{x}_V^d + \sum _V^{All}\ \end{aligned}$$
(24)

with

$$\begin{aligned} \sum _V^{All}:= & {} F_\Phi ^V(S_\varepsilon ^{{e_V}}(\varepsilon _V^{{e_V}})(p_\text {upper}^{{e_V}} - p_\text {lower}^{{e_V}})\mathrm{{ + }}p_\text {lower}^{{e_V}},\Phi ) \\&- \dot{x}_V^d\mathrm{{ + }}\bar{\sum }_V^{p,\dot{p}}.\ \end{aligned}$$

Due to the boundedness of arguments, the continuous function \(\sum _V^{All}\) also is bounded, denoted by \({\text {abs}}\left( {\sum _V^{All}} \right) \le \bar{\sum }_V^{All}\) with \(\bar{\sum }_V^{All} \in {\Re _{ > 0}}\).

Define Lyapunov function

$$\begin{aligned} W_V^{{e_V}} = \frac{1}{2}{\left( {z_V^{{e_V}}} \right) ^2}\ \end{aligned}$$
(25)

Taking time derivative along (25) and employing (24), we get

$$\begin{aligned} \dot{W}_V^{{e_V}}= & {} z_V^{{e_V}}\dot{z}_V^{{e_V}} \nonumber \\\le & {} d_\varepsilon ^V\bar{\sum }_V^{All}\mathrm{{abs}}\left( {z_V^{{e_V}}} \right) - k_V^{{\Phi _d}}{\left( {z_V^{{e_V}}} \right) ^2} \nonumber \\= & {} d_\varepsilon ^V\mathrm{{abs}}\left( {z_V^{{e_V}}} \right) \nonumber \\&\times \left( {\bar{\sum }_V^{All} - k_V^{{\Phi _d}}\mathrm{{abs}}\left( {z_V^{{e_V}}} \right) } \right) \ \end{aligned}$$
(26)

If \({\text {abs}}\left( {z_V^{{e_V}}} \right) > \bar{\sum }_V^{All}/k_V^{{\Phi _d}}\), we have \(\dot{W}_V^{{e_V}} < 0\) and further obtain \({\text {abs}}\left( {z_V^{{e_V}}} \right) \le \min \left\{ {{\text {abs}}\left( {z_V^{{e_V}}\left( 0 \right) } \right) ,\frac{{\bar{\sum }_V^{All}}}{{k_V^{{\Phi _d}}}}} \right\} \). Thereby, the boundedness of \({\Phi _d}\) is guaranteed, and \(\Phi - {\Phi _d}\) also is bounded. The Lyapunov function is chosen as \({W_{{s_V}}} = \frac{1}{2}s_V^2\). Then, by utilizing (20), we know

$$\begin{aligned} {{\dot{W}}_{{s_V}}}= & {} \frac{{{s_V}{{\dot{s}}_V}}}{{{d_{\varepsilon _V^{{e_V}}}}}} \nonumber \\= & {} - {k_{{s_V}}}{s_V}\arctan \left( {{s_V}} \right) + \iota _\Phi ^V{s_V}\left( {\Phi - {\Phi _d}} \right) \nonumber \\\le & {} - \mathrm{{abs}}\left( {{s_V}} \right) {k_{{s_V}}}\mathrm{{abs}}\left( {\arctan \left( {{s_V}} \right) } \right) \nonumber \\&+ \mathrm{{abs}}\left( {{s_V}} \right) \iota _\Phi ^V\mathrm{{abs}}\left( {\Phi - {\Phi _d}} \right) \end{aligned}$$
(27)

When \({k_{{s_V}}}\frac{\pi }{2}> {k_{{s_V}}}{\text {abs}}\left( {\arctan \left( {{s_V}} \right) } \right) {>} \iota _\Phi ^V{\text {abs}}\left( {\Phi {-} {\Phi _d}} \right) \), i.e., \({k_{{s_V}}} > \frac{{2\iota _\Phi ^V}}{\pi }{\text {abs}}\left( {\Phi - {\Phi _d}} \right) \), we have \({\dot{W}_{{s_V}}} < 0\). Thus, \(s_{V}\) is bounded. Noting that \(z_V^{{e_V}} = \varepsilon _V^{{e_V}}(t) - {s_V}\), we conclude that the transformed error \(\varepsilon _V^{{e_V}}(t)\) also is bounded. We choose the upper bound of \(\varepsilon _V^{{e_V}}(t)\) as \(\bar{\varepsilon }_V^{{e_V}} \in {\Re _{ > 0}}\). On the basis of Theorem 1 presented in [16], it is derived from (19) that \(\frac{{{e_V} - p_\text {lower}^{{e_V}}(t)}}{{p_\text {upper}^{{e_V}}(t) - p_\text {lower}^{{e_V}}(t)}}{\text { = }}\frac{{\exp \left( {\varepsilon _V^{{e_V}}(t)} \right) }}{{1{\text { + }}\exp \left( {\varepsilon _V^{{e_V}}(t)} \right) }}\) and \(0< \frac{{\exp \left( { - \bar{\varepsilon }_V^{{e_V}}} \right) }}{{1{\text { + }}\exp \left( { - \bar{\varepsilon }_V^{{e_V}}} \right) }} \le \frac{{\exp \left( {\varepsilon _V^{{e_V}}(t)} \right) }}{{1{\text { + }}\exp \left( {\varepsilon _V^{{e_V}}(t)} \right) }} \le \frac{{\exp \left( {\bar{\varepsilon }_V^{{e_V}}} \right) }}{{1{\text { + }}\exp \left( {\bar{\varepsilon }_V^{{e_V}}} \right) }} < 1\). Finally, we obtain \(p_\text {lower}^{{e_V}}(t)< {e_V} < p_\text {upper}^{{e_V}}(t)\). Thereby, the spurred prescribed performance can be guaranteed.

3.2 Altitude controller

In this subsection, we will exploit a constrained controller \({\delta _e} \in [{\delta _e}_{\min },{\delta _e}_{\max }]\) to let \(x_h^h \rightarrow x_h^{h,d},x_h^\gamma \rightarrow x_h^{\gamma ,d},x_h^\theta \rightarrow x_h^{\theta ,d}\) and \(x_h^Q \rightarrow x_h^{Q,d}\) in finite-time with readjusting prescribed performance being guaranteed for \(e_h^h,e_h^\gamma ,e_h^\theta \) and \(e_h^Q\), where \(x_h^{\gamma ,d},x_h^{\theta ,d}\) and \(x_h^{Q,d}\) are virtual controllers devised using back-stepping, while their time derivatives aren’t required for feedback control, effectively avoiding the problem of “explosion of terms”.

The tracking errors \(e_h^i = x_h^i - x_h^{i,d},i = h,\gamma ,\theta ,Q\) should satisfy the following readjusting prescribed performance

$$\begin{aligned} p_\text {lower}^{e,i}\left( t \right)< e_h^i < p_\text {upper}^{e,i}\left( t \right) ,i = h,\gamma ,\theta ,Q\ \end{aligned}$$
(28)

with \(p_\text {lower}^{e,i}\left( t \right) = - p_{upper}^{e,i}\left( t \right) \) and

$$\begin{aligned} p_{upper}^{e,i}\left( t \right) = \left\{ \begin{array}{l} {\left( {\frac{{T_{FT}^{e,i} - t}}{{T_{FT}^{e,i}}}} \right) ^{{l_{e,i}}}}\left( {p_0^{e,i} - p_{T_{FT}^{e,i}}^{e,i}} \right) \\ + p_{T_{FT}^{e,i}}^{e,i} + p_{{\delta _e}}^{e,i}\left( t \right) ,\mathrm{{if }}\ 0 < t \le T_{FT}^{e,i},\\ p_{T_{FT}^{e,i}}^{e,i} + p_{{\delta _e}}^{e,i}\left( t \right) ,\mathrm{{if }}\ t > T_{FT}^{e,i},\\ i = h,\gamma ,\theta ,Q, \end{array} \right. \ \end{aligned}$$
(29)

where \(p_0^{e,i}\left( { \in {\Re _{> 0}}} \right)> p_{T_{FT}^{e,i}}^{e,i}\left( { \in {\Re _{ > 0}}} \right) \) and \({l_{e,i}} \in {\Re _{ > 0}}\) are design parameters with \(i = h,\gamma ,\theta ,Q\), and \(T_{FT}^{e_h^i} \in {\Re _{ > 0}}(i = h,\gamma ,\theta ,Q)\) are convergence times. \(p_{{\delta _e}}^{e,i}\left( t \right) = \kappa _{{\delta _e},2}^{e,i}tanh\left( {\kappa _{{\delta _e},1}^{e,i}{\text {abs}}\left( {{\delta _e} - {\delta _e}_d} \right) } \right) ,i = h,\gamma ,\theta ,Q\) are readjusting terms with \(\kappa _{{\delta _e},1}^{e,i} \in {\Re _{ > 0}}(i = h,\gamma ,\theta ,Q)\) and \(\kappa _{{\delta _e},2}^{e,i} \in {\Re _{ > 0}}(i = h,\gamma ,\theta ,Q)\).

(28) is equivalently expressed as

$$\begin{aligned} e_h^i= & {} S_h^{e,i}\left( {\varepsilon _h^{e,i}} \right) \left( {p_{upper}^{e,i}(t) - p_{lower}^{e,i}(t)} \right) \nonumber \\&\mathrm{{ + }}p_{lower}^{e,i}(t),i = h,\gamma ,\theta ,Q,\ \end{aligned}$$
(30)

with \(\varepsilon _h^{e,i} \in \Re \) and \(S_h^{e,i}\left( {\varepsilon _h^{e,i}} \right) = \frac{{{e^{\varepsilon _h^{e,i}}}}}{{1 + {e^{\varepsilon _h^{e,i}}}}}:\Re \rightarrow \left( {0,1} \right) \), where \(i = h,\gamma ,\theta ,Q.\)

From (30), we further get the formulation of transformed errors \(\varepsilon _h^{e,i} \in \Re ,i = h,\gamma ,\theta ,Q\)

$$\begin{aligned} \varepsilon _h^{e,i} = \ln \left( {\frac{{e_h^i - p_{lower}^{e,i}\left( t \right) }}{{p_{upper}^{e,i}\left( t \right) - e_h^i}}} \right) ,i = h,\gamma ,\theta ,Q\ \end{aligned}$$
(31)

Invoking (13) and (30), \(\dot{\varepsilon }_h^{e,i},i = h,\gamma ,\theta ,Q\) are given by

$$\begin{aligned} \frac{{\dot{\varepsilon }_h^{e,h}}}{{{d_{\varepsilon ,h,h}}}}= & {} F_\gamma ^h + \iota _\gamma ^hx_h^\gamma - \dot{x}_h^{h,d} + \sum _{h,h}^{p,\dot{p}}, \nonumber \\ \frac{{\dot{\varepsilon }_h^{e,\gamma }}}{{{d_{\varepsilon ,h,\gamma }}}}= & {} F_\theta ^h + \iota _\theta ^hx_h^\theta - \dot{x}_h^{\gamma ,d} + \sum _{h,\gamma }^{p,\dot{p}}, \nonumber \\ \frac{{\dot{\varepsilon }_h^{e,\theta }}}{{{d_{\varepsilon ,h,\theta }}}}= & {} F_Q^h + \iota _Q^hx_h^Q - \dot{x}_h^{\theta ,d} + \sum _{h,\theta }^{p,\dot{p}}, \nonumber \\ \frac{{\dot{\varepsilon }_h^{e,Q}}}{{{d_{\varepsilon ,h,Q}}}}= & {} F_{{\delta _e}}^h + \iota _{{\delta _e}}^h{\delta _e} - \dot{x}_h^{Q,d} + \sum _{h,Q}^{p,\dot{p}},\ \end{aligned}$$
(32)

with

$$\begin{aligned} {d_{\varepsilon ,h,i}}= & {} \frac{{{1 \big /{\left( {p_{upper}^{e,i}\left( t \right) - p_{lower}^{e,i}\left( t \right) } \right) }}}}{{S_h^{e,i}\left( {\varepsilon _h^{e,i}} \right) \left[ {1 - S_h^{e,i}\left( {\varepsilon _h^{e,i}} \right) } \right] }} \\> & {} 0,i = h,\gamma ,\theta ,Q, \\ \sum _{h,i}^{p,\dot{p}}:= & {} \frac{{\dot{p}_{lower}^{e,i}(t) - \dot{p}_{upper}^{e,i}(t)}}{{p_{upper}^{e,i}(t) - p_{lower}^{e,i}(t)}}S_h^{e,i}\left( {\varepsilon _h^{e,i}} \right) p_{upper}^{e,i}(t) \\&- \frac{{\dot{p}_{lower}^{e,i}(t) - \dot{p}_{upper}^{e,i}(t)}}{{p_{upper}^{e,i}(t) - p_{lower}^{e,i}(t)}}S_h^{e,i}\left( {\varepsilon _h^{e,i}} \right) p_{lower}^{e,i}(t) \\&\mathrm{{ + }}\frac{{\dot{p}_{lower}^{e,i}(t) - \dot{p}_{upper}^{e,i}(t)}}{{p_{upper}^{e,i}(t) - p_{lower}^{e,i}(t)}}p_{lower}^{e,i}(t) \\&+ \frac{{\dot{p}_{upper}^{e,i}(t)p_{lower}^{e,i}(t) - \dot{p}_{lower}^{e,i}(t)p_{upper}^{e,i}(t)}}{{p_{upper}^{e,i}(t) - p_{lower}^{e,i}(t)}}, \\ i= & {} h,\gamma ,\theta ,Q.\ \end{aligned}$$

Due to the boundedness of arguments, \(\sum _{h,i}^{p,\dot{p}},i = h,\gamma ,\theta ,Q\) also are bounded. Based on the back-stepping procedure, we design the following virtual control laws

$$\begin{aligned} x_h^{\gamma ,d}= & {} - \frac{{k_h^h}}{{\iota _\gamma ^h}}\varepsilon _h^{e,h}, \nonumber \\ x_h^{\theta ,d}= & {} - \frac{{k_h^\gamma }}{{\iota _\theta ^h}}\varepsilon _h^{e,\gamma }, \nonumber \\ x_h^{Q,d}= & {} - \frac{{k_h^\theta }}{{\iota _Q^h}}\varepsilon _h^{e,\theta },\ \end{aligned}$$
(33)

with \(k_h^i \in {\Re _{ > 0}},i = h,\gamma ,\theta \).

Substituting (33) into (32) and using (30), we obtain

$$\begin{aligned} \frac{{\dot{\varepsilon }_h^{e,h}}}{{{d_{\varepsilon ,h,h}}}}= & {} F_\gamma ^h + \iota _\gamma ^h\left( {e_h^\gamma + x_h^{\gamma ,d}} \right) - \dot{x}_h^{h,d} + \sum _{h,h}^{p,\dot{p}} \nonumber \\= & {} - k_h^h\varepsilon _h^{e,h} + \sum _{h,h}^{All}, \nonumber \\ \frac{{\dot{\varepsilon }_h^{e,\gamma }}}{{{d_{\varepsilon ,h,\gamma }}}}= & {} F_\theta ^h + \iota _\theta ^h\left( {e_h^\theta + x_h^{\theta ,d}} \right) - \dot{x}_h^{\gamma ,d} + \sum _{h,\gamma }^{p,\dot{p}} \nonumber \\= & {} - k_h^\gamma \varepsilon _h^{e,\gamma } + \sum _{h,\gamma }^{All}, \nonumber \\ \frac{{\dot{\varepsilon }_h^{e,\theta }}}{{{d_{\varepsilon ,h,\theta }}}}= & {} F_Q^h + \iota _Q^h\left( {e_h^Q + x_h^{Q,d}} \right) - \dot{x}_h^{\theta ,d} + \sum _{h,\theta }^{p,\dot{p}} \nonumber \\= & {} - k_h^\theta \varepsilon _h^{e,\theta } + \sum _{h,\theta }^{All},\ \end{aligned}$$
(34)

with

$$\begin{aligned} \sum _{h,h}^{All}:= & {} F_\gamma ^h - \dot{x}_h^{h,d} + \sum _{h,h}^{p,\dot{p}}\mathrm{{ + }}\iota _\gamma ^hp_{lower}^{e,h}(t) \\&+ \iota _\gamma ^hS_h^{e,h}\left( {\varepsilon _h^{e,h}} \right) \left( {p_{upper}^{e,h}(t) - p_{lower}^{e,h}(t)} \right) ,\\ \sum _{h,\gamma }^{All}:= & {} F_\theta ^h - \dot{x}_h^{\gamma ,d} + \sum _{h,\gamma }^{p,\dot{p}}\mathrm{{ + }}\iota _\gamma ^hp_{lower}^{e,\gamma }(t) \\&+ \iota _\gamma ^hS_h^{e,\gamma }\left( {\varepsilon _h^{e,\gamma }} \right) \left( {p_{upper}^{e,\gamma }(t) - p_{lower}^{e,\gamma }(t)} \right) , \\ \sum _{h,\theta }^{All}:= & {} F_Q^h - \dot{x}_h^{\theta ,d} + \sum _{h,\theta }^{p,\dot{p}}\mathrm{{ + }}\iota _\gamma ^hp_{lower}^{e,\theta }(t) \\&+ \iota _\gamma ^hS_h^{e,\theta }\left( {\varepsilon _h^{e,\theta }} \right) \left( {p_{upper}^{e,\theta }(t) - p_{lower}^{e,\theta }(t)} \right) .\ \end{aligned}$$

We easily conclude that \(\sum _{h,i}^{All},i = h,\gamma ,\theta \) are bounded since their arguments are bounded, that is, there exist constants \(\bar{\sum }_{h,i}^{All} \in {\Re _{ > 0}},i = h,\gamma ,\theta \) such that \({\text {abs}}\left( {\sum _{h,i}^{All}} \right) \le \bar{\sum }_{h,i}^{All},i = h,\gamma ,\theta \).

Define Lyapunov function

$$\begin{aligned} W_h^{\varepsilon ,e,i} = \frac{1}{2}{\left( {\varepsilon _h^{e,i}} \right) ^2},i = h,\gamma ,\theta \ \end{aligned}$$
(35)

Taking time derivative of (35) and utilizing (34), we know

$$\begin{aligned} \dot{W}_h^{\varepsilon ,e,i}= & {} {d_{\varepsilon ,h,i}}\left[ {\varepsilon _h^{e,i}\sum _{h,i}^{All} - k_h^i{{\left( {\varepsilon _h^{e,i}} \right) }^2}} \right] ,i = h,\gamma ,\theta \nonumber \\\le & {} {d_{\varepsilon ,h,i}}\left[ {\bar{\sum }_{h,i}^{All} - k_h^iabs\left( {\varepsilon _h^{e,i}} \right) } \right] \nonumber \\&\times abs\left( {\varepsilon _h^{e,i}} \right) .\ \end{aligned}$$
(36)

Once \(abs\left( {\varepsilon _h^{e,i}} \right) > {{\bar{\sum }_{h,i}^{All}} \big / {k_h^i}},i = h,\gamma ,\theta \), we have \(\dot{W}_h^{\varepsilon ,e,i} < 0,i = h,\gamma ,\theta \). Thereby, we conclude that \(abs\left( {\varepsilon _h^{e,i}} \right) \le \min \left\{ {{{abs\left( {\varepsilon _h^{e,i}(0)} \right) ,\bar{\sum }_{h,i}^{All}} \big / {k_h^i}}} \right\} ,i = h,\gamma ,\theta .\)

It is difficult to guarantee the stability of altitude subsystem under the saturation condition. Thus, we develop the following compensated system.

$$\begin{aligned} {{\dot{s}}_h}= & {} - {k_{{s_h}}}{d_{\varepsilon ,h,Q}}\arctan \left( {{s_h}} \right) \nonumber \\&+ \iota _{{\delta _e}}^h{d_{\varepsilon ,h,Q}}\left( {{\delta _e} - {\delta _e}_d} \right) ,\ \end{aligned}$$
(37)

where \({k_{{s_h}}} \in {\Re _{ > 0}}\) is a design parameter, and the state \({s_h} \in \Re \) is used to modify \(\varepsilon _h^{e,Q}\)

$$\begin{aligned} z_h^{e,Q} = \varepsilon _h^{e,Q} - {s_h}.\ \end{aligned}$$
(38)

Combining (32) and (37), the time derivative of \(z_h^{e,Q}\) is given by

$$\begin{aligned} \dot{z}_h^{e,Q}= & {} {d_{\varepsilon ,h,Q}}\dot{\varepsilon }_h^{e,Q} - {d_{\varepsilon ,h,Q}}{{\dot{s}}_h} \nonumber \\= & {} {d_{\varepsilon ,h,Q}}F_{{\delta _e}}^h - {d_{\varepsilon ,h,Q}}\dot{x}_h^{Q,d} \nonumber \\&+ {d_{\varepsilon ,h,Q}}\sum _{h,Q}^{p,\dot{p}} + \iota _{{\delta _e}}^h{d_{\varepsilon ,h,Q}}{\delta _e}_d \nonumber \\&+ {k_{{s_h}}}{d_{\varepsilon ,h,Q}}\arctan {\left( {{s_h}} \right) _e}.\ \end{aligned}$$
(39)

The altitude controller is developed as

$$\begin{aligned} {\delta _e}_d = - \frac{{k_h^{{\delta _e}}}}{{\iota _{{\delta _e}}^h}}z_h^{e,Q} - \frac{{{k_{{s_h}}}}}{{\iota _{{\delta _e}}^h}}\arctan \left( {{s_h}} \right) \ \end{aligned}$$
(40)

with \(k_h^{{\delta _e}} \in {\Re _{ > 0}}\).

Substituting (40) into (39) leads to

$$\begin{aligned} \dot{z}_h^{e,Q} = - k_h^{{\delta _e}}{d_{\varepsilon ,h,Q}}z_h^{e,Q} + {d_{\varepsilon ,h,Q}}\Sigma _{{\delta _e}}^{All,h}.\ \end{aligned}$$
(41)

where \(\Sigma _{{\delta _e}}^{All,h}: = F_{{\delta _e}}^h - \dot{x}_h^{Q,d} + \sum _{h,Q}^{p,\dot{p}}\) is bounded since \(\dot{x}_h^{Q,d} = - \frac{{k_h^Q}}{{\iota _{x_h^Q}^h}}\dot{\varepsilon }_h^{e,Q} = - \frac{{k_h^Q}}{{\iota _{x_h^Q}^h}}\left( {F_{{\delta _e}}^h - \dot{x}_h^{Q,d} + \sum _{h,Q}^{p,\dot{p}}} \right) \) is bounded, that is, there is a constant \(\bar{\Sigma }_{{\delta _e}}^{All,h} \in {\Re _{ > 0}}\) such that \({\text {abs}}\left( {\Sigma _{{\delta _e}}^{All,h}} \right) \le \bar{\Sigma }_{{\delta _e}}^{All,h}\).

Define Lyapunov function

$$\begin{aligned} W_h^{\varepsilon ,e,Q} = \frac{1}{2}{\left( {z_h^{e,Q}} \right) ^2}.\ \end{aligned}$$
(42)

Taking time derivative along (42) and employing (41), we obtain

$$\begin{aligned} \frac{{\dot{W}_h^{\varepsilon ,e,Q}}}{{{d_{\varepsilon ,h,Q}}}} = \left( { - k_h^{{\delta _e}}abs\left( {z_h^{e,Q}} \right) + \Sigma _{{\delta _e}}^{All,h}} \right) abs\left( {z_h^{e,Q}} \right) .\ \end{aligned}$$
(43)

It can be seen that \(\dot{W}_h^{\varepsilon ,e,Q}\) will be negative if \(abs\left( {z_h^{e,Q}} \right) > {{\bar{\Sigma }_{{\delta _e}}^{All,h}} \big / {k_h^{{\delta _e}}}}\). Thus, we know that \(abs\left( {z_h^{e,Q}} \right) \le \min \left\{ {{{abs\left( {z_h^{e,Q}(0)} \right) ,\bar{\Sigma }_{{\delta _e}}^{All,h}} \big / {k_h^{{\delta _e}}}}} \right\} \), which further guarantees the boundedness of \({\text {abs}}\left( {{\delta _e} - {\delta _e}_d} \right) \). By defining the Lyapunov function \({W_{{s_h}}} = \frac{1}{2}s_h^2\) and utilizing (37), we have

$$\begin{aligned} {{\dot{W}}_{{s_h}}}= & {} {s_h}{{\dot{s}}_h} \nonumber \\= & {} - {k_{{s_h}}}{s_h}\arctan ({s_h}) + \iota _{{\delta _e}}^h{s_h}\left( {{\delta _e} - {\delta _e}_d} \right) \nonumber \\\le & {} - \mathrm{{abs}}\left( {{s_h}} \right) {k_{{s_h}}}\mathrm{{abs}}\left( {\arctan ({s_h})} \right) \nonumber \\&+ \mathrm{{abs}}\left( {{s_h}} \right) \iota _{{\delta _e}}^h\mathrm{{abs}}\left( {{\delta _e} - {\delta _e}_d} \right) \ \end{aligned}$$
(44)

Let \({k_{{s_h}}}\frac{\pi }{2}> {k_{{s_h}}}{\text {abs}}\left( {\arctan \left( {{s_h}} \right) } \right) > \iota _{{\delta _e}}^h{\text {abs}}\left( {{\delta _e} - {\delta _e}_d} \right) \) (i.e., \({k_{{s_h}}} > {{2\iota _{{\delta _e}}^h{\text {abs}}\left( {{\delta _e} - {\delta _e}_d} \right) } \big / \pi }\)). We obtain \({\dot{W}_{{s_h}}} < 0\). It is further concluded that \({s_h}\) and \(z_h^{e,Q}\left( {: = \varepsilon _h^{e,Q} - {s_h}} \right) \) are bounded.

The above discussions prove the boundedness of \(\varepsilon _h^{e,i},i = h,\gamma ,\theta ,Q\), given by \({\text {abs}}\left( {\varepsilon _h^{e,i}} \right) \le \bar{\varepsilon }_h^{e,i} \in {\Re _{ > 0}},i = h,\gamma ,\theta ,Q\). Based on Theorem 1 of [16], we conclude from (31) that \(\frac{{e_h^i - p_{lower}^{e,i}(t)}}{{p_{upper}^{e,i}(t) - p_{lower}^{e,i}(t))}}{\text { = }}\frac{{\exp \left( {\varepsilon _h^{e,i}} \right) }}{{1{\text { + }}\exp \left( {\varepsilon _h^{e,i}} \right) }},i = h,\gamma ,\theta ,Q\) and \(0< \frac{{\exp \left( { - \bar{\varepsilon }_h^{e,i}} \right) }}{{1{\text { + }}\exp \left( { - \bar{\varepsilon }_h^{e,i}} \right) }} \le \frac{{\exp \left( {\varepsilon _h^{e,i}} \right) }}{{1{\text { + }}\exp \left( {\varepsilon _h^{e,i}} \right) }} \le \frac{{\exp \left( {\bar{\varepsilon }_h^{e,i}} \right) }}{{1{\text { + }}\exp \left( {\bar{\varepsilon }_h^{e,i}} \right) }} < 1,i = h,\gamma ,\theta ,Q\),. Finally, we obtain \(p_{lower}^{e,i}(t)< e_h^i < p_{upper}^{e,i}(t),i = h,\gamma ,\theta ,Q\). Thereby, the spurred prescribed performance can be guaranteed for \(e_h^i,i = h,\gamma ,\theta ,Q\).

Remark 3

Controllers (33) and (40), developed utilizing back-stepping, don’t contain the time derivatives of virtual control laws, which eliminates the problem of “explosion of terms”. Moreover, there is no need of any fuzzy/neural approximation for (33) and (40). Hence, the problem of computational complexity is avoided.

Remark 4

From [5, 16], we know that \(\iota _\Phi ^V\), \(\iota _\gamma ^h\), \(\iota _\theta ^h\), \(\iota _Q^h\) and \(\iota _{{\delta _e}}^h\) satisfy: \(\iota _\Phi ^V > \frac{1}{2}\frac{{\partial f_\Phi ^V\left( {{x_V},\Phi } \right) }}{{\partial \Phi }}\), \(\iota _\gamma ^h > \frac{1}{2}\frac{{\partial f_\gamma ^h\left( {x_h^h,x_h^\gamma } \right) }}{{\partial x_h^\gamma }}\), \(\iota _\theta ^h > \frac{1}{2}\frac{{\partial f_\theta ^h\left( {x_h^h,x_h^\gamma ,x_h^\theta } \right) }}{{\partial x_h^\theta }}\), \(\iota _Q^h > \frac{1}{2}\frac{{\partial f_Q^h\left( {x_h^Q} \right) }}{{\partial x_h^Q}}\) and \(\iota _{{\delta _e}}^h > \frac{1}{2}\frac{{\partial f_{{\delta _e}}^h\left( {x_h^h,x_h^\gamma ,x_h^\theta ,x_h^Q,{\delta _e}} \right) }}{{\partial {\delta _e}}}\). In the simulation, we can select suitable constants for \(\iota _\Phi ^V\), \(\iota _\gamma ^h\), \(\iota _\theta ^h\), \(\iota _Q^h\) and \(\iota _{{\delta _e}}^h\). \(p_0^{{e_V}} \in {\Re _{ > 0}}\) denotes the initial value of the performance function, and its value can be chosen as a constant that satisfies \(p_0^{{e_V}} > {\text {abs}}\left( {{e_V}(0)} \right) \). \(p_{T_{FT}^{{e_V}}}^{{e_V}} \in {\Re _{ > 0}}\) means the upper bound of \({e_V}\), and its value should be suitably designed according to the desired control accuracy. \(T_{FT}^{{e_V}} \in {\Re _{ > 0}}\) and \({l_{{e_V}}} \in {\Re _{ > 0}}\) should be set as suitable values according to the desired convergence time and rate of \({e_V}\). \(\kappa _{\Phi ,2}^{{e_V}} \in {\Re _{ > 0}}\) and \(\kappa _{\Phi ,1}^{{e_V}} \in {\Re _{ > 0}}\) mainly affect the amplitude and rate of the readjusting term \(p_\Phi ^{{e_V}}\left( t \right) \). Similarly, \(\kappa _{{\delta _e},2}^{e,i}\), \(i = h,\gamma ,\theta ,Q\) and \(\kappa _{{\delta _e},1}^{e,i},i = h,\gamma ,\theta ,Q\) mainly affect the amplitudes and rates of readjusting terms \(p_{{\delta _e}}^{e,i}\left( t \right) ,i = h,\gamma ,\theta ,Q\). The value of \({k_{{s_V}}}\) should be designed based on the response of \({s_V}\), and it should satisfy \({k_{{s_V}}} > \frac{{2\iota _\Phi ^V}}{\pi }{\text {abs}}\left( {\Phi - {\Phi _d}} \right) \). \(k_V^{{\Phi _d}} \in {\Re _{ > 0}}\) should be set as a suitable value according to the response of \(z_V^{{e_V}}\). \(p_0^{e,i} \in {\Re _{ > 0}},i = h,\gamma ,\theta ,Q\) mean the initial values of the performance functions, and their values can be chosen as constants satisfying \(p_0^{e,i} > {\text {abs}}\left( {e_h^i(0)} \right) ,i = h,\gamma ,\theta ,Q\). \(p_{T_{FT}^{e,i}}^{e,i} \in {\Re _{ > 0}},i = h,\gamma ,\theta ,Q\) denote the upper bounds of \(e_h^i,i = h,\gamma ,\theta ,Q\), and their values should be suitably designed based on the desired control accuracy. \(T_{FT}^{e_h^i},i = h,\gamma ,\theta ,Q\) and \({l_{e,i}} \in {\Re _{ > 0}},i = h,\gamma ,\theta ,Q\) should be set as suitable values according to the desired convergence times and rates of \(e_h^i,i = h,\gamma ,\theta ,Q\). The values of \(k_h^i \in {\Re _{ > 0}},i = h,\gamma ,\theta \) and \(k_h^{{\delta _e}} \in {\Re _{ > 0}}\) should be chosen according to the responses of \(\varepsilon _h^{e,h},\varepsilon _h^{e,\gamma }\varepsilon _h^{e,\theta }\) and \(z_h^{e,Q}\). \({k_{{s_h}}}\) should be set as a suitable value based on the response of \({s_h} \in \Re \), and it should satisfy \({k_{{s_h}}} > 2\iota _{{\delta _e}}^h{\text {abs}}\left( {{\delta _e} - {\delta _e}_d} \right) /\pi \).

Fig. 3
figure 3

Velocity control input of [17,18,19] under actuator saturation

Full size image
Fig. 4
figure 4

Velocity tracking error of [17,18,19] under actuator saturation

Full size image
Fig. 5
figure 5

Transformed errors of [17,18,19] under actuator saturation

Full size image
Fig. 6
figure 6

Velocity tracking performance of the proposed method

Full size image
Fig. 7
figure 7

Altitude tracking performance of the proposed method

Full size image
Fig. 8
figure 8

Velocity tracking error of the proposed method

Full size image
Fig. 9
figure 9

Altitude tracking error of the proposed method

Full size image
Fig. 10
figure 10

Flight-path angle tracking error of the proposed method

Full size image
Fig. 11
figure 11

Pitch angle tracking error of the proposed method

Full size image
Fig. 12
figure 12

Pitch rate tracking error of the proposed method

Full size image
Fig. 13
figure 13

Velocity control input of the proposed method

Full size image
Fig. 14
figure 14

Altitude control input of the proposed method

Full size image
Fig. 15
figure 15

Compensated systems’ states of the proposed method

Full size image
Fig. 16
figure 16

Transformed errors of the proposed method

Full size image

4 Simulation results

The purpose of this section is to validate the effect of the proposed method via compared simulation. The addressed controllers (23), (33), and (40) with compensated systems (20) and (37) are tested in the MATLAB/Simulink environment by utilizing the fourth-order Runge–Kutta algorithm with a fixed-step of 0.01 s. Based on the discussions presented in Remark 3 and the actual simulation performance, we choose the following values for the design parameters: \(\iota _\Phi ^V = 1.3\), \(\iota _\gamma ^h = 1.3\), \(\iota _\theta ^h = 1.3\), \(\iota _Q^h = 1.3\), \(\iota _{{\delta _e}}^h = 1.3\), \(p_0^{{e_V}} = 6\), \(p_{T_{FT}^{{e_V}}}^{{e_V}} = 2\), \({l_{{e_V}}} = 3\), \(T_{FT}^{{e_V}} = 6\), \(\kappa _{\Phi ,1}^{{e_V}} = 1.5\), \(\kappa _{\Phi ,2}^{{e_V}} = 20\), \({k_{{s_V}}} = 1.5\), \(k_V^{{\Phi _d}} = 0.6\), \(p_0^{e,h} = 1.6\), \(p_{T_{FT}^{e,h}}^{e,h} = 0.4\), \({l_{e,h}} = 3\), \(T_{FT}^{e_h^h} = 8\), \(p_0^{e,\gamma } = 0.08\), \(p_{T_{FT}^{e,\gamma }}^{e,\gamma } = 0.017\), \({l_{e,\gamma }} = 3\), \(T_{FT}^{e_h^\gamma } = 8\), \(p_0^{e,\theta } = 0.12\), \(p_{T_{FT}^{e,\theta }}^{e,\theta } = 0.025\), \({l_{e,\theta }} = 3\), \(T_{FT}^{e_h^\theta } = 8\), \(p_0^{e,Q} = 0.3\), \(p_{T_{FT}^{e,Q}}^{e,Q} = 0.05\), \({l_{e,Q}} = 3\), \(T_{FT}^{e_h^Q} = 8\), \(\kappa _{{\delta _e},1}^{e,h} = 1.2\), \(\kappa _{{\delta _e},2}^{e,i} = 0.5(i = h,\gamma ,\theta ,Q)\), \(\kappa _{{\delta _e},1}^{e,i} = 1.2\pi /180(i = \gamma ,\theta ,Q)\), \(k_h^h = 0.05\), \(k_h^\gamma = 0.06\), \(k_h^\theta = 0.13\), \(k_h^Q = 0.9\), and \({k_{{s_h}}} = 0.5\). We assume that the control inputs are constrained by: \(\Phi \in [0.05,0.95]\) and \({\delta _e} \in [ - 20{\text { }}\deg ,20{\text { }}\deg ]\). The proposed readjusting prescribed performance controller is compared with the traditional PPC [17,18,19]. Moreover, to test the robust performance, we consider parameter uncertainty up to 45

$$\begin{aligned} C = \left\{ {\begin{array}{*{20}{c}} {{C_0},}&{}{0\mathrm{{ }}s \le t< 50\mathrm{{ }}s}\\ {{C_0}\left[ {1 + 0.4\sin (0.01\pi t)} \right] ,}&{}{50\mathrm{{ }}s \le t < 80\mathrm{{ }}s} \end{array}} \right. \ \end{aligned}$$
(45)

where C denotes the value of uncertain coefficient and \({C_0}\) means the nominal value of C.

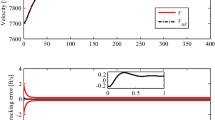
The obtained simulation results are depicted in Figs. 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 and 16. Figures 3, 4, and 5 clearly infer that the traditional PPC [17,18,19] exhibits fragility to the actuator saturation. If the actuator is saturated (See Fig. 3), the tracking error \({e_V}\) increases gradually so that \({e_V}\) reaches the traditional prescribed funnel [17,18,19] (See Fig. 4). As a result, the transformed errors tend to diverge (See Fig. 5). Thereby, as to the traditional PPC [17,18,19], the actuator saturation will result in the singular problem. As a contrast, the proposed method can effectively guarantee tracking errors with desired prescribed performance in the presence of actuator saturation, as shown in Figs. 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 and 16. The velocity tracking performance and the altitude tracking performance are presented in Figs. 6 and 7. Figs. 8, 9, 10, 11, 12, 13 and 14 indicate that the addressed method is capable of adaptively readjusting the prescribed funnels (See Figs. 8, 9, 10, 11 and 12) when actuators are saturated (See Figs. 13 and 14), while avoiding the fragile problem associated with traditional PPC [17,18,19]. Besides, the developed compensated system can provide timely compensations when actuators are saturated (See Fig. 15). Finally, Fig 16 shows the boundedness of transformed errors.

5 Conclusions

The non-fragile tracking control methodology is exploited for WVs subject to actuator saturation. A new type of PPC with readjusting prescribed performance is proposed to handle the fragile problem. Moreover, the improved back-stepping is used to devised velocity controller and altitude controller, while the problem of “explosion of terms” is avoided. Besides, compensated systems are developed to provide effective compensations for actuator saturations. Finally, the presented simulation results prove the effectiveness and superiority of the proposed design. In our future work, we will try to handle the actuator saturation utilizing the Bessel function.