1 Introduction

Out-of-equilibrium systems often exhibit multistability, that is, by setting the parameters of the system, and for different initial conditions, these systems can exhibit different equilibrium states [1, 2]. In the case that these equilibria account for the orientation of some physical quantities (vector fields), the union of three different domains is characterized by exhibiting a vortex [1, 3]. These vortices correspond to points or lines where the magnitude of the vector quantity is zero, and its respective phase value is undefined, phase singularity. Examples of everyday vortices are eddies or tornadoes in fluids, hair whorl, umbilic defects in liquid crystals, and skyrmions in magnetic systems.

In the last decades, a great effort has been developed to understand spiral-out light beams about their axis of propagation, orbital angular momentum of light or optical vortex [4,5,6,7,8]. These beams have a donut-like structure, that is, the beam intensity cancels out into the center, generating a phase singularity into the envelope. In addition, the light beams are characterized by fading asymptotically from the center. Around the point of zero intensity, the phase distribution forms an N-armed spiral, with N being the topological charge [3, 5,6,7,8]. These optical vortices have aroused interest from both the fundamental and applied point of view. The photonic applications range from optical tweezers [9,10,11], enhancement of astronomical images [12], quantum computation [13], wavefront sensors [14], and data transmission [15]. From a fundamental point of view, the interchange of angular momentum between light and matter has attracted attention (see the collected articles [8] and references therein). Different methods have been used to generate optical vortices based on diffractive elements [16], deformable mirrors [17], holograms [18], spiral phase plates [19], nanostructured glass plates [20], planar chiral meta-surfaces [21], wavelength-adaptable effective q-plates with passively tunable retardance [22], and helical structures of liquid crystals [23,24,25,26]. In most of these methods, the light beam interacts with a material object which has an intrinsic helicity. Hence, to control the optical vortex, it is important to have an adequate alignment between the light beam, the helical target, and the geometry of it. In the case of liquid crystals, the light induces a vortex in the matter (umbilical defect), with which interacts, generating an optical vortex by photoconductor walls [26, 27], photovoltaics walls [28], temperature gradients [29], combination of a magnetic ring and oscillatory electric field [30, 31], combining an external pressure and electric field on a homeotropic liquid crystal cell [39], and azo dye dopants [33]. The vortex-like defects have accompanied liquid crystals since their discovery in 1889 by Lehmann [34]; later, Friedel solved its detailed topological structure [35], which was complemented by the elastic theory of crystals by Frank [36]. Because of the topological structure of these defects corresponding to a rodlike object in three dimensions, these defects are usually called nematic umbilical defects [37]. Microstructured pillar patterns [38], interaction between the vortices and the excitation of stationary waves [39], and low-frequency-driven voltage [40] can induce patterns of tunable umbilical defects. The dynamics and properties of umbilic defects can be described employing the Frank–Oseen free energy [41,42,43]. This description includes an order parameter that accounts for molecular orientation, the director \(\mathbf {n}\). The dynamic behavior of the director is based on the minimization of the free energy with the restriction of the conservation of the director norm. This minimization generates complex vector dynamics to describe the defects of liquid crystals. However, a more accessible approach that captures the dynamics of umbilic defects is through the dynamics of a critical mode of the director, which satisfies the Ginzburg–Landau amplitude equation with real coefficients [27, 45]. When a sufficiently large electric field is applied to a nematic liquid crystal cell with homeotropic anchoring and a negative anisotropic dielectric constant, a gas of umbilical defects emerges (see Fig. 1). These defects later begin to be annihilated by pairs with opposite charges to minimize the free energy [41]. Figure 1c shows two vortices of opposite charge under circular crossed polarizers. To our knowledge, the emergence process and statistical rules governing this phase singularity gas have not been established.

Fig. 1
figure 1

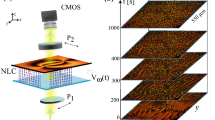
Vortex nucleation in a nematic liquid crystal light cell with homeotropic anchoring and negative dielectric anisotropic constant. The rods represent schematically the typical direction in which the molecules are oriented. a Schematic representation of the experimental setup. The setup consists of white light, a thermal control chamber (thermal stage) with a nematic liquid crystal cell (NLC) inside to which a vertical voltage is applied. The thermal control chamber is between two cross-polarizers (linear or circular). An objective of magnification N (5 or 50) and a CMOS camera monitor the nematic liquid crystal cell. b Snapshot of a vortex gas obtained in a nematic liquid crystal cell between linear cross-polarizer, using an objective of magnifications \(N=5\). The lower inset is a schematic representation of the director and its associated complex amplitude. c Vortices of positive and negative charge observed with crossed circular polarizers and using an objective of magnifications \(N=50\). d Snapshot of a vortex gas obtained in a nematic liquid crystal cell between circular cross-polarizer, using an objective of magnifications \(N=5\)

Full size image

The paper aims to establish the nucleation mechanisms of the matter vortices in nematic liquid crystal cells and provide statistical laws that govern them. Based on a stochastic amplitude equation, the Ginzburg–Landau equation with additive noise, we establish the law for the number of nucleated vortices as a function of anisotropy, bifurcation parameter, and intensity of the noise level. Experimentally, we consider a nematic liquid crystal cell with homeotropic anchoring and a negative anisotropic dielectric constant under the influence of a transverse electric field. The average number of umbilical defects as a function of the applied voltage and temperature shows a qualitative agreement with the theoretical findings.

The article has the following structure: Liquid crystal cells, the experimental setup, and experimental vortices nucleation and annihilation are described in Sect. 2. The amplitude equation that accounts for the reorientation dynamics of a nematic liquid crystal cell is presented in Sect. 3. In addition, a numerical and experimental analysis of vortex nucleation is presented. Our conclusions and comments are left for the final section.

2 Nematic liquid crystal cell

Nematic liquid crystals are nonlinear optical media [41,42,43], composed of rodlike molecules that have a preferential orientation order but not a positional one. This state of matter shares features of solids and liquids, such as fluidity and birefringence. Introducing a liquid crystal inside a cell, that is, it is sandwiched between two confining glass layers, the molecules are oriented according to anchoring conditions. Homeotropic anchoring is characterized by molecules that are oriented orthogonal to cell walls, as illustrated in Fig. 1a by rods. If the dielectric anisotropic constant of the liquid crystal is negative, when applying a vertical electric field, the molecules tend to orient orthogonal to it. The elastic and electric energy determines the equilibrium angle of the average molecular orientation to the vertical axis. This generates different domains connected by orientation defects or phase singularities, matter vortices [41]. Figure 1b shows the umbilical defects observed in a liquid crystal nematic cell. The defects correspond to the intersection of two black fringes.

2.1 Experimental setup

Let us consider a 15-\(\upmu \)m-thick cell (SB100A150uT180 manufactured by Instec), filled with nematic liquid crystal LC BYVA- 01 (Instec) with dielectric anisotropy \(\epsilon _{a}=-4.89\), birefringence \(\varDelta n=n_e-n_o=0.1\), rotation viscosity \(\gamma = 204\) mPas, splay and bend elastic constant, respectively, \(K_1=17.65\) pN and \(K_3=21.39\) pN. To guarantee the thickness of the liquid crystal cell, there are randomly distributed 15-\(\mu \)m-thick glass beads inside it. This liquid crystal is nematic in the \(-20\)–\( 92^\circ \)C; at \( 92^\circ \)C, it exhibits a nematic–isotropic transition. This liquid crystal cell is placed inside a thermal control chamber (Linkam LTS420), which in turn is inserted inside a microscope (Leica DM2700P), in between the crossed linear or circular polarizers. Figure 1a shows a schematic representation of the experimental setup. To monitor the images, an objective of magnification N (5 and 50) and a CMOS camera is connected to the microscope. A sinusoidal voltage with a frequency of 100 Hz is applied to the sample.

2.2 Experimental vortices nucleation

Maintaining the temperature at 26 \(^\circ \)C, the voltage is turned on and the dynamics of vortex nucleation and annihilation are recorded. Figure 2 depicts the temporal evolution of the observed umbilical defects. To figure out vortex evolution, we have considered a voltage sweep between 9.0 Vpp and 30.0 Vpp. Likewise, keeping the voltage at 15 Vpp it is switched on and sweeping the temperature between 25 and 80\( ^\circ \)C, the dynamics of vortex nucleation is analyzed. From the chart in Fig. 2a, we infer that there is an abrupt process of vortex nucleation. Once the voltage is turned on, we immediately observe the appearance of domains. These domains are separated by interfaces that are recognized by the camera. All these different and complicated domains are a consequence of inert thermal fluctuations and spatial inhomogeneity (spacer and cell imperfections), which cause the molecules to orient themselves in different directions transverse to the applied electric field. Later, the domain interfaces are destabilized, through the emergence of vortices. The above process occurs in fractions of a second. Hence, vortices quickly emerge, as illustrated in Fig. 2. Once established a vortex gas, the vortices are subsequently annihilated by pairs of opposite charges (see insets in Fig. 2b), generating a coarsening processes characterized by a power law [46].

In brief, once the voltage is applied to the nematic liquid crystal cell, vortices are generated rapidly by thermal agitation and evolve through a pair interaction process.

Fig. 2
figure 2

Nucleation and evolution of umbilical defects in a nematic liquid crystal cell driven by an electric field. a Experimental temporal evolution of the number of vortices as a function of time. The painted and unpainted region accounts for the vortex nucleation and annihilation regime. b Panels account for a temporal sequence of snapshots of a liquid crystal cell driven by an electric field, under cross-circular polarizers, and constant temperature (\(t_1=0\) s, \(t_2=1\) s, \(t_3=4\) s, and \( t_4=7\) s). c Numerical temporal sequence of polarized field \(\varPsi (\mathbf {r},t)=Re(A)Im(A)\) obtained by the numerical simulations of the stochastic Ginzburg–Landau Eq. (4) with \(\mu =1.0\), \(\delta =0.0\), and \(T=0.01\) (\(t_1<t_2<t_3<t_4\))

Full size image

3 Theoretical description of the vortices nucleation

Nematic liquid crystals are a state of the matter characterized by present molecular orientation, but not a positional order [41, 42]. Considering a fixed temperature, this molecular orientation is characterized and described by the normalized director vector field \(\mathbf {n}(\mathbf {r},t)\) [41, 42]. The dynamics of the director \(\mathbf {n}\) satisfies a Frank–Oseen free energy minimization principle [41, 42]

$$\begin{aligned} \mathcal{{F}}[\mathbf {n}]= \int&\left( \frac{K_1}{2} (\mathbf {\nabla }\cdot \mathbf {n})^2+\frac{K_2}{2} (\mathbf {n} \cdot \mathbf {\nabla }\times \mathbf {n})^2 \right. \nonumber \\&+\left. \frac{K_3}{2} (\mathbf {n} \times \mathbf {\nabla }\times \mathbf {n})^2 + \frac{\epsilon _a}{2} (\mathbf {E} \cdot \mathbf {n})^2 \right) dV, \end{aligned}$$
(1)

with the restriction \(|\mathbf {n}|^2=1\), where \(K_1\), \(K_2\), and \(K_3\) are the elastic constants that account for the splay, twist, and bend deformation of the liquid crystals, respectively. \(\epsilon _a\) is the anisotropic dielectric constant, and \(\mathbf {E}\) is an electric field. Hence, the director equation reads [41, 42]

$$\begin{aligned} \gamma \mathbf {n} \times \frac{\partial \mathbf {n}}{\partial t}=- \mathbf {n} \times \frac{\delta \mathcal{{F}}}{\delta \mathbf {n}}, \end{aligned}$$
(2)

where \(\gamma \) is the rotation viscosity.

When one considers a nematic liquid crystal cell with homeotropic anchoring (molecules are oriented perpendicular to the walls), as a result of elastic interaction, all molecules are oriented orthogonal to the wall cells. Hence, the homeotropic state satisfies \(\mathbf {n}=\hat{z}\), where \(\hat{z}\) accounts for the unitary vector orthogonal to the wall cells. In the case that the liquid crystal has a negative anisotropic dielectric constant (\(\epsilon _a<0\)), when applying a sufficiently large vertical electric field \(\mathbf {E}=\mathbf {E}_c=\sqrt{-K_3 \pi ^2/d^2 \epsilon _a} \hat{z}\), molecules become misaligned with the direction of the electric field, reorientation instability [41, 42, 44]. This instability is known as the Freédericksz transition [44]. Close to the orientational instability of molecules, the director can be approached by [27]

$$\begin{aligned} \mathbf {n} (r,\theta ,z)\approx \left( \begin{array}{c} u(r,\theta ,t)\sin ({\pi z \over d})\\ w(r,\theta ,t)\sin ({\pi z \over d})\\ 1-\frac{(u^{2}+w^{2})}{2}\sin ^{2}({\pi z \over d}) \end{array} \right) , \end{aligned}$$
(3)

where d is the thickness of the cell and \(\{r,\theta , z\}\) are the cylindrical coordinates. Introducing the complex order parameter \(A=u+i w\) in the director equation (2) close to the reorientational instability and imposing the solvability condition for small director corrections after straightforward calculations, the amplitude equation of the order parameter reads (the stochastic Ginzburg–Landau equation) [27, 45, 47]

$$\begin{aligned} \partial _t A=\mu A- a|A|^2A+\nabla ^2A+\delta \partial _{\eta ,\eta }\bar{A}+\sqrt{T}\zeta (\mathbf {r},t), \end{aligned}$$
(4)

where the complex field \(A(\mathbf {r},t)\) accounts for the amplitude of the critical elastic mode that describes the deviation of the molecular director with respect to the vertical direction. \(\bar{A}\) accounts for the complex conjugate of A. \(\mu \) is the bifurcation parameter that is proportional to the voltage minus the critical Frédericksz voltage \(V_{FT}\equiv \sqrt{ K_3\pi ^2 / |\epsilon _a |}\) [27, 45, 47], which is related to the physical parameters as follows:

$$\begin{aligned} \mu =-K_3\frac{\pi ^2}{d^2}-\epsilon _a \mathbf {E}_c^2={ K_3\frac{\pi ^2 }{d^2}\left( \frac{V^2}{V_{FT}^2}-1\right) }, \end{aligned}$$
(5)

where d is the cell thickness and \(V=-||\mathbf {E}||/d\) is the voltage applied to the liquid crystal cell. The temporal and spatial scales are in units of rotation viscosity \(\gamma \) and elastic constants \(K_1+K_2\), respectively. \(\delta =K_1-K_2/(K_1+K_2)\) is the parameter that accounts for the elastic anisotropy of the nematic liquid crystal. \(\partial _\eta \equiv \partial _x+i\partial _y\) is the Wirtinger differential operator; note that the Laplacian operator satisfies \(\nabla ^2=\partial _{\eta ,\bar{\eta }}\). \(a=-K_3\pi ^2/d^2 4-3 \epsilon _a \mathbf {E}^2/4\) accounts for the nonlinear saturation coefficient. Our system presents noise due to the inherent fluctuations of the liquid crystal cell as a result of thermal fluctuations and noise in the electrical control and measurement system; particularly, the latter is difficult to control. Hence, we have included an additive noise in the amplitude Eq. (4), where \(\zeta (\mathbf {r},t)\) is a Gaussian white noise with zero mean value \(\langle \zeta \rangle =0\) and correlation \(\langle \zeta (\mathbf {r},t) \bar{\zeta }(\mathbf {r}',t') \rangle =\delta (t-t')\delta (\mathbf {r}-\mathbf {r}')\). T accounts for the noise intensity level. A detailed derivation of the model Eq. (4) and its parameters from the dynamics of the director is presented in Ref. [27]. Note that the bifurcation parameter \(\mu \) close to the Fréedericksz voltage behaves linearly, and as one increases the voltage, this parameter depends nonlinearly on it.

3.1 Theoretical vortices nucleation

For \(\mu \leqslant 0\), the Ginzburg–Landau Eq. (4) has a null solution \(A=0\) as a stable equilibrium, which corresponds to that the molecules are not reoriented, that is, homeotropic state is the stable configuration. For \(\mu > 0\), the homeotropic state \(A=0\) becomes unstable by means of a degenerate pitchfork bifurcation, giving rise to the appearance of vortices [47]. This instability is a second-order transition that originates different domains of equilibria \(A=\sqrt{\mu /a}e^{i \theta _0}\) where \(\theta _0\) is an arbitrary constant. This instability is well known as the Fréedericksz transition [48]. In this regime of parameters, the stochastic fluctuations induce different domains connected by point defects (phase singularities). Figure 2b shows the emergence of vortices in model Eq. (4) as a result of stochastic fluctuations. To compare with the experimental observations, Fig. 2b shows a color map of the auxiliary field \(\varPsi \equiv Re(A)Im(A)\), usually called the polarization field [27]. Note that \(\varPsi (\mathbf {r},t)\) vanishes for any of nullclines of A, \(Re(A)=0\) or \(Im(A)=0\). The intersection of two nullclines, black fringes in Fig. 2b, accounts for a vortex. As in the experiment, initially the noise nucleates a large number of vortices (see the inset \(t_1\) in Fig. 2b), which are subsequently annihilated by opposite pairs. The dynamics of vortex annihilation followed a coarsening process [3], which is illustrated in the sequence of colormaps in Fig. 2b. It is important to note that the amplitude equation does not fully describe all the dynamics observed experimentally. In particular, model Eq. (4) does not account for the initial creation of domains. However, it gives an adequate description of the vortices and their respective dynamics. Numerical simulations of the model Eq. (4) were implemented using a finite differences scheme in space that uses a centered stencil of five grid points with Runge–Kutta order-4 algorithm, with a \(500 \times 500\) points grid temporal step d\(t=0.0004\) and Neumann boundary conditions.

Fig. 3
figure 3

The number of defects in a given instant as a function of the bifurcation parameter. a The number of defects obtained from numerical simulations of Eq. (4) with \(\mu =1.0\) and a=1, different anisotropy \(\delta \) and intensity of the level of noise T at \(t=12\) (top panel) and \(t=60\) (bottom panel). The points with a bar account for mean value and standard deviation obtained after carrying out for each parameter 30 realizations. The continuous curves account for the linear trend exhibited by the numerical data. b Number of umbilical defects as a function of the driven voltage at \(t=0.5\) s (top panel) and \(t=1.0\) s (bottom panel). The points with a bar account for mean value and standard deviation divided by the square root of the realization number of measurements, which were obtained after five experimental realizations. The dashed curves (linear fits) account for the linear trend exhibited by the experimental data. In the lower panel, two zones have also been considered in which a parabolic one (local fit 1) follows a linear fit (local fit 2)

Full size image

Numerically, we have monitored the number of vortices at a given instant as a function of the bifurcation parameter \(\mu \). Figure 3a summarizes the results found. From these charts, we infer that the number of vortices grows to a good approximation linearly with the bifurcation parameter. Likewise, we note that this behavior is not substantively modified when we change the anisotropy \(\delta \). To compare and validate this numerical result, we have experimentally studied the number of umbilical defects N at an instant as a function of the voltage applied to the liquid crystal sample. We found that the number of defects grows with the voltage, which shows a qualitative agreement with the numerical results (cf. Fig. 3b). From these experimental charts, one can infer that the tendency to the number of defects increases as a function of the applied voltage. For an instant of premature elapsed time, we observe a trend of the linear type (see the top panel of cf. Fig. 3b); however, we observe a more nonlinear trend as a function of applied voltage for longer elapsed times (see the bottom panel of cf. Fig. 3b). This may be a consequence of the strong nonlinear response of the system that we have ignored in our simple model, which is approximated by taking the first dominant nonlinearities [cf. Eq. (4)]. The dependency of these high nonlinear terms and the voltage has a complex relation, as illustrated by the cubic coefficient formula (4).

The defects emerge from the homeotropic state, due to the inherent fluctuations of the system. The imperfections in the experiment, electronic noise, and elements ignored in our theory, such as black flow and movements of charges, may be responsible for the differences in fine-tuning between simulations and experiments.

3.2 Statistical law of vortex nucleation

To figure out the nucleation process, we approximate the model Eq. (4) by its deterministic linear part and consider the Fourier mode decomposition

$$\begin{aligned} A(x,y,t)=A_k e^{\sigma t+i(k_x x+k_y y)}, \end{aligned}$$
(6)

after straightforward calculations, we get

$$\begin{aligned} \sigma =\mu -k_x^2(1+\delta )-k_y^2(1-\delta )\pm 2i \delta k_x k_y, \end{aligned}$$
(7)

where \(Re[\sigma ]\equiv \mu -k_x^2(1+\delta )-k_y^2(1-\delta )\) is the growth rate mode, and \(k_x\) and \(k_y\) are wavenumber modes in the horizontal directions. The \(Im[\sigma ]=\pm 2 \delta k_x k_y\) accounts for the dispersion relation. The condition \(Re[\sigma (k_x,k_y)]>0\) corresponds to unstable spatial modes. Notice that white noise is characterized by excited in the same manner all modes [49]. Indeed, the stochastic fluctuations of a white noise on average excite all spatial modes in the same manner. The boundary conditions and geometric dimensions of the system determine the wavenumbers of modes. For simplicity, if we consider periodic boundary conditions and a square domain wavenumbers take the form \(k_x=2\pi n/L\) and \(k_y=2\pi m/L\), where L is the size of the box and \(\{n, m\}\) are integer numbers. Then, the amplitude of a mode (n, m) can be written in the form

$$\begin{aligned}&Re\left[ A_{(n,m)}\right] \nonumber \\&\quad =a_0 \cos \left( \frac{2\pi n}{L} x+\phi _0 \right) \sin \left( \frac{2\pi m}{L} y+\phi _1\right) , \end{aligned}$$
(8)

where \(a_0\), \(\phi _0\), and \(\phi _1\) are constants characterizing the spatial mode. The nodes of the spatial modes correspond to zeros of the amplitude, \(A_{(n,m)}=0\); that is, these nodes correspond to phase singularities for the spatial modes. The spatial mode with the maximum number of vortices (nodes) corresponds to \(Re(\sigma ) = 0\). To calculate this maximum number of vortices, we proceed by calculating the number of nodes in one direction

$$\begin{aligned} Re[\sigma (n^c,k_y=0)]=\mu -\left( \frac{2\pi n^c}{L}\right) ^2(1+\delta )=0. \end{aligned}$$
(9)

Then, the critical number of nodes is

$$\begin{aligned} n^c=\left( \frac{L}{2\pi } \right) \sqrt{\frac{\mu }{(1+\delta )}}. \end{aligned}$$
(10)

Applying the same condition in the other direction, that is, \(Re[\sigma (k_x=0,m^c)]=0\), we get

$$\begin{aligned} m^c=\left( \frac{L}{2\pi } \right) \sqrt{\frac{\mu }{(1-\delta )}}. \end{aligned}$$
(11)

Finally, we determine the maximum number of vortices (nodes) of the critical spatial modes by

$$\begin{aligned} N = n^cm^c=\left( \frac{L}{2\pi } \right) ^2\frac{\mu }{\sqrt{(1-\delta ^2)}}. \end{aligned}$$
(12)
Fig. 4
figure 4

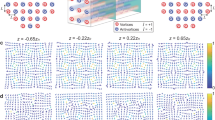
The number of defects in a given instant as a function of the anisotropic parameter \(\delta \) obtained from numerical simulations of Eq. (4) with a=1 at \(t=12\) (a) and \(t=60\) (b). The points with a bar account for mean value and standard deviation obtained after carrying out for each parameter 20 realizations. The continuous curves were obtained using the fitting function \(N=A/(1-\delta ^2)^b+C\). The simulations and fitting parameters are specified in insets. c The number of defects in a given moment as a function of the noise intensity level T. d Umbilical defects number as a function of the temperature after 1 second of applying voltage 15 Vpp. The points with a bar account for mean value and standard deviation divided by the square root of the realization number of measurements, which were obtained after carrying out five experimental realizations. The dashed curve (linear fit) accounts for the linear trend exhibited by the experimental data

Full size image

Notice that all other unstable modes also have a number of nodes proportional to the previous expression multiplied by a proper fraction. As we have mentioned, the stochastic fluctuations generated by white noise excite both the stable and unstable modes in the same manner. On the other hand, the stable modes are damped, and the unstable ones grow as a consequence of the linear dynamics of the model Eq. (4). Hence, the number of vortices is proportional to the previous expression, in particular to the bifurcation parameter, which is consistent with what is observed numerically and experimentally (see Fig. 3). Then, Formula (12) predicts that the number of vortices grows linearly with the voltage close to the Frédericksz voltage (experimentally \(V_{FT}= 6.57 \) Vpp). This result is consistent with the linear fit considered in Figure 3b (upper panel). For higher voltage values, it has nonlinear corrections due to nonlinear saturation. However, for longer times, the interaction of the vortices and their dependence on the voltage change this tendency, which could explain what was observed experimentally (lower panel). A more detailed study of this phenomenon is in progress.

Likewise, we note that expression (12) predicts that the number of vortices diverges when \(\delta \) tends to 1. This result is natural from a physical point of view, because if \(\delta ^2 = 1\), then some of the elastic constants diverge or disappear, which corresponds to a transition from a nematic liquid crystal to another matter state [41]. Figure 4 shows the number of vortices at a given moment as a function of the anisotropy parameter \(\delta \). This type of result shows an excellent agreement with analytical expression (12). To study its trend, we have used a more general fitting function of the form \(N=A/(1-\delta ^2)^b+C\), which can take into account the nonlinear effects and errors of the vortex measurement method. From charts, Fig. 4a, b, notices that the critical exponent b evaluated at higher times is dissimilar that predicted theoretically. This effect is due to the fact that nonlinear terms begin to play a non-negligible role. Note that Formula (12) only contains the effects of linear theory. Experimentally, we cannot carry out a similar analysis since elastic anisotropy \(\delta \) is determined by intermolecular interactions that we cannot control. One possibility of carrying out the experimental study of the dependence of the number of vortices as a function of anisotropy \(N(\delta )\) would be to use different liquid crystals with different elastic constants. However, different liquid crystals have different rotational viscosities and dielectric anisotropic constants [41,42,43]; therefore, the noise level would change, not allowing an adequate analysis. Likewise, one could study the nucleation of vortices close to a nematic–smectic transition of the liquid crystal, where the constants \(K_2\) and \(K_3\) increase significantly [41]. However, the more overwhelming growth of \(K_3\) generates important modifications in the size of the vortex and in the voltage applied to generate the orientation transition, producing, in turn, an uncontrolled increase in noise in the system. Therefore, it makes the study of vortex nucleation equally complex.

Formula (12) does not depend on the noise intensity level T. Indeed, the number of vortices (nodes) does not depend on the intensity of the noise; however, their presence is essential to stimulate unstable modes. Figure 4c shows that effectively the noise intensity level does not affect the number of vortices created. When the noise intensity is large, \(T>20\), the deterministic linear theory is no longer valid and the vortices are no longer related to the linear modes (see Fig. 4c). Indeed, for these levels of noise values the system can be approximated by a purely stochastic one. Experimentally to study the effect of the inherent fluctuations of our physical system, we have studied the number of vortices in a given moment as a function of temperature. Figure 4d summarizes the results found. We infer that there is a tendency to increase the number of vortices with temperature. The increase in temperature has a double effect; on the one hand, it increases the thermal fluctuations and, in turn, modifies the elastic constants [50]. This combined effect is responsible for the increase found in the number of vortices.

4 Conclusions and remarks

During the last decades, much effort has been focused on understanding topological defects and their dynamics. However, the emergency processes of these intriguing solutions have been scarcely addressed. Based on linear theory and stochastic fluctuations, we can establish that the matter vortices are a consequence of the different excited unstable spatial modes. The above is summarized by Formula (12) multiplied by a constant that accounts for the effect of all unstable modes. Therefore, we can establish that the number of vortices grows proportional to the bifurcation parameter; it is inverse to the square of the elastic anisotropy and does not depend on the level of the noise intensity. Experimental observations show a qualitative agreement with theoretical findings. Discrepancies between experimental observations and theoretical predictions are mainly due to vortex interactions, spatial inhomogeneities, imperfections, and glass beads (spacers), inherent in all experiments, which are not considered in our simplified theory. Incorporating these effects in theory and their respective experimental analysis is in progress.

An interesting result of Formula (12) is the divergence of the nucleation of vortices when the anisotropy \(\delta = 1\). Experimentally carried out, this study is complex since the modifications of \(\delta \) (change of liquid crystal, nematic–smectic transitions) entail strong fluctuations due to the fluctuation–dissipation relationship.

The number of vortices for long times, where the nonlinear theory governs the dynamics of the system, can no longer be given by Formula (12) since the interaction of the vortex pair begins to annihilate vortices, as illustrated in Fig. 2. The complete expression of the number of vortices as a function of time is an open problem.