Ghost attractor in fractional order blinking system and its application

Abstract

In this paper, the occurrence of ghost attractor is verified in three cases of a proposed fractional order Rössler blinking system. Firstly, the dynamical behaviors of the short memory fractional order prototype-4 Rössler system with Chua’s diode are explored via bifurcation diagrams and Lyapunov exponents. It is depicted that this system exhibits a variety of dynamics including limit cycles, period doubling and chaos. Then, a proposed non-autonomous fractional order Rössler blinking system is introduced. Numerical simulations are employed to confirm the existence of ghost attractors at specific cases which involve very fast switching time between two composing autonomous fractional subsystems. It is found that the presented fractional order blinking system is very sensitive to system parameters, initial conditions, and stochastic process parameters. Thus, the induced chaotic ghost attractor is utilized in a suggested ghost attractor-based chaotic image encryption scheme for first time. Finally, a detailed security analysis is carried out and reveals that the proposed image cryptosystem is immune against different types of attacks such as differential attacks, brute force attacks, cropping and statistical attacks.

1 Introduction

In recent decades, the applications of fractional calculus in the area of dynamical systems have attracted great interest. Indeed, many theoretical and experimental studies indicated that fractional order derivatives have many advantages in modeling intricate systems in contrast to conventional treatment using integer order calculus [1]. The essential reason is that fractional derivative possesses hereditary properties and can mimic memory effects in some nonlinear systems [2]. So, fractional order differential equations have successfully modeled many real applications, such as neural networks [3, 4], biological systems [5, 6], financial systems [7, 8], secure communications [9], electronic circuit models [10,11,12], nonlinear mechanical problems [13, 14] and many more. The fractional order differential equations with chaotic behaviors can be physically realized using op-amp-based approximations of fractional-order integrators or embedded circuits uses FPGAs or DSPs [15,16,17,18]. Fractional order switched system which includes switching parameter based on logical rule has recently drawn the attention of several researchers [19, 20].

Switched system is a hybrid dynamical system that is composed of a number of dynamical subsystems and has a specific rule to control the switching between its subsystems with time [21, 22]. Stochastic processes are usually employed to externally drive these blinking non-autonomous systems at the specified values of switching time scales. More specifically, there is a predetermined fixed period of time $\tau$ through which the dynamics of blinking system is determined by one of its composing subsystems then a random switching to another subsystem is done for the same time interval $\tau$ and the process continues in this way as long as the blinking system is running. The blinking systems have appeared in many realistic models in biology, the internet networks, and circuits like power converters where the connections are randomly switched on and off in time. Assuming that the blinking system has n subsystems, the coupling between subsystems in each time interval of duration $\tau$ is done stochastically with probability $p_i, i=1,2,...,n$.

In blinking systems, there are two time-scales belonging to the stochastic process and the blinking system itself. In fast-switching blinking systems, the time scale of stochastic process is much faster than intrinsic time scale of the dynamical subsystems of the blinking system. This means that the switching is considered to be fast according to its value in comparison with intrinsic time scale of the blinking system [23]. The switching occurs randomly and independently for different time intervals and connections in the system. It is found that the blinking systems can exhibit non-trivial and unexpected nonlinear behaviors which surprisingly do not exist in each of the composing subsystems [24]. The averaged systems associated to the blinking systems which are given by the expectation of stochastic variables have attractors called ghost attractors of the blinking systems if they are different from the set of attractors in the composing subsystems [25].

Up to now, the study and investigation of blinking systems have been reported in few works. For example, Belykh et al. [26] showed an example of a blinking system and the corresponding synchronization in small-world networks. Barabash and Belykh [24] proved the existence of ghost attractors for certain parameter ranges in the blinking piecewise-linear Lorenz-type system being unexpectedly different with respect to the attractors of composing systems. Levanova et al. [25] obtained a ghost attractor in blinking Lorenz and Hindmarsh-Rose systems in spite of the trivial dynamics of the associated subsystems at selected values of parameters which is defined by stable equilibrium points. Hasler et al. [27], investigated the dynamics, finite time properties and asymptotic properties of a stochastically blinking system. The authors proven that any trajectory of the blinking system closely follows the trajectory of the averaged system, starting from the same initial condition, during a certain interval of time T when the switching is fast enough. They reported an explicit relation between the distance between the two trajectories, the switching time, and the length of the time interval T. Hasler et al. [28], discussed the relation between the trajectories of the averaged and blinking systems when time goes to infinity. They demonstrated that two trajectories usually cannot stay together, but they may converge to the same attractor. The work in [27, 28] can be extended to fractional order in separate paper as a future work.

In recent years, because of the rapid development of multimedia technologies and the increased exchange of multimedia data over the internet, the need to devise effective tools to make the transmitted multimedia secured and well preserved is becoming increasingly important [29]. Images have main features such as redundancy, a strong correlation between adjacent pixels, and a large amount of data. According to these features, the need to encryption schemes suitable for image encryption rather than traditional encryption algorithms such as DES, AES and RSA [30] for text encryption is required. In the last decades, researchers have developed algorithms based on chaos theory that are suitable for images encryption [31,32,33]. Chaotic systems are extremely sensitive to control parameters and initial values. In additions, inherent characteristics such as unpredictability, pseudo-randomness and ergodicity are employed for keystream generation [34, 35]. The required cryptographic characteristics through image diffusion and confusion can be achieved through the fascinating features of the image encryption techniques relying on chaotic systems [36]. The applicability of the fractional order chaotic systems and fractional order chaotic maps to image encryption are investigated to further enhance the security of the cryptosystem and increase key-space in several articles [37,38,39,40]. Chaos based encryption algorithms can be used in authentication systems for safely storing vital images in database [41].

It is worth mentioning that all the aforementioned works are only concerned with blinking systems in integer order forms. Inspired by the above discussion, the main contribution of this paper is to study fractional order blinking system composed of two fractional order Rössler prototype-4 autonomous continuous time subsystems based on Chua’s diode nonlinearity. Random switching between internal parameters of the proposed system occurs stochastically and evolves over time. To the best of authors knowledge, this first time to explore of the ghost attractor in fractional order blinking systems. This work is organized such that firstly, the short memory fractional order Rössler system is studied using Lyapunov spectrum, bifurcation diagrams. Secondly, a fractional order blinking system is presented in three cases involving different values of intrinsic parameters of the fractional order Rössler system. The randomly and rapidly switching time between two values of fractional blinking system parameter is verified to yield a chaotic attractor which goes near the chaotic ghost attractor of the associated fractional order averaged system. Detailed numerical simulations are utilized to explore chaotic ghost attractors. Thirdly, fractional order blinking system is considered for the first time to present an image encryption scheme to improve cryptosystem security and further increase the secret key space. Finally, the proposed scheme is analyzed by several security tests to show the immunity against different attacks.

The layout of this paper is structure as follows: The mathematical preliminaries and definitions are summarized in Sect. 2. The fractional order blinking Rössler system is introduced in Sect. 3 along with its detailed numerical investigation. In Sect. 4, the chaotic image encryption scheme based on fractional order blinking system is proposed and the security analysis is conducted. The discussion and future work are concluded in Sect. 5.

2 Mathematical preliminaries

This section addresses the definition of fractional order Caputo derivative, the definition of short memory fractional differential equation, the definition of fractional blinking system and the associate fractional order averaged system.

Recently, many definitions for fractional order derivatives have been well-established. We focus on the Caputo fractional derivative [1]. The Caputo fractional derivative of order $\alpha$ of function f(t) is defined as follows

$$\begin{aligned} ^{C}_{t_{0}}D^{\alpha }_{t} f(t) = \frac{1}{\Gamma (1-\alpha )}\int ^{t}_{t_{0}}\frac{\grave{f}(s)}{(t-s)^{\alpha }} ds, \qquad 0< \alpha < 1,\nonumber \\ \end{aligned}$$

(1)

where $\Gamma (.)$ is the Gamma function.

The standard fractional order system in Caputo sense is defined as follows [42]

$$\begin{aligned} ^{C}_{t_{0}}D_{t}^{\alpha } x(t) = f(t,x(t)), \qquad x(t_{0}) = x_{0}, \end{aligned}$$

(2)

where $t_{0}$ is a fixed starting point of the fractional derivative.

2.1 Definition of short memory fractional order system

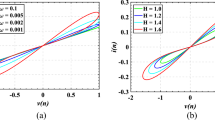
The standard fractional order system (2) holds the memory from $t = t_{0}$. The weight coefficients of $x(t_{0})$ become smaller as the time t increases. The meaning of short memory is summarized in Fig. 1 [43].

Fig. 1

Short memory fractional order system

Let the interval $[t_{0}, T]$ is divided to m subinterval with length nh and n is an integer number such that $[T - t_{0}] = [t_{0}, t_{l}] \cup [t_{l}, t_{2}] \cup ... \cup [t_{(m-1)}, t_{m}], h = (T - t_{0})/N$. In the first subinterval $t \in [t_{0},t_{1}]$, the fractional order system is described as $^{C}_{t_{0}}D_{t}^{\alpha } x(t) = f(t,x)$, then in the second subinterval $t \in [t_{1},t_{2}]$, the fractional order system is described as $^{C}_{t_{1}}D_{t}^{\alpha } x(t) = f(t,x)$ so, the intial point is updated to $t_{1}$ and so on until the last subinterval.

Subsequently, the short memory fractional order system which holds short memory effect is defined as follows [43]

$$\begin{aligned} \begin{aligned} ^{C}_{t_{*}}D_{t}^{\alpha } x(t)&= f(t,x), \qquad x(t_{0}) = x_{0},\\ t_{*}&= t_{k}, \quad t \in [t_{k}, \, , t_{k+1}], \, k=0,..., m-1. \end{aligned} \end{aligned}$$

(3)

The Eq. (3) has different initial points $t_{*}$ in the Caputo fractional derivative (1). This provides more freedom degrees in real-world applications.

2.2 Definition of the fractional order blinking system

The blinking system is presented in [27, 28] and it is defined in the form of time dependent ordinary differential equations. Here, we generalize the concept to the fractional order blinking system by defining it as

$$\begin{aligned} \begin{aligned} ^{C}_{t_{*}}D_{t}^{\alpha } x(t) = f(x(t) , s(t)),\qquad \qquad \qquad \qquad \qquad \\ x \in R^{N}, \qquad f: R^{N+M} \rightarrow R^{N}, \qquad s(t) \in \{0,1\}^{M}, \end{aligned}\nonumber \\ \end{aligned}$$

(4)

where $^{C}_{t_{*}}D_{t}^{\alpha }$ is a short memory derivative and the function s(t) is a binary random constant discrete scalar value such that $s^{i} = (s_{1}^{i},..., s_{M}^{i})$ with the probability $p_{i}$ at each $i^{th}$ time piecewise constant in the time interval $[i\tau , (i+1)\tau ]$ and $\tau$ is a constant switching period. All variables $s_{j}^{i}$ are random variables and independent and they take the value 1 with probability p and the value 0 with probability $1-p$. So, the switching sequence of the stochastic process is determined according to s(t) . Hence this system is considered as a special case of random dynamical systems and its solution also is a stochastic process. The signal $s_{i}$ can be viewed as a closing and opening eye lid therefore, the system (4) is called a blinking system. The trajectories of M autonomous systems are blinded together at $t = i \tau$ to consist the trajectories of system (4). In this type of system, there are two-time scales which are the one associated with the dynamical system itself and the other of the switching process. In this work, the switching process is considered to be much faster than the dynamical subsystems.

2.3 Definition of the fractional order averaged system

The fractional order averaged system associated with the fractional order blinking system (4) reads as

$$\begin{aligned} ^{C}_{t_{*}}D_{t}^{\alpha } x(t) = \Phi (x(t)), \end{aligned}$$

(5)

where

$$\begin{aligned} \Phi (x) = E (f (x, s)) = \sum _{s \in \{0,1\}^{M}} f(x,s) p_{s}, \end{aligned}$$

(6)

and E(f(x, s)) denotes the average or expected value of f(x, s) .

3 Proposed fractional order blinking systems

3.1 Fractional order prototype-4 Rössler system with short memory

We propose the following fractional order version of the prototype-4 Rössler system with short memory [44] as follows

$$\begin{aligned} \begin{aligned} ^{C}_{t_{*}}D_{t}^{\alpha } x&= y + q z, \quad \\ ^{C}_{t_{*}}D_{t}^{\alpha } y&= - \beta x , \quad \, \,\, \,\\ ^{C}_{t_{*}}D_{t}^{\alpha } z&= g(y)-\gamma z. \end{aligned} \end{aligned}$$

(7)

where $q, \beta$ and $\gamma$ have positive values and g(y) is a piecewise-linear function with definition as

$$\begin{aligned} g(y) = m_{1} y+ \dfrac{1}{2}(m_{0}-m_{1})(\arrowvert y+1 \arrowvert - \arrowvert y -1 \arrowvert ), \end{aligned}$$

(8)

where $m_{0}$ and $m_{1}$ are constants. Nonlinearity in (7) is known as a nonlinear component which called the Chua’s diode [45]. We call (7) a short memory fractional differential equation since the fractional derivative is defined from $t_{*}$ not from the fixed $t_{0}$ or 0.

3.1.1 Stability analysis

For the fractional order model (7), the phase space S can be divided into three linear subsets as follow:

$$\begin{aligned} S = \left\{ \begin{array}{ll} S_{-} = (x,y,z) &{} | \,\, y < -1 , \\ S_{0} = (x,y,z)&{} | \,\, -1 \le y \le 1 , \\ S_{+} = (x,y,z)&{} | \,\, y > 1 .\\ \end{array} \right. \end{aligned}$$

Let $D^{\alpha }_{t} x = D^{\alpha }_{t} y = D^{\alpha }_{t} z = 0$. The equilibrium points are studied so, the system Eq. (7) has three equilibrium points as $E_{\mp } =(0 , \mp q \upsilon , \pm \upsilon )$ and $E_{0} = (0,0,0)$, where $\upsilon = \frac{m_{1} - m_{0}}{q m_{1} + \gamma }$ with condition $\gamma \ne - q m_{1}$ to avoid infinite coordinates. The system has the next Jacobian matrix:

$$\begin{aligned} J = \begin{bmatrix} 0 &{} 1 &{} q \\ - \beta &{} 0 &{} 0 \\ 0 &{} m _{i}&{} -\gamma \end{bmatrix}, \end{aligned}$$

with $m _{i} = m _{0}$ in $S _{0}$ and $m _{i} = m _{1}$ in $S _{\mp }$. The Jacobian matrix has a characteristic equation as follow

$$\begin{aligned} H(\lambda ) = \lambda ^{3} + \gamma \lambda ^{2} + \beta \lambda + \beta (\gamma + q m_{i}). \end{aligned}$$

(9)

Based on the stability criterion of fractional Routh Hurwitz [46], if the system (7) has $|arg (\lambda _{i}(J))|> \dfrac{\alpha \pi }{2} , \forall \lambda _{i} , i = 1,2,3$ where $\lambda _{i}$ is an eigenvalue of matrix J then the system is locally asymptotically stable at the associated equilibrium point.

To get the stability region for system (7) depending on its parameter, we solve characteristic equation (9) and based on the stability condition $|arg (\lambda _{i}(J))|> \dfrac{\alpha \pi }{2} , \forall \lambda _{i} , i = 1,2,3$. The stability region for the system in the phase space $S_{0}$ and their dependance on different parameters are depicted in Fig. (2) and in the phase space $S_{\mp }$ is displayed in Fig. 3.

Fig. 2

The stability region for the fractional system in the phase space $S_{0}$

Fig. 3

The stability region for the fractional system in the phase space $S _{\mp }$

Fig. 4

Phase portrait for the system (7) with different parameter values. a $m_0 = -1.4, \gamma =2.2$, b $m_0 = -1.4, \gamma =0.65$, c $q= 0.2 , \gamma = 0.8$, d $q =4.2 , \gamma = 0.8$, e $m_1 = 0.3, \gamma =2.5$, (f) $m_1 = 0.3, \gamma =0.5$

To solve (7) numerically, starting from initial conditions at $t =0$ and updating initial conditions at each stage. We can get each subsystem as follows. For $t \in ( 0,t_{1})$ and the initial conditions $(x_{0},y_{0},z_{0})$ are known, we solve the following subsystem

$$\begin{aligned} \begin{aligned} ^{C}_{0}D_{t}^{\alpha } x&= y + q z, \quad \\ ^{C}_{0}D_{t}^{\alpha } y&= - \beta x, \quad \, \,\, \,\\ ^{C}_{0}D_{t}^{\alpha } z&= g(y)-\gamma z. \end{aligned} \end{aligned}$$

(10)

Then, for $t \in [ t_{k}, t_{k+1}]$ with $(x_{k},y_{k},z_{k})$ is known from the system on $[ t_{k-1}, t_{k}]$ and we get the subsystem

$$\begin{aligned} \begin{aligned} ^{C}_{t_{m-1}}D_{t}^{\alpha } x&= y + q z, \quad \\ ^{C}_{t_{m-1}}D_{t}^{\alpha } y&= - \beta x, \quad \, \,\, \,\\ ^{C}_{t_{m-1}}D_{t}^{\alpha } z&= g(y)-\gamma z. \end{aligned} \end{aligned}$$

(11)

We solve the system (7) numerically with some parameters values to confirm the stability region. In Fig. 2, the stability region based parameters on $m_0$ and $\gamma$ is verified by phase portrait with $m_0 = -1.4, \gamma =2.2$ and $m_0 = -1.4, \gamma =0.65$ as displayed in Fig. 4a and b, respectively. Also, the stability region based on parameters q and $\gamma$ is confirmed by phase portrait with $q= 0.2 , \gamma = 0.8$ and $q =4.2 , \gamma = 0.8$ as shown in Fig. 4c and d, respectively. In Fig. 3, the stability region based on parameters $m_1$ and $\gamma$ is verified by phase portrait with $m_1 = 0.3 ,\gamma =2.5$ and $m_1 = 0.3, \gamma =0.5$ as plotted in Fig. 4e and f, respectively.

We study the effect of varying parameter q in the interval [0, 4.5] as displayed in Fig. 7a and b. The system is stable in the interval [0, 0.7] then goes to 2- period doubling and 4- period doubling in the range [0.7, 1.9] after that the system exhibits chaotic behavior.

3.1.2 Influence of system parameters

The bifurcation strategies have been successfully deployed to handle nonlinear properties of complex systems. Different bifurcation parameters have been explored in this section to investigate the dynamical behaviors of the system (7). Firstly, all the system parameters are fixed at values $\alpha =0.98 , \gamma = 1 , m_{0} =-1.5 , m_{1} = 0.3 , q =3$ and we start analyzing the sensitivity of system by varying each parameter individually. Figure 5a and b show the bifurcation diagram and Lyapunov exponents spectrum, respectively, for bifurcation parameter $\beta$ in the range [0.2, 3]. For $0.4\le \beta \le 0.85$ there is 6- period doubling and $0.85\le \beta \le 3$ the system goes to chaos. By fixing $\beta = 1$ and varying parameter $\gamma$ in range [0.6, 3.6] , the bifurcation diagram and Lyapunov exponents plots are illustrated in Fig. 5c and d, respectively. In range [0.6, 1.3] the system exhibits chaotic behavior and goes to 4-period doubling then 2-period doubling in the range [1.3, 3.6] .

Fig. 5

a and b bifurcation diagram of the proposed fractional-order system and Lyapunov exponents, respectively, versus $\beta$ for $\beta \in [0.2,3]$. c and d bifurcation diagram of the proposed fractional-order system and Lyapunov exponents, respectively, versus $\gamma$ for $\gamma \in [0.6,3.6]$

Fig. 6

a and b bifurcation diagram of the proposed fractional-order system and Lyapunov exponents, respectively, versus $m_{0}$ for $m_{0} \in [-2,-0.5]$. c and d bifurcation diagram of the proposed fractional-order system and Lyapunov exponents, respectively, versus $m_{1}$ for $m_{1} \in [0,0.36]$

Fig. 7

a and b bifurcation diagram of the proposed fractional-order system and Lyapunov exponents, respectively, versus q for $q \in [0,4.5]$

Fig. 8

a and b bifurcation diagram of the proposed fractional-order system and Lyapunov exponents, respectively, versus $\alpha$ for $\alpha \in [0.5,1]$

Then, we fix $\gamma = 1$ and explore the parameter $m_{0}$ within range $-2 \le m_{0} \le -0.5$. It is noticed that from $m_{0} = -2$ to $m_{0} = -1.8$ and from $m_{0} = -1.6$ to $m_{0} = -0.75$ the system has chaotic behavior soon after that it tends to period doubling in two ranges $[-1.8,-1.6]$ and $[-0.75,-0.5]$ as displayed in Fig. 6a and b. In addition, the value of parameter $m_{0} = -1.5$ is fixed to analyze the effect of changing the value of parameter $m_{1}$ in range $0 \le m_{1} \le 0.36$. It can be seen from Fig. 6c and d that the system is stable in the interval [0, 0.01] then it undergoes period doubling within the interval [0.01, 0.07] until it reaches the chaos behavior in the interval $m_{1} \in [0.07, 0.36]$.

The fractional order $\alpha$ is now considered as the bifurcation parameter to show its effects on the dynamics of the proposed system (7). The dynamics of the system with varying fractional order $\alpha$ in the range 0.5 to 1 . We fix $q = 3$ and varying fractional order $\alpha$, the bifurcation diagram and Lyapunov exponents plots are obtained in Fig. 8a and b, respectively.

Fig. 9

Fractional order blinking system Case 1: phase portrait for first subsystem $R_{1}(q_{1} = 0.75)$

It is shown that from $\alpha = 0.5$ to $\alpha = 0.68$ it is a stable region. A cascade of period doublings in ranges [0.68, 0.78] and [0.875, 0.91] are observed. Then the system (7) shows chaotic dynamics over the ranges of $0.78 \le \alpha \le 0.875$ and $0.91 \le \alpha \le 1$.

In spite of the simplicity of system (7), the dynamical behaviors of this system are complex depending on the value of the bifurcation parameters. Firstly, unlike the case of limit cycle presence in integer order systems, the limit set of a solution trajectory of fractional order system cannot be a constant periodic solution of the system. In additions, the nonexistence of periodic solutions was proved in time-invariant fractional order systems in [47]. However, some examples were given where the solutions of the fractional order system are not periodic, but they asymptotically converge to periodic signals [48]. Summarizing these results, the limit cycle that appears in phase portrait of the fractional order system is not a solution of the system, but it attracts nearby solutions. Secondly, the fractional order blinking system and some aspects of nonlinear dynamics of the model will be investigated in the following subsections.

Fig. 10

Fractional order blinking system Case 1: phase portrait for second subsystem $R_{2}(q_{2} = 3.83)$

3.2 Fractional order blinking system

We propose fractional order blinking Rössler system R(q) with Chua’s diode non-linearity as follows

$$\begin{aligned} \begin{aligned} {}^{C}_{t_{*}}D_{t}^{\alpha } x&= y + q(t) z, \\ {}^{C}_{t_{*}}D_{t}^{\alpha } y&= - \beta x, \quad \, \,\, \,\\ {}^{C}_{t_{*}}D_{t}^{\alpha } z&= g(y)-\gamma z, \end{aligned} \end{aligned}$$

(12)

with time-varying parameter $q(t) = (q_{1}- q_{2}) s(t) + q_{2}$. Based on random sequence, the parameter s(t) switches in the non-autonomous system (12) between two subsystem $R_{1}(q_{1})$ for $s =1$ with probability $p_{1}$ and subsystem $R_{2}(q_{2})$ for $s = 0$ with probability $p_{2}$.

Fig. 11

Fractional order blinking system Case 1: phase portrait for averaged system $q_{avg} = p_{1}*q_{1} + p_{2}*q_{2}$ at $q_{avg} = 3.1524$

Fig. 12

Fractional order blinking System Case 1: phase portrait for switching $R{s}(q_{1},q_{2})$ and averaged system $R{a}(q_{avg})$

Fig. 13

Fractional order blinking system Case 1: time series for first subsystem, second subsystem, averaged system and blinking system

For sufficiently fast switching time, it is expected that the fractional order blinking system follows the corresponding fractional order averaged system as the case of integer order systems studied previously in literature. The emerging attractor of fractional order averaged system is referred to as ghost attractor if it is different from the set of attractors in the subsystems of corresponding fractional order blinking system. The careful numerical simulation will indicate that when the switching is very fast, the trajectory of the fractional order blinking system evolves rapidly towards the neighborhood of the ghost attractor and then stays most of the time close to ghost attractor.

3.3 Numerical simulation for fractional order blinking system

In this subsection, the numerical simulations have been presented via phase portraits for three cases of fractional order blinking system based on different values for parameter q as follows

3.3.1 Case 1

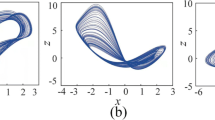
In first case, the solution trajectory of the system (7) is attracted to periodic orbit in phase space at $q = 0.75$ as shown in Fig. 9 and at $q = 3.83$ as shown in Fig. 10 with other parameters values $\beta = 1,\gamma =1, m_{0} = -1.5 , m_{1} = 0.3, \alpha =0.98$ and $T= 500$, using a unit step $h =0.005$. Accordingly, the blinking system (12) switches in random between first subsystem $R_{1}(q_{1} = 0.75)$ with probability $p_{1} = \frac{22}{100}$ and second subsystem $R_{2}(q_{2} = 3.83)$ with probability $p_{2} = \frac{78}{100}$. The fractional order averaged autonomous system associated with the fractional order blinking system (12) where E(R(q, s(t))) is the expected value of R(q, s(t)) is $R_{a}( q_{avg} = 3.1524)$ where $q_{avg} = p_{1}*q_{1} + p_{2}*q_{2}$. The induced interesting ghost attractor is shown in Fig. 11. It is noticed that the trajectory of blinking system moves around the ghost attractor and after sufficient time remains close to the ghost attractor which means that it reaches a small neighborhood of the ghost attractor with appropriate fast switching. Indeed, the chaotic attractor of the fractional order averaged system represents the ghost attractor for the fractional order blinking system as shown in Fig. 12. Time series from the systems for first subsystem, second subsystem, averaged system and switching system are all depicted in Fig. 13.

Fig. 14

Fractional order blinking system Case 2: phase portrait for the first subsystem $R_{1}(q_{1} = 1.8)$

Fig. 15

Fractional order blinking system Case 2: phase portrait for the second subsystem $R_{2}(q_{2} = 3.34)$

Fig. 16

Fractional order blinking system Case 2: phase portrait for averaged autonomous system $q_{avg} = p_{1}*q_{1} + p_{2}*q_{2}$ with $q_{avg} = 2.878$

3.3.2 Case 2

In second case, the system (7) has like a periodic behavior at $q = 1.8$ as shown in Fig. 14 and at $q = 3.34$ as shown in Fig. 15 with other parameters values as in Case 1 except $m_{1} =0.35$. Thus, the blinking system (12) randomly switches between first subsystem $R_{1}(q_{1} = 1.8)$ with probability $p_{1} = \frac{30}{100}$ and second subsystem $R_{2}(q_{2} = 3.34)$ with probability $p_{2} = \frac{70}{100}$. The fractional order averaged system associated with the fractional order blinking system (12) where E(R(q, s(t))) is the expected value of R(q, s(t)) as $R_{a}(q_{avg} = 2.878)$ where $q_{avg} = p_{1}*q_{1} + p_{2}*q_{2}$. The ghost attractor of fractional order averaged system is shown in Fig. 16. For fast switching time, Fig. 17 displays the trajectory of fractional order blinking system reaches a small neighborhood of the ghost attractor and remains there. Time series of the solutions of first subsystem, second subsystem, averaged system and blinking system are depicted in Fig. 18.

Fig. 17

Fractional order blinking system Case 2: phase portrait for switching $R{s}(q_{1},q_{2})$ and averaged system $R{a}(q_{avg})$

Fig. 18

Fractional order blinking system Case 2: time series for first subsystem, second subsystem, averaged system and blinking system

Fig. 19

Fractional order blinking system Case 3: phase portrait for the first subsystem $R_{1}(q_{1} = 0.8, \gamma _{1} = 2.4)$

Fig. 20

Fractional order blinking system Case 3: phase portrait for second subsystem $R_{2}(q_{2} = 2.58, \gamma _{2} = 0.8)$

Fig. 21

Fractional order blinking system Case 3: phase portrait for averaged system $q_{avg} = p_{1}*q_{1} + p_{2}*q_{2}$ with $q_{avg} = 2.4643$ and $\gamma _{avg} = p_{1}*\gamma _{1} + p_{2}*\gamma _{2}$ with $\gamma _{avg} = 0.904$

3.3.3 Case 3

In third case, the system (7) has a stable equilibrium point at $q = 0.8 , \gamma _{1} = 2.4$ as shown in Fig. 19 and the solution trajectory of the system is attracted to periodic orbit in phase space at $q = 2.58 , \gamma _{2} = 0.8$ as shown in Fig. 20 with other parameters values $\beta = 1,\gamma =1, m_{0} = -1.5 , m_{1} = 0.3, \alpha =0.98$ and $T= 700$, using a unit step $h =0.005$. Thus, the blinking system (12) randomly switches between first subsystem $R_{1}(q_{1} = 0.8, \gamma _{1} = 2.4)$ with probability $p_{1} = \frac{6.5}{100}$ and second subsystem $R_{2}(q_{2} = 2.58, \gamma _{2} = 0.8)$ with probability $p_{2} = \frac{93.5}{100}$. The fractional order averaged autonomous system associated with the fractional order blinking system (12) where E(R(q, s(t))) is the expected value of R(q, s(t)) as $R_{a}(q_{avg} = 2.4643 ,\gamma _{avg} = 0.904)$ where $q_{avg} = p_{1}*q_{1} + p_{2}*q_{2}$ and $\gamma _{avg} = p_{1}*\gamma _{1} + p_{2}*\gamma _{2}$. The behavior of the averaged system is shown in Fig. 21. The trajectory of blinking system remains in a small neighborhood of the ghost attractor as shown in Fig. 22. Time series solutions of the first subsystem, second subsystem, averaged system and switching system are depicted in Fig. 23.

Fig. 22

Fractional order blinking system Case 3: phase portrait for switching $R{s}(q_{1},\gamma _{1}, q_{2},\gamma _{2} )$ and averaged system $R{a}(q_{avg}, \gamma _{avg})$

Fig. 23

Fractional order blinking system Case 3: time series for first subsystem, second subsystem, averaged system and blinking system

Fig. 24

The distance $\delta (\tau )$ for the three proposed cases of fractional order Rössler blinking system a Case 1, b Case 2 and (3) Case 3

Fig. 25

The experiment realization using Arduino Uno. a circuit simulation, b circuit implementation, c C code

3.3.4 Euclidean distance

In this part, we calculate the Euclidean distance between the attractor of the blinking system and the ghost attractor. The Euclidean distance approximates the distance between invariant measures of the blinking system attractor and the ghost attractor. It is defined as [25]

$$\begin{aligned} \delta (\tau ) = \frac{1}{N}\left( \sum _{j=1}^{N}(h_{j}^{\tau } - h_{j}^{a})^{2}\right) ^{1/2}, \end{aligned}$$

(13)

where $h_{j}^{\tau } = \dfrac{h_{1}^{\tau }}{T_{s}}, \dfrac{h_{2}^{\tau }}{T_{s}},..., \dfrac{h_{N}^{\tau }}{T_{s}}$ represents a distribution of $T_{s}$ calculated phase points which is taken from the attractor of blinking system after neglecting the sufficient transient interval at chosen value of switching period $\tau$. Similarly, $h_{j}^{a} = {\dfrac{h_{1}^{a}}{T_{s}}, \dfrac{h_{2}^{a}}{T_{s}},..., \dfrac{h_{N}^{a}}{T_{s}}}$ is a distribution which is taken from the ghost attractor of fractional averaged system from these $T_{s}$ points to the box $D_j, \, j = 1,...,\,N$. These calculations are considered in the selected domain defined as $D : {x_{i}^{-}< x_{i} <x_{i}^{+}, i = 1,2 , 3}$ which contains both two attractors of the blinking system and the averaged system. The two boundaries in each $i^{th}$ direction of domain D are denoted by $x_{i}^{-}$ and $x_{i}^{+}$. The D region is divided into $N = \prod _{i}^{n} N_{i}$ small boxes. The value of $h_j$ represents the number of times that the solution trajectory hits the boundaries of box j after the initial transient time is ignored.

The Euclidean distance $\delta (\tau )$ has been used to quantify the closeness of the attractors of blinking system with those of the averaged system when the value of switching time is varied. In numerical simulations, the Euclidean distance is evaluated in the domain $D: x\in [ -11, 13], y\in [-13 ,13 ], z\in [ -5.5, 5.5]$ and divide it into $N = N_{x} \times N_{y} \times N_{z}$. For simplicty, we take $N_{x} = N_{y} = N_{z}$ i.e. equal number of boxes in each direction such that $N = 10^{6}$. We select interval length $T = 500$ and $T = 700$ as it is used in the previous numerical simulation with the integration step 0.005 after neglecting $2*10^{4}$ iterations of the transition interval. For the switching period $\tau \in [0.005, 1]$, the Euclidean distance $\delta (\tau )$ is evaluated and displayed in Fig. 24. It is noticed that the distance $\delta (\tau )$ rapidly increases for very small values of $\tau$ then undergoes slight changes for further values till $\tau =0.1$. This means that the attractor of system (12) changes under fast switching time $\tau <1$ in a slight way. The attractors of the fractional blinking system (12) for the three presented cases are shown in Figs. 12, (17) and 22. Accordingly, it is highly probable that the ghost attractor and the attractor of fractional order blinking system sufficiently remain close to each other with the advance of time.

3.3.5 Hardware implementation

Hardware experiment is realized using Arduino Uno board which is a board based on ATmega-328 microcontroller as illustrated in Fig. 25. The implementation consists of Arduino Uno platform which pulse width modulated signals are applied to resistor - capacitor low pass filter to generate chaotic outputs across capacitor terminals. All the used components are mentioned in Table (1). Through a fractional Euler discretization, the program is coded in C / Arduino language to validate the averaged system in case 2. The chaotic behavior is monitored through 500 ms Oscilloscope for the presented system.

4 Image encryption algorithm

In this section, we are motivated by the characteristics of the proposed system (12) as its high sensitivity to initial conditions, parameter values of chaotic system and the stochastic process to propose an image encryption scheme that utilizes this system.

4.1 Algorithm steps

The algorithm is mainly composed of two parts: plain image pixel shuffling without changing the pixels values and image diffusion. The block diagram to demonstrate the steps of encryption algorithm is given in Fig. 26.

The steps of the encryption strategy are detailed as follows

Step 1:

Read the plain image $I_{M\times N}$ as a matrix with dimensions $M\times N$, where M is the length and M is the width.

Step 2:

Evaluate a constant $img_{c}$ as a perturbation value which depends only on the image to be ciphered, and it is defined as

$$\begin{aligned}&img_{c} = \frac{1}{(M\times N)^{2} }\sum _{i=1}^{M}\sum _{j=1}^{N} I(i,j), \end{aligned}$$

(14)

where i and j are the pixel positions of original image I. The image constant $img_{c}$ is added to one of the system parameters as a perturbation value to make the original image contributes to evaluate the secret key. We choose to add $img_{c}$ to the fractional derivative $\alpha$ in the three examples that are used in our procedure.

Step 3:

To get the chaotic time series as x(i), y(i), z(i), $i = 1,2,...,n$, $n= M \times N$, we first eliminate the transient values, then we take the time series with the required size where x, y, z are the solutions of fractional order blinking system.

Step 4:

Standardize the values of the state variables as follows

$$\begin{aligned}&key_{i} = mod(floor(x_{i}\times 10^{15}),256),\,\,\quad \nonumber \\&row_{i} = mod(floor(y_{i}\times 10^{15}),512)+1,\,\, \nonumber \\&col_{i} = mod(floor(z_{i}\times 10^{15}),512)+1.\nonumber \\ \end{aligned}$$

(15)

We get $x_{i}, y_{i}, z_{i}$ from solving fractional order blinking system (7) as the state variables. To obtain the value of the secret key $key_{i}$ value within range [0, 256] as image pixels value, we use mod operation among the state variable $x_{i}$ and 256. Also, we use mod operation between the state variables $y_{i} , z_{i}$ and 512 to get a new position for pixels value image matrix I as shuffling process.

Step 5:

Rearrange the pixels position as shuffle process as follows

$$\begin{aligned}&I_{sh}(i,j) = I(RW(i),CL(j)), \end{aligned}$$

(16)

where $I_{sh}$ and I are the matrix for shuffle and plain images, respectively, where $i= 1,2,...,M$ and $j= 1,2,...,N$ are the image matrix dimensions. We set a simple scheme from three steps to get the shuffled matrix $I_{sh}$ as follows S1 We used the generated values row and col to select from them first 512 different values as RW and CL. S2 Use the first value RW(1) in RW(j) in ascending order with all values in CL(j) where the pixels position in the plain image matrix are reposition in the shuffled image matrix and $j=1,2,...,512$. S3 To fit all the position of matrix I, repeat the second step 511 times where the pixels value remains unchanged.

Step 6:

To set the secret key in matrix form the reshape function is used as follows

$$\begin{aligned}&Key_{s} = reshape(key,M,N). \end{aligned}$$

(17)

Step 7:

Apply bitwise XOR operation between $Key_{s}$ and $I_{sh}$ to establish the encrypted image $I_{en}$ as follows

$$\begin{aligned}&I_{en}(i,j) = I_{sh}(i,j) \oplus Key_{s}(i,j). \end{aligned}$$

(18)

To reconstruct the original image, the encryption steps are reversed. So, the decryption procedure is presented as

Step 1:

Apply the bitwise XOR operation between $I_{en}$ and $Key_{s}$ to attain decrypted image $I_{de}$ as follows

$$\begin{aligned}&I_{de}(i,j) = I_{en}(i,j) \oplus K_{s}(i,j). \end{aligned}$$

(19)

Step 2:

The image pixel positions are reversed to obtain the original image $I_{dsh}$ as

$$\begin{aligned}&I_{dsh}(RW(i),CL(j)) = I_{de}(i,j). \end{aligned}$$

(20)

The proposed encryption scheme is applied on three different images as shown in Fig. 27 which depicts the original, shuffled, encrypted and decrypted images for the presented algorithm.

4.2 Security analysis

A good encryption scheme should defend against all sorts of known and common attacks such as differential attack, the brute force attacks and statistical attacks. Various security tests have been used on encrypted images to assess the proposed image cryptosystem. These tests include histogram, information entropy, pixel correlation, differential attack, key space and cropping attack. We have chosen three images: Pepper, Man and Baboon image of size $512 \times 512$ to explore the security of the proposed encryption scheme. The chaotic time series from the third case of fractional order blinking system has been used to generate new row, column image pixel positions and the secret key. In addition, the perturbation values $img_{c}$ for Pepper, Man and Baboon are $4.5710 \times 10^{-4}$ , $2.9686 \times 10^{-4}$ and $4.9284 \times 10^{-4}$, respectively are used to make the system solutions depend on the plain image and increase the robust the encryption scheme.

4.2.1 Histogram analysis

Image histogram is an important criterion to measure the performance of encryption algorithm. It can describe the intensity distribution of image gray-scale level. In order to protect the information of the plain image to stand up against the statistical attacks, the statistical characteristics of pixel values in plain image should be eliminated to bear no statistical similarity to the original image. The good image encryption algorithm will lead to a flat or uniform histogram of encrypted image. Figure 28 depicts the results of histogram analysis which is evaluated to Pepper, Man and Baboon images. It is shown that the encrypted image histogram is uniform and is different from the original image so, it is effectively resisting the statistical attacks.

The variance related to histograms is evaluated using [49]

$$\begin{aligned} Var(h)= \frac{1}{G_{L}^{2}}\sum _{i=0}^{G_{L}-1}\sum _{j=0}^{G_{L}-1}\frac{1}{2}(h_{i}-h_{j}), \end{aligned}$$

(21)

where $G_{L} = 256$ is the grey level and $h = [h_{1},h_{2},...,h_{256}]$ where $h_{i}$ and $h_{j}$ are the numbers of pixels. The histogram variances for original and ciphered images are depicted in Table 2. The reduction for Pepper, Man and Baboon images is verified with values approximate $99.8\%$.

4.2.2 Information entropy

In this subsubsection, we explore one of main features of randomness which is the information entropy. The greater information entropy means image pixels are less feasible to show information for the encryption scheme. The information entropy calculated by the following formula

$$\begin{aligned} H(X) = \sum _{i=1}^{2^{N}-1} p_{i}\log _{2}\dfrac{1}{p_{i}}, \end{aligned}$$

(22)

where X is an input symbol, $p_{i}$ is probability value of symbol X and H(X) is the entropy in bits. Image pixels are more invisible when $H(X) \simeq 8$ for an encrypted image. The entropy values for Pepper, Man and Baboon images for the proposed algorithm have been compared with other algorithms in Refs. [9, 36, 50] are shown in Table 3. Consequently, the calculated entropy is approximately 8 therefore, the proposed scheme is equivalent to the existing algorithms and has a good property of information entropy and decoding encrypted image is less possible from attackers.

4.2.3 Correlation analysis

The characteristic of image data is inherited by high correlation of adjacent pixels. Therefore, the correlation of adjacent pixels in the encrypted images should be as small as possible. To test the correlation coefficient $r_{uv}$ between u, v as the gray-scale values of two adjacent pixels, the $r_{uv}$ formula is defined as

$$\begin{aligned} r_{uv} = \frac{cov(u,v)}{\sqrt{\sigma _{u}\sigma _{v}}}, \end{aligned}$$

(23)

where cov(u, v) is the covariance function, $E(u) = \frac{1}{N} \sum _{i=1}^{N}u_{i}$ and $\sigma _{u} = \frac{1}{N} \sum _{i=1}^{N}(u_{i}-E(u))^{2}$. In vertical, horizontal, and diagonal directions of the plain image and encrypted image, the value of correlation between two adjacent pixels are calculated for Pepper, Man and Baboon images of the proposed algorithm is shown in Table 4 with the comparison of our proposed algorithm with other methods mentioned in Refs. [9, 36, 50] and it is cleared that the superiority of the proposed algorithm to other algorithms. Through the obtained results, we noticed that the correlations in the plain image are strong since the correlation coefficients are all around to 0.8 and 0.97. And the correlation coefficients of the ciphered image are smaller and all around zero in the presented scheme, which demonstrates the insignificant correlation between adjacent pixels.

4.2.4 Differential attack

The cryptosystem should be kept safe from the different types of attacks. For a robust cryptosystem, an essential feature as differential attack is needed to analyze. To reflect the differences in the ciphers due to the changes in the encrypting keys which means that a slight change of secret key will cause an obvious distinction in the cipher-image. In order to test this feature, there are two benchmark values (NPCR) and (UACI) as in [51]. These evaluate the difference among the encrypted images obtained from an original image and its slightly modified copy. NPCR is used to calculate the total number of different pixels in the original cipher and modified ciphers. It is defined as

$$\begin{aligned} NPCR(\%)= & {} \sum _{i=1}^{M} \sum _{j=1}^{N} \frac{|sign(C_{1}(i,j) - C_{2}(i,j))|}{M\times N} \nonumber \\&\times 100, \end{aligned}$$

(24)

where $C_{i}$ is the ciphered image and sign() is the sign function. The UACI is used to obtain average difference in the pixel intensity in the original cipher $C_{1}$ and the modified cipher $C_{2}$. It is calculated by

$$\begin{aligned} UACI(\%)= & {} \frac{1}{M\times N} \sum _{i=1}^{M} \sum _{j=1}^{N} \frac{|C_{1}(i,j) - C_{2}(i,j)|}{255}\nonumber \\&\times 100. \end{aligned}$$

(25)

Table 1 The components that are used for hardware implementation

Fig. 26

The structure of the proposed image encryption algorithm

The ideal results to NPCR and UACI tests for encryption schemes should be near to $100\%$ and $33.33\%$, respectively as ideal results. Results of these two tests and the comparison with different algorithms is reported in Refs. [36, 50] are introduced in Tables 5 and 6. It is obvious that proposed encryption algorithm achieves equal or higher performance by comparing the other algorithms. The calculated NPCR and UACI for the proposed encryption algorithm are very close to the ideal value and is highly sensitive to image pixel change and mismatched keys.

Fig. 27

The plain, shuffled, encrypted and decrypted images in first, second, third and fourth row, respectively for Pepper, Man and Baboon images

Fig. 28

Histograms for Pepper, Man and Baboon images in first, second and third column, respectively. First row: plain images, second row: shuffled images, third row: encrypted images

Table 2 The variances for original, encrypted images for Pepper, Man and Baboon and their reduction

Table 3 Comparison of the entropy of encrypted images with some existing algorithms

Table 4 Comparison of correlation coefficients in vertical, horizontal and diagonal directions of the plain image and encrypted image with other algorithms are presented for Pepper, Man and Baboon images

4.2.5 Key space

The robust image encryption algorithm should have key space with value greater than $2^{100}$ at least [52] to withstand brute-force attacks. In the presented scheme, the secret key is composed of the double precision based on the parameters of the chaotic systems, $q_{1}, q_{2}, \gamma _{1}, \gamma _{2},p_{1}, p_{2}, m_{0},$ $m_{1} , \alpha , (x_{0}, y_{0}, z_{0}), img_{c}$. The digits number are to be at least $10^{-15}$ in each parameter. The key space of the presented scheme is $10^{195}$ and it is effectively enough to stand up against violent attack.

4.2.6 Cropping attack

The cropping attacks are used to examine the immunity of encryption scheme to information loss. To study the robustness in defend the cropping attack [53], we replaced an internal block of the ciphered image with size $512 \times 100$ into black with left, middle, and right positions. The black blocks inside the ciphered image and the decrypted images are displayed in Fig. 29. It is noticed that recovered images are all recognizable despite the significant information loss.

Table 5 Comparison of $NPCR(\%)$ results for Pepper, Man, and Baboon with different existing algorithms

Table 6 Comparison of $UACI(\%)$ results for Pepper, Man, and Baboon with different existing algorithms

5 Conclusion

Over the past twenty years, the study of integer order blinking systems has been considered in few works. In this work, we have presented a blinking system in fractional order model for first time. We have shown through thorough numerical simulation that the attractor of fractional order blinking system follows the ghost attractor of the corresponding fractional order averaged system when the switching time is sufficiently fast. We utilized the chaotic time series of resulting ghost attractor in a novel encryption scheme. The presented image encryption scheme successfully stands against different types of attacks with a high level of security. Nevertheless, the achieved results prove that the proposed image encryption algorithm preserves good encryption performance while comparing with existing algorithms. The theoretical work of fractional order blinking system with more numerical simulation can be reported in our subsequent studies. In addition, for independent navigation of a differential drive mobile robot, the chaotic signals that are generated from fractional blinking system can be utilized which could be used for search, firefighting, or patrol activities.

Fig. 29

The first row displays the encrypted image with the internal black block in different positions, while the second row views the respective decrypted images as results of the cropping attack