1 Introduction

Reeving systems are used in many engineering applications such as elevators, cable-driven robots, all types of cranes, or hoisting machines for mining. In these systems, ropes are winded on sheaves or reels to transmit large amounts of power and force to relatively large distances. Due to their lightweight and mechanical simplicity, these mechanisms are widely used in many different industries. However, the attention that the research community of flexible multibody dynamics has paid to these systems is not proportional to their use in the industry. Reeving systems show specific properties that require specialized methods for their modeling and simulation:

  1. 1.

    Special structural properties of the rope: non-solid cross section, very low bending stiffness, axial-torsion coupling, and bending-torsion coupling.

  2. 2.

    Axially moving mass that results in rope spans with varying length.

  3. 3.

    Long load-free, low-deformation segments (free spans) next to short, highly loaded, high-deformation segments (rope-sheave contact).

The simplest and very efficient rope models consider them as linear spring with length-dependent stiffness, thus neglecting the inertia or weight forces [1]. These models can be accurate enough in some applications. However, this approach has been shown to be energetically inconsistent [2]. The lumped mass approach considers the rope as a set of point masses connected with spring-dashpot systems [3]. These models can be adapted to the modeling of length-varying rope span, and they account for gravity and inertia forces. Most real-time simulators of ropes are based on these lumped mass models. The Rayleigh–Ritz method can also be used to model the elasticity, and inertial forces in ropes with little computational effort [2]. Of course, the finite element model (FEM) can also be used to model ropes. FEM models are well-suited to develop detailed models of the different wires and strands in a rope and their interaction [4]. However, these detailed models are computationally too expensive for the dynamic analysis of reeving systems. The Absolute Nodal Coordinate Formulation (ANCF) [5] is a finite element method for the efficient modeling of very slender structures that undergo large displacements and deformations. The ANCF allows the development of efficient models of cables [6, 7]. The ANCF has also been used to model belt drives [8, 9]. For the modeling of belt drives, the ANCF method requires a large number of elements to account accurately for the belt-sheave contact interaction.

Ropes are neither beams nor rods and their dynamics may not be well-modeled when applying geometrically exact beams models (GEBM) [10] or the ANCF . In the last decade, new specialized models have started to be developed for the efficient and accurate modeling and simulation of reeving systems as flexible multibody systems. The key aspect of these models is the use of an arbitrary Lagrangian–Eulerian (ALE) description of the continuum. The following discussion deals with pulley mechanisms that include uni-rigid solids, that is, solids that are very rigid when subjected to axial forces and very flexible when the loads are compressive. These solids can be wire ropes, textile ropes, belts, chains, strands, or coated wires. They will be called next simply cable-pulley mechanisms or reeving systems. Recently developed ALE formulations can be applied to the modeling and simulation of two types of cable-pulley mechanisms, as shown in Fig. 1. Shape-preserving mechanisms are those that under the assumptions of: (1) perfectly rigid cable in the axial direction, (2) perfectly flexible cable in the transverse direction and (3) no-slip in the cable-pulley interface, keep the shape of the cable constant throughout the mechanism motion. On the contrary, non-shape-preserving mechanisms do not keep that shape constant; therefore, the length of the cable-free spans varies throughout the mechanism motion. Shape-preserving cable-pulley mechanisms are used, for example, in belt or chain transmissions in machines or in ropeways. Non-shape-preserving cable-pulley mechanisms are used, for example, in elevators, cranes, or 3D-printers.

Fig. 1
figure 1

Cable-pulley mechanisms. a Shape-preserving and, b non-shape-preserving

Full size image

Under assumptions (1)–(3), the reference kinematics of the shape-preserving mechanisms is simple. All the cable cross sections move with an axial velocity V that coincides with the peripheral velocity of all the pulleys. If the cable transports rigid bodies, as in ropeways, the velocity of these rigid bodies is V too. However, the reference kinematics of non-shape-preserving mechanisms is far more complex. As it can be observed in the example shown in the right of Fig. 1, each of the rope spans may have different axial velocities, each of the pulleys may have different angular and peripheral velocities and each of the rigid bodies that are attached to the cables may have different velocities. In the example shown in Fig. 1, the counterweight moves with a velocity V that is 4 times the velocity of the car. Out of the five rope spans, two of them have an axial velocity that is V, two of them have an axial velocity that is V/2, and one has zero axial velocity. The four pulleys have different angular velocities, being \(\omega \), \(3\omega /4\), \(\omega /2\), and \(\omega /4\), where \(\omega = V/R\), where R is the radius of the pulleys.

Pechstein and Gerstmayr [11] developed an ALE formulation for the modeling and simulation of axially moving beams. The beam discretization is carried out with the absolute nodal coordinate formulation (ANCF). In this work, the axial velocity is prescribed and assumed constant throughout the beam. The principal benefit of the ALE approach is the use of different mesh refinements along the beam. In the case of cable-pulley mechanisms, the mesh is coarse in the free-span regions and fine in the contact areas. Therefore, this method is appropriate for the dynamic analysis of shape-preserving cable-pulley mechanisms. As an example, the paper presents a simple belt transmission like the one shown in Fig. 1 on the left, without transported masses. An important detail of this paper is the use of the Lagrange equations for systems with non-material volumes previously developed by Irschik and Holl [12]. A recent publication of the research group of Gerstmayr by Ntarladima et al. [13] follows the same approach as [11]. However, the axial velocity of the beam is no longer prescribed but described by a new generalized coordinate called the Eulerian coordinate s of the beam. This Eulerian coordinate is shared by all the finite elements, which is a valid approach for shape-preserving reeving systems. The other beam coordinates are again the ANCF nodal coordinates that are considered as the Lagrangian coordinates of the system. The use of the Eulerian coordinate allows the stability analysis of axially moving beams. In the work of the group of Gerstmayr, the meaning of the ALE approach is to consider a Lagrangian finite element mesh with a superimposed material motion that is described with the unique Eulerian coordinate. As mentioned, this approach is valid for the simulation of shape-preserving cable-pulley mechanisms.

Vetyukov [14] developed a similar approach as the group of Gerstmayr for the study of the vibrations of axially moving strings and beams. He does not call this approach ALE but “mixed Eulerian–Lagrangian description” and developed the variational formulation of D’Alamberts principle of virtual work for this mixed formulation using a spatially fixed range of integration. He also demonstrated the equivalence of this principle and the Lagrange equations with kinematic boundary conditions. The formulation developed by Vetyukov was applied by Oborin et al. [15] to the belt-pulley problem with dry friction, to an axially moving plate [16], to the deformation of a metal sheet in rolling mill [17], to the steady motion of a slack belt drive [18] and, recently, to an endless elastic beam travelling on a moving surface [19]. Grundl et al [20] developed a general method based on the floating frame of reference and the ALE method for the modeling and simulation of belt drives, ropeways, or strings in flexible multibody systems. This work can be considered in line of the work of Gerstmayr and Vetyukov in the sense that it is applicable to shape-preserving cable-pulley mechanisms.

The research group of Ren has been very productive in the formulation of beam finite elements under the ALE approach. Hong and Ren [21] also defined an ALE formulation with the ANCF discretization method. However, this approach is very different and more general than the one defined in [11]. Each finite element node includes a set of nodal coordinates (absolute position vectors and slopes) for the description of the deformation of the beam and one material coordinate that defines the instantaneous position of the node in the reference-undeformed configuration of the beam. Therefore, this ALE-ANCF beam element can describe an arbitrary input and output material flow through the boundaries of the element. The formulation described Hong and Ren [21] was applied to flexible multibody systems with sliding joints. This formulation was applied by Escalona [22] for the modeling and simulation of arbitrary reeving systems. The conceptual difference between the ALE formulation of the groups of Gerstmayr or Vetyukov, described in the previous two paragraphs, and the ALE formulation of the group of Ren is that, while the former is a mixed Lagrangian and Eulerian approach, the latter is neither Lagrangian nor Eulerian, because the finite element nodes do not have to be fixed in material points and do not have to be fixed in space. Therefore, the approach used in the ALE formulation of Ren is truly arbitrary. “Arbitrary” means here “according to the convenience of the user”. If you want the node to be fixed to a material point (Lagrangian node), you can do it, if you want the node to be fixed in space (Eulerian node), you can do it, and if you want it neither to be fixed to a material point nor to a spatial point, you can do it too. As shown by Escalona [23], the use of nodal material coordinates together with kinematic constraints allows all these possibilities when modeling reeving systems. Thanks to this freedom in the definition of the mesh, this formulation can be applied to the modeling and simulation of arbitrary non-shape-preserving cable-pulley mechanisms. Consider the cable-pulley mechanism at the left of Fig. 1. Points that are tangent to the fixed sheaves or the endpoint of the cable that is clamped can be defined as Eulerian nodes, the connecting point of the cable to the counterweight can be defined as a Lagrangian node. The points that are tangent to the pulleys that move with the car can be defined as nodes that are neither Eulerian nor Lagrangian, that is, pure ALE nodes.

Following with the work of the group of Ren, in the paper by Liu et al. [24], they extended the ALE approach defined in [21] for ANCF beams to GEBM beams using again the nodal material coordinates for the definition of the position of the nodes and absolute position and absolute rotation vectors for the description of the displacement and deformation at the nodal points. In this paper, the application was the motion of beam through a curved tube with frictional contact. The idea of the paper was the definition of a spatially fixed fine mesh in the areas of high curvature of the tube next to a coarse mesh in the areas of small curvature of the tube. The equations of motion were obtained using the principle of virtual work. This is another difference with the work of the group of Gerstmayr that used Lagrange equations for non-material volumes instead. However, Chen et al. [25] of the group of Ren demonstrated analytically the equivalence of Lagrange equations for non-material volumes and the principle of virtual work without any additional correction terms due to the material flow. The ultimate contribution of the group of Ren in this area is the paper by Zhang et al. [26] in which they model a reeving system using the ALE-GEBM procedure. The modeled system is an arresting mechanism used to decelerate aircraft when landing in aircraft carriers. The model is 2D, including aircraft to rope contact with friction and length-varying rope spans. The rope to pulley contact areas is not modeled. To this end, pulleys are considered as a dimensionless point. Pulleys are treated as points where the orientation of the cross-sectional frame is discontinuous. The ALE approach of Hong and Ren [21] has been applied to the modeling of non-shape-preserving reeving systems by Qi et al. [27] and Wang et al. [28].

Escalona [22] applied the ALE-ANCF method developed by Hong and Ren [21] for the first time for the modeling and simulation of non-shape-preserving reeving systems. In this work, the benefits of the ALE approach for an efficient discretization of reeving systems were highlighted. The formulation presented by Escalona [22] is a general and systematic method for the simulation of arbitrary 3D reeving systems. To this end, the different types of nodes and their associated constraints and generalized forces were defined. This formulation was extended by Escalona [23] including a systematic computational method to get the equations of motion of reeving systems and the consideration of the axial-torsion coupling in the constitutive behavior of wire ropes. In the paper by Escalona et al. [29], the ANCF beam model was abandon and substituted by a description of the transverse deformation of the ropes using modal amplitudes, being the modal shape functions defined in an element fixed frame. Due to this change in the description of deformation, the method was recalled ALEM (ALE-modal). The ALEM method allows the accurate discretization of long rope spans using a single element. This paper is the last step in the development of this ALEM method.

This paper is organized as follows. Section 2 is a summary of the ALEM method. Section 3 explains the changes to be made in this formulation to account for the sheaves’ rotary inertia. Section 4 is devoted to the addition of new modal coordinates in the axial direction that allows the definition of ALEM elements with space varying tension force. Section 5 applies these advances to the simulation of a 100-m height elevator with 2:1 suspension. Numerical results show the influence of the rotary inertia and the space-varying tension force in the overall dynamics of the system.

2 Modeling reeving systems with the ALEM method

2.1 Kinematics of the ALEM finite elements

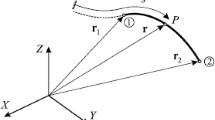
Figure 2 shows an ALEM finite element in an arbitrary position in space. The element occupies part of the volume of a rope. Nodes 1 and 2 do not have a fixed position in space. In other words, nodes 1 and 2 are not material points. The instantaneous location of the nodes in the rope is determined by the value of the time-dependent variable \(s_1(t)\) and \(s_2(t)\) that can be observed in the right of the figure (parameter space). Variables \(s_1(t)\) and \(s_2(t)\), which are also called material coordinates, are considered as nodal coordinates of the element.

The ALEM element coordinates are divided into four different sets, as follows:

$$\begin{aligned} {\mathbf{q}} = \left[ {\begin{array}{*{20}{c}} {{{\mathbf{q}}_a}}\\ {{{\mathbf{q}}_{\theta }}}\\ {{{\mathbf{q}}_m}}\\ {{{\mathbf{q}}_s}} \end{array}} \right] \,, \end{aligned}$$
(1)

where \({{\mathbf{q}}_a} = {\left[ {\begin{array}{*{20}{c}}{{{\mathbf{r}}_1}}&{{{\mathbf{r}}_2}} \end{array}} \right] ^T}\) includes the absolute position coordinates of the end nodes 1 and 2, \({{\mathbf{q}}_{\theta }} = \left[ { \begin{array}{*{20}{c}} \theta _{1}&\theta _{2} \end{array}} \right] ^T\) includes the twist angles at the end nodes, \({{\mathbf{q}}_s} = {\left[ {\begin{array}{*{20}{c}} {{s_1}}&{{s_2}} \end{array}} \right] ^T}\) includes the material coordinates and

$$\begin{aligned} {{\mathbf{q}}_m} = {\left[ {\begin{array}{*{20}{c}} {{q_{y,1}}}&{{q_{y,2}}}&\cdots&{{q_{y,nmy}}}&{{q_{z,1}}}&{{q_{z,2}}}&\cdots&{{q_{z,nmz}}} \end{array}} \right] ^T} \end{aligned}$$
(2)

is the set of \(nmy + nmz\) modal amplitudes in the local \(y_e\) and \(z_e\) directions (axes of the element local frame) used to describe transverse deformation.

Fig. 2
figure 2

Kinematics of an ALEM finite element. (1) Physical Space, (2) Parameter Space

Full size image

The absolute position vector of an arbitrary point P in the centerline of the element resolved in the global frame is obtained as:

$$\begin{aligned} {\mathbf{r}} = {{\mathbf{r}}_a} + {{\mathbf{u}}_t} = {\mathbf{N}}\left( {s,{{\mathbf{q}}_s}} \right) \,\,{{\mathbf{q}}_a} + {{\mathbf{A}}_e}\left( {{{\mathbf{q}}_a}} \right) {{{\bar{\mathbf{u}}}}_t} \end{aligned}$$
(3)

where \({\mathbf{r}}_a\) and \({{\mathbf{u}}_t}\) are the axial position vector and transverse displacement vector, respectively, both resolved in the global frame, \(\mathbf {N}\) is a linear-interpolating functions matrix that depends on the nodal coordinates \({\mathbf{q}}_s\) and the parameter s associated with point P, as follows:

$$\begin{aligned} \begin{array}{l} {\mathbf{N}}\left( {s,{{\mathbf{q}}_s}} \right) = \left[ {\begin{array}{*{20}{c}} {{N_1}{{\mathbf{1}}_{3 \times 3}}}&{}{{N_2}{{\mathbf{1}}_{3 \times 3}}} \end{array}} \right] \\ {N_1} = \frac{{1 - \xi }}{2},\mathrm{{ }}{N_2} = \frac{{1 + \xi }}{2},\mathrm{{ }}\\ \xi = \frac{{2s - {s_1} - {s_2}}}{{{s_2} - {s_1}}}. \end{array} \end{aligned}$$
(4)

In Eq. 3, the term \({{{\bar{\mathbf{u}}}}_t}\) contains the components of the transverse elastic displacement in the element frame \(\left\langle {{{\mathbf{i}}_e},\,\,{{\mathbf{j}}_e},\,\,{{\mathbf{k}}_e}} \right\rangle \). Vector \({{{\bar{\mathbf{u}}}}_t}\) can be calculated using linear interpolation as follows:

$$\begin{aligned} {{{\bar{\mathbf{u}}}}_t} = {\mathbf{S}}\left( {s,{{\mathbf{q}}_s}} \right) \,\,{{\mathbf{q}}_m}\,, \end{aligned}$$
(5)

where \(\mathbf {S}\) is the following shape functions matrix:

$$\begin{aligned} \begin{array}{l} {\mathbf{S}}\left( {s,{{\mathbf{q}}_s}} \right) \, = \left[ {\begin{array}{*{20}{c}} 0&{}0&{} \cdots &{}0&{}0&{}0&{} \cdots &{}0\\ {{S_1}}&{}{{S_2}}&{} \cdots &{}{{S_{nmy}}}&{}0&{}0&{} \cdots &{}0\\ 0&{}0&{} \cdots &{}0&{}{{S_1}}&{}{{S_2}}&{} \cdots &{}{{S_{nmz}}} \end{array}} \right] ,\\ {S_i} = \sin \left[ {\frac{{i\pi \left( {s - {s_1}} \right) }}{{{s_2} - {s_1}}}} \right] ,\,\,\,i = i=1,2,..., \end{array} \end{aligned}$$
(6)

The first row of \(\mathbf {S}\) is zero because \({{{\bar{\mathbf{u}}}}_t}\) is a transverse displacement, that is, it has zero component along the \(x_e\) direction. Therefore, in the original ALEM formulation, the axial displacement \({\mathbf{r}}_a\) of the arbitrary point P is a function of the absolute position coordinates \({\mathbf{q}}_a\) and the transverse displacement \({{{\bar{\mathbf{u}}}}_t}\) is a function of the modal coordinates \({\mathbf{q}}_m\). This geometric interpretation of the vectors and the functional dependency changes in the work presented in this paper.

2.2 Dynamics of the ALEM finite elements

Using this kinematic description and Lagrange equations, the equations of motion (EOM) of the ALEM finite element are given as:

$$\begin{aligned} \mathbf {M}{\ddot{\mathbf {q}}} = {{\mathbf {Q}}_v} + {{\mathbf {Q}}_{elas}} + {{\mathbf {Q}}_{ap}} + {{\mathbf {Q}}_{reac}} \end{aligned}$$
(7)

where \(\mathbf {M}\) is a coordinate-dependent mass matrix, \({\mathbf {Q}}_{v}\) is the generalized quadratic-velocity inertia force, \({\mathbf {Q}}_{elas}\) is the generalized elastic force vector, \(\mathbf {Q}_{ap}\) is the generalized applied forces vector, and \(\mathbf {Q}_{reac}\) is a vector of generalized reaction forces that may appear due to kinematic constraints. Details about the calculation of these terms can be found in [29].

2.3 Modeling reeving systems with ALEM finite elements

The ALEM method presented here to model and simulate the dynamics of reeving systems is valid to analyze the overall dynamics of the system. This method has not been developed for detailed dynamic analysis, as the behavior of the individual wires within the rope. Another very important assumption is related to the rope-sheave contact. So far, the method does not model the wire rope to sheave contact. The no-slip condition is assumed all along the contact segment. That means that this method is not used to analyze the rope-sheave contact stress or the micro-slip area. This is future work that is already under preparation. In a rope winded in a sheave, it is assumed that the location of the tangent points at the sheave is known in advance. This assumption is quite reasonable in most reeving systems.

A reeving system, like the tower crane shown in Fig. 3, is considered as a multibody system that includes rigid bodies as well as ALEM finite elements to discretize the ropes. Other bodies in the system could also be considered as flexible and modeled with the floating frame of reference approach. However, this possibility is not developed in this paper. Therefore, the set of coordinates used to model the reeving system is divided in two groups: (1) the set \({{{\mathbf {q}}^{WR}}}\) (WR stands for wire ropes) that includes the nodal coordinates of the wire rope ALE-FEM elements, and (2) the set \({{{\mathbf {q}}^{RB}}}\) (RB stands for rigid bodies) that includes the coordinates used to describe the global position and orientation of the rigid bodies in the system. The total set of coordinates used to model the reeving systems, which is called here \(\mathbf {p}\), is given by:

$$\begin{aligned} \begin{array}{l} {{\mathbf {p}}} = {\left[ {\begin{array}{*{20}{c}} {{{\mathbf {q}}^{RB}}^T}&{}{{{\mathbf {q}}^{WR}}^T} \end{array}} \right] ^T}\\ {{\mathbf {q}}^{WR}} = {\left[ {\begin{array}{*{20}{c}} {{{\mathbf {q}}^{WR1}}^T}&{}{{{\mathbf {q}}^{WR2}}^T}&{} \cdots &{}{{{\mathbf {q}}^{WRne}}^T} \end{array}} \right] ^T} \end{array} \end{aligned}$$
(8)

where \({\mathbf {q}}^{WRi}\) are the coordinates of the wire rope element i and ne is the total number of elements used to model the reeving system.

Fig. 3
figure 3

Example of reeving system: tower crane

Full size image

2.4 Node types in reeving systems

Ropes in reeving systems have two ends, obviously, and they are winded in sheaves or reels. It is common in this type of mechanisms to attach the end of the ropes using flexible supports that can be modeled as spring-damper force elements. There are two types of sheaves: deviation sheaves and drive sheaves. Therefore, four different types of element nodes are needed to model reeving systems: continuous node, fixed node, node attached to an elastic support and node tangent to a sheave or reel. Figure 4 shows a reeving system that is discretized with five elements and includes the four types of node. Each node can be systematically treated, as explained in Ref. [23], for the automatic generation of the EOM of reeving systems. To this end, each node has a set of associated constraints, which are linear or nonlinear, as a set of generalized forces. In this paper, the constraints used to model the node tangent to a sheave are going to be modified to account for the sheave rotary inertia.

Fig. 4
figure 4

Nodes used in reeving systems

Full size image

The continuous node, which is located in the middle of the span of the rope in Fig. 4, is not used in practice. In case it is used, its definition requires the usual connectivity conditions used in the FEM. However, in the ALEM approach, because the transverse deformation is described using the modal amplitudes (sines) \({{{\mathbf {q}}_{m}}}\), an additional set of constraints would be needed to guarantee tangent continuity at that node, thus avoiding the appearance of a kink. In practice, the continuous node is not used because, in the ALEM method, thanks to the developments described in this paper, the complete free span of the rope can be modeled with a single variable-length ALEM element.

Most of the constraints needed to model the reeving systems are linear in terms of the \({\mathbf {q}}^{WR}\), as shown in Ref. [23]. These linear constraints can be eliminated systematically and, as a result, the following velocity transformation can be easily obtained:

$$\begin{aligned} {\dot{\mathbf {p}}} = {\mathbf {B}}\left( {{{\mathbf {q}}^{RB}}} \right) {\dot{\mathbf {q}}} + {\mathbf {D}}\left( t \right) \end{aligned}$$
(9)

where \(\mathbf {q}\) is a new set of generalized coordinates that is a subset of \(\mathbf {p}\) and includes coordinates that are not independent but are subjected to a minimum set of nonlinear constraints. Matrix \(\mathbf {B}\) and vector \(\mathbf {D}\) are given in Ref. [23]. Typically, the nonlinear constraints are due to the torque balance at the nodes tangent to a sheave. In the work presented in this paper, these nonlinear constraints are eliminated, thus leading to a more convenient set of independent system coordinates \(\mathbf {q}\).

2.5 Equations of motion of reeving systems

The equations of motion of the reeving system include the equations of the rigid body parts and the equations of the wire rope elements, as follows:

$$\begin{aligned}&\left[ {\begin{array}{*{20}{c}} {{{\mathbf {M}}^{RB}}}&{}{\mathbf {0}}&{} \cdots &{}{\mathbf {0}}\\ {\mathbf {0}}&{}{{{\mathbf {M}}^{WR1}}}&{} \cdots &{}{\mathbf {0}}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {\mathbf {0}}&{}{\mathbf {0}}&{} \cdots &{}{{{\mathbf {M}}^{WRne}}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {\ddot{\mathbf {q}}}^{RB}\\ {\ddot{\mathbf {q}}}^{WR1}\\ \vdots \\ {\ddot{\mathbf {q}}}^{WRne} \end{array}} \right] \nonumber \\&\quad = \left[ {\begin{array}{*{20}{c}} {{{\mathbf {Q}}^{RB}}}\\ {{{\mathbf {Q}}^{WR1}}}\\ \vdots \\ {{{\mathbf {Q}}^{WRne}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\mathbf {Q}}_{reac}^{RB}}\\ {{\mathbf {Q}}_{reac}^{WR1}}\\ \vdots \\ {{\mathbf {Q}}_{reac}^{WRne}} \end{array}} \right] \Rightarrow \nonumber \\&\quad \Rightarrow {{{{\hat{\mathbf {M}}}}}}{\ddot{\mathbf {p}}} = {{{{\hat{\mathbf {Q}}}}}^{RS}} + {{\hat{\mathbf {Q}}}}_{reac} \end{aligned}$$
(10)

where \({\mathbf {M}}^{RB}\) and \({\mathbf {Q}}^{RB}\) are the mass matrix and generalized force vector (including applied forces and quadratic-velocity inertia vector) associated with the rigid bodies and \({\mathbf {Q}}_{reac}^{RB}\) is the vector of generalized reaction forces of the rigid bodies. The mass matrices \({\mathbf {M}}^{WRi}\) and generalized force vectors \({\mathbf {Q}}^{WRi}\) and \({\mathbf {Q}}_{reac}^{WRi}\) for the ne ALEM elements are as those given in Eq. 7.

The velocity transformation matrix given in Eq. 9 is used to turn these equations into a set of equations written in terms of \(\mathbf {q}\), as follows:

$$\begin{aligned} {{\mathbf {M}}}\ddot{\mathbf {q}} = {{\mathbf {Q}}} + {\mathbf {Q}}_{reac} \end{aligned}$$
(11)

where

$$\begin{aligned} \begin{array}{l} {{\mathbf {M}}} = {{\mathbf {B}}^T}{{{{\hat{\mathbf {M}}}}}}{\mathbf {B}},\,\,\,\\ {{\mathbf {Q}}} = {{\mathbf {B}}^T}\left( {{{{{\hat{\mathbf {Q}}}}}} - {{{{\hat{\mathbf {M}}}}}}\left( {\dot{\mathbf {B}}\dot{\mathbf {q}}} + \dot{\mathbf {D}} \right) } \right) ,\\ {\mathbf {Q}}_{reac} = {{\mathbf {B}}^T}{{\hat{\mathbf {Q}}}}_{reac} \end{array} \end{aligned}$$
(12)

The procedure followed to obtain the equations of motion Eq. 11 is borrowed from the well-known coordinate-partitioning method [30]. From this method, it is known that the rows of the matrix \({{\mathbf {B}}}\) are perpendicular to the Jacobian of the (linear) constraint equations that are used to obtain Eq. 9. This means that the vector of reaction forces associated with the reduced set of coordinates \(\mathbf {q}\) is associated only with the nonlinear reaction constraints that are not accounted for in Eq. 9. The vector of reaction forces can be included into the system of equations of motion using the Lagrange multipliers method as:

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {{\mathbf {M}}}&{}{{\mathbf {C}}_{\mathbf {q}}^T}\\ {{{\mathbf {C}}_{\mathbf {q}}}}&{}{\mathbf {0}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{{\ddot{\mathbf {q}}}}}\\ {\mathbf {\lambda }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\mathbf {Q}}}}\\ { - {{\dot{\mathbf {C}}}_{\mathbf {q}}}{{\dot{\mathbf {q}}}} - {{{\dot{\mathbf {C}}}_t}}} \end{array}} \right] \end{aligned}$$
(13)

where

$$\begin{aligned} \begin{array}{l} {{\mathbf {C}}_{\mathbf {q}}} = \frac{{\partial {\mathbf {C}}_{nl}}}{{\partial {{\mathbf {p}}}}}\frac{{\partial {{\mathbf {p}}}}}{{\partial {{\mathbf {q}}}}} = {{\mathbf {C}}_{nl}}_{\mathbf {p}}{\mathbf {B}} \end{array} \end{aligned}$$
(14)

is the Jacobian matrix on the nonlinear constraints \({\mathbf {C}}_{nl}\) that are given in terms of \(\mathbf {p}\). Equations 13 has a standard form in multibody dynamics and it can be solved using standard methods.

3 Adding the sheaves rotary inertia

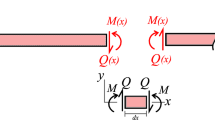
Figure 5 shows a wire rope winded in a sheave, the axial loads \(T_1\) and \(T_2\) at the two tangent points, the external torque applied on the sheave \(M_{ext}\) that can be a drive torque or a resistance torque, and the torque due to the rotary inertia \(M_{inertia} = - I\ddot{\alpha }\), where I is the moment of inertia of the sheave and \(\alpha \) its angle of rotation. This value of the rotary inertia is just an approximation since the pulley may be attached to a rigid body with its own angular acceleration. However, in reeving systems, the rotation of the sheaves about their axis use to be much higher than other rotations.

Fig. 5
figure 5

Wire rope rolled in a sheave

Full size image

The torque balance in the sheave yields:

$$\begin{aligned} \left( {{T_2} - {T_1}} \right) R + {M_{ext}} = I\ddot{\alpha }\end{aligned}$$
(15)

If the moment of inertia is small such that the term \(\left( {{T_2} - {T_1}} \right) R\) is much larger than the rotary inertia (this assumption is reasonable in most reeving systems), the following equation can be used to find the axial load difference:

$$\begin{aligned} \left( {{T_2} - {T_1}} \right) R + {M_{ext}} = 0 \end{aligned}$$
(16)

In a deviation sheave, that is, a sheave where \({M_{ext}} = 0\), this equation yields the equal-axial force condition, as follows:

$$\begin{aligned} \left( {{T_2} - {T_1}} \right) R = 0\,\,\, \Rightarrow \,\,\,{T_2} = {T_1} \end{aligned}$$
(17)

This simple condition is used as nonlinear constraints in the nodes tangent to a sheave in reeving systems.

Consider the sheave attached to the rigid body i shown in Fig. 6. Regardless of being a drive sheave (\(M_{ext} \ne 0\)) or a deviation sheave (\(M_{ext}=0\)), the following linear constraints apply:

$$\begin{aligned} {{\mathbf{C}}_{lin}} = \left[ {\begin{array}{*{20}{c}} {{\mathbf{r}}_2^j - \left( {{{\mathbf{r}}^i} + {{\mathbf{A}}^i}{{\bar{\mathbf{u}}}}_{t1}^i} \right) }\\ {{\mathbf{r}}_1^k - \left( {{{\mathbf{r}}^i} + {{\mathbf{A}}^i}{{\bar{\mathbf{u}}}}_{t2}^i} \right) }\\ {s_2^j - s_1^k}\\ \end{array}} \right] = {\mathbf{0}} \end{aligned}$$
(18)

where the first two sets of equations guarantee that the absolute position of the end nodes of the elements j and k coincide with the absolute position of the tangent points to the sheave, t1 and t2. The fact that the position of the tangent points in the body frame, \({{\bar{\mathbf{u}}}}_{t1}^i\) and \({{\bar{\mathbf{u}}}}_{t1}^i\), is known is a reasonable approximation in reeving systems. The third constraint is a continuity constraint that makes sense because, in the formulation presented in this paper, the rope segment winded in the sheave is not modeled.

In addition to the constraint equations given in Eq. 18, a constraint equation has to be added to fulfill the torque balance given in Eq. 16. This equation is written in terms of the coordinates of elements j and k as follows:

$$\begin{aligned} {\mathbf {C}}_{nl} = \left( {F_{ax}^{j2}\left( {{{\mathbf {q}}^j}} \right) - F_{ax}^{k1}\left( {{{\mathbf {q}}^k}} \right) } \right) {R_s} - {M_{ext}}\left( t \right) = 0\nonumber \\ \end{aligned}$$
(19)

where the axial force at element j, \(F_{ax}^{j2}\) and the axial force at element k, \(F_{ax}^{k1}\), can be calculated as functions of the element coordinates. This equation is a rheonomic constraint if the torque applied on the sheave is a known function of time, \({M_{ext}} \left( t \right) \) . In the case of a deviation sheave, in which typically \({M_{ext}} = 0\), this equation turns into:

$$\begin{aligned} {\mathbf {C}}_{nl} = {F_{ax}^{j2}\left( {{{\mathbf {q}}^j}} \right) - F_{ax}^{k1}\left( {{{\mathbf {q}}^k}} \right) } = 0 \end{aligned}$$
(20)

The linear constraint equations given in Eq. 18 plus the nonlinear constraint equation given in Eq. 19 (drive sheave) or the nonlinear constraint equation given in Eq. 20 (deviation sheave) are required to model sheaves in reeving systems. Note that the angle rotated by the sheave \(\theta _s^i\) is not used in these equations. In fact, this angle is not needed as a generalized coordinate of the reeving system. Besides, this angle has little interest in the system dynamics.

Fig. 6
figure 6

Rope rolled in a sheave

Full size image

The method based on the set of constraint equations defined above to model sheaves of reeving systems has two drawbacks:

  1. 1.

    The sheaves may have a sufficiently large moment of inertia, such that the rotary inertia (right-hand side of Eq. 15) is not negligible but has an influence in the system dynamics. This large moment of inertia can be due not to the sheave itself but to the contribution of a gear motor. As known from elementary mechanics, the moment of inertia of the motor is divided by the square of the gear ratio to obtain the equivalent moment of inertia of the sheave. For low gear ratios (speed reducer), the contribution of the moment of inertia of the motor can be very important.

  2. 2.

    Equation 19 is useful to model torque-driven sheaves. However, in the case of a kinematically driven sheave, the angle \(\theta _s^i\) has to be obtained in the dynamic simulation. This is the case, for example, when simulating the dynamics of an elevator with a given velocity profile. In this case, the equations given above are useless to find the drive torque.

The alternative is, of course, to add the sheave rotation angle \(\theta _s^i\) as a generalized coordinate and to eliminate the torque balance in the sheaves (Eq. 19 or Eq. 20) of the set of constraints. When using this method, the sheave rotation \(\theta _s^i\) must be linked to the rope material coordinate to guarantee the no-slip condition. In this case, the linear constraint turns into:

$$\begin{aligned} {{\mathbf{C}}_{lin}} = \left[ {\begin{array}{*{20}{c}} {{\mathbf{r}}_2^j - \left( {{{\mathbf{r}}^i} + {{\mathbf{A}}^i}{{\bar{\mathbf{u}}}}_{t1}^i} \right) }\\ {{\mathbf{r}}_1^k - \left( {{{\mathbf{r}}^i} + {{\mathbf{A}}^i}{{\bar{\mathbf{u}}}}_{t2}^i} \right) }\\ {s_2^j - s_1^k}\\ {s_2^j - \left( {s_{20}^j - \theta _s^iR} \right) } \end{array}} \right] = {\mathbf{0}}, \end{aligned}$$
(21)

where the first three sets of constraints are the same as those in Eq. 18, and the fourth one guarantees that the rope does not slip with respect to the groove of the sheave. In the examples, the results of both types of modeling of sheaves in reeving systems will be compared.

Regardless of the better accuracy that can be obtained when considering the sheaves rotary inertia, the method described in this section has a clear computational benefit. The substitution of the equal-axial force nonlinear constraint equations with the no-slip linear constraint equations results into equations of motion that unless the rigid body coordinates set \({{{\mathbf {q}}^{RB}}}\) were subjected to other nonlinear constraints, are ordinary differential equations (ODE) instead of differential-algebraic equations (DAE). As it is well-known, ODE are more easily solved than DAE.

Fig. 7
figure 7

Deformation of a rod under its own weight

Full size image

4 ALEM elements with axial modes

In the kinematic description of the ALEM elements given in Section 2.1, Eq. 3, the longitudinal displacement of the cross sections of the rope is given by \({{\mathbf{r}}_a}\) and the transverse displacement by \({{\mathbf{u}}_t}\). The longitudinal displacement is a linear function of the absolute coordinates \({{\mathbf{q}}_a}\) and also linear in terms of the parameter s, since the shape functions in matrix \(\mathbf {N}\) are linear polynomials. The axial strain, which is a function of the partial derivative of the longitudinal displacement \({{\mathbf{r}}_a}\) with respect to s, is constant along the element. Due to Hooke’s law, the axial force along the element is also constant.

In hoisting machines in which the wire ropes work vertically, the weight of the ropes can be an important force for long rope spans. Think, for example, about the elevators of skyscrapers. In these cases, the axial load along the ropes varies approximately linearly with s and the constant axial load is not admissible. The solution to simulate non-constant axial load distributions in the context of the ALEM method is to assume in the kinematic description, a modal contribution also in the axial direction. In this case, vector \({{{\bar{\mathbf{u}}}}_t}\) is no longer considered as transverse displacement because it also carries part of the axial displacement of the cross sections. The new definition of vector \({{\mathbf{u}}_t}\) is given by:

$$\begin{aligned} \begin{array}{llll} {{{\bar{\mathbf{u}}}}_t} = {\mathbf{S}}\left( {s,{{\mathbf{q}}_s}} \right) \,\,{\mathbf{q}}_m,\\ \\ {\mathbf{S}}\left( {s,{{\mathbf{q}}_s}} \right) = \left[ {\begin{array}{*{20}{c}} {{S_1}}&{} \cdots &{}{{S_{nmx}}}&{}0&{} \cdots &{}0&{}0&{} \cdots &{}0\\ 0&{} \cdots &{}0&{}{{S_1}}&{} \cdots &{}{{S_{nmy}}}&{}0&{} \cdots &{}0\\ 0&{} \cdots &{}0&{}0&{} \cdots &{}0&{}{{S_1}}&{} \cdots &{}{{S_{nmz}}} \end{array}} \right] ,\\ \\ {S_i} = \sin \left[ {\frac{{i\pi \left( {s - {s_1}} \right) }}{{{s_2} - {s_1}}}} \right] ,\,\,\,i = \mathrm{{1}}\mathrm{{,2}}i=1,2,...\\ \\ {{\mathbf{q}}_m} = {\left[ {\begin{array}{*{20}{c}} {{q_{x,1}}}&{} \cdots &{}{{q_{x,nmx}}}&{}{{q_{y,1}}}&{} \cdots &{}{{q_{y,nmy}}}&{}{{q_{z,1}}}&{} \cdots &{}{{q_{z,nmz}}} \end{array}} \right] ^T} \end{array} \end{aligned}$$
(22)

where \({{\mathbf{q}}_m}\) includes nmx modal amplitudes in the local \(x_e\) direction, nmy modal amplitudes in the local \(y_e\) direction and nmz modal amplitudes in the local \(z_e\) direction.

In order to check the capability of the sine functions to represent a linear axial force distribution accurately, a simple quasi-static structural problem has been solved. Figure 7 shows a uniform cantilever rod under the action of its own weight, \(\rho Ag\), being \(\rho \) mass density, A cross-sectional area and g acceleration of gravity. The axial force distribution along the rod is of course linear, \({F_{ax}}\left( s \right) = \rho g\left( {L - s} \right) \), where L is the length of the cantilever. Modeling the axial displacement with a linear mode and a set of nm sine modes:

$$\begin{aligned} u\left( {s,t} \right) = \frac{s}{L}{u_L} + \sum \limits _{i = 1}^{nm} {\sin \frac{{i\pi s}}{L}{q_i}}, \end{aligned}$$
(23)

being \(u_L\) the amplitude of the linear mode and \({q_i}\) the amplitude of the ith mode, the modal amplitudes can be obtained analytically, yielding:

$$\begin{aligned}&{u_L} = {{m{L^2}} \big /{2EA}},\,\,\,\,{q_1} = {{4m{L^2}} \big / {{\pi ^3}EA}},\,\,\,{q_2} = 0,\,\,\,\,\nonumber \\&\quad {q_3} = {{4m{L^2}} \big / {27{\pi ^3}EA}} \end{aligned}$$
(24)

where m is the total mass of the cantilever and EA is the stiffness per unit length. Using this model, the resulting axial force distribution along the cantilever is plotted in Fig. 8. As it can be observed in the figure on the left, without modal contribution (\(nm=0\)) the resulting axial force distribution is constant and an average of the exact linear distribution. The central plot shows that adding just one sine mode (\(nm=1\)) approximates the linear distribution, while the plot on the right shows that using three modes (\(nm=3\)), the approximation becomes quite acceptable. The second mode does not contribute to the result for symmetry reasons. This simple example shows that the axial modes can be used to obtain a reasonable approximation of the axial force distribution along the ropes.

Fig. 8
figure 8

Deformation of a rod under its own weight

Full size image

The simple quasi-static problem used in this section is not representative of the dynamics of ropes in reeving systems because no payload has been assumed, and inertia forces are not considered. Results just show that a few axial modes are sufficient for an acceptable description of a triangular tension field along the ropes. It can be shown that the trapezoidal tension field appearing under the presence of the payload is equally well-described. In dynamics, tension is affected by axial elastic waves. It is well-known from the theory of vibrations of continuous systems that a sufficient number of axial modes can be used to describe axial elastic waves along a rope.

5 Example: simulation of an elevator with a 2:1 suspension

The reeving system modeled with the presented method is the 2:1-suspension electric driven elevator shown in Fig. 9. The model includes a motor elastically supported in the vertical direction, a cabin, a counterweight, one drive sheave attached to the motor and two deflection sheaves attached to the cabin and the counterweight. Figure 10 shows the cabin target velocity during a 12 seconds-ride with a nominal value of 6 m/s. The cabin displacement during the ride is 80 m. The simulation is kinematically driven. To this end, the rotation of the drive sheave is prescribed to produce the mentioned cabin velocity profile in the ideal conditions of perfectly rigid ropes (axially) and zero ropes-to-drive sheave slipping. Four wire ropes elements are used to model the elevator reeving system, labeled as a, b, c and d. Only the longitudinal dynamics of the system are modeled here. The main parameters of the elevator system are given in Table 1.

Fig. 9
figure 9

Electric driven elevator with 2:1 suspension system

Full size image
Fig. 10
figure 10

Commanded velocity profile of the cabin

Full size image
Table 1 Elevator parameters
Full size table

5.1 Model without sheaves inertia and without axial modes

This is the model that could be built with the ALEM method developed previously by the authors. This model includes three rigid body coordinates. For the wire rope elements, four coordinates per node and eight nodal coordinates per element are used. Figure 9 shows the global frame where the heights of the different bodies and nodes are measured. The set of total coordinates \(\mathbf {p}\) is given by:

$$\begin{aligned} \begin{array}{l} {{\mathbf {q}}^{RB}} = {\left[ {\begin{array}{*{20}{c}} {{z_{cab}}}&{}{{z_{cw}}}&{}{{z_{mot}}} \end{array}} \right] ^T}\\ {{\mathbf {q}}^{i}} = \left[ {\begin{array}{*{20}{c}} {z_1^{i}}&{}{z_2^{i}}&{}{s_1^i}&{}{s_2^{i}} \end{array}} \right] ^{T},\,\,\,\,i = a,...,d\\ {{\mathbf {q}}^{WR}} = \left[ {\begin{array}{*{20}{c}} {{{\mathbf {q}}^{a}}^T}&{}{{{\mathbf {q}}^{b}}^T}&{}{{{\mathbf {q}}^{c}}^T}&{}{{{\mathbf {q}}^{d}}^T} \end{array}} \right] \\ {\mathbf {p}} = {\left[ {\begin{array}{*{20}{c}} {{{\mathbf {q}}^{RB}}^T}&{}{{{\mathbf {q}}^{WR}}^T} \end{array}} \right] ^T} \end{array} \end{aligned}$$
(25)

Using the standard nodal coordinate constraints defined in Section 2.4, the following set of 16 linear constraints can be deduced:

$$\begin{aligned} {{\mathbf {C}}_{lin}}\left( {{\mathbf {p}},t} \right) = \left[ \begin{array}{l} z_2^{a} - \left( {{z_{cab}} + {d_{cab}}} \right) \\ z_2^{a} - z_1^{b}\\ z_2^{b} - {z_{mot}}\\ z_2^{b} - z_1^{c}\\ z_2^{c} - \left( {{z_{cw}} + {d_{cw}}} \right) \\ z_2^{c} - z_1^{d}\\ s_1^{a}\\ s_2^{a} - s_1^{b}\\ s_2^{b} - s_1^{c}\\ s_2^{c} - s_1^{d}\\ s_2^{d} - l\\ s_2^{b} - \left( {s_{20}^{b} + 2\int _0^t {V\left( t \right) dt} } \right) \end{array} \right] = {\mathbf {0}} \end{aligned}$$
(26)

where \(d_{cab}\) and \(d_{cw}\) are the distances from the center of gravity of the cabin and counterweight to the deviation sheaves, respectively, l is the total length of the wire rope, \(s_{20}^{b}\) is the initial value of \(s_{2}^{b}\) and V(t) is the commanded velocity of the cabin shown in Fig. 10. Note that the last of the linear equations is a mobility constraint that drives the entire system forcing the cabin to approximately follow the velocity profile V(t). The factor ‘2’ that multiplies the integral of V(t) is due to the 2:1 suspension. In this problem, the angle rotated by the drive sheave is a function of time given by:

$$\begin{aligned} \alpha \left( t \right) = - \frac{2}{R}\int _0^t {V\left( t \right) dt}, \end{aligned}$$
(27)

where the negative sign means that the sheave has to be rotated counter-clockwise for a positive velocity of the cabin in the upward direction. Since no generalized coordinates are used to model the rotation of the deviation sheaves, the nonlinear constraints that establish the equal-axial loads of the wire ropes have to be used as follows:

$$\begin{aligned} {{\mathbf {C}}_{nonlin}}\left( {{\mathbf {p}},t} \right) = \left[ {\begin{array}{*{20}{c}} {F_{ax}^{a2}\left( {{{\mathbf {q}}^a}} \right) - F_{ax}^{b1}\left( {{{\mathbf {q}}^b}} \right) }\\ {F_{ax}^{c2}\left( {{{\mathbf {q}}^c}} \right) - F_{ax}^{d1}\left( {{{\mathbf {q}}^d}} \right) } \end{array}} \right] = {\mathbf {0}} \end{aligned}$$
(28)

In this equation, the axial forces \(F_{ax}^{i}\left( {{{\mathbf {q}}^j}} \right) \) are constant along the elements because no axial modes are considered. In the model with axial modes presented next, the axial forces are also functions of s, that is, \(F_{ax}^{ai} = F_{ax}^{i}\left( s, {{{\mathbf {q}}^j}} \right) \).

In this problem, \(n = 3 + 4 \times 4 = 19\), \(m_l = 12\), \(m_{nl} = 2\), and the number of degrees of freedom is \(g = 19-(12+2) = 5\). The set of generalized coordinates \(\mathbf {q}\) used in this example is given by:

$$\begin{aligned} {\mathbf {q}} = {\left[ {\begin{array}{*{20}{c}} {{z_{cab}}}&{{z_{cw}}}&{{z_{mot}}}&{z_1^a}&{z_2^d}&{s_2^a}&{s_2^c} \end{array}} \right] ^T} \end{aligned}$$
(29)

and the subsets of independent and dependent coordinates in \(\mathbf {q}\) can be established as:

$$\begin{aligned} \begin{array}{l} {{\mathbf {q}}^{ind}} = {\left[ {\begin{array}{*{20}{c}} {{z_{cab}}}&{}{{z_{cw}}}&{}{{z_{mot}}}&{}{z_1^a}&{}{z_2^d} \end{array}} \right] ^T}\\ {{\mathbf {q}}^{dep}} = {\left[ {\begin{array}{*{20}{c}} {s_2^a}&{}{s_2^c} \end{array}} \right] ^T} \end{array} \end{aligned}$$
(30)

The reason for this separation is that \(s_2^a\) and \(s_2^c\) can be easily obtained solving Eq. 28 once the value of \({{\mathbf {q}}^{ind}}\) is known. With the values of \(\mathbf {q}\) and time t, all other coordinates in \(\mathbf {p}\) can be obtained using the linear constraints given in Eq. 26.

The velocity transformation matrix \(\mathbf {B}\) that appears in Eq. 9 is constant for this example, it can be simply obtained from the time-derivative of Eq. 26 and it takes the form:

$$\begin{aligned} {\mathbf {B}} = \left[ {\begin{array}{*{20}{c}} {{{\mathbf {B}}^{RB}}}\\ {{{\mathbf {B}}^a}}\\ {{{\mathbf {B}}^b}}\\ {{{\mathbf {B}}^c}}\\ {{{\mathbf {B}}^d}} \end{array}} \right] \end{aligned}$$
(31)

where

$$\begin{aligned} \begin{array}{l} {{\mathbf {B}}^{RB}} = \left[ {\begin{array}{*{20}{c}} {{{\mathbf {I}}_{3 \times 3}}}&{}{{{\mathbf {0}}_{3 \times 4}}} \end{array}} \right] ,\\ {{\mathbf {B}}^a} = \left[ {\begin{array}{*{20}{c}} 0&{}0&{}0&{}1&{}0&{}0&{}0\\ 1&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}1&{}0 \end{array}} \right] ,\,\,\,{{\mathbf {B}}^b} = \left[ {\begin{array}{*{20}{c}} 1&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}1&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}1&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0 \end{array}} \right] ,\\ {{\mathbf {B}}^c} = \left[ {\begin{array}{*{20}{c}} 0&{}0&{}1&{}0&{}0&{}0&{}0\\ 0&{}1&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}1 \end{array}} \right] ,\,\,\,{{\mathbf {B}}^d} = \left[ {\begin{array}{*{20}{c}} 0&{}1&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}1&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}1\\ 0&{}0&{}0&{}0&{}0&{}0&{}0 \end{array}} \right] , \end{array}\nonumber \\ \end{aligned}$$
(32)

And array \(\mathbf {D}\) in Eq. 9 is given by:

$$\begin{aligned} {\mathbf {D}} = \left[ {\begin{array}{*{20}{c}} {{{\mathbf {D}}^{RB}}}\\ {{{\mathbf {D}}^a}}\\ {{{\mathbf {D}}^b}}\\ {{{\mathbf {D}}^c}}\\ {{{\mathbf {D}}^d}} \end{array}} \right] , \end{aligned}$$
(33)

where

$$\begin{aligned} \begin{array}{l} {{\mathbf {D}}^{RB}} = {{\mathbf {0}}_{3 \times 1}},\,\,\,{{\mathbf {D}}^a} = {{\mathbf {D}}^d} = {{\mathbf {0}}_{4 \times 1}},\\ {{\mathbf {D}}^b} = {\left[ {\begin{array}{*{20}{c}} 0&{}0&{}0&{}{2V\left( t \right) } \end{array}} \right] ^T}\\ {{\mathbf {D}}^c} = {\left[ {\begin{array}{*{20}{c}} 0&{}0&{}{2V\left( t \right) }&{}0 \end{array}} \right] ^T} \end{array} \end{aligned}$$
(34)

5.2 Model with sheaves rotary inertia and without axial modes

In the model with sheaves rotary inertia, the number of rigid body coordinates is 5 instead of 3 because the angle rotated by the deviation sheave of the cabin, \(\theta ^{cab}\), and the counterweight, \(\theta ^{cw}\), have to be added. The nonlinear equal-axial load constraints Eq. 28 are not needed. These nonlinear constraints are substituted by the no-slip constraints at the deviation sheaves, which are linear and given by:

$$\begin{aligned} \begin{array}{l} s_2^a - s_{20}^a - {\theta ^{cab}}{R^{cab}} = 0\\ s_2^c - s_{20}^c - {\theta ^{cw}}{R^{cw}} = 0 \end{array} \end{aligned}$$
(35)

where \(s_{20}^a\) and \(s_{20}^c\) are initial values of the arc-length nodal coordinates and \(R^{cab}\) and \(R^{cw}\) are the radius of the cabin and counterweight deviation sheaves. Equations 35 have to be added to the set of linear equations given in Eq. 26 that also apply to this model. Therefore, in this problem \(n = 5 + 4 \times 4 = 21\), \(m_l = 14\), \(m_{nl} = 0\), and the number of degrees of freedom is \(g = 21-(14+0) = 7\). The model with sheave’s inertia has two more degrees of freedom than the model without it. Of course, these are the rotations of the deviation sheaves. The set of generalized coordinates \(\mathbf {q}\) used in this example is given by:

$$\begin{aligned} {\mathbf {q}} = {\left[ {\begin{array}{*{20}{c}} {{z_{cab}}}&{{z_{cw}}}&{{z_{mot}}}&{\theta ^{cab}}&{\theta ^{cw}}&{z_1^a}&{z_2^d} \end{array}} \right] ^T} \end{aligned}$$
(36)

This problem does not include non-linear constraints and all coordinates are treated as independent:

$$\begin{aligned} {{\mathbf {q}}^{ind}} = {{\mathbf {q}}},\, {{\mathbf {q}}^{dep}} = {\left[ \, \right] } \end{aligned}$$
(37)

In this model, matrices \(\mathbf {B}\) and \(\mathbf {D}\) that appear in the velocity transformation Eq. 9 are built similarly to the previous model, but in this case accounting for the additional linear constraint equations (Eq. 35).

5.3 Models with axial modes

Using the results shown in Fig. 8, in the models built to simulate non-constant axial forces along the rope elements, three axial modal amplitudes per element are considered. Therefore, the number of coordinates per element becomes 7, as follows:

$$\begin{aligned} {{\mathbf {q}}^{WRi}} = \left[ {\begin{array}{*{20}{c}} {z_1^{i}}&{z_2^{i}}&{s_1^i}&{s_2^{i}}&{q_{x,1}^{i}}&{q_{x,2}^{i}}&{q_{x,3}^{i}} \end{array}} \right] ^{T},\,\,\,\,i = a,...,d\nonumber \\ \end{aligned}$$
(38)

The models with axial modes keep the same constraints than the models without them. Therefore, the model with axial modes but without sheaves rotary inertia has \(n = 3 + 4 \times 7 = 31\), \(m_l = 12\), \(m_{nl} = 2\), and the number of degrees of freedom is \(g = 31-(12+2) = 17\). The model with axial modes and with sheaves rotary inertia has \(n = 5 + 4 \times 7 = 33\), \(m_l = 14\), \(m_{nl} = 0\), and the number of degrees of freedom is \(g = 33-(14+0) = 19\).

5.4 Simulation results

In the figures shown in this section, Figs. 11, 12, 13, and 14, the plots on the left are the results of the models without axial deformation modes (constant tension on ropes), while plots on the right are the results of the models with three axial deformation modes (length-varying tension on ropes). Both plots, left and right plots, include the results of the models with and without considering the sheaves rotary inertia (SRI).

Figure 11 shows the cabin acceleration during the ride. The triangular shapes that appear at the beginning and the end of the ride are due to the triangular shape of the acceleration profiles that are used in the elevator industry. These triangular shapes can also be observed in the forces and torques involved in the system dynamics. As it can be observed in the figure, all models provide very similar results. There is little influence of the sheave rotary inertia or the tension variation along the ropes. Figure 12 shows the vibration of the cabin. Because the cabin is modeled as a rigid body, this plot can be interpreted as the vibration of the ropes during the ride. These curves are obtained by subtracting to the real cabin displacement the ideal displacement considering a perfectly rigid system. Conclusions drawn from this figure are the same as those from Fig. 11. Therefore, in the simulated system, results show that the influence of the sheaves rotary inertia and the tension variation along the ropes in the dynamic response of the system is not significant.

Fig. 11
figure 11

Cabin acceleration

Full size image
Fig. 12
figure 12

Vibration of cabin

Full size image

Figure 13 shows the tension of ropes a and b at the deviation sheave of the cabin. There are four curves per plot. However, because both tensions are equal in the models without sheaves rotary inertia, it seems there are only three. As can be observed, the effect of the sheave rotary inertia is important in the resulting tension. In this example, differences in the order of 1 KN can be observed. It is also true that the assumed sheaves moment of inertia has been 10 kgm\(^2\), which is a very high value. Regarding the effect of the length-varying tension, its effect is very important as well. There are differences of the order of 3 KN in the tensions shown in the left and the right plots, being larger in the models with constant tension along the ropes (without axial modes). The reason is that being the tension measured at the bottom of the ropes, the length-averaged value provided by the constant-tension models overestimates the real one, as it occurs with the simple result shown in Fig. 8.

Fig. 13
figure 13

Tension of ropes at cabin deviation sheave

Full size image

Figure 14 shows the motor torque. In this case, results show again that both the sheave rotary inertia and the variation of tension along the ropes influence the resulting motor torque, being the effect of the tension variation much more important. Contrary to what is observed in Fig. 13, in this case, the models with constant tension underestimate the motor torque. The reason is that being the tension measured at the top of the ropes, the length-averaged value provided by the constant-tension models underestimates the real one, as it occurs with the simple result shown in Fig. 8. Differences of the order of 1 KNm can be observed. It is also interesting to observe that the static equilibrium values of the motor torque (brake torques) are also different. In the initial instant, the motor torque is negative in the models with constant tension (counterweight tends to fall) while positive in the models with length-varying tension (cabin tends to fall).

Fig. 14
figure 14

Motor torque

Full size image

It can be concluded that in the simulated example that represents the reeving system of the elevator of a tall building (100 m), the effect of the sheaves rotary inertia and the variation of tension along the ropes have very little effect on the dynamic response of the system but important effect in the resulting forces and torques that produce or are transmitted during the ride.

Results of this section just show the dynamics of the cabin-side (ropes a and b), but not the dynamics of the counterweight-side (ropes c and d). The reason is that the dynamics in the counterweight-side is totally equivalent, and their simulation results do not add any new qualitative information.

6 Comparison with the ALE-ANCF formulation

The formulation presented in this paper, originally developed in [29], cannot be considered as ANCF formulation because the selected generalized coordinates are not all absolute, and they are not all nodal. Modal coordinates do not fulfill these two properties. The use of an arbitrary number of mode shapes and modal coordinates allows the description of elastic waves along the element. With the work presented in this paper, not only transverse elastic waves, but also axial elastic waves can be described. The ALE-ANCF formulation developed in [21] and applied to reeving systems in [23] cannot be used to describe elastic waves within the elements. That is why rope spans should not be modeled with a single element if the elastic wave propagation is important in a particular problem. However, because the elements of the ALE-ANCF use line-parametrized cubic shape functions, the axial strain may vary quadratically. Therefore, linear tension distributions are naturally described because the straight line is a particular case of a quadratic polynomial. In other words, the capability that is approximated in this work with axial modes is exactly obtained with the original ALE-ANCF formulation. Therefore, in that sense, the ALE-ANCF can be considered superior. This section describes the modeling and simulation of the elevator system shown in Fig. 9 and compares the results with the ALEM method presented in this paper with three axial deformation modes.

The ALE-ANCF kinematic description uses a set of 14 nodal coordinates per element, \({\mathbf{q}} = {\left[ {{{\begin{array}{*{20}{c}} {{{\mathbf{q}}_a}^T}&{{{\mathbf{q}}_s}} \end{array}}^T}} \right] ^T}\), that are separated into absolute and material coordinates. The kinematic description of an arbitrary point within the element can be summarized as:

$$\begin{aligned}&{\mathbf{r}} = {\mathbf{N}}\left( {s,{{\mathbf{q}}_s}} \right) {{\mathbf{q}}_a}\nonumber \\&{{\mathbf{q}}_a} = {\left[ {\begin{array}{*{20}{c}} {{{\mathbf{r}}_1}^T}&{{{{\mathbf{r'}}}_1}^T}&{{{\mathbf{r}}_2}^T}&{{{{\mathbf{r'}}}_2}^T} \end{array}} \right] ^T},\,\,\,\,\,{{\mathbf{q}}_s} = {\left[ {\begin{array}{*{20}{c}} {{s_1}}&{{s_2}} \end{array}} \right] ^T}\nonumber \\&{{{\mathbf{r'}}}_i} = \frac{{\partial {{\mathbf{r}}_i}}}{{\partial s}},\mathrm{{ }}i = \mathrm{{1}}\mathrm{{,2}}\mathrm{{.}}\nonumber \\&{\mathbf{N}} = \left[ {\begin{array}{*{20}{c}} {{N_1}\left( s \right) {{\mathbf{1}}_{3 \times 3}}}&{{N_2}\left( s \right) {{\mathbf{1}}_{3 \times 3}}}&{{N_3}\left( s \right) {{\mathbf{1}}_{3 \times 3}}}&{{N_4}\left( s \right) {{\mathbf{1}}_{3 \times 3}}} \end{array}} \right] \nonumber \\&{N_1} = \frac{1}{4}{\left( {\xi - 1} \right) ^2}\left( {2 + \xi } \right) \mathrm{{, }}{N_2} = \frac{{{s_2} - {s_1}}}{8}{\left( {\xi - 1} \right) ^2}\left( {\xi + 1} \right) \nonumber \\&{N_3} = \frac{1}{4}{\left( {\xi + 1} \right) ^2}\left( {2 - \xi } \right) \mathrm{{, }}{N_4} = \frac{{{s_2} - {s_1}}}{8}{\left( {\xi + 1} \right) ^2}\left( {\xi - 1} \right) \nonumber \\&\xi = \frac{{2s - {s_1} - {s_2}}}{{{s_2} - {s_1}}}\mathrm{{ }} \end{aligned}$$
(39)

When modeling the 2:1 elevator with ALE-ANCF elements with sheaves rotary inertia the number of coordinates and constraints are \(n = 5 + 4 \times 6 = 29\), \(m_l = 14\), \(m_{nl} = 0\), and the number of degrees of freedom is \(g = 29-(14+0) = 15\). In this calculation, the number of nodal coordinates per element is 6 instead of 14 because the problem is 1D.

Figure 15 shows the tension along ropes a and b in the static equilibrium position at the initial configuration. It can be observed that the ALE-ANCF provides the exact linear distribution, while the ALEM method describes a quite acceptable approximation with modal superposition. The results obtained with the ALEM method slightly overestimates the tension in the lower end of the rope and slightly overestimates it in the higher end. The error is approximately \(1.5\%\). Figure 16 shows the time history of the tension of the rope a simulated with both methods. It is apparent that the ALEM method provides slightly higher values of that tension. This is a clear consequence of the modal superposition as shown in the static result of Fig. 15. Therefore, from that figure, it can be interpreted that near the ends of the rope is where the maximum error in the rope tension is obtained, and its value is about \(1.5\%\) of the average. It is also apparent for Fig. 16 that the ALEM method is able to capture higher frequency contents.

Regarding the simulation times, using MATLAB R2021b on an Intel i7 8th Gen laptop and ode45 as solver, the computational time was 80.23s for the ALE-ANCF solution and 149.45s for the ALEM solution. Therefore, the ALEM solution takes a little less than the double time of the ALE-ANCF solution. The increase in simulation time is due to two facts. First, the ALE-ANCF model has fewer degrees of freedom. Second, the higher frequency content of the ALEM solution forces the solver to select smaller time steps during integration. Recall that ode45 is a variable time-step solver.

Results of this section can be used to compare the ALEM method presented in this paper with the existing ALE-ANCF with line-parametrized cubic polynomials in terms of ease of implementation, accuracy, and computational efficiency, as follows:

  1. 1.

    Ease of implementation. The ALE-ANCF method is easier to implement because the kinematics is less involved. The number of coordinates per element is fixed (14) for the ALEANCF method but variable for the ALEM method, since it depends on the selected modal coordinates in each direction.

  2. 2.

    Accuracy. While the ALE-ANCF method can represent exactly linear variations of axil forces along the ropes, the ALEM method just approximates it, but the error is relatively small. The maximum error has been estimated in about \(1.5\%\) of the average value of the tension. However, the ALEM method is able to describe higher frequency vibrations at the ropes. The limit frequency depends on the selected number of modal coordinates. That property allows the ALEM method to discretize the complete rope span using a single element while showing a high-frequency response. That is not possible with the ALE-ANCF method.

  3. 3.

    Efficiency. The ALE-ANCF is more efficient computationally. This is due to the simpler kinematics but also because the resulting model just captures relatively low-frequency vibrations. In other words, the ALEM model takes longer to simulate, but the results include higher frequency content.

It is worth to mention that these conclusions are taken based on an example that just models axial vibrations. However, the ALEM method what originally developed in [29] to model transverse vibrations. That is why only modal coordinates in the transverse direction were used. For the description of transverse vibrations in ropes, the ALE-ANCF simply cannot compete with the ALEM method when using a coarse mesh. The cubic polynomials are not adequate to model the sinusoidal modal shapes that appear in taut ropes.

Fig. 15
figure 15

Comparison of tension along the ropes in static equilibrium with ALE-ANCF and ALEM methods

Full size image
Fig. 16
figure 16

Comparison of time history of tension at cabin side with ALE-ANCF and ALEM methods

Full size image

7 Summary and conclusions

This paper includes two new modeling features of the ALEM method for the modeling and simulation of reeving systems under the multibody dynamics framework. These features are the consideration of the sheaves rotary inertia and the use of new modal coordinates to simulate free rope spans with non-constant axial forces along the rope. The paper begins with a detailed introduction of the different ALE methods that have been developed by different research groups in the last decade for the simulation of axially moving beam-like structures. To make the paper self-contained and to understand the reasons and effects of the new features, Sect. 2 summarizes the ALEM method.

Section 3 explains the changes needed to account for the sheaves rotary inertia. To this end, the system coordinates have to be augmented with new coordinates that describe the rotation of the sheaves, thus increasing the number of degrees of freedom of the model. Besides, the nonlinear axial force constraints are substituted with linear no-slip constraints. As a consequence, in most typical reeving systems, the EOM of the reeving systems are ODE instead of DAE when considering the rotary inertia of the sheaves. Section 4 explains the method followed to add new modal coordinates in the axial direction. These new coordinates allow the description of non-constant axial forces along the elements. When using this new set of modal coordinates, the modal superposition not only describes the transverse deformation but it also carries part of the axial deformation. A simple quasi-static example shows that the use of three axial modal coordinates is enough to model linearly varying axial forces that typically appear due to the own-weight of the ropes.

Section 5 includes the simulation results. The system modeled is an electrically driven elevator with a 2:1 suspension and a height of 100 m. Four models are simulated and compared, the result of the combination of considering or not considering the sheave’s rotary inertia and using or not using axial modal coordinates. Simulation results show that in the selected example, both new features have little effect in the system dynamics, that is, in the resulting motion of the rigid bodies, but they have a significant effect on the forces and torques that produce or appear during the ride.

Section 6 compares the presented ALEM method with the ALE-ANCF method developed in [21] and applied to reeving systems in [23] in terms of ease of implementation, accuracy, and computational efficiency. It is shown that the increase in complexity and decrease in computational efficiency of the ALEM model are not very significant. In turn, the method provides an accurate representation of non-constant tension along the ropes, and it can be used to model high-frequency vibrations. These conclusions are taken from an example that is dominated by axial vibrations. In problems where the transverse vibrations of the ropes are of interest, the benefits of the ALEM model with respect to the ALE-ANCF model are much more important.