General planar motion modeling and control of a smart rigid-flexible satellite considering large deflections

Abstract

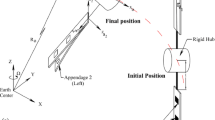
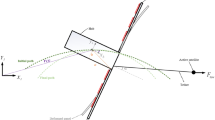
In this paper, the motion of a smart rigid-flexible satellite considering large deflections for its flexible appendages in general planar motion is modeled. Also, the satellite can experience translational and rotational motions. In addition, its flexible appendages can vibrate arbitrarily in the motion plane. Two control forces perpendicular to each other and one control torque are responsible for controlling the motion of the satellite on the desired trajectories. Also, piezoelectric actuators and sensors suppress vibrations and estimate the transverse displacement of the satellite's flexible appendages, respectively. The coupled ordinary-partial differential equations of motion, equations of the sensors and boundary conditions of the system are obtained using the extended Hamilton's principle. Then, these equations are discretized using the Galerkin method. The discretized equations of motion are a set of coupled nonlinear ordinary differential equations due to the consideration of the large rotation angle of the satellite and large deflections for its flexible appendages. An adaptive super-twisting global nonlinear sliding mode controller is designed to satisfy the control objectives including position and attitude control, as well as suppressing vibrations of the flexible appendages in the presence of uncertainties and external disturbances. Eventually, numerical simulations are presented to validate the proposed dynamic model of a smart flexible satellite and illustrate the effectiveness of the proposed controller.

Appendices

Appendix A

Applying the variation operator to Eqs. (3) and (10) leads to Eqs. (A.1) and (A.2), respectively.

$$ \begin{aligned} \delta T = & M\dot{X}\delta \dot{X} + \left( {\rho A} \right)_{{La}} \int\limits_{0}^{{l_{a} }} {\delta \dot{X}{{d}}x} \\ & + \left( {\rho A} \right)_{{Ra}} \int\limits_{0}^{{l_{a} }} {\delta \dot{X}{{d}}x} \\ & + \sum\limits_{{i = 1}}^{N} {\left( {\rho A} \right)_{{LP_{i} }} \int\limits_{{LP_{i} }} {\left\{ {\left[ {\left( {\dot{X}\cos \theta + \dot{Y}\sin \theta - \dot{\theta }w_{L} } \right)\cos \theta } \right] + \left[ {\left( {\dot{Y}\cos \theta - \dot{X}\sin \theta - \left( {x + r} \right)\dot{\theta } + \dot{w}_{L} } \right)\left( { - \sin \theta } \right)} \right]} \right\}\delta \dot{X}{{d}}x} } \\ & + \sum\limits_{{i = 1}}^{N} {\left( {\rho A} \right)_{{RP_{i} }} \int\limits_{{RP_{i} }} {\left\{ {\left[ {\left( {\dot{X}\cos \theta + \dot{Y}\sin \theta - \dot{\theta }w_{R} } \right)\cos \theta } \right] + \left[ {\left( {\dot{Y}\cos \theta - \dot{X}\sin \theta + \left( {x + r} \right)\dot{\theta } + \dot{w}_{R} } \right)\left( { - \sin \theta } \right)} \right]} \right\}\delta \dot{X}{{d}}x} } \\ & + M\dot{Y}\delta \dot{Y} + \left( {\rho A} \right)_{{La}} \int\limits_{0}^{{l_{a} }} {\delta \dot{Y}{{d}}x} \\ & + \left( {\rho A} \right)_{{Ra}} \int\limits_{0}^{{l_{a} }} {\delta \dot{Y}{{d}}x} \\ & + \sum\limits_{{i = 1}}^{N} {\left( {\rho A} \right)_{{LP_{i} }} \int\limits_{{LP_{i} }} {\left\{ {\left[ {\left( {\dot{X}\cos \theta + \dot{Y}\sin \theta - \dot{\theta }w_{L} } \right)\sin \theta } \right] + \left[ {\left( {\dot{Y}\cos \theta - \dot{X}\sin \theta - \left( {x + r} \right)\dot{\theta } + \dot{w}_{L} } \right)\left( {\cos \theta } \right)} \right]} \right\}\delta \dot{Y}{{d}}x} } \\ & + \sum\limits_{{i = 1}}^{N} {\left( {\rho A} \right)_{{RP_{i} }} \int\limits_{{RP_{i} }} {\left\{ {\left[ {\left( {\dot{X}\cos \theta + \dot{Y}\sin \theta - \dot{\theta }w_{R} } \right)\sin \theta } \right] + \left[ {\left( {\dot{Y}\cos \theta - \dot{X}\sin \theta + \left( {x + r} \right)\dot{\theta } + \dot{w}_{R} } \right)\left( {\cos \theta } \right)} \right]} \right\}\delta \dot{Y}{d}x} } \\ & + J\dot{\theta }\delta \dot{\theta } + \left( {\rho A} \right)_{{La}} \int\limits_{0}^{{l_{a} }} {\left\{ {\left[ {\left( {\dot{X}\cos \theta + \dot{Y}\sin \theta - \dot{\theta }w_{L} } \right)\left( { - w_{L} } \right)} \right] + \left[ {\left( {\dot{Y}\cos \theta - \dot{X}\sin \theta - \left( {x + r} \right)\dot{\theta } + \dot{w}_{L} } \right)\left( { - \left( {x + r} \right)} \right)} \right]} \right\}\delta \dot{\theta }{{d}}x} \\ & + \left( {\rho A} \right)_{{Ra}} \int\limits_{0}^{{l_{a} }} {\left\{ {\left[ {\left( {\dot{X}\cos \theta + \dot{Y}\sin \theta - \dot{\theta }w_{R} } \right)\left( { - w_{R} } \right)} \right] + \left[ {\left( {\dot{Y}\cos \theta - \dot{X}\sin \theta + \left( {x + r} \right)\dot{\theta } + \dot{w}_{R} } \right)\left( {x + r} \right)} \right]} \right\}\delta \dot{\theta }{d}x} \\ & + \sum\limits_{{i = 1}}^{N} {\left( {\rho A} \right)_{{LP_{i} }} \int\limits_{{LP_{i} }} {\left\{ {\left[ {\left( {\dot{X}\cos \theta + \dot{Y}\sin \theta - \dot{\theta }w_{L} } \right)\left( { - w_{L} } \right)} \right] + \left[ {\left( {\dot{Y}\cos \theta - \dot{X}\sin \theta - \left( {x + r} \right)\dot{\theta } + \dot{w}_{L} } \right)\left( { - \left( {x + r} \right)} \right)} \right]} \right\}\delta \dot{\theta }{d}x} } \\ & + \sum\limits_{{i = 1}}^{N} {\left( {\rho A} \right)_{{RP_{i} }} \int\limits_{{RP_{i} }} {\left\{ {\left[ {\left( {\dot{X}\cos \theta + \dot{Y}\sin \theta - \dot{\theta }w_{R} } \right)\left( { - w_{R} } \right)} \right] + \left[ {\left( {\dot{Y}\cos \theta - \dot{X}\sin \theta + \left( {x + r} \right)\dot{\theta } + \dot{w}_{R} } \right)\left( {x + r} \right)} \right]} \right\}\delta \dot{\theta }{d}x} } \\ & + \left( {\rho A} \right)_{{La}} \int\limits_{0}^{{l_{a} }} {\delta \theta {d}x} \\ & + \left( {\rho A} \right)_{{Ra}} \int\limits_{0}^{{l_{a} }} {\delta \theta {d}x} \\ & + \sum\limits_{{i = 1}}^{N} {\left( {\rho A} \right)_{{LP_{i} }} \int\limits_{{LP_{i} }} {\left\{ {\left( {\dot{X}\cos \theta + \dot{Y}\sin \theta - \dot{\theta }w_{L} } \right)\left( {\dot{Y}\cos \theta - \dot{X}\sin \theta } \right) + \left( {\dot{Y}\cos \theta - \dot{X}\sin \theta - \left( {x + r} \right)\dot{\theta } + \dot{w}_{L} } \right)\left( { - \left( {\dot{Y}\sin \theta + \dot{X}\cos \theta } \right)} \right)} \right\}\delta \theta {d}x} } \\ & + \sum\limits_{{i = 1}}^{N} {\left( {\rho A} \right)_{{RP_{i} }} \int\limits_{{RP_{i} }} {\left\{ {\left( {\dot{X}\cos \theta + \dot{Y}\sin \theta - \dot{\theta }w_{R} } \right)\left( {\dot{Y}\cos \theta - \dot{X}\sin \theta } \right) + \left( {\dot{Y}\cos \theta - \dot{X}\sin \theta + \left( {x + r} \right)\dot{\theta } + \dot{w}_{R} } \right)\left( { - \left( {\dot{Y}\sin \theta + \dot{X}\cos \theta } \right)} \right)} \right\}\delta \theta {d}x} } \\ & + \left( {\rho A} \right)_{{La}} \int\limits_{0}^{{l_{a} }} {\left\{ {\left( {\dot{Y}\cos \theta - \dot{X}\sin \theta - \left( {x + r} \right)\dot{\theta } + \dot{w}_{L} } \right)} \right\}\delta \dot{w}_{L} {d}x} \\ & + \sum\limits_{{i = 1}}^{N} {\left( {\rho A} \right)_{{LP_{i} }} \int\limits_{{LP_{i} }} {\left\{ {\left( {\dot{Y}\cos \theta - \dot{X}\sin \theta - \left( {x + r} \right)\dot{\theta } + \dot{w}_{L} } \right)} \right\}\delta \dot{w}_{L} {d}x} } \\ & + \left( {\rho A} \right)_{{La}} \int\limits_{0}^{{l_{a} }} {\left\{ {\left( {\dot{X}\cos \theta + \dot{Y}\sin \theta - \dot{\theta }w_{L} } \right)\left( { - \dot{\theta }} \right)} \right\}\delta w_{L} {d}x} \\ & + \sum\limits_{{i = 1}}^{N} {\left( {\rho A} \right)_{{LP_{i} }} \int\limits_{{LP_{i} }} {\left\{ {\left( {\dot{X}\cos \theta + \dot{Y}\sin \theta - \dot{\theta }w_{L} } \right)\left( { - \dot{\theta }} \right)} \right\}\delta w_{L} {d}x} } \\ & + \left( {\rho A} \right)_{{Ra}} \int\limits_{0}^{{l_{a} }} {\left\{ {\left( {\dot{Y}\cos \theta - \dot{X}\sin \theta + \left( {x + r} \right)\dot{\theta } + \dot{w}_{R} } \right)} \right\}\delta \dot{w}_{R} {d}x} \\ & + \sum\limits_{{i = 1}}^{N} {\left( {\rho A} \right)_{{RP_{i} }} \int\limits_{{RP_{i} }} {\left\{ {\left( {\dot{Y}\cos \theta - \dot{X}\sin \theta + \left( {x + r} \right)\dot{\theta } + \dot{w}_{R} } \right)} \right\}\delta \dot{w}_{R} {d}x} } \\ & + \left( {\rho A} \right)_{{Ra}} \int\limits_{0}^{{l_{a} }} {\left\{ {\left( {\dot{X}\cos \theta + \dot{Y}\sin \theta - \dot{\theta }w_{R} } \right)\left( { - \dot{\theta }} \right)} \right\}\delta w_{R} {d}x} \\ & + \sum\limits_{{i = 1}}^{N} {\left( {\rho A} \right)_{{RP_{i} }} \int\limits_{{RP_{i} }} {\left\{ {\left( {\dot{X}\cos \theta + \dot{Y}\sin \theta - \dot{\theta }w_{R} } \right)\left( { - \dot{\theta }} \right)} \right\}\delta w_{R} {d}x} } \\ \end{aligned} $$

(A.1)

$$ \begin{aligned} \delta U = & \int\limits_{La} {\left[ {\left( {EI} \right)_{La} w^{\prime\prime}_{L} - \frac{1}{2}\left( {EQ} \right)_{La} \left( {w^{\prime}_{L} } \right)^{2} } \right]\delta w^{\prime\prime}_{L} {d}x + \int\limits_{La} {\left[ { - \left( {EQ} \right)_{La} w^{\prime\prime}_{L} w^{\prime}_{L} + \frac{1}{2}\left( {EA} \right)_{La} \left( {w^{\prime}_{L} } \right)^{3} } \right]\delta w^{\prime}_{L} {d}x} } \\ & \; + \int\limits_{Ra} {\left[ {\left( {EI} \right)_{Ra} w^{\prime\prime}_{R} - \frac{1}{2}\left( {EQ} \right)_{Ra} \left( {w^{\prime}_{R} } \right)^{2} } \right]\delta w^{\prime\prime}_{R} {d}x + \int\limits_{Ra} {\left[ { - \left( {EQ} \right)_{Ra} w^{\prime\prime}_{R} w^{\prime}_{R} + \frac{1}{2}\left( {EA} \right)_{Ra} \left( {w^{\prime}_{R} } \right)^{3} } \right]\delta w^{\prime}_{R} {d}x} } \\ & \; + \sum\limits_{i = 1}^{N} {\int\limits_{{LP_{i} }} {\left[ {\left( {E_{p} I_{p} } \right)_{{LP_{i} }} w^{\prime\prime}_{L} - \frac{1}{2}\left( {E_{p} Q_{p} } \right)_{{LP_{i} }} \left( {w^{\prime}_{L} } \right)^{2} } \right]\delta w^{\prime\prime}_{L} {d}x + \int\limits_{{LP_{i} }} {\left[ { - \left( {E_{p} Q_{p} } \right)_{{LP_{i} }} w^{\prime\prime}_{L} w^{\prime}_{L} + \frac{1}{2}\left( {E_{p} A_{p} } \right)_{{LP_{i} }} \left( {w^{\prime}_{L} } \right)^{3} } \right]\delta w^{\prime}_{L} {d}x} } } \\ & \; + \sum\limits_{i = 1}^{{N_{a} }} { - \int\limits_{{LA_{i} }} {\left( {\frac{{e_{31} \left( { - Q_{p} } \right)V_{p} }}{{t_{p} }}} \right)_{{LA_{i} }} \delta w^{\prime\prime}_{L} {d}x} - \int\limits_{{LA_{i} }} {\left( {\frac{{e_{31} A_{p} V_{p} }}{{t_{p} }}} \right)_{{LA_{i} }} w^{\prime}_{L} \delta w^{\prime}_{L} {d}x} } \\ & \; + \sum\limits_{i = 1}^{N} {\int\limits_{{RP_{i} }} {\left[ {\left( {E_{p} I_{p} } \right)_{{RP_{i} }} w^{\prime\prime}_{R} - \frac{1}{2}\left( {E_{p} Q_{p} } \right)_{{RP_{i} }} \left( {w^{\prime}_{R} } \right)^{2} } \right]\delta w^{\prime\prime}_{R} {d}x + \int\limits_{{RP_{i} }} {\left[ { - \left( {E_{p} Q_{p} } \right)_{{RP_{i} }} w^{\prime\prime}_{R} w^{\prime}_{R} + \frac{1}{2}\left( {E_{p} A_{p} } \right)_{{RP_{i} }} \left( {w^{\prime}_{R} } \right)^{3} } \right]\delta w^{\prime}_{R} {d}x} } } \\ & \; + \sum\limits_{i = 1}^{{N_{a} }} { - \int\limits_{{RA_{i} }} {\left( {\frac{{e_{31} \left( { - Q_{p} } \right)V_{p} }}{{t_{p} }}} \right)_{{RA_{i} }} \delta w^{\prime\prime}_{R} {d}x} - \int\limits_{{RA_{i} }} {\left( {\frac{{e_{31} A_{p} V_{p} }}{{t_{p} }}} \right)_{{RA_{i} }} w^{\prime}_{R} \delta w^{\prime}_{R} {d}x} } \\ & \; + \sum\limits_{i = 1}^{{N_{s} }} {\left\{ {\left( {\frac{{e_{31} Q_{p} }}{{t_{p} }}} \right)_{{LS_{i} }} \int\limits_{{LS_{i} }} {w^{\prime\prime}_{L} {d}x} - \frac{1}{2}\left( {\frac{{e_{31} A_{p} }}{{t_{p} }}} \right)_{{LS_{i} }} \int\limits_{{LS_{i} }} {\left( {w^{\prime}_{L} } \right)^{2} {d}x} + \left( {\frac{{\varepsilon_{p} A_{p} l_{p} }}{{t_{p}^{2} }}} \right)_{{LS_{i} }} V_{{LS_{i} }} } \right\}\delta V_{{LS_{i} }} } \\ & \; + \sum\limits_{i = 1}^{{N_{s} }} {\left\{ {\left( {\frac{{e_{31} Q_{p} }}{{t_{p} }}} \right)_{{RS_{i} }} \int\limits_{{RS_{i} }} {w^{\prime\prime}_{R} {d}x} - \frac{1}{2}\left( {\frac{{e_{31} A_{p} }}{{t_{p} }}} \right)_{{RS_{i} }} \int\limits_{{RS_{i} }} {\left( {w^{\prime}_{R} } \right)^{2} {d}x} + \left( {\frac{{\varepsilon_{p} A_{p} l_{p} }}{{t_{p}^{2} }}} \right)_{{RS_{i} }} V_{{RS_{i} }} } \right\}\delta V_{{RS_{i} }} } \\ \end{aligned} $$

(A.2)

Appendix B

The relations obtained from integration by parts (B.1) and (B.2) are used in the simplification of Eqs. (A.1) and (A.2) to obtain the equations of motion, the equations of sensors and the boundary conditions of the system.

$$ \left\{ \begin{gathered} \int\limits_{{t_{1} }}^{{t_{2} }} {\int\limits_{a}^{b} {\dot{w}\delta \dot{w}{d}x} {d}t = \int\limits_{a}^{b} {\left( {\dot{w}\delta w\left| {_{{t_{1} }}^{{t_{2} }} } \right. - \int\limits_{{t_{1} }}^{{t_{2} }} {\ddot{w}\delta w{d}t} } \right){d}x} } \hfill \\ \int\limits_{a}^{b} {w^{\prime}\delta w^{\prime}{d}x = w^{\prime}\delta w\left| {_{a}^{b} } \right.} - \int\limits_{a}^{b} {w^{\prime\prime}\delta w{d}x} \hfill \\ \int\limits_{a}^{b} {w^{\prime\prime}\delta w^{\prime\prime}{d}x = w^{\prime\prime}\delta w^{\prime}\left| {_{a}^{b} } \right.} - \int\limits_{a}^{b} {w^{\prime\prime\prime}\delta w^{\prime}{d}x = \int\limits_{a}^{b} {w^{\prime\prime\prime\prime}\delta w{d}x + w^{\prime\prime}\delta w^{\prime}\left| {_{a}^{b} } \right.} } - w^{\prime\prime\prime}\delta w\left| {_{a}^{b} } \right. \hfill \\ \int\limits_{a}^{b} {\delta w^{\prime\prime}{d}x = \int\limits_{a}^{b} {[\delta_{D} (x - b) - \delta_{D} (x - a)]\delta w^{\prime}{d}x = [\delta_{D} (x - b) - \delta_{D} (x - a)]\delta w\left| {_{a}^{b} } \right.} } - \int\limits_{a}^{b} {[\delta^{\prime}_{D} (x - b) - \delta^{\prime}_{D} (x - a)]\delta w{d}x} \hfill \\ \end{gathered} \right. $$

(B.1)

$$\begin{gathered} \delta U^{*} = \overbrace {{\int_{a}^{b} {\underbrace {{\left[ {EIw^{\prime\prime} - \frac{1}{2}EQw^{{\prime}{2}} } \right]}}_{u}\underbrace {{\delta w^{\prime\prime}{d}x}}_{{{d}v}}} }}^{{I_{1} }} + \overbrace {{\int_{a}^{b} {\underbrace {{\left[ { - EQw^{\prime\prime}w^{\prime} + \frac{1}{2}EAw^{{\prime}{3}} } \right]}}_{{u_{2} }}\underbrace {{\delta w^{\prime}{d}x}}_{{{d}v_{2} }}} }}^{{I_{2} }} \hfill \\ \left\{ \begin{gathered} {d}u = \left( {EIw^{\prime\prime\prime} - EQw^{\prime}w^{\prime\prime}} \right){d}x \hfill \\ v = \delta w^{\prime} \hfill \\ \end{gathered} \right. \hfill \\ \to \left. {I_{1} = \left( {EIw^{\prime\prime} - \frac{1}{2}EQw^{{\prime}{2}} } \right)\delta w^{\prime}} \right|_{a}^{b} - \overbrace {{\int_{a}^{b} {\underbrace {{\left( {EIw^{\prime\prime\prime} - EQw^{\prime}w^{\prime\prime}} \right)}}_{{u_{1} }}\underbrace {{\delta w^{\prime}{d}x}}_{{{d}v_{1} }}} }}^{{I_{11} }} \hfill \\ \left\{ \begin{gathered} {d}u_{1} = \left( {EIw^{\prime\prime\prime\prime} - EQ\left( {w^{{\prime\prime}{2}} + w^{\prime}w^{\prime\prime\prime}} \right)} \right){d}x \hfill \\ v_{1} = \delta w \hfill \\ \end{gathered} \right. \hfill \\ \to I_{11} = \left. {\left( {EIw^{\prime\prime\prime} - EQw^{\prime}w^{\prime\prime}} \right)\delta w} \right|_{a}^{b} - \int_{a}^{b} {\left( {EIw^{\prime\prime\prime\prime} - EQ\left( {w^{{\prime\prime}{2}} + w^{\prime}w^{\prime\prime\prime}} \right)} \right)\delta w{d}x} \hfill \\ \to I_{1} = \left. {\left( {EIw^{\prime\prime} - \frac{1}{2}EQw^{{\prime}{2}} } \right)\delta w^{\prime}} \right|_{a}^{b} - \left. {\left( {EIw^{\prime\prime\prime} - EQw^{\prime}w^{\prime\prime}} \right)\delta w} \right|_{a}^{b} + \int_{a}^{b} {\left( {EIw^{\prime\prime\prime\prime} - EQ\left( {w^{{\prime\prime}{2}} + w^{\prime}w^{\prime\prime\prime}} \right)} \right)\delta w{d}x} \hfill \\ \left\{ \begin{gathered} {d}u_{2} = \left( { - EQ\left( {w^{\prime\prime\prime}w^{\prime} + w^{{\prime\prime}{2}} } \right) + \frac{3}{2}EAw^{{\prime}{2}} w^{\prime\prime}} \right){d}x \hfill \\ v_{2} = \delta w \hfill \\ \end{gathered} \right. \hfill \\ \to I_{2} = \left. {\left( { - EQw^{\prime\prime}w^{\prime\prime} + \frac{1}{2}EAw^{{\prime}{3}} } \right)\delta w} \right|_{a}^{b} - \int_{a}^{b} {\left( { - EQ\left( {w^{\prime\prime\prime}w^{\prime} + w^{{\prime\prime}{2}} } \right) + \frac{3}{2}EAw^{{\prime}{2}} w^{\prime\prime}} \right)\delta w{d}x} \hfill \\ \delta U^{*} = 0 \to \left\{ \begin{gathered} + \int_{a}^{b} {\left( {EIw^{\prime\prime\prime\prime} - EQ\left( {w^{{\prime\prime}{2}} + w^{\prime}w^{\prime\prime\prime}} \right)} \right)\delta w{d}x} - \int_{a}^{b} {\left( { - EQ\left( {w^{\prime\prime\prime}w^{\prime} + w^{{\prime\prime}{2}} } \right) + \frac{3}{2}EAw^{{\prime}{2}} w^{\prime\prime}} \right)\delta w{d}x} = 0 \hfill \\ \to \int_{a}^{b} {\left( {EIw^{\prime\prime\prime\prime} - \frac{3}{2}EAw^{{\prime}{2}} w^{\prime\prime}} \right){d}x = 0 \to Eq.} \hfill \\ - \left. {\left( {EIw^{\prime\prime\prime} - EQw^{\prime}w^{\prime\prime}} \right)\delta w} \right|_{a}^{b} + \left. {\left( { - EQw^{\prime\prime}w^{\prime\prime} + \frac{1}{2}EAw^{{\prime}{3}} } \right)\delta w} \right|_{a}^{b} = 0 \to \mathrm{Boundary\;condition} \hfill \\ \left. {\left( {EIw^{\prime\prime} - \frac{1}{2}EQw^{{\prime}{2}} } \right)\delta w^{\prime}} \right|_{a}^{b} = 0 \to \mathrm{Boundary\;condition} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $$

(B.2)

Appendix C

The relations obtained from integration by parts (C.1) are used in the process of reducing the order of Eqs. (15) and (16) after the discretization process.

$$ \left\{ \begin{gathered} \int\limits_{a}^{b} {vw^{\prime\prime\prime\prime}{d}x = \int\limits_{a}^{b} {v^{\prime\prime}w^{\prime\prime}{d}x + vw^{\prime\prime\prime}\left| {_{a}^{b} - v^{\prime}w^{\prime\prime}\left| {_{a}^{b} } \right.} \right.} } \hfill \\ \int\limits_{a}^{b} {vw^{\prime\prime}(w^{\prime})^{2} {d}x = \frac{1}{3}v(w^{\prime})^{3} \left| {_{a}^{b} } \right. - \frac{1}{3}\int\limits_{a}^{b} {v^{\prime}(w^{\prime})^{3} {d}x} } \hfill \\ \int\limits_{a}^{b} {v[\delta^{\prime}_{D} (x - b) - \delta^{\prime}_{D} (x - a)]{d}x = v[\delta_{D} (x - b) - \delta_{D} (x - a)]\left| {_{a}^{b} } \right. - \int\limits_{a}^{b} {v^{\prime}[\delta_{D} (x - b) - \delta_{D} (x - a)]{d}x} } \hfill \\ = v[\delta_{D} (x - b) - \delta_{D} (x - a)]\left| {_{a}^{b} - [v^{\prime}(b) - v^{\prime}(a)] = } \right.v[\delta_{D} (x - b) - \delta_{D} (x - a)]\left| {_{a}^{b} } \right. - \int\limits_{a}^{b} {v^{\prime\prime}(x){d}x} \hfill \\ \end{gathered} \right. $$

(C.1)