On closed-loop vibrational control of underactuated mechanical systems

Abstract

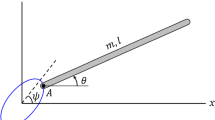
This paper discusses vibrational stabilization of a class of single-input, two degree-of-freedom mechanical systems. Considering two different control formulations—position-input and force-input—and both open- and closed-loop control, we find that the sets of attainable equilibrium positions for the unactuated coordinate are identical in every case. The subset of positions that are stabilizable, however, depends on the formulation. In general, the set of equilibria that can be stabilized using open-loop force-input is larger than the set that can be stabilized using open-loop position-input. And the use of feedback expands this stabilizable set even further. As examples, this paper presents the dynamic analysis, open- and closed-loop vibrational control, and the mechanics behind the stability of two underactuated systems, the Kapitza pendulum and a one-link horizontal pendulum.

Appendix

1.1 Averaged potential of a class of Lagrangian systems

The following presents an abstract of the concept of averaged potential based on [2, 50].

Consider an $(n+1)$-DOF, underactuated mechanical system with the n unactuated generalized coordinates $\varvec{q}_{\mathrm{u}}=(q_1,\ldots ,q_n)^T$, one actuated coordinate $q_{\mathrm{a}}$, and Lagrangian

$$\begin{aligned} L(\varvec{q}_{\mathrm{u}},\dot{\varvec{q}}_{\mathrm{u}};v)= & {} \frac{1}{2}\dot{\varvec{q}}_{\mathrm{u}}^T {\mathbb {M}}(\varvec{q}_{\mathrm{u}}) \dot{\varvec{q}}_{\mathrm{u}} \nonumber \\&+ v \varvec{A}^T(\varvec{q}_{\mathrm{u}}) \dot{\varvec{q}}_{\mathrm{u}} - V_{\mathrm{a}}(\varvec{q}_{\mathrm{u}};v) \end{aligned}$$

(A.1)

where $v=v(t)={\dot{q}}_{\mathrm{a}}$ is the control input, ${\mathbb {M}}(\varvec{q}_{\mathrm{u}})$ is the $n\times n$ inertia matrix, $\varvec{A}(\varvec{q}_{\mathrm{u}})$ is an $n\times 1$ inertial coupling vector, and $V_{\mathrm{a}}(\varvec{q}_{\mathrm{u}};v)$ is called the augmented potential.

Defining the momentum vector $\varvec{p}=(p_1,\ldots ,p_n)^T$, where $p_i=\frac{\partial L}{\partial {\dot{q}}_i}$, $i\in \{1,\ldots ,n\}$, and using the Legendre transformation $H(\varvec{q}_{\mathrm{u}},\varvec{p};v)=\varvec{p}^T \dot{\varvec{q}}_{\mathrm{u}}-L$, the Hamiltonian corresponding to (A.1) is in the form

$$\begin{aligned} H(\varvec{q}_{\mathrm{u}},\varvec{p};v)= & {} \frac{1}{2}\big (\varvec{p}-v\varvec{A}(\varvec{q}_{\mathrm{u}})\big )^T {\mathbb {M}}^{-1}(\varvec{q}_{\mathrm{u}})\big (\varvec{p}-v\varvec{A}(\varvec{q}_{\mathrm{u}})\big ) \nonumber \\&+ V_{\mathrm{a}}(\varvec{q}_{\mathrm{u}};v) \end{aligned}$$

(A.2)

Note that since $v=v(t)$, the Hamiltonian H is not conserved. If v is a T-periodic function, then the Hamiltonian (A.2) is also a T-periodic function and its average, called the averaged Hamiltonian can be determined as

$$\begin{aligned} {\bar{H}}(\bar{\varvec{q}}_{\mathrm{u}},\bar{\varvec{p}};{\bar{v}})=\frac{1}{T}\int _0^T H\big (\bar{\varvec{q}}_{\mathrm{u}},\bar{\varvec{p}};v(t)\big ) \mathrm{d}t \end{aligned}$$

(A.3)

where $\bar{\varvec{q}}_{\mathrm{u}}$ is the vector of the unactuated coordinates of the averaged dynamics and $\bar{\varvec{p}}$ is the vector of the average momenta. Replacing H from (A.2) and simplifying, the averaged Hamiltonian ${\bar{H}}$ is determined in the form

$$\begin{aligned} {\bar{H}}(\bar{\varvec{q}}_{\mathrm{u}},\bar{\varvec{p}})= & {} \frac{1}{2}\big (\bar{\varvec{p}}-{\bar{v}}\varvec{A}(\bar{\varvec{q}}_{\mathrm{u}})\big )^T {\mathbb {M}}^{-1}(\bar{\varvec{q}}_{\mathrm{u}})\big (\bar{\varvec{p}}-{\bar{v}}\varvec{A}(\bar{\varvec{q}}_{\mathrm{u}})\big ) \nonumber \\&+ V_{\mathrm{A}}(\bar{\varvec{q}}_{\mathrm{u}};{\bar{v}}) \end{aligned}$$

(A.4)

where the averaged potential $V_{\mathrm{A}}$ is

$$\begin{aligned} V_{\mathrm{A}}(\bar{\varvec{q}}_{\mathrm{u}};{\bar{v}}) = \mu \varvec{A}^T(\bar{\varvec{q}}_{\mathrm{u}}) {\mathbb {M}}^{-1}(\bar{\varvec{q}}_{\mathrm{u}})\varvec{A}(\bar{\varvec{q}}_{\mathrm{u}}) + {\bar{V}}_{\mathrm{a}}(\bar{\varvec{q}}_{\mathrm{u}}) \end{aligned}$$

(A.5)

and where the input parameter

$$\begin{aligned} \mu = \frac{1}{2} \left( \bar{v^2}-{\bar{v}}^2\right) \end{aligned}$$

(A.6)

and

$$\begin{aligned} {\bar{v}}=\frac{1}{T}\int _0^T v(t) \mathrm{d}t \end{aligned}$$

(A.7)

and

$$\begin{aligned} \bar{v^2}=\frac{1}{T}\int _0^T v^2(t) \mathrm{d}t \end{aligned}$$

(A.8)

Note that if the velocity function v(t) is zero-mean, then ${\bar{v}}=0$. However, for any function $v(t) \not \equiv 0$, one finds $\bar{v^2}\ne 0$.

For the averaged Hamiltonian ${\bar{H}}$, one can write

$$\begin{aligned} \frac{\partial {\bar{H}}}{\partial t}=0 \end{aligned}$$

(A.9)

Therefore, the equilibria and stability of the averaged dynamics, and according to the averaging theorem, the existence and stability of the periodic orbits of the original time-periodic system, can be studied using the averaged potential $V_{\mathrm{A}}(\bar{\varvec{q}}_{\mathrm{u}};{\bar{v}})$.

1.2 Averaging of mechanical control-affine systems

The following theorem is based on the results developed in Bullo [11], Bullo and Lewis [12], and as presented in Tahmasian et al. [44].

Consider an n-DOF mechanical control-affine system with m inputs. The dynamics of the system can be written in the general form

$$\begin{aligned} \ddot{\varvec{q}}= & {} \varvec{f}(\varvec{q},\dot{\varvec{q}})+\displaystyle \sum \limits _{i=1}^{m} \varvec{g}_i(\varvec{q}) u_i(t), \nonumber \\ \varvec{q}(0)= & {} \varvec{q}_0,\; \dot{\varvec{q}}(0)= \varvec{v}_0 \end{aligned}$$

(A.10)

where $\varvec{q}=(q_1, \;\ldots , \; q_n)^T$ is the vector of generalized coordinates and $u_i(t)$ are the inputs. Suppose that $\varvec{f}(\varvec{q},\dot{\varvec{q}})$ and $\varvec{g}_i(\varvec{q})$ depend polynomially on their arguments, are twice differentiable in $\varvec{q}$, and that the components of $\varvec{f}(\varvec{q},\dot{\varvec{q}})$ are homogeneous in $\dot{\varvec{q}}$ of degree two and less. Consider high-frequency, high-amplitude inputs $u_i(t)$, $i\in \{1,\ldots ,m\}$, in the following form:

$$\begin{aligned} u_i(t)=\omega v_i(\omega t) \end{aligned}$$

(A.11)

where $\omega$ is the (high) frequency, and $v_i(t)$ are zero-mean, T-periodic functions.

Using the state vector $\varvec{x}=(\varvec{q}^T, \; \dot{\varvec{q}}^T)^T$ and the inputs defined in (A.11), system (A.10) can be written in the first-order form

$$\begin{aligned} \dot{\varvec{x}}= & {} \varvec{Z}(\varvec{x})+\displaystyle \sum \limits _{i=1}^{m}\varvec{Y}_i(\varvec{x}) \omega v_i (\omega t), \nonumber \\ \varvec{x}(0)= & {} \varvec{x}_0=(\varvec{q}_0^T\, ,\, \varvec{v}_0^T)^T \end{aligned}$$

(A.12)

where $\varvec{Z}(\varvec{x})=\left( \dot{\varvec{q}}^T, \; \varvec{f}^T(\varvec{q},\dot{\varvec{q}})\right) ^T$ is the drift vector field and $\varvec{Y}_i(\varvec{x})=\left( \varvec{0}_{1\times n}, \; \varvec{g}_i^T(\varvec{q})\right) ^T$ are the input vector fields.

For the inputs (A.11), define scalar parameters $\kappa _i$, $\lambda _{ij}$, and $\mu _{ij}$, for $i,j\in \{1,\ldots ,m\}$, as follows

$$\begin{aligned} \kappa _i= & {} \frac{1}{T}\int _0^T \int _0^t v_i(\tau )\mathrm{d}\tau \mathrm{d}t \end{aligned}$$

(A.13)

$$\begin{aligned} \lambda _{ij}= & {} \frac{1}{T}\int _0^T \left( \int _0^t v_i(\tau )\mathrm{d}\tau \right) \left( \int _0^t v_j(\tau )\mathrm{d}\tau \right) \mathrm{d}t \nonumber \\ \end{aligned}$$

(A.14)

and

$$\begin{aligned} \mu _{ij}=\frac{1}{2}(\lambda _{ij}-\kappa _i \kappa _j) \end{aligned}$$

(A.15)

Also, consider the symmetric product between two input vector fields $\varvec{Y}_i(\varvec{x})$ and $\varvec{Y}_j(\varvec{x})$ defined as

$$\begin{aligned} \langle \varvec{Y}_i:\varvec{Y}_j \rangle (\varvec{x})= \langle \varvec{Y}_j:\varvec{Y}_i \rangle (\varvec{x}) = \left[ \varvec{Y}_j(\varvec{x}),[\varvec{Z}(\varvec{x}),\varvec{Y}_i(\varvec{x})]\right] \nonumber \\ \end{aligned}$$

(A.16)

where $[\cdot ,\cdot ]$ denotes the Lie bracket of vector fields.

The averaged dynamics of time-periodic system (A.12) then is determined as

$$\begin{aligned} \dot{\bar{\varvec{x}}}=\varvec{Z}(\bar{\varvec{x}})-\displaystyle \sum \limits _{i,j=1}^{m} \mu _{ij} \langle \varvec{Y}_i: \varvec{Y}_j \rangle (\bar{\varvec{x}}) \end{aligned}$$

(A.17)

with the initial condition $\bar{\varvec{x}}(0)=\bar{\varvec{x}}_0=\varvec{x}_0+\sum \nolimits _{i=1}^m \kappa _i \varvec{Y}_i(\varvec{x}_0)$, where $\bar{\varvec{x}}=(\bar{\varvec{q}}^T, \; \dot{\bar{\varvec{q}}}^T)^T$ is the state vector of the averaged dynamics [12, 44].