Wave propagation in nonlinear monoatomic chains with linear and quadratic damping

Abstract

Due to the substantial role of damping in the performance of real-life structures, many researchers are interested in analyzing its various effects on the dynamic behavior of systems. In this work, a theoretical investigation is performed on the wave propagation in monoatomic nonlinear chains in the presence of energy dissipation. Both linear and quadratic damping models are considered and the time-dependent dispersion relations for the weakly nonlinear monoatomic chains are obtained using the multiple-scale method. Also, a numerical simulation is carried out to verify the results obtained by the analytical formulations. In addition to the comparison of the dispersion relations for chains with hardening and softening nonlinearities, their wave-filtering performances in the presence of linear and quadratic damping are compared. According to the results, increasing the damping ratio in chains with hardening nonlinearity leads to lower dispersion branches compared to their linear counterparts. On the other hand, in systems with softening nonlinearity, higher dispersion branches than the linear chains are achieved by increasing the damping ratio. The results of this work bring us one step closer to modeling the real behavior of nonlinear phononic crystals and lattice materials to have a better perception of their extraordinary dynamic capabilities.

Appendices

Appendix 1

The three terms on the right-hand side of Eq. (6) can be expanded in the following forms:

$$ \begin{gathered} 2D_{0} D_{1} u_{n}^{\left( 0 \right)} = i\omega_{0} D_{1} A\left( {T_{1} } \right)e^{{i\omega_{0} T_{0} }} e^{i\kappa nd} - i\omega_{0} D_{1} \overline{A}\left( {T_{1} } \right)e^{{ - i\omega_{0} T_{0} }} e^{ - i\kappa nd} \hfill \\ = i\omega_{0} D_{1} A\left( {T_{1} } \right)e^{{i\omega_{0} T_{0} }} e^{i\kappa nd} + c.c., \hfill \\ \end{gathered} $$

(42)

$$ \begin{gathered} \alpha \left( {u_{n}^{\left( 0 \right)} - u_{n - 1}^{\left( 0 \right)} } \right)^{3} + \alpha \left( {u_{n}^{\left( 0 \right)} - u_{n + 1}^{\left( 0 \right)} } \right)^{3} \hfill \\ = \alpha \left\{ {\left[ {\frac{A}{2}\left( {1 - e^{ - i\kappa d} } \right)e^{{i\omega_{0} T_{0} }} e^{i\kappa nd} + \frac{{\overline{A}}}{2}\left( {1 - e^{i\kappa d} } \right)e^{{ - i\omega_{0} T_{0} }} e^{ - i\kappa nd} } \right]^{3} } \right. \hfill \\ \left. { + \left[ {\frac{A}{2}\left( {1 - e^{i\kappa d} } \right)e^{{i\omega_{0} T_{0} }} e^{i\kappa nd} + \frac{{\overline{A}}}{2}\left( {1 - e^{ - i\kappa d} } \right)e^{{ - i\omega_{0} T_{0} }} e^{ - i\kappa nd} } \right]^{3} } \right\} \hfill \\ = \frac{3}{8}\alpha A^{2} \overline{A}\left( {6 - 4e^{i\kappa d} - 4e^{ - i\kappa d} + e^{ - 2i\kappa d} + e^{2i\kappa d} } \right)e^{{i\omega_{0} T_{0} }} e^{i\kappa nd} \hfill \\ + \frac{{A^{3} }}{8}\left( {1 - 3e^{ - \kappa d} + 3e^{ - 2\kappa d} - e^{ - 3i\kappa d} } \right) + c.c. \hfill \\ = \frac{3}{8}\alpha A^{2} \overline{A}\left( {6 - 8\cos \kappa d + 2\cos 2\kappa d} \right)e^{{i\omega_{0} T_{0} }} e^{i\kappa nd} \hfill \\ + \frac{{A^{3} }}{8}\left( {1 - 3e^{ - \kappa d} + 3e^{ - 2\kappa d} - e^{ - 3i\kappa d} } \right)e^{{3i\omega_{0} T_{0} }} e^{3i\kappa nd} + c.c., \hfill \\ \end{gathered} $$

(43)

$$ \begin{gathered} \mu_{l} D_{0} \left( {2u_{n}^{\left( 0 \right)} - u_{n - 1}^{\left( 0 \right)} - u_{n + 1}^{\left( 0 \right)} } \right) = \mu_{l} i\omega_{0} \left[ {\begin{array}{*{20}c} {\frac{A}{2}\left( {2 - e^{ - i\kappa d} - e^{i\kappa d} } \right)e^{{i\omega_{0} T_{0} }} e^{i\kappa nd} } \\ { + \overline{\frac{A}{2}} \left( {2 - e^{ - i\kappa d} - e^{i\kappa d} } \right)e^{{ - i\omega_{0} T_{0} }} e^{ - i\kappa nd} } \\ \end{array} } \right] \hfill \\ = \frac{{\mu_{l} i\omega_{0} A}}{2}\left( {2 - e^{ - i\kappa d} - e^{i\kappa d} } \right)e^{{i\omega_{0} T_{0} }} e^{i\kappa nd} + c.c. . \hfill \\ \end{gathered} $$

(44)

Appendix 2

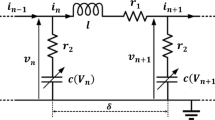
The governing equation of the quadratically damped phononic crystal of Fig. 1 is as follows:

$$ \begin{gathered} m\frac{{\partial^{2} u_{n} }}{{\partial t^{2} }} + k\left( {2u_{n} - u_{n - 1} - u_{n + 1} } \right) + \varepsilon \tilde{\alpha }\left( {u_{n} - u_{n - 1} } \right)^{3} + \varepsilon \tilde{\alpha }\left( {u_{n} - u_{n + 1} } \right)^{3} \hfill \\ + \varepsilon c_{quad} \left\{ {\left( {\frac{{\partial u_{n} }}{\partial t} - \frac{{\partial u_{n - 1} }}{\partial t}} \right)\left| {\frac{{\partial u_{n} }}{\partial t} - \frac{{\partial u_{n - 1} }}{\partial t}} \right|} \right\} \hfill \\ + \varepsilon c_{quad} \left\{ {\left( {\frac{{\partial u_{n} }}{\partial t} - \frac{{\partial u_{n + 1} }}{\partial t}} \right)\left| {\frac{{\partial u_{n} }}{\partial t} - \frac{{\partial u_{n + 1} }}{\partial t}} \right|} \right\} = 0. \hfill \\ \end{gathered} $$

(45)

Introducing nondimensional time $\tau = \omega_{nat} t$, the governing equation can be expressed as

$$ \begin{gathered} \ddot{u}_{n} + \left( {2u_{n} - u_{n - 1} - u_{n + 1} } \right) + \varepsilon \alpha \left( {u_{n} - u_{n - 1} } \right)^{3} + \varepsilon \alpha \left( {u_{n} - u_{n + 1} } \right)^{3} \hfill \\ + \varepsilon \mu_{quad} \left\{ {\left( {\dot{u}_{n} - \dot{u}_{n - 1} } \right)\left| {\dot{u}_{n} - \dot{u}_{n - 1} } \right| + \left( {\dot{u}_{n} - \dot{u}_{n + 1} } \right)\left| {\dot{u}_{n} - \dot{u}_{n + 1} } \right|} \right\} = 0, \hfill \\ \end{gathered} $$

(46)

where $= \frac{{\tilde{\alpha }}}{k}$ $\mu_{quad} = \frac{{c_{q} \omega_{nat}^{2} }}{k} = \frac{{c_{q} }}{m}$.

Appendix 3

Starting from Eq. (23), the term ${f}_{d}$ can be expressed as:

$$ f_{d} = \mu_{q} \dot{u}_{n}^{\left( 0 \right)} \left| {\dot{u}_{n}^{\left( 0 \right)} } \right|\left[ {\left( {1 - e^{ - i\kappa d} } \right)\left| {1 - e^{ - i\kappa d} } \right| + \left( {1 - e^{i\kappa d} } \right)\left| {1 - e^{i\kappa d} } \right|} \right] = \mu_{q} P\dot{u}_{n}^{\left( 0 \right)} \left| {\dot{u}_{n}^{\left( 0 \right)} } \right|, $$

(47)

where

$$ P = \left( {1 - e^{ - i\kappa d} } \right)\left| {1 - \left( {\cos \kappa d - i\sin \kappa d} \right)} \right| + \left( {1 - e^{i\kappa d} } \right)\left| {1 - \left( {\cos \kappa d + i\sin \kappa d} \right)} \right|. $$

(48)

Considering the absolute values of the complex terms in Eq. (48), we can write:

$$ \begin{gathered} \left| {1 - \left( {\cos \kappa d - i\sin \kappa d} \right)} \right| = \left| {1 - \left( {\cos \kappa d + i\sin \kappa d} \right)} \right| = \hfill \\ \sqrt {\left( {1 - \cos \kappa d} \right)^{2} + \sin^{2} \kappa d} = \sqrt {2 - 2\cos \kappa d} . \hfill \\ \end{gathered} $$

(49)

Substituting from Eq. (49) in Eq. (48), the following expression for $f_{d}$ can be obtained:

$$ \begin{gathered} \mu_{q} \dot{u}_{n}^{\left( 0 \right)} \left| {\dot{u}_{n}^{\left( 0 \right)} } \right|\left[ {\left( {1 - e^{ - i\kappa d} } \right)\sqrt {2 - 2\cos \kappa d} + \left( {1 - e^{i\kappa d} } \right)\sqrt {2 - 2\cos \kappa d} } \right] \hfill \\ = \mu_{q} \dot{u}_{n}^{\left( 0 \right)} \left| {\dot{u}_{n}^{\left( 0 \right)} } \right|\sqrt {2 - 2\cos \kappa d} \left( {2 - 2\cos \kappa d} \right) = \mu_{q} \left( {2 - 2\cos \kappa d} \right)^{\frac{3}{2}} { }\dot{u}_{n}^{\left( 0 \right)} \left| {\dot{u}_{n}^{\left( 0 \right)} } \right| \hfill \\ \end{gathered} $$

(50)