Skip to main content
SpringerLink
Log in

Hopf bifurcation of a fractional-order double-ring structured neural network model with multiple communication delays

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

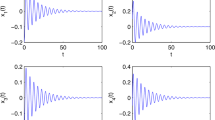
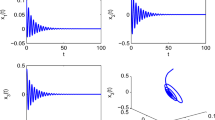
In this paper, we delve into the Hopf bifurcation of a novel high-dimensional delayed fractional neural network model with bicyclic structure sharing a node. Under some mild assumptions, the developed model is equivalently transformed into a system with two delays representing, respectively, the sum of delays in each ring. By applying the formula of Coates’s flow graph, we first derive the associated characteristic equation of the transformed system. Then, picking one delay as a control parameter and regarding the other one as a constant in its stable interval, we establish the respective critical value of each delay for the occurrence of Hopf bifurcation. It is shown that the stability behavior remains unchanged for the small control delay and will be lost once the delay passes through the critical value. Numerical simulations and sensitivity analysis are performed to validate the theoretical results and identify the most sensitive parameter to the Hopf bifurcation point.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Data availability

Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.

References

  1. Forti, M., Tesi, A.: New conditions for global stability of neural networks with application to linear and quadratic programming problems. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 42(7), 354–366 (1995). https://doi.org/10.1109/81.401145

    Article  MathSciNet  MATH  Google Scholar 

  2. Kulkarni, S.R., Rajendran, B.: Spiking neural networks for handwritten digit recognition supervised learning and network optimization. Neural Netw. 103, 118–127 (2018). https://doi.org/10.1016/j.neunet.2018.03.019

    Article  Google Scholar 

  3. Fröhlich, F., Bazhenov, M.: Coexistence of tonic firing and bursting in cortical neurons. Phys. Rev. E 74(3), 031922 (2006). https://doi.org/10.1103/PhysRevE.74.031922

    Article  Google Scholar 

  4. Herry, C., Johansen, J.P.: Encoding of fear learning and memory in distributed neuronal circuits. Nat. Neurosci. 17(12), 1644–1654 (2014). https://doi.org/10.1038/nn.3869

    Article  Google Scholar 

  5. Morita, M.: Associative memory with nonmonotone dynamics. Neural Netw. 6(1), 115–126 (1993). https://doi.org/10.1016/S0893-6080(05)80076-0

    Article  Google Scholar 

  6. Anderson, J.A.: A simple neural network generating an interactive memory. Math. Biosci. 14(3–4), 197–220 (1972). https://doi.org/10.1016/0025-5564(72)90075-2

    Article  MATH  Google Scholar 

  7. Cao, J.D., Xiao, M.: Stability and Hopf bifurcation in a simplified BAM neural network with two time delays. IEEE Trans. Neural Netw. 18(2), 416–430 (2007). https://doi.org/10.1109/TNN.2006.886358

    Article  MathSciNet  Google Scholar 

  8. Cohen, M.A., Grossberg, S.: Absolute stability of global pattern formation and parallel memory storage by competitive neural networks. IEEE Trans. Syst. Man Cybern. 13(5), 815–826 (1983). https://doi.org/10.1109/TSMC.1983.6313075

    Article  MathSciNet  MATH  Google Scholar 

  9. Podlubny, I.: Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications. Academic Press, New York (1999)

    MATH  Google Scholar 

  10. Chen, Y.Q.: Ubiquitous fractional order controls? IFAC Proc. Vol. 39(11), 481–492 (2006). https://doi.org/10.3182/20060719-3-PT-4902.00081

    Article  Google Scholar 

  11. Koeller, R.: Applications of fractional calculus to the theory of viscoelasticity. J. Appl. Mech. 51(2), 299–307 (1984). https://doi.org/10.1115/1.3167616

    Article  MathSciNet  MATH  Google Scholar 

  12. Heymans, N., Bauwens, J.C.: Fractal rheological models and fractional differential equations for viscoelastic behavior. Rheol. Acta 33(3), 210–219 (1994). https://doi.org/10.1007/BF00437306

    Article  Google Scholar 

  13. Chen, W., Sun, H.G., Zhang, X.D., Korošak, D.: Anomalous diffusion modeling by fractal and fractional derivatives. Comput. Math. Appl. 59(5), 1754–1758 (2010). https://doi.org/10.1016/j.camwa.2009.08.020

    Article  MathSciNet  MATH  Google Scholar 

  14. Henry, B.I., Wearne, S.L.: Existence of turing instabilities in a two-species fractional reaction–diffusion system. SIAM J. Appl. Math. 62(3), 870–887 (2002). https://doi.org/10.1137/S0036139900375227

    Article  MathSciNet  MATH  Google Scholar 

  15. Pu, Y.F., Wang, W.X., Zhou, J.L., Wang, Y.Y., Jia, H.D.: Fractional differential approach to detecting textural features of digital image and its fractional differential filter implementation. Sci. China Inf. Sci. F 51(9), 1319–1339 (2008). https://doi.org/10.1007/s11432-008-0098-x

    Article  MathSciNet  MATH  Google Scholar 

  16. Chen, L.P., Yin, H., Huang, T.W., Yuan, L.G., Zheng, S., Yin, L.S.: Chaos in fractional-order discrete neural networks with application to image encryption. Neural Netw. 125, 174–184 (2020). https://doi.org/10.1016/j.neunet.2020.02.008

    Article  Google Scholar 

  17. Wang, F.Z., Shi, L.P., Wu, H.Q., He Lian, N., Chua, L.O.: Fractional memristor. Appl. Phys. Lett. 111(24), 243502 (2017). https://doi.org/10.1063/1.5000919

    Article  Google Scholar 

  18. Pu, Y.F., Yuan, X., Yu, B.: Analog circuit implementation of fractional-order memristor: arbitrary-order lattice scaling fracmemristor. IEEE Trans. Circuits Syst. I Regul. Pap. 65(9), 2903–2916 (2018). https://doi.org/10.1109/TCSI.2018.2789907

    Article  MathSciNet  Google Scholar 

  19. Lundstrom, B.N., Higgs, M.H., Spain, W.J., Fairhall, A.L.: Fractional differentiation by neocortical pyramidal neurons. Nat. Neurosci. 11(11), 1335–1342 (2008). https://doi.org/10.1038/nn.2212

    Article  Google Scholar 

  20. Anastasio, T.J.: The fractional-order dynamics of brainstem vestibulo-oculomotor neurons. Biol. Cybern. 72(1), 69–79 (1994). https://doi.org/10.1007/BF00206239

    Article  Google Scholar 

  21. Goldfain, E.: Fractional dynamics and the standard model for particle physics. Commun. Nonlinear Sci. Numer. Simul. 13(7), 1397–1404 (2008). https://doi.org/10.1016/j.cnsns.2006.12.007

    Article  MathSciNet  MATH  Google Scholar 

  22. Chen, L.P., Chai, Y., Wu, R.C., Ma, T.D., Zhai, H.Z.: Dynamic analysis of a class of fractional-order neural networks with delay. Neurocomputing 111, 190–194 (2013). https://doi.org/10.1016/j.neucom.2012.11.034

    Article  Google Scholar 

  23. Chen, J.J., Zeng, Z.G., Jiang, P.: Global Mittag–Leffler stability and synchronization of memristor-based fractional-order neural networks. Neural Netw. 51, 1–8 (2014). https://doi.org/10.1016/j.neunet.2013.11.016

    Article  MATH  Google Scholar 

  24. Kaslik, E., Sivasundaram, S.: Nonlinear dynamics and chaos in fractional-order neural networks. Neural Netw. 32, 245–256 (2012). https://doi.org/10.1016/j.neunet.2012.02.030

    Article  MATH  Google Scholar 

  25. Liu, H., Li, S.G., Wang, H.X., Sun, Y.G.: Adaptive fuzzy control for a class of unknown fractional-order neural networks subject to input nonlinearities and dead-zones. Inf. Sci. 454, 30–45 (2018). https://doi.org/10.1016/j.ins.2018.04.069

    Article  MathSciNet  MATH  Google Scholar 

  26. Marcus, C.M., Westervelt, R.M.: Stability of analog neural networks with delay. Phys. Rev. A 39(1), 347 (1989). https://doi.org/10.1103/PhysRevA.39.347

    Article  MathSciNet  Google Scholar 

  27. Wu, J.H.: Introduction to Neural Dynamics and Signal Transmission Delay, vol. 6. Walter de Gruyter, Berlin (2011)

    Google Scholar 

  28. Han, F., Wang, Z.J., Du, Y., Sun, X.J., Zhang, B.: Robust synchronization of bursting Hodgkin–Huxley neuronal systems coupled by delayed chemical synapses. Int. J. Nonlinear Mech. 70, 105–111 (2015). https://doi.org/10.1016/j.ijnonlinmec.2014.10.010

    Article  Google Scholar 

  29. Grossberg, S.: Nonlinear difference-differential equations in prediction and learning theory. Proc. Natl. Acad. Sci. U.S.A. 58(4), 1329 (1967). https://doi.org/10.1073/pnas.58.4.1329

    Article  MathSciNet  MATH  Google Scholar 

  30. Chen, Y.M.: Global stability of neural networks with distributed delays. Neural Netw. 15(7), 867–871 (2002). https://doi.org/10.1016/S0893-6080(02)00039-4

    Article  Google Scholar 

  31. Zou, S.F., Huang, L.H., Chen, Y.M.: Linear stability and Hopf bifurcation in a three-unit neural network with two delays. Neurocomputing 70(1–3), 219–228 (2006). https://doi.org/10.1016/j.neucom.2006.03.003

    Article  Google Scholar 

  32. Xiao, M., Zheng, W.X., Cao, J.D.: Hopf bifurcation of an \((n+1)\)-neuron bidirectional associative memory neural network model with delays. IEEE Trans. Neural Netw. Learn. Syst. 24(1), 118–132 (2012). https://doi.org/10.1109/TNNLS.2012.2224123

    Article  Google Scholar 

  33. Jefferson, M.F., Pendleton, N., Lucas, C.P., Lucas, S.B., Horan, M.A.: Evolution of artificial neural network architecture: prediction of depression after mania. Methods Inf. Med. 37(03), 220–225 (1998). https://doi.org/10.1055/s-0038-1634532

    Article  Google Scholar 

  34. Hoffman, R.E., Quinlan, D.M., Mazure, C.M., McGlashan, T.M.: Cortical instability and the mechanism of mania: a neural network simulation and perceptual test. Biol. Psychiatr. 49(6), 500–509 (2001). https://doi.org/10.1016/S0006-3223(00)01071-4

    Article  Google Scholar 

  35. Curry, J.H., Yorke, J.A.: A transition from Hopf bifurcation to chaos: computer experiments with maps on \({\mathbf{R}}^2\). In: The Structure of Attractors in Dynamical Systems, pp. 48–66 (1978). https://doi.org/10.1007/BFb0101779

  36. Hassard, B.D., Hassard, B., Kazarinoff, N.D., Wan, Y.H., Wan, Y.W.: Theory and Applications of Hopf Bifurcation, vol. 41. Cambridge University Press, Cambridge (1981)

    MATH  Google Scholar 

  37. Zhou, S., Xiao, M., Wang, L., Cheng, Z.S.: Bifurcation and oscillations of a multi-ring coupling neural network with discrete delays. Cognit. Comput. 13, 1233–1245 (2021). https://doi.org/10.1007/s12559-021-09920-y

    Article  Google Scholar 

  38. Kandasamy, U., Rajan, R.: Hopf bifurcation of a fractional-order octonion-valued neural networks with time delays. Discrete Contin. Dyn. Syst. Ser. S 13(9), 2537 (2020). https://doi.org/10.3934/dcdss.2020137

    Article  MathSciNet  MATH  Google Scholar 

  39. Huang, C.D., Wang, J., Chen, X.P., Cao, J.D.: Bifurcations in a fractional-order BAM neural network with four different delays. Neural Netw. 141, 344–354 (2021). https://doi.org/10.1016/j.neunet.2021.04.005

    Article  Google Scholar 

  40. Xu, C.J., Liu, Z.X., Yao, L.Y., Aouiti, C.: Further exploration on bifurcation of fractional-order six-neuron bi-directional associative memory neural networks with multi-delays. Appl. Math. Comput. 410, 126458 (2021). https://doi.org/10.1016/j.amc.2021.126458

    Article  MathSciNet  MATH  Google Scholar 

  41. Szentagothai, J.: The module-concept in cerebral cortex architecture. Brain Res. 95(2–3), 475–496 (1975). https://doi.org/10.1016/0006-8993(75)90122-5

    Article  Google Scholar 

  42. Guo, Z.V., Inagaki, H.K., Daie, K., Druckmann, S., Gerfen, C.R., Svoboda, K.: Maintenance of persistent activity in a frontal thalamocortical loop. Nature 545(7653), 181–186 (2017). https://doi.org/10.1038/nature22324

    Article  Google Scholar 

  43. Milo, R., Shen-Orr, S., Itzkovitz, S., Kashtan, N., Chklovskii, D., Alon, U.: Network motifs: simple building blocks of complex networks. Science 298(5594), 824–827 (2002). https://doi.org/10.1126/science.298.5594.824

    Article  Google Scholar 

  44. Hu, H.J., Huang, L.H.: Stability and Hopf bifurcation analysis on a ring of four neurons with delays. Appl. Math. Comput. 213(2), 587–599 (2009). https://doi.org/10.1016/j.amc.2009.03.052

    Article  MathSciNet  MATH  Google Scholar 

  45. Ge, J.H., Xu, J.: Stability and Hopf bifurcation on four-neuron neural networks with inertia and multiple delays. Neurocomputing 287, 34–44 (2018). https://doi.org/10.1016/j.neucom.2018.01.081

    Article  Google Scholar 

  46. Zhao, D.X., Wang, J.M.: Exponential stability and spectral analysis of a delayed ring neural network with a small-world connection. Nonlinear Dyn. 68(1), 77–93 (2012). https://doi.org/10.1007/s11071-011-0205-1

    Article  MathSciNet  MATH  Google Scholar 

  47. Huang, C.D., Cao, J.D., Xiao, M., Alsaedi, A., Hayat, T.: Effects of time delays on stability and Hopf bifurcation in a fractional ring-structured network with arbitrary neurons. Commun. Nonlinear Sci. Numer. Simul. 57, 1–13 (2018). https://doi.org/10.1016/j.cnsns.2017.09.005

    Article  MathSciNet  MATH  Google Scholar 

  48. Zhang, Y.Z., Xiao, M., Cao, J.D., Zheng, W.X.: Dynamical bifurcation of large-scale-delayed fractional-order neural networks with hub structure and multiple rings. IEEE Trans. Syst. Man Cybern. (2020). https://doi.org/10.1109/TSMC.2020.3037094

    Article  Google Scholar 

  49. Xing, R.T., Xiao, M., Zhang, Y.Z., Qiu, J.L.: Stability and Hopf bifurcation analysis of an (n+m)-neuron double-ring neural network model with multiple time delays. J. Syst. Sci. Complex 2021, 1–20 (2021). https://doi.org/10.1007/s11424-021-0108-2

    Article  Google Scholar 

  50. Deng, W.H., Li, C.P., Lü, J.H.: Stability analysis of linear fractional differential system with multiple time delays. Nonlinear Dyn. 48(4), 409–416 (2007). https://doi.org/10.1007/s11071-006-9094-0

    Article  MathSciNet  MATH  Google Scholar 

  51. Li, C.P., Ma, Y.T.: Fractional dynamical system and its linearization theorem. Nonlinear Dyn. 71(4), 621–633 (2013). https://doi.org/10.1007/s11071-012-0601-1

    Article  MathSciNet  MATH  Google Scholar 

  52. Desoer, C.A.: The optimum formula for the gain of a flow graph or a simple derivation of Coates’ formula. Proc. IRE 48(5), 883–889 (1960). https://doi.org/10.1109/JRPROC.1960.287625

  53. Diethelm, K., Ford, N.J., Freed, A.D.: A predictor–corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 29(1), 3–22 (2002). https://doi.org/10.1023/A:1016592219341

    Article  MathSciNet  MATH  Google Scholar 

  54. Chitnis, N., Hyman, J.M., Cushing, J.M.: Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model. Bull. Math. Biol. 70(5), 1272–1296 (2008). https://doi.org/10.1007/s11538-008-9299-0

    Article  MathSciNet  MATH  Google Scholar 

  55. Kong, J.D., Salceanu, P., Wang, H.: A stoichiometric organic matter decomposition model in a chemostat culture. J. Math. Biol. 76(3), 609–644 (2018). https://doi.org/10.1007/s00285-017-1152-3

    Article  MathSciNet  MATH  Google Scholar 

  56. Rihan, F., Al-Mdallal, Q., AlSakaji, H., Hashish, A.: A fractional-order epidemic model with time-delay and nonlinear incidence rate. Chaos Solitons Fractals 126, 97–105 (2019). https://doi.org/10.1016/j.chaos.2019.05.039

    Article  MathSciNet  MATH  Google Scholar 

Download references

Funding

This work was supported by the National Natural Science Foundation of China [Grant Numbers 12071293, 11671260].

Author information

Authors and Affiliations

  1. College of Science, University of Shanghai for Science and Technology, Shanghai, 200093, China

    Shuai Li & Sanling Yuan

  2. School of Mathematics and Statistics, Xinyang Normal University, Xinyang, 464000, China

    Chengdai Huang

Authors
  1. Shuai Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chengdai Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Sanling Yuan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sanling Yuan.

Ethics declarations

Conflict of interest

The authors declared that they have no conflict of interest.

Code availability

Not applicable.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, S., Huang, C. & Yuan, S. Hopf bifurcation of a fractional-order double-ring structured neural network model with multiple communication delays. Nonlinear Dyn 108, 379–396 (2022). https://doi.org/10.1007/s11071-021-07177-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-021-07177-6

Keywords

Search

Navigation