Skip to main content

Advertisement

SpringerLink
Log in

Dynamics of circular oscillator arrays subjected to noise

  • Feature Article
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

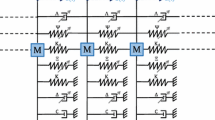
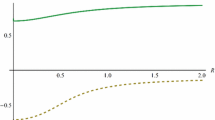
Energy localization, which are spatially confined response patterns, have been observed in turbomachinery applications, micro-electromechanical systems, and atomic crystals. While confined energy can reduce a device’s life-span, in sensing and energy harvesting applications, it can be beneficial to steer a system’s response into a localized mode. Building on earlier studies, in this article, the authors extend the research on localization by considering an array of coupled Duffing oscillators arranged in a circle. The system is composed of multiple nonlinear oscillators each connected to two neighboring oscillators via springs. Due to the periodic boundary conditions waves can propagate through the boundaries. These oscillators are hardening in most of the considered cases, and softening in the others. In the studied parameter range, the system is characterized by multi-stable behavior and a localized mode as well as a unison-low-amplitude motion coexist. The possibility that white noise can drive the system response from the localized mode to the low amplitude mode and thus suppresses energy localization is investigated. For different noise levels, the duration needed to stop energy localization as well as the probability to suppress localization within a certain time is numerically studied. In addition, the effects of linear coupling and nonlinear coupling between the oscillators on the strength of localization and the minimum noise addition needed to suppress energy localization are examined in depth. Moreover, modeling of large array dynamics with smaller subsystems is explored and dynamics with non-Gaussian noise is also considered.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Data Availability Statement

Data used in this work are available as time series data and results provided within the manuscript.

Notes

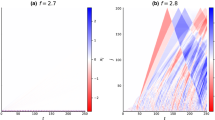
  1. The average over the transitioned samples is included in Fig. 8 for comparison. Since many samples have been discarded, this mean collapse time at \(\sigma =0.005\) is not completely equivalent to the other transition times with \(\sigma >0.005\).

References

  1. He, Z., Epureanu, B.I., Pierre, C.: Parametric study of the aeroelastic response of mistuned bladed disks. Comput. Struct. 85(11–14), 852–865 (2007)

    Article  Google Scholar 

  2. Sievers, A.J., Takeno, S.: Intrinsic localized modes in anharmonic crystals. Phys. Rev. Lett. 61(8), 970 (1988)

    Article  Google Scholar 

  3. Perkins, E., Chabalko, C., Balachandran, B.: Noise-influenced transient energy localization in an oscillator array. Nonlinear Theory Appl. IEICE 4(3), 232–243 (2013)

    Article  Google Scholar 

  4. Vakais, A.F., Cetinkaya, C.: Mode localization in a class of multidegree-of-freedom nonlinear systems with cyclic symmetry. SIAM J. Appl. Math. 53(1), 265–282 (1993)

    Article  MathSciNet  Google Scholar 

  5. Dick, A.J., Balachandran, B., Mote, C.D., Jr.: Intrinsic localized modes in microresonator arrays and their relationship to nonlinear vibration modes. Nonlinear Dyn. 54(1–2), 13–29 (2008)

    Article  Google Scholar 

  6. Dauxois, T., Peyrard, M.: Energy localization in nonlinear lattices. Phys. Rev. Lett. 70(25), 3935 (1993)

    Article  Google Scholar 

  7. Papangelo, A., Fontanela, F., Grolet, A., Ciavarella, M., Hoffmann, N.: Multistability and localization in forced cyclic symmetric structures modelled by weakly-coupled duffing oscillators. J. Sound Vib. 440, 202–211 (2019)

    Article  Google Scholar 

  8. Agarwal, V., Zheng, X., Balachandran, B.: Influence of noise on frequency responses of softening duffing oscillators. Phys. Lett. A 382(46), 3355–3364 (2018)

    Article  MathSciNet  Google Scholar 

  9. Perkins, E., Kimura, M., Hikihara, T., Balachandran, B.: Effects of noise on symmetric intrinsic localized modes. Nonlinear Dyn. 85(1), 333–341 (2016)

    Article  MathSciNet  Google Scholar 

  10. Marin, J.L., Aubry, S.: Breathers in nonlinear lattices: numerical calculation from the anticontinuous limit. Nonlinearity 9(6), 1501 (1996)

    Article  MathSciNet  Google Scholar 

  11. Nayfeh, A.H., Balachandran, B.: Applied Nonlinear Dynamics: Analytical, Computational, and Experimental Methods. Wiley, Hoboken (2008)

    MATH  Google Scholar 

  12. Dankowicz, H., Schilder, F.: Recipes for continuation. SIAM (2013)

  13. Kloeden, P. E., Platen, E.: Numerical solution of stochastic differential equations. Applications of mathematics 23. Springer, Berlin [etc, (3rd corrected printing) edition, (1999)

  14. Oksendal, B.: Stochastic Differential Equations: an Introduction with Applications. Springer, Berlin (2013)

    MATH  Google Scholar 

  15. Higham, D.J.: An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM Rev. 43(3), 525–546 (2001)

    Article  MathSciNet  Google Scholar 

  16. Freidlin, M. I., Wentzell, A. D.: Random perturbations. In: Random Perturbations of Dynamical Systems, pages 15–43. Springer, (1998)

  17. Matkowsky, B.J., Schuss, Z.: The exit problem for randomly perturbed dynamical systems. SIAM J. Appl. Math. 33(2), 365–382 (1977)

    Article  MathSciNet  Google Scholar 

  18. Dick, A.J., Balachandran, B., Mote, C.D., Jr.: Localization in microresonator arrays: influence of natural frequency tuning. J. Comput. Nonlinear Dyn. 5(1), 011002 (2010)

    Article  Google Scholar 

  19. Balachandran, B., Perkins, E., Fitzgerald, T.: Response localization in micro-scale oscillator arrays: influence of cubic coupling nonlinearities. Int. J. Dyn. Control 3(2), 183–188 (2015)

    Article  MathSciNet  Google Scholar 

  20. Cilenti, L., Balachandran, B.: Transient probability in basins of noise influenced responses of mono and coupled duffing oscillators. Chaos: Interdiscip. J. Nonlinear Sci. 31(6), 063117 (2021)

    Article  MathSciNet  Google Scholar 

  21. Golubitsky, M., Stewart, I., Schaeffer, David G.: Singularities and Groups in Bifurcation Theory: Volume II. volume 69. Springer Science & Business Media (2012)

  22. Crawford, J.D., Knobloch, E.: Symmetry and symmetry-breaking bifurcations in fluid dynamics. Annu. Rev. Fluid Mech. 23(1), 341–387 (1991)

    Article  MathSciNet  Google Scholar 

  23. Rhoads, J.F., Shaw, S.W., Turner, K.L.: Nonlinear dynamics and its applications in micro-and nanoresonators. J. Dyn. Syst. Measurement Control 132(3), 034001 (2010)

    Article  Google Scholar 

  24. Amabili, M., Païdoussis, M.P.: Review of studies on geometrically nonlinear vibrations and dynamics of circular cylindrical shells and panels, with and without fluid-structure interaction. Appl. Mech. Rev. 56(4), 349–381 (2003)

    Article  Google Scholar 

  25. Masud, A., Bergman, L. A.: Solution of the four dimensional fokker-planck equation: Still a challenge. In: Icossar. volume 2005, pages 1911–1916. Citeseer, (2005)

  26. Kogan, S.: Electronic Noise and Fluctuations in Solids. Cambridge University Press, Cambridge (2008)

    Google Scholar 

  27. Press, W.H.: Flicker noises in astronomy and elsewhere. Comments Astrophys. 7, 103–119 (1978)

    Google Scholar 

  28. Smith, J. O.: Mathematics of the discrete Fourier transform (DFT): with audio applications. Julius Smith, (2007)

  29. Timmer, J., Koenig, M.: On generating power law noise. Astron. Astrophys. 300, 707 (1995)

    Google Scholar 

  30. Caughey, T.K.: Nonlinear theory of random vibrations. Adv. Appl. Mech. 11, 209–253 (1971)

    Article  Google Scholar 

  31. King, M.E., Aubrecht, J., Vakakis, A.F.: Experimental study of steady-state localization in coupled beams with active nonlinearities. J. Nonlinear Sci. 5(6), 485–502 (1995)

    Article  Google Scholar 

  32. Niedergesaß, B., Papangelo, A., Grolet, A., Vizzaccaro, A., Fontanela, F., Salles, L., Sievers, A., Hoffmann, N.: Experimental observations of nonlinear vibration localization in a cyclic chain of weakly coupled nonlinear oscillators. J. Sound Vib. 497, 115952 (2021)

    Article  Google Scholar 

Download references

Acknowledgements

The authors are grateful for the support received from the U.S. National Science Foundation, through Grant CMMI-1760366.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, University of Maryland, College Park, MD, 20742, USA

    Balakumar Balachandran, Thomas Breunung & Abdulrahman Alofi

  2. Department of Mechanical Engineering, Stevens Institute of Technology, Hoboken, NJ, 07030, USA

    Gizem D. Acar

  3. Department of Mathematics, University of Maryland, College Park, MD, 20742, USA

    James A. Yorke

Authors
  1. Balakumar Balachandran
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Thomas Breunung
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Gizem D. Acar
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Abdulrahman Alofi
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. James A. Yorke
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Balakumar Balachandran.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Balachandran, B., Breunung, T., Acar, G.D. et al. Dynamics of circular oscillator arrays subjected to noise. Nonlinear Dyn 108, 1–14 (2022). https://doi.org/10.1007/s11071-021-07165-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-021-07165-w

Keywords

Search

Navigation