Nonholonomic dynamics of the Twistcar vehicle: asymptotic analysis and hybrid dynamics of frictional skidding

Abstract

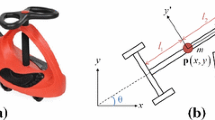
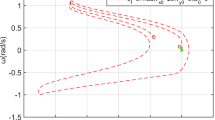
The Twistcar vehicle is a classic example of a nonholonomic dynamical system. The vehicle model consists of two rigid links connected by an actuated rotary joint and supported by wheeled axles, where nonholonomic constraints are assumed to impose no skidding of the wheels. Recent experimental measurements conducted with a robotic Twistcar prototype have shown disagreements with previous theoretical analyses. In particular, significant skidding has been observed, in addition to discrepancies with respect to theoretical predictions of divergence in oscillations of the vehicle’s speed and orientation, as well as direction reversal depending on the vehicle’s structure. The goal of our research is to resolve this disagreement by generalizing the theoretical analysis. First, we extend previous asymptotic analysis by incorporating the effects of links’ inertia and oscillation amplitude of the input angle on the direction of net motion. Next, we formulate the vehicle’s hybrid dynamics under frictional bounds and skid-state transitions. Using numerical analysis, we obtain optimal values for the vehicle’s mean speed and energetic cost-of-transport as a function of the input frequency. Our results improve the agreement between theory and experiments and suggest directions for further experimental investigation.

Appendix—singularity analysis of the hybrid dynamics

Table 2 Determinants $\Delta _{ijk}$ of the system’s dynamics for all cases

Table 3 Singularity conditions

The dynamics of the constrained system in (7) and (9) can be rearranged into differential algebraic system as:

(31)

The inertia matrix ${{\mathbf {M}}}$ is positive definite, except for degenerate cases where $m_2$ and/or $I_1$ vanish ($\kappa ,\eta _1=0$), which result in ${{\mathbf {M}}}$ being only positive semi-definite (i.e., singular). Singularity of the constrained dynamics (31) depends on rank of the $6 \times 6$ matrix ${{\mathbf {A}}}$, whose determinant is denoted $\Delta$. It has been shown in [29] that this matrix has full rank ($\Delta \ne 0$) even for the degenerate point-mass model where $\kappa =\eta _1=0$ and $\mathrm {rank}({{\mathbf {M}}})=2$, as long as ${\beta }_1 \ne 0$.

We now investigate conditions for singularity of the dynamics under all possible skid states, considering both cases of controlled actuation torque $\tau (t)$ or controlled steering angle $\phi (t)$. In the latter case of controlled angle, since $\tau$ appears only in the fourth row of (31), and $\phi (t)$ is no longer unknown, both $\tau$ and ${\ddot{\phi }}$ can be eliminated by removing both fourth row and fourth column of ${{\mathbf {A}}}$ and reducing (31) to a $5 \times 5$ system. If the first axle skids, ${\sigma }_1(t)={{\mathbf {w}}}_1(q) \cdot {{\dot{\mathbf{q}}}}\ne 0$, the constraint in the fifth row of (31) no longer holds, and ${\lambda }_1$ can be eliminated from (31). Therefore, both the fifth row and fifth column of ${{\mathbf {A}}}$ should be removed. Similarly, if the second axle skids, the sixth row and sixth column of ${{\mathbf {A}}}$ should be removed. If additionally, the input is the steering angle, the fourth row and column of ${{\mathbf {A}}}$ should be removed as well. That is, each case is associated with removing the fourth and/or fifth and/or sixth row and column from ${{\mathbf {A}}}$. This results in $n \times n$ matrix for $n \in \{3,4,5,6\}$, which is still positive semi-definite. Singularity of each case can be assessed by analyzing the determinant $\Delta _{ijk}$ of the matrix obtained by removing the $\{i,j,k\}^{th}$ rows and columns of ${{\mathbf {A}}}$. (For example, we denote $\Delta _4$, $\Delta _{56}$, $\Delta _{456}$ etc.). For convenience, the matrix ${{\mathbf {A}}}$ is calculated using the nondimensional quantities defined in (10). Due to rotational invariance of (31), evaluation is made for ${\theta }=0$ without loss of generality. Expressions for the $n \times n$ determinants for all cases are given in Table 2. Conditions for singularity in all possible skid states and choice of controlled input are summarized in Table 3. We assume that ${\alpha }\in (0,1)$ and ${\beta }_1,{\beta }_2 \in [0,1]$, but alternative limits can be considered as well. The results in Table 3 show that in most of the skid states, the overly simplifying assumptions of massless link (${\kappa }=0$) and/or point masses ($\eta _i=0$) lead to singularity of the dynamics, where wither accelerations or constraint forces may grow unbounded.