Virtual target approach-based optimal guidance law with both impact time and terminal angle constraints

Abstract

To attack a stationary target with both impact time and angle constraints, a novel two-stage guidance strategy is proposed based on the virtual target approach. A moving virtual target that satisfies both impact time and angle requirements is introduced, which substantially simplifies the problem without estimating the time-to-go and its feasibility has been theoretically proved in this paper. For the first stage, taking into account the nonlinear engagement dynamics, an energy optimal closed-loop guidance law is derived to intercept the virtual target with zero impact angle, which is in an analytical form so it can be implemented without any numerical algorithms. Then for the second stage, the proportional navigation guidance law is employed to enhance the robustness against potential disturbances, which also offers the property that the overall two-stage guidance law is almost-smooth at the switching time. The proposed methodology is capable to accommodate the all-aspect attacking scenario with arbitrary initial conditions and arbitrary terminal impact constraints. At last, the effect of navigation coefficients as well as the performance of the proposed guidance law in different engagement scenarios is assessed by several numerical simulations.

Appendices

Appendix A: Proof of Theorem and Corollary

1.1 Appendix A.1: Proof of Theorem 1

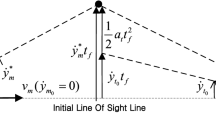
From the triangular geometry in Fig. 2, following equations are derived based on the Law of Cosines.

$$\begin{aligned}&r_v^2(t)=r_t^2(t)+V^2\left( T_{\mathrm{imp}}-t\right) ^2\nonumber \\&\quad -2r_t(t)V\left( T_{\mathrm{imp}}-t\right) \nonumber \\&\quad \cos \left( \lambda _t(t)-\gamma _v\right) \end{aligned}$$

(A.1)

$$\begin{aligned}&r_t^2(t)=r_v^2(t)+V^2\left( T_{\mathrm{imp}}-t\right) ^2-\nonumber \\&\quad 2r_v(t)V\left( T_{\mathrm{imp}}-t\right) \nonumber \\&\quad \cos \left( \pi +\gamma _v-\lambda _{v}(t)\right) \end{aligned}$$

(A.2)

Sufficiency We will proof $r_v(t)=0,\forall t\in [t^*,T_{\mathrm{imp}}]$ by contradiction, so we firstly assume $\exists t_1\in [t^*,T_{\mathrm{imp}}]:r_v(t_1)=C$ where $C\ne 0$ is a positive constant. Considering that the condition $\exists t^*\le T_{\mathrm{imp}}: \lambda _t(t)=\theta _{\mathrm{imp}}=\gamma _v,\forall t\in \left[ t^*, T_{\mathrm{imp}}\right]$ indicates ${\dot{\lambda }}_t(t)=0,\forall t\in \left[ t^*, T_{\mathrm{imp}}\right]$, it can be obtained from following equation that $\lambda _t(t)=\gamma (t),\forall t\in \left[ t^*, T_{\mathrm{imp}}\right]$

$$\begin{aligned} r_t(t){\dot{\lambda }}_t(t)=V\sin \left( \lambda _t(t)-\gamma (t)\right) =0 \end{aligned}$$

(A.3)

Thus $\gamma _{v}=\gamma (t)$ holds, then substitute it into

$$\begin{aligned} {\dot{r}}_v(t)=V\left( \cos (\lambda _v(t)-\gamma _v)-\cos (\lambda _v(t)-\gamma (t))\right) \end{aligned}$$

(A.4)

we have ${\dot{r}}_v(t)=0$, so $r_v(t)=C, \forall t\in \left[ t^*, T_{\mathrm{imp}}\right]$ is derived.

Again, since $\lambda _t(t)=\gamma _v,\forall t\in \left[ t^*, T_{\mathrm{imp}}\right]$, Eq. (A.1) can be rewritten in the form of

$$\begin{aligned} r_v^2(t)=\left( r_t(t)-V\left( T_{\mathrm{imp}}-t\right) \right) ^2 \end{aligned}$$

(A.5)

Take into account the fact that ${r_t}/{V}\le T_{\mathrm{imp}}-t$, it is obtained from (A.5) that

$$\begin{aligned} r_t(t)=V\left( T_{\mathrm{imp}}-t\right) -r_v(t)=V\left( T_{\mathrm{imp}}-t\right) -C \end{aligned}$$

(A.6)

which, however, contradicts to the condition that $r_t(T_{\mathrm{imp}})=0$, hence the assumption $\exists t_1\in [t^*,T_{\mathrm{imp}}]:r_v(t_1)=C\ne 0$ does not holds. Now we have completed the proof of $\exists t^*\le T_{\mathrm{imp}}, r_v(t)=0, \forall t\in [t^*,T_{\mathrm{imp}}]$.

Necessity Considering $r_v(t)=0,\forall t\in [t^*,T_{\mathrm{imp}}]$, from (A.2) we know that $r_t(t)=V\left( T_{\mathrm{imp}}-t\right)$ holds for $\forall t\in [t^*,T_{\mathrm{imp}}]$ then $r_t(T_{\mathrm{imp}})=0$ is obtained.

Now on the basis of $r_v(t)=0$ and $r_t(t)=V\left( T_{\mathrm{imp}}-t\right) , \forall t\in [t^*,T_{\mathrm{imp}}]$, Eq. (A.1) can be rewritten as

$$\begin{aligned} 2r_t^2(t)\left( 1-\cos \left( \lambda _t(t)-\gamma _v\right) \right) =0 \end{aligned}$$

(A.7)

thus $\lambda _t(t)=\gamma _v=\theta _{\mathrm{imp}},\forall t\in [t^*,T_{\mathrm{imp}}]$ is obtained.

1.2 Appendix A.2: Proof of Corollary 1

Since $\exists t^*\le T_{\mathrm{imp}}:r_v(t^*)=0$, substituting it into (A.2), we have

$$\begin{aligned} r_t(t^*)=V\left( T_{\mathrm{imp}}-t^*\right) \end{aligned}$$

(A.8)

which indicates that the triangle in Fig. 2 is isosceles and two following base angles at this moment are therefore equal, i.e.,

$$\begin{aligned} \pi +\gamma _v-\lambda _{v}(t^*)=\lambda _v(t^*)-\lambda _t(t^*) \end{aligned}$$

(A.9)

According to Theorem 1, $r_v(t^*)=0$ implies $\lambda _t(t^*)=\gamma _v$, then substitute it into (A.9), we have

$$\begin{aligned} \lambda _v(t^*)=\gamma _v+\frac{\pi }{2} \end{aligned}$$

(A.10)

holds. Now rewrite the first time derivative of $r_v(t)$ as

$$\begin{aligned} \begin{aligned} {\dot{r}}_v(t)&=V\left( \cos (\lambda _v(t)-\gamma _v)-\cos (\lambda _v(t)-\gamma (t))\right) \\&=2V\sin \left( \frac{2\lambda _{v}(t)-\gamma _v-\gamma (t)}{2}\right) \sin \left( \frac{\gamma _v-\gamma (t)}{2}\right) \\ \end{aligned}\nonumber \\ \end{aligned}$$

(A.11)

then substitute (A.10) into (A.11), we have ${\dot{r}}_v(t^*)=V\sin \left( \gamma (t^*)-\gamma _v\right)$. The objective in Problem 2, namely $r_v(t)=0, \forall t\in [t^*,T_{\mathrm{imp}}]$, indicates that ${\dot{r}}_v(t^*)=0$ holds, hence $\gamma (t^*)=\gamma _v$ is derived.

Appendix B: Derivation of ${\dot{\lambda }}_v$

From (1) and (4), we have

$$\begin{aligned} \begin{aligned}&r_t{\dot{\lambda }}_t=V\sin \left( \lambda _t-\gamma \right) \\&r_v{\dot{\lambda }}_v=V\left( \sin (\lambda _v-\gamma )-\sin (\lambda _v-\gamma _v)\right) \end{aligned} \end{aligned}$$

(B.1)

such that

$$\begin{aligned}&{\dot{\lambda }}_v=\frac{r_t{\dot{\lambda }}_t}{r_v\sin (\lambda _t-\gamma )} \left( \sin (\lambda _v-\lambda _t)\cos (\lambda _t-\gamma )\nonumber \right. \\&\quad \left. +\sin (\lambda _t-\gamma )\cos (\lambda _v-\lambda _t)-\sin (\lambda _v-\gamma _v)\right) \end{aligned}$$

(B.2)

Then according to the Rule of Sines and Cosines, the triangle geometry in Fig. 2 give us

$$\begin{aligned}&\sin (\lambda _v-\lambda _t)=\frac{(T_{\mathrm{imp}}-t)V}{r_v}\sin (\lambda _t-\gamma _v) \end{aligned}$$

(B.3)

$$\begin{aligned}&\sin (\lambda _v-\gamma _v)=\frac{r_t}{r_v}\sin (\lambda _t-\gamma _v) \end{aligned}$$

(B.4)

$$\begin{aligned}&\cos (\lambda _v-\lambda _t)=\frac{r_t^2+r_v^2-(T_{\mathrm{imp}}-t)^2V^2}{2r_tr_v} \end{aligned}$$

(B.5)

$$\begin{aligned}&r_t^2-(T_{\mathrm{imp}}-t)^2V^2=r_v^2\nonumber \\&\quad +2(T_{\mathrm{imp}}-t)Vr_v\cos (\lambda _v-\gamma _v) \end{aligned}$$

(B.6)

And we know that

$$\begin{aligned} \cos (\lambda _t-\gamma )=-\frac{{\dot{r}}_t}{V} \end{aligned}$$

(B.7)

from (1). Now substitute (B.3)-(B.7) into (B.2) which becomes

$$\begin{aligned} \begin{aligned} {\dot{\lambda }}_v =&\frac{r_t{\dot{\lambda }}_t}{r_v\sin (\lambda _t-\gamma )}\left( \frac{(T_{\mathrm{imp}}-t)V}{r_v}\sin (\lambda _t-\gamma _v)\right. \\&\left. \left( -\frac{{\dot{r}}_t}{V}\right) -\frac{r_t}{r_v}\sin (\lambda _t-\gamma _v)\right) \\&+\frac{r_t{\dot{\lambda }}_t}{r_v\sin (\lambda _t-\gamma )}\sin (\lambda _t-\gamma )\\&\frac{r_t^2+r_v^2-(T_{\mathrm{imp}}-t)^2V^2}{2r_tr_v}\\ =&-\frac{V{\dot{r}}_t}{r_v^2}\sin (\lambda _t-\gamma _v)\left( T_{\mathrm{imp}}-t -\left( -\frac{r_t}{{\dot{r}}_t}\right) \right) +\frac{{\dot{\lambda }}_t}{2}\\&+\frac{r_t{\dot{\lambda }}_t}{r_v}\left( \frac{r_v^2+2(T_{\mathrm{imp}}-t)Vr_v\cos (\lambda _v-\gamma _v)}{2r_tr_v}\right) \\ =&\left( 1+\frac{(T_{\mathrm{imp}}-t)V\cos (\lambda _v-\gamma _v)}{r_v}\right) {\dot{\lambda }}_t\\&-\frac{V{\dot{r}}_t}{r_v^2}\sin (\lambda _t-\gamma _v)\left( T_{\mathrm{imp}}-t \right. \\&\left. -\left( -\frac{r_t}{{\dot{r}}_t}\right) \right) \\ \end{aligned}\nonumber \\ \end{aligned}$$

(B.8)

then Eq. (37) is derived.