Basins and bifurcations of a delayed feedback control system and its experimental verification for a DC bus circuit

Abstract

The present study deals with the basins of the equilibrium points embedded within the normal forms of Bogdanov–Takens bifurcation with delayed feedback control. It is numerically shown that the unstable periodic orbit that coexists with the equilibrium point stabilized by delayed feedback control is associated with the basin of the stabilized point. The relation between the periodic orbit and the basin indicates that for enlarging the basin, a homoclinic bifurcation for the orbit and a saddle point can provide useful information for the design of delayed feedback controllers. These results are experimentally confirmed in a real direct-current bus circuit that has dynamics similar to that of the normal form .

Appendices

Appendix A: Solutions of time-delayed dynamical systems

This appendix gives a brief explanation of the solutions of autonomous time-delayed dynamical systems. For simplicity, we consider a time-delayed system with single scalar variable $x \in {\mathbb {R}}$ and a single constant delay $\tau \ge 0$,

$$\begin{aligned} \dot{x}(t) = f\left( x(t), x(t-\tau )\right) . \end{aligned}$$

(19)

The dynamics depends on both the current state x(t) and the previous state $x(t-\tau )$. Therefore, a time function,

$$\begin{aligned} x(t) = \phi (t),\quad t\in [-\tau , 0], \end{aligned}$$

(20)

is required as an initial condition for the time development of time-delayed system (19).

Appendix B: Saddle-node bifurcation of UPOs in a DC bus circuit with DFC

This appendix explains the bifurcation scenario that includes the saddle-node bifurcation of UPOs described by the gray lines in Fig. 9. With an increase in k from 0 for a fixed delay time $\tau \in [6.52, 10.00]$, a pair of UPOs appear at the saddle-node bifurcation curve. As an example, the bifurcation scenario with a fixed $\tau = 8.0$ is shown in Fig. 15. The top panel shows an enlarged view of the bifurcation curves in Fig. 9; the bottom panel shows a bifurcation diagram for $x_1$. The red symbols $\text {HP}_\text {sub}$, HC, and SN denote the bifurcation points of the Hopf bifurcation of equilibrium point $[x_{1+}^*, x_{2+}^*]^\text {T}$, the homoclinic bifurcation of a UPO, and the saddle-node bifurcation of UPOs, respectively.

We now review the bifurcation scenario in Fig. 15 with an increase in k from 0. The unstable equilibrium point $[x_{1+}^*, x_{2+}^*]^\text {T}$ is stabilized and UPO 1 appears via a subcritical Hopf bifurcation at $k \approx 0.07$ ($\text {HP}_\text {sub}$). With a further increase in k, UPO 1 enlarges and then disappears via the homoclinic bifurcation at $k \approx 0.18$ (HC). At $k \approx 0.25$, UPO 2 and UPO 3 are created by the saddle-node bifurcation (SN). The equilibrium point $[x_{1+}^*, x_{2+}^*]^\text {T}$ becomes unstable and UPO 2 disappears via a subcritical Hopf bifurcation at $k \approx 0.35$ ($\text {HP}_\text {sub}$).

Appendix C: Procedure for setting initial functions

This appendix describes an experimental procedure for setting three restricted initial functions. The implementation of the CPL and the delay unit can be found in our previous study [42]. Figure 16 shows a DC bus circuit with a delayed feedback controller.

Fig. 15

Bifurcation curves (top) and bifurcation diagram (bottom) of system (15) along feedback gain k with fixed delay $\tau = 8.0$. The top panel shows an enlarged view of Fig. 9 and the bottom panel shows a bifurcation diagram for the $x_1$ component of $[x_{1+}^*, x_{2+}^*]^\text {T}$ and UPOs

Fig. 16

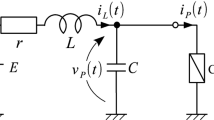
DC bus circuit diagram for circuit used in our experiments. The delayed feedback controller is represented by the shaded area. E and $v_\text {0}$ are bipolar power supplies; two switches are opened at time $t = 0$; the delay unit (PIC18F2550) controls output voltage $v_\text {out}(t)$ using the open/close status of the switches

Two bipolar power supplies⁸, which can output both positive and negative currents, are used for voltage E and initial voltage $v_\text {0}$. The power supply that supplies $v_\text {0}$ is connected to the DC bus line by a switch. This switch is paired with another switch; they open and close at the same time. The lower switch is connected to a 5-V power supply. The delay unit detects whether the switch is open or closed. The delay unit is implemented using a peripheral interface controller (PIC: PIC18F2550-I/SP, Microchip Technology). The unit was modified from a previous one [42] to read the switch’s open/close status and to handle a voltage range of $v_\text {P} \in [6.0, 20.0]\ \text {V}$. The output voltage $v_\text {out}(t)$ of the delay unit can be adjusted in accordance with programs implemented in PIC.

The experimental procedure used for setting the initial functions is as follows. First, set $v_\text {0}$ to a voltage in voltage set (18) and close the switches. Second, after a sufficient amount of time, open the switches at $t = 0$. Third, set the output voltage $v_\text {out}(t)$ to

$$\begin{aligned}&{\varvec{\varPhi }}_1(t):\quad v_\text {out}(t) = v_\text {P}(t-\varGamma ) \quad t \ge 0, \end{aligned}$$

(21)

$$\begin{aligned}&{\varvec{\varPhi }}_2(t):\quad v_\text {out}(t) = \left\{ \begin{array}{ll} v^*_\text {P} &{} t \in [0,\varGamma )\\ v_\text {P}(t-\varGamma ) &{} t \ge \varGamma \end{array}\right. , \end{aligned}$$

(22)

$$\begin{aligned}&{\varvec{\varPhi }}_3(t):\quad v_\text {out}(t) = \left\{ \begin{array}{ll} v_\text {P}(t) &{} t \in [0,\varGamma )\\ v_\text {P}(t-\varGamma ) &{} t \ge \varGamma \end{array}\right. , \end{aligned}$$

(23)

where $v^*_\text {P} = {12.0}\ \text {V}$ corresponds to the equilibrium point (i.e., the operating point) of $v_\text {P} (t)$. We can easily see that $v_\text {out}(t)$ in Eqs. (21) and (22) realizes the initial functions ${\varvec{\varPhi }}_1(t)$ and ${\varvec{\varPhi }}_2(t)$, respectively. $v_\text {out}(t)$ in Eq. (23) realizes ${\varvec{\varPhi }}_3(t)$ in a shifted time scale. That is, the DC bus system starts with initial point $v_\text {out}(0) = v_\text {0}$ and runs without control (i.e., $i_\text {u} = 0$) from $t = 0$ to $t = \varGamma$; DFC works from $t = \varGamma$.