1 Introduction

The singular nonlinear models are of great significance in the variety of fields, i.e., biology, technology, applied mathematics, engineering and physics. The typical mathematical representation of the singular Emden–Fowler equation is written as [1,2,3,4,5]:

$$ \left\{ {\begin{array}{*{20}l} {\frac{{{\text{d}}^{2} U}}{{{\text{d}}X^{2} }} + \frac{\Upsilon }{X}\frac{{{\text{d}}U}}{{{\text{d}}X}} + g(X)h(U) = 0,} \hfill & {0 < X \le 1,\Upsilon \ge 0,} \hfill \\ {U(0) = \alpha ,} \hfill & {\frac{{{\text{d}}U(0)}}{{{\text{d}}X}} = 0,} \hfill \\ \end{array} } \right. $$
(1)

where \(\alpha\) is constant, \(\Upsilon\) represents the shape factor and X shows the singular point. The singular model (1) has been applied to mathematically development of the numerous model arising in broad fields like stellar structure, astrophysics, isothermal gas spheres and mathematical physics [6,7,8]. It is always considered tough to solve the singular nonlinear models due to singular points at the origin. Few numerical/analytical techniques available in the literature to solve the singular models. Parand et al. [9] introduced meshfree numerical computing procedure for Emden–Fowler system, and Singh et al. [10] used Haar wavelet quasi linearization method for numerical solution of Emden–Fowler model. Bencheikh [11] applied Bernstein polynomial method for nonlinear singular Emden–Fowler equations. Parand et al. [6] implemented Hermite functions based collocation scheme for solving the singular models. Sabir et al. [12] solved third-order nonlinear singular functional differential model using the differential transformation scheme. Sadaf et al. [13] introduced Legendre-homotopy method for boundary value problems (BVPs) with higher order terms. Dizicheh et al. [14] present a Legendre wavelet spectral technique to solve the Lane–Emden differential systems. Parand et al. [15] solved singular astrophysics problems using the rational Chebyshev based collocation procedures.

The said approaches have their specific potential, exactness, sensitivity and competence as well as accountabilities and defects over another. The present study is related to solve the third-order Emden–Fowler model using the Gudermannian neural network (GNN) as an activation function along with the optimization of global search with particle swarm optimization (PSO) and local search with active set (AS) scheme, i.e., GANN-PSOAS approach. The general form of the nonlinear third-order Emden–Fowler model (NTO-EFM) is written as [16]:

$$ \left\{ {\begin{array}{*{20}l} {\frac{{{\text{d}}^{3} U}}{{{\text{d}}X^{3} }} + \frac{2\Upsilon }{X}\frac{{{\text{d}}^{2} U}}{{{\text{d}}X^{2} }} + \frac{\Upsilon (\Upsilon - 1)}{{X^{2} }}\frac{{{\text{d}}U}}{{{\text{d}}X}} + g(X)h(U) = 0,} \hfill & {} \hfill \\ {U(0) = \alpha ,} \hfill & {\frac{{{\text{d}}U(0)}}{{{\text{d}}X}} = \frac{{{\text{d}}^{2} U(0)}}{{{\text{d}}X^{2} }} = 0.} \hfill \\ \end{array} } \right. $$
(2)

The above model clearly indicates the double singular points at X = 0 and X2 = 0. Few current applications of the stochastic solvers are seen in broad fields [17,18,19,20,21] and particularly, in plasma physics problems [22], financial model [23], dusty plasma models [24], bioinformatics problem of HIV infection spresd [25], Thomas–Fermi atom's models [26, 27], nonlinear reactive transport model [28], fin model [29], neuro-fuzzy model [30], nonlinear singular models [16, 31], doubly singular nonlinear models [32], prey-predator models [33], nonlinear models [34], model of heartbeat dynamics [35], corneal shape model [36], multi-point boundary value problems [37], atomic physics model [38], temperature distribution dynamics of human head [39], singular functional differential system [40] and novel COVID-19 dynamics with nonlinear SITR system [41]. These motivations demonstrated the worth of the stochastic numerical solvers due to their better precision/accuracy and convergence. Thus, we are interested to exploit/explore the stochastic computing paradigm to design a reliable methodology based on GANN, trained with PSO and AS scheme to solve the NTO-EFM including single/multi singularities.

The innovative characteristics of the GANN-PSOAS scheme are listed as follows:

  • A new continuous differential mappings of GANN models are presented for the solution of singular NTO-EFMs by construction of merit function in mean square sense and optimization is performed with combined heuristics of PSOAS.

  • The proposed GANN-PSOAS scheme is efficiently implemented to solve three problems of the NTO-EFM with singularity at origin with reasonable precision.

  • The achieved numerical outcomes of proposed GANN-PSOAS approach matched with the reference exact solutions for each variant of singular NTO-EFM that indicates the exactness, precision and consistency.

  • The outcome of statistics for proposed GANN-PSOAS approach of on sufficient large multiple execution through performance measures on median, mean, standard deviation, Nash–Sutcliffe efficiency (NSE), semi-interquartile range (S.IR), and Theil's inequality coefficient (TIC) further certify the worth.

The remaining portions of the present investigation are described as: Sect. 2 shows the proposed structure and optimization schemes. Section 3 represents the performance indices. Section 4 indicates the details of the numerical outcomes. The conclusions along with future research studies are shown in Sect. 5.

2 Proposed methodology

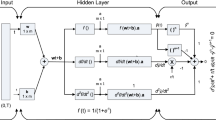
In this section, the differential operators of GNN are designed along with the necessary description for solving the NTO-EFM. The mathematical modeling, the objective function and its learning process are provided here for proposed solver GANN-PSOAS.

2.1 Gudermannian Function based Mathematical Modeling

The capability of GNN systems is presented for consistent, reliable and trustworthy results for the optimization of the proposed problem. \(U(X)\) represents the continuous mapping results, and its derivatives are written as:

$$ \begin{aligned} & \hat{U}(X) = \sum\limits_{i\, = \,1}^{k} {\beta_{i} Z(w_{i} X + c_{i} )} , \\ & \hat{U}^{(n)} = \sum\limits_{i = 1}^{k} {\beta_{i} Z^{(n)} (w_{i} X + c_{i} )} , \\ \end{aligned} $$
(3)

where k and Z represent the number of neurons and activation function, whereas \(\beta\), \(w\) and \(c\) are the unknown weight vectors ‘W’ given as: \({\varvec{W}} = [\user2{\beta ,w,c}]\), for \({\varvec{\beta}} = [\beta_{1} ,\beta_{2} ,\beta_{3} ,...,\beta_{m} ]\),\({\varvec{w}} = [w_{1} ,w_{2} ,w_{3} ,...,w_{m} ]\) and \({\varvec{c}} = [c_{1} ,c_{2} ,c_{3} ,...,c_{m} ]\).

The Gudermannian-based NN is given as:

$$ U(X) = 2\left( {\tan^{ - 1} e^{X} - \frac{1}{4}\pi } \right). $$
(4)

Using the Gudermannian-based activation function provided in Eq. (3), the continuous mapping of differential operators takes the form as

$$ \begin{aligned} & \hat{U}(X) = \sum\limits_{i = 1}^{m} {2\beta_{i} \left( {\tan^{ - 1} e^{{(w_{i} X + c_{i} )}} - \frac{1}{4}\pi } \right)} , \\ & \hat{U}^{{\prime }} (X) = \sum\limits_{i = 1}^{m} {2\beta_{i} w_{i} \left( {\frac{{e^{{(w_{i} X + c_{i} )}} }}{{1 + \left( {e^{{(w_{i} X + c_{i} )}} } \right)^{2} }}} \right)} , \\ & \hat{U}^{{\prime \prime }} (X) = \sum\limits_{i = 1}^{m} {2\beta_{i} w_{i}^{2} \left( {\frac{{e^{{(w_{i} X + c_{i} )}} }}{{1 + \left( {e^{{(w_{i} X + c_{i} )}} } \right)^{2} }} - \frac{{2e^{{(w_{i} X + c_{i} )^{3} }} }}{{\left( {1 + \left( {e^{{(w_{i} X + c_{i} )}} } \right)^{2} } \right)^{2} }}} \right)} . \\ \end{aligned} $$
(5)

To solve the NTO-EFM, an objective function using the sense of mean squared error becomes as:

$$ \xi_{{{\text{FIT}}}} = \xi_{{{\text{FIT}} - 1}} + \xi_{{{\text{FIT}} - 2}} , $$
(6)

where \(\xi_{FIT}\) is an error function associated with NTO-EFM, \(\xi_{FIT - 1}\) and \(\xi_{FIT - 2}\) denote the fitness functions of the model differential form and boundary conditions, written as

$$ \xi_{{{\text{FIT}} - 1}} = \frac{1}{N}\sum\limits_{k = 1}^{N} {\left( {\frac{{{\text{d}}^{3} \hat{U}_{k} }}{{{\text{d}}X_{k}^{3} }} + \frac{2\Upsilon }{{X_{k} }}\frac{{{\text{d}}^{2} \hat{Z}_{k} }}{{{\text{d}}X_{k}^{2} }} + \frac{\Upsilon (\Upsilon - 1)}{{X_{k}^{2} }}\frac{{{\text{d}}\hat{U}_{k} }}{{{\text{d}}X_{k} }} + g_{k} h(\hat{U}_{k} )} \right)}^{2} , $$
(7)
$$ \xi_{{{\text{FIT}} - 2}} = \frac{1}{2}\left( {(\hat{U}_{0} - \alpha )^{2} + \left( {\frac{{{\text{d}}\hat{U}_{0} }}{{{\text{d}}X_{k} }}} \right)^{2} + \left( {\frac{{{\text{d}}^{2} \hat{U}_{0} }}{{{\text{d}}X_{k}^{2} }}} \right)^{2} } \right), $$
(8)

where \(hN = 1,\,\,\hat{U}_{k} = \hat{U}(X_{k} ),\,\,\,g_{k} = f(U_{k} ),\,\) and \(X_{k} = kh\).

2.2 Optimization of the network

The optimization of the parameters is performed for the solution of NTO-EFM by incorporating the strength of hybrid-computing infrastructure based on swarm intelligence global technique PSO along with local AS approach.

PSO is an effective search scheme used as an alternate optimization procedure of genetic algorithms. PSO ascertained by Eberhart and Kennedy at the end of the nineteenth century [42,43,44] and applied as an easy technique with less memory requirements. In the system of search space, a single candidate outcome of decision variables for the optimization is called a particle and the set of these particles form a swarm. For the adaptation of optimization variables, PSO works through the optimization process based on the local and global positions \({\varvec{P}}_{LB}^{\Omega - 1}\) and \({\varvec{P}}_{GB}^{\Omega - 1}\) in the swarm. It metaheuristic technique and capable of searching very large spaces of candidate solutions. Particle swarm optimization does not require too many assumptions in optimization. The mathematical notations of the position and velocity are given as:

$$ {\varvec{X}}_{i}^{\Omega } = {\varvec{V}}_{i}^{\Omega - 1} + {\varvec{X}}_{i}^{\Omega - 1} , $$
(9)
$$ {\varvec{V}}_{i}^{\Omega } = \sigma {\varvec{V}}_{i}^{\Omega - 1} + \zeta_{1} ({\varvec{P}}_{LB}^{\Omega - 1} - {\varvec{X}}_{i}^{\Omega - 1} ){\varvec{\gamma}}_{1} + \zeta_{2} ({\varvec{P}}_{GB}^{\Omega - 1} - {\varvec{X}}_{i}^{\Omega - 1} ){\varvec{\gamma}}_{2} , $$
(10)

where \(\sigma\) is the inertia weight vector lie between [0, 1], \(\Omega\) is the flight index, \(\zeta_{1}\) and \(\zeta_{2}\) are the social/global and cognitive/local constants of the accelerations, whereas \({\varvec{\gamma}}_{1}\) and \({\varvec{\gamma}}_{2}\) are the vectors lie between 0 and 1. Recently, a wide-ranging review on hypothetical and experimental studies on PSO has been discussed by the research community in various dimensions, i.e., geotechnical modeling [45], optimize the performance of induction generator [46], traveling salesman problem [47], nonlinear electric circuits [48], mobile robot in a complex dynamic environment [49], physical model systems [50], combinatorial optimization problems [51] and permanent magnets optimization of synchronous motor [52].

The quick performance of PSO is the rapid convergence due to the hybridization with a suitable local search approach by taking the best values of PSO as a primary weight. Therefore, an appropriate local search active-set (AS) approach is applied for fast refinements of the results obtained by the PSO algorithm. Recently, AS approach is used in the scalable elastic net subspace clustering [53], nonlinear fluid mechanic models [54], multistage nonlinear nonconvex problems [55], symmetric eigenvalue complementarity problem [55] and embedded model predictive control [56].

The hybrid of PSOAS algorithm trains the GNNs as well as vital parameter setting for PSOAS scheme provided in Algorithm 1. The parameter setting is a crucial and critical step in the optimization process of the algorithms, i.e., PSO and AS, a slight variation of the parameter setting of these algorithm results in premature convergence, so all these parameters are adjusted with extensive care, after exhaustive experimentation, experience and knowledge of both optimization procedures and problem under consideration etc.

figure a

3 Performance matrices

The performance processes of two different measures of the system (1) based on TIC and NSE are presented. The global presentations of G.TIC and NSE are used to examine the proposed methodology for solving the NTO-EFM. The mathematical representations of these indices are provided as follows:

$$ \begin{aligned} & {\text{NSE = }}\left\{ {\begin{array}{*{20}l} {1 - \frac{{\sum\limits_{i = 1}^{n} {\left( {U_{i} - \hat{U}_{i} } \right)}^{2} }}{{\sum\limits_{i = 1}^{n} {\left( {U_{i} - \overline{U}_{i} } \right)}^{2} }},} \hfill & {\overline{U}_{i} = \frac{1}{n}\sum\limits_{i = 1}^{n} {U_{i} } ,} \hfill \\ \end{array} } \right. \\ & {\text{ENSE = 1}} - {\text{NSE}}{.} \\ \end{aligned} $$
(11)
$$ {\text{TIC = }}\frac{{\sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {U_{i} - \hat{U}_{i} } \right)}^{2} } }}{{\left( {\sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {U_{i}^{2} } } + \sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {\hat{U}_{i}^{2} } } } \right)}}, $$
(12)
$$ {\text{S}}{\text{.IR = }}\left\{ {\begin{array}{*{20}l} {0.5 \times \left( {Q_{3} - Q_{1} } \right),} \hfill \\ {Q_{3} = 3{{{\text{rd}}}} \,{\text{quartile,}}\,Q_{1} = 1{{{\text{st}}}} \,{\text{quartile}}{.}} \hfill \\ \end{array} } \right. $$
(13)

4 Simulation and results

In this section, the detail results are presented for the numerical outcomes to solve three problems of the NTO-EFM using the GANN-PSOAS approach.

Problem 1:

Consider the NTO-EFM-based example is shown as:

$$ \left\{ {\begin{array}{*{20}l} {\frac{{{\text{d}}^{3} U}}{{{\text{d}}X^{3} }} + \frac{2}{T}\frac{{{\text{d}}^{2} U}}{{{\text{d}}X^{2} }} - \frac{9}{8}(8 + X^{6} )U^{ - 5} = 0,} \hfill \\ {U(0) = 1,\frac{{{\text{d}}U(0)}}{{{\text{d}}X}} = \frac{{{\text{d}}^{2} U(0)}}{{{\text{d}}X^{2} }} = 0.} \hfill \\ \end{array} } \right. $$
(14)

The exact result of the above equation is \(\sqrt {1 + X^{3} }\), and the error function becomes as:

$$ \xi_{{{\text{FIT}}}} = \frac{1}{N}\sum\limits_{m = 1}^{N} {\left( {8X_{m} \frac{{{\text{d}}^{3} \hat{U}}}{{{\text{d}}X_{m}^{3} }} + 16\frac{{{\text{d}}^{2} \hat{U}}}{{{\text{d}}X_{m}^{2} }} - 9X_{m} (X_{m}^{6} + 8)\hat{U}^{ - 5} } \right)^{2} } + \frac{1}{3}\left( {\left( {\hat{U}_{0} - 1} \right)^{2} + \left( {\frac{{{\text{d}}\hat{U}_{0} }}{{{\text{d}}X_{0} }}} \right)^{2} + \left( {\frac{{{\text{d}}^{2} \hat{U}_{0} }}{{{\text{d}}X_{0}^{2} }}} \right)^{2} } \right). $$
(15)

Problem 2:

Consider the NTO-EFM including multi-singularities is shown as:

$$ \left\{ {\begin{array}{*{20}l} {\frac{{{\text{d}}^{3} U}}{{{\text{d}}X^{3} }} + \frac{4}{X}\frac{{{\text{d}}^{2} U}}{{{\text{d}}X^{2} }} + \frac{2}{{X^{2} }}\frac{{{\text{d}}U}}{{{\text{d}}X}} - 9(4 + 10X^{3} + 3X^{6} )U = 0,} \hfill \\ {U(0) = 1,\frac{{{\text{d}}U(0)}}{{{\text{d}}X}} = \frac{{{\text{d}}^{2} U(0)}}{{{\text{d}}X^{2} }} = 0.} \hfill \\ \end{array} } \right. $$
(16)

The exact result of the above equation is \(e^{{X^{3} }}\) along with the fitness/error function provided below:

$$ \begin{aligned} \xi_{{{\text{FIT}}}} = & \frac{1}{N}\sum\limits_{m = 1}^{N} {\left( {X_{m}^{2} \frac{{{\text{d}}^{3} \hat{U}}}{{{\text{d}}X_{m}^{3} }} + 4X_{m} \frac{{{\text{d}}^{2} \hat{U}}}{{{\text{d}}X_{m}^{2} }} + 2\frac{{{\text{d}}\hat{U}}}{{{\text{d}}X_{m} }} - 9X_{m}^{2} (4 + 10X_{m}^{3} + 3X_{m}^{6} )\hat{U}} \right)^{2} } \\ & + \frac{1}{3}\left( {\left( {\hat{U}_{0} - 1} \right)^{2} + \left( {\frac{{{\text{d}}\hat{U}_{0} }}{{{\text{d}}X_{0} }}} \right)^{2} + \left( {\frac{{{\text{d}}^{2} \hat{U}_{0} }}{{{\text{d}}X_{0}^{2} }}} \right)^{2} } \right). \\ \end{aligned} $$
(17)

Problem 3:

Consider the NTO-EFM including multi-singularities at the origin is shown as:

$$ \left\{ {\begin{array}{*{20}l} {\frac{{{\text{d}}^{3} U}}{{{\text{d}}X^{3} }} + \frac{8}{X}\frac{{{\text{d}}^{2} U}}{{{\text{d}}X^{2} }} + \frac{12}{{X^{2} }}\frac{{{\text{d}}U}}{{{\text{d}}X}} + 1 = 0,} \hfill \\ {U(0) = 1,\frac{{{\text{d}}U(0)}}{{{\text{d}}X}} = \frac{{{\text{d}}^{2} U(0)}}{{{\text{d}}X^{2} }} = 0.} \hfill \\ \end{array} } \right. $$
(18)

The exact result of the above equation is \(- \left( {\frac{1}{90}X^{3} - 1} \right)\), and the error function becomes as:

$$ \begin{aligned} \xi_{{{\text{FIT}}}} = & \frac{1}{N}\sum\limits_{m = 1}^{N} {\left( {X_{m}^{2} \frac{{{\text{d}}^{3} \hat{U}}}{{{\text{d}}X_{m}^{3} }} + 8T_{m} \frac{{{\text{d}}^{2} \hat{U}}}{{{\text{d}}X_{m}^{2} }} + 12\frac{{{\text{d}}\hat{U}}}{{{\text{d}}X_{m} }} + X_{m}^{2} } \right)^{2} } \\ & \quad + \frac{1}{3}\left( {\left( {\hat{U}_{0} - 1} \right)^{2} + \left( {\frac{{{\text{d}}\hat{U}_{0} }}{{{\text{d}}X_{0} }}} \right)^{2} + \left( {\frac{{{\text{d}}^{2} \hat{U}_{0} }}{{{\text{d}}X_{0}^{2} }}} \right)^{2} } \right). \\ \end{aligned} $$
(19)

Problem 4:

Consider the NTO-EFM including multi-singularities at the origin is shown as:

$$ \left\{ {\begin{array}{*{20}l} {\frac{{{\text{d}}^{3} U}}{{{\text{d}}X^{3} }} + \frac{4}{X}\frac{{{\text{d}}^{2} U}}{{{\text{d}}X^{2} }} + \frac{2}{{X^{2} }}\frac{{{\text{d}}U}}{{{\text{d}}X}} + XU^{2} = 0,} \hfill \\ {U(0) = 1,\frac{{{\text{d}}U(0)}}{{{\text{d}}X}} = \frac{{{\text{d}}^{2} U(0)}}{{{\text{d}}X^{2} }} = 0.} \hfill \\ \end{array} } \right. $$
(20)

The exact result of the above equation is \(1 + X^{10}\), while the error-based fitness is expressed as:

$$ \begin{aligned} \xi_{{{\text{FIT}}}} = & \frac{1}{N}\sum\limits_{m = 1}^{N} {\left( {X_{m}^{2} \frac{{{\text{d}}^{3} \hat{U}}}{{{\text{d}}X_{m}^{3} }} + 4T_{m} \frac{{{\text{d}}^{2} \hat{U}}}{{{\text{d}}X_{m}^{2} }} + 2\frac{{{\text{d}}\hat{U}}}{{{\text{d}}X_{m} }} + X_{m}^{2} \hat{U}^{2} } \right)^{2} } \\ & \quad + \frac{1}{3}\left( {\left( {\hat{U}_{0} - 1} \right)^{2} + \left( {\frac{{{\text{d}}\hat{U}_{0} }}{{{\text{d}}X_{0} }}} \right)^{2} + \left( {\frac{{{\text{d}}^{2} \hat{U}_{0} }}{{{\text{d}}X_{0}^{2} }}} \right)^{2} } \right). \\ \end{aligned} $$
(21)

Optimization of the NTO-EFM-based examples 1–4 is accomplished by manipulating the PSOAS approach using the Gudemannian function as an objective function for fifty independent executions to find the parameters of the system. A set of best weights are provided to authenticate the projected numerical values of the model given in Eq. (1) for 10 neurons. The mathematical notations of the projected numerical outcomes are written as:

$$ \begin{aligned} \hat{U}_{1} (X) = & - 0.07\left( {2\tan^{ - 1} e^{( - 3.004X - 5.985)} - \frac{1}{2}\pi } \right) + 5.4845\left( {2\tan^{ - 1} e^{(2.8075X + 6.7644)} - \frac{1}{2}\pi } \right) \\ & \quad - 3.1639\left( {2\tan^{ - 1} e^{( - 1.739X - 1.653)} - \frac{1}{2}\pi } \right) + 1.5746\left( {2\tan^{ - 1} e^{( - 3.257X - 5.6424)} - \frac{1}{2}\pi } \right) \\ & \quad + 3.7517\left( {2\tan^{ - 1} e^{( - 1.131X - 6.608)} - \frac{1}{2}\pi } \right) + 12.588\left( {2\tan^{ - 1} e^{(0.0977X + 0.4688)} - \frac{1}{2}\pi } \right) \\ & \quad - 4.776\left( {2\tan^{ - 1} e^{( - 0.5593X + 2.6131)} - \frac{1}{2}\pi } \right) - 0.3478\left( {2\tan^{ - 1} e^{(1.7898X - 0.6415)} - \frac{1}{2}\pi } \right) \\ & \quad + 2.527\left( {2\tan^{ - 1} e^{(2.1674X + 0.7886)} - \frac{1}{2}\pi } \right) + 5.2395\left( {2\tan^{ - 1} e^{( - 1.903X - 0.8656)} - \frac{1}{2}\pi } \right), \\ \end{aligned} $$
(22)
$$ \begin{aligned} \hat{U}_{2} (X) = & 0.9743\left( {2\tan^{ - 1} e^{(8.0030X + 4.4796)} - \frac{1}{2}\pi } \right) - 1.4746\left( {2\tan^{ - 1} e^{(13.073X + 6.5331)} - \frac{1}{2}\pi } \right) \\ & \quad - 1.4746\left( {2\tan^{ - 1} e^{( - 2.2933X + 2.8480)} - \frac{1}{2}\pi } \right) + 3.4100\left( {2\tan^{ - 1} e^{(7.3623X + 8.2833)} - \frac{1}{2}\pi } \right) \\ & \quad - 1.8858\left( {2\tan^{ - 1} e^{( - 6.916X + 9.6506)} - \frac{1}{2}\pi } \right) + 0.8247\left( {2\tan^{ - 1} e^{( - 7.266X + 9.1292)} - \frac{1}{2}\pi } \right) \\ & \quad - 6.0506\left( {2\tan^{ - 1} e^{( - 6.646X + 9.2707)} - \frac{1}{2}\pi } \right) - 4.8015\left( {2\tan^{ - 1} e^{(0.8626X - 10.835)} - \frac{1}{2}\pi } \right) \\ & \quad + 0.7639\left( {2\tan^{ - 1} e^{( - 0.706X + 0.0.890)} - \frac{1}{2}\pi } \right) - 1.4884\left( {2\tan^{ - 1} e^{(0.5684X - 2.049)} - \frac{1}{2}\pi } \right), \\ \end{aligned} $$
(23)
$$ \begin{aligned} \hat{U}_{3} (X) = & 16.885\left( {2\tan^{ - 1} e^{(19.959X + 19.998)} - \frac{1}{2}\pi } \right) + 14.570\left( {2\tan^{ - 1} e^{( - 18.37X - 19.916)} - \frac{1}{2}\pi } \right) \\ & \quad - 15.547\left( {2\tan^{ - 1} e^{(14.147X + 13.0948)} - \frac{1}{2}\pi } \right) + 19.619\left( {2\tan^{ - 1} e^{(0.0012X + 1.7629)} - \frac{1}{2}\pi } \right) \\ & \quad + 15.139\left( {2\tan^{ - 1} e^{(2.7368X - 8.9748)} - \frac{1}{2}\pi } \right) + 14.8743\left( {2\tan^{ - 1} e^{(1.1241X - 10.309)} - \frac{1}{2}\pi } \right) \\ & \quad - 5.4440\left( {2\tan^{ - 1} e^{( - 19.996X - 19.963)} - \frac{1}{2}\pi } \right) - 11.486\left( {2\tan^{ - 1} e^{( - 19.996X + 19.956)} - \frac{1}{2}\pi } \right) \\ & \quad + 19.990\left( {2\tan^{ - 1} e^{( - 2.4909X + 8.6705)} - \frac{1}{2}\pi } \right) + 14.558\left( {2\tan^{ - 1} e^{(11.4909X + 19.9451)} - \frac{1}{2}\pi } \right). \\ \end{aligned} $$
(24)

The best set of weights and result comparison based on the reference exact/proposed outcomes for all the problems of the NTO-EFM are illustrated in Fig. 1. It can be seen that the proposed results from the GANN-PSOAS approach and reference/exact solutions matched over one another for all four problems of the NTO-EFM. This matching of the numerical results indicates the perfection, correctness and excellence of the projected GANN-PSOAS approach. Figure 2 shows the absolute error (AE) values and performance investigations through GANN-PSOAS approach for three problems of the NTO-EFM and similar trend is observed for problem 4. Figure 2(a) depicts the AE values that have been found for higher decimal places of accuracy, i.e., 10–5 to 10–6, 10–4 to 10–5 and 10–6 to 10–7 for problems 1, 2 and 3 of the NTO-EFM. Figure 2(b) indicates the performance studies based on \(\xi_{FIT}\), ENSE and TIC for the problems 1–3 of the NTO-EFM. One may clearly observed that the \(\xi_{FIT}\) closely lie 10–7 to 10–8, 10–6 to 10–7 and 10–8 to 10–9, for examples 1, 2 and 3 of the NTO-EFM, respectively. The ENSE values lie in the domain from 10–9 to 10–10 for problems 1 and 3, while for problem 2, ENSE lie 10–8 to 10–9. TIC metric, for examples, 1 and 2 lie in the interval 10–8 to 10–9, while for problem 3 in the interval between 10–9 and 10–10.

Fig. 1
figure 1

Set of weights and proposed/true solutions for all the problems of the NTO-EFM model

Full size image
Fig. 2
figure 2

AE values and performance measures based on GANN-PSOAS approach for all the problems of the NTO-EFM

Full size image
Fig. 3
figure 3

Statistical studies for the GANN-PSOAS scheme through Fitness using the histogram/boxplots for all the problems of the NTO-EFM

Full size image
Fig. 4
figure 4

Statistical studies for the GANN-PSOAS scheme through ENSE using the histogram/boxplots for all the problems of the NTO-EFM

Full size image
Fig. 5
figure 5

Statistical studies for the GANN-PSOAS scheme through TIC using the histogram/boxplots for all the problems of the NTO-EFM

Full size image

The performance operators plots/illustrations based on fitness, ENSE and TIC have been drawn together with the boxplots and histogram values for all the problems of the NTO-EFM are given in Figs. 3, 4, 5. The values of the fitness for Problems 1 and 2 lie in 10–2 to 10–6, whereas for problem 3, mostly fitness lies in 10–06 to 10–08. The ENSE for problems 1 and 3 lie in range of 10–3 to 10–7, while for third problem, the ENSE lie in 10–7 to 10–10. The TIC values for problems 1 and 2 lie in 10–4 to 10–8, while for problem 3 lie in 10–8 to 10–10. In view of these statistical results, one can accomplish that the near to optimal levels of ENSE and TIC have been attained.

The statistical assessments studies have been described using the GANN-PSOAS approach to solve all the problems of the NTO-EFM for 50 independent executions using the measure of central tendency and variation including the minimum (Min), mean, median (Med), semi-interquartile range (S.IR) and standard deviation (SD). The obtained statistical outcomes have been provided in Table 1. These statistical performances for all the problems of the NTO-EFM are calculated and presented, which describe the accuracy/precision of the proposed GANN-PSOAS approach. The convergence investigations of GANN-PSOAS approach are further showed on the global performance measures based on G.FIT, G. ENSE and G-TIC for 50 independent executions are given in Table 2. The mean/average levels of the G.FIT, G.ENSE as well as of G.TIC lie in 10−5 to 10−8, 10−8 to 10−9, 10−7 to 10−8, respectively, while the S.IR of G.FIT, G.ENSE as well as G.TIC lie in 10−4 to 10−7, 10−7 to 10−9 and 10−5 to 10−8, respectively, for problems 1 to 3. The close optimal values of these global level presentations supplementary authenticate the precision of the projected GANN-PSOAS solver.

Table 1 Statistics investigation via designed GANN-PSOAS approach for all the problems of the NTO-EFM
Full size table
Table 2 Global presentations for all the problems of the NTO-EFM
Full size table

The computational bourdon of the proposed GANN-PSOAS scheme is perceived via completed generations, parameter adaptation’s execution time and executed counts of the function under the procedure to get the decision variables of the GANNs. Complexity examinations for each problem of the NTO-EFM mathematical models are evaluated, and the results based on numerical data are provided in Table 3. One may notice that the average generations, execution of time as well as function counts are 1962.8067 and 76,713.32, for all three problems of the NTO-EFM, respectively, of the proposed GANN-PSOAS scheme. These complexity index can be used in future for necessary comparison studies with state-of-the-art computing procedures based on exploitation of artificial intelligence methodologies. Beside the accurate and efficient solutions obtained from GANN-PSOAS, other advantages include ease of the concept with smooth implementation, provision of continuous solutions, reliable, stable, extendable and applicable to different nonlinear systems.

Table 3 Complexity performance for all the problems of the NTO-EFM
Full size table

5 Conclusions

A new design of neuroswarming heuristics is presented to solve the third-order nonlinear singular Emden–Fowler model by introducing Gudermannian activation function for the formulation of Gudermannian artificial neural networks which is used for the modeling of the equation by the construction of the objective function. The fitness/merit function of the nonlinear singular system is optimized with optimization ability of global search with particle swarm optimization combined with quick/rapid local search strength of active-set approach. The designed intelligent solver GANN-PSOAS is effectively implemented to solve three variants of NTO-EFMs by exploiting in 10 neurons in hidden layer structure of the networks. The convergence, precision and accuracy of the stochastic numerical solver are estimated by accomplishing the overlapping results with the true/exact solutions having an acceptable level of accuracy for solving the NTO-EFMs. Moreover, statistical amplifications based on 50 executions/runs have been performed to solve the NTO-EFM on the basis of mean, standard deviation, semi-interquartile range and median scales which evidently authenticate the trustworthiness, accurateness, exactness and robustness of the proposed Gudermannian activation function based neural network models trained with hybrid of particle swarm optimization with active set scheme. The proposed methodology GANN-PSOSA is stochastic in nature, therefore have limitation better performance cannot be given guarantee/assurance that algorithm converges in each independent trial. Additionally, a slight change in parameters settings of the optimization algorithms also results in premature convergence.

In the future, the designed GANN-PSOAS scheme can be applied to investigate the dynamics of nonlinear fluidic systems, bioinformatics models, computer virus propagation models, nonlinear circuit theory problem, systems in energy and power sector.