Planar dynamics of a dimer on a wave

Abstract

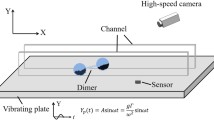
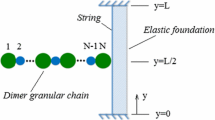
We study the 2D dynamics of a rigid dimer, a dumbbell-shaped extended body, on an elastic surface carrying a harmonic traveling wave. The impact of the dimer with the surface is modeled using Routh’s impact diagram which assumes inelastic normal interaction along with frictional constraint in the tangential direction. The impulse correlation ratio is used while working at double impact. The surface provides a kinematic boundary condition corresponding to the mode of motion. As a result, the dimer exhibits various modes of motion consisting of rolling with or without slip, hopping, and double stick/slide as a function of wave parameters and initial conditions. The dimer drifts through various modes, namely drift and jump–drift, while realizing period-doubling and novel complex/mixed-periodic behavior (different impact periodicity admitted by each ball) with coexisting attractors. Noticeably, the flutter mode, as observed in bouncing dimer problem on rigid surface, appears to be absent in the present system due to the persistent drift. The transport properties of a dimer as a function of initial conditions, surface and geometric parameters bring forth interesting conclusions. This study is expected to be useful in developing and understanding the novel idea of wave-induced transport of elongated granular particles.

Appendix A

Coefficients of contact forces in equation of motion (Eq. 10) are as follows.

$$\begin{aligned} S_{n1}^{x1}&=\dfrac{-I_2\sin \theta _{s1}-ml^2\sin (2\theta -\theta _{s1})}{8mI}\\ S_{t1}^{x1}&=\dfrac{I_2\cos \theta _{s1}+ml(4r\sin \theta -l\cos (2\theta -\theta _{s1}))}{8mI}\\ S_{n2}^{x1}&=\dfrac{-I_3\sin \theta _{s2}+ml^2\sin (2\theta -\theta _{s2})}{8mI}\\ S_{t2}^{x1}&=\dfrac{I_3\cos \theta _{s2}+ml(4r\sin \theta +l\cos (2\theta -\theta _{s2}))}{8mI}\\ S_{n1}^{y1}&=\dfrac{I_2\cos \theta _{s1}+ml^2\cos (2\theta -\theta _{s1})}{8mI}\\ S_{t1}^{y1}&=\dfrac{I_2\sin \theta _{s1}-ml(4r\cos \theta +l\sin (2\theta -\theta _{s1}))}{8mI}\\ S_{n2}^{y1}&=\dfrac{I_3\cos \theta _{s2}-ml^2\cos (2\theta -\theta _{s2})}{8mI}\\ S_{t2}^{y1}&=\dfrac{I_3\sin \theta _{s2}-ml(4r\cos \theta -l\sin (2\theta -\theta _{s2}))}{8mI}\\ S_{n1}^{\theta }&=-\dfrac{l\cos (\theta -\theta _{s1})}{2I},\ S_{t1}^{\theta }=\dfrac{2r+l\sin (\theta -\theta _{s1})}{2I}\\ S_{n2}^{\theta }&=\dfrac{l\cos (\theta -\theta _{s2})}{2I},\ S_{t2}^{\theta }=\dfrac{2r-l\sin (\theta -\theta _{s2})}{2I} \end{aligned}$$

Coefficients of contact forces in equation of motion (Eq. 11) are as follows.

$$\begin{aligned} S_{n1}^{x2}&=\dfrac{-I_3\sin \theta _{s1}+ml^2\sin (2\theta -\theta _{s1})}{8mI}\\ S_{t1}^{x2}&=\dfrac{I_3\cos \theta _{s1}-ml(4r\sin \theta -l\cos (2\theta -\theta _{s1}))}{8mI}\\ S_{n2}^{x2}&=\dfrac{-I_2\sin \theta _{s2}-ml^2\sin (2\theta -\theta _{s2})}{8mI}\\ S_{t2}^{x2}&=\dfrac{I_2\cos \theta _{s2}-ml(4r\sin \theta +l\cos (2\theta -\theta _{s2}))}{8mI}\\ S_{n1}^{y2}&=\dfrac{I_3\cos \theta _{s1}-ml^2\cos (2\theta -\theta _{s1})}{8mI}\\ S_{t1}^{y2}&=\dfrac{I_3\sin \theta _{s1}+ml(4r\cos \theta +l\sin (2\theta -\theta _{s1}))}{8mI}\\ S_{n2}^{y2}&=\dfrac{I_2\cos \theta _{s2}+ml^2\cos (2\theta -\theta _{s2})}{8mI}\\ S_{t2}^{y2}&=\dfrac{I_2\sin \theta _{s2}+ml(4r\cos \theta -l\sin (2\theta -\theta _{s2}))}{8mI} \end{aligned}$$

where $I_1=I+\frac{1}{4}ml^2$, $I_2=8I_1-ml^2=8I+ml^2$ and $I_3=8I_1-3ml^2=8I-ml^2$.

Note: Appendix B and the simulation videos are given as electronic supplementary material (ESM).