1 Introduction

Vibro-impact systems can be found in many areas of science and engineering. Even with a simple structure, they are strongly nonlinear. Therefore, there are no general analytical solutions or strategies for dynamic problems of this type. Many approximate analytical methods designed for nonlinear systems are based on the classical perturbation approach, and they can be applied only to weakly nonlinear problems [18, 24]. In recent decades, some analytical techniques have been developed to cope with vibro-impact systems by imposing certain conditions on their motion (e.g., periodicity at the resonant state): the power-law phenomenological modeling, the non-smooth temporal transformation (NSTT), the concept of impact modes, the Ivanov non-smooth coordinate transformation, and few others [12, 27, 28].

There is also a solution strategy that particularly fits in with the asymptotic approach to nonlinear problems and near-resonant dynamics. It consists in combining the multiple time scales method (MTSM) with a use of a sawtooth function which describes the non-smooth nature of the given system. In recent years the technique has been applied to the systems including vibro-impact nonlinear energy sink (VI NES) [9,10,11, 13,14,15,16]. Problems of this kind are strictly connected with the increasingly extensive studies on targeted energy transfer (TET) and energy harvesting [32].

Approximate analytical solutions and the related stability analysis can be useful, among others, in the control and improvement of periodic orbits of vibro-impact systems [4]. However, in the framework of the ’MTSM—sawtooth function’ approach, there is a lack of comprehensive works on stability studies of the periodic steady-state near-resonant solutions. Perhaps the most commonly cited work related to stability of impact dampers is the PhD thesis by Masri [19]. The proposed conception and results were also discussed in later papers [20, 21]. Similar method was presented, for example, by Popplewell et al. [29]. Unfortunately, in all these works, motion of the primary system between impacts is described by the general solution for a piecewise linear oscillator with viscous damping and periodic excitation. Such a model is usually inconsistent with the approximate solution formulated with the method of multiple scales under the assumption of small forcing and/or damping.

Results of the stability analysis focused on an approximate analytical solution can be verified numerically, by computation of Lyapunov exponents associated with the given system. For nonlinear discontinuous problems (with impacts and/or dry friction), the standard, well-established technique for determination of Lyapunov spectrum [23, 25, 26] need to be modified in order to handle the discontinuities (jumps). A theoretically based and straightforward generalization of the method was proposed by Müller [22]. This approach has been successfully applied to various multi-degree-of-freedom systems with impacts (e.g., see [1,2,3]).

In practical applications, machine components that undergo impacts are often interconnected with other, non-colliding parts (e.g., in percussive machines/tools such as hammer drills). Mostly, these couplings are strong. The mechanical system under consideration consists of two coupled oscillators, of which one includes an internally colliding small body. Due to the assumption of weak coupling, the paper can be treated as a preliminary work towards more realistic and practical problems. The main aim of this paper is to adapt and discuss the conception of the stability studies suited for the ’MTSM – sawtooth function’ approach.

The paper is divided into six sections. A mathematical formulation of the problem is presented in Sect. 2. Section 3 includes an outline of the approximate analytical procedure of solution, and admissibility of the steady-state solutions is discussed from the viewpoint of different criteria. Analytical results and their verification via numerical simulations are reported in Sect. 4. Section 5 includes some remarks on limitations and extensibility of the presented approach. Conclusions and final remarks are given in Sect. 6.

2 Physical and mathematical model

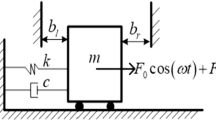
Let us consider the system illustrated schematically in Fig. 1. The primary part is a vibro-impact unit comprised of a damped linear oscillator (box) of mass \(m_1\) and an embedded block of mass \(m_2\). The latter one can move freely between two rigid stops (L is the symmetric gap size). The unit is driven by a harmonic force \(F_1\), and the components undergo mutual impact interactions. The secondary part of the system, in turn, is an ordinary damped linear oscillator of mass \(m_3\), elastically coupled with the block. The stiffness constants associated with the linear springs are denoted by \(k_1\), \(k_3\) and \(k_{23}\); the viscous damping coefficients are \(c_1\), \(c_3\).

It is assumed that the masses of the block and the secondary oscillator are identical (\(m_2 = m_3\)) and relatively small (\(m_2 \ll m_1\) and \(m_3 \ll m_1\)). Impacts of the block against the main body are characterized by the restitution coefficient \(\kappa \). The case of imperfectly elastic collisions is considered, that is \(0< \kappa < 1\). Moreover, the spring coupling between the left and right subsystem is assumed to be weak (\(k_{23} \ll k_1,\, k_3\)). The external force is harmonic: \(F_1(t) = F_{10}\sin (\omega _{1}t)\).

Fig. 1
figure 1

The analyzed vibro-impact system

Full size image

Let \(x_1\), \(x_2\) and \(x_3\) be the displacements of the components from equilibrium (\(-L \le x_2-x_1 \le L\)). The equations of motion of the three-degree-of-freedom system between impacts (for \(|x_2-x_1| < L\)) take the form:

$$\begin{aligned} \begin{aligned}&m_1\ddot{x}_1+ c_1 \dot{x}_1 + k_1 x_1 = F_{10}\sin (\omega _{1}t)\,, \\&m_2\ddot{x}_2 + k_{23} (x_2 - x_3) = 0\,, \\&m_3\ddot{x}_3 + c_3 \dot{x}_3 + k_3 x_3 + k_{23} (x_3 - x_2) = 0\,. \end{aligned} \end{aligned}$$
(1)

Classically, it is assumed that the duration of the collisions is very short, and any external forces are negligible compared to the impact force. When Newton’s restitution rule is used together with the momentum conservation principle [31], the change in momentum of the main oscillator due to an impact is given by

$$\begin{aligned} \varDelta p_1 = m_1 (\dot{x}_{1}^{+}-\dot{x}_{1}^{-}) = - \mu (1 + \kappa )(\dot{x}_{1}^{-} - \dot{x}_{2}^{-}) \end{aligned}$$
(2)

where

$$\begin{aligned} \mu = \frac{m_1 m_2}{m_1+m_2} \end{aligned}$$

and \(\dot{x}_{i}^{-}\), \(\dot{x}_{i}^{+}\) denote the velocities of the ith body just before the impact and just after the impact, respectively. Including the effect of consecutive collisions, the dynamic equations (for \(|x_2-x_1| \le L\)) become

$$\begin{aligned} \begin{aligned}&m_1\ddot{x}_1 + c_1 \dot{x}_1 + k_1 x_1 = F_{10}\sin (\omega _{1}t) +\\&\quad - \mu (1 + \kappa )\sum \limits _{j} (\dot{x}_{1} - \dot{x}_{2}) \delta (t - t_j^{-})\,, \\&m_2\ddot{x}_2 + k_{23} (x_2 - x_3) \\&\quad = \mu (1 + \kappa )\sum \limits _{j} (\dot{x}_{1} - \dot{x}_{2}) \delta (t - t_j^{-})\,, \\&m_3\ddot{x}_3 + c_3 \dot{x}_3 + k_3 x_3 + k_{23} (x_3 - x_2) = 0 \,, \end{aligned} \end{aligned}$$
(3)

where \(\delta (\bullet )\) is the Dirac delta function, and \(t_j\) is the time instant of the \(j\hbox {th}\) impact.

For convenience of analytical studies, we introduce the dimensionless time and displacements:

$$\begin{aligned} \tau = \omega _{10}t,\quad \omega _{10}^2 = \frac{k_1}{m_1},\quad X_i = \frac{x_i}{L}\,. \end{aligned}$$

Now, Eq. (3) can be rewritten in their counterpart non-dimensional form (cf. [9,10,11]):

$$\begin{aligned}&\ddot{X}_1 + \gamma _{1}\dot{X}_1 + X_1 = f_{10}\sin (\varOmega _{1}\tau ) \nonumber \\&\qquad - \varepsilon \frac{1 + \kappa }{1+\varepsilon }\sum \limits _{j} (\dot{X}_1 - \dot{X}_2) \delta (\tau - \tau _{j}^{-})\,, \nonumber \\&\varepsilon \ddot{X}_2 + \alpha _{23}(X_2 - X_3) = \varepsilon \frac{1 + \kappa }{1+\varepsilon }\sum \limits _{j} (\dot{X}_1 - \dot{X}_2) \delta (\tau - \tau _{j}^{-})\,, \nonumber \\&\varepsilon \ddot{X}_3 + \gamma _{3}\dot{X}_3 + \varOmega _{30}^2 X_3 + \alpha _{23}(X_3 - X_2) = 0 \,, \end{aligned}$$
(4)

where the overdots denote differentiation with respect to \(\tau \), and the dimensionless parameters are as follows:

$$\begin{aligned} \varepsilon = \frac{m_2}{m_1} = \frac{m_3}{m_1},\qquad f_{10}= \frac{F_{10}}{m_1 L \omega _{10}^2},\qquad \varOmega _{1}= \frac{\omega _{1}}{\omega _{10}},\\ \gamma _i = \frac{c_i}{m_1\omega _{10}},\qquad \varOmega _{30}^2 = \frac{k_{3}}{m_1\omega _{10}^2},\qquad \alpha _{23}= \frac{k_{23}}{m_1\omega _{10}^2}. \end{aligned}$$

In order to cope with the impulsive right-hand sides of the equations, we define new variables, namely the coordinates describing (approximately) the displacement of the center of mass of the vibro-impact unit, and the relative displacement of the main body:

$$\begin{aligned} U = X_1 + \varepsilon X_2,\qquad W = X_1 - X_2\,. \end{aligned}$$
(5)

Introducing these variables into Eq. (4) leads to

$$\begin{aligned} \begin{aligned} \ddot{U}&+ \gamma _{1}\frac{\dot{U} + \varepsilon \dot{W}}{1+\varepsilon } + \frac{U + \varepsilon W}{1+\varepsilon } + \\&+ \alpha _{23}\frac{U - W}{1+\varepsilon } - \alpha _{23}X_{3}= f_{10}\sin (\varOmega _{1}\tau )\,, \\ \ddot{W}&+ \gamma _{1}\frac{\dot{U} + \varepsilon \dot{W}}{1+\varepsilon } + \frac{U + \varepsilon W}{1+\varepsilon } +\\&- \frac{\alpha _{23}}{\varepsilon } \frac{U - W}{1+\varepsilon } + \frac{\alpha _{23}}{\varepsilon }X_{3}= f_{10}\sin (\varOmega _{1}\tau ) + \\&-(1 + \kappa )\sum \limits _{j} \dot{W}_j\delta (\tau - \tau _{j}^{-})\,, \\ \varepsilon \ddot{X}_{3}&+ \gamma _{3}\dot{X}_{3}+ (\varOmega _{30}^2 + \alpha _{23})X_{3}- \alpha _{23}\frac{U - W}{1+\varepsilon } = 0\,. \end{aligned} \end{aligned}$$
(6)

Although the left-hand sides of the equations are more complicated than before, only one differential equation (corresponding to the relative displacement) includes the impact-related sum.

3 Analytical approach to the problem

3.1 Analytical approximate solution

Let the mass ratio \(\varepsilon \) play a role of the small parameter (\(\varepsilon \ll 1\)). Some factors within the mechanical system, such as damping, elastic coupling and dynamic excitation, are assumed to be weak, and the rescaled parameters \(\hat{\gamma }_{1}\), \(\hat{\gamma }_{3}\), \(\hat{\alpha }_{23}\), \(\hat{f}_{10}\) are formally introduced:

$$\begin{aligned} \gamma _{1}= \varepsilon \hat{\gamma }_{1},\;\; \gamma _{3}= \varepsilon ^2\hat{\gamma }_{3},\;\; \alpha _{23}= \varepsilon ^2\hat{\alpha }_{23},\;\; f_{10}= \varepsilon \hat{f}_{10}\,.\nonumber \\ \end{aligned}$$
(7)

Since the construction of a general solution of the non-smooth dynamical problem is essentially impossible, certain restrictions on the system’s motion are indispensable. Our considerations are focused on a specific vibro-impact regime, i.e., the periodic motion with two symmetric impacts per cycle, near 1:1 resonance. As it was indicated by experimental investigations, this particular type of behavior predominates in dynamics of such vibro-impact systems, and is the most efficient from the perspective of targeted energy transfer [16, 19]. Accordingly, we assume that

$$\begin{aligned} \varOmega _{1}= 1 + \varepsilon \hat{\sigma }_{1},\quad \varOmega _{30}^2 = \varepsilon (1 + \varepsilon \hat{\sigma }_{30})\,, \end{aligned}$$
(8)

where \(\hat{\sigma }_{1}\) and \(\hat{\sigma }_{30}\) are the detuning parameters.

Fig. 2
figure 2

Description of the SIM of the system: a the sawtooth function, b the relation B(C), c the relation \(\rho (\kappa )\)

Full size image

Applying the method of multiple scales [18, 24], we express the approximate solution in terms of two different time scales:

$$\begin{aligned} \begin{aligned}&U = U_{0}(\tau _{0},\, \tau _{1}) + \varepsilon U_{1}(\tau _{0},\, \tau _{1})\,, \\&W = W_{0}(\tau _{0},\, \tau _{1}) + \varepsilon W_{1}(\tau _{0},\, \tau _{1})\,, \\&X_{3}= X_{3 0}(\tau _{0},\, \tau _{1}) + \varepsilon X_{3 1}(\tau _{0},\, \tau _{1})\,, \end{aligned} \end{aligned}$$
(9)

where \(\tau _k = \varepsilon ^k \tau \) for \(k = 0,\, 1\). Substituting parameters (8) and (7) as well as expansions (9) into Eqs. (6), and then equating coefficients of order \(\varepsilon ^0\) leads to

$$\begin{aligned}&D_0^2 U_{0} + U_{0} = 0\,, \end{aligned}$$
(10)
$$\begin{aligned}&D_0^2 W_{0} = - (1 + \kappa )\sum \limits _{j} D_0 W_{0}\; \delta (\tau _{0}- \tau _{0,j}^{-}) - U_{0}\,, \end{aligned}$$
(11)
$$\begin{aligned}&D_0^2 X_{3 0} + X_{3 0} = 0\,, \end{aligned}$$
(12)

where \(D_k^n(\bullet ) = \frac{\partial ^n}{\partial \tau _k^n}(\bullet )\). Obviously, the solutions of Eqs. (10) and (12) can be written as

$$\begin{aligned} \begin{aligned}&U_{0} = B(\tau _{1}) \sin (\tau _{0}+ \phi (\tau _{1}))\,,\\&X_{3 0} = A_3(\tau _{1}) \sin (\tau _{0}+ \phi _{3}(\tau _{1}))\,, \end{aligned} \end{aligned}$$
(13)

while for Eq. (11) we postulate

$$\begin{aligned} W_{0} = B(\tau _{1}) \sin (\tau _{0}+ \phi (\tau _{1})) + Z(\tau _{0},\, \tau _{1}), \end{aligned}$$
(14)

where \(Z\) is the sawtooth function

$$\begin{aligned} Z(\tau _{0},\, \tau _{1})= \frac{2}{\pi } C(\tau _{1}) \arcsin [\cos (\tau _{0}- \theta (\tau _{1}))]. \end{aligned}$$
(15)

Its role is to reflect the non-smooth nature of the solution as an effect of the cyclic symmetric impacts that occur at \(\tau _{0,j}= j\pi + \theta \) where \(j = 0,\, 1,\, 2,\,\ldots \). The sawtooth function is illustrated in Fig. 2a for constant C and \(\theta \). Expanding the inverses of Eqs. (5)

$$\begin{aligned} X_1 = \frac{U+\varepsilon W}{1+\varepsilon }\,,\qquad X_2 = \frac{U-W}{1+\varepsilon } \end{aligned}$$
(16)

in a Taylor series with respect to \(\varepsilon \), and keeping terms up to second order, we obtain

$$\begin{aligned} X_1\approx & {} B \sin (\tau _{0}+ \phi ) + \varepsilon (1-\varepsilon ) \frac{2}{\pi } C \arcsin [\cos (\tau _{0}- \theta )]\,,\nonumber \\ X_2\approx & {} -(1-\varepsilon +\varepsilon ^2) \frac{2}{\pi } C \arcsin [\cos (\tau _{0}- \theta )]\,. \end{aligned}$$
(17)

Thus, in the near-resonant case, the block is bounced against the inner wall of the box (from \(W_{0} = -1\) to \(W_{0} = 1\) and vice versa) whose harmonic motion is slightly disturbed by the impacts. What is more, B as well as C multiplied by the \(\varepsilon \)-related factor play the role of the amplitudes.

Due to the geometric constraints, B and C are mutually dependent. As discussed in Refs. [9, 10], analysis of the impact conditions (\(W_{0} = 1\) at \(\tau _{0}= \theta \)) described by Eq. (11) together with solutions (14) and (13) produces

$$\begin{aligned}&B \sin (\theta + \phi ) + C = 1\,,\nonumber \\&\quad -\frac{4}{\pi }C + (1+\kappa ) \left[ B \cos (\theta + \phi ) + \frac{2}{\pi } C \right] = 0\,.\qquad \end{aligned}$$
(18)

Combining these two equations leads to the relationship between the slow-time-scale variables

$$\begin{aligned} B^2 = 1 - 2C + (1+\rho ^2) C^2 \quad \text {with} \quad \rho = \frac{2(1 - \kappa )}{\pi (1 + \kappa )} \end{aligned}$$
(19)

which describes the so called slow invariant manifold (SIM) of the problem. Moreover, the phase angles are defined by

$$\begin{aligned} \sin (\theta + \phi ) = \frac{1-C}{B},\qquad \cos (\theta + \phi ) = \frac{\rho C}{B}. \end{aligned}$$
(20)

Geometrically speaking, the curve B(C) is a set of points \((C,\, B)\) corresponding to potential steady-states of the dynamical system. An exemplary curve B(C) is shown in Fig. 2b. The minimal possible value of B and the related value of C are

$$\begin{aligned} B_{\min }= \frac{\rho }{\sqrt{1+\rho ^2}}\,,\qquad C_{\min }= \frac{1}{1+\rho ^2}\,. \end{aligned}$$
(21)

Moreover, the relation between \(\rho \) and \(\kappa \) is graphically presented in Fig. 2c. Parameter \(\rho \) changes from \(2/\pi \) to 0 over the whole range of the restitution coefficient.

For the studies of evolution of the system on the SIM, the equations corresponding to U and \(X_{3}\) at the \(\varepsilon ^1\) order of approximation are necessary:

$$\begin{aligned} D_0^2 U_{1} + U_{1}= & {} \hat{f}_{10}\sin (\varOmega _{1}\tau _{0}) \nonumber \\&+ U_{0} - W_{0} - \hat{\gamma }_{1}D_0U_{0} - 2 D_0 D_1 U_{0}\,, \nonumber \\ D_0^2 X_{3 1} + X_{3 1}= & {} \hat{\alpha }_{23}(U_{0} - W_{0} - X_{3 0}) \nonumber \\&- \hat{\sigma }_{30}X_{3 0} - \hat{\gamma }_{3}D_0 X_{3 0} - 2 D_0 D_1 X_{3 0}\,.\nonumber \\ \end{aligned}$$
(22)

Function \(Z\) involved in \(W_{0}\) can be expanded into a Fourier series with respect to \(\tau _{0}\). Eliminating secular terms from \(U_{1}\) and \(X_{3 1}\), we obtain the solvability conditions which form a system of differential equations for the amplitudes and phases:

$$\begin{aligned} \begin{aligned}&D_1 B = g_{B}(\tau _{1},\, B,\, \phi ,\, C,\, \theta )\,,\\&D_1 \phi = g_{\phi }(\tau _{1},\, B,\, \phi ,\, C,\, \theta )\,,\\&D_1 A_3 = g_{A3}(\tau _{1},\, \phi ,\, A_3,\, \phi _{3},\, C,\, \theta )\,,\\&D_1 \phi _{3}= g_{\phi 3}(\tau _{1},\, \phi ,\, A_3,\, \phi _{3},\, C,\, \theta )\,. \end{aligned} \end{aligned}$$
(23)

For the sake of brevity, functions \(g_{B}\), \(g_{\phi }\), \(g_{A3}\), \(g_{\phi 3}\) are not presented in a full detailed form. System (23) can be transformed into an autonomous one

$$\begin{aligned} \begin{aligned}&D_1 B = h_{B}(B,\, \psi ,\, C)\,, \\&D_1 \psi = h_{\psi }(B,\, \psi ,\, C)\,,\\&D_1 A_3 = h_{A3}(B,\, A_3,\, \psi _3,\, C)\,, \\&D_1 \psi _3 = h_{\psi 3}(B,\, \psi ,\, A_3,\, \psi _3,\, C) \end{aligned} \end{aligned}$$
(24)

by using formulae (20), and introducing the modified phases

$$\begin{aligned} \psi = \hat{\sigma }_{1}\tau _{1}- \phi \,,\qquad \psi _3 = \phi - \phi _3\,. \end{aligned}$$
(25)

The full form of the autonomous system is

$$\begin{aligned} D_1 B= & {} -\frac{\hat{\gamma }_{1}B}{2} - \frac{4\rho C^2}{\pi ^2 B} + \frac{\hat{f}_{10}}{2} \sin \psi \,, \nonumber \\ D_1 \psi= & {} \hat{\sigma }_{1}+ \frac{\hat{f}_{10}}{2B}\cos \psi + \frac{4 C(C-1)}{\pi ^2 B^2}\,, \nonumber \\ D_1 A_3= & {} -\frac{\hat{\gamma }_{3}A_3}{2} - \frac{4\rho \hat{\alpha }_{23}C^2}{\pi ^2 B}\cos \psi _3 +\nonumber \\&+ \frac{4\hat{\alpha }_{23}C(C-1)}{\pi ^2 B} \sin \psi _3\,, \nonumber \\ D_1 \psi _3= & {} -\frac{\hat{\alpha }_{23}+ \hat{\sigma }_{30}}{2} - \frac{4 C(C-1)}{\pi ^2 B^2} + \frac{\hat{f}_{10}}{2}\cos \psi + \nonumber \\&+ \frac{4\hat{\alpha }_{23}C(C-1)}{\pi ^2 B A_3}\cos \psi _3 + \frac{4\rho \hat{\alpha }_{23}C^2}{\pi ^2 B A_3}\sin \psi _3 \,.\nonumber \\ \end{aligned}$$
(26)

The steady-state near-resonant motions correspond to the fixed points of (26). Thus, the set of algebraic equations must be solved:

$$\begin{aligned} h_{B} = 0\,,\quad h_{\psi } = 0\,,\quad h_{A3} = 0\,,\quad h_{\psi 3} = 0\,. \end{aligned}$$
(27)

Eliminating \(\psi \) and \(\psi _3\), we obtain

$$\begin{aligned} \begin{aligned}&\frac{64 C^2 [1-2C+(1+\rho ^2)C^2]}{\pi ^4 \hat{f}_{10}^2 B^2} + \frac{(\hat{\gamma }_{1}^2 + 4\hat{\sigma }_{1}^2) B^2}{\hat{f}_{10}^2} \\&+ \frac{16 C [(\rho \hat{\gamma }_{1}+2\hat{\sigma }_{1})C - 2\hat{\sigma }_{1}]}{\pi ^2 \hat{f}_{10}^2} = 1\,,\\&\frac{ \pi ^4 B^2 A_3^2 (\hat{\alpha }_{23}^2 + \hat{\gamma }_{3}^2) }{ 64\hat{\alpha }_{23}^2 C^2 [1-2C+(1+\rho ^2)C^2] }\\&+ \frac{ \pi ^4 B^2 A_3^2 \varDelta \hat{\sigma }(2\hat{\alpha }_{23}+\varDelta \hat{\sigma }) }{ 64\hat{\alpha }_{23}^2 C^2 [1-2C+(1+\rho ^2)C^2] } = 1\,, \end{aligned} \end{aligned}$$
(28)

where \(\varDelta \hat{\sigma }= \hat{\sigma }_{30}-2\hat{\sigma }_{1}\). Now, recalling the relation B(C) given by (19), we determine two solutions for C:

$$\begin{aligned} C^{(1)} = \frac{p_{1} - \sqrt{p_{2}}}{q}\,,\qquad C^{(2)} = \frac{p_{1} + \sqrt{p_{2}}}{q}\,, \end{aligned}$$
(29)

where

$$\begin{aligned} \begin{aligned} p_1&= 16\hat{\sigma }_{1}+ \pi ^2 (\hat{\gamma }_{1}^2 + 4\hat{\sigma }_{1}^2)\,,\\ p_2&= \hat{f}_{10}^2 \left[ 16\pi ^2(\rho \hat{\gamma }_{1}+ 2\hat{\sigma }_{1}) + \right. \\&\left. + \pi ^4(\rho ^2+1)(\hat{\gamma }_{1}^2 + 4\hat{\sigma }_{1}^2) + 64 \right] +\\&- \left[ \hat{\gamma }_{1}(\pi ^2\rho \hat{\gamma }_{1}+ 8) + 4\pi ^2\rho \hat{\sigma }_{1}^2 \right] , \\ q&= 16(\rho \hat{\gamma }_{1}+ 2\hat{\sigma }_{1}) + \pi ^2 (\rho ^2+1)(\hat{\gamma }_{1}^2 + 4\hat{\sigma }_{1}^2) + \frac{64}{\pi ^2}\,. \end{aligned} \end{aligned}$$
(30)

The dependence of B on C follows from (19), while amplitude \(A_3\) can be written as

$$\begin{aligned} A_3^{(s)} = \frac{8\hat{\alpha }_{23}C^{(s)}}{ \pi ^2 \sqrt{ \hat{\alpha }_{23}^2 + \hat{\gamma }_{3}^2 + \varDelta \hat{\sigma }(2\hat{\alpha }_{23}+ \varDelta \hat{\sigma }) }} \end{aligned}$$
(31)

for \(s = 1,\, 2\). Thus, B and C are dependent on \(\rho \), \(\hat{f}_{10}\), \(\hat{\sigma }_{1}\), \(\hat{\gamma }_{1}\) whereas \(A_3\) is a function of all model parameters. Projections \(P_{s}\) of the fixed points \((B^{(s)},\, C^{(s)},\, A^{(s)})\) onto the plane (B, C) are schematically shown in Fig. 2b.

3.2 Classification of periodic solutions

Numerical experiments presented in Sect. 5 are conducted by treating some model coefficients as control parameters. However, not all of the theoretically possible responses (14) are admissible. Assessment of the steady-state periodic solutions will be based on the three factors:

  • geometric constraints,

  • stability of fixed points,

  • stability of periodic motions.

They will be the source of certain restrictions on values of amplitude C. In further considerations, the inverse of relation (19) is used

$$\begin{aligned} C_{L,\, R} = \frac{ 1 {\mp } \sqrt{(1+\rho ^2) B^2 - \rho ^2} }{1+\rho ^2}\,, \end{aligned}$$
(32)

where the curve B(C) is divided into the left (L) and right (R) branches. Moreover, the following set of dimensionless parameters is treated as the basic one:

$$\begin{aligned} \begin{aligned} \varepsilon = 0.1,\quad \kappa = 0.75,\quad \hat{f}_{10}= 1.5,\quad \hat{\sigma }_{1}= 0.5,\\ \hat{\gamma }_{1}= 0.5,\quad \hat{\alpha }_{23}= 1,\quad \hat{\sigma }_{30}= 0.5,\quad \hat{\gamma }_{3}= 1\,. \end{aligned} \end{aligned}$$
(33)
Fig. 3
figure 3

Geometric restrictions on C: a degenerate (bold black) and non-degenerate (solid and dashed blue) solutions for \(\kappa = 0.75\), b the maximal value of C as a function of \(\kappa \). (Color figure online)

Full size image

Firstly, degenerate solutions should be excluded. By degenerate solutions we mean such functions W that violate the unilateral geometric constraints \(|W| \le 1\), i.e., the no-penetration condition. As illustrated in Fig. 3a, negative values of C are not allowed, although the condition \(W(\tau _{0,j}) = \pm 1\) is satisfied. On the other hand, high positive values lead to local extrema which may exceed the constraints. The maximum in the interval \((\theta ,\, \theta +\pi )\) can be easily determined:

$$\begin{aligned} \begin{aligned} W_{\max }&= \frac{2}{\pi } C \arcsin \left[ \cos \left( \arccos { \frac{2C}{\pi B} } + \right. \right. \\&\left. \left. - \arctan { \frac{1-C}{\rho C} } \right) \right] + \sqrt{ B^2 - \frac{4 C^2}{\pi ^2} } \end{aligned} \end{aligned}$$
(34)

and, taking into account relation (32) for the right branch, the equation \(W_{\max } = 1\) can be solved numerically for the critical value of B. The geometrically acceptable range of C is given by

$$\begin{aligned} 0< C < C_{G\max }(\kappa )\,, \end{aligned}$$
(35)

where the upper limit as a function of \(\kappa \) is shown in Fig. 3b. For example, when \(\kappa = 0.75\), \(C_{G\max }\approx 6.07\) for which \(B \approx 5.1\).

In the next step, linear stability of the steady-states corresponding to fixed points \(P_{s}\) should be verified. The autonomous system (26) in vector notation can be expressed as follows:

$$\begin{aligned} \mathbf {y}' = \mathbf {h}(\mathbf {y},\, C)\,, \end{aligned}$$
(36)

where prime denotes the derivative with respect to \(\tau _{1}\), and

$$\begin{aligned} \begin{aligned}&\mathbf {y} = [B,\, \psi ,\, A_3,\, \psi _3]^{T},\\&\mathbf {h} = [h_{B},\, h_{\psi },\, h_{A3},\, h_{\psi 3}]^{T}. \end{aligned} \end{aligned}$$
(37)

Eliminating C through the relations (32), the Jacobian matrix can be evaluated analytically for both the branches of SIM:

$$\begin{aligned} {\mathbf {J}}_L = \frac{\partial \mathbf {h}(\mathbf {y},{C_L})}{\partial \mathbf {y}},\qquad {\mathbf {J}}_R = \frac{\partial \mathbf {h}(\mathbf {y},{C_R})}{\partial \mathbf {y}} . \end{aligned}$$
(38)

For a given fixed point \(P_{s}\), the eigenvalues of \({\mathbf {J}}_L\) (if \(C^{(s)} < C_{\min }\)) or \({\mathbf {J}}_R\) (if \(C^{(s)} > C_{\min }\)) are calculated numerically. Classically, the corresponding steady-state periodic solution is asymptotically stable if all the eigenvalues have negative real parts [24, 30]. The analytical form of the Jacobian matrix has been reported in Appendix 1. Unfortunately, its complexity does not allow to present concise stability conditions in terms of the model parameters.

Fig. 4
figure 4

Restrictions on C related to the stability of periodic motions: a relative displacement and velocity—the original (bold blue) and perturbed (gray) solutions, b absolute displacement and velocity—\(X_1\), \(\dot{X_1}\) (bold blue) and \(X_2\), \(\dot{X_2}\) perturbed (gray). (Color figure online)

Full size image

Perhaps the most important restrictions imposed on C can be specified by stability studies of periodic motions of the vibro-impact unit. Such analysis is not an easy task due to the non-smooth character of the solution. It may be conducted by means of the method proposed by Masri [19,20,21]. Similar approaches to this kind of systems were presented for example in [6, 7, 29]. The general idea is to analyze the propagation of small initial perturbations in the solution (see Fig. 4a). However, it should be emphasized that in all of the abovementioned works, the motion of the main body between impacts was described by the general solution for a periodically excited linear oscillator with viscous damping. Then, periodicity conditions were used together with Newton’s restitution rule and the principle of momentum conservation. In the next subsection, we adapt this method to the form of the presented approximate analytical solution.

3.3 Stability analysis of the periodic motion

Let us rewrite the approximate periodic solutions (17) in an equivalent form:

$$\begin{aligned} \begin{aligned} X_1&= B \sin (\tau _{0}- \theta + \varPhi ) + \\&+ \varepsilon (1-\varepsilon ) \frac{2}{\pi } C \arcsin [\cos (\tau _{0}- \theta )]\,,\\ X_2&= -(1-\varepsilon +\varepsilon ^2) \frac{2}{\pi } C \arcsin [\cos (\tau _{0}- \theta )]\,, \end{aligned} \end{aligned}$$
(39)

so that \(\varPhi = \phi + \theta \) is the phase shift between the motion of the box and the internal block. For the sake of brevity, the zero subscript of \(\tau \) is dropped, and \(\tau _{j}\) denotes the time instant of the \(j\hbox {th}\) impact (\(\tau _{j} = \tau _{0,j}\)). The displacement and velocity of the box can be expressed in a piecewise manner for the intervals between the impacts of number j and \((j+1)\) as well as between the impacts of number \((j+1)\) and \((j+2)\):

$$\begin{aligned} X_1= & {} \left\{ \begin{array}{ll} B \sin (\tau - \tau _{j} + \varPhi ) + &{} \\ - \varepsilon v_{2}(\tau - \tau _{j} - \pi /2)\,, &{} \tau _{j}< \tau \le \tau _{j+1} \\ -B \sin (\tau - \tau _{j+1} + \varPhi ) + &{} \\ - \varepsilon v_{2}(\tau - \tau _{j+1} - \pi /2)\,, &{} \tau _{j+1}< \tau \le \tau _{j+2} \end{array} \right. \nonumber \\ \dot{X}_1= & {} \left\{ \begin{array}{ll} B \cos (\tau - \tau _{j} + \varPhi ) + &{} \\ - \varepsilon v_{2}\,, &{} \tau _{j}< \tau \le \tau _{j+1} \\ -B \cos (\tau - \tau _{j+1} + \varPhi ) + &{} \\ - \varepsilon v_{2}\,, &{} \tau _{j+1} < \tau \le \tau _{j+2} \end{array} \right. \nonumber \\ \end{aligned}$$
(40)

where \(v_{2}= \dot{X}_2\) denotes the steady-state absolute velocity of the block. In the case of the original (unperturbed) motion, we have \(v_{2}= \pm (1-\varepsilon +\varepsilon ^2)\frac{2}{\pi } C\) and \(\tau _{j+1}-\tau _{j}=\tau _{j+2}-\tau _{j+1} = \pi \). Similarly to the stability analysis discussed in [19], we initially take

$$\begin{aligned} {\mathbf {z}^{*}} = [X_1,\ \dot{X}_1,\ \varPhi ,\ \dot{X}_2]^{T} \end{aligned}$$

as the state vector of the subsystem.

Using formulae (40) for the first interval (with positive \(v_{2}\), see Fig. 4b), we can describe position and velocity of the main body immediately after the \(j\hbox {th}\) impact in both the original and disturbed case:

$$\begin{aligned} \left\{ \begin{array}{l} d_{1}= X_1(\tau _{j}^{+},\, v_{2},\, \varPhi ) \\ v_{1}^{+}= \dot{X}_1(\tau _{j}^{+},\, v_{2},\, \varPhi ) \end{array} \right. \end{aligned}$$
(41)
$$\begin{aligned} \left\{ \begin{array}{l} \widetilde{d}_1= d_{1}+ \varDelta _{j} X_{1} = X_1(\tau _{j}^{+},\, \widetilde{v}_2,\, \widetilde{\varPhi }) \\ \widetilde{v}_{1}^{+}= v_{1}^{+}+ \varDelta _{j} \dot{X}_{1} = \dot{X}_1(\tau _{j}^{+},\, \widetilde{v}_2,\, \widetilde{\varPhi }) \end{array} \right. \end{aligned}$$
(42)

where \(d_{1}\) and \(v_{1}^{+}\) are the given displacement and velocity of the box at the impact; the tilde denotes the steady-state values perturbed by small variations at \(\tau = \tau _{j}^{+}\):

$$\begin{aligned} \widetilde{v}_2= v_{2}+\varDelta _{j} \dot{X}_{2}\,,\qquad \widetilde{\varPhi }= \varPhi +\varDelta _{j} \varPhi \,. \end{aligned}$$
(43)

Equations (42), and all the subsequent ones describing the disturbed state, can be linearized near the original motion (the first-order approximation). Hence, a comparison of the unperturbed and perturbed behavior, i.e., Eqs. (41) with (42), provides the relationships between the deviations:

$$\begin{aligned} \begin{aligned}&\varDelta _{j} X_{1} = \frac{\pi }{2}\varepsilon \varDelta _{j} \dot{X}_{2} + \varDelta _{j} \varPhi \, B\cos {\varPhi } \,, \\&\varDelta _{j} \dot{X}_{1} = -\varepsilon \varDelta _{j} \dot{X}_{2} - \varDelta _{j} \varPhi \, B\sin {\varPhi }\,. \end{aligned} \end{aligned}$$
(44)

For the time instant just before the \((j+1)\hbox {th}\) impact, we have

$$\begin{aligned} \left\{ \begin{array}{l} -d_{1}= X_1(\tau _{j+1}^{-},\, v_{2},\, \varPhi ) \\ v_{1}^{-}= \dot{X}_1(\tau _{j+1}^{-},\, v_{2},\, \varPhi ) \end{array} \right. \end{aligned}$$
(45)
$$\begin{aligned} \left\{ \begin{array}{l} -\widetilde{d}_1= -(d_{1}+ \varDelta _{j+1} X_{1}) = X_1(\tau _{j+1}^{-},\, \widetilde{v}_2,\, \widetilde{\varPhi }) \\ \widetilde{v}_{1}^{-}= \dot{X}_1(\tau _{j+1}^{-},\, \widetilde{v}_2,\, \widetilde{\varPhi }) \end{array} \right. \end{aligned}$$
(46)

where

$$\begin{aligned} \widetilde{\tau }_{j+1}^{-} = \tau _{j+1}^{-}+\varDelta \tau \,,\quad \varDelta \tau = \varDelta _{j+1} \varPhi -\varDelta _{j} \varPhi \,. \end{aligned}$$
(47)

Comparing the second equations of (45) and (46) leads to

$$\begin{aligned} \widetilde{v}_{1}^{-}= -\varepsilon \widetilde{v}_2- B(\cos {\varPhi } - \varDelta _{j+1} \varPhi \sin {\varPhi }) \end{aligned}$$
(48)

The time of the block motion between the stops is given by

$$\begin{aligned} \left\{ \begin{array}{l} \pi = \dfrac{l_{2}}{v_{2}} = \dfrac{(-d_{1}+ 1) - (d_{1}-1)}{v_{2}} \\ \pi + \varDelta \tau = \dfrac{\widetilde{l}_2}{\widetilde{v}_2} \end{array} \right. \end{aligned}$$
(49)

where

$$\begin{aligned} \begin{aligned}&l_{2}= 2d_{2}\,,\\&\widetilde{l}_2= [-(d_{1}+ \varDelta _{j+1} X_{1}) + 1] - [(d_{1}+\varDelta _{j} X_{1})-1]\,. \end{aligned} \end{aligned}$$
(50)

From Eqs. (49) we obtain

$$\begin{aligned} \begin{aligned} \varDelta \tau&= \varDelta _{j+1} \varPhi -\varDelta _{j} \varPhi = \\&= - \frac{ \varDelta _{j} X_{1} + \varDelta _{j+1} X_{1} + \pi \varDelta _{j} \dot{X}_{2} }{v_{2}}\,. \end{aligned} \end{aligned}$$
(51)

Moreover, using solutions (40) for the second interval (with negative \(v_{2}\)), we can describe the motion immediately after the \((j+1)\hbox {th}\) impact:

$$\begin{aligned} \left\{ \begin{array}{l} -d_{1}= X_1(\tau _{j+1}^{+},\, -v_{2},\, \varPhi ) \\ -v_{1}^{+}= \dot{X}_1(\tau _{j+1}^{+},\, -v_{2},\, \varPhi ) \end{array} \right. \end{aligned}$$
(52)
$$\begin{aligned} \left\{ \begin{array}{l} -\widetilde{d}_1= -(d_{1}+ \varDelta _{j+1} X_{1}) = X_1(\tau _{j+1}^{+},\, -\widetilde{v}_2,\, \widetilde{\varPhi }) \\ -\widetilde{v}_{1}^{+}= \dot{X}_1(\tau _{j+1}^{+},\, -\widetilde{v}_2,\, \widetilde{\varPhi }) \end{array} \right. \end{aligned}$$
(53)

where the perturbed values at \(\tau = \tau _{j+1}^{+}\) are

$$\begin{aligned} \widetilde{v}_2= v_{2}+\varDelta _{j+1} \dot{X}_{2}\,,\qquad \widetilde{\varPhi }= \varPhi +\varDelta _{j+1} \varPhi \,. \end{aligned}$$
(54)

Confronting (42) and (53) yields

$$\begin{aligned} \begin{aligned} \varDelta _{j+1} X_{1}&= \varDelta _{j} X_{1} + \frac{\pi }{2}\varepsilon (\varDelta _{j+1} \dot{X}_{2}-\varDelta _{j} \dot{X}_{2}) +\\&\quad + \varDelta \tau \, B\cos {\varPhi } \,, \\ \varDelta _{j+1} \dot{X}_{1}&= \varDelta _{j} \dot{X}_{1} - \varepsilon (\varDelta _{j+1} \dot{X}_{2}-\varDelta _{j} \dot{X}_{2}) + \\&\quad - \varDelta \tau \, B\sin {\varPhi } \end{aligned} \end{aligned}$$
(55)

Now, the discontinuities in the velocities should be described. From Newton’s rule and the momentum conservation it follows that

$$\begin{aligned} \begin{aligned} \dot{X}_{1, j+1}^{-} = \frac{\kappa -\varepsilon }{\kappa (1+\varepsilon )} \dot{X}_{1, j+1}^{+} + \frac{\varepsilon (1+\kappa )}{\kappa (1+\varepsilon )} \dot{X}_{2, j+1}^{+} \,, \\ \dot{X}_{2, j+1}^{-} = \frac{1+\kappa }{\kappa (1+\varepsilon )} \dot{X}_{1, j+1}^{+} - \frac{1-\varepsilon \kappa }{\kappa (1+\varepsilon )} \dot{X}_{2, j+1}^{+}\,. \end{aligned} \end{aligned}$$
(56)

In the unperturbed case, one can put

$$\begin{aligned} \begin{aligned}&\dot{X}_{1, j+1}^{-} = v_{1}^{-}\,, \quad \dot{X}_{2, j+1}^{-} = v_{2}\,, \\&\dot{X}_{1, j+1}^{+} = -v_{1}^{+}\,, \quad \dot{X}_{2, j+1}^{+} = -v_{2}\,, \end{aligned} \end{aligned}$$
(57)

where \(v_{1}^{-}\) is described by (45). In the disturbed state, in turn, the velocities should be replaced with their perturbed values:

$$\begin{aligned} \widetilde{v}_{1}^{-},\, (v_{2}+ \varDelta _{j} \dot{X}_{2}),\, -\widetilde{v}_{1}^{+},\, -(v_{2}+\varDelta _{j+1} \dot{X}_{2})\,, \end{aligned}$$
(58)

where \(\widetilde{v}_{1}^{-}\) is given by (48). Again, by comparing the original and perturbed motion, we get the new relations:

$$\begin{aligned}&\varepsilon \kappa (1+\varepsilon )\varDelta _{j} \dot{X}_{2} + (\varepsilon -\kappa )\varDelta _{j+1} \dot{X}_{1} \nonumber \\&\quad - \varepsilon (1+\kappa )\varDelta _{j+1} \dot{X}_{2} - \kappa (1+\varepsilon )\varDelta _{j+1} \varPhi \, B\sin {\varPhi } = 0, \nonumber \\&\kappa (1+\varepsilon )\varDelta _{j} \dot{X}_{2} + (1+\kappa )\varDelta _{j+1} \dot{X}_{1} \nonumber \\&\quad - (1-\varepsilon \kappa )\varDelta _{j+1} \dot{X}_{2}= 0\,. \end{aligned}$$
(59)

As can be seen from Eqs. (44) and (55), the perturbations of the components of \(\mathbf {z}^{*}\) are not mutually independent. Thus, it is possible to reduce the state vector to

$$\begin{aligned} \mathbf {z} = [\varPhi ,\ \dot{X}_2]^{T}. \end{aligned}$$

Substituting (44) and (55) into Eq. (51) gives

$$\begin{aligned} \begin{aligned}&\pi \left( 1+\frac{\varepsilon }{2} \right) \varDelta _{j} \dot{X}_{2} + (-v_{2}+B\cos {\varPhi })\varDelta _{j} \varPhi \\&\quad + \frac{\pi }{2}\varepsilon \varDelta _{j+1} \dot{X}_{2} + (v_{2}+B\cos {\varPhi })\varDelta _{j+1} \varPhi = 0\,. \end{aligned} \end{aligned}$$
(60)

Again, using (44) and (55) combined with Eqs. (59) leads to one and the same relation:

$$\begin{aligned} \begin{aligned}&(1+\varepsilon ) ( \varDelta _{j+1} \dot{X}_{2} - \kappa \varDelta _{j} \dot{X}_{2} ) + \\&\quad + (1+\kappa )\varDelta _{j+1} \varPhi \, B\sin {\varPhi } = 0. \end{aligned} \end{aligned}$$
(61)

Finally, Eqs. (60) and (61) form the system of relationships between the perturbations occurring after the consecutive impacts:

$$\begin{aligned} \varDelta \mathbf {z}_{j+1} = {\mathbf {D}}_{j} \varDelta \mathbf {z}_{j}\,, \end{aligned}$$
(62)

where

$$\begin{aligned} \varDelta \mathbf {z}_{j} = [\varDelta _{j} \varPhi ,\ \varDelta _{j} \dot{X}_{2}]^T, \end{aligned}$$
(63)

and \({\mathbf {D}}_{j}\) is a kind of transition matrix. Its elements are dependent on C, \(\kappa \) and \(\varepsilon \) in the considered problem.

By analogy, this whole procedure can be applied to the second half period of the analyzed cyclic motion, which gives

$$\begin{aligned} \varDelta \mathbf {z}_{j+2} = {\mathbf {D}}_{j+1} \varDelta \mathbf {z}_{j+1}\,. \end{aligned}$$
(64)

However, the two-impact motion is assumed to be symmetric, therefore \({\mathbf {D}}_{j+1}={\mathbf {D}}_{j}\) and the final transformation has the form

$$\begin{aligned} \varDelta \mathbf {z}_{j+2} = {\mathbf {D}}\, \varDelta \mathbf {z}_{j} \quad \text {with}\quad {\mathbf {D}}= {\mathbf {D}}_{j+1} {\mathbf {D}}_{j} = {\mathbf {D}}_{j}^2. \end{aligned}$$
(65)

Stability of the periodic motion can be determined on the basis of the eigenvalues \(r_1\) and \(r_2\) (real or complex) of constant matrix \({\mathbf {D}}\). The motion is asymptotically stable if \(|r_i| < 1\) for every i [19, 21].

The resulting stability regions on the planes \((\kappa ,\, C)\) and \((\varepsilon ,\, C)\) are shown in Fig. 5. The acceptable range of C can be written as

$$\begin{aligned} C_{S\min }(\kappa ,\, \varepsilon ) \le C \le C_{S\max }(\kappa ,\, \varepsilon )\,. \end{aligned}$$
(66)

Although formally the lower boundary depends on both \(\kappa \) and \(\varepsilon \), the dependence on \(\varepsilon \) is negligible; \(C_{S\min }\) turns out to be a monotonically increasing function of \(\kappa \), and it practically coincides with \(C_{\min }(\kappa )\) given by formula (21). The upper stability boundary, in turn, is weakly dependent on both the restitution coefficient and small parameter. When \(\kappa = 0.75\) and \(\varepsilon = 0.1\), the critical values are \(C_{S\min }\approx 0.99\) and \(C_{S\max }\approx 1.68\).

Fig. 5
figure 5

Restrictions on C related to the stability of periodic motions: stability regions and stability boundaries for varying \(\kappa \) and \(\varepsilon \)

Full size image
Fig. 6
figure 6

Stability region on the plane \((\xi ,\, \kappa )\) for \(\varepsilon = 0.05\)

Full size image
Fig. 7
figure 7

SIM of the system and different stability regions: a the regions of stable fixed points (SFP) and stable periodic motions (SPM), b the stable branch (bold) and two fixed points

Full size image

For comparison with literature results, the stability region has been plotted on another plane (see Fig. 6), in terms of the dimensionless factor

$$\begin{aligned} \xi = \frac{2L}{F_{10}/k_1} = \frac{2}{\varepsilon \hat{f}_{10}}\,. \end{aligned}$$

Such a graphical representation of stability boundaries was shown, for example, by Masri [19, 21]. His results were reported for the mass ratio \(\varepsilon = 0.05\) and damping ratio

$$\begin{aligned} \zeta = \frac{c_1}{c_{1\mathrm {cr}}} = \frac{c_1}{2\sqrt{k_1 m_1}} = 0.01\,, \end{aligned}$$

that is \(\zeta = \varepsilon \hat{\gamma }_{1}/2 = 0.01\). These values have been taken into account in Fig. 6. A visual comparison of the results reveals a close similarity of the boundaries shapes and, above all, a high agreement of the characteristic \(\xi \) values at \(\kappa = 0\) and \(\kappa = 1\).

Fig. 8
figure 8

Analytical solutions corresponding to the stable fixed point (\(\hat{f}_{10}= 1.5\)): a time histories, b phase diagrams

Full size image

The analytical expression for matrix \({\mathbf {D}}_{j}\) as well as an approximation of \(C_{S\min }\) and \(C_{S\max }\) have been presented in Appendix 1. Unfortunately, the resulting complicated form of the eigenvalues \(r_1\) and \(r_2\) does not allow to formulate concise stability conditions.

Figure 7 presents different parts of the SIM related to the three considered criteria. The geometrically allowable solutions can be found along the branch of stable fixed points (SFP) within the range of stable periodic motions (SPM, see Fig. 7a). The final stability region (S) is illustrated in Fig. 7b. For the basic data set (33), only one fixed point belongs to the stable branch. It is worth noting that the location and length of the stable segment of the SIM are comparable with the results reported in Refs. [13,14,15,16].

4 Analytical and numerical results

Let us start with the results of an analytical nature. The time histories of U, W and \(X_1\), \(X_2\), \(X_3\) corresponding to the stable fixed point \(P_{2}\) (Fig. 7b) are plotted in Fig. 8a. As can be seen, the effect of collision on the box motion is hardly visible. Due to the very weak coupling between the block and the secondary oscillator, the latter one moves harmonically. The smooth and non-smooth types of the components behavior can be better seen in the phase diagrams (Fig. 8b).

The size of the stability zone and the location of fixed points on the SIM are strongly affected by the model parameters. For instance, when treating the excitation amplitude \(\hat{f}_{10}\) as a control parameter, we can observe various changes in the existence and stability of the periodic solutions (see Fig. 9). As \(\hat{f}_{10}\) is decreased to 1.2, points \(P_{1}\) and \(P_{2}\) get closer to each other, and \(P_{2}\) still remains stable. For \(\hat{f}_{10}= 0.6\), \(P_{2}\) is shifted to the left branch and becomes unstable. However, increasing the forcing amplitude from \(\hat{f}_{10}= 1.5\) to \(\hat{f}_{10}= 2.5\) also lead to instability of \(P_{2}\). In the case of two unstable fixed points, the assumed periodic solution with two symmetric impacts per cycle is not valid. Therefore, the actual motion of the mechanical system should be determined via numerical simulations.

Fig. 9
figure 9

Fixed points on the SIM of the system with stable (bold solid) and unstable (dashed) branches: a \(\hat{f}_{10}= 1.2\), b \(\hat{f}_{10}= 0.6\), c \(\hat{f}_{10}= 2.5\)

Full size image

Figure 10 contains the plots of the frequency–response curves for various values of \(\hat{f}_{10}\) and \(\hat{\gamma }_{1}\). The result corresponds only to the right branch of the SIM (\(C > C_{S\min }\)). The characteristics resemble the case of linear system, but they consist of stable and unstable segments. Functions \(C(\hat{\sigma }_{1})\) and \(A_3(\hat{\sigma }_{1})\) are mostly single-valued, since there is no spring-related nonlinearity bending the response curves. Only for low forcing amplitudes and small damping, one stable and one unstable branch occur simultaneously for \(\hat{\sigma }_{1}< 0\). Although the two subsystems are weakly coupled, amplitude \(A_3\) noticeably increases with \(\hat{f}_{10}\). However, it should be emphasized that \(A_3\) is a function of the parameters that are crucial for stability of the system as well as the other parameters (\(\hat{\alpha }_{23}\), \(\hat{\sigma }_{30}\), \(\hat{\gamma }_{3}\)).

Fig. 10
figure 10

Frequency–response curves of the system: a effect of \(\hat{f}_{10}\), b effect of \(\hat{\gamma }_{1}\); stable (bold solid) and unstable (dashed) branches

Full size image
Fig. 11
figure 11

Amplitude C as a function of the excitation amplitude \(\hat{f}_{10}\) for positive (a) and negative (b) values of the detuning parameter \(\hat{\sigma }_{1}\); stable (bold solid) and unstable (dashed) branches

Full size image
Fig. 12
figure 12

The effect of selected pairs of parameters on existence and stability of periodic solutions: no solutions (white), at least one stable solution (blue), one or two unstable solutions (gray). (Color figure online)

Full size image

The variation of amplitude C with the excitation amplitude for several values of the detuning parameter is presented in Fig. 11. Naturally, the curves can also be divided into stable and unstable segments. Functions \(C(\hat{f}_{10})\) seem to be linear for \(\hat{\sigma }_{1}> 0\), and they take more complicated shapes for \(\hat{\sigma }_{1}< 0\). In the two cases, the length of the stable branches increases with increasing \(|\hat{\sigma }_{1}|\).

In order to get a deeper insight into the effect of various parameters on the occurrence of the steady-state periodic response of the system, more systematic calculations have been conducted. Figure 12 shows several parameter planes with the regions of existence and stability of the solutions. The variation ranges and steps of the parameters are given in Table 1. The domains of one stable solution are filled with blue. In the gray-shaded areas the two existing solutions are unstable. The white areas, in turn, relates to the lack of periodic solutions. As it could be expected, low amplitudes of the excitation are insufficient to ensure a steady state in the form of two-impact symmetric motion. Such regions and the stability zones are usually separated by relatively narrow instability strips. Moreover, unstable regions arise near the axis \(\hat{\sigma }_{1}= 0\). Apart from amplitude \(\hat{f}_{10}\), the restitution coefficient is crucial for the existence and stability of the solutions. On the plane \((\kappa ,\, \hat{f}_{10})\), for example, the stable region is bounded from above and below. Similar effect can be observed for the pair \((\hat{\gamma }_{1},\, \hat{f}_{10})\), but the upper critical force level increases with \(\hat{\gamma }_{1}\). When it comes to the interplay between \(\kappa \) and \(\hat{\gamma }_{1}\), high damping values together with low restitution coefficient may exclude the occurrence of the periodic response.

Now let us turn to purely numerical results. It should be noted that simulation studies of vibro-impact dynamics can be a challenging task from the computational viewpoint. Firstly, long-term motion of the system should be analyzed to omit the transient response, which becomes cumbersome in parametric investigations. Secondly, a special attention must be paid to collision detection, i.e., a very accurate determination of the impact time instants. In what follows, Eq. (1) in a non-dimensional form are integrated numerically between impacts by using the Runge–Kutta–Fehlberg method (RKF45). As soon as the unilateral constraints are violated, the algorithm switches to the classical fourth-order Runge-Kutta method (RK4) modified with the concept of time-step bisection.

Numerical solutions for the basic data set as well as for \(\hat{f}_{10}= 0.6\) are presented in Fig. 13. In the first case, function W has a similar shape as the sinusoidal-sawtooth response given in Fig. 8. The numerically obtained amplitudes of \(X_1\) and \(X_3\) are very close to the analytical ones. Time histories for the unstable case are shown for a longer time interval. As can be seen, time history of the relative displacement W is composed of resonant subintervals (two-impact motion) and shorter episodes of irregular motion. The main oscillator exhibits the so-called strongly modulated response (SMR). Such a behavior was reported in many papers devoted to VI NES of this kind (e.g., see [9, 11, 15, 16]). What is more, the secondary oscillator coupled with the colliding block undergoes a similar beating-like motion, but with a slighter amplitude modulation. Completely different complexity of the system behavior in the two cases is also reflected in the phase portraits.

As a result of parametric studies, the bifurcation diagrams of the displacement \(X_2\) are shown in Fig. 14a. The excitation amplitude is the control parameter. The first diagram was calculated for \(0.5 \le \hat{f}_{10}\le 5\) with a step \(\varDelta \hat{f}_{10}= 0.01\). The initial \(n_t = 400\) excitation periods were discarded, and then motion of the system was analyzed for \(n_{s} = 800\) periods. At the beginning of a new step, the last solution (for the previous value of \(\hat{f}_{10}\)) was used as the initial conditions. Instead of using the Poincare map, local maxima of \(X_2\) were found in each period [26].

The system dynamics turns out to be regular in a large part of the analyzed range. The motion is mostly periodic in the subintervals \(0.9 \le \hat{f}_{10}\le 2.8\), \(2.9 \le \hat{f}_{10}\le 3.4\) and \(3.8 \le \hat{f}_{10}\le 4\). The periodic windows are surrounded and separated by regions of chaotic behavior. The relatively narrow smears of points at the transition between these two regimes may indicate quasi-periodic motion. More details of the qualitative changes in the system dynamics can be seen in the second diagram computed with the same technique for \(1.9 \le \hat{f}_{10}\le 4\) with higher resolution: \(\varDelta \hat{f}_{10}= 0.002\).

In order to more precisely specify the character of vibro-impact motion, spectra of the Lyapunov exponents (LEs) \(\{\lambda _1,\, \lambda _2,\, \ldots ,\, \lambda _7\}\) of the system were determined within the same ranges of \(\hat{f}_{10}\). In the procedure of numerical integration of the variational equations along with the equations of motion, we have applied the Müller algorithm for non-smooth dynamical systems [22] and the Gram-Schmidt reorthonormalization [25, 26]. The calculations were performed over \(n_{\lambda } = 1500\) excitation periods, and were terminated if the maximal value of standard deviation of the set of LEs within the last \(m_{\lambda }\) steps decreased below a given threshold.

Table 1 The variation ranges and steps of the model parameters used in the numerical studies
Full size table
Fig. 13
figure 13

Numerical solutions—time histories and phase portraits: a the basic data set with \(\hat{f}_{10}= 1.5\), b \(\hat{f}_{10}= 0.6\)

Full size image
Fig. 14
figure 14

The effect of \(\hat{f}_{10}\) on the system response: a bifurcation diagrams, b diagrams of the three largest Lyapunov exponents

Full size image

The diagrams of the three largest Lyapunov exponents are presented in Fig. 14b. As can be seen, the ranges of the control parameter where the maximal exponent \(\lambda _1 = 0\) correspond to the periodic windows. In the regions of chaotic behavior, in turn, \(\lambda _1\) becomes positive and \(\lambda _2 = 0\). Moreover, it seems that \(\lambda _1 = \lambda _2 = 0\) at some single points. The third LE is always negative.

Table 2 contains the LE spectra in a numeric form for selected values of the excitation amplitude. Now it is clear that when \(\hat{f}_{10}\) increases and the periodic motion with two symmetric impacts loses its stability, the system exhibits a sequence of period-doubling bifurcations. Next, a relatively narrow range of chaotic motion arises. Within the next two periodic windows, this classical route to chaos is not so evident, but it can be observed that 2T- and 4T-periodic motions predominate. Phase portraits of the periodic and chaotic solutions for \(\hat{f}_{10}> 2\) are shown in Fig. 15.

It should be noticed that the bifurcation diagram based on local maxima can be confronted directly with the amplitude of the periodic steady-state motion investigated analytically. According to Eq. (17) the amplitude of \(X_2\) is given by \(A_2 = (1-\varepsilon +\varepsilon ^2) C\). By analogy to Fig. 11, we can plot \(A_2\) as a function of \(\hat{f}_{10}\) when the other parameters are kept constant. The resulting force–response curve overlaid on the bifurcation diagram of \(X_2\) is depicted in Fig. 16. As can be seen, there is a quite good agreement between the results. The amplitude based on the approximate analytical solution is slightly lower than the numerical values. Moreover, although the length of the stable periodic range may seem to be overestimated, it can be observed that the numerical solutions at \(\hat{f}_{10}\approx 1\) and \(\hat{f}_{10}\approx 2.1\) are mostly 1T-periodic.

5 Limitations and extensibility of the approach

The approximate analytical approach can be regarded as a specific perturbation technique, where the small parameter, equivalent to the mass ratio, plays the central role. Usually, in the investigations of various VI NESs the parameter value is assumed to be very small, i.e., \(\varepsilon \le 0.02\). On the contrary, in our studies, we have taken \(\varepsilon = 0.1\) as the limiting value: the masses \(m_2\) and \(m_3\) are at least one order of magnitude smaller than \(m_1\). So, a question about sufficiency of this assumption and accuracy of the solutions arises.

A graphical comparison between the analytical and numerical time histories of U and W for three values of \(\varepsilon \) is shown in Fig. 17a. For the sake of clarity, the plots are focused on one period of the system motion. Although the vibro-impact behavior reflected by W (always limited by the values \(A_W = 1\) and \(-1\)) is constantly well approximated, the differences for U increase with \(\varepsilon \) considerably. Obviously, it has its consequences for solutions \(X_1\), \(X_2\) and \(X_3\) (it is visible, for example, in Fig. 16). The broader results included in Fig. 17b indicate that the discrepancies in the amplitudes B, \(A_1\), \(A_2\) and \(A_3\) grow linearly with the small parameter. When \(\varepsilon = 0.1\), the amplitude differences for B and \(A_1\) are about \(20\%\) (with reference to the numerical values), while the differences in the other amplitudes do not exceed \(8\%\).

Table 2 The spectra of the Lyapunov exponents for selected values of \(\hat{f}_{10}\)
Full size table
Fig. 15
figure 15

Phase portraits of periodic and chaotic solutions: a \(\hat{f}_{10}= 2.2\), b \(\hat{f}_{10}= 2.4\), c \(\hat{f}_{10}= 2.5\), d \(\hat{f}_{10}= 2.523\), e \(\hat{f}_{10}= 2.8\), f \(\hat{f}_{10}= 3\), g \(\hat{f}_{10}= 3.6\), h \(\hat{f}_{10}= 4.5\)

Full size image

It should be noticed that the small parameter is involved in many stages of the procedure, which leads to various simplifications. For instance, the assumption \(m_2/m_1 = m_3/m_1 = \varepsilon \) (i.e., \(m_2 = m_3\)) together with \(\alpha _{23}= \varepsilon ^2\hat{\alpha }_{23}\) results in a very specific idealization of the system. Indeed, the coupling between the colliding block and the secondary oscillator is weak (of order \(\varepsilon ^1\)), and their interaction is neglected at the first approximation. Consequently, the stability analysis of the periodic motion can be restricted to the vibro-impact unit, and dynamics of the body of mass \(m_3\) is considered only in the stability analysis of the steady states.

Fig. 16
figure 16

Comparison of the analytical and numerical results: the force-amplitude curve \(A_2(\hat{f}_{10})\) overlaid on the bifurcation diagram

Full size image
Fig. 17
figure 17

Comparison of the analytical (solid line) and numerical (markers) results: a steady-state solutions U and W for \(\varepsilon \in \left\{ 0.02,\, 0.05,\, 0.1 \right\} \), b steady-state amplitudes as functions of \(\varepsilon \). Results obtained for the basic data set

Full size image

Moreover, the analytical approach has been applied just to the simplest type of the system behavior: the periodic motion with two symmetric impacts per cycle. As it can be concluded from numerous simulations conducted for this and similar systems, the 2T-, 4T- or 8T-periodic motions do not include simple impacts patterns (e.g., equal time intervals between impacts, only full-span travels between the stops), which practically makes it impossible to construct analytical solutions to such vibro-impact problems.

As a potential extension of our considerations, we will outline the analysis suited to the case when the assumption \(m_3/m_1 = \varepsilon \) is eliminated. So, let \(m_2/m_1 = \varepsilon \) while \(m_3/m_1 \approx 1\). Now, the equations of motion are given by [cf. Eq. (4)]

$$\begin{aligned}&\ddot{X}_1 + \gamma _{1}\dot{X}_1 + X_1 = f_{10}\sin (\varOmega _{1}\tau ) + \nonumber \\&\quad - \varepsilon \frac{1 + \kappa }{1+\varepsilon }\sum \limits _{j} (\dot{X}_1 - \dot{X}_2) \delta (\tau - \tau _{j}^{-})\,, \nonumber \\&\quad \varepsilon \ddot{X}_2 + \alpha _{23}(X_2 - X_3) = \nonumber \\&\quad = \varepsilon \frac{1 + \kappa }{1+\varepsilon }\sum \limits _{j} (\dot{X}_1 - \dot{X}_2) \delta (\tau - \tau _{j}^{-})\,, \nonumber \\&\quad \ddot{X}_3 + \gamma _{3}\dot{X}_3 + \varOmega _{30}^2 X_3 + \alpha _{32}(X_3 - X_2) = 0 \,, \end{aligned}$$
(67)

where

$$\begin{aligned} \varOmega _{30}^2 = \frac{k_{3}}{m_3\omega _{10}^2},\qquad \gamma _3 = \frac{c_3}{m_3\omega _{10}},\qquad \\ \alpha _{23}= \frac{k_{23}}{m_1\omega _{10}^2},\qquad \alpha _{32}= \frac{k_{23}}{m_3\omega _{10}^2}. \end{aligned}$$

Let \(\varOmega _{30}^2 = 1 + \varepsilon \hat{\sigma }_{30}\). If \(\alpha _{23}= \varepsilon \hat{\beta }^2\) and \(\alpha _{32}= \varepsilon \mu _{13}\hat{\beta }^2\) where \(\mu _{13}= m_1/m_3\), at the level of the first approximation the vibro-impact motion of the block will be affected by vibrations of the secondary oscillator (but not vice versa). After all, the resulting model will be much more realistic.

For the case of weak damping, Eqs. (10) and (12) remain unchanged, but Eq. (11) becomes

$$\begin{aligned} D_0^2 W_{0} + \hat{\beta }^2W_{0}= & {} - (1 + \kappa )\sum \limits _{j} D_0 W_{0}\; \delta (\tau _{0}- \tau _{0,j}^{-}) + \nonumber \\&- (1-\hat{\beta }^2)U_{0} -\hat{\beta }^2 X_{3 0} \,. \end{aligned}$$
(68)

The solution of this equation can be written as

$$\begin{aligned} \begin{aligned} W_{0}(\tau _{0},\, \tau _{1})&= B \sin (\tau _{0}+ \phi ) + \\&+ \frac{\hat{\beta }^2}{1-\hat{\beta }^2} A_3 \sin (\tau _{0}+ \phi _{3}) + Z^{*}(\tau _{0},\, \tau _{1})\,, \end{aligned}\nonumber \\ \end{aligned}$$
(69)

where \(Z^{*}\) is the modified sawtooth function [5, 8]:

$$\begin{aligned} Z^{*}= \frac{C}{\sin \hat{\beta }} \left\{ \begin{array}{lll} -\sin \left[ \frac{2}{\pi }\hat{\beta }(\tau _{0}- \frac{\pi }{2}) \right] , &{} \, &{} 0 \le \tau _{0}\le \pi \\ \sin \left[ \frac{2}{\pi }\hat{\beta }(\tau _{0}- \frac{3\pi }{2}) \right] , &{} \, &{} \pi \le \tau _{0}\le 2\pi \end{array} \right. \nonumber \\ \end{aligned}$$
(70)

For computational purposes, \(Z^{*}\) can be expressed as a continuous function, by analogy to formula (15). It should be noticed that \(Z^{*}\) reduces to \(Z\) in the limiting case for \(\hat{\beta }= 0\) (see Fig. 18).

Fig. 18
figure 18

The modified sawtooth function (solid) for \(\hat{\beta }= 1.2\) and the original sawtooth function (dashed)

Full size image

Due to the extended form of \(W_{0}\), the relationship between the slow-time-scale variables is much more complicated than before, and involves not only B and C, but also \(A_3\), \(\phi \) and \(\phi _3\) [cf. Eq. (19)]:

$$\begin{aligned} \begin{aligned} B^2&= 1 - 2C + (1+ w_1^2 \rho ^2) C^2 + \\&- w_3^2 A_3^2 - 2 w_3 A_3 B \cos (\phi -\phi _{3}) \end{aligned} \end{aligned}$$
(71)

with

$$\begin{aligned} w_1 = \hat{\beta }\cot {\hat{\beta }}\,,\quad w_3 = \frac{\hat{\beta }^2}{1-\hat{\beta }^2}. \end{aligned}$$

Therefore, searching for the steady states becomes hindered. Moreover, the stability analysis of the periodic motions is more difficult, since the spring described by \(\hat{\beta }\) participates in the travel of the block between the stops and this motion is not uniform.

Fig. 19
figure 19

Comparison of the analytical (solid line) and numerical (markers) results for the modified vibro-impact problem

Full size image

A comparison between the analytical and numerical solutions to the modified problem is shown in Fig. 19. The results have been obtained for the following data set:

$$\begin{aligned}&\varepsilon = 0.1,\quad \kappa = 0.75,\quad \mu _{13}= 1,\quad \hat{f}_{10}= 1.5,\quad \hat{\sigma }_{1}= 0.5,\\&\hat{\gamma }_{1}= 0.5,\quad \hat{\beta }= 0.7,\quad \hat{\sigma }_{30}= 0.5,\quad \hat{\gamma }_{3}= 1\,. \end{aligned}$$

As can be seen, despite the high value of the small parameter, the discrepancies in the amplitudes obtained analytically and numerically are relatively small.

6 Conclusions

The three-degree-of-freedom system under a harmonic force has been considered. The analytical studies have been restricted to a periodic steady-state motion with two symmetric impacts per cycle near 1:1 resonance. The multiple scales method combined with the sawtooth-function-based modelling of the non-smooth dynamics has been successfully applied to the problem.

Taking into account geometric constraints and stability criteria, certain restrictions on the amplitudes have been specified. The central role belongs to the stability studies of periodic motions. The presented method is something between the approach involving the general solution for a periodically excited, viscously damped piecewise linear oscillator [19, 29] and the studies of the Poincaré sections of periodic solutions for discrete dynamical systems (e.g., see [17]).

The approximate analytical approach has allowed us to determine both the frequency–response and force–response curves having stable and unstable branches. Moreover, the interplay between the model parameters and their effect on the existence and stability of the periodic solutions have been determined on various parameter planes. When treating the excitation amplitude as the control parameter, one can make the system leave the stability zone. Consequently, the response of the primary oscillator is strongly modulated. This kind of motion is largely followed by the secondary oscillator, in spite of a weak coupling between the subsystems.

The bifurcation diagrams and the Lyapunov exponents spectra have shown that the window of stable 1T-periodic solution is surrounded by the regions of chaotic motion and period-doubling route to chaos. The theoretical predictions have turned out to be in good agreement with the purely numerical results.

To sum up, in the area of near-resonant dynamics, the analytical approach is a useful tool in stability studies, estimation of the motion amplitudes, and systematic parametric studies. However, an extension of the applicability of the method to more complex problems with weaker assumptions (e.g., strong and/or nonlinear coupling, mass ratio of order 1) is highly desirable.