Dynamics and wave propagation in nonlinear piezoelectric metastructures

Abstract

This paper reports dynamical effects in one-dimensional locally resonant piezoelectric metastructures leveraged by nonlinear electrical attachments featuring either combined quadratic and quartic, or essentially quartic potentials. The nonlinear electromechanical unit cell is built upon a linear host oscillator coupled to a nonlinear electrical circuit via piezoelectricity. Semi-analytical harmonic balance (HB)-based dispersion relations are derived to predict the location and edges of the nonlinear attenuation band. Numerical responses show that weakly and moderately nonlinear piezoelectric metastructures (NPMSs) promote a class of nonlinear attenuation band where a bandgap and a wave supratransmission band coexist, while also imparting nonlinear attenuation at the resonances around the underlying linear bandgap. Besides, strongly nonlinear regimes are shown to elicit broadband chaotic attenuation. Negative capacitance (NC)-based essentially cubic piezoelectric attachments are found to expand the aforementioned effects over a broader bandwidth. Excellent agreement is found between the predictions of the HB-based dispersion relations and the nonlinear transmissibility functions of undamped and weakly damped NPMSs at weakly and moderately nonlinear regimes, even in the presence of NC circuits. This research is expected to pave the way toward fully tunable smart periodic metastructures for vibration control via nonlinear piezoelectric attachments.

Appendices

Appendix A

Since an NC is an active, linear electrical component (cf. Eq. 16), stability bounds for $\mu _N$ should be given such that the eigenvalues of the underlying linear system of Eq. 22 are kept at the left half complex plane. Then, by making $\alpha _N=0$ in Eq. 22, the system’s characteristic equation can be obtained as follows:

$$\begin{aligned}&\gamma \varOmega ^4 - \left( \mu _N\delta _{sc}^2 + K^2\gamma + \gamma \right) \varOmega ^2 + \mu _N\delta _{sc}^2\left( 1+K^2\right) \nonumber \\&- K^2\delta _{sc}^2 = 0, \end{aligned}$$

(53)

from which an expression for the system’s resonances are:

$$\begin{aligned} \left\{ \varOmega _1,\ \varOmega _2\right\}&= \mp \frac{1}{2\gamma }\left\{ \gamma \left( \mu _N\delta _{sc}^2 + \gamma \left( 1 + K^2\right) \right. \right. \nonumber \\&\left. \left. \pm \left[ \mu _N\delta _{sc}^4 - 2\mu _NK^2\gamma \delta _{sc}^2 + K^4\gamma ^2 + 4K^2\gamma \delta _{sc}^2 \right. \right. \right. \nonumber \\&\left. \left. \left. - 2\mu _N\gamma \delta _{sc}^2+ 2K^2\gamma ^2 + \gamma ^2\right] ^{-1/2}\right) \right\} ^{-1/2}. \end{aligned}$$

(54)

The NC circuit being dealt with in this manuscript is the S-type one [29], which is known for reducing the short-circuit electroelastic resonances [19, 53]. Although the practical operation bound might be determined by the analog circuitry limitations [5, 6], the theoretical stability limit is actually found by investigating the $\mu$ value that makes the lowest resonance to be placed at exactly the DC frequency. Then, by enforcing the RHS of Eq. 54 to be positive, an expression for $\mu _N$ can be obtained as follows:

$$\begin{aligned} \mu _N>\frac{K^2}{K^2+1}, \end{aligned}$$

(55)

where K is given by either Eq. 12 or 13 for the LPUC. It can be shown that Eq. 55 can be further generalized for a LPMS (multiple LPUCs), as follows:

$$\begin{aligned} \mu >det\left( \left[ \left( \mathbf{K} ^2+\mathbf{I} \right) ^{-1}{} \mathbf{K} ^2\right] -\mathbf{I} \right) . \end{aligned}$$

(56)

The stability limit has been determined for the LPUC and several LPMSs, formed by 5, 10, 15, and 20 LPUCs, with the parameters reported in Sect. 3.1 by using Eq. 56. The $\mu _N$ limits have been obtained as follows: LPUC: 0.01; 5-LPUC LPMS: 0.06; 10-LPUC LPMS: 0.23; 15-LPUC LPMS: 0.48; and 20-LPUC LPMS: 0.78. These values show that, as the number of cells grows to form the piezoelectric metastructure, the $\mu _N$ parameter should be reduced to keep the linear stability. Yet, this does not imply in that the twofold NC effects in reducing the inherent piezoelectric capacitance while increasing the electromechanical coupling are degraded in some way, as it will be shown next.

Figure 13 shows the LPUC’s and the LPMS’ transmissibilities (LPMSs formed by 5, 10, 15, and 20 LPUCs), wherein the main plot illustrates the denser amount of resonances that arise as the number of cells increases, whereas the inset evidences the location of the first resonance at almost $\varOmega =0$, placed at that frequency by the effect of the previously found $\mu _N$ values close to the linear stability bound. Any attempt to improve $\mu _N$ above the obtained stability bounds renders the linear electroelastic system unstable.

Fig. 13

Transmissibilities of several LPMS with $\mu _N$ values set equal to the stability bound given by Eq. 56

Another form of gaining insights into the stability of the linear electroelastic system under the effect of the S-type NC circuit is by iteratively calculating the generalized electromechanical coupling coefficient, $K_{eff}^2$, by using:

$$\begin{aligned} K_{eff}^2=\frac{\omega _{NC,1}^2-\omega _1^2}{\omega _1^2}, \end{aligned}$$

(57)

where $\omega _1$ refers to the first eigenvalue of the generalized eigenvalue problem that is formed with matrices M and K without NC (cf. Eq. 22 with $\mu _N=1$ and $\gamma =1$), and $\omega _{NC,1}$ refers to the first eigenvalue of the generalized eigenvalue problem that is formed with the same matrices, yet with $0<\mu _N<1$. Equation 57 can be recursively calculated as $\mu \rightarrow -1$, which shows that, as $\omega _{NC}\rightarrow 0^+$, $K_{eff}^2\rightarrow \infty$. Moreover, as $\omega _{NC}$ becomes a complex-valued eigenvalue due to $\mu _N$ values that overcome the stability limit given by either Eq. 55 or 56, the negative real part of $\omega _{NC}$ makes $K_{eff}^2$ to take negative, meaningfulness values [53].

Fig. 14

Generalized electromechanical coupling coefficient for the LPUC and for a set of LPMS

Fig. 15

Amplitude behaviors of selected discrete frequencies as a function of the nonlinear coefficient: a NTRFs; b amplitude transmission as a function of $\alpha _N$. Legend for the left-column plots: L or LC: ; $\varvec{\alpha }_{N,1}$: ; $\varvec{\alpha }_{N,2}$: ; $\varvec{\alpha }_{N,3}$: ; $\varvec{\alpha }_{N,5}$: ; $\varvec{\alpha }_{N,6}$:

Figure 14 illustrates the trends of $K_{eff}^2$ as a function of $\mu _N$, for the LPUC and a set of LPMS formed with 5, 10, 15, and 20 LPUCs. The figure has been set so as to show $K_{eff}^2$ values between the $K_{eff}^2$ value that corresponds to the electromechanical coupling without NC and $K_{eff}^2=2.5$, but even larger values are—theoretically—possible. Figure 14 also shows that a certain $K_{eff}^2$ value can be attained by either the LPUC or a LPMS with several LPUCs, by properly fixing the $\mu _N$ value of all the LPUCs in the LPMS. That is to say, the same generalized electromechanical coupling and inherent piezoelectric capacitance reduction effects can be attained by one or several sequentially connected LPUCs, by properly setting all the $\mu _N$’s to the same value, yet the numerical value should be increased toward zero as the number of LPUCs increases. This explains the small $\mu _N$ value that was chosen for the LPMS with 20 unit cells shunted with negative capacitances, although it produces the same net effect as $\mu _N=0.01$ for the LPUC case, i.e., $K_{eff}^2=1.0$. From this discussion, it becomes straightforward to see that the $\mu _N$ value that makes $K_{eff}^2=1.0$ for the LPMS with 20 LPUCs will cause a rather small effect in the electroelastic system consisting of one single LPUC, cf. Fig. 2, but the obtainment of the LPMS effects shown in Fig. 7 follows from repeating 20 times the investigated LPUC with $\mu _N=0.85$.

Figure 14 evidences that all the simulations in this paper have considered linearly stable electroelastic systems, both for the NPUC and the 20-NPUC NPMS cases. The inclusion of $\alpha _N$ with the values reported in Sect. 3.2 was not shown to change the system’s stability. An analytical expression and bounds for $\alpha _N$ that ensure the electroelastic system’s stability are left for future works.

Appendix B

In uniform nonlinear metamaterials⁴ with cubic restoring forces [25, 35, 38, 51], the saddle-node bifurcation that emerges and shifts to the right side in the spectrum as a function of the input amplitude has been associated with the onset of transmission within the underlying linear bandgap [70]. It is through this essentially nonlinear mechanism that wave propagation becomes enabled within the otherwise forbidden band. As the periodic solutions lose their stability through the several saddle-node bifurcations of the unit cells in the metastructure, the essentially nonlinear wave supratransmission phenomenon becomes enabled in the host structure [70].

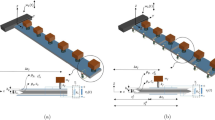
Wave supratransmission is the essentially nonlinear phenomenon that allows the metamaterial host to underpin waves within the forbidden band [69, 70]. The most research has focused on nonlinear hosts that are able to respond to amplitude-level variations. On the one hand, the versatility of nonlinear mechanical host structures is found to be limited, from the point of view of designing, realizing, and controlling the degree of their nonlinearity, which makes the input amplitude variations to be a better approach in practical terms. On the other hand, piezoelectric metastructures based on the nonlinear electrical circuit shown in Fig. 1b can achieve a great level of versatility, since their coefficients are synthesized in the electrical domain with some analog circuits and passive components, whose parameters are comparatively easier to tailor. In this line, the input excitation given for the linear mechanical host can be kept at the same level, whereas the nonlinear coefficients are varied by adjusting the electrical circuit’s parameters [57, 60]. According to Eq. 24, this approach is also a means for exciting and controlling the overall system’s level of nonlinearity, which has a direct relationship with enabling and enhancing the nonlinear wave supratransmission phenomenon across the NPMS.

From the results shown in Fig. 7 for a set of $\alpha _N$ values, five discrete frequencies that fall into the forbidden band have been chosen to demonstrate the nonlinear wave supratransmission phenomenon, as shown in Fig. 15. In special, the frequencies located at $\varOmega =1.002$, $\varOmega =1.003$, and $\varOmega =1.004$ that fall into the forbidden band show similar trends to those found in the specialized literature concerning amplitude-induced wave supratransmission, cf. right column of Fig. 15. The frequencies $\varOmega =1.001$ and $\varOmega =1.004$, which are located at the left and right bandgap edges, respectively, also show the same behavior of rising their amplitudes and reaching a stable value, which is similar to those observed at the remaining frequencies, yet the initial amplitude of the latter frequencies is lesser than the one of the former frequencies because they are located at the bandgap edges.

The plots at the left column of Fig. 15 also help visualize the behaviors inside the bandgap and at its edges, for the same set of $\alpha$ coefficients defined in Sect. 3.1.