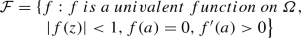Existence of a smooth Lyapunov function for any smooth planar dynamical system with one limit cycle

Abstract

The existence of a smooth Lyapunov function for any smooth planar dynamical system with one limit cycle is proved, which is based on a novel decomposition of the dynamical system from the perspective of mechanics and some definitions and known theorems. By considering the smooth simple closed curve in the complex plane corresponding to the limit cycle of a smooth planar dynamical system and the definition of Morse decomposition, we first prove a theorem in which the limit cycle is diffeomorphic to the unit circle for any smooth planar dynamical system with one limit cycle, and we deduce another theorem, that any two smooth planar systems with one limit cycle are diffeomorphic (or smoothly equivalent). Next, through the definition of the potential function, the explicit construction of a smooth Lyapunov function for a smooth planar dynamical system with one circular limit cycle is given. Then, according to these results, we obtain the following theorem: there always exists a smooth Lyapunov function for any smooth planar dynamical system with one limit cycle. Additionally, two examples are given. Finally, with respect to the coexistence of the limit cycle and Lyapunov function, we discuss two criteria related to system dissipation (divergence and dissipative power) in an example, find that they are not consistent, and explain the meaning of dissipation in infinitely repeated motion in the limit cycle. This result may provide a deeper understanding of the existence of a Lyapunov function for systems with limit cycles.

Appendix

In this “Appendix”, we consider only a smooth planar dynamical system with one limit cycle and we prove Theorem 1.

As discussed in Sect. 3.1, the limit cycle of a smooth planar dynamical system is a smooth simple closed curve, and we can study this kind of curve in the complex plane. In addition, the area surrounded by this kind of curve is a simply connected region. Combining Morse decomposition (Definition 3) and the work of Kwon, Ao and Thouless [32], we can only consider a smooth planar dynamical system with one equilibrium point and one limit cycle here. Then, in view of the results of Lemma 2, we combine some known theorems, such as the Schoenflies theorem, the Riemann mapping theorem, the boundary correspondence theorem, and differential geometry theory, to derive Theorem 1.

Proof of Theorem 1

The proof process is divided into three parts: Part I will prove that there exists a bijection mapping from the region bounded by a smooth simple closed curve(smooth limit cycle) to the unit disk; Part II will prove that the obtained bijection is a bijection at the boundary; Part III will prove that the obtained bijection is a diffeomorphic mapping at the boundary.

• Part I: Prove that there exists a mapping that maps the region $\varOmega$ enclosed by the smooth simple closed curve J to the unit disk W. The idea is to prove the existence of such a mapping by using some properties of the normal family [34]: for any point $a \in \varOmega$, there exists a unique biholomorphic mapping f that maps $\varOmega$ to the unit disk W, such that $f(a)=0$, $f'(a)>0$. The proof consists of the following six steps:

  • Step 1 Construct the function family ${\mathcal {F}}$ on the bounded region $\varOmega$ with the following properties

    

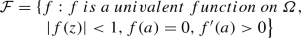    (43)

    Clearly, ${\mathcal {F}}$ is not empty; for example, ${{z - a}}/{d}$ belongs to ${\mathcal {F}}$, and d is the diameter of $\varOmega$.

  • Step 2 Ensure that the derivative $f'(z)$ of the selected function f in ${\mathcal {F}}$ has the highest possible value at a.

    Set $\{ \varOmega _n^ * \}$ as a compact subset sequence of $\varOmega$, so that $\mathop \cup \limits _{n = 1}^\infty \varOmega _n^ * = \varOmega$ and $a \in \varOmega _n^ *$. Then, $\{ f(\varOmega _n^ * )\}$ is a compact subset sequence of $W = \left\{ {z:\left| z \right| < 1} \right\}$. As $n\rightarrow \infty$, $\mathop \cup \limits _{n = 1}^\infty f(\varOmega _n^ * )$ increases, and it tries to fill the unit circle ${\partial W}$. We choose f from ${\mathcal {F}}$, and the derivative $f'(a)$ has the highest possible value, so that we select the “fastest spreading” function at $z=a$ and f has the greatest opportunity to satisfy $\bigcup \limits _{n = 1}^{ + \infty } {f(\varOmega _n^ * )} = W$.

    Note that

    $$\begin{aligned} v = \sup \left\{ {\left| {f'(a)} \right| :f \in {\mathcal {F}}} \right\} . \end{aligned}$$

    (44)

    Because $\varOmega$ is an open region, there certainly exists a neighborhood $U(a,\kappa ) \subset \varOmega$, $\kappa >0$. Let $\forall w \in W$, $\varphi (w) = \kappa w + a$: then, $\varphi$ maps the unit disk W to $U(a,\kappa )$, and $\varphi (0) = a$. For $\forall f \in {\mathcal {F}}$, the composite function $f \circ \varphi$ maps the unit disk to the unit disk origin to origin. Using Schwarz’s lemma [34], we have $\left| {f'(a) \varphi '(0)} \right| \le 1$. Moreover, $\varphi '(0) = r$, and we obtain $\left| {f'(a)} \right| \le {1}/{r}$ and $v < + \infty$.

  • Step 3 The mapping function is expressed as a solution of an extremum problem through some properties of the analytic function family.

    By (44), there exists a function sequence ${f_n}(z) \in {\mathcal {F}}(n = 1,2, \ldots )$ such that

    $$\begin{aligned} \left| {{f_n}'(a)} \right| \ge v - \frac{1}{n}. \end{aligned}$$

    (45)

    Because ${\mathcal {F}}$ is uniformly bounded on $\varOmega$, by the condensation principle [41], there exists an inner closed uniformly convergent subsequence $\left\{ {{f_{{n_j}}}(z)} \right\}$ in $\left\{ {{f_n}(z)} \right\}$. Set $\left\{ {{f_{{n_j}}}(z)} \right\}$ to uniformly converge to some holomorphic function f(z) on $\varOmega$. By the Weierstrass theorem [34], $\{ f_{{n_j}}^{'}(z)\}$ uniformly converges to $f'(z)$ and f(z) is an analytic function on $\varOmega$. Moreover, $f'(a) = \mathop {\lim }\limits _{j \rightarrow + \infty } f_{{n_j}}^{'}(a) = v > 0$, which shows that f(z) is not a constant. Clearly, $\left| {f(z)} \right| < 1$. Therefore, f(z) is the solution to the extremum problem.

  • Step 4 Prove that the obtained f(z) is an injection.

    That is, for $\forall {z_0} \in \varOmega$, the function value $w_0=f(z_0)$ cannot be taken at a point different from $z_0$. Therefore, $f(z)-w_0$ has no zero point in $\varOmega \backslash \left\{ {{z_0}} \right\}$. Let ${w_j} = {f_{{n_j}}}(z_0)$, by ${f_{{n_j}}} \in {\mathcal {F}}$, ${f_{{n_j}}}$ is a one-to-one function, so ${f_{{n_j}}}(z) - {w_j}$ has no zero point in $\varOmega \backslash \left\{ {{z_0}} \right\}$. Clearly, the sequence $\left\{ {{f_{{n_j}}}(z) - {w_j}} \right\}$ shows internal closed uniform convergence to $f(z) - {w_0}$. By Hurwitz’s theorem [42], $f(z) - {w_0}$ has no zero point in $\varOmega \backslash \left\{ {{z_0}} \right\}$, so f(z) is a one-to-one function in W.

  • Step 5 Prove that the obtained f(z) is a surjection.

    In other words, we have $f(\varOmega )=W$. If $f(\varOmega )\ne W$, there exists at least one point $c \in W$ so that $c \notin f(\varOmega )$, $0< \left| c \right| < 1$. Combined with the facts that $f(a)=0$ and f(z) is one-to-one, perform the fraction linear transformation

    $$\begin{aligned} {\psi _1}(z) = \frac{{f(z) - c}}{{1 - {{\overline{c}}} f(z)}}. \end{aligned}$$

    (46)

    Because ${\psi _1}(z)$ is simply connected and has no zero point, $\sqrt{{\psi _1}(z)}$ can have a single branch in $\varOmega$, which is written as ${{\psi _2}(z)}$. Clearly, we have $\left| {{\psi _2}(z)} \right| < 1$. Noting that ${\psi _2}(a) = \sqrt{ - c} \ne 0$, perform the fraction linear transformation

    $$\begin{aligned} {\psi _3}(z) = {e^{i\theta }}\frac{{{\psi _2}(z) - {\psi _2}(a)}}{{1 - {{{{\overline{\psi }}} }_2}(a){\psi _2}(z)}},\theta = \arg {\psi _2}(a).\nonumber \\ \end{aligned}$$

    (47)

    It is easy to obtain $\left| {{\psi _3}(z)} \right| < 1$, $\left| {{\psi _3}(a)} \right| =0$. Because $- c = {\psi _1}(a) = \psi _2^2(a)$, we have

    $$\begin{aligned} \psi _3^{'}(a)= & {} {e^{i\theta }}\frac{{\psi _2^{'}(a)}}{{1 - {{\left| {{\psi _2}(a)} \right| }^2}}} \nonumber \\= & {} {e^{i\theta }}\frac{{\psi _1^{'}(a)}}{{2{\psi _2}(a)}}\frac{1}{{1 - {{\left| {{\psi _2}(a)} \right| }^2}}} \nonumber \\= & {} \frac{{1 + {{\left| {{\psi _2}(a)} \right| }^2}}}{{2\left| {{\psi _2}(a)} \right| }}f'(a) \nonumber \\> & {} f'(a) \nonumber \\= & {} v. \end{aligned}$$

    (48)

    By the property of fraction linear transformation, ${\psi _3}(z) \in {\mathcal {F}}$, so $\psi _3^{'}(a) \le v$, which yields a contradiction. Therefore, f is surjective. Combined with step 2, we have that f is a biholomorphic mapping from $\varOmega$ to W and that $f (a) = 0, f '(a) > 0$.

  • Step 6 Prove that f is unique.

    Suppose g is also a biholomorphic mapping from $\varOmega$ to W, and $g(a) = 0,g'(a) > 0$. Then, $g \circ {f^{ - 1}}$ is a mapping from the unit disk to the unit disk, and it maps zero to zero. By the Schwarz lemma [34], we have $\left| {g({f^{ - 1}}(w))} \right| \le \left| w \right| ,\forall w:\left| w \right| < 1.$ Let $w = f(z)$: then, $\left| {g(z)} \right| \le \left| {f(z)} \right|$, $\forall z \in \varOmega$. Similarly, we can have $\left| {g(z)} \right| \ge \left| {f(z)} \right|$, $\forall z \in \varOmega$. Then, we have $\left| {g(z)} \right| = \left| {f(z)} \right|$, and there exists a constant $\theta _0$ satisfying $g(z) = {e^{i\theta _0 }}f(z)$. Because $f'(a)>0, g'(a)>0$, we have ${e^{i\theta _0 }}=1$, and then $g(z) \equiv f(z)$.

    • Part II: Prove that the obtained f is a continuous bijection that can map the smooth simple closed curve J to the unit circle, we use the following four steps:

    • Step 7 Generalize the domain of f(z) from $\varOmega$ to its boundary $\partial \varOmega$ (also written as J).

      Since the boundary $\partial \varOmega$ is a smooth simple closed curve, the points on the boundary $\partial \varOmega$ are accessible boundary points. Let $\zeta \in \partial \varOmega ,$ $\left\{ {{z_n}} \right\} \subset \varOmega ,\mathop {\lim }\limits _{n \rightarrow + \infty } {z_n} = \zeta .$ The function f(z) is proved to be uniformly continuous in $\varOmega$ by Yu [43]. That is, for $\forall \varepsilon> 0,\exists \delta > 0$, if $z',z'' \in \varOmega$ and $\left| {z' - z''} \right| < \delta$, then

      $$\begin{aligned} \left| {f(z') - f(z'')} \right| < \varepsilon . \end{aligned}$$

      (49)

      By the Cauchy criterion for convergence, when n is sufficiently large, there exists a positive integer $p = 1,2, \ldots$ such that $\left| {{z_{n + p}} - {z_n}} \right| < \delta$. Combined with (49), we have

      $$\begin{aligned} \left| {f({z_{n + p}}) - f({z_n})} \right| < \varepsilon . \end{aligned}$$

      (50)

      Then, the sequence $\left\{ {f(z_n)} \right\}$ converges to a finite complex number w.

      Set another sequence $\{ z_n^{'}\} \subset \varOmega$ that converges to $\zeta$. Similarly, the sequence $\{ f(z_n^{'})\}$ converges to a finite complex number $w'$. We have

      $$\begin{aligned}&\left| {w - w'} \right| = \left| {w - f({z_n}) + f({z_n}) - f(z_n^{'}) + f(z_n^{'}) - w'} \right| \nonumber \\&\quad \le \left| {w - f({z_n})} \right| + \left| {f({z_n}) - f(z_n^{'})} \right| \nonumber \\&\qquad + \left| {f(z_n^{'}) - w'} \right| . \end{aligned}$$

      (51)

      By

      $$\begin{aligned} \left| {{z_n} - z_n^{'}} \right|= & {} \left| {{z_n} - \zeta + \zeta - z_n^{'}} \right| \nonumber \\\le & {} \left| {{z_n} - \zeta } \right| + \left| {\zeta - z_n^{'}} \right| , \end{aligned}$$

      (52)

      and sequences $\left\{ {{z_n}} \right\}$, $\{ z_n^{'}\}$ all have the limit $\zeta$. Therefore, when n is large enough, we have

      $$\begin{aligned} \left| {{z_n} - z_n^{'}} \right| < \delta . \end{aligned}$$

      (53)

      Combined with (53),(49)and (51), we obtain

      $$\begin{aligned} \left| {w - w'} \right|< & {} \varepsilon + \varepsilon + \varepsilon =3\varepsilon . \end{aligned}$$

      (54)

      From the arbitrariness of $\varepsilon$, there must be $\left| {w - w'} \right| = 0$, so we have

      $$\begin{aligned} {w = w'}. \end{aligned}$$

      (55)

      This shows that

      $$\begin{aligned} \exists \mathop {\lim }\limits _{z \rightarrow \zeta ,z \in G} f(z) = w, written ~as ~f(\zeta ). \end{aligned}$$

      (56)

    • Step 8 Prove that the function $w = f(z)$ is continuous on $\partial \varOmega$.

      Let $\zeta ,{\zeta ^ * } \in \partial \varOmega$, $\left| {\zeta - {\zeta ^ * }} \right| < {\delta }/{3}$ and $\left\{ {{z_n}} \right\} ,\left\{ {z_n^{*}} \right\} \subset \varOmega$, ${z_n} \rightarrow \zeta ,z_n^ * \rightarrow {\zeta ^ * },n \rightarrow + \infty$; we have

      $$\begin{aligned}&\left| {f(\zeta ) - f({\zeta ^ * })} \right| \nonumber \\&\quad = \left| {f(\zeta ) - f({z_n}) + f({z_n}) - f(z_n^ * ) + f(z_n^ * ) - f({\zeta ^ * })} \right| \nonumber \\&\quad \le \left| {f(\zeta ) - f({z_n})} \right| + \left| {f({z_n}) - f(z_n^ * )} \right| + \nonumber \\&\qquad \left| {f(z_n^ * ) - f({\zeta ^ * })} \right| . \end{aligned}$$

      (57)

      Fig. 5

      

      Differentiable mapping

      Due to

      $$\begin{aligned} \left| {{z_n} - z_n^*} \right|= & {} \left| {{z_n} - \zeta + \zeta - {\zeta ^*} + {\zeta ^*} - z_n^*} \right| \nonumber \\\le & {} \left| {{z_n} - \zeta } \right| + \left| {\zeta - {\zeta ^*}} \right| + \left| {{\zeta ^*} - z_n^*}\right. | \end{aligned}$$

      (58)

      select the appropriate ${{z_n}, z_n ^ *}$ such that

      $$\begin{aligned} \left| {{z_n} - z_n^ * } \right| < \delta . \end{aligned}$$

      (59)

      Then, combining with (59),(49) and (57), when $\left| {\zeta - {\zeta ^ * }} \right| < {\delta }/{3}$, we have

      $$\begin{aligned} \left| {f(\zeta ) - f({\zeta ^ * })} \right|< & {} \varepsilon + \varepsilon + \varepsilon =3\varepsilon . \end{aligned}$$

      (60)

      That is, the function $w = f(\zeta )$ is continuous on $\partial \varOmega$.

    • Step 9 Prove that $w = f(z)$ is an injection from $\partial \varOmega$ to $\partial W = \left\{ {\left. w \right| \left| w \right| = 1} \right\}$.

      When $\zeta \in \partial \varOmega$, there are two cases for the value of $\left| {f(\zeta )} \right|$: $\left| {f(\zeta )} \right| < 1$ and $\left| {f(\zeta )} \right| = 1$.

      Let$\left\{ {{z_n}} \right\} \subset \varOmega$, $\mathop {\lim }\limits _{n \rightarrow + \infty } {z_n} = \zeta$; suppose $w = f(z)$ satisfies $\left| w \right| = \left| {f(z)} \right| < 1$ and there exists $z' \in \varOmega$ such that $w = f(z')$.

      Select a sufficiently small neighborhood of $z'$, written as ${\varOmega _{z'}}$; when n is sufficiently large, ${z_n} \notin {\varOmega _{z'}}$.

      According to the consistency of f(z), we have $f({z_n}) \notin f({\varOmega _{z'}})$. That is, $\mathop {\lim }\limits _{n \rightarrow + \infty } f({z_n}) = f(\zeta ) = w \notin f({\varOmega _{z'}})$, which is contrary to the assumption that $w = f(z') \in f({\varOmega _{z'}})$, so $\left| {f(\zeta )} \right| = 1$.

      Now we prove that $w = f(z)$ is an injection on $\left| w \right| = 1$. That is, for $\forall \zeta ,{\zeta ' } \in \partial \varOmega$ and $\zeta \ne \zeta '$, we have $f(\zeta ) \ne f(\zeta ')$.

      Letting $\left\{ {{z_n}} \right\}$, $\{ z_n^{'}\} \subset \varOmega$, $\mathop {\lim }\limits _{n \rightarrow + \infty } {z_n} = \zeta ,\mathop {\lim }\limits _{n \rightarrow + \infty } z_n^{'} = \zeta '$, we have $\left| {f(\zeta )} \right| = \left| {f(\zeta ')} \right| = 1$. Select a sufficiently small neighborhood of $\zeta$, written as ${\varOmega _{\zeta }}$; when n is sufficiently large, ${z_n} \in {\varOmega _\zeta },z_n^{'} \notin {\varOmega _\zeta }$. Then $f({z_n}) \in f({\varOmega _\zeta }),f(z_n^{'}) \notin f({\varOmega _\zeta })$, so $f(z_n^{'}) \rightarrow f({z_n}) \in f({\varOmega _\zeta })$ is not possible. Hence, $w = f(z)$ is an injection on $\partial \varOmega$.

    • Step 10 Prove that $w = f(z)$ is a surjection from $\partial \varOmega$ to $\partial W = \left\{ {\left. w \right| \left| w \right| = 1} \right\}$.

      Without loss of generality, assume there exists ${w_0} \in \left| w \right| = 1$ such that $f(z) - {w_0} \ne 0, z \in \partial \varOmega$, and we obtain $\left| {f(z) - {w_0}} \right| > 0$. Then, there must be some $r>0$ such that

      $$\begin{aligned} \left| {f(z) - {w_0}} \right|> r > 0. \end{aligned}$$

      (61)

      This contradicts the conclusion of step 8 that $w = f(\zeta )$ is continuous on $\partial \varOmega$. Therefore, $w = f(z)$ is a surjection on $\left| w \right| = 1$.

  • Part III: Prove that the obtained bijection f is a diffeomorphic mapping. The proof contains the following two steps:

    • Step 11 To prove that f is a homeomorphism: (i) f is a continuous bijection, which has been demonstrated above; (ii) f and $f^{-1}$ are continuous. The continuity of f has been obtained. Since the smooth simple closed curve J and the unit circle $\partial W$ are both closed sets, that is, compact, it can be known that the inverse mapping $f^{-1}$ is also continuous.

      Thus, f is a homeomorphic mapping.

    • Step 12 Prove that f is differentiable.

      According to the definition of a differentiable mapping [30], Fig. 5 can be obtained.

      Before proving this theorem, we consider the limit cycle in the phase plane as a smooth simple closed curve in the complex plane. Here, we discuss these manifolds from the complex plane to the phase plane (Euclidean plane).

      The smooth simple closed curve J and unit circle $\partial W$ in the complex plane are one-dimensional differentiable manifolds. For the mapping $f\!\!\!\!:\!\!\!J to\partial W$,Jand $\partial W$ can, respectively, obtain a coordinate in the Euclidean plane by the chart $\left( J_{i}, \varphi _{i}\right)$ (belonging to the atlas $\left\{ \left( J_{i}, \varphi _{i}\right) \right\} )$ and$\left( \partial W_{i}, \psi _{i}\right)$ (belonging to the atlas $\left\{ \left( \partial W_{i}, \psi _{i}\right) \right\}$). For $\forall p \in {J}$, any selected coordinate $({J_i},{\varphi _i})$ satisfies $p \in {J_i}$ and ${\varphi _i}(p) \in \overline{{J_i}}$, and the coordinate $({\partial W_i},{\psi _i})$ satisfies $f(p) \in \partial W_{i}$ and ${\psi _i}(f(p)) \in \overline{\partial W_{i}}$. Then, the mapping of the domains of Euclidean spaces ${\psi _i} \circ f \circ \varphi _i^{-1}$, which is defined in a neighborhood of the point $\varphi _{i}(p)$, must be differentiable.

      The geometric interpretation of complex numbers is noted: a one to one correspondence is established between each complex number and ordered pair(x, y) which is a point in the Cartesian plane coordinate system. Therefore, the 2-dimensional Euclidean space can be identified with the 1-dimensional complex linear space [44]. The specific process is as follows: let M be a 1-dimensional manifold in a complex plane, where its atlas is $\left\{ U_{\beta }\right\}$. In addition, let $\varphi _{\beta } : U_{\beta } \rightarrow V_{\beta } \subset R^{2}$ be a coordinate homeomorphic mapping. Then, a point z yields two real coordinates (x, y), $z= x + iy$.

      Then, the two coordinate functions ${x_\beta }(p)$ and ${y_\beta }(p)$ in chart $U_{\beta }$ transform into one complex-valued function ${z_\beta } = {x_\beta }(p) + i{y_\beta }(p)$, and ${x_\beta }(p)$ and ${y_\beta }(p)$ are called the complex coordinates of a point in chart $U_{\beta }$. Therefore, the coordinate homeomorphic mapping $\psi _{i}$ and $\varphi _{i}$ can be expressed as an identity mapping from the complex plane to two-dimensional Euclidean space. Then, the differentiable mapping ${\psi _i} \circ f \circ \varphi _i^{-1}$ can be rewritten as f which is differentiable at point p. For the arbitrariness of point p, we derive that f is a differentiable mapping from the smooth simple closed curve J to the unit circle $\partial W$. Similarly, the inverse mapping $f^{-1}$ is also differentiable. Finally, Theorem 1 is proved. $\square$