Skip to main content
SpringerLink
Log in

Analysis and control of a Stewart platform as base motion compensators—part II: dynamics

  • Original paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

A Correction to this article was published on 14 March 2022

This article has been updated

Abstract

For a Stewart platform installed on a moving base-mount, analytical equations of motion are derived utilizing velocities of constituent bodies, computed in the part I-paper. To derive the equations, the principle of virtual work is variationally derived from Hamilton’s principle by examining the variations in rotation matrices since the configuration space of the Stewart platform is defined utilizing both vectors in ℝ3 and rotation matrices in the special orthogonal group, SO(3). The variations in rotation matrices define virtual angular displacements, and the integrability condition of rotation matrices yields the constrained variations in virtual angular velocities. The latter is essential for the variational derivation of the principle. The principle of virtual work seamlessly bridges the gap between the Newton–Euler method and Lagrange’s method (if configuration spaces are defined by generalized coordinates only). Starting from the principle, a systematic method for deriving equations of motion is presented for general multi-body systems and subsequently for a base-moving Stewart platform. The resulting equations in matrix form facilitate the computation of actuator axial forces for inverse dynamics control (IDC). Finally, experiments were performed on a scale model to illustrate the superiority of IDC to the inverse kinematics control, presented in the part I-paper.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Change history

References

  1. Do, W.Q.D., Yang, D.C.H.: Inverse dynamic analysis and simulation of a platform type of robot. J. Field Robot. 5(3), 209–227 (1988)

    MATH  Google Scholar 

  2. Dasgupta, B., Mruthyunjaya, T.: A Newton–Euler formulation for the inverse dynamics of the Stewart platform manipulator. Mech. Mach. Theory 33(8), 1135–1152 (1998)

    Article  MathSciNet  Google Scholar 

  3. Becerra-Vergus, M. Belo, E.: Dynamic modeling of a six degree-of-freedom flight simulator motion base. J. Comput. Nonlinear Dyn. 10(5), 051020 (2015)

  4. Lee, S.-H., Song, J.-B., Choi, W.-C., Hong, D.: Position control of a Stewart platform using inverse dynamics control with approximate dynamics. Mechatronics 13, 605–619 (2003)

    Article  Google Scholar 

  5. Xiaolin, D., Shijie, S., Wenbo, X., Zhangchao, H., Dawei, G.: Modal space neural network compensation control for Gough–Stewart robot with uncertain load. Neurocomputing 449, 245–257 (2021)

    Article  Google Scholar 

  6. Liu, K., Fitzgerald, M., Dawson, D., Lewis, F.L.: Modelling and Control of a Stewart Platform Manipulator. ASME DSC Vol. 33, Control of Systems with Inexact Dynamic Models, pp. 83–89 (1991)

  7. Geng, Z., Haynes, L.S., Lee, J.D., Carroll, R.L.: On the dynamic model and kinematic analysis of a class of Stewart platforms. J. Robot. Autonom. Syst. 9(4), 237–254 (1992)

    Article  Google Scholar 

  8. Lebret, G., Liu, K., Lewis, F.L.: Dynamic analysis and control of a stewart platform manipulator. J. Field Robot. 10(5), 629–655 (1993)

    MATH  Google Scholar 

  9. Sohei-l, S.A., Arash, R.: Nonlinear model predictive control of a stewart platform based on improved dynamic model. Int. J. Theor. Appl. Mech. 5, 8–26 (2020)

    Google Scholar 

  10. Gallardo, J., Rico, J.M., Frisoli, A., Checcacci, D., Bergamasco, M.: Dynamics of parallel manipulators by means of screw theory. Mech. Mach. Theory 38(11), 1113–1131 (2003)

    Article  MathSciNet  Google Scholar 

  11. Ophaswongse, C., Murray, R.C., Agrawal, S.K.: Wrench capability of a stewart platform with series elastic actuators. J. Mech. Robot. 10(2), paper 021002, 8 pages (2018)

  12. Liu, M.J., Li, C.X., Li, C.N.: Dynamics analysis of the Gough–Stewart platform manipulator. IEEE Trans. Robot. Autom. 16(1), 94–98 (2000)

    Article  Google Scholar 

  13. Wittenburg, J.: Dynamics of Multibody Systems, 2nd ed. Springer, Berlin, ISBN 978-3-540-73913-5 (2008)

  14. Murakami, H.: A moving frame method for multi-body dynamics. In: Proceedings of the ASME 2013 International Mechanical Engineering Congress & Exposition, IMECE2013-62833: pp. V04AT04A079; 12 pages. San Diego, CA, November 15–21 (2013)

  15. Murakami, H.: A moving frame method for multi-body dynamics using SE(3). In: Proceedings of the ASME 2015 International Mechanical Engineering Congress & Exposition, IMECE2015-51192: pp. V04BT04A003; 19 pages. Houston, Texas, November 13–19 (2015)

  16. Frankel, T.: The Geometry of Physics: An Introduction, 3rd edn. Cambridge University Press, New York (2012)

    MATH  Google Scholar 

  17. Asada, H., Slotine, J.J.-E.: Robot Analysis and Control. Wiley, New York (1986)

    Google Scholar 

  18. Murray, R.M., Li, Z., Sastry, S.S.: A Mathematical Introduction to Robotics Manipulation. CRC Press, Boca Raton (1994)

    MATH  Google Scholar 

  19. Holm, D.D.: Geometric Mechanics: Part II: Rotating, Translating, Rolling. Imperial College Press, London (2008)

    Book  Google Scholar 

  20. Byron, F.W., Jr., Fuller, R.W.: Mathematics of Classical and Quantum Physics. Dover, New York (1992)

    MATH  Google Scholar 

  21. Smith, D.R.: Variational Methods in Optimization. Prentice-Hall Inc, Englewood Cliffs, NJ (1974)

    MATH  Google Scholar 

  22. Ono, T., Eto, R., Yamakawa, J., Murakami, H.: Development of equations of motion for a Stewart platform under prescribed mount motion. In: Proceedings of the ASME 2018 International Mechanical Engineering Congress & Exposition, IMECE2018–87253, 21 pages (2018)

  23. Leshchenko, D., Ershkov, S., Kozachenko, T.: Evolution of a heavy rigid body rotation under the action of unsteady restoring and perturbation torques. Nonlinear Dyn. 103(5), 1517–1528 (2021). https://doi.org/10.1007/S11071-020-06195-0

    Article  Google Scholar 

  24. Ershkov, S.V., Shamin, R.V.: The dynamics of asteroid rotation, governed by YORP effect: The kinematic Ansatz. Acta Astronaut. 149, 47–54 (2018)

    Article  Google Scholar 

Download references

Funding

Not applicable.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, The National Defense Academy, 1-10-20, Hashirimizu, Yokosuka, Kanagawa, 239-8686, Japan

    Takeyuki Ono, Ryosuke Eto & Junya Yamakawa

  2. Department of Mechanical and Aerospace Engineering, University of California, San Diego, 9500 Gilman Drive, La Jolla, CA, 92093-0411, USA

    Hidenori Murakami

Authors
  1. Takeyuki Ono
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ryosuke Eto
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Junya Yamakawa
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Hidenori Murakami
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Takeyuki Ono.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix A: Equation of motion for \({{\varvec{\phi}}}_{3}^{\left(2{\varvec{k}}/2{\varvec{k}}-1\right)}({\varvec{t}})\)

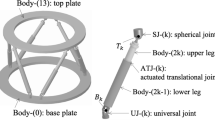
The upper body of leg-(k), body-(2 k), is a circular cylinder with a spherical ball at one end, as illustrated in Fig. I-7. One first observes that (i) the damping couple induced at a spherical joint is negligible since \({\mu }_{SJ}\) is small, and (ii) there is no external couple. The equations of motion for axial rotation \({\phi }_{3}^{\left(2k/2k-1\right)}\left(t\right)\) of body-(2 k) relative to body-(2 k-1) is written including viscous damping couple as:

$${\widehat{J}}_{3C}^{\left(2k\right)}{\ddot{\phi }}_{3}^{\left(2k/2k-1\right)}\left(t\right)+\mu {\dot{\phi }}_{3}^{\left(2k/2k-1\right)}\left(t\right)=0,$$
(A1)

with the initial conditions:

$${\phi }_{3}^{\left(2k/2k-1\right)}\left(0\right)={\dot{\phi }}_{3}^{\left(2k/2k-1\right)}\left(0\right)=0.$$
(A2)

However, the inertia term in Eq. (A1) is negligible since \({\widehat{J}}_{3C}^{\left(2k\right)}\ll {\widehat{J}}_{1C}^{\left(2k\right)}={\widehat{J}}_{2C}^{(2k)}\) and the axial rotational acceleration is of order (1). Neglecting the inertial term in Eq. (A1), the resulting equation with Eq. (A2) yields \({\phi }_{3}^{\left(2k/2k-1\right)}\left(t\right)=0\).

Appendix B: Time derivatives of \(\left[{{\varvec{B}}}^{\boldsymbol{*}}\right]\) submatrices

\(\left[{\dot{B}}_{TP/TP}^{*}(t)\right]\) and \(\left[{\dot{B}}_{TP/BP}^{*}(t)\right]\) are obtained, respectively, by taking the time derivatives of \(\left[{B}_{TP/TP}^{*}(t)\right]=\left[{B}_{TP/TP}(t)\right]\) defined in Eq. (29c) and \(\left[{B}_{TP/TP}^{*}(t)\right]=\left[{B}_{TP/TP}(t)\right]\) in Eq. (29d).

$$\left[{\dot{B}}_{TP/TP}^{*}(t)\right]=\left[\begin{array}{c}\begin{array}{cc}{R}^{\left(0\right)}\left(t\right){\overleftrightarrow{{\omega }^{\left(0\right)}\left(t\right)}} & {0}_{3\times 3}\\ {0}_{3\times 3} & {0}_{3\times 3}\end{array}\\ \begin{array}{cc}{ R}^{\left(0\right)}\left(t\right){\overleftrightarrow{{\omega }^{\left(0\right)}\left(t\right)}}& -{R}^{\left(13\right)}\left(t\right){\overleftrightarrow{{\omega }^{\left(13\right)}\left(t\right)}} {\overleftrightarrow{{e}_{3}{\widehat{h}}^{(14/13)}}}\\ {0}_{3\times 3}& {0}_{3\times 3}\end{array}\end{array}\right],$$
(A3)
$$\left[{\dot{B}}_{TP/BP}^{*}(t)\right]=\left[ \begin{array}{c}\begin{array}{cc}{0}_{3\times 3}& -{R}^{\left(0\right)}(t)\left(\overleftrightarrow{{\omega }^{\left(0\right)}(t)} \overleftrightarrow{{s}_{C}^{\left(13/0\right)}(t)}+\overleftrightarrow{{\dot{s}}_{C}^{\left(13/0\right)}(t)}\right)\\ {0}_{3\times 3}& -\overleftrightarrow{{\omega }^{\left(13/0\right)}\left(t\right)} {\left({R}^{\left(13/0\right)}(t)\right)}^{T} \\ {0}_{3\times 3}& -{R}^{\left(0\right)}(t)\left\{\begin{array}{c}\overleftrightarrow{{\omega }^{\left(0\right)}\left(t\right)} \overleftrightarrow{{s}_{C}^{\left(13/0\right)}\left(t\right)+{R}^{\left(13/0\right)}\left(t\right){e}_{3}{\widehat{h}}^{\left(14/13\right)}}\\ +\overleftrightarrow{{\dot{s}}_{C}^{\left(13/0\right)}\left(t\right)+{R}^{\left(13/0\right)}\left(t\right)\overleftrightarrow{{\omega }^{\left(13/0\right)}\left(t\right)} {e}_{3}{\widehat{h}}^{(14/13)}}\end{array}\right\}\\ {0}_{3\times 3}& -\overleftrightarrow{{\omega }^{\left(13/0\right)}\left(t\right)} {\left({R}^{\left(13/0\right)}(t)\right)}^{T}\end{array}\end{array}\right].$$
(A4)

Taking the time derivatives of Eqs. (44c) and (44d), respectively, one finds

$$\left[{\dot{B}}_{L/TP}^{(k)*}(t)\right]=\left[{\dot{B}}_{L/L}^{(k)}(t)\right]\left[{T}_{L/TP}^{\left(k\right)}(t)\right]+\left[{B}_{L/L}^{\left(k\right)}(t)\right]\left[{\dot{T}}_{L/TP}^{\left(k\right)}(t)\right],$$
(A5)
$$\left[{\dot{B}}_{L/BP}^{\left(k\right)*}(t)\right]=\left[{\dot{B}}_{L/L}^{\left(k\right)}(t)\right]\left[{T}_{L/BP}^{\left(k\right)}(t)\right]+\left[{B}_{L/L}^{\left(k\right)}(t)\right]\left[{\dot{T}}_{L/BP}^{\left(k\right)}(t)\right]+\left[{\dot{B}}_{L/BP}^{\left(k\right)}(t)\right].$$
(A6)

In Eqs. (A5) and (A6), \(\left[{\dot{B}}_{L/L}^{(k)}(t)\right]\) and \(\left[{\dot{B}}_{L/BP}^{\left(k\right)}(t)\right]\) are computed from Eqs. (31c, d) as:

$$\left[{\dot{B}}_{L/L}^{\left(k\right)}(t)\right]=\left[\begin{array}{c}\begin{array}{c}-{R}^{\left(2k-1\right)}(t)\left\{\overleftrightarrow{{\omega }^{\left(2k-1\right)}(t)} {\overleftrightarrow{{\widehat{s}}_{C/{B}_{k}}^{(2k-1)}}} {\left({R}_{2{B}_{k}\mathrm{UJ}}({\phi }_{2}^{\left(k\right)}\left(t\right))\right)}^{T}{e}_{1}+{\overleftrightarrow{{\widehat{s}}_{C/{B}_{k}}^{(2k-1)}}} {e}_{3}{\dot{\phi }}_{2}^{\left(k\right)}(t)\right\}\\ {e}_{3}{\dot{\phi }}_{2}^{\left(k\right)}(t)\end{array}\\ \begin{array}{c}-{R}^{\left(2k-1\right)}(t)\left\{\begin{array}{c}{\overleftrightarrow{{\omega }^{\left(2k-1\right)}}\left(t\right)} \overleftrightarrow{{e}_{3}\left({\widehat{l}}_{\mathrm{UJ}}^{\left(2k-1\right)}+{d}^{\left(k\right)}\left(t\right)\right)} {\left({R}_{2{B}_{k}\mathrm{UJ}}\left({\phi }_{2}^{\left(k\right)}\left(t\right)\right)\right)}^{T}{e}_{1}\\ +\overleftrightarrow{{e}_{3}{\dot{d}}^{\left(k\right)}(t)}{\left({R}_{2{B}_{k}\mathrm{UJ}}({\phi }_{2}^{\left(k\right)}\left(t\right))\right)}^{T}{e}_{1}+\overleftrightarrow{{e}_{3}\left({\widehat{l}}_{\mathrm{UJ}}^{(2k-1)}+{d}^{\left(k\right)}(t)\right)} {e}_{3}{\dot{\phi }}_{2}^{\left(k\right)}(t)\end{array}\right\}\\ {e}_{3}{\dot{\phi }}_{2}^{\left(k\right)}(t)\end{array}\end{array}\right.\left.\begin{array}{c}\begin{array}{cc}-{R}^{\left(2k-1\right)}\left(t\right)\overleftrightarrow{{\omega }^{\left(2k-1\right)}\left(t\right)}{\widehat{s}}_{C/{B}_{k}}^{(2k-1)}{e}_{2}& {0}_{3\times 1}\\ {0}_{3\times 1}& {0}_{3\times 1} \\ -{R}^{\left(2k-1\right)}\left(t\right)\left\{\overleftrightarrow{{\omega }^{\left(2k-1\right)}\left(t\right)} \overleftrightarrow{{e}_{3}\left({\widehat{l}}_{\mathrm{UJ}}^{\left(2k-1\right)}+{d}^{\left(k\right)}\left(t\right)\right)} {e}_{2}+\overleftrightarrow{{e}_{3}{\dot{d}}^{\left(k\right)}(t)} {e}_{2}\right\}& {R}^{\left(2k-1\right)}\left(t\right)\overleftrightarrow{{\omega }^{\left(2k-1\right)}\left(t\right)} {e}_{3}\\ {0}_{3\times 1}& {0}_{3\times 1}\end{array}\end{array}\right]$$
(A7)
$$\left[{\dot{B}}_{L/BP}^{\left(k\right)}(t)\right]=\left[\begin{array}{c}\begin{array}{cc}{0}_{3\times 1} & -{R}^{\left(0\right)}(t)\left\{\begin{array}{c}{\overleftrightarrow{{\omega }^{\left(0\right)}\left(t\right)}} {\overleftrightarrow{{R}^{\left(2k-1/0\right)}\left(t\right){\widehat{s}}_{C/{B}_{k}}^{\left(2k-1\right)}}+{\widehat{s}}_{{B}_{k}}^{\left(0\right)}}\\ +\overleftrightarrow{{R}^{\left(2k-1/0\right)}\left(t\right){\overleftrightarrow{{\omega }^{\left(2k-1/0\right)}\left(t\right)}{\widehat{s}}_{C/{B}_{k}}^{(2k-1)}}}\end{array}\right\}\\ {0}_{3\times 1} & -\overleftrightarrow{{\omega }^{\left(2k-1/0\right)}(t)}{\left({R}^{\left(2k-1/0\right)}(t)\right)}^{T} \\ {0}_{3\times 1}& -{R}^{\left(0\right)}(t)\left\{\begin{array}{c}\overleftrightarrow{{\omega }^{\left(0\right)}\left(t\right)} \overleftrightarrow{{R}^{\left(2k-1/0\right)}\left(t\right){e}_{3}({\widehat{l}}_{\mathrm{UJ}}^{\left(2k-1\right)}+{d}^{\left(k\right)}\left(t\right))+{\widehat{s}}_{{B}_{k}}^{\left(0\right)}}\\ +\overleftrightarrow{{R}^{\left(2k-1/0\right)}\left(t\right)\left(\overleftrightarrow{{\omega }^{\left(2k-1/0\right)}\left(t\right)}{e}_{3}\left({\widehat{l}}_{\mathrm{UJ}}^{\left(2k-1\right)}+{d}^{\left(k\right)}\left(t\right)\right)+{e}_{3}{\dot{d}}^{\left(k\right)}(t)\right)}\end{array}\right\}\\ {0}_{3\times 1}& -\overleftrightarrow{{\omega }^{\left(2k-1/0\right)}(t)}{\left({R}^{\left(2k-1/0\right)}(t)\right)}^{T}\end{array}\end{array}\right].$$
(A8)

In Eqs. (A5) and (A6), \(\left[{\dot{T}}_{L/TP}^{\left(k\right)}(t)\right]\) is computed from Eq. (39b).

$$\left[{\dot{T}}_{L/TP}^{\left(k\right)}(t)\right]=-\left(\frac{{\rm d}}{{\rm d}t}{\left[{A}_{L}^{\left(k\right)}(t)\right]}^{-1}\right){\left({R}^{\left(2k-1/0\right)}(t)\right)}^{T}\left[\begin{array}{cc}{I}_{3}& -{R}^{\left(13/0\right)}(t){\overleftrightarrow{{\widehat{s}}_{{T}_{k}}^{(13)}}}\end{array}\right]+{\left[{A}_{L}^{\left(k\right)}(t)\right]}^{-1}\left\{{\overleftrightarrow{{\omega }^{\left(2k-1/0\right)}(t)}{\left({R}^{\left(2k-1/0\right)}(t)\right)}}^{T}\left[\begin{array}{cc}{I}_{3}& -{R}^{\left(13/0\right)}(t){\overleftrightarrow{{\widehat{s}}_{{T}_{k}}^{(13)}}}\end{array}\right]\right.\left.-{\left({R}^{\left(2k-1/0\right)}(t)\right)}^{T}\left[\begin{array}{cc}{0}_{3\times 3}& -{R}^{\left(13/0\right)}\left(t\right){\overleftrightarrow{{\omega }^{(13/0)}\left(t\right)}} {\overleftrightarrow{{\widehat{s}}_{{T}_{k}}^{(13)}}}\end{array}\right]\right\},$$
(A9)

where

$$\frac{{\rm d}}{{\rm d}t}{\left[{A}_{L}^{\left(k\right)}(t)\right]}^{-1}=\left[\begin{array}{ccc}0& \frac{-{\dot{d}}^{\left(k\right)}(t)\mathrm{cos}{\phi }_{2}^{\left(k\right)}\left(t\right)+{l}^{\left(k\right)}(t){\dot{\phi }}_{2}^{\left(k\right)}(t)\mathrm{sin}{\phi }_{2}^{\left(k\right)}(t)}{{\left({l}^{\left(k\right)}(t)\mathrm{cos}{\phi }_{2}^{\left(k\right)}(t)\right)}^{2}}& 0 \\ \frac{{\dot{d}}^{\left(k\right)}(t)}{{({l}^{\left(k\right)}\left(t\right))}^{2}}& 0& 0\\ 0& 0& 0\end{array}\right].$$
(A10)

In Eq. (A6), \(\left[{\dot{T}}_{L/BP}^{\left(k\right)}(t)\right]\) is computed from Eq. (41b) as:

$$\left[{\dot{T}}_{L/BP}^{\left(k\right)}(t)\right]=\left(\frac{{\rm d}}{{\rm d}t}{\left[{A}_{L}^{\left(k\right)}(t)\right]}^{-1}\right){\left({R}^{\left(2k-1/0\right)}(t)\right)}^{T}{\overleftrightarrow{\Delta {s}_{CL}^{\left(k\right)}(t)}}\left[\begin{array}{cc}{0}_{3\times 3}& {I}_{3}\end{array}\right]+{\left[{A}_{L}^{\left(k\right)}(t)\right]}^{-1}\left\{-{\overleftrightarrow{{\omega }^{\left(2k-1/0\right)}\left(t\right)}}{\left({R}^{\left(2k-1/0\right)}\left(t\right)\right)}^{T}{\overleftrightarrow{\Delta {s}_{CL}^{\left(k\right)}\left(t\right)}} +{\left({R}^{\left(2k-1/0\right)}(t)\right)}^{T}{\overleftrightarrow{\dot{\Delta {s}_{CL}^{\left(k\right)}}(t)}}\right\}\left[\begin{array}{cc}{0}_{3\times 3}& {I}_{3}\end{array}\right],$$
(A11)

where from Eq. (35c),

$$\dot{\Delta {s}_{CL}^{\left(k\right)}}\left(t\right)={\dot{s}}_{C}^{\left(13/0\right)}\left(t\right)+{R}^{\left(13/0\right)}\left(t\right){\overleftrightarrow{{\omega }^{\left(13/0\right)}(t)}}{\widehat{s}}_{{T}_{k}}^{(13)}-{R}^{\left(2k-1/0\right)}\left(t\right)\left({\omega }^{\left(2k-1/0\right)}\left(t\right){e}_{3}{l}^{\left(k\right)}\left(t\right)+{e}_{3}{\dot{d}}^{\left(k\right)}\left(t\right)\right).$$
(A12)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ono, T., Eto, R., Yamakawa, J. et al. Analysis and control of a Stewart platform as base motion compensators—part II: dynamics. Nonlinear Dyn 106, 3161–3182 (2021). https://doi.org/10.1007/s11071-021-06749-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-021-06749-w

Keywords

Search

Navigation