1 Introduction

Vertical sloshing is a phenomenon that occurs on structures that undergo strong vertical accelerations. Among these, we find the aeronautical structures that withstand load occurring from gusts, turbulence and landing impacts. The jolt of fuel generally stowed in the wings caused by vertical accelerations is coupled with the structural dynamics of the aircraft. This type of sloshing is well known to provide a noticeable increase in structural damping but nevertheless remains generally not modeled in the design phase of modern aircraft. This work is therefore part of the research activity within the European project H2020 SLOshing Wing Dynamics (SLOWD) and aims at providing reduced-order models (ROMs) for the study of slosh dynamics (Ref. [1]). Vertical slosh dynamics is one of the possible dynamics of the fluid stowed in the tanks which, when it occurs, manifests different characteristics compared to the classic sloshing, generally occurring with rotations and lateral motion of the tank. The latter generates standing waves inside the cavity that provide dynamic coupling with structure and possible modification of flutter margins. Specifically, the effects of sloshing on aircraft aeroelastic flutter stability were considered in Refs. [2, 3]. On the other hand, the subject of this paper is sloshing induced by high vertical acceleration of the tank, hence perpendicular to the free surface. As long as the acceleration is kept below a certain threshold the free surface does not break. However, the crossing of this acceleration threshold triggers Rayleigh–Taylor instabilities (Ref. [4]), determining a chaotic flow regime with air/water mixing. Turbulence, impacts and the continuous generation of the free surface cause additional dissipation of energy (Refs. [5, 6]). The total balancing of elastic potential energy and fluid energy results in a noticeable increase in the effective damping of the structural motion. Moreover, considering vertical harmonic motions, it would be noticeable that the dissipative characteristics depend on the amplitude of the motion and on the frequency.

This work involves the use of acceleration data from sloshing experiments carried out in the laboratories of the Universidad Politécnica de Madrid (UPM). The experimental object consists of an elastically scaled single-degree-of-freedom mass–spring system coupled with the slosh dynamics within a hydrodynamically scaled tank. An equivalent mechanical model of a bouncing ball is then used to emulate the fluid behavior inside the tank (specifically the impacts with the tank wall) and provide a numerical model of a tank isolated from the structure on which it is possible to perform simulations with seismic excitation. Indeed, classical sloshing ROMs are intrinsically based on potential fluid theory or small lateral perturbations [7,8,9,10] and, the identification of impulsive forces that vertical sloshing dynamics provides is not covered by these models. On the other hand, the main interests of fluid dynamics are addressed on the study of Rayleigh–Taylor instabilities and Faraday waves phenomena [8], thus focusing more on getting the stability margins rather than providing ROMs for multi-disciplinary analyses. As far as it concerns the bouncing ball model, in the framework of SLOWD, a one-free-parameter model has been recently proposed in Ref. [11]. However, the model presented in Ref. [11] provides infinitesimal-time impulsive sloshing forces making it not fitting for its use in the neural network framework, thus requiring the introduction of a further model with more extensive features. However, it is worth specifying that the bouncing ball model being introduced in this paper replaces what in the authors’ minds will have to be represented either by a long experimental campaign with different arrangements for a complete investigation of the behavior of the fluid or by Computational Fluid Dynamics (CFD) simulations. Finally in the last part of the paper, we will present a reduced-order model based on neural networks. Indeed, The use of neural network is getting attention in providing ROM for fluid–structure interaction (FSI) as it was already done for external aerodynamics in Ref. [12]. Artificial neural network can be seen as a parallel distributed processors made up of the so-called neurons: simple processing units, having the natural capability of storing accumulated knowledge, and then, make it available for subsequent use. In particular, knowledge is acquired by the network from its environment through a learning process, and then stored by synaptic weights. Due to their useful properties and capabilities (Ref. [13]), neural networks are increasingly used in nonlinear system identification. Indeed, they are a powerful tool for approximating nonlinear dynamic systems, even when the system structure is unknown and only input–output data are available, thus allowing a sort of generalized black-box modeling. Specifically, the sloshing forces will be estimated on the basis of the unsteady boundary condition time series. The feed forward natural network (Ref. [14]) is trained with an appropriate data series (consisting of motion of the tank and forces provided by bouncing ball model) spanning different values of frequencies and amplitude in order to provide a complete characterization of the fluid dissipative behavior. Once the neural network is identified and integrated in the simulation framework, the results provide a good agreement with simulations with the bouncing ball model and experiments as well.

2 Experimental setup and related experiments

In order to scale down the actual wing to the SDOF tests, it is important to consider the dimensional analysis of the problem. Applying the \(\Pi \) theorem to a reference variable [15], for example the dissipated power by the fluid, one can find a dimensional relation between this variable and several non-dimensional numbers, such as the Reynolds number, Froude number and filling level. It is common practice in sloshing problems to perform a Froude scaling [15] where \(Fr= \sqrt{w_0^2 h/N g}\) is defined based on the maximum acceleration of the problem which is N times the gravity. In the Froude number definition, \(w_0\) is the characteristic angular frequency of the problem, h represents the height of the tank, Ng is the maximum acceleration of the problem, being \(N \approx 10\) in our case. Then, a perfect geometrical scaling parameter is considered \(\lambda = h_{SDOF}/h_W\) defined as the ratio between the heights of the SDOF tank and the wing tank. For the SDOF sloshing tests, a 1:5 scale was selected (\(\lambda = 0.2\)) which results in a tank geometry of 10x6x6 cm. The scaled tank is filled up to 50 \(\%\) of its volume with a water mass of \(m_l= 0.18\) kg and it oscillates at a characteristic frequency of \(f_0=6.56\) Hz.

Fig. 1
figure 1

(1) Load cell, (2) metallic plate, (3) upper springs \(k_1=1904.4\) N/m, (4) lower springs \(k_2=1904.4\) N/m, (5) laser sensor, (6) mechanical guide, (7) accelerometer, (8) methacrylate tank and C-shaped wooden structure and (9) solenoids for release mechanism

Full size image

A picture of the experimental setup at the Model Basin Research group sloshing laboratory of the UPM and a simplified outline are both shown in Fig. 1. The sloshing rig is a SDOF system composed of a mechanical guide that allows the 1-degree-of-freedom constraint. This guide is attached to a C-shaped wooden structure that holds the tank with a structural mass of \(m= 2.06\) kg. Similarly, the C-shaped wooden structure is attached to a set of 6 springs, 3 on the upper side and 3 on the lower side. The lower springs are mechanically embedded into the floor, and on the opposite side, the upper set of springs is attached to a metallic plate that acts as a joint between them and the embedded load cell. This setup also includes an accelerometer glued to the C-shaped wooden structure, a laser sensor pointing at the wooden block and two solenoids acting as a release mechanism. The structure is deflected an initial amplitude until it is fixed by the action of the solenoids. When the electrical current is turned on, they release the structure triggering the beginning of the experiment where acceleration and position of the tank as well as load cell measurements are recorded allowing the calculation of the sloshing force acting on the system. A more detailed description of the sloshing rig and the sloshing force can be found in Ref. [16].

3 Bouncing ball model replacing slosh dynamics

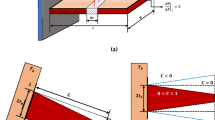
In the present model, the sloshing forces are replaced by the forces exchanged between the tank wall (floor and ceiling) and a ball bouncing inside the rigid tank. The energy balance after each impact is negative due to the presence of viscoelastic element inside the ball that characterizes energy dissipation. Indeed, the behavior of the fluid inside the tank is such that it is possible to appreciate impacts of the fluid mass on the tank walls (see Fig. 2b and c) as well as instants when the most of water mass is floating inside the cavity (see Fig. 2a). As illustrated in Fig. 3, the bouncing ball model aims at reproducing this behavior. Specifically, three different conditions are illustrated representing the ball floating in the tank and, respectively, the impacts with the ceiling and floor. The system is ideally represented as a rigid bubble without mass properties that has a concentrated mass inside hanged to its wall by means of a spring-damper system. Part of the fluid total mass is considered associated with the ball \(m_b\), whereas another portion is considered frozen \(m_f\), namely attached to the wall. When the rigid bubble touches the ceiling or the floor of the tank, the impact condition is verified so causing viscoelastic forces exchanged between the case and the bouncing ball. The equation of motion of the bouncing ball can be thus summarized as follows

$$\begin{aligned} m_{b} \ddot{z}_{b} = -m_{b} g + F_b(z_{b}(t),z_T(t)) \end{aligned}$$
(1)

where \(F_b\) is the force exchanged at the wall, \(z_T(t)\) represents the motion of the tank whereas \({z}_{b}\) is the absolute vertical motion of the bouncing ball. The latter will be expressed as \(\left( 1-\beta \right) m_l\) being \(m_l\) the total fluid mass of the ball and \(\beta \) a parameter that can take values between zero and 1.

Fig. 2
figure 2

Snapshots of the sloshing experiment

Full size image
Fig. 3
figure 3

Bouncing ball motion phases

Full size image

In this framework, it is convenient to introduce a new variable s such that \(s = z_{b} - z_T - r_0\) (where \(r_0\) is the radius of the bubble and h is the height of the tank) if the ball is impacting in the floor region, \(s = z_{b} - z_T - h + r_0\) if the ball is impacting in the ceiling region and zero elsewhere. Moreover it is introduced also the variable \(\nu = \dot{z_{b}} - {\dot{z}}_T\). It follows that we can define the viscoelastic forces as

$$\begin{aligned} F_b(s(t),\nu (t)) = k_b s + c_b \nu \end{aligned}$$
(2)

where \(k_b\) and \( {c_b}\) are, respectively, the stiffness and damping associated with the bouncing ball. It is worth to notice that \(k_b = {\hat{k}}_b f_{nl}(s)\) may eventually be, in turn, nonlinear function of s(t) by introducing a penalty function \(f_{nl}(s) = 1 + \alpha s^2/(r_0-|s|)\) that avoid the ball to go out by the limits of the tank. The overall sloshing force exchanged between the tank and fluid mass inside consists of two terms yielded by bouncing ball impacts and frozen mass inertia:

$$\begin{aligned} F_s(s(t),\nu (t)) = F_b(s(t),\nu (t)) - m_f (\ddot{z}_T+g). \end{aligned}$$
(3)

3.1 The simulation environment

The experimental reality was modeled within a Simulink®  simulation environment by replacing the sloshing dynamics with the bouncing ball model. The structural system consists of mass–spring–damper identified during the conducted experimental campaign. It is worth noting that the structural damping model includes viscous and Coulomb damping to represent the identified frictious. The flowchart of the overall system (structure and sloshing) is shown in Fig. 4 where the input of the structural subsystem is represented by the sloshing forces, while the input of the sloshing subsystem is represented by the vertical rigid displacement and the velocity of the tank. In particular, the latter can be studied separately from the structure by assigning a suitable seismic excitation, or connected in a closed loop with the structure.

Fig. 4
figure 4

Flowchart of the fluid–structure interaction problem

Full size image

3.2 Bouncing ball tuning via experimental test

The main parameters of the bouncing ball are then estimated from the experimental data by means of an optimization process, in order to obtain a virtual equivalent configuration such as to present the model of the ball in place of the sloshing liquid. This optimization process takes into account the vertical acceleration of the tank. The reference experimental analysis was characterized by a free response with initial displacement equal to \(z_T = 0.064\) m. From this vertical acceleration (blue curve in Fig.5a) the first step was to get the envelope in order to estimate the instantaneous damping ratio via logarithmic decay, subsequently expressed as a function of the acceleration amplitude (see blue curve in Fig.5b). This function, that is influenced also by the structural damping (viscous and Coulomb), represents the target function to fit. By exploiting the model presented in Sec.3.1 it is possible to get the acceleration signal related to the free response analysis (red curve in Fig.5a). By repeating the procedure above we are able to obtain the virtual instantaneous damping as a function of the acceleration amplitude as the red curve in Fig.5b. This curve comes from an already optimized problem with the objective function \(J = \sum _{i=1}^{N} \left( \zeta _i^{exp} - \zeta _i^{sim}\right) ^2 \). The design variables are reported in Table1 (where the liquid mass \(m_l\) and the tank height h are kept fixed and equal, respectively, to 0.18 Kg and 0.06 cm).

Table 1 Optimal parameters of the bouncing ball
Full size table
Fig. 5
figure 5

Identification of the optimal bouncing ball parameters

Full size image
Fig. 6
figure 6

Hysteresis cycle and loss fact map of the optimal bouncing ball ROM

Full size image

3.3 Nonlinear dissipative behavior

In order to show the dissipative capabilities of the reduced-order model of the identified bouncing ball, an open-loop simulation campaign of the sloshing subsystem (i.e., bouncing ball) is carried out. Since the dissipative content is dependent on the amplitude and frequency of the imposed motion, several analyses have been performed with permanent harmonic motion considering different amplitude–frequency pairs covering a range of acceleration that is even beyond the range of interest of the performed experiment. For each of these simulations, the sloshing forces produced by the equivalent mechanical model were obtained as output. The hysteresis cycles were plotted (see Fig. 6a) from which the work dissipated by the sloshing forces was computed, once a stationary regime is reached, by evaluating the area subtended by the cycle. This last quantity allows to define the loss factor as the ratio between the dissipated work and the kinetic energy of the overall system (sloshing and structure) in the case of frozen fluid (  \(\eta := W_D / (\pi \, (m + m_l) \, \Omega ^2 A^2) \, \)). Finally, Fig. 6b shows the dependency of the loss factor from both amplitude and frequency by means of pseudo-color plot. It looks evident how there exists a specific value of amplitude A (that appears to be between 1 cm and 3 cm) that maximizes the loss factor (darker region). A contour line plot of maximum values of g-force is also superimposed on the loss factor map. Moreover, the occurrence of something similar to Rayleigh–Taylor instabilities, that is the detachment of the ball from the bottom of the tank, is verified when the maximum value of acceleration reaches approximately 2g. Before the 2g frontier, since there is no impact, the dissipation is negligible. On the contrary, for acceleration values greater than this threshold value, the ball detaches and impacts cause dissipation.

4 Neural-network-based reduced-order models

Identification techniques based on the use of neural networks (NN) can therefore be exploited to obtain a new class of ROMs for vertical sloshing. In order to identify the NN-based ROM, input/output data related to the vertical sloshing system are needed. In this paper, in order to cover the lack of experimental and CFD data, the NN is trained by exploiting data that are output by low-fidelity bouncing ball model. This model is now considered as a black-box to be identified that provides sloshing forces as a function of the history of the assigned vertical displacement. Before the integration of the NN-based ROM into a simulation framework in Sec. 4.2, a training campaign for the identification of the network is provided in Sec. 4.1.

Fig. 7
figure 7

Feed forward neural network flowchart

Full size image

4.1 Training phase

The training phase consists in the definition of a neural network able to emulate vertical slosh dynamics. In this framework, the use of a proper data set is critical, thus requiring an investigation among different types of inputs, after which, the choice fell on a pseudo-harmonic signal with amplitude and frequency slowly varying over time (\(z_T = A(t) \sin (\int _0^t \Omega (\tau ) \, \mathrm{d}\tau )\)). This time law is such as to suitably cover the amplitude–frequency domain of interest as in Fig. 6b , that, in turn, covers the range of accelerations provided by the performed experiments. The time derivative of \(z_T\) is used as input for the training. On the other hand, the output consists of the sloshing force that the ball returns when the tank is set on motion. The need to cover the more frequency–amplitude pairs leads to a data set represented by time series (velocity as input and sloshing force as output) obtained by only one 200 s long simulation with a sample frequency of 1 kHz. Among the wide variety of NN architectures feed forward neural network (FF NN) has been considered, in which the information simply propagates from left to right in the network through a manifold of hidden layers. The proposed scheme of the identified neural network shown in Fig. 7 consists of 7 hidden layers with 35 nodes/neurons each. Moreover, 50 tapped delay lines are considered for the input. This kind of NN is proved to work efficiently by using non-polynomial activation functions like radial basis functions (Refs. [17, 18]). As a consequence, these latter are employed as activation functions in all nodes of the considered hidden layers, whereas the output layer is made up with a simple linear function. The choice of the number of hidden nodes and layers is based on a qualitative sensitivity analysis that did not require the use of specific techniques. Specifically, given the same number of epochs considered in the network training, the selected NN is the one that proved to provide more fitting results when the ROM is introduced in the FSI environment that follows in Sec. 4.2. The algorithm used for the training consists of Bayesian Regularization, implemented in Matlab®  through the trainbr function (Ref. [14]), with a fixed number of epochs equal to 1000, in which the mean-squared error performance is observed to converge to a constant value, thus guaranteeing the convergence of the network. The total time spent for the NN training is 44 hours without employing any kind of parallel computing.

Fig. 8
figure 8

Comparison between FFNN, bouncing ball and experiment

Full size image

4.2 Integration of Neural Network into closed-loop simulation

Subsequently, the equivalent mechanical model of bouncing ball was replaced by the identified neural-network-based ROM in the simulation framework depicted in Fig. 5. The same free response analysis as in the experiments and simulation in Sec. 3.2 has been performed. It is worth to highlight that this kind of response has nothing to do with the data used to train the network. Since the sloshing tank system is of the type single input/single output, the simulation takes only a few seconds to perform the fluid–structure interaction analysis where the sloshing block is replaced with a neural network. Fig. 8a, b and c provides, respectively, the acceleration response, the instantaneous damping ratio as a function of the acceleration envelope, and the sloshing force comparing the experiments, the simulation with the bouncing ball and the one with the neural-network-based ROM. Specifically, Fig. 8a shows that response in terms of acceleration obtained with the NN-based ROM for sloshing is close to the response obtained with the bouncing ball model (used to train the network) and the experimental response as well. Fig. 8b demonstrates the capability of the NN-based ROM to provide a value of the instantaneous damping ratio matching the one of the bouncing ball model at each value of response amplitude even though better performances are noticeable at higher acceleration values. The results show that although the methodology is at its preliminary stage, the NN-based ROM is able to reproduce the behavior of the model with the bouncing ball and, in turn, also of the experiments. Moreover, as shown in Fig. 8c, the neural network is also capable to reproduce the nonlinear behavior of the bouncing ball impact force.

5 Conclusions

The goal of this paper was to study and provide a reduced-order model to describe the dissipative behavior of nonlinear vertical sloshing (involving Rayleigh–Taylor instability) of fuel-inside-wing tanks by means of a feed forward neural network. The data used to build an equivalent mechanical model (EMM) was provided by an experimental study about the coupling between fluid sloshing and a 1-DoF system performed at UPM. The EMM consists of a boxed-in bouncing ball model, able to emulate the fluid sloshing into the tank and to replace the fluid behavior in FSI simulations for different scenarios than the one of the experiments. Next, the network was trained using a large data set, consisting of a long simulation of the bouncing ball model with pseudo-periodic motion assigned as unsteady boundary condition spanning different values of oscillation amplitude and frequency. Indeed, the vertical sloshing forces were proved to be highly nonlinear and dependent on the amplitude of oscillation and its frequency content. Despite the training phase of the neural network has revealed time-consuming, it has provided a sufficiently fast reduced-order model able to reproduce the behavior of sloshing forces. The obtained neural network input–output model was included in a Simulink®  environment for closed-loop fluid–structure interaction simulations showing good matching with the experiments.

In the framework of SLOWD project, this research will go toward several directions, such as the use of higher fidelity data provided by CFD simulations specific for vertical sloshing or by proper experiments even though large tank sizes requires for important facilities to assign motion to trigger such a dissipative behavior. On the other hand, neural networks may allow for generalization of tank motion including all 6 DoFs of the tank instead of the only vertical motion at the cost of increasing the computational cost in the identification since more inputs and more outputs increase the complexity of the network. Moreover, a specific issue to be faced in the next future concerns the integration of the network into a multiple-degree-of-freedom system, in which the behavior of the ROM will need to be assessed for multi-harmonic motion. Although the neural network is computationally more expensive in both training and simulation phases, these points mark the difference with the bouncing ball model. NN-based ROM, following an adequate learning phase employing the right data set (also taking into consideration different types of inputs with respect to the pseudo-harmonic), has the potential to accurately replace the behavior of the sloshing forces even by increasing the degree of complexity of the FSI environment.