A novel nonlinear filter through constructing the parametric Gaussian regression process

Abstract

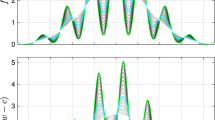
In this paper, a new variational Gaussian regression filter (VGRF) is proposed by constructing the linear parametric Gaussian regression (LPGR) process including variational parameters. Through modeling the measurement likelihood by LPGR to implement the Bayesian update, the nonlinear measurement function will not be directly involved in the state estimation. The complex Monte Carlo computation used in traditional methods is also avoided well. Hence, in PVFF, the inference of state posteriori and variational parameters can be achieved tractably and simply by using variational Bayesian inference approach. Secondly, a filtering evidence lower bound (F-ELBO) is proposed as a quantitative evaluation rule of different filters. Compared with traditional methods, the higher estimation accuracy of VGRF can be explained by the F-ELBO. Thirdly, a relationship between F-ELBO and the monitored ELBO (M-ELBO) is found, i.e., F-ELBO is always larger than M-ELBO. Based on this finding, the accuracy performance improvement of VGRF can be theoretically explained. Finally, three numerical examples are employed to illustrate the effectiveness of VGRF.

Appendices

Appendix A: The proof of theorem 1

Given $p({x_k},\mu ,\beta ,\lambda ,Z_1^k)$, use the mean field theory to yield that

$$\begin{aligned}&{\log q({x_k})q(\beta )}{ = {E_{{q_t}(\mu ,\lambda )}}\left\{ {\log p({x_k},\mu ,\beta ,\lambda ,Z_1^k)} \right\} + const}\\&{ = - \frac{1}{{\mathrm{2}}}{E_{{q_t}(\mu ,\lambda )}}\left[ {\lambda D({z_k} - {H_k}{x_k} - \mu ,{\bar{R}})} \right] + \log prio({x_k})}\\&{} { + \sum \limits _{j = 1}^{k - 1} {\left[ {\frac{1}{{\mathrm{2}}} \log \beta - \frac{\beta }{{\mathrm{2}}}{E_{{q_t}(\mu ,\lambda )}}\left[ {\lambda D({z_j} - {H_j}{{{\bar{x}}}_j} - \mu ,{\bar{R}}_j^*)} \right] } \right] } }\\&{} { + ({a_0} - 1)\log \beta - \beta {b_0} + const} \end{aligned}$$

where for the brevity u is omitted in our derivation the filter’s structure and will be brought back into the final result. We have

$$\begin{aligned}&{E_{{q_t}(\mu ,\lambda )}}\left[ {\lambda D({z_k} - {H_k}{x_k} - \mu ,{\bar{R}})} \right] \\&{\mathrm{= }}{E_{{q_t}(\mu ,\lambda )}}{\mathrm{[}}\lambda {\mathrm{]}}D({z_k} - {H_k}{x_k} - {{{\hat{\mu }} }_t},{\bar{R}}) + const\\&{E_{{q_t}(\mu ,\lambda )}}\left[ {\lambda D({z_j} - {H_j}{{{\bar{x}}}_j} - \mu ,{\bar{R}}_j^*)} \right] \\&{\mathrm{= }}{E_{{q_t}(\mu ,\lambda )}}{\mathrm{[}}\lambda {\mathrm{]}}D({z_j} - {H_j}{{{\bar{x}}}_j} - {{{\hat{\mu }} }_t},{\bar{R}}_j^*) + Tr[{\bar{R}}_j^*\hat{M}_t^{ - 1}]\\&{E_{{q_t}(\mu ,\lambda )}}[\lambda ]={E_{{q_t}(\lambda )}}[\lambda ]=\frac{{\hat{c}}_t}{{\hat{d}}_t}. \end{aligned}$$

For the following deduction, we define

$$\begin{aligned}&prio({z_k})\\&\buildrel \varDelta \over = \int {N{\mathrm{(}}{z_k}{\mathrm{|}}{H_k}{x_k}{\mathrm{+ }}{{{\hat{\mu }} }_t},[\frac{{\hat{c}}_t}{{\hat{d}}_t} {\bar{R}}]^{-1} {\mathrm{)}}} N({x_j}|{{{\bar{x}}}_k},{\bar{P}}_k^{ - 1})d{x_k}\\&=N{\mathrm{(}}{z_k}{\mathrm{|}}{H_k}{{{\bar{x}}}_k}{\mathrm{+ }}{{{\hat{\mu }} }_t},{H_k}{\bar{P}}_k^{ - 1}H_k^T + [\frac{{\hat{c}}_t}{{\hat{d}}_t} \bar{R}]^{-1} {\mathrm{)}}. \end{aligned}$$

Obviously, $prio({z_k})$ is a constant independent of state. By rewriting ${\log q({x_k})q(\beta )}$ with $prio({z_k})$ , we have

$$\begin{aligned}&\log q({x_k})q(\beta ) \\&= \log \frac{{N{\mathrm{(}}{z_k}{\mathrm{|}}{H_k}{x_k}{\mathrm{+ }}{{{\hat{\mu }} }_t},[\frac{{\hat{c}}_t}{{\hat{d}}_t} {\bar{R}}]^{-1} {\mathrm{)}}N({x_j}|{{{\bar{x}}}_k},{\bar{P}}_k^{ - 1})}}{{prio({z_k})}}\\&\quad + ({a_0}{\mathrm{+ }}\frac{{k - 1}}{{\mathrm{2}}} - 1)\log \beta + const\\&\quad - \beta \left( {{b_0} + \frac{1}{{\mathrm{2}}}\sum \limits _{j = 1}^{k - 1} {\left[ {{E_{{q_t}(\mu ,\lambda )}}\left[ {\lambda D({z_j} - {H_j}{{{\bar{x}}}_j} - \mu ,\bar{R}_j^*)} \right] } \right] } } \right) . \end{aligned}$$

Then, by re-organizing $\log q({x_k})q(\beta )$, (30)-(33) are obtained.

Appendix B: The proof of theorem 2

According to the mean field theory, from $p({x_k},\mu ,\beta ,\lambda , Z_1^k)$ it is easy to obtain

$$\begin{aligned}&\log q(\mu ,\lambda ) \\&= {E_{{q_{t + 1}}({x_k}){q_{t + 1}}(\beta )}}\left\{ {\log p({x_k},\mu ,\beta ,\lambda ,Z_1^k)} \right\} + const\\&= \frac{1}{{\mathrm{2}}}\log \lambda - \frac{\lambda }{{\mathrm{2}}}{E_{{q_{t + 1}}({x_k})}}\left[ {D({z_k} - {H_k}{x_k} - \mu ,{\bar{R}})} \right] \\&{} + \sum \limits _{j = 1}^{k - 1} {\left\{ {\frac{1}{{\mathrm{2}}}\log \lambda - \frac{{\lambda {E_{{q_{t + 1}}(\beta )}}[\beta ]}}{{\mathrm{2}}}D({z_j} - {H_j}{{{\bar{x}}}_j} - \mu ,{\bar{R}}_j^*)} \right\} } \\&{}+ \log N{\mathrm{(}}\mu {\mathrm{|}}{\mu _{\mathrm{0}}},{\lambda ^{ - 1}}{ M}_{\mathrm{0}}^{ - 1}{\mathrm{)}} + ({c_0} - 1)\log \lambda - \lambda {d_0}{\mathrm{+ const}} \end{aligned}$$

where

$$\begin{aligned}&{E_{{q_{t + 1}}({x_k})}}\left[ {D({z_k} - {H_k}{x_k} - \mu ,{\bar{R}})} \right] \\&{\mathrm{= }}D({z_k} - {H_k}{\hat{x}}_k^{t + 1} - \mu ,{\bar{R}}){\mathrm{+ Tr}}[{H_k}{(P_k^{t + 1}{\mathrm{)}}^{ - 1}}H_k^T{\bar{R}}]\\&{{ {E_{{q_{t + 1}}(\beta )}}[\beta ]}}=\frac{{\bar{a}}_{t+1}}{\bar{b}_{t_+1}}. \end{aligned}$$

For the following deduction, we define

$$\begin{aligned}&{p({{{\bar{Z}}}_k})}\\&{ = \int {N({{{\bar{Z}}}_k}{\mathrm{|}}(e \otimes {I_m})\mu ,{\lambda ^{ - 1}}{\bar{R}}_k^{ - 1})N(\mu {\mathrm{|}}\mu _0,{\lambda ^{ - 1}}{M}_{\mathrm{0}}^{ - 1})d\mu } }\\&{ = N\left( {{{{\bar{Z}}}_k}{\mathrm{|}}(e \otimes {I_m}){\mu _{\mathrm{0}}},\lambda ^{ - 1} B^{-1}} \right) } \end{aligned}$$

where $B = {\left( {[e \otimes {I_m}]{M}_{\mathrm{0}}^{ - 1}{{[e \otimes {I_m}]}^T} + {\bar{R}}_k^{ - 1}} \right) ^{ - 1}}$. Obviously, $p({\bar{Z}_k})$ is independent of states and decomposed as

$$\begin{aligned} {\log p({{{\bar{Z}}}_k})} =&\frac{1}{{\mathrm{2}}}\log \lambda - \frac{\lambda }{{\mathrm{2}}}D\left[ {{{{\bar{Z}}}_k} - (e \otimes {I_m}){\mu _{\mathrm{0}}}, B } \right] \\&+ const \end{aligned}$$

Then, rewriting ${\log q(\mu ,\lambda )}$ with ${\log p({{\bar{Z}}_k})}$, we have

$$\begin{aligned}&{\log q(\mu ,\lambda )}\\&{ = {E_{{q_{t + 1}}({x_k}){q_{t + 1}}(\beta )}}\left\{ {\log p({x_k},\mu ,\beta ,\lambda ,Z_1^k)} \right\} + const}\\&{ = \log \frac{{N({{{\bar{Z}}}_k}{\mathrm{|}}(e \otimes {I_m})\mu ,{\lambda ^{ - 1}}{\bar{R}}_k^{ - 1})N(\mu {\mathrm{|}}{\mu _{\mathrm{0}}},{{(\lambda )}^{ - 1}}{M}_{\mathrm{0}}^{ - 1})}}{{p({{{\bar{Z}}}_k})}}}\\&+ ({c_0}{\mathrm{+ }}\frac{1}{{\mathrm{2}}} - 1)\log \lambda - \lambda \left( {{d_0} + \frac{1}{{\mathrm{2}}}{\mathrm{Tr}}\left[ {{H_k}{{(P_k^{t + 1}{\mathrm{)}}}^{ - 1}}H_k^T{\bar{R}}} \right] } \right) \\&{ - \frac{\lambda }{{\mathrm{2}}}D\left[ {{{{\bar{Z}}}_k} - (e \otimes {I_m}){\mu _{\mathrm{0}}}, B } \right] {\mathrm{+ const}}}. \end{aligned}$$

Then, by re-organizing ${\log q(\mu ,\lambda )}$, Theorem 2 is derived.

$$\begin{aligned}&{L_{M - ELBO}}(q)=\int q_t({x_k},\mu ,\lambda ,\beta )\nonumber \\&\quad \ln \frac{{p({x_k},\mu ,\lambda ,\beta ,Z_1^k)}}{{q_t({x_k},\mu ,\lambda ,\beta )}}d\left\{ {{x_k},\mu ,\lambda ,\beta } \right\} \nonumber \\&\quad = {E_{}}\left[ {p({z_k}|{x_k},\mu ,\lambda )} \right] + {E_{}}\left[ {prio({x_k})} \right] \nonumber \\&\qquad + \sum \limits _{J = 1}^{k - 1} {{E_{}}\left[ {p({z_j}|\mu ,\lambda ,\beta )} \right] } \nonumber \\&\quad {}+ {E_{}}\left[ {p(\mu |\lambda )} \right] + {E_{}}\left[ {p(\lambda )} \right] + {E_{}}\left[ {p(\beta )} \right] - {E_{}}\left[ {q_t({x_k})} \right] \nonumber \\&\qquad - {E_{}}\left[ {q_t(\mu |\lambda )} \right] - {E_{}}\left[ {q_t(\lambda )} \right] - {E_{}}\left[ {q_t(\beta )} \right] \end{aligned}$$

(82)

$$\begin{aligned}&{E_{}}\left[ {p({z_k}|{x_k},\mu ,\lambda )} \right] = - \frac{{{D_m}}}{2}\log 2\pi \nonumber \\&\quad + \frac{{{D_m}}}{2}{\lambda _e} + \frac{1}{2}\log \left| {{R^{ - 1}}} \right| \nonumber \\&\quad - \frac{1}{2}\left( D\left( {{z_k} - {H_k}{\hat{x}}_k^t - {{{\hat{\mu }} }_t} - {u_k},{l_e}{R^{ - 1}}} \right) \right. \nonumber \\&\left. \qquad + Tr\left[ {\left( {{H_k}{{(P_k^t)}^{ - 1}}H_k^T{l_e} + {\hat{M}}_t^{ - 1}} \right) {R^{ - 1}}} \right] \right) \end{aligned}$$

(83)

$$\begin{aligned}&{E_{}}\left[ {prio({x_k})} \right] = - \frac{{{D_n}}}{2}\log 2\pi - \frac{1}{2}\log \left| {{\bar{P}}_j^{ - 1}} \right| \nonumber \\&\qquad - \frac{1}{2}\left( {D\left( {{\hat{x}}_k^t - {{{\bar{x}}}_k},{\bar{P}}_j^{}} \right) + Tr\left[ {{{(P_k^{t + 1})}^{ - 1}}{\bar{P}}_j^{}} \right] } \right) \end{aligned}$$

(84)

$$\begin{aligned}&{E_{}}\left[ {p({z_j}|\mu ,\lambda ,\beta )} \right] = - \frac{{{D_m}}}{2}\log 2\pi + \frac{{{D_m}}}{2}\left( {{\lambda _e} + {\beta _e}} \right) \nonumber \\&\qquad + \frac{1}{2}\log \left| {r{r_j}} \right| - \frac{1}{2}\left( D\left( {{z_j} - {H_j}{\hat{x}}_j^t - {{{\hat{\mu }} }_t} - {u_j},{l_e}{b_e}r{r_j}} \right) \right. \nonumber \\&\qquad \left. + Tr\left[ {{\hat{M}}_t^{ - 1}{b_e}r{r_j}} \right] \right) \end{aligned}$$

(85)

$$\begin{aligned}&{E_{}}\left[ {p(\mu |\lambda )} \right] = - \frac{{{D_m}}}{2}\log 2\pi + \frac{{{D_m}}}{2}{\lambda _e} + \frac{1}{2}\log \left( {\left| {{M_0}} \right| } \right) \nonumber \\&\qquad - \frac{{{l_e}}}{2}D\left( {{{{\hat{\mu }} }_t} - {\mu _0},{M_0}} \right) - \frac{1}{2}Tr\left[ {{\hat{M}}_t^{ - 1}M_0^{ - 1}} \right] \end{aligned}$$

(86)

$$\begin{aligned}&{E_{}}\left[ {p(\lambda )} \right] = - \log \varGamma \left( {{c_0}} \right) + {c_0}\log {d_0} + \left( {{c_0} - 1} \right) {\lambda _e} - {d_0}{l_e} \end{aligned}$$

(87)

$$\begin{aligned}&{E_{}}\left[ {p(\beta )} \right] = - \log \varGamma \left( {{a_0}} \right) + {a_0}\log {b_0} + \left( {{a_0} - 1} \right) {\beta _e} - {b_0}{b_e} \end{aligned}$$

(88)

$$\begin{aligned}&{E_{}}\left[ {q_t({x_k})} \right] = - \frac{{{D_n}}}{2}\log 2\pi - \frac{1}{2}\log \left| {{{(P_k^t)}^{ - 1}}} \right| - \frac{{{D_n}}}{2} \end{aligned}$$

(89)

$$\begin{aligned}&{E_{}}\left[ {q_t(\mu |\lambda )} \right] = - \frac{{{D_m}}}{2}\log 2\pi + \frac{{{D_m}}}{2}{\lambda _e} + \frac{1}{2}\log \left( {\left| {{\hat{M}}_t^{}} \right| } \right) - \frac{{{D_m}}}{2} \end{aligned}$$

(90)

$$\begin{aligned}&{E_{}}\left[ {q_t(\lambda )} \right] = - \log \varGamma \left( {{{{\hat{c}}}_t}} \right) + {{{\hat{c}}}_t}\log {{{\hat{d}}}_t} + \left( {{{{\hat{c}}}_t} - 1} \right) {\lambda _e} - {{{\hat{d}}}_t}{l_e} \end{aligned}$$

(91)

$$\begin{aligned}&{E_{}}\left[ {q_t(\beta )} \right] = - \log \varGamma \left( {{{{\hat{a}}}_t}} \right) + {{{\hat{a}}}_t}\log {{{\hat{b}}}_t} + \left( {{{{\hat{a}}}_t} - 1} \right) {\beta _e} - {{{\hat{b}}}_t}{b_e} \end{aligned}$$

(92)

Appendix C: Calculation of M-ELBO

Based on (42), M-ELBO is expressed as (82). Then, the calculations of expectations in (82) are given by (83)–(92). For the convenience of expression, the subscript for expectation computation is omitted.