High-energy orbit sliding mode control for nonlinear energy harvesting

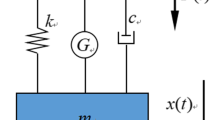
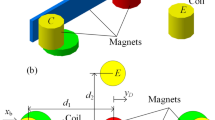
Abstract

Vibration energy harvesting has extensive application prospects in many significant occasions, such as mechanical structure health monitoring, vehicle tire pressure monitoring, IoT devices and human health monitoring. The nonlinearity is an effective method to improve the energy harvesting efficiency where there are low- and high-energy orbits in the multi-solution region of the system. The harvested power will be increased significantly when the system is guided from the low-energy orbit to the high-energy orbit. The sliding mode control is regarded as an easy, robust and adaptive method for orbit jump, but the implementation of this nonlinear control method has not been discussed. This paper proposes a high-energy sliding mode control method through rotatable magnets actuated by micro-motor. The electromechanical model of mono-stable and bi-stable systems with the identified nonlinear restoring force is established to design a sliding mode control algorithm for enhancing the energy harvesting performance. Simulation and experiment results demonstrate that the rotatable magnets with sliding mode control have a positive influence on reaching the high-energy orbit for both mono-stable and bi-stable systems within the multi-solution region. Moreover, the rotatable magnets method with a sliding mode control actuates the small magnets in the system for a short time with little theoretical consumption of energy. This research has provided a potential practical application of sliding mode control for high-energy orbit jump of the nonlinear energy harvesting.

Appendix 1: Nonlinear restoring force calculation for multi-stable energy harvester

According to the research [48] on the restoring force modeling, the force condition of tip magnet in given configuration is shown in Fig. 

Fig. 28

Diagram of force balance for tip magnet

28. The nonlinear restoring force here is along y direction.

The governing equation of tip magnet along y and z directions can be obtained as:

$$\left\{ {\begin{array}{*{20}l} {F_{r} - F_{{my}} - F_{{e1}} - F_{{e2}} \sin \beta = 0} \hfill \\ {F_{{mz}} + F_{{e2}} \cos \beta - F_{g} = 0} \hfill \\ \end{array} } \right.$$

(20)

where F_my, F_mz are magnetic force along y direction and z direction, respectively; F_e1 is elastic force along y direction; F_e2 is the elastic force of cantilever beam along axial direction; F_g is the gravity force of tip magnets; F_r is the nonlinear restoring force.

In order to solve Eq. (20) to obtain the nonlinear restoring force, it is necessary to calculate the magnetic force between the tip magnet and the external magnets. The detailed expression of magnetic force between two cubic magnets can be seen in the research [49]. In terms of two cubic magnets with the magnetization J, the size is a × b × c and a′ × b′ × c′ along x, y and z directions, respectively. The relative coordinates between these two magnets are (x₀₁, y₀₁, z₀₁), and relative rotational angle along x direction is θ.

The magnetic force along z direction is

$$\begin{aligned} F_{z} \left( {\theta ,x_{{01}} ,y_{{01}} ,z_{{01}} ,a,b,c,a',b',c',J} \right) & = - F_{{zp}} \left( {\theta ,0,y_{{01}} ,z_{{01}} ,a,b,a',b',J} \right) \\ & \quad + F_{{zp}} \left( {\theta ,0,y_{{01}} - c'\sin \theta ,z_{{01}} + c'\cos \theta ,a,b,a',b',J} \right) \\ & \quad - F_{{zp}} \left( {\theta ,0,y_{{01}} - c'\sin \theta ,z_{{01}} - c + c'\cos \theta ,a,b,a',b',J} \right) \\ & \quad + F_{{zp}} \left( {\theta ,0,y_{{01}} ,z_{{01}} - c,a,b,a',b',J} \right) \\ \end{aligned}$$

(21)

When θ ≠ kπ, it has

$$\begin{aligned} F_{{zp}} \left( {\theta ,x_{{01}} ,y_{{01}} ,z_{{01}} ,a,b,a',b',J} \right) & = \frac{{F_{{pp}} \left( {\theta ,x_{{01}} ,y_{{01}} ,z_{{01}} ,a,b,a',b',J} \right)}}{{\sin \theta }} \\ & \quad - \frac{{F_{{yp}} \left( {\theta ,x_{{01}} ,y_{{01}} ,z_{{01}} ,a,b,a',b',J} \right)}}{{\tan \theta }} \\ \end{aligned}$$

(22)

$$\begin{aligned} F_{{yp}} \left( {\theta ,x_{{01}} ,y_{{01}} ,z_{{01}} ,a,b,a',b',J} \right) & = - f_{{1p}} \left( {x_{{01}} ,x_{{01}} + a',y_{{01}} ,z_{{01}} ,\theta ,0,b',J} \right) \\ & \quad + f_{{1p}} \left( {x_{{01}} - a,x_{{01}} - a + a',y_{{01}} ,z_{{01}} ,\theta ,0,b',J} \right) \\ & \quad - f_{{1p}} \left( {x_{{01}} - a,x_{{01}} - a + a',y_{{01}} ,z_{{01}} ,\theta ,b,b',J} \right) \\ & \quad + f_{{1p}} \left( {x_{{01}} ,x_{{01}} + a',y_{{01}} ,z_{{01}} ,\theta ,b,b',J} \right) \\ \end{aligned}$$

(23)

$$f_{{1p}} \left( {u,w,y_{{01}} ,z_{{01}} ,\theta ,b,b',J} \right) = - \frac{{J^{2} }}{{4\pi \mu _{0} }}f_{2} \left( {v,w,y_{{01}} ,z_{{01}} ,\theta ,b,0,b',0} \right)$$

(24)

When θ = kπ, it has

$$F_{{zp}} \left( {\theta = k\pi ,x_{{01}} ,y_{{01}} ,z_{{01}} ,a,b,a',b',J} \right) = - \frac{{J^{2} f_{{1z}} \left( {x_{{01}} ,y_{{01}} ,z_{{01}} ,a,b,a',b'} \right)}}{{4\pi \mu _{0} }}$$

(25)

$$\begin{aligned} f_{{1z}} \left( {x_{{01}} ,y_{{01}} ,w,a,b,a',b'} \right) & = - f_{{2z}} \left( {x_{{01}} ,x_{{01}} + a',y_{{01}} ,y_{{01}} + b',w} \right) \\ & \quad + f_{{2z}} \left( {x_{{01}} ,x_{{01}} + a',y_{{01}} - b,y_{{01}} + b' - b,w} \right) \\ & \quad + f_{{2z}} \left( {x_{{01}} - a,x_{{01}} + a' - a,y_{{01}} ,y_{{01}} + b',w} \right) \\ & \quad - f_{{2z}} \left( {x_{{01}} - a,x_{{01}} + a' - a,y_{{01}} - b,y_{{01}} + b' - b,w} \right) \\ \end{aligned}$$

(26)

$$f_{{2z}} \left( {a_{1} ,a_{2} ,b_{1} ,b_{2} ,w} \right) = f_{{3z}} \left( {a_{2} ,b_{2} ,w} \right) - f_{{3z}} \left( {a_{1} ,b_{2} ,w} \right) - f_{{3z}} \left( {a_{2} ,b_{1} ,w} \right) + f_{{3z}} \left( {a_{1} ,b_{1} ,w} \right)$$

(27)

$$\begin{aligned} f_{{3z}} \left( {u,v,w} \right) & = uv\arctan \left( {\frac{{uv}}{{w\sqrt {u^{2} + v^{2} + w^{2} } }}} \right) + \frac{1}{2}uw\ln \left( {\frac{{u + \sqrt {u^{2} + v^{2} + w^{2} } }}{{ - u + \sqrt {u^{2} + v^{2} + w^{2} } }}} \right) \\ & \quad - \frac{1}{2}vw\ln \left( {\frac{{ - v + \sqrt {u^{2} + v^{2} + w^{2} } }}{{v + \sqrt {u^{2} + v^{2} + w^{2} } }}} \right) - w\sqrt {u^{2} + v^{2} + w^{2} } \\ \end{aligned}$$

(28)

Then, the magnetic force along y direction is

$$\begin{aligned} F_{y} \left( {\theta ,x_{{01}} ,y_{{01}} ,z_{{01}} ,a,b,c,a',b',c',J} \right) & = f_{1} \left( {x_{{01}} ,x_{{01}} + a',y_{{01}} ,z_{{01}} ,\theta ,0,0,b',c',J} \right) \\ & \quad - f_{1} \left( {x_{{01}} - a,x_{{01}} - a + a',y_{{01}} ,z_{{01}} ,\theta ,0,0,b',c',J} \right) \\ & \quad + f_{1} \left( {x_{{01}} - a,x_{{01}} - a + a',y_{{01}} ,z_{{01}} ,\theta ,b,0,b',c',J} \right) \\ & \quad - f_{1} \left( {x_{{01}} ,x_{{01}} + a',y_{{01}} ,z_{{01}} ,\theta ,b,0,b',c',J} \right) \\ & \quad + f_{1} \left( {x_{{01}} - a,x_{{01}} - a + a',y_{{01}} ,z_{{01}} ,\theta ,0,c,b',c',J} \right) \\ & \quad - f_{1} \left( {x_{{01}} ,x_{{01}} + a',y_{{01}} ,z_{{01}} ,\theta ,0,c,b',c',J} \right) \\ & \quad + f_{1} \left( {x_{{01}} ,x_{{01}} + a',y_{{01}} ,z_{{01}} ,\theta ,b,c,b',c',J} \right) \\ & \quad - f_{1} \left( {x_{{01}} - a,x_{{01}} - a + a',y_{{01}} ,z_{{01}} ,\theta ,b,c,b',c',J} \right) \\ \end{aligned}$$

(29)

$$\begin{aligned} f_{1} \left( {v,w,y_{{01}} ,z_{{01}} ,\theta ,b,c,b',c',J} \right) & = \frac{{J^{2} }}{{4\pi \mu _{0} }}\left( {f_{2} \left( {v,w,y_{{01}} ,z_{{01}} ,\theta ,b,c,b',c'} \right)} \right) \\ & \quad - f_{2} \left( {v,w,y_{{01}} ,z_{{01}} ,\theta ,b,c,b',0} \right) \\ \end{aligned}$$

(30)

$$\begin{aligned} f_{2} \left( {v,w,y_{{01}} ,z_{{01}} ,\theta ,b,c,b',z'} \right) & = f_{3} \left( {w,y_{{01}} ,z_{{01}} ,\theta ,b,c,0,z'} \right) \\ & \quad - f_{3} \left( {v,y_{{01}} ,z_{{01}} ,\theta ,b,c,b',z'} \right) \\ & \quad - f_{3} \left( {w,y_{{01}} ,z_{{01}} ,\theta ,b,c,0,z'} \right) \\ & \quad + f_{3} \left( {v,y_{{01}} ,z_{{01}} ,\theta ,b,c,0,z'} \right) \\ \end{aligned}$$

(31)

$$\begin{aligned} f_{3} \left( {u,y_{{01}} ,z_{{01}} ,\theta ,b,c,y',z'} \right) & = uf_{6} \left( {y_{{01}} ,z_{{01}} ,\theta ,b,c,y'} \right)\ln \left( { - u + f_{4} \left( {y_{{01}} ,z_{{01}} ,\theta ,b,c,y',z'} \right)} \right) \\ & \quad - uf_{6} \left( {y_{{01}} ,z_{{01}} ,\theta ,b,c,y'} \right) \\ & \quad - u^{2} \ln \left( {f_{4} \left( {y_{{01}} ,z_{{01}} ,\theta ,b,c,y',z'} \right) + f_{6} \left( {y_{{01}} ,z_{{01}} ,\theta ,b,c,y'} \right)} \right) \\ & \quad + uf_{5} \left( {y_{{01}} ,z_{{01}} ,\theta ,b,c,z'} \right)\arctan \left( {\frac{{ - f_{5}^{2} \left( {y_{{01}} ,z_{{01}} ,\theta ,b,c,y'} \right) - u^{2} + uf_{4} \left( {y_{{01}} ,z_{{01}} ,\theta ,b,c,y',z'} \right)}}{{f_{5} \left( {y_{{01}} ,z_{{01}} ,\theta ,b,c,z'} \right)f_{6} \left( {y_{{01}} ,z_{{01}} ,\theta ,b,c,y'} \right)}}} \right) \\ & \quad + \frac{1}{2}u\pi \left| {f_{5} \left( {y_{{01}} ,z_{{01}} ,\theta ,b,c,z'} \right)} \right|sign\left( {f_{6} \left( {y_{{01}} ,z_{{01}} ,\theta ,b,c,y'} \right)} \right) \\ & \quad + \frac{1}{2}f_{6} \left( {y_{{01}} ,z_{{01}} ,\theta ,b,c,y'} \right)f_{4} \left( {y_{{01}} ,z_{{01}} ,\theta ,b,c,y',z'} \right) \\ & \quad + \frac{1}{2}\left( {u^{2} + f_{5}^{2} \left( {y_{{01}} ,z_{{01}} ,\theta ,b,c,y',z'} \right)} \right)\ln \left( {f_{4} \left( {y_{{01}} ,z_{{01}} ,\theta ,b,c,y',z'} \right) + f_{6} \left( {y_{{01}} ,z_{{01}} ,\theta ,b,c,y'} \right)} \right) \\ \end{aligned}$$

(32)

$$f_{4} \left( {y_{{01}} ,z_{{01}} ,\theta ,b,c,y',z'} \right) = \sqrt {u^{2} + f_{5}^{2} \left( {y_{{01}} ,z_{{01}} ,\theta ,b,c,z'} \right) + f_{6}^{2} \left( {y_{{01}} ,z_{{01}} ,\theta ,b,c,y'} \right)}$$

(33)

$$f_{5} \left( {y_{{01}} ,z_{{01}} ,\theta ,b,c,z'} \right) = - y_{{01}} \sin \theta + z_{{01}} \cos \theta + b\sin \theta - ccos\theta + z'$$

(34)

$$f_{6} \left( {y_{{01}} ,z_{{01}} ,\theta ,b,c,y'} \right) = y_{{01}} \cos \theta + z_{{01}} \sin \theta - b\cos \theta - c\sin \theta + y'$$

(35)