Abstract
Nonlinearities in rotating systems have been seen to cause a wide variety of rich phenomena; however, the understanding of these phenomena has been limited because numerical approaches typically rely on “brute force” time simulation, which is slow due to issues of step size and settling time, cannot locate unstable solution families, and may miss key responses if the correct initial conditions are not used. This work uses numerical continuation to explore the responses of such systems in a more systematic way. A simple isotropic rotor system with a smooth nonlinearity is studied, and the rotating frame is used to obtain periodic solutions. Asynchronous responses with oscillating amplitude are seen to initiate at certain drive speeds due to internal resonance, in a manner similar to that observed for nonsmooth rotor–stator contact systems in the previous literature. These responses are isolated, in the sense that they will only meet the more trivial synchronous responses in the limit of zero damping and out of balance forcing. In addition to increasing our understanding of the responses of these systems, the work establishes the potential of numerical continuation as a tool to systematically explore the responses of nonlinear rotor systems.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
In nonlinear dynamic systems, the response can change qualitatively with small changes in system parameters, so being able to systematically locate these so-called bifurcations is vital in nonlinear mechanical systems. This complication is accentuated in rotating machinery because of gyroscopic coupling which makes the response modes complex and whirl frequencies dependent on the rotor speed. These systems exhibit rich phenomena including period doubling, aperiodicity, and even chaos in the system’s response [1, 5, 37].
Nonlinearity in rotordynamics can originate from sources such as rotor–stator interactions, faults such as cracks, nonlinear bearing forces, and geometric nonlinearity when shafts are flexible [13, 16, 24]. The rotor–stator contacting phenomenon in turbomachinery can result from a loss of blade, supports being misaligned, fatigue cracks shafts [2, 17], and depending on the bearing type can lead to destructive oil whips [4]. By contrast with turbomachinery, long drilling shafts with low stiffness have been documented to demonstrate nonlinearity due to rotor–stator contact [3, 31, 36]. Ehrich [10] described the following phenomena occurring in the nonlinear response of rotating systems: asynchronous response, changing amplitude for constant rotor speed, discontinuous amplitude response as rotor speed changes. Synchronous partial contact response have been observed [5, 8].
The response of an isotropic rotor system is typically in the form of a constant radius circular motion known as whirling—in linear and weakly nonlinear cases this is generally synchronous, meaning it occurs at the speed of the shaft rotation, excited by unbalanced mass. While the presence of friction can lead to a dangerous case known as dry backward whirl [13], more intriguing are responses where the amplitude of shaft displacement from its rotation centre continually oscillates, also known as bouncing motions or intermittent contact cycles [34]. These can be synchronous, in that the period of the response is in a real ratio with the period of shaft rotation. However, the more challenging case is that of asynchronous responses, where the response frequencies bear no obvious relation to the shaft speed [8, 39]. It has been shown that the intermittent contact can be asynchronous, yet it can be estimated by an internal resonance condition, relating integer multiples of whirl frequencies [34]. It is crucial to note that because the underlying linear frequencies depend on the rotor speed, different underlying modes may take part in internal resonance combinations at different drive speeds.
Many approaches have been used to analyse such response. Some research considered fully rigid models for the stator contact. Cole and Keogh [8] analysed the asynchronous intermittent contact phenomenon. The fundamental frequency of the harmonic balance method (HBM) they used was set to the contacting frequency which was found from the contact energy conservation. They concluded that in the high frequency range the number of possible contact modes decreased with increasing damping. The study gave upper and lower limits of unbalance to achieve the periodic contacting motions. Mora et al. [23] employed a rigid impact model for the contacting interactions, and explained the transition into bouncing motions as a grazing bifurcation.
Further studies use smooth or piecewise linear functions to represent nonlinearity due to contact. Karpenko et al. [18] analytically solved the two-degree-of-freedom (2-dof) Jeffcott system. Depending on the accuracy of Taylor expansion during contact, time simulations were approximated very closely. Gyroscopic effects, friction, and snubber mass were not considered. Karpenko et al. [19] observed that higher damping and lower stiffness eliminated multi-periodic and chaotic solutions on a similar model. A preloaded snubber ring in [27] shifted the bifurcation plots, added new bifurcations, and decreased the response amplitudes of the retainer ring. The position of the massless snubber ring was found from the energy spent on the ring during contact, with the help of a Lagrange multiplier. The experimental validation of this mathematical model was published by Karpenko et al. [20].
Zilli et al. [39] investigated a snubbed overhung rotor with 2-dof, and time-simulated a blade loss scenario by introducing an unbalance. The analytical model had a piecewise linear stiffness to define contact. A synchronisation condition was derived using phasors of system frequencies. The frequencies where the intermittent contacts occurred in the bifurcation diagrams were closely approximated with this synchronisation condition. In a rapid deceleration test, higher transient energy was found more likely to yield sustained bouncing motion.
Shaw et al. [34] expanded the internal resonance idea to higher-degree-of-freedom systems by setting the condition to involve any two whirl modes. In the study, soft contact with no damping and stiff contact with damping were investigated on a finite element (FE) model that is further reduced with some of the linear eigenmodes. As observed in [39], the authors reported the stiffening effect that causes the predicted rotor speeds to be lower than the numerical ones. Chipato et al. introduced friction [6] and gravity [5] to the overhung rotor system in [39]; they noted that the synchronisation condition holds in both cases. With gravity, multi-periodic and even chaotic responses appeared. However, increased rotor stiffness nullified the effect of gravity. Varney and Green [37] presented a rotor speed threshold after which the gravity can be ignored.
Analytical and semi-analytical methods to solve the nonlinear equation of motions include the use of normal forms, harmonic balance method (HBM), and alternating frequency/time domain methods (AFT), [35]. In the study by Von Groll and Ewins [38], after the equations of motion were converted to algebraic equations by HBM, arclength continuation was performed to efficiently find solutions, with the help of AFT to update contact forces. The method was demonstrated on a Jeffcott rotor in penalty–contact interaction with a stator of nonzero mass. Subharmonics were allowed in HBM formulations which was stated to be required by the intermittent contact motion.
Quasi-periodic solutions were investigated by Peletan et al. [29] who used HBM with pseudo-arclength continuation, both of which were modified to automate the selection of harmonics and continuation of quasi-periodic solution branches. A previous study [28] showed that for the stability analysis, the time domain methods were more accurate than the frequency domain methods that are based on the modified Hill’s method. A study [30] assessed the limitations of HBM in the rotor–stator contact modelling.
Salles et al. [32] used HBM and numerical continuation to obtain the bifurcation diagram of an entire aeroengine with three shaft and four snubber elements. Component mode synthesis was used to reduce the FE model, which was further reduced to the nonlinear degrees of freedom. A special treatment of the method allowed them to find isolated solutions in bifurcation diagram. However, the analysis of the asynchronous response was not their objective.
The fact that the intermittent contact response can be seen as the synchronisation of resonant frequencies of the rotating system, make the use of the normal forms technique a useful procedure to solve the nonlinear equations [35]. Shaw et al. [35] employed the normal forms method on a reduced order model together with an AFT method to update the nonlinear forces. The proposed method was demonstrated on a 2-dof overhung snubbed rotor system and a multi-disc system involving rotor–stator contact. The importance of the use of rotating coordinates was emphasised to get a periodic response for the bouncing cycles, as also mentioned by Cole and Keogh [8].
Geometric nonlinearity in rotors has been discussed in the context of rotordynamics by Nagasaka et al. [25]. The mathematical model of a continuous slender shaft with nonlinear cross section was constrained longitudinally through bearings at each end. The gyroscopic effects were small due to the lack of a disc. Thus, the 1:1 internal resonance in the stationary frame was investigated for both major and secondary critical speeds. The cause of the nonlinear response such as Hopf bifurcations and quasi-periodic motions was linked to the internal resonance. Findings were experimentally confirmed. Previous works accompanied that study such as [14, 15, 26]. In the book by Ishida and Yamamoto [16], further discussions of geometric nonlinearity and their solutions were given. The book [16], represented the weak nonlinearity in stiffness as one for which the potential energy can be expressed as a power series, whose derivatives with respect to the dimensions of the system give restoring forces. The harmonic and subharmonic responses, as well as combination resonances, were investigated in the stationary coordinate frame.
Aside from experimental investigations, the primary tools for understanding rotordynamics have thus far been time simulation [5,6,7, 12, 34, 37, 39] and analytical and semi-analytical approaches based on the harmonic balance method [29, 30, 32, 35, 38]. The time simulation approach is slow; solutions must be continued for some arbitrary amount of time to converge to a steady state which make it excessively time-consuming for low damping cases [33]. Also, many simulations must be run with different initial conditions if multiple solutions are to be found [34]. Even when this has been done, there is no guarantee that all responses have been found, making time simulation quite an inefficient method to investigate these systems. Analytical and semi-analytical approaches require sometimes complex formulations to transform the equations of motion to algebraic form, and still leave doubt that all solutions have been found, depending on the numerical solver’s start point. However, the use of arclength continuation does offer significant benefits in exploring the space around a given solution in the sense that it allows a complete solution family to be found without the interruption of jumping phenomenon, a common phenomenon for time simulations. It can pass the turning points, the so-called folds, possibly progressing to the unstable region [30], which make the method feasible for high-resolution bifurcation diagrams [33]. However, an initial time to set up the continuation parameters such as those that define accuracy is required in continuation [9]. Given the rich complexity of solutions in rotor systems, it is perhaps surprising the method of numerical continuation, where continuation is applied directly to the equations of motion, has not previously been applied more extensively.
Considering the literature above, the present work seeks the analysis of a 2-dof mathematical model of an overhung rotor with an isotropic cubic stiffness nonlinearity. The main focus is asynchronous periodic orbits that are caused by internal resonance in the case of geometric nonlinearity, and we see similarities to the behaviours seen with contacting nonlinearity. The results are compared to studies with discontinuous stiffness contact definitions. The continuation method is applied directly to the systems of ODE, in contrast to Refs. [29, 32, 38]. The autonomous rotating coordinate frame equations of motion are used in the numerical continuation procedures; the observed periodic solution families correspond to quasi-periodic solutions in the stationary frame.
In the rest of this paper, Sect. 2 presents the theoretical background: the equations of motion are derived using Lagrange’s method, nondimensionalised and transformed to the rotating frame. Section 2 ends with a plot of the natural frequency map featuring signed natural frequencies [35]. Section 3 contains time simulations set-up using the MATLAB function ode45. The numerical continuation procedures are explained in Sect. 4 with a summary of the continuation theory. Then the results of the continuation runs and time simulations are presented in Sect. 5 with an extra validation of the continuation results using time simulations. Conclusions from the results, along with the future work ideas, are given in Sect. 6.
2 Theoretical background
2.1 Derivation of equations of motion
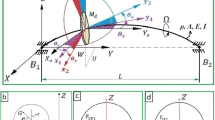
The system subject to analysis here is a two-degree-of-freedom (2-dof) overhung rotor system, as shown in Fig. 1. Here, a and b are distances from point O, up to the disc and the stiffness element, respectively; \(k_r\) is the isotropic linear stiffness; \(k_3\) is the isotropic cubic stiffness; \(c_r\) is the linear damping coefficient; \(\theta ,\psi ,\phi \) are the angles of rotation about x, y, z axes, respectively; \(\varOmega \) is the rotor speed \((\phi =\varOmega t)\); \(I_p\) and \(I_d\) are polar and diametral moments of inertia, respectively. This system is in some ways similar to the contacting system in [39], although the piecewise linear contact is replaced by a smooth cubic stiffness \(k_3\). As an isotropic stiffening effect, this cubic stiffness can represent effects such as a bend–stretch coupling due to fixed positions of the bearings, for example, in a pinned–pinned shaft [16]. Note that the derivation of the equations of motion in the next section assumes constant rotational speed, \({\dot{\varOmega }}=0\), and small transverse angles \(\theta \) and \(\psi \).
2.2 Equations of motion
In this section, the derivation of equations of motion is given which takes the transverse angles \(\theta \) and \(\psi \) as the generalised coordinates. The derivation uses Lagrange’s energy method [13].
2.2.1 Kinetic energy
Kinetic energy resulting from the translational motion of the disc is,
where \(m_d\) is the disc mass, \(x_g=x_c+e\cos {\phi }\) and \(y_g=y_c+e\sin {\phi }\) are the transverse translations of the disc centre of gravity,
and \(x_c\) and \(y_c\) point to the disc centre of rotation. For small motions, the angles \(\theta ,\psi \) can be defined in terms of \(x_c,y_c\) and linearised to give,
It is convenient to express the rotational kinetic energy with respect to the body-fixed frame of reference, i.e. a coordinate system that is fixed onto the disc. The method requires that the Euler angles be obtained from position with zero angles of rotation by applying rotations. Let the order of rotations be:
-
\(\psi \) about y-axis,
-
\(\theta \) about resulting x-axis,
-
\(\phi \) about resulting z-axis.
The transformation matrices needed for these transformations are:
These matrices are be used to find the angular speeds in the body-fixed frame of reference as,
where \(\omega _{{\bar{x}}},\omega _{{\bar{y}}},\omega _{{\bar{z}}}\) are the angular speed with respect to the body-fixed frame. As a result, the rotational kinetic energy can be expressed as,
Therefore, the total kinetic energy of the disc becomes \(T_{d}=T_{\mathrm{tra}}+T_{\mathrm{rot}}\), with small angles \(\theta \) and \(\psi \):
where \(I_d^o=I_d+m_da^2\) is the diametral moment of inertia of the disc with respect to centre of the fixed-frame of reference.
2.2.2 Potential energy
All potential energy is due to the nonlinear spring, acting in the radial direction. The conservative force can be expressed as the superposition of the linear and cubic stiffness contributions,
where \(r=b \sqrt{\theta ^2+\psi ^2}\). Therefore, the potential energy is given by:
2.2.3 Lagrangian equations of motion
The Lagrangian function \(L=T-V\) is found from Eqs. (7) and (9) as,
The following nonconservative forces are introduced to include the effects of linear damping in the restoring force:
The 2nd type Lagrange equations,
yield the following equations of motion in the angular coordinates, \((q_1,q_2)=(\theta ,\psi )\),
2.3 Nondimensionalised equations of motion
A nondimensionalisation of Eq. (13) is performed by dividing by \(k_t=k_rb^2\), which represents the angular equivalent of the radial stiffness \(k_r\), and it is related to the natural frequency of the underlying linear system through \(\omega _n^2=k_t/I_d^o\). A new term \(\gamma \) is introduced to express the ratio of linear and cubic returning forces:
If one keeps b constant, the ratio \(\gamma \) is a direct measure of cubic stiffness, which is the geometric nonlinearity used here. Thus, the nondimensional equations of motion are,
where the following identities are used,
Hats on \(\theta \) and \(\psi \) were placed for consistency within the equations. Here, \((\cdot )^\prime \) is the derivative with respect to the nondimensionalised time, \(\tau \).
The parameters were chosen to provide a system that can be reasonably compared to the system presented in [39]. Clearly, there is no direct equivalence between the coefficients describing the smooth nonlinearity in this work with the piecewise nonlinear stiffness in [39], but the values chosen give oscillating limit cycles at similar amplitudes found by Zilli. A comparison of the nonlinear functions used in this work and [39] is shown in Fig. 2.
a Restoring force and b potential energy comparison between piecewise contact stiffness model that is used in [39] and cubic stiffness model used here
2.4 Stationary frame equations in displacement coordinates
The displacement of the disc in the stationary frame can be derived from the equation of motion in Eq. (15) by simply applying the transformation,
where \({\hat{x}}=\frac{x_c}{a},\ {\hat{y}}=\frac{y_c}{a}\) from Eqs. (3) and (16).
The nondimensionalised stationary frame displacement equations of motion are then obtained as:
In matrix form with \(\hat{{\mathbf {X}}}=[{\hat{x}},{\hat{y}}]^T\) this is,
where \({\hat{r}}=\sqrt{{{\hat{x}}}^2+{{\hat{y}}}^2}=r/b\) is the distance of the centre of the disc from the equilibrium position in the nondimensional form, and \({\mathbf {J}}\) is the skew symmetric matrix:
2.5 Rotating frame equations of motion
A transformation in \(\phi \), the rotor angular position, has to be applied in the following form,
where \(\hat{{\mathbf {U}}}=\left[ {\hat{u}},{\hat{v}}\right] ^T\) is the rotating coordinate vector, and the transformation \({\mathbf {T}}\) is,
During the transformations, the first and second normalised derivatives of \({\mathbf {X}}\) are needed,
where the first and second normalised derivative of \({\mathbf {T}}\) are,
After substituting Eqs. (23) and (24) to Eq. (19), and multiplying on the left by \({\mathbf {T}}^T\), the rotating frame equations of motion are obtained as,
The state-space representation is:
where \({\mathbf {q}}_{1-4}\) are \(\left[ u,v,{\dot{u}},{\dot{v}}\right] ^T\).
2.6 Natural frequency map
The natural frequency of the underlying linear system changes with rotor speed due to the gyroscopic couplings, or additionally through the dependence of the system parameters such as stiffness and damping on the rotor speed [13]. A natural frequency map, plotting the natural frequency with respect to the rotor speed, can help identify the critical speeds, where harmonic, subharmonic, or internal resonance occur [16]. The natural frequencies are shown in Fig. 3, from an eigenvalue analysis of the linear conservative parts of the equations of motion. Figure 3a shows a traditional representation of the Campbell diagram, where unsigned stationary frame frequencies are plotted. Figure 3b shows the form suggested in [35] where a signed frequency in the rotating frame is presented. Anticlockwise whirling is indicated by a positive value, whereas clockwise whirling is indicated by a negative value. This form is invaluable for highlighting drive speeds where combination resonances can occur.
The natural frequency map in a stationary frame, and b rotating frame. 1st engine order (EO) is also shown in stationary frame frequency map. Whirl frequencies are signed positive and negative for forward and backward whirl, respectively. The 3:1 and 2:1 internal resonance points are marked in the rotating frame
3 Time simulation set-up
The explicit time marching was performed in [22] using the built in ode45 function. In this study, three cases of simulations were designed: constant initial condition simulations, sweep tests, and starting data generation for AUTO.
For constant initial condition simulations, a randomly generated stationary frame initial condition was used in the entire drive speed range to initiate the simulation. The initial conditions of the rotating frame simulations were derived from this initial condition using the transformations at \(\tau =0\) (nondimensionalised time) given by,
where the subscripts \(\hat{\theta }\hat{\psi }\), \({\hat{x}}{\hat{y}}\), and \({\hat{u}}{\hat{v}}\) represent nondimensional coordinates in their respective frames of reference. Simulations were run with damping ratio \(\zeta =0.01\), duration of nondimensional time, \(\tau _{\mathrm{end}}=3000\), and the relative tolerance, \(\hbox {tol} = 1e-7\). This relative tolerance value was adequate as lower tolerances did not show qualitative changes to the converged solution while increasing the computational time. Then, initial conditions were varied randomly to capture the responses of the system with different response types. The parfor looping provided by MATLAB was used to utilise 12 CPU threads in parallel.
For sweep tests, the drive speed, \(\hat{\varOmega }\), was swept in the range of 0.01–7.01 in the forward and backward directions. Each time a simulation of a particular drive speed finished, the last datum of the trajectory was selected as initial condition for the next \(\hat{\varOmega }\). To do this in the rotating coordinates, the last datum was transformed to the stationary frame using Eqs. (27) and (28), and then back to the rotating frame at the next drive speed using Eq. (29). Because of the need of one simulation to finish for the next to start, parallel computing was not available for the sweep tests. Different initial conditions were used until the full synchronous solution families were obtained without jumps to periodic orbits. Also, the asynchronous responses found using the constant initial condition simulations were swept in the same manner. For sweep tests, the same damping ratio \(\zeta \), simulation duration \(\tau _{\mathrm{end}}\), and relative tolerance values were used as mentioned above for the constant initial condition simulations. Lastly, the synchronous and asynchronous sweep test results were plotted to form a single bifurcation diagram.
Starting data generation for AUTO was created in the rotating frame for different \(\zeta \); the duration of simulation was increased as the damping ratio, \(\zeta \), was decreased, to ensure that the transient decayed within at most half the simulation duration. For stationary solutions in the rotating frame, the last data points in the time series generated by the time simulations were used. The time and state variable data that belong to one single period of the converged periodic orbits were stored in a .dat file to be used as starting periodic orbits in AUTO runs. More details of .dat file generation can be found in “Appendices”.
4 Numerical continuation set-up
4.1 Background
Compared to the time simulations of ode45, numerical continuation theory provides a different way to extracting the response of the numerical system from a previously known solution. The method [33] is based on the implicit function theorem which states that a regular solution point \(x_0=\left( u_0,\lambda _0\right) \) satisfying the system of equations of form \(G(u,\lambda )=0,\quad G:R^n\times R\rightarrow R^n\) has a continuous family of solutions provided that the Jacobian \(G_u(u_0,\lambda _0)\) is nonsingular and the function is continuously differentiable at this point. So, the derivative of the system gives:
where \(G_\lambda \) is the derivative of the equations \(G(u.\lambda )=0\) with respect to \(\lambda \). However, due to the problem that arises when the Jacobian is singular at the so-called folds of a solution family, its arclength, s, is introduced as a free parameter, with an accompanying parametrisation:
In this way, the extended Jacobian, \(G_x=[G_u,G_\lambda ]\), is kept full rank. An initial guess for the next point of a solution branch can be written as [33],
where \(\sigma \) is a step length. A correction with a Newton method is then,
Once the convergence is achieved, the next direction vector is found from the derivative of Eq. (31),
The new direction vector is rescaled by normalising its norm \({||}{\dot{x}}_1{||}^2={||}{\dot{u}}_1{||}^2+\lambda _1^2=1\).
A boundary value problem’s continuation procedure can be used [33] to follow periodic solution branches of an n-dimensional ODE, \(y^\prime =Tf(y,\lambda )\), with the derivative being with respect to normalised time, t with \(0\le ~t\le ~1\). The ODE problem then needs to be augmented with a periodicity condition, \(y(0)=y(1)\), and a phase condition, e.g. \(p(y(0),\lambda )={{\dot{y}}}_k(t=0)=0\). Accompanying these are the statements of the period and continuation parameter, \(\lambda \) not changing for a certain periodic solution: \(T^\prime =0\) and \(\lambda ^\prime =0\). The continuation of a branch of periodic solutions then take the form,
where P is a parametrisation such as arclength parametrisation of Eq. (31), and p is a phase condition. The discretisation of the ODE part will ultimately result in an algebraic equation of the form \(F(y,T,\lambda )=0\) [33].
Discussion of stability is covered well in the text books, for example [33]. AUTO, the numerical continuation software employed in this study, uses a method proposed by Fairgrieve and Jepson [11], where the Floquet multipliers are calculated without explicit calculation of the monodromy matrix.
4.2 AUTO files
The AUTO-07p open source numerical continuation software [9] was used to apply pseudo-arclength continuation. This software is operated through a Unix Command Language User Interface (CLUI), and can be written in a Python CLUI which supports Python 3 syntax. AUTO set-up basically includes filling three dedicated files: equations file, constants file, Python CLUI files.
4.2.1 Equations file
The equations file requires information on the equation of motion, as well as the starting conditions of parameters and a regular solution on a branch of solutions that is to be continued.
The rotating frame equation of motion (Eq. 26) was used since in the rotating frame the forcing becomes constant, which facilitates the analysis by making the system of equations autonomous. Also, asynchronous solutions appear periodic (although quasi-periodic in the stationary frame, as the Poincare map has closed loops). Therefore, the synchronous solutions are sought with the stationary continuation solver \((\hbox {IPS}=1)\); whereas asynchronous solutions are found by employing periodic continuation solver of AUTO \((\hbox {IPS}=2)\).
Amplitude was defined to be a solution measure in the PVLS subroutine of the equations file. The amplitudes of stationary and periodic solutions were calculated as,
where the nondimensional time, \(\tau \), is defined between \(0\le \tau \le 1\).
The constants file is where the user mainly specifies the continuation software’s solution control parameters. The main adjustments of these constants concern those that define the accuracy. More detail can be found in “Appendices”.
4.2.2 Continuation solution process
The Python CLUI file contains the chronological flow of runs. The complete content of this file can be written in the AUTO CLUI shell. However, the usage of Python CLUI eases the use of the software by a complete view of the runs. The flow of runs is shown in Table 1. The references to the single- and double-loop families in Table 1 indicate the shape of the orbits corresponding to the 3:1 and 2:1 internal resonances, respectively, as seen in Fig. 4.
Damping ratio, \(\zeta \), was selected as the main continuation parameter because the level of damping might explain the rotor speed range where the asynchronous solutions could be expected, e.g. earlier in the range and more likely to appear particularly with low damping (see in Sect. 5). In Table 1, A, B and C are different ways the continuation was carried out:
- A::
-
A first continuation run with \(\zeta =0.01\) is performed through homotopy of the \({\hat{m}},\gamma \) and \(\hat{\varOmega }\) from zero, initialised with the known analytical values for synchronous solutions and simulation results for periodic solutions. Then, continuation in \(\zeta \) is performed from a selected point of the solution family. After, from the data sampled at various \(\zeta \) during this \(\zeta \)-continuation, new solution branches are found with continuation in \(\hat{\varOmega }\).
- B::
-
Only time simulation starting data is used in \(\hat{\varOmega }\)-continuation for different \(\zeta \) values
- C::
-
Folds in \(\hat{\varOmega }\) are continued in \(\zeta \) to trace the effect of the change of \(\zeta \).
and the cases 1, 2, and 3 are,
- 1::
-
Synchronous solution branch continuation
- 2::
-
Single-loop branch continuation
- 3::
-
Double-loop branch continuation
5 Results and discussion
Results of the numerical continuation are presented first; then, in Sect. 5.2, the time simulation data used to validate these results and provide starting solutions is discussed.
5.1 Numerical continuation
Figure 5 shows the bifurcation diagram in nondimensionalised amplitude versus rotor speed, for all of the solutions from the different \(\zeta \) values investigated. Labels SS, DL, and SL in the figure refer to the solution families of synchronous, double-loop asynchronous, and single-loop asynchronous solutions, respectively. Synchronous and asynchronous solutions are also referred to as stationary and periodic as only the rotating frame equations of motion were used in AUTO.
For the lower \(\zeta \), the SS branch exceeds the limit of the plot. A close-up view of the SS branch is shown in Fig. 5d. For the increased damping values, the synchronous peaks merge and form a stiffened nonlinear response peak. As the damping is further increased, the unstable solutions, which are shown with dashed lines, are lost. At higher drive speeds the amplitude of SS branch decreases very slightly with increased damping.
The bifurcation diagram generated from AUTO using the autonomous rotating frame equations of motion. Both stationary (synchronous) and periodic (asynchronous) solutions are included. The zoom views at b and c show the change in double-loop and single-loop solution families with \(\zeta \), respectively. The zoom view in d shows the synchronous region. The zoom view in e shows the cyan-coloured single-loop periodic solutions with \(\zeta =0.082\). In the figure, ’SS’, ’DL’, and ’SL’ stand for synchronous, double-loop, and single-loop solution families, respectively. The legends show \(\zeta \) values of periodic solutions in b and c, and of synchronous solutions in d. (Color figure online)
Figure 5 also shows that there is a region of nondimensionalised rotor speed between \(\hat{\varOmega }=1.5-2.3\) where jumps would only happen between the synchronous solutions. Chipato et al. [6] and Zilli et al. [39] also documented this phenomenon in their overhung models with frictionless contact definitions.
Zoom view at the bifurcation diagram where stationary and single-loop periodic solutions meet in the lower-\(\zeta \) extreme. Turquoise and purple lines show \(\zeta =1e-4\) and \(1e-5\), respectively, and “SS” stands for synchronous solutions. The stacked lines below the 0.413 amplitude level show the synchronous branches where higher amplitudes correspond to lower \(\zeta \). (Color figure online)
As damping increases, the fold at the lower end of both the DL and SL solution branches moves higher in terms of both amplitude and drive speed, with the SL branch moving beyond the range of drive speeds considered at higher damping values. The various \(\zeta \) value sampling of periodic solution families was done through the continuation of the \(\zeta =0.01\) orbits in AUTO, for Methods A2 and A3 (see Table 1). The results are given in Fig. 6. The higher damping ratio limit to the existence of SL and DL are \(\zeta =0.0828\) and \(\zeta =0.0117\), respectively. This shows that the increase in damping in the system would first eliminate DL solutions. SL solution families show that the increased \(\zeta \) shrinks and eliminates this type of periodic solution family out of the investigated drive speed region (see Fig. 5e). This can be observed in Fig. 5e where the brown, dark turquoise, and cyan coloured branches correspond to \(\zeta \) of 0.050, 0.075, and 0.082, respectively. Note that in this figure the dark blue dashed line shows the fold continuation (Method C2) of the SL solutions. Increased \(\zeta \) for DL branches, however, kept these solution families as isolated amplitude circles within the drive speed region of interest until the damping ratio is above the 0.0117 limit.
a Bifurcation diagram for the angular equations of motion with initial condition [0.0; 0.6; \(-1.246\); 0.0]. b and c show the double-loop response from the perspective of stationary and rotating frame of references, respectively. d and e show single-loop response in stationary and rotating frame, respectively. The orange dots in b and d show the stroboscopic Poincare sampling at the drive speed after the convergence. (Color figure online)
Figure 5b and c shows that the decrease in damping extends the left-hand side of the periodic solution families downwards, closing into the synchronous solutions at \(\hat{\varOmega }=2.31\) and \(\hat{\varOmega }=3.46\) for DL and SL solution families, respectively. Figure 5b also shows the locus of folds as zeta is freed in addition to rotor speed. At the place where the periodic and stationary solutions meet, the periodic solution branches become quite sharp, making it difficult to perform continuation. As a result, the SL solution family for \(\zeta =1e-5\) converged only with increased number of Newton–Chord correction iterations. The results are seen in Fig. 7.
The Campbell diagram of the linear, undamped system (Fig. 3) shows possible locations of the internal resonances at \(\hat{\varOmega }=1.81\) for 4:1, \(\hat{\varOmega }=2.18\) for 3:1, \(\hat{\varOmega }=3.33\) for 2:1, \(\hat{\varOmega }=5.84\) for 3:2. Therefore, DL solution families could be related to 3:1 internal resonances, and SL periodic solutions could arise from 2:1 internal resonances. To investigate the relationship of the 3:1 internal resonance to DL families, the fold with \(\zeta =1e-5\) was continued in eccentricity as an extra continuation parameter to the drive speed. The results are presented in Fig. 8. A decrease in eccentricity, \({\hat{e}}\) from 0.353 to 0.092 made DL solution family’s left tip frequency to go down to 2.19, much closer to the 3:1 frequency of 2.18 from the Campbell diagram (Fig. 3). As the forcing is decreased, the amplitude reduces. By reducing the amplitude, the stiffening effect of amplitude is also decreased, so that the underlying frequencies that are in internal resonance move closer to their linear values. And as a result, the solution moves closer to the critical drive speed predicted using the Campbell plot (Fig. 3). In the vicinity of these points, any synchronous response would take very little disturbance to move onto and beyond the unstable part of the periodic solutions, possibly converging onto the stable limit cycle. Nonetheless, the brute force bifurcation diagrams do not show the periodic solution families at the place they are expected, because the time simulations only show \(\zeta =0.01\) data, which appear with higher amplitudes, and hence with higher nonlinearity. In the limit of zero out of balance force and zero damping, the fold reached the intersection point on the linear Campbell diagram. In fact, as forcing and damping increase, the solutions become more isolated as the fold point increases in amplitude. Even in that asymptotic condition, the stiffening with amplitude would cause these points to diverge from what is expected from the Campbell diagram.
Validation of single-loop orbits with \(\zeta =0.01\) from AUTO and MATLAB. The bottom row shows the trajectory history (from left to right) during the transition from UPO to SPO at \(\hat{\varOmega }=3.47\). The green squares are stroboscopic Poincare sampling of the data at the rotor speed. Floquet multipliers indicate the stability. (Color figure online)
Validation of single-loop orbits with \(\zeta =0.01\) from AUTO and MATLAB. The bottom row shows the trajectory history (from left to right) during the transition from UPO to SPO at \(\hat{\varOmega }=3.47\). The green squares are stroboscopic Poincare sampling of the data at the rotor speed. Floquet multipliers indicate the stability. (Color figure online)
These results compare to those of contact nonlinearity studies. For example, in Ref. [35] on a similar 2-dof model with piecewise-linear stiffness contact model, the periodic solutions were observed to start in a similar range after \(\hat{\varOmega }=3.5\), with similar amplitudes for a 2:1 internal resonance. Zilli et al. [39] also observed the intermittent contact motions after \(\hat{\varOmega }=3.4\).
No asynchronous response under contacting level amplitude can be seen in the studies that model a clearance as the underlying system is linear. However, the cubic stiffness model here removes this limit and bridges the gap between the synchronous and asynchronous responses. This possibly reveals the transition from synchronous to asynchronous response, as discussed above. As a result, the stiffening effect that is seen in the contact-featuring studies is available at all amplitudes in the cubic stiffness continuous stiffness model.
The present isotropic cubic stiffness model did not produce period doubling in the continuation runs, which is an identified route to chaos in systems with stiffness asymmetry [18, 37]. Asymmetry due to gravity also resulted in the chaos in [6]. Li and Païdoussis [21] reported the quasi-periodic route to chaos in the presence of rubbing friction, which is not a part of the model in this study, although we observe quasi-periodicity. These indicate that the isotropic cubic stiffness model used here does not present a way to explain the chaotic behaviour. Thus, the numerical simulations with various initial conditions did not result in chaos. However, a homotopy parameter can be used to include the friction, gravity, contact (e.g. via hyperbolic tangent functions), making the cubic stiffness a base to explore these responses.
Contrary to the systems with impact definitions in the contact [8, 23], the smoothness of the trajectories of the cubic stiffness model is not broken. Also the effect of contact dissipation cannot be seen in the present model, on which Shaw et al. [34] noted that stiffer, dissipative contact definitions eliminated most of the sustained intermittent bouncing cycles.
5.2 Time simulations
5.2.1 Constant initial condition
The simulations with constant initial conditions in the entire rotor speed range yielded different bifurcation diagrams. The 12 thread CPU parallelisation decreased the simulation time by 5 times. Figure 9 shows the response of the system to the initial conditions [0.0; 0.6; \(-1.246\); 0.0] in angular coordinates (physical coordinates). Asynchronous solutions appear quasi-periodic in the stationary frame and periodic in the rotating frame. It can be noted here that the quasi-periodic solutions disappear at higher drive speeds, while easily achieved in the 3.5–5.0 region.
The double-loop orbits were only discovered as the initial condition was increased in amplitude (Fig. 9a and b), With the greater initial energy due to higher magnitude position and/or speed, the orbits settle more readily onto the asynchronous orbits, which were recorded in the transient study in Ref. [39].
In order to extract the most significant features of the complete bifurcation plot, a number of random initial conditions in the order of 100 was selectively merged and is illustrated in Fig. 10a. The stable synchronous high- and low-amplitude solution families, as well as two distinct asynchronous solution families can be identified. The difficulty of finding the double-loop orbits was noted in the process.
5.2.2 Sweep
Figure 10b shows the forward and backward sweep test results as a bifurcation diagram for both synchronous and asynchronous responses. Once the different solution families are identified with constant initial condition simulations (Fig. 10a), it is more likely for sweep tests to discover a given family of solutions (Fig. 10b). Also note that in backward sweep and periodic solution sweep tests, the unstable parts of the solution families are not seen, which are clearly visible in the AUTO numerical continuation results.
In the sweep tests, the next increment in the same family of solutions converges with less transient motion, thereby making the extraction of system response quicker than each time simulation in the case of constant initial condition simulations. However, the advantage of multi-core processors cannot be utilised because in sweep test the last point of the trajectory of the previous step is required in the next step. Nonetheless, in terms of computational speed, time simulations cannot compare to numerical continuations: for example, the computation of Fig. 5 took under 10 min, while time for the simulations easily reached an hour.
With these constant initial condition and sweep test results, it is clear that the numerical continuation is computationally more efficient and reveals more of the system response characteristics.
5.2.3 MATLAB: AUTO validation
The single-loop orbits were compared to those of AUTO for validation of both simulations and the continuation with each other. An unstable single-loop periodic orbit at \(\hat{\varOmega }=3.47\) with \(\zeta =0.01\), was given to MATLAB as initial condition for ode45 simulations. Results are illustrated in Fig. 11. The trajectory in the ode45 simulations stayed on the unstable periodic orbit (UPO) for the first few cycles, then diverged from this unstable periodic orbit to converge onto the stable periodic orbit (SPO). This diverging speed is much higher for the higher amplitude case (Fig. 12), where also the greater rotation of the orbit is visible. A close match was obtained between the two solution methods with respect to the stable and unstable orbits. As seen in Figs. 11 and 12, the absolute value of one Floquet multiplier is greater than unity for the unstable orbits.
6 Conclusion
This study considered the responses of an overhung rotor with an isotropic cubic stiffness. Direct application of continuation method on the equations of motion was set up and validated with time simulations. The following conclusions were drawn:
-
1.
It was shown in the present work that the previously reported bouncing cycle phenomenon for the models of hard impact and compliant snubbing rings can also be observed with a geometric nonlinearity of cubic stiffness replacing contact interaction definitions.
-
2.
If a discontinuous stiffness was defined, then the bouncing cycles would not be present under the clearance level amplitude, due to the rotor not experiencing nonlinearity below this level. On the contrary, nonlinearity is present in all amplitude levels for the cubic nonlinearity; thus, the bouncing cycle amplitudes could get very close to the synchronous solutions.
-
3.
Depending on the level of damping, the periodic orbit region can expand and shrink. Especially for higher \(\zeta \) damping ratio values, the periodic orbits’ region vanishes from the nondimensionalised rotor speed region of interest.
-
4.
As damping tends to zero, the lower limit of drive speeds that see these responses tends towards the critical speed predicted with linear frequencies in the natural frequency map. Decreasing the eccentricity level (or out of balance mass) makes this match closer.
-
5.
As damping tends towards zero, the periodic solution family approaches the synchronous orbit. It might be inferred that the gap closes asymptotically as \(\zeta \) and oscillation amplitude approaches zero.
-
6.
This indicates that this region requires very little to no disturbance to jump to the periodic orbits because of the closeness of the unstable side of periodic solutions to the stable synchronous solutions.
-
7.
As the results were compared to the previous studies featuring nonsmooth contact models, the synchronous solution jump, and the nondimensional rotor speed where periodic solutions first appeared were reproduced with the cubic stiffness model adopted here.
The application of numerical continuation theory directly to the system equations proved practical and accurate in this study when compared to the brute force bifurcation diagrams. The type of low order model studied, with a simple smooth stiffening nonlinearity, is also relevant to many rotating machines with flexible shafts, that may exhibit bend stretch coupling, or overhung rotors that may show nonlinear displacements in the case of large out of balance force.
In future work, we are looking to extend the work to consider smooth approximations to contact phenomena that are seen in wide range of industrial applications, particularly where bearings are present. A further aim is to explore systems with multiple degrees of freedom. If these aims can be achieved, numerical continuation will be proven as a highly efficient tool for exploring complex phenomena in industrial rotating machinery.
References
Adiletta, G., Guido, A.R., Rossi, C.: Chaotic motions of a rigid rotor in short journal bearings. Nonlinear Dyn. 10(3), 251–269 (1996). https://doi.org/10.1007/BF00045106
Ahmad, S.: Rotor casing contact phenomenon in rotor dynamics-literature survey. J. Vib. Control 16(9), 1369–1377 (2010). https://doi.org/10.1177/1077546309341605
AlZibdeh, A., AlQaradawi, M., Balachandran, B.: Effects of high frequency drive speed modulation on rotor with continuous stator contact. Int. J. Mech. Sci. 131–132(June), 559–571 (2017). https://doi.org/10.1016/j.ijmecsci.2017.08.004
de Castro, H.F., Cavalca, K.L., Nordmann, R.: Whirl and whip instabilities in rotor-bearing system considering a nonlinear force model. J. Sound Vib. 317(1–2), 273–293 (2008). https://doi.org/10.1016/j.jsv.2008.02.047
Chipato, E., Shaw, A.D., Friswell, M.I.: Effect of gravity-induced asymmetry on the nonlinear vibration of an overhung rotor. Commun. Nonlinear Sci. Numer. Simul. 62, 78–89 (2018). https://doi.org/10.1016/j.cnsns.2018.02.016
Chipato, E., Shaw, A.D., Friswell, M.I.: Frictional effects on the nonlinear dynamics of an overhung rotor. Commun. Nonlinear Sci. Numer. Simul. 78, 104875 (2019). https://doi.org/10.1016/j.cnsns.2019.104875
Chu, F., Lu, W.: Stiffening effect of the rotor during the rotor-to-stator rub in a rotating machine. J. Sound Vib. (2007). https://doi.org/10.1016/j.jsv.2007.03.059
Cole, M.O., Keogh, P.S.: Asynchronous periodic contact modes for rotor vibration within an annular clearance. Proc. Inst. Mech. Eng. Part C: J. Mech. Eng. Sci. 217(10), 1101–1116 (2003). https://doi.org/10.1243/095440603322517126
Doedel, E.J., Oldeman, B.E.: AUTO-07P: Continuation and Bifurcation Software for Ordinary Differential Equations. Concordia University and McGill HPC Centre (2019)
Ehrich, F.F.: Observations of nonlinear phenomena in rotordynamics. J. Syst. Des. Dyn. 2(3), 641–651 (2008). https://doi.org/10.1299/jsdd.2.641
Fairgrieve, T., Jepson, A.D., Floquet, O.K.: Multipliers. SIAM J. Numer. Anal. 28(5), 1446–1462 (1991)
Feng, Z.C., Zhang, X.Z.: Rubbing phenomena in rotor–stator contact. Am. Soc. Mech. Eng. Appl. Mech. Div. 241, 81–88 (2000). https://doi.org/10.1016/S0960-0779(01)00231-4
Friswell, M.I., Penny, J.E., Garvey, S.D., Lees, A.W.: Dynamics of Rotating Machines. Cambridge University Press, Cambridge (2010). https://doi.org/10.1017/cbo9780511780509
Ishida, Y., Nagasaka, I., Inoue, T., Lee, S.: Forced oscillations of a vertical continuous rotor with geometric nonlinearity. Nonlinear Dyn. (1996). https://doi.org/10.1007/BF00044997
Ishida, Y., Nagasaka, I., Inoue, T., Lee, S.W.: Forced oscillations of a continuous rotor with nonlinear spring characteristics (vertical shaft with geometric nonlinearity). Trans. Jpn. Soc. Mech. Eng. Ser. C (1994). https://doi.org/10.1299/kikaic.60.2684
Ishida, Y., Yamamoto, T.: Linear and Nonlinear Rotordynamics: A Modern Treatment with Applications, 2nd edn. Wiley, Hoboken (2012). https://doi.org/10.1002/9783527651894
Jacquet-Richardet, G., Torkhani, M., Cartraud, P., Thouverez, F., Nouri Baranger, T., Herran, M., Gibert, C., Baguet, S., Almeida, P., Peletan, L.: Rotor to stator contacts in turbomachines: review and application. Mech. Syst. Signal Process. 40(2), 401–420 (2013). https://doi.org/10.1016/j.ymssp.2013.05.010
Karpenko, E.V., Wiercigroch, M., Cartmell, M.P.: Regular and chaotic dynamics of a discontinuously nonlinear rotor system. Chaos Solitons Fractals 13(6), 1231–1242 (2002). https://doi.org/10.1016/S0960-0779(01)00126-6
Karpenko, E.V., Wiercigroch, M., Pavlovskaia, E.E., Cartmell, M.P.: Piecewise approximate analytical solutions for a Jeffcott rotor with a snubber ring. Int. J. Mech. Sci. 44(3), 475–488 (2002). https://doi.org/10.1016/S0020-7403(01)00108-4
Karpenko, E.V., Wiercigroch, M., Pavlovskaia, E.E., Neilson, R.D.: Experimental verification of Jeffcott rotor model with preloaded snubber ring. J. Sound Vib. 298(4–5), 907–917 (2006). https://doi.org/10.1016/j.jsv.2006.05.044
Li, G., Païdoussis, M.: Impact phenomena of rotor-casing dynamical systems. Nonlinear Dyn. 5(1), 53–70 (1994). https://doi.org/10.1007/BF00045080
MATLAB: Version 9.8.0 (R2020a) (2020)
Mora, K., Champneys, A.R., Shaw, A.D., Friswell, M.I.: Explanation of the onset of bouncing cycles in isotropic rotor dynamics; a grazing bifurcation analysis. Proc. R. Soc. A: Math. Phys. Eng. Sci. 476(2237), 20190549 (2020). https://doi.org/10.1098/rspa.2019.0549
Muszynska, A.: Rotordynamics. Taylor & Francis, Boca Raton (2005). https://doi.org/10.4324/9781315235097
Nagasaka, I., Ishida, Y., Liu, J.: Forced oscillations of a continuous asymmetrical rotor with geometric nonlinearity (Major critical speed and secondary critical speed). J. Vib. Acoust. Trans. ASME 130(3), 1–7 (2008). https://doi.org/10.1115/1.2890734
Nagasaka, I., Liu, J., Ishida, Y., Katou, K.: Forced oscillations of a continuous rotor with strong geometric nonlinearity (separation of resonance point by effect of gravity and axial force). Nippon Kikai Gakkai Ronbunshu, C Hen/Trans. Jpn. Soc. Mech. Eng. Part C (2002). https://doi.org/10.1299/kikaic.68.3268
Pavlovskaia, E.E., Karpenko, E.V., Wiercigroch, M.: Non-linear dynamic interactions of a Jeffcott rotor with preloaded snubber ring. J. Sound Vib. 276(1–2), 361–379 (2004). https://doi.org/10.1016/j.jsv.2003.07.033
Peletan, L., Baguet, S., Torkhani, M., Jacquet-Richardet, G.: A comparison of stability computational methods for periodic solution of nonlinear problems with application to rotordynamics. Nonlinear Dyn. 72(3), 671–682 (2013). https://doi.org/10.1007/s11071-012-0744-0
Peletan, L., Baguet, S., Torkhani, M., Jacquet-Richardet, G.: Quasi-periodic harmonic balance method for rubbing self-induced vibrations in rotor–stator dynamics. Nonlinear Dyn. 78(4), 2501–2515 (2014). https://doi.org/10.1007/s11071-014-1606-8
Peletan, L., Baguet, S., Jacquet-Richardet, G., Torkhani, M.: Use and limitations of the harmonic balance method for rub-impact phenomena in rotor-stator dynamics. In: Proceedings of the ASME Turbo Expo, Vol. 7(PARTS A AND B), pp. 647–655 (2012). https://doi.org/10.1115/GT2012-69450
Saldivar, B., Boussaada, I., Mounier, H., Mondié, S., Niculescu, S.I.: An overview on the modeling of oilwell drilling vibrations. In: IFAC Proceedings Volumes (IFAC-PapersOnline) (2014). https://doi.org/10.3182/20140824-6-za-1003.00478
Salles, L., Staples, B., Hoffmann, N., Schwingshackl, C.: Continuation techniques for analysis of whole Aeroengine dynamics with imperfect bifurcations and isolated solutions. Nonlinear Dyn. 86(3), 1897–1911 (2016). https://doi.org/10.1007/s11071-016-3003-y
Seydel, R.: From Equilibrium to Chaos. Elsevier, New York (1988)
Shaw, A.D., Champneys, A.R., Friswell, M.I.: Asynchronous partial contact motion due to internal resonance in multiple degree-of-freedom rotordynamics. Proc. R. Soc. Math. Phys. Eng. Sci. 472(2192), 20160303 (2016). https://doi.org/10.1098/rspa.2016.0303
Shaw, A.D., Champneys, A.R., Friswell, M.I.: Normal form analysis of bouncing cycles in isotropic rotor stator contact problems. Int. J. Mech. Sci. 155(2018), 83–97 (2019). https://doi.org/10.1016/j.ijmecsci.2019.02.035
Stroud, D.R., Lines, L.A., Minett-Smith, D.J.: Analytical and experimental backward whirl simulations for rotary steerable bottom hole assemblies. In: SPE/IADC Drilling Conference, Proceedings (2011). https://doi.org/10.2118/140011-ms
Varney, P., Green, I.: Nonlinear phenomena, bifurcations, and routes to chaos in an asymmetrically supported rotor–stator contact system. J. Sound Vib. 336, 207–226 (2015). https://doi.org/10.1016/j.jsv.2014.10.016
Von Groll, G., Ewins, D.J.: The harmonic balance method with arc-length continuation in rotor/stator contact problems. J. Sound Vib. 241(2), 223–233 (2001). https://doi.org/10.1006/jsvi.2000.3298
Zilli, A., Williams, R.J., Ewins, D.J.: Nonlinear dynamics of a simplified model of an overhung rotor subjected to intermittent annular rubs. J. Eng. Gas Turbine Power 137(6), 1–10 (2015). https://doi.org/10.1115/1.4028844
Acknowledgements
This research was funded by the Ministry of National Education of the Republic of Turkey.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Code availability
The code used in this research is available through the Zenodo DOI link https://doi.org/10.5281/zenodo.4586405.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendices
1.1 A1: Constants file
The constants file that is used in AUTO set-up is where the user mainly specifies,
-
type of solution (IPS=1 for stationary, IPS=2 for periodic),
-
the continuation parameters (ICP list, e.g. rotational speed, damping),
-
tolerances of convergence conditions (EPSL, EPSU, EPSS),
-
minimum, maximum, and starting step sizes (DSMIN, DSMAX, DS)
-
number of Newton–Chord iterations (ITNW, NWTN) to be performed before re-attempt of solution,
-
mesh discretisation (NTST) for accuracy control
-
user requested data points (UZR)
-
stopping conditions for continuation (STOP, UZSTOP, NMX) or parameter lower and upper limits (RL0, RL1).
It is suggested [9] that the mesh interval count should be as low as possible for convergence. A tolerance of convergence (EPSL, EPSU) of 1e\(-\)6 to 1e\(-\)7 is recommended, and a special solution (such as branch points) an accuracy (EPSS) of 1e2–1e3 times the tolerance of convergence is advised. These limits were kept in all continuation runs of this study. The constants-file content that is used to start the synchronous AUTO runs is given below:
-
unames\(\mathrm {=1: ``u'', 2: ``v'',3:`` u\_dot'' , 4:``v\_dot''}\)
-
parnames\(\mathrm {=1:``gamma'',2:``Omeg'',3:``mH'',4:}\mathrm {``JpH'',5:``epsH'',}\)
-
\(\mathrm {6:``zeta'',7:``OmegP'',9:``Amplitude''}\)
-
NDIM= 4, IPS = 1, ICP = [3,9], IPLT= 9, IRS = 0, ILP = 1,
-
ISW = 1, ISP = 2, UZSTOP = 3:0.9
-
NTST= 200, DS = 0.005, DSMIN= 1e-4, DSMAX= 0.05,
-
IADS= 1, EPSL= 1e-06, EPSU = 1e-06, EPSS =1e-4,
-
NMX = 10000, ITMX= 8, ITNW= 7, NWTN= 5
-
NCOL= 4, IAD = 3
-
NBC = 0, NINT= 0
-
NPR = 1000, IID = 3
-
MXBF= 5, JAC = 0, NPAR= 36, THU = {}, THL = {}
Particularly, ICP, NTST, NMX, EPSL, EPSU, EPSS, DS, DSMIN, DSMAX, UZSTOP, RL0, RL1 were checked specifically for each run, with some level of experimentation for better accuracy and convergence [9].
1.2 A2: Auto-data file generation
Synchronous solution initial conditions are given in Table 2.
Table 2 also shows the simulation duration in nondimensional time \(\tau _{\mathrm{end}}\) for both synchronous and asynchronous responses. After a simulation completed, the converged orbit’s data of time versus all four states were stored in a tab-separated .dat file [9] to be used as starting data in AUTO.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Akay, M.S., Shaw, A.D. & Friswell, M.I. Continuation analysis of a nonlinear rotor system. Nonlinear Dyn 105, 25–43 (2021). https://doi.org/10.1007/s11071-021-06589-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-021-06589-8