Perturbation incremental method of limit cycle for a nonlinear conveyor belt system

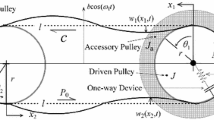
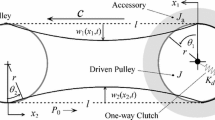
Abstract

In this paper, we study the limit cycle of a nonlinear conveyor belt system by utilizing the perturbation incremental method. We first divide the system into two subclasses. On account of the former is heteroclinic orbit and the latter is not, there are some differences in the process of employing this method. Next two steps are introduced, the perturbation part provides the zero-order perturbation solution and takes it as the initial value of the incremental part, and in the incremental part, the corresponding limit cycle is obtained by controlling the value of the parameter $\lambda$. Under this circumstance, approximate analytical expressions of limit cycles of those classes are found. Then, numerical simulations are presented to prove the effectiveness of the results by comparison with numerical integration using the fourth-order Runge–Kutta method. Finally, some conclusions and expectations are given.

Appendices

Appendix A

$$\begin{aligned}&\bigg (\frac{\partial V}{\partial a}\bigg )_0= \sum \limits _{k=1}^M\alpha _{2k} cos (2k\varphi ),\\&H(a_0,\Phi _0,\varphi )= \sum \limits _{k=1}^M(\gamma _{1,2k} cos(2k\varphi )+\delta _{1,2k}sin(2k\varphi )),\\&\bigg (\frac{\partial H}{\partial a}\bigg )_0= \sum \limits _{k=1}^M(\gamma _{2,2k} cos(2k\varphi )+\delta _{2,2k}sin(2k\varphi )),\\&\bigg (\frac{\partial H}{\partial \Phi }\bigg )_0= \sum \limits _{k=1}^M(\gamma _{3,2k} cos(2k\varphi )+\delta _{3,2k}sin(2k\varphi )),\\&\Phi _0 sin^2\varphi =\sum \limits _{k=1}^M(\zeta _{1,2k} cos(2k\varphi )+\eta _{1,2k}sin(2k\varphi )),\\&\frac{1}{2} (\Phi _0 sin\varphi )^2+V(a_0,\varphi )\\&\quad =\sum \limits _{k=1}^M(\zeta _{2,2k} cos(2k\varphi )+\eta _{2,2k}sin(2k\varphi )). \end{aligned}$$

Appendix B

$$\begin{aligned}&A_{0}=\alpha _{0}-\lambda \sum \limits _{k=1}^M \frac{1}{k}\delta _{2,k},\\&A_{2i}=\alpha _{i}+\lambda \frac{1}{2i}\delta _{2,2i},\\&A_{2(M+i-1)}=-\lambda \frac{1}{2i}\gamma _{2,2i},\\&A_{2(2M-1)}=\sum \limits _{k=1}^M (-1)^{k}\alpha _{k}-\lambda \sum \limits _{k=1}^M \frac{1}{k}[1-(-1)^{k}] \delta _{2,k},\\&A_{4M}=\gamma _{2,0},\\&A_{0,2j}=\frac{1}{2}(\zeta _{1,-2j}+\zeta _{1,2j})-\frac{1}{2}\lambda \\&\quad \sum \limits _{k=1}^M \frac{1}{k}(\delta _{3,2(k-j)}-\delta _{3,2(j-k)}+\delta _{3,2(j+k)}),\\&A_{2i,2j}=\frac{1}{2}(\zeta _{1,2(i-j)}+\zeta _{1,2(j-i)}+\zeta _{1,2(j+i)})\\&\quad +\frac{1}{4i}\lambda (\delta _{3,2(i-j)}-\delta _{3,2(j-i)}+\delta _{3,2(j+i)}),\\&A_{2(M+i-1),2j}=\frac{1}{2}(\eta _{1,2(i-j)}-\eta _{1,2(j-i)}+\eta _{1,2(j+i)})\\&\quad -\frac{1}{4i}\lambda (\gamma _{3,2(i-j)}+\gamma _{3,2(j-i)}+\gamma _{3,2(j+i)}),\\&A_{2(2M-1),2j}=-\frac{1}{2}\lambda \sum \limits _{k=1}^M\\&\quad \frac{[1-(-1)^{k}]}{k}(\delta _{3,2(k-j)}-\delta _{3,2(j-k)}+\delta _{3,2(j+k)}),\\&A_{4M,2j}=\frac{1}{2}(\gamma _{3,-2j}+\gamma _{3,2j}),\\&B_{0,2j}=\frac{1}{2}(\eta _{1,-2j}+\eta _{1,2j})-\frac{1}{2}\lambda \\&\quad \sum \limits _{k=1}^M \frac{1}{k}(\gamma _{3,2(k-j)}+\gamma _{3,2(j-k)}-\gamma _{3,2(j+k)}),\\&B_{2i,2j}=\frac{1}{2}(\eta _{1,2(j-i)}+\eta _{1,2(j+i)}-\eta _{1,2(i-j)})\\&\quad +\frac{1}{4i}\lambda (\gamma _{3,2(i-j)}+\gamma _{3,2(j-i)}-\gamma _{3,2(j+i)}),\\&B_{2(M+i-1),2j}=\frac{1}{2}(\zeta _{1,2(i-j)}+\zeta _{1,2(j-i)}-\zeta _{1,2(j+i)}))\\&\quad -\frac{1}{4i}\lambda (\delta _{3,2(j-i)}+\delta _{3,2(j+i)}-\delta _{3,2(i-j)}),\\&B_{2(2M-1),2j}=-\frac{1}{2}\lambda \sum \limits _{k=1}^M \frac{[1-(-1)^{k}]}{k}(\gamma _{3,2(k-j)}\\&\quad +\gamma _{3,2(j-k)}-\gamma _{3,2(j+k)}),\\&B_{4M,2j}=\frac{1}{2}(\delta _{3,2j}-\delta _{3,-2j}),\\&R_{0}=-\zeta _{2,0}+\lambda \sum \limits _{k=1}^M \frac{1}{k}\delta _{1,k},\\&R_{2i}=-\zeta _{2,2i}-\lambda \frac{1}{2i}\delta _{1,2i},\\&R_{2(M+i-1)}=-\eta _{2,2i}+\lambda \frac{1}{2i}\gamma _{1,2i},\\&R_{2(2M-1)}=-\sum \limits _{k=1}^M (-1)^{k}\zeta _{2,k}+\lambda \\&\quad \sum \limits _{k=1}^M \frac{[1-(-1)^{k}]}{k}\delta _{1,k},\\&R_{4M}=-\gamma _{1,0}, \end{aligned}$$

where

$$\begin{aligned} i=1,2,\ldots ,M-1, \ \ \ j=0,1,2,\ldots ,M-1, \end{aligned}$$

for $k<0$, $\zeta _{1,k}=\eta _{1,k}=\gamma _{3,k}=\delta _{3,k}=0$.

Appendix C

$$\begin{aligned}&\bigg (\frac{\partial V}{\partial a}\bigg )_0= \sum \limits _{k=1}^M\alpha _{k} cos k\varphi ,\\&\bigg (\frac{\partial V}{\partial b}\bigg )_0= \sum \limits _{k=1}^M\beta _{k} cos k\varphi ,\\&H(a_0,\Phi _0,\varphi )= \sum \limits _{k=1}^M(\gamma _{1,k} cos k\varphi +\delta _{1,k}sin k\varphi ),\\&\bigg (\frac{\partial H}{\partial a}\bigg )_0= \sum \limits _{k=1}^M(\gamma _{2,k} cos k\varphi +\delta _{2,k}sin k\varphi ),\\&\bigg (\frac{\partial H}{\partial b}\bigg )_0= \sum \limits _{k=1}^M(\gamma _{3,k} cos k\varphi +\delta _{3, k}sin k\varphi ),\\&\bigg (\frac{\partial H}{\partial \Phi }\bigg )_0= \sum \limits _{k=1}^M(\gamma _{4,k} cos k\varphi +\delta _{4,k}sin k\varphi ),\\&\Phi _0 sin^2\varphi =\sum \limits _{k=1}^M(\zeta _{1,k} cos k\varphi +\eta _{1,k}sin k\varphi ),\\&\frac{1}{2} (\Phi _0 sin\varphi )^2+V(a_0,\varphi )\\&\quad =\sum \limits _{k=1}^M(\zeta _{2,k} cos k\varphi +\eta _{2,k}sin k\varphi ). \end{aligned}$$

Appendix D

$$\begin{aligned}&A_{0}=\alpha _{0}-\lambda \sum \limits _{k=1}^M \frac{1}{k}\delta _{2,k},\\&A_{i}=\alpha _{i}+\lambda \frac{1}{i}\delta _{2,i},\\&A_{M+i}=-\lambda \frac{1}{i}\gamma _{2,i},\\&A_{2M+1}=\sum \limits _{k=1}^M (-1)^{k}\alpha _{k}-\lambda \sum \limits _{k=1}^M \frac{1}{k}[1-(-1)^{k}] \delta _{2,k},\\&A_{2M+2}=\gamma _{2,0},\\&B_{0}=\beta _{0}-\lambda \sum \limits _{k=1}^M \frac{1}{k}\delta _{3,k},\\&B_{i}=\beta _{i}+\lambda \frac{1}{i}\delta _{3,i},\\&B_{M+i}=-\lambda \frac{1}{i}\gamma _{3,i},\\&B_{2M+1}=\sum \limits _{k=1}^M (-1)^{k}\beta _{k}-\lambda \sum \limits _{k=1}^M \frac{1}{k}[1-(-1)^{k}] \delta _{3,k},\\&B_{2M+2}=\gamma _{3,0},\\&A_{0,j}=\frac{1}{2}(\zeta _{1,-j}+\zeta _{1,j})-\frac{1}{2}\lambda \sum \limits _{k=1}^M\\&\quad \frac{1}{k}(\delta _{4,k-j}-\delta _{4,j-k}+\delta _{4,j+k}),\\&A_{i,j}=\frac{1}{2}(\zeta _{1,i-j}+\zeta _{1,j-i}+\zeta _{1,j+i})\\&\quad +\frac{1}{2i}\lambda (\delta _{4,i-j}-\delta _{4,j-i}+\delta _{4,j+i}),\\&A_{M+i,j}=\frac{1}{2}(\eta _{1,i-j}-\eta _{1,j-i}+\eta _{1,j+i})\\&\quad -\frac{1}{2i}\lambda (\gamma _{4,i-j}+\gamma _{4,j-i}+\gamma _{4,j+i}),\\&A_{2M+1,j}=-\frac{1}{2}\lambda \sum \limits _{k=1}^M\\&\quad \frac{[1-(-1)^{k}]}{k}(\delta _{4,k-j}-\delta _{4,j-k}+\delta _{4,j+k}),\\&A_{2M+2,j}=\frac{1}{2}(\gamma _{4,-j}+\gamma _{4,j}),\\&B_{0,j}=\frac{1}{2}(\eta _{1,-j}+\eta _{1,j})-\frac{1}{2}\lambda \sum \limits _{k=1}^M\\&\quad \frac{1}{k}(\gamma _{4,k-j}+\gamma _{4,j-k}-\gamma _{4,j+k}),\\&B_{i,j}=\frac{1}{2}(\eta _{1,j-i}+\eta _{1,j+i}-\eta _{1,i-j})\\&\quad +\frac{1}{2i}\lambda (r_{4,i-j}+r_{4,j-i}-r_{4,j+i}),\\&B_{M+i,j}=\frac{1}{2}(\zeta _{1,i-j}+\zeta _{1,j-i}-\zeta _{1,j+i})\\&\quad -\frac{1}{2i}\lambda (\delta _{4,j-i}+\delta _{4,j+i}-\delta _{4,i-j}),\\&B_{2M+1,j}=-\frac{1}{2}\lambda \sum \limits _{k=1}^M \frac{[1-(-1)^{k}]}{k}(\gamma _{4,k-j}\\&\quad +\gamma _{4,j-k}-\gamma _{4,j+k}),\\&B_{2M+2,j}=\frac{1}{2}(\delta _{4,j}-\delta _{4,-j}),\\&R_{0}=-\zeta _{2,0}+\lambda \sum \limits _{k=1}^M \frac{1}{k}\delta _{1,k},\\&R_{i}=-\zeta _{2,i}-\lambda \frac{1}{i}\delta _{1,i},\\&R_{M+i}=-\eta _{2,i}+\lambda \frac{1}{i}\gamma _{1,i},\\&R_{2M+1}=-\sum \limits _{k=1}^M (-1)^{k}\zeta _{2,k}\\&\quad +\lambda \sum \limits _{k=1}^M \frac{[1-(-1)^{k}]}{k}\delta _{1,k},\\&R_{2M+2}=-\gamma _{1,0}, \end{aligned}$$

where

$$\begin{aligned} i=1,2,\ldots ,M, \ \ \ j=0,1,2,\ldots ,M, \end{aligned}$$

for $k<0$, $\zeta _{1,k}=\eta _{1,k}=r_{4,k}=\delta _{4,k}=0$.