1 Introduction

Several methodologies are available to formulate the equations of motion of constrained mechanical systems. When combined with notational differences and a wide range of terminology, this variety can be bewildering for students, researchers, and instructors alike. As summarized in the survey [31], these formulations include (but are not limited to) the Newton–Euler balance laws, Lagrange’s equations of motion, Maggi’s equations of motion, Gibbs–Appell equations of motion, Kane’s equation of motion, and the Boltzmann–Hamel equations of motion.

One framework that can help to relate the formulations is to exploit an idea championed by Hertz [18] and imagine a representative particle moving on a configuration manifold \({\mathcal {M}}\) that is embedded in a high-dimensional Euclidean space. While the representative particle has been exploited by Synge [36] and used by Lesser [21] and Essén [13] to explore the geometry of Kane’s equations, explicit constructions of the representative particle for a system of particles and a single rigid body were only recently developed by Casey [10, 11]. In the paper [12], this construction was then extended to constrained systems comprised of particles and rigid bodies.

Fig. 1
figure 1

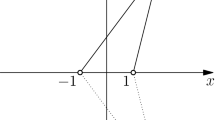
A system of two particles that is used as a model for Chaplygin sleigh. The unit vector \(\mathbf{e}_1\) points from \(m_1\) to \(m_2\) and can be defined by an angle \(\vartheta \): \(\mathbf{e}_1 = \cos \left( \vartheta \right) \mathbf{E}_1 + \sin \left( \vartheta \right) \mathbf{E}_2\). A unit vector \(\mathbf{e}_2 = \cos \left( \vartheta \right) \mathbf{E}_2 - \sin \left( \vartheta \right) \mathbf{E}_1\) can be defined where \(\dot{\mathbf{e}}_1 = {\dot{\vartheta }} \mathbf{e}_2\)

Full size image

In the present paper, the representative particle is constructed for a system of two particles. The dynamics of the system is then represented by a single particle of mass m that is constrained to move on a manifold \({\mathcal {M}} \subset {\mathbb {E}}^6\). This construction is used to show that the equations of motion can be considered as particular linear combinations of the balance laws \(\mathbf{F}_1 = m_1 \dot{\mathbf{v}}_1\) and \(\mathbf{F}_2 = m_2 \dot{\mathbf{v}}_2\) in partnership with judicious choices of coordinates, inspired use of the derivatives of the kinetic energy function, and, possibly, a Gibbs-Appell function S.

Referring to Fig. 1, we start by considering the simplest possible non-holonomically constrained mechanical system. This system consists of two particles connected by a massless rod of length \(\ell \) that is free to move on a smooth horizontal surface. The second particle is subject to a non-holonomic constraint: \(\mathbf{v}_2\cdot \mathbf{e}_2 = 0\). This system can be considered as a simple realization of Chaplygin’s sleigh [4, 37] or a skate [9]; two classic examples that have been discussed in numerous texts and papers (e.g., [7, 15, 16, 25, 26, 34] and [3, 29]). The configuration manifold \({\mathcal {M}} = {\mathbb {E}}^2\oplus S^1\) for the system of particles can be embedded in \({\mathbb {E}}^4\) but not in \({\mathbb {E}}^3\) (see Fig. 2). Six formulations of the equations of motion for this system are presented: Newton–Euler, Lagrange, Maggi, Gibbs–Appell, Kane, and Boltzmann–Hamel.

To explore the connections between these formulations, a single representative particle is then constructed in Sects. 3–6. Explicit expressions for the forces acting on the single particle and tangent vectors to \({\mathcal {M}}\) are developed. These expressions are then used in Sect. 7 to show the interrelationships between the five formulations and the balances of linear momenta \(\mathbf{F}_1 = m_1 \dot{\mathbf{v}}_1\) and \(\mathbf{F}_2 = m_2 \dot{\mathbf{v}}_2\) for the system of particles. By explicitly constructing two sets of bases vectors for the tangent space \(T_P{\mathcal {M}}\) at a point \(P \in {\mathcal {M}}\), we are able to demonstrate the advantages of using quasi-velocities and their associated basis vectors when non-holonomic constraints are present (cf. Eqs. (7.11) and (7.12)).

Fig. 2
figure 2

Schematic of the configuration manifold \({\mathcal {M}} = {\mathbb {E}}^2\oplus S^1\) for the system of particles. Each position and orientation of the system of particles corresponds to a unique point on \({\mathcal {M}}\)

Full size image

Given the classic nature of the subject and a recent resurgence of interest in the dynamics of non-holonomic systems [7, 20, 34], our expository work has overlap with the works of several authors. These works include, but are not limited to, Storch and Gates [35] who show that Kane’s equations are linear combinations (or projections) of balances of linear momenta, and Blajer [6], Essén [13], Lesser [21], and Soltakhanov et al. [34] who explored related developments using a representative particle. Our paper complements these works by presenting a considerable amount of additional detail on the representative particle and exploring these developments with the aid of the simplest non-holonomically constrained mechanical system. We are assisted greatly in this endeavor by the construction presented by Casey [10] supplemented by the treatment of constraint forces in [27]. While the works [11, 12] can be used to explore equations of motion for more complex mechanical systems, many of the relationships between different formulations of the resulting equations of motion can be captured using the simple system of two particles presented in this paper.

The electronic supplementary material for this paper is a short video showing a summary of the paper and animations of the motions of the systems of particles.

2 Six formulations of the equations of motion for the system of particles

Consider the system of two particles shown in Fig.  1. To determine the equations of motion, we can parameterize the motion of \(m_1\) using a Cartesian coordinate system and the motion of \(m_2\) relative to \(m_1\) using an angle \(\vartheta \) and an associated unit vector \(\mathbf{e}_1\):

$$\begin{aligned} \begin{aligned}&\mathbf{r}_1 = x \mathbf{E}_1 + y\mathbf{E}_2, \qquad \mathbf{r}_2 = \mathbf{r}_1 + \ell \mathbf{e}_1,\\&\mathbf{v}_1 = {\dot{x}} \mathbf{E}_1 + {\dot{y}}{} \mathbf{E}_2, \qquad \mathbf{v}_2 = \mathbf{v}_1 + \ell {\dot{\vartheta }} \mathbf{e}_2. \end{aligned} \end{aligned}$$
(2.1)

Here, \(\left\{ \mathbf{E}_1, \mathbf{E}_2, \mathbf{E}_3 = \mathbf{E}_1\times \mathbf{E}_2\right\} \) is a Cartesian basis for \({\mathbb {E}}^3\) and planar motions of the system have been assumed.

The motion of \(m_2\) is such that its velocity vector \(\mathbf{v}_2\) must be parallel to the rod connecting \(m_1\) and \(m_2\). This constraint can be expressed in the compact form

$$\begin{aligned} \mathbf{e}_2 \cdot \mathbf{v}_2 = 0. \end{aligned}$$
(2.2)

As discussed in the texts [27, 32], this constraint is the simplest possible non-integrable (non-holonomic) constraint. In addition to gravitational, tension, and normal reaction forces acting on \(m_1\) and \(m_2\), a constraint force \(\mu \mathbf{e}_2\) acts on \(m_2\) to enforce the velocity constraint:

$$\begin{aligned} \begin{aligned}&\mathbf{F}_1 = p \mathbf{e}_1 + \left( N_1 - m_1 g\right) \mathbf{E}_3,\\&\mathbf{F}_2 = - p \mathbf{e}_1 + \left( N_2 - m_2 g\right) \mathbf{E}_3 + \mu \mathbf{e}_2. \end{aligned} \end{aligned}$$
(2.3)

The generalized coordinates for the system are \(q^1 = x\), \(q^2 = y\), and \(q^3 = \vartheta \). The kinetic energy \({\tilde{T}}\) of the system of particles is

$$\begin{aligned} \begin{aligned} {\tilde{T}}&= \frac{m_1 + m_2}{2} \left( {\dot{x}}^2 + {\dot{y}}^2\right) + \frac{m_2 \ell ^2}{2} {\dot{\vartheta }}^2\\&+ m_2 \ell \left( {\dot{y}}{\dot{\vartheta }} \cos \left( \vartheta \right) - {\dot{x}}{\dot{\vartheta }} \sin \left( \vartheta \right) \right) . \end{aligned} \end{aligned}$$
(2.4)

For any motion of this system of particles, the kinetic energy will be conserved.

Another formulation, one that uses quasi-velocities (or generalized speeds), \(u^K\), can be used. We choose these quantities so that the constraint \(\mathbf{v}_2\cdot \mathbf{e}_2 = 0\) can be expressed in terms of a single kinematical quantity (\(u^3 = 0\)):

$$\begin{aligned} \begin{aligned} u^1&= \mathbf{v}_1 \cdot \mathbf{e}_1 = {\dot{x}}\cos \left( \vartheta \right) + {\dot{y}}\sin \left( \vartheta \right) ,\\ u^2&= {\dot{\vartheta }},\\ u^3&= \mathbf{v}_2 \cdot \mathbf{e}_2 = \ell {\dot{\vartheta }} - {\dot{x}}\sin \left( \vartheta \right) + {\dot{y}} \cos \left( \vartheta \right) . \end{aligned} \end{aligned}$$
(2.5)

With the help of the inverse relations

$$\begin{aligned} \left[ \begin{array}{c} {\dot{x}} \\ {\dot{y}} \\ {\dot{\vartheta }} \end{array}\right] = {\mathsf {H}}_1\left[ \begin{array}{c} u^1 \\ u^2 \\ u^3 \end{array}\right] , \end{aligned}$$
(2.6)

where

$$\begin{aligned} {\mathsf {H}}_1 = \left[ \begin{array}{c c c} \cos \left( \vartheta \right) &{} \ell \sin \left( \vartheta \right) &{} - \sin \left( \vartheta \right) \\ \sin \left( \vartheta \right) &{} - \ell \cos \left( \vartheta \right) &{} \cos \left( \vartheta \right) \\ 0 &{} 1 &{} 0 \end{array}\right] , \end{aligned}$$
(2.7)

we find that \(\mathbf{v}_1 = u_1 \mathbf{e}_1 + \left( u_3 - \ell u_2\right) \mathbf{e}_2\) and \(\mathbf{v}_2 = u_1 \mathbf{e}_1 + u_3 \mathbf{e}_2\). These relations enable us to change variables from \(\left( q^k, {\dot{q}}^i\right) \) to \(\left( q^k, u^i\right) \) in the representation (2.4) for T.

Following Maggi [23], a pair of kinetic characteristics are defined:

$$\begin{aligned} e^1 = u^1, \qquad e^2 = u^2. \end{aligned}$$
(2.8)

Thus,

$$\begin{aligned} \left[ \begin{array}{c} {\dot{x}} \\ {\dot{y}} \\ {\dot{\vartheta }} \end{array}\right] = {\mathsf {E}}_1 \left[ \begin{array}{c} e^1 \\ e^2 \end{array}\right] , \quad {\mathsf {E}}_1 = \left[ \begin{array}{c c} \cos \left( \vartheta \right) &{} \ell \sin \left( \vartheta \right) \\ \sin \left( \vartheta \right) &{} - \ell \cos \left( \vartheta \right) \\ 0 &{} 1 \end{array}\right] .\nonumber \\ \end{aligned}$$
(2.9)

Observe that (2.9) can be obtained from (2.6) by setting \(u^3 = 0\).

2.1 A Newton–Euler formulation of the equations of motion

By taking components (projections) of the pair of balances of linear momenta,

$$\begin{aligned} m_1 \dot{\mathbf{v}}_1 = \mathbf{F}_1, \qquad m_2 \dot{\mathbf{v}}_2 = \mathbf{F}_2, \end{aligned}$$
(2.10)

with respect to \(\mathbf{E}_1\), \(\mathbf{E}_2\), and \(\mathbf{E}_3\), we will find six equations for the seven unknowns x, y, \(\vartheta \), p, \(\mu \), \(N_1\), and \(N_2\):

$$\begin{aligned} \begin{aligned}&m_1 \ddot{x} = p \cos \left( \vartheta \right) ,\\&m_1 \ddot{y} = p \sin \left( \vartheta \right) ,\\&0 = N_1 - m_1 g,\\&m_2 \frac{d}{\mathrm{d}t}\left( {\dot{x}} - \ell {\dot{\vartheta }} \sin \left( \vartheta \right) \right) = - p\cos \left( \vartheta \right) - \mu \sin \left( \vartheta \right) ,\\&m_2 \frac{d}{\mathrm{d}t}\left( {\dot{y}} + \ell {\dot{\vartheta }} \cos \left( \vartheta \right) \right) = - p\sin \left( \vartheta \right) + \mu \cos \left( \vartheta \right) ,\\&0 = N_2 - m_2 g. \end{aligned} \end{aligned}$$
(2.11)

To close the system of Eq. (2.11) is supplemented by the constraint equation \(\mathbf{e}_2\cdot \mathbf{v}_2 = 0\). The determination of the motion of the system from (2.11) is not readily apparent.

As we shall see, projections of \(\mathbf{F}_\alpha = m_\alpha \dot{\mathbf{v}}_\alpha \) other than onto \(\mathbf{E}_1\), \(\mathbf{E}_2\), and \(\mathbf{E}_3\) are more fruitful. These projections, combined with taking linear combinations of the projections, and judiciously choosing coordinates and speeds, result in the five other formulations that we will now present.

2.2 Lagrange’s equations of motion

The equations of motion can be computed from the following form of Lagrange’s equations of motion:

$$\begin{aligned} \frac{d}{\mathrm{d}t}\left( \frac{\partial {\tilde{T}}}{\partial {\dot{q}}^K} \right) - \frac{\partial {\tilde{T}}}{\partial {q}^K} = Q_K, \end{aligned}$$
(2.12)

where \(K = 1,2,3\) and

$$\begin{aligned} Q_K = \mathbf{F}_1 \cdot \frac{\partial \mathbf{v}_1}{\partial {\dot{q}}^K} + \mathbf{F}_2 \cdot \frac{\partial \mathbf{v}_2}{\partial {\dot{q}}^K}. \end{aligned}$$
(2.13)

The resulting equations of motion are supplemented by the constraint \(\mathbf{v}_2\cdot \mathbf{e}_2 = 0\). Thus,

$$\begin{aligned} \begin{aligned}&\frac{d}{\mathrm{d}t}\left( \left( m_1 + m_2\right) {\dot{x}} - m_2 \ell {\dot{\vartheta }} \sin \left( \vartheta \right) \right) = - \mu \sin \left( \vartheta \right) ,\\&\frac{d}{\mathrm{d}t}\left( \left( m_1 + m_2\right) {\dot{y}} + m_2 \ell {\dot{\vartheta }} \cos \left( \vartheta \right) \right) = \mu \cos \left( \vartheta \right) ,\\&m_2 \ell ^2 \ddot{\vartheta } + m_2 \ell \left( \ddot{y} \cos \left( \vartheta \right) - \ddot{x} \sin \left( \vartheta \right) \right) = \mu \ell ,\\&\ell {\dot{\vartheta }} - {\dot{x}}\sin \left( \vartheta \right) + {\dot{y}} \cos \left( \vartheta \right) = 0, \end{aligned} \end{aligned}$$
(2.14)

form a determinate system of four equations for four unknowns (x(t), y(t), \(\vartheta (t)\), and \(\mu \)).

2.3 Maggi’s equations of motion

We observe that, unlike Eq. (2.11), the tension p and normal forces \(N_1\) and \(N_2\) are absent from Eq. (2.14). That is, the constraint forces for the integrable (holonomic) constraints have been eliminated. However, the constraint force enforcing the constraint \(\mathbf{v}_2\cdot \mathbf{e}_2 = 0\) is still present in Eq. (2.14). As a result, Eq. (2.14) cannot be readily integrated to determine the motion of the system.

Maggi’s equations of motion ( [22, Section 493] cf. [8, 23, 30]) are computed by taking linear combinations of Lagrange’s equations of motion (2.12):

$$\begin{aligned} {\mathsf {E}}^T_1 \left[ \begin{array}{c} \frac{d}{\mathrm{d}t}\left( \frac{\partial {\tilde{T}}}{\partial {\dot{x}}} \right) - \frac{\partial {\tilde{T}}}{\partial {x}} \\ \frac{d}{\mathrm{d}t}\left( \frac{\partial {\tilde{T}}}{\partial {\dot{y}}} \right) - \frac{\partial {\tilde{T}}}{\partial {y}} \\ \frac{d}{\mathrm{d}t}\left( \frac{\partial {\tilde{T}}}{\partial {\dot{\vartheta }}} \right) - \frac{\partial {\tilde{T}}}{\partial {\vartheta }} \end{array}\right] = {\mathsf {E}}^T_1 \left[ \begin{array}{c} Q_1 \\ Q_2 \\ Q_3 \end{array}\right] . \end{aligned}$$
(2.15)

The resulting pair of equations are supplemented by the constraint \(\mathbf{v}_2\cdot \mathbf{e}_2 = 0\):

$$\begin{aligned} \begin{aligned}&\ell {\dot{\vartheta }} - {\dot{x}}\sin \left( \vartheta \right) + {\dot{y}} \cos \left( \vartheta \right) = 0,\\&\left( m_1 + m_2\right) \left( \ddot{x}\cos \left( \vartheta \right) + \ddot{y}\sin \left( \vartheta \right) \right) - m_2 \ell {\dot{\vartheta }}^2 = 0,\\&m_1 \ell \left( \ddot{x}\sin \left( \vartheta \right) - \ddot{y}\cos \left( \vartheta \right) \right) = 0. \end{aligned} \end{aligned}$$
(2.16)

Observe that \(\mu \) is remarkably absent from the right-hand side of Maggi’s equations (2.16). Consequently, (2.16) can be integrated using standard methods to determine the motion of the system.

If we were to replace \({\mathsf {E}}_1\) with \({\mathsf {H}}_1\) in Maggi’s equations (2.15), then the additional equation

$$\begin{aligned} m_2 \ell ^2 \ddot{\vartheta } + m_2\ell \left( \ddot{y}\cos \left( \vartheta \right) - \ddot{x}\sin \left( \vartheta \right) \right) = \mu \ell \end{aligned}$$
(2.17)

would be present in (2.16). This additional equation can be used to compute the constraint force \(\mu \mathbf{e}_2\) as a function of the motion of the system.

2.4 Boltzmann–Hamel equations of motion

A fourth formulation can be achieved by the explicit use of quasi-velocities. Thus, with the help of the inverse relations (2.6), we recall that

$$\begin{aligned} \begin{aligned} \mathbf{v}_1&= u^1 \mathbf{e}_1 + \left( u^3 - \ell u^2\right) \mathbf{e}_2, \\ \mathbf{v}_2&= u^1 \mathbf{e}_1 + u^3 \mathbf{e}_2, \end{aligned} \end{aligned}$$
(2.18)

and compute the following expression for the kinetic energy:

$$\begin{aligned} {\bar{T}} = \frac{m_1 + m_2}{2} \left( u^1 u^1 + u^3 u^3\right) + \frac{m_1}{2} \left( \ell ^2 u^2 u^2 - 2 \ell u^2 u^3\right) . \end{aligned}$$
(2.19)

The equations of motion can now be determined from the Boltzmann–Hamel equations of motion [16]. We write the latter in a non-standard, but compact, form:Footnote 1

$$\begin{aligned} \frac{d}{\mathrm{d}t}\left( \frac{\partial {\bar{T}}}{\partial u^K}\right)&- \sum _{\alpha = 1}^2 m_\alpha \mathbf{v}_\alpha \cdot \frac{d}{\mathrm{d}t} \left( \frac{\partial \mathbf{v}_\alpha }{\partial u^K}\right) = R_K, \end{aligned}$$
(2.20)

where

$$\begin{aligned} R_K = \mathbf{F}_1 \cdot \frac{\partial \mathbf{v}_1}{\partial u^K} + \mathbf{F}_2 \cdot \frac{\partial \mathbf{v}_2}{\partial u^K} = \sum _{I=1}^3 H_{IK}Q_I. \end{aligned}$$
(2.21)

The resulting equations of motion are

$$\begin{aligned} \begin{aligned}&\left( m_1+m_2\right) {\dot{u}}^1 + m_1\ell u^2u^2 = 0,\\&m_1\ell ^2{\dot{u}}^2-m_1 \ell u^1u^2 = 0,\\&-m_1 \ell {\dot{u}}^2 + \left( m_1 + m_2\right) u^1 u^2 = \mu . \end{aligned} \end{aligned}$$
(2.22)

In contrast to the previous formulations (2.11), (2.14), and (2.16), the Boltzmann–Hamel equations (2.22) provide a set of equations of motion that are decoupled from the constraint force associated with the constraint \(\mathbf{v}_2\cdot \mathbf{e}_2 = 0\). That is, (2.22)\(_{1,2}\) can be used to solve for \(u^K(t)\) where \(u^3 = 0\) and (2.6) integrated to determine x(t), y(t) and \(\vartheta (t)\).

The phase portrait of Eq. (2.22)\(_{1,2}\) is shown in Fig. 3 and representative examples of the motions of the system are shown in Fig. 4. Closed-form analytical expressions for the motion can be inferred from Carathéodory’s classic paper [9]. We note that the system has a preferred direction of motion with \(m_1\) leading \(m_2\). This phenomenon is similar to another non-holomically constrained mechanical system, the rattleback, having a preferred rotational motion [5].

Eq. (2.22)\(_{3}\), can be used to compute the constraint force on \(m_2\) that enforces the constraint \(\mathbf{v}_2\cdot \mathbf{e}_2 = 0\): \(\mu = m_2 u^1 u^2 = m_2 {\dot{\vartheta }} \mathbf{v}_1\cdot \mathbf{e}_1\). Thus, as was perhaps to be expected, this force vanishes if the velocities of both particles are identical. If there is no interest in computing \(\mu \), then \(u^3\) can be set to 0 in the expression for \({\bar{T}}\) in (2.19) and K set to 1 and 2 in evaluating the Boltzmann–Hamel equations (2.20).

Fig. 3
figure 3

Phase portrait of the governing equations for the system of particles: (2.22)\(_{1,2}\). Observe that the equilibria on the positive \(u^1\) axis are unstable and those on the negative \(u^1\) axis are stable. The orbits correspond to level sets of \({\bar{T}}\)

Full size image
Fig. 4
figure 4

A pair of representative motions of the system of particles. The corresponding orbits are labeled in the phase portrait shown in Fig. 3. These motions show that the heteroclinic orbits connecting the equilibria correspond to motions of the system where \(\left( \mathbf{v}_1 = \mathbf{v}_2\right) \cdot \mathbf{e}_1 > 0\) asymptote to a motion where \(\left( \mathbf{v}_1 = \mathbf{v}_2\right) \cdot \mathbf{e}_1 < 0\)

Full size image

2.5 Gibbs–Appell equations of motion

The Gibbs–Appell equations [2, 14, 33] provide the fifth formulation of the equations of motion. To compute the Gibbs–Appell function S, we first compute the acceleration vectors and set \(u^3 = {\dot{u}}^3 = 0\):

$$\begin{aligned} \begin{aligned} \dot{\mathbf{v}}_1&= \left( {\dot{u}}^1+\ell u^2 u^2\right) \mathbf{e}_1+\left( u^1u^2-\ell {\dot{u}}^2\right) \mathbf{e}_2,\\ \dot{\mathbf{v}}_2&= {\dot{u}}^1\mathbf{e}_1+u^1 u^2\mathbf{e}_2. \end{aligned} \end{aligned}$$
(2.23)

The expression for S is computed as follows:

$$\begin{aligned} \begin{aligned} S&= \frac{m_1}{2} \dot{\mathbf{v}}_1\cdot \dot{\mathbf{v}}_1 + \frac{m_2}{2} \dot{\mathbf{v}}_2\cdot \dot{\mathbf{v}}_2\\&= \frac{m_1}{2}\left( \left( {\dot{u}}^1+\ell u^2 u^2\right) ^2+\left( u^1u^2-\ell {\dot{u}}^2\right) ^2\right) \\&+\frac{m_2}{2}\left( {\dot{u}}^1{\dot{u}}^1+\left( u^1u^2\right) ^2\right) . \end{aligned} \end{aligned}$$
(2.24)

The Gibbs–Appell equations are computed from

$$\begin{aligned} \frac{\partial S}{\partial {\dot{u}}^K} = R_K = \sum _{\alpha =1}^2 \mathbf{F}_\alpha \cdot \frac{\partial \mathbf{v}_\alpha }{\partial u^K}. \end{aligned}$$
(2.25)

Using (2.24), the equations of motion for the system of particles are computed:

$$\begin{aligned} \begin{aligned} \frac{\partial S}{\partial {\dot{u}}^1}&= \left( m_1+m_2\right) {\dot{u}}^1+m_1\ell u^2 u^2 = 0,\\ \frac{\partial S}{\partial {\dot{u}}^2}&= m_1\ell ^2{\dot{u}}^2-m_1\ell u^1 u^2 = 0. \end{aligned} \end{aligned}$$
(2.26)

We observe that these equations are identical to the Boltzmann–Hamel equations of motion (2.22)\(_{1,2}\).

2.6 Kane’s equations of motions

Kane’s equations of motion for this system will be identical to the Gibbs–Appell equations (2.26). For completeness, we note (using Kane’s notation from [19, Section 6.1]), that Kane’s equations of motion are obtained from \({\tilde{F}}_K+{\tilde{F}}_K^* = 0\) where \(K = 1,2\) and

$$\begin{aligned} \begin{aligned}&{\tilde{F}}_K = R_K,\\&{\tilde{F}}_K^* = -\sum _{\alpha =1}^2m_\alpha \dot{\mathbf{v}}_\alpha \cdot \frac{\partial \mathbf{v}_\alpha }{\partial u^K}. \end{aligned} \end{aligned}$$
(2.27)

Kane refers to \({\tilde{F}}_K\) as the non-holonomic generalized active forces and \({\tilde{F}}_K^*\) as the non-holonomic generalized inertia forces. The reason that \(\mu \) is absent from \(R_{1,2}\) will be revealed at the conclusion of Sect. 7.

3 The single particle and the pair of particles

To explore the geometric relationships between the formulations of the equations of motion, we follow [10] and construct a particle of mass m. Thus, we consider a system of two particles that are each free to move in \({\mathbb {E}}^3\). The respective masses and position vectors are denoted by \(m_1\) and \(\mathbf{r}_1\) and \(m_2\) and \(\mathbf{r}_2\), respectively. The resultant forces acting on the respective particles are \(\mathbf{F}_1\) and \(\mathbf{F}_2\) (see Fig. 5).

Fig. 5
figure 5

a A system of two particles that are each free to move in \({\mathbb {E}}^3\). b The representative particle of mass m for the system of particles. This particle is free to move in \({\mathbb {E}}^6\)

Full size image

The kinetic energy of the system of particles is

$$\begin{aligned} T = \frac{m_1}{2}{} \mathbf{v}_1 \cdot \mathbf{v}_1 + \frac{m_2}{2}{} \mathbf{v}_2 \cdot \mathbf{v}_2. \end{aligned}$$
(3.1)

Referring to Fig. 5, we now define a representative particle of mass \(m > 0\) that is free to move in \({\mathbb {E}}^6\). The position vector \(\mathbf{r}\) of this particle is chosen such that the kinetic energy of the particle \(\frac{m}{2} \dot{\mathbf{r}}\cdot \dot{\mathbf{r}}\) is identical to the kinetic energy of the system of particles. One prescription for \(\mathbf{r}\) that satisfies this requirement is (from [10])

$$\begin{aligned} \mathbf{r} = \sum _{\alpha =1}^2 \sum _{\beta = 1}^3 \sqrt{\frac{m_\alpha }{m}} \left( \mathbf{r}_\alpha \cdot \mathbf{E}_\beta \right) {\bar{\mathbf{e}}}_{3 \alpha + \beta - 3}, \end{aligned}$$
(3.2)

where \(\left\{ {\bar{\mathbf{e}}}_1, \ldots , {\bar{\mathbf{e}}}_6\right\} \) is a fixed orthonormal basis for \({\mathbb {E}}^6\). It is straightforward to show using (3.2) that the Gibbs–Appell function for the representative particle is identical to the Gibbs–Appell function for the system of particles:

$$\begin{aligned} S = \frac{m}{2} \dot{\mathbf{v}}\cdot \dot{\mathbf{v}} = \frac{m_1}{2} \dot{\mathbf{v}}_1 \cdot \dot{\mathbf{v}}_1 + \frac{m_2}{2} \dot{\mathbf{v}}_2 \cdot \dot{\mathbf{v}}_2. \end{aligned}$$
(3.3)

This equivalence will be exploited in the sequel.

We assume that the equations governing the motion of the pair of particles are

$$\begin{aligned} m_1 \dot{\mathbf{v}}_1 = \mathbf{F}_1, \qquad m_2 \dot{\mathbf{v}}_2 = \mathbf{F}_2. \end{aligned}$$
(3.4)

The resultant force \(\varvec{\Phi }\) acting on the single particle of mass m is prescribed such that

$$\begin{aligned} m \ddot{\mathbf{r}} = \varvec{\Phi }, \end{aligned}$$
(3.5)

where \(\mathbf{r}\) is prescribed by (3.2). Thus, from [10],

$$\begin{aligned} \varvec{\Phi }= \sum _{\alpha =1}^2 \sum _{\beta = 1}^3 \sqrt{\frac{m}{m_\alpha }} \left( \mathbf{F}_\alpha \cdot \mathbf{E}_\beta \right) {\bar{\mathbf{e}}}_{3 \alpha + \beta - 3}. \end{aligned}$$
(3.6)

It is crucial to note that the dynamics of the particle of mass m is equivalent to the dynamics of the system of particles. By construction, this equivalence will hold when constraints are imposed.

4 Coordinates, bases vectors, and quasi-velocities

We next assume that a set of 6 coordinates has been chosen to parameterize the motion of the system of particles:

$$\begin{aligned} \mathbf{r}_\alpha = \mathbf{r}_\alpha \left( q^1, \ldots , q^6\right) , \qquad \left( \alpha = 1, 2\right) . \end{aligned}$$
(4.1)

The selection of these coordinates is typically dictated by the integrable constraints on the system. Appealing to (3.2), position vector \(\mathbf{r}\) can also be expressed as a function of the coordinates \(q^1, \ldots , q^6\). Furthermore,

$$\begin{aligned} \mathbf{v} = \dot{\mathbf{r}} = \sum _{K=1}^6 {\dot{q}}^K \mathbf{a}_K, \end{aligned}$$
(4.2)

where \(\mathbf{a}_K = \frac{\partial \mathbf{r}}{\partial q^K}\) are covariant basis vectors for \({\mathbb {E}}^6\). The contravariant basis vectors \(\left\{ \mathbf{a}^1 = \nabla q^1, \ldots , \mathbf{a}^{6} = \nabla q^6\right\} \) satisfy the relations

$$\begin{aligned} \mathbf{a}^K\cdot \mathbf{a}_I = \delta ^K_I \end{aligned}$$
(4.3)

where \(\delta ^K_I\) is the Kronecker delta: \(\delta ^K_I = 1\) if \(I = K\) and is otherwise 0. The gradient operator \(\nabla \) is defined in a manner that parallels the prescription (3.6):

$$\begin{aligned} \nabla f = \sum _{\alpha =1}^2 \sum _{\beta = 1}^3 \sqrt{\frac{m}{m_\alpha }} \left( \frac{\partial f}{\partial \mathbf{r}_\alpha } \cdot \mathbf{E}_\beta \right) {\bar{\mathbf{e}}}_{3 \alpha + \beta - 3}. \end{aligned}$$
(4.4)

where \(f = f\left( \mathbf{r}_1, \mathbf{r}_2\right) = {\hat{f}}\left( q^1, \ldots , q^6\right) \).

4.1 Mass matrix

The mass matrix \({\mathsf {M}}\) for the system can be defined using the kinetic energy:

$$\begin{aligned} T = \frac{1}{2} \dot{{\mathsf {q}}}^T {\mathsf {M}} \dot{{\mathsf {q}}} = \frac{m_1}{2} \mathbf{v}_1 \cdot \mathbf{v}_1 + \frac{m_2}{2} \mathbf{v}_2 \cdot \mathbf{v}_2, \end{aligned}$$
(4.5)

where \({\mathsf {q}} = \left[ q^1, \ldots , q^6\right] ^T\). The components \(M_{IK}\) of the \(6\times 6\) matrix \({\mathsf {M}}\) have the representations

$$\begin{aligned} \begin{aligned} M_{IK}&= m \mathbf{a}_I\cdot \mathbf{a}_K\\&= m \sum _{\alpha =1}^2 \sum _{\beta = 1}^3 \frac{m_\alpha }{m} \left( \frac{\partial \mathbf{r}_\alpha }{\partial q^I}\cdot \mathbf{E}_\beta \right) \left( \frac{\partial \mathbf{r}_\alpha }{\partial q^K}\cdot \mathbf{E}_\beta \right) . \end{aligned} \end{aligned}$$
(4.6)

It can be shown that \(\left\{ \mathbf{a}_1, \ldots \mathbf{a}_6\right\} \) are linearly independent if, and only if, \({\mathsf {M}}\) is invertible, otherwise the coordinate system \(\left\{ {q}^1, \ldots q^6\right\} \) for \({\mathbb {E}}^6\) is said to have a singularity [17].

Rather than using (4.3) to compute the contravariant basis vectors, another approach (that we attribute to Blajer [6]) uses \({\mathsf {M}}\). Assuming that \({\mathsf {M}}\) is invertible, it is straightforward to show that

$$\begin{aligned} m \mathbf{a}_K = \sum _{L = 1}^{6} M_{KL} \mathbf{a}^L, \qquad \frac{1}{m} \mathbf{a}^K = \sum _{L = 1}^{6} A^{KL} \mathbf{a}_L, \end{aligned}$$
(4.7)

where \(A^{KR}\) are the components of \({\mathsf {M}}^{-1}\).

4.2 Identities

Application of the chain rule reveals the useful identities

$$\begin{aligned} \begin{aligned}&\mathbf{a}_K = \frac{\partial \mathbf{r}}{\partial q^K} = \frac{\partial \mathbf{v}}{\partial {\dot{q}}^K} = \frac{\partial \dot{\mathbf{v}}}{\partial \ddot{q}^K},\\&\frac{\partial \mathbf{r}_\alpha }{\partial q^K} = \frac{\partial \mathbf{v}_\alpha }{\partial {\dot{q}}^K} = \frac{\partial \dot{\mathbf{v}}_\alpha }{\partial \ddot{q}^K},\\&\dot{\mathbf{a}}_K = \frac{d}{\mathrm{d}t}\left( \frac{\partial \mathbf{v}}{\partial {\dot{q}}^K}\right) = \frac{\partial \mathbf{v}}{\partial {q}^K},\\&\frac{d}{\mathrm{d}t}\left( \frac{\partial \mathbf{v}_\alpha }{\partial {\dot{q}}^K}\right) = \frac{\partial \mathbf{v}_\alpha }{\partial {q}^K}. \end{aligned} \end{aligned}$$
(4.8)

The identities (4.8)\(_{1,2}\) are sometimes referred to as “cancellation of the dots.”

4.3 Quasi-velocities

An appropriate choice of the coordinates \(q^K\) is sufficient to enable Lagrange’s equations (6.3) to produce a set of reactionless equations of motion when the system of particles is subject to holonomic constraints and dynamic Coulomb friction is absent. However, Lagrange’s equations are unable to achieve this decoupling when non-holonomic constraints are present. At the turn of the 20th century, the notion of using quasi-velocities to produce a set of reactionless equations of motion was starting to become appreciated.

In the sequel, a set of quasi-velocities \(u^1, \ldots , u^6\) will be defined by invertible functions of \(q^K\) and \({\dot{q}}^K\):

$$\begin{aligned} \begin{aligned} u^K&= {\hat{u}}^K\left( {\dot{q}}^1, \ldots , {\dot{q}}^6, {q}^1, \ldots , {q}^6\right) = \sum _{L=1}^6 J_{LK} {\dot{q}}^L,\\ {\dot{q}}^K&= \hat{{\dot{q}}}^K\left( u^1, \ldots , u^6, {q}^1, \ldots , {q}^6\right) = \sum _{L=1}^6 H_{KL} {u}^L, \end{aligned} \end{aligned}$$
(4.9)

where \(J_{LK}\) are functions of \(q^1, \ldots , q^6\) and

$$\begin{aligned} {\mathsf {J}} = \left[ J_{LK}\right] , \qquad {\mathsf {H}} = \left[ H_{KL}\right] , \qquad {\mathsf {H}}^{-T} = {\mathsf {J}}. \end{aligned}$$
(4.10)

The functions \({\hat{u}}^K\) and \(\hat{{\dot{q}}}^K\) enable us to define a second representation for \(\mathbf{v}\):

$$\begin{aligned} \mathbf{v} = \sum _{K=1}^6 {u}^K \mathbf{b}_K = \sum _{K=1}^6 {\dot{q}}^K \mathbf{a}_K. \end{aligned}$$
(4.11)

With the help of the chain rule, it can be shown by taking the partial derivatives of \(\mathbf{v}\) with respect to \(u^K\) and \({\dot{q}}^K\) that

$$\begin{aligned} \begin{aligned}&\frac{\partial \mathbf{v}}{\partial {\dot{q}}^K} = \mathbf{a}_K = \sum _{L=1}^6 \frac{\partial {\hat{u}}^L}{\partial {\dot{q}}^K} \mathbf{b}_L = \sum _{L=1}^6 J_{KL} \mathbf{b}_L,\\&\frac{\partial \mathbf{v}}{\partial {u}^K} = \mathbf{b}_K = \sum _{L=1}^6 \frac{\partial \hat{{\dot{q}}}^L}{\partial u^K} \mathbf{a}_L = \sum _{L=1}^6 H_{LK} \mathbf{a}_L, \\&\mathbf{b}_K = \frac{\partial \mathbf{v}}{\partial u^K} = \frac{\partial \dot{\mathbf{v}}}{\partial {\dot{u}}^K}. \end{aligned} \end{aligned}$$
(4.12)

The invertibility of the functions \({\hat{u}}^K\) and \(\hat{{\dot{q}}}^K\) implies that \({\mathsf {J}}\) is invertible. Thus, \(\left\{ \mathbf{b}_1, \ldots , \mathbf{b}_6\right\} \) is a basis for \({\mathbb {E}}^6\) if and only if \(\left\{ \mathbf{a}_1, \ldots , \mathbf{a}_6\right\} \) is a basis for \({\mathbb {E}}^6\).

A contravariant basis \(\left\{ \mathbf{b}^1, \ldots , \mathbf{b}^6\right\} \) can also be defined: \(\mathbf{b}_L \cdot \mathbf{b}^K = \delta ^K_L\). By paralleling the developments leading to the relations (4.7), we find that

$$\begin{aligned} m \mathbf{b}_K = \sum _{L = 1}^{6} N_{KL} \mathbf{b}^L, \quad \frac{1}{m} \mathbf{b}^K = \sum _{L = 1}^{6} B^{KL} \mathbf{b}_L, \end{aligned}$$
(4.13)

where \(N_{KL}\) and \(B^{KR}\) are the components of \({\mathsf {H}}^{T}{\mathsf {M}} {\mathsf {H}}\) and \({\mathsf {J}}^{T}{\mathsf {M}}^{-1}{\mathsf {J}}\), respectively.

4.4 Powers and projections of forces

An identity that will play a key role in the sequel pertains to the components of the forces acting on the particles. A related identity for the power of the forces acting on the system can be established in a similar manner. With help of the representations (3.2) for \(\mathbf{r}\) and (3.6) for \(\varvec{\Phi }\), direct calculations demonstrate that

$$\begin{aligned} \begin{aligned}&\varvec{\Phi }\cdot \mathbf{v} = \mathbf{F}_1 \cdot \mathbf{v}_1 + \mathbf{F}_2 \cdot \mathbf{v}_2,\\&\varvec{\Phi }\cdot \frac{\partial \mathbf{v}}{\partial w} = \mathbf{F}_1 \cdot \frac{\partial \mathbf{v}_1}{\partial w} + \mathbf{F}_2 \cdot \frac{\partial \mathbf{v}_2}{\partial w}. \end{aligned} \end{aligned}$$
(4.14)

Here, w can represent either \({\dot{q}}^K\) or \(u^L\).

Fig. 6
figure 6

Schematic of the path \({\mathcal {C}}\) of the representative particle of mass m on the n-dimensional configuration manifold \({\mathcal {M}}\). The generalized coordinates \(\left( q^1, \ldots , q^n\right) \) form a curvilinear coordinate system on \({\mathcal {M}}\) and \(\left\{ \mathbf{a}_1, \ldots , \mathbf{a}_n\right\} \) form a basis for the n-dimensional tangent space \(T_P{\mathcal {M}}\). For the example discussed in this paper, \(n =3\) and \({\mathcal {M}} = {\mathbb {E}}^2\oplus S^1\)

Full size image

5 Constraints and constraint forces

A single integrable constraint \(\varPsi = 0\) on the system of two particles can be expressed in the equivalent forms

$$\begin{aligned} \varPsi = {\hat{\varPsi }}\left( \mathbf{r}_1, \mathbf{r}_2, t\right) = q^6 - f(t), \end{aligned}$$
(5.1)

where, after computing \({\dot{\varPsi }} = 0\),

$$\begin{aligned} \begin{aligned}&\frac{\partial {\hat{\varPsi }}}{\partial \mathbf{r}_1}\cdot \mathbf{v}_1 + \frac{\partial {\hat{\varPsi }}}{\partial \mathbf{r}_2}\cdot \mathbf{v}_2 = \mathbf{a}^6\cdot \mathbf{v} = {\dot{q}}^6,\\&\frac{\partial {\hat{\varPsi }}}{\partial t} = - {\dot{f}}. \end{aligned} \end{aligned}$$
(5.2)

The surface \({\mathcal {M}} \in {\mathbb {E}}^6\) corresponding to \(q^6 = f(t)\) is the configuration manifold. A point P on this 5-dimensional manifold at time t has a 5-dimensional tangent plane \(T_P{\mathcal {M}}\).Footnote 2 The vectors \(\left\{ \mathbf{a}_1, \ldots , \mathbf{a}_5\right\} \) form a basis for \(T_P{\mathcal {M}}\) and \(\mathbf{a}^6\) is normal to \({\mathcal {M}}\) at P (cf. Fig. 6).

If the constraint \(\varPsi = 0\) is ideal, then the constraint forces acting on the particles that enforce the constraint \(\varPsi = 0\) are prescribed as follows:

$$\begin{aligned} \mathbf{F}_{c_1} = \lambda \frac{\partial \varPsi }{\partial \mathbf{r}_1}, \qquad \mathbf{F}_{c_2} = \lambda \frac{\partial \varPsi }{\partial \mathbf{r}_2}. \end{aligned}$$
(5.3)

Here, \(\lambda \) is a function that is determined by the equations of motion. As \(\nabla \varPsi = \nabla q^6 = \mathbf{a}^6\), with the help of (3.6) and (4.4) it can be shown that the corresponding constraint force on the particle of mass m is simply

$$\begin{aligned} \varvec{\Phi }_c = \lambda \mathbf{a}^6. \end{aligned}$$
(5.4)

Examples of ideal constraints include a particle in motion on a smooth surface or particles connected by massless rods [27].

A non-holonomic constraint on the system of particles can be expressed in the equivalent forms:Footnote 3

$$\begin{aligned} \mathbf{f}_1\cdot \mathbf{v}_1 + \mathbf{f}_2\cdot \mathbf{v}_2 + e = 0, \qquad \mathbf{f}\cdot \mathbf{v} + e = 0. \end{aligned}$$
(5.5)

where the functions \(\mathbf{f}\), \(\mathbf{f}_1\), \(\mathbf{f}_2\), and e depend on the position vectors and time. The functions \(\mathbf{f}_1\) and \(\mathbf{f}_2\) are used to construct \(\mathbf{f}\) using a relation of the form (3.6). It is standard to assume that the constraint forces enforcing this constraint are

$$\begin{aligned} \mathbf{F}_{c_1} = \mu \mathbf{f}_1, \qquad \mathbf{F}_{c_2} = \mu \mathbf{f}_2, \qquad {\varvec{\Phi }}_{c} = \mu \mathbf{f}, \end{aligned}$$
(5.6)

where \(\mu \) is a function that is determined by the equations of motion.

As discussed in [28], even though the constraint forces discussed in this section have simple prescriptions, they are both the necessary and sufficient to ensure that the constraints are satisfied.

6 Equations of motion for the single particle

Consider a system of two particles subject to three ideal integrable constraints. The coordinates \(q^K\) can be chosen so that each of the constraints can be expressed in terms of one coordinate (as in (5.1)). Thus, \(q^1\), \(q^2\), and \(q^3\) are unconstrained and are known as the generalized coordinates. Furthermore,

$$\begin{aligned} \varvec{\Phi }_c = \lambda _1 \mathbf{a}^4 + \lambda _2 \mathbf{a}^5 + \lambda _3 \mathbf{a}^6. \end{aligned}$$
(6.1)

The configuration manifold \({\mathcal {M}}\) is a three-dimensional surface in \({\mathbb {E}}^6\)—that is often challenging to visualize. Lagrange’s equations of motion are ideally suited to this situation and lead to a set of decoupled equations: three second-order differential equations for the generalized coordinates.

To elaborate, by virtue of (4.8)\(_{3}\) and the identities

$$\begin{aligned} \frac{\partial T}{\partial {\dot{q}}^K} = m \mathbf{v}\cdot \mathbf{a}_K, \qquad \frac{\partial T}{\partial {q}^K} = m \mathbf{v}\cdot \dot{\mathbf{a}}_K, \end{aligned}$$
(6.2)

it is straightforward to show that Lagrange’s equations of motion are equivalent to projections of the balance law \(\varvec{\Phi }= m\dot{\mathbf{v}}\):

$$\begin{aligned} \frac{d}{\mathrm{d}t}\left( \frac{\partial T}{\partial {\dot{q}}^K} \right) - \frac{\partial T}{\partial {q}^K} = m \dot{\mathbf{v}}\cdot \mathbf{a}_K = \varvec{\Phi }\cdot \mathbf{a}_K, \end{aligned}$$
(6.3)

where \(K =1, \ldots , 6\). With the help of (4.8)\(_{1,2}\), the right-hand side of (6.3) can be expressed in several alternative manners including

$$\begin{aligned} \begin{aligned} \varvec{\Phi }\cdot \mathbf{a}_K&= \varvec{\Phi }\cdot \frac{\partial \mathbf{v}}{\partial {\dot{q}}^K}\\&= \mathbf{F}_1 \cdot \frac{\partial \mathbf{r}_1}{\partial q^K} + \mathbf{F}_2 \cdot \frac{\partial \mathbf{r}_2}{\partial q^K}\\&= \mathbf{F}_1 \cdot \frac{\partial \mathbf{v}_1}{\partial {\dot{q}}^K} + \mathbf{F}_2 \cdot \frac{\partial \mathbf{v}_2}{\partial {\dot{q}}^K}. \end{aligned} \end{aligned}$$
(6.4)

Because \(\varvec{\Phi }_c = \lambda _1 \mathbf{a}^4 + \lambda _2 \mathbf{a}^5 + \lambda _3 \mathbf{a}^6\) is orthogonal to \(\mathbf{a}_1\), \(\mathbf{a}_2\), and \(\mathbf{a}_3\), the first three of (6.3) are unaffected by \(\varvec{\Phi }_c\) and the last three of (6.3) can be used to determine \(\lambda _{1,2,3}\).

In practice, the decoupling mentioned above is assumed to be possible, only the generalized coordinates are selected, and only the first three of Lagrange’s equations (6.3) are computed. Indeed, this was the strategy used earlier in Sect. 2.2. One of the purposes for the construction of the single particle is to demonstrate the geometric reasoning behind the decoupling. However, as demonstrated by the example discussed in Sect. 2, it is possible to compute Lagrange’s equations without ever explicitly constructing the single particle.

A non-integrable constraint on the system of particles cannot be expressed simply in terms of the coordinates. To decouple the equations of motion in this case, quasi-velocities are chosen. For example, \(u^K\) are chosen such that the constraint (5.5) is expressed in the equivalent forms

$$\begin{aligned} u^3 - e = 0, \qquad \mathbf{b}^3\cdot \mathbf{v} - e = 0. \end{aligned}$$
(6.5)

Representations for T and S in terms of \(u^K\) and \(q^L\) are also computed:

$$\begin{aligned} \begin{aligned} T = {\bar{T}}&= {\bar{T}}\left( u^K, q^L\right) = \frac{1}{2} {\mathsf {u}}^T \left( {\mathsf {H}}^T {\mathsf {M}} {\mathsf {H}}\right) {\mathsf {u}},\\ S = {\bar{S}}&= {\bar{S}}\left( {\dot{u}}^L, u^K, q^L\right) = \frac{1}{2} m \dot{\mathbf{v}} \cdot \dot{\mathbf{v}}, \end{aligned} \end{aligned}$$
(6.6)

where \({\mathsf {u}} = \left[ u^1, \ldots , u^6\right] ^T\) and (3.3) was used to compute S. With the help of (4.12)\(_3\), we find the remarkable result:

$$\begin{aligned} \frac{\partial {\bar{S}}}{\partial {\dot{u}}^K} = m \dot{\mathbf{v}} \cdot \frac{\partial \dot{\mathbf{v}}}{\partial {\dot{u}}^K} = m \dot{\mathbf{v}} \cdot \mathbf{b}_K. \end{aligned}$$
(6.7)

We now consider the possibility of establishing the equations of motion for an unconstrained particle as projections of \(m \dot{\mathbf{v}} = \varvec{\Phi }\) onto \(\mathbf{b}_1, \ldots , \mathbf{b}_6\):

$$\begin{aligned} m\dot{\mathbf{v}}\cdot \mathbf{b}_K = R_K \end{aligned}$$
(6.8)

where, with the help of (4.14),

$$\begin{aligned} R_K = \varvec{\Phi }\cdot \mathbf{b}_K = \mathbf{F}_1 \cdot \frac{\partial \mathbf{v}_1}{\partial u^K} + \mathbf{F}_2 \cdot \frac{\partial \mathbf{v}_2}{\partial u^K}. \end{aligned}$$
(6.9)

The left-hand side of (6.8) can be computed in a variety of manners. We list here, in order, the Kane, MaggiFootnote 4, Boltzmann-Hamel, and Gibbs-Appell formulations:

$$\begin{aligned} \begin{aligned} m\dot{\mathbf{v}}\cdot \mathbf{b}_K&= \sum _{L=1}^6 H_{LK}\left( \frac{d}{\mathrm{d}t}\left( \frac{\partial T}{\partial {\dot{q}}^L}\right) - \frac{\partial T}{\partial {q}^L} \right) \\&=\frac{d}{\mathrm{d}t}\left( \frac{\partial {\bar{T}}}{\partial u^K}\right) -\sum _{L=1}^6\frac{\partial {\bar{T}}}{\partial q^L}\frac{\partial \hat{{\dot{q}}}^L}{\partial u^K}\\&-\sum _{L=1}^6\sum _{M=1}^6\frac{\partial {\bar{T}}}{\partial u^M}\frac{\partial {\hat{u}}^M}{\partial {\dot{q}}^L}\frac{d}{\mathrm{d}t}\left( \frac{\partial \hat{{\dot{q}}}^L}{\partial u^K}\right) \\&= \frac{\partial {\bar{S}}}{\partial {\dot{u}}^K}. \end{aligned} \end{aligned}$$
(6.10)

In our developments thus far we have not imposed constraints. We take this opportunity to note that other representations for (6.10) including those attributed to Cenov, Chaplygin, Nielsen, and Tzénoff, among others, are available (cf. [1, 34, 38]).

As in the example we will consider in Sect. 7, suppose the particle is subject to three integrable constraints and one non-integrable constraint:

$$\begin{aligned} u^3 = e, \qquad u^K = {\dot{f}}_K, \qquad \left( K = 4, 5, 6\right) , \end{aligned}$$
(6.11)

where \(u^4 = {\dot{q}}^4\), \(u^5 = {\dot{q}}^5\), and \(u^6 = {\dot{q}}^6\). We choose \(u^i\) to be functions of \({\dot{q}}^k\) where \(i, k = 1, 2, 3\). Consequently, \(\mathbf{b}^4 = \mathbf{a}^4\), \(\mathbf{b}^5 = \mathbf{a}^5\), and \(\mathbf{b}^6 = \mathbf{a}^6\). Furthermore,

$$\begin{aligned} \varvec{\Phi }_c&= \mu \mathbf{b}^3 + \lambda _1 \mathbf{a}^4 + \lambda _2 \mathbf{a}^5 + \lambda _3 \mathbf{a}^6. \end{aligned}$$
(6.12)

In this instance, the equations of motion (6.8–6.10) provide a set of decoupled equations: equations for \(\mu \), \(\lambda _1\), \(\lambda _2\), and \(\lambda _3\) and differential equations for \(u^1\) and \(u^2\). This would not be possible with Lagrange’s equations of motion (6.3) as these equations are equivalent to projections of \(\varvec{\Phi }= m\dot{\mathbf{v}}\) onto \(\mathbf{a}_K\).

7 The example revisited

We now return to the system of two particles presented in Sect. 2. There are four constraints on the system:

$$\begin{aligned} \begin{aligned}&\Vert \mathbf{r}_2 - \mathbf{r}_1 \Vert - \ell = 0, \qquad \mathbf{r}_1\cdot \mathbf{E}_3 = 0, \\&\mathbf{r}_2\cdot \mathbf{E}_3 = 0, \qquad \mathbf{e}_2\cdot \mathbf{v}_2 = 0. \end{aligned} \end{aligned}$$
(7.1)

The integrable constraints (7.1)\(_{1,2,3}\) motivate us to use an angle \(\vartheta \) and scalar variable \(r \ge 0\) to parameterize \(\mathbf{r}_2 - \mathbf{r}_1\) and a set of Cartesian coordinates to parameterize \(\mathbf{r}_1\):

$$\begin{aligned} \begin{aligned}&\mathbf{r}_1 = x\mathbf{E}_1 + y \mathbf{E}_2 + z_1\mathbf{E}_3,\\&\mathbf{r}_2 = x\mathbf{E}_1 + y \mathbf{E}_2 + r \mathbf{e}_1 + z_2 \mathbf{E}_3. \end{aligned} \end{aligned}$$
(7.2)

Thus, for the system of particles,

$$\begin{aligned} \begin{aligned}&q^1 = x = \mathbf{r}_1 \cdot \mathbf{E}_1, \qquad q^2 = y = \mathbf{r}_1 \cdot \mathbf{E}_2, \\&q^3 = \vartheta , \qquad q^4 = r = \Vert \mathbf{r}_2-\mathbf{r}_1\Vert , \\&q^5 = z_1 = \mathbf{r}_1 \cdot \mathbf{E}_3, \qquad q^6 = z_2 = \mathbf{r}_2 \cdot \mathbf{E}_3. \end{aligned} \end{aligned}$$
(7.3)

The position vector of the representative particle can be computed using (3.2):

$$\begin{aligned} \mathbf{r}= & {} \sqrt{\frac{m_1}{m}}\left( x {\bar{\mathbf{e}}}_1 + y {\bar{\mathbf{e}}}_2 + z_1 {\bar{\mathbf{e}}}_3\right) + \sqrt{\frac{m_2}{m}} \left( x + r \cos \left( \vartheta \right) \right) {\bar{\mathbf{e}}}_4 \nonumber \\&+ \sqrt{\frac{m_2}{m}} \left( y + r \sin \left( \vartheta \right) \right) {\bar{\mathbf{e}}}_5 + \sqrt{\frac{m_2}{m}} \left( z_2\right) {\bar{\mathbf{e}}}_6. \end{aligned}$$
(7.4)

The lengthy expressions for the covariant \(\mathbf{a}_K\) and contravariant \(\mathbf{a}^K\) basis vectors for \({\mathbb {E}}^6\) are recorded in (A.1) and (A.6), respectively.

We next choose the quasi-velocities \(u^K\) with the constraints in mind:

$$\begin{aligned} \begin{aligned}&u^1 = \mathbf{v}_1 \cdot \mathbf{e}_1 = {\dot{x}}\cos \left( \vartheta \right) + {\dot{y}}\sin \left( \vartheta \right) ,\\&u^2 = {\dot{\vartheta }}, \qquad u^{3+i} = {\dot{q}}^{3+i}, \,\, \left( i=1,2,3\right) , \\&u^3 = \mathbf{v}_2 \cdot \mathbf{e}_2 = - {\dot{x}}\sin \left( \vartheta \right) + {\dot{y}}\cos \left( \vartheta \right) + r {\dot{\vartheta }}. \end{aligned} \end{aligned}$$
(7.5)

Observe that the functions \({\hat{u}}^K\) and \(\hat{{\dot{q}}}^K\) can be readily computed from (7.5). The corresponding expressions for \(\mathbf{b}_K\) are computed with the help of (4.12) and are presented in (A.8).

Fig. 7
figure 7

Schematic of \(T_P{\mathcal {M}}\) showing the covariant bases vectors, the constraint force \(\mu \mathbf{b}^3\) and the velocity vector \(\mathbf{v} = u_1 \mathbf{b}_1 + u_2 \mathbf{b}_2 = {\dot{x}}{} \mathbf{a}_1 + {\dot{y}}{} \mathbf{a}_2 + {\dot{\vartheta }}{} \mathbf{a}_3\). Because of the constraint \(\mathbf{v}\cdot \mathbf{b}^3 = 0\), \(\mathbf{v}\) is constrained to lie in the plane spanned by \(\mathbf{b}_1\) and \(\mathbf{b}_2\). Expressions for the bases vectors can be found in Appendix A

Full size image

7.1 Configuration manifold

The constraints on the systems of particles that they are free to move on a smooth horizontal surface and connected by a rigid massless rigid rod are integrable. This collection of constraints implies that the corresponding single particle of mass m can be considered to move on a 3-dimensional surface that is contained in \({\mathbb {E}}^6\): the configuration manifold \({\mathcal {M}} = {\mathbb {E}}^2\oplus S^1\). As can be inferred from Fig. 2, \({\mathcal {M}}\) for this system cannot be embedded in \({\mathbb {E}}^3\). Each point P of the configuration manifold has a 3-dimensional tangent space \(T_P{\mathcal {M}}\) (cf. Fig. 6). As displayed in Fig. 7, the vectors \(\left\{ \mathbf{a}_1, \mathbf{a}_2, \mathbf{a}_3\right\} \) and \(\left\{ \mathbf{b}_1, \mathbf{b}_2, \mathbf{b}_3\right\} \) form bases for \(T_P{\mathcal {M}}\). Moreover, the vectors \(\mathbf{a}^4 = \mathbf{b}^4\), \(\mathbf{a}^5 = \mathbf{b}^5\), and \(\mathbf{a}^6 = \mathbf{b}^6\) are normal to the velocity vector

$$\begin{aligned} \mathbf{v} = {\dot{q}}^1 \mathbf{a}_1+{\dot{q}}^2 \mathbf{a}_2 + {\dot{q}}^3 \mathbf{a}_3 = u^1 \mathbf{b}_1 + u^2 \mathbf{b}_2 \end{aligned}$$
(7.6)

of the particle of mass m and are normal to \({\mathcal {M}}\).

7.2 Constraint forces

There are four constraints (7.1) on the system. The forces acting on the particles that enforce these constraints are prescribed using (5.3):

$$\begin{aligned} \begin{aligned}&\mathbf{F}_{c_1} = - \lambda _1 \mathbf{e}_1 + \lambda _2 \mathbf{E}_3,\\&\mathbf{F}_{c_2} = \lambda _1 \mathbf{e}_1 + \mu \mathbf{e}_2 + \lambda _3 \mathbf{E}_3. \end{aligned} \end{aligned}$$
(7.7)

Here, \(\lambda _2 \mathbf{E}_3\) and \(\lambda _3 \mathbf{E}_3\) are normal forces, \(-\lambda _1 \mathbf{e}_1\) is the tension force in the rod connecting the particles, and \(\mu \mathbf{e}_2\) is the constraint force enforcing the non-integrable constraint.

The pair of constraint forces, \(\mathbf{F}_{c_1}\) and \(\mathbf{F}_{c_2}\), is equivalent to a force \(\varvec{\Phi }_c\) acting on the particle of mass m. We use the definition of \(\varvec{\Phi }\) presented in (3.6), the expressions for \(\mathbf{F}_{c_{1}}\) and \(\mathbf{F}_{c_2}\), and the expressions (A.6) for \(\mathbf{a}^K\) and (A.9) for \(\mathbf{b}^K\) to establish representations for \(\varvec{\Phi }_c\):

$$\begin{aligned} \begin{aligned} \varvec{\Phi }_c&= \lambda _1 \mathbf{a}^4 + \mu \mathbf{f} + \lambda _2 \mathbf{a}^5+\lambda _3 \mathbf{a}^6\\&= \lambda _1 \mathbf{b}^4 + \mu \mathbf{b}^3 + \lambda _2 \mathbf{b}^5+\lambda _3 \mathbf{b}^6, \end{aligned} \end{aligned}$$
(7.8)

where

$$\begin{aligned} \begin{aligned} \mathbf{f}&= \sqrt{\frac{m}{m_2}}\sum _{\beta = 1}^3 \left( \mathbf{e}_2 \cdot \mathbf{E}_\beta \right) {\bar{\mathbf{e}}}_{3 + \beta }\\&= \sqrt{\frac{m}{m_2}}\left( \cos \left( \vartheta \right) {\bar{\mathbf{e}}}_5 - \sin \left( \vartheta \right) {\bar{\mathbf{e}}}_4 \right) \\&= - \sin \left( \vartheta \right) \mathbf{a}^1 + \cos \left( \vartheta \right) \mathbf{a}^2 + r \mathbf{a}^3\\&= \mathbf{b}^3. \end{aligned} \end{aligned}$$
(7.9)

In computing the final representation for \(\mathbf{f}\), the expressions (A.6) for \(\mathbf{a}^K\) and (A.9)\(_3\) for \(\mathbf{b}^3\) were used (cf. Fig. 7).

For completeness, we note that the resultant force \(\varvec{\Phi }\) acting on the particle is

$$\begin{aligned} \varvec{\Phi }= \varvec{\Phi }_c - m_1 g \mathbf{a}^5 - m_2 g \mathbf{a}^6. \end{aligned}$$
(7.10)

This expression was computed with the help of (3.6). Referring to (A.9)\(_{5,6}\), for future reference we note that \(\mathbf{b}^5 = \mathbf{a}^5\) and \(\mathbf{b}^6 = \mathbf{a}^6\).

7.3 Equations of motion

The right-hand side of Lagrange’s equations of motion (cf. (6.3)\(_{K=1,2,3}\)) contain contributions from \(\varvec{\Phi }_c\cdot \mathbf{a}_K\):

$$\begin{aligned} \begin{aligned}&Q_1 = \varvec{\Phi }\cdot \mathbf{a}_1 = - \mu \sin \left( \vartheta \right) ,\\&Q_2 = \varvec{\Phi }\cdot \mathbf{a}_2 = \mu \cos \left( \vartheta \right) ,\\&Q_3 = \varvec{\Phi }\cdot \mathbf{a}_3 = \mu \ell . \end{aligned} \end{aligned}$$
(7.11)

It is straightforward to see from (7.8), (7.9), and (7.11) that \(\mu \mathbf{f}\) lies in \(T_p{\mathcal {M}}\). This is the reason that this force appeared previously in Lagrange’s equations of motion (2.14).

For the formulations of the equations of motion using quasi-velocities and Maggi’s formulation, the basis vectors \(\left\{ \mathbf{b}_1, \mathbf{b}_2, \mathbf{b}_3\right\} \) for \(T_p{\mathcal {M}}\) are employed:

$$\begin{aligned} \begin{aligned}&R_1 = \varvec{\Phi }\cdot \mathbf{b}_1 = 0,\\&R_2 = \varvec{\Phi }\cdot \mathbf{b}_2 = 0,\\&R_3 = \varvec{\Phi }\cdot \mathbf{b}_3 = \mu . \end{aligned} \end{aligned}$$
(7.12)

These expressions illustrate the geometric reason for the success of Maggi’s formulation (cf. (2.15) and (2.16)) and we invite the reader to compare them to the corresponding expressions for \(Q_{1,2,3}\) displayed in (7.11). Suppose, as in the Gibbs–Appell, Kane, and Boltzmann–Hamel formulations, the non-integrable constraint is simply expressed as \(u^3 =0\). Then, the projections of \(m \dot{\mathbf{v}} = \varvec{\Phi }\) onto \(\mathbf{b}_1\) and \(\mathbf{b}_2\) provide ordinary differential equations for \(u^1\) and \(u^2\) that are free of constraint forces (cf. the Boltzmann–Hamel equations (2.22) and the Gibbs–Appell and Kane’s equations (2.26)).

8 Closing remarks

The equations \(\mathbf{F}_1 = m_1 \dot{\mathbf{v}}_1\) and \(\mathbf{F}_2 = m_2 \dot{\mathbf{v}}_2\) along with prescriptions for constraint forces can in principle be used to determine the equations of motion for a system of particles. The advantage of using Lagrange’s equations of motion becomes apparent if the constraints are holonomic and ideal (i.e., no dynamic Coulomb friction) and the coordinates are chosen appropriately. Geometrically, the generalized coordinates parameterize \({\mathcal {M}}\) and the constraint forces are orthogonal to \({\mathcal {M}}\). Lagrange’s formulation remarkably selects linear combinations of components of \(\mathbf{F}_1 = m_1 \dot{\mathbf{v}}_1\) and \(\mathbf{F}_2 = m_2 \dot{\mathbf{v}}_2\) to produce a set of equations of motion that are uncoupled from the constraint forces. This decoupling can be explained using the covariant basis vectors for \(T_P{\mathcal {M}}\).

In the late 1800s, Lagrange’s formulation was extended to encompass systems with non-holonomic constraints. It was quickly appreciated that the remarkable decoupling mentioned above was no longer produced by the formulation. Geometrically, the construction of the representative particle shows that the reason for the lack of decoupling is because the constraint force associated with the non-holonomic constraint has components in \(T_P{\mathcal {M}}\) (see, e.g., the expressions for \(Q_{1,2,3} = \varvec{\Phi }\cdot \mathbf{a}_{1,2,3}\) in (7.11)).

Fortunately, at the turn of the 20th century, researchers including Appell, Boltzmann, Gibbs, Hamel, and Maggi, realized that a decoupling could be produced by carefully selecting quasi-velocities and using them in place of \({\dot{q}}^K\) in the formulation of the equations of motion (cf. [32]). The construction of the single particle shows that the use of quasi-velocities \(u^L\) is equivalent to constructing a different basis for \(T_P{\mathcal {M}}\)—one where the constraint force \(\varvec{\Phi }_c\) and velocity \(\mathbf{v}\) have representations that are conducive to uncoupling the equations of motion from the constraint forces enforcing the non-holonomic constraint. The expressions for \(R_{1,2,3} = \varvec{\Phi }\cdot \mathbf{b}_{1,2,3}\) in (7.12) are illustrative examples.

The distinction between the aforementioned equations lies in their left-hand sides. Maggi’s equations are expressed in terms of the generalized coordinates \(q^K\) and their derivatives \({\dot{q}}^K\). Since the number of generalized coordinates are the same, say n, while the number of equations is decreased to \(n - m\) where m is the number of non-holonomic constraints, one needs to supplement the Maggi’s equations with the m constraint equations to obtain a determinate system of equations of motion. The left-hand side of the Boltzmann–Hamel equations is obtained in terms of the quasi-velocities and generalized coordinates through careful applications of the chain rule to the left-hand side of Maggi’s equations. The Gibbs–Appell equations forgo these complications by introducing the Gibbs–Appell function. Kane’s equations employ similar ideas but bypass the calculation of the Gibbs-Appell function.

Perhaps one of the most remarkable aspects of the geometric construction we have used to explore connections between six formulations of the equations of motion for a system of particles, is that the construction can also be extended to systems comprised of particles and rigid bodies [12, 17]. For our present purposes, we chose to consider the simplest example of a non-holonomically constrained mechanical system to illustrate and illuminate these connections. We close by noting that the representative particle can be used to quickly demonstrate that if the quasi-velocities are chosen to be identical to the generalized velocities, then the Gibbs-Appell equations of motion become identical to Lagrange’s equations of motion.