Efficiency comparison of various friction models of a hydraulic cylinder in the framework of multibody system dynamics

Abstract

Dynamic simulation of mechanical systems can be performed using a multibody system dynamics approach. The approach allows to account systems of other physical nature, such as hydraulic actuators. In such systems, the nonlinearity and numerical stiffness introduced by the friction model of the hydraulic cylinders can be an important aspect to consider in the modeling because it can lead to poor computational efficiency. This paper couples various friction models of a hydraulic cylinder with the equations of motion of a hydraulically actuated multibody system in a monolithic framework. To this end, two static friction models, the Bengisu–Akay model and Brown–McPhee model, and two dynamic friction models, the LuGre model and modified LuGre model, are considered in this work. A hydraulically actuated four-bar mechanism is exemplified as a case study. The four modeling approaches are compared based on the work cycle, friction force, energy balance, and numerical efficiency. It is concluded that the Brown–McPhee approach is numerically the most efficient approach and it is well able to describe usual friction characteristics in dynamic simulation of hydraulically actuated multibody systems.

1 Introduction

Dynamic simulation of mechanical systems can be performed using multibody system dynamics. In this approach, the equations of motion describe a force equilibrium for the mechanical system under consideration. This approach allows to describe systems of other physical nature, such as hydraulic actuators [32, 33, 43]. Hydraulic systems are highly nonlinear systems, which are caused, in part, by the friction model of the hydraulic cylinders. The friction model of the hydraulic cylinders can introduce numerical stiffness [38], and as a consequence, time integration of hydraulically actuated systems may become cumbersome, especially, in real-time applications [30, 31, 50]. Moreover, a physically incorrect friction model of the hydraulic cylinders can lead to inaccurate simulations and control errors.

Friction models can, in general, be categorized into two main groups, namely, static friction models and dynamic friction models [5, 37, 45]. Static friction models describe only the steady-state relation between the friction force and the relative velocity [5]. The well-known friction model was developed by Coulomb in 1785, and over the years, various friction models have been proposed that capture Coulomb, stiction, viscous, and Stribeck [29] friction effects, as in [14, 27]. The exponential Stribeck friction model described by Bo and Pavelescu [14] is popular, however, it can lead to numerical problems because of the discontinuity of the friction force at zero relative velocity. To overcome this numerical problem, a separate equation can be used to describe friction at zero relative velocity [2,3,4, 10]. For example, Bengisu and Akay [10] utilize two separate equations for the adhesion regime and Stribeck effect. However, when this approach is adopted, the use of different equations during the simulation can lead to poor numerical efficiency. To address this problem, Brown and McPhee [16] recently developed a continuous velocity-based friction model suitable for computationally challenging applications and optimization problems. Their model [16] does not consider the time lag [11], micro-slip [2] or pre-slip displacement [11], and dwell-time dependence of friction [23]. In this study, the friction models developed by Bengisu and Akay [10] and Brown and McPhee [16] are referred to as the Bengisu–Akay and Brown–McPhee friction models, respectively.

Dynamic friction models evaluate the friction force based on the actual state of contact and the contact history [5, 38]. In general, extra state variables, such as the average bristle deflection, are used with relative velocity to model the evolution of the friction force [37]. Unlike most static friction models, dynamic friction models consider frictional phenomena such as pre-slip displacement [11] and frictional lag, and dynamic friction models eliminate the discontinuity at zero relative velocity. The Dahl friction model [20] was the first dynamic friction model in which the friction force is considered proportional to the average bristle deflection. It did not, however, consider the static friction. Based on the Dahl friction model, a number of friction models, such as the reset integrator model [24], Bliman–Sorine model [12, 13], LuGre model [21], Leuven model [51], and generalized Maxwell slip model [1, 36], are described accounting for various frictional phenomena. The LuGre friction model [21] is widely used and it captures the Stribeck and stiction effects, as well as the pre-slip displacement and frictional lag. Subsequently, a modified LuGre friction model [57] was developed that considered the dynamics of the lubricant film formation. In the modified LuGre friction model, the lubricant film dynamics is computed using a first-order lag element in which the time constant is varied between the deceleration, acceleration, and dwell periods [57]. It should be noted that dynamic friction models can introduce numerical stiffness to systems and, consequently, increasing the computational cost [38].

In the literature, experiments have been conducted to measure the friction force of hydraulic cylinders with different reciprocating seals operating under various conditions [42]. Additionally, a number of studies have been carried out that utilize different seal friction models for simulation of hydraulic cylinders. For example, the exponential Stribeck friction model [14] was used in [53, 54] and the stick-slip friction model [3, 4] in [39]. Furthermore, the dynamic friction behavior of hydraulic cylinders was studied using the LuGre friction model in [41, 53] and a modified LuGre friction model [57] in [52, 53]. Yanada and Sekikawa [57] found that compared with the LuGre friction model, the modified LuGre friction model [57] can simulate the real friction characteristics of a hydraulic cylinder with a good accuracy. Other work has used simple pressure-dependent friction models [15, 25] that either had discontinuity at zero relative velocity [25] or were case-dependent [15]. Ylinen et al. [58] combined a pressure-dependent function with the LuGre friction model to study multibody simulation of a hydraulic cylinder.

In the framework of multibody system dynamics [35, 46], a large number of studies have been presented that demonstrate coupling of multibody systems and hydraulic actuators [22, 40]. Coupling has been carried out using either monolithic [48, 49] or co-simulation approaches [44, 47]. There are even studies using a monolithic approach that demonstrate this coupling for real-time applications, such as [6] and [31]. Despite widespread interest in the field, detailed comparative study on the inclusion of various friction models of a hydraulic cylinder with the equations of motion of hydraulically actuated multibody systems has been overlooked in the literature.

The objective of this paper is to couple various friction models of a hydraulic cylinder with the equations of motion of a hydraulically actuated multibody system in a monolithic framework. To this end, the Bengisu–Akay model [10] and the Brown–McPhee model [16], in the category of static friction models, and the LuGre model [21] and the modified LuGre model [57], in the category of dynamic friction models, are considered in this work. In the monolithic coupling scheme, the multibody system is described using a semi-recursive formulation [8, 18] and the hydraulic system is described using the lumped fluid theory [56]. In the study, only a fixed step-size integrator is considered because the interest of the authors lies in the area of real-time simulation. The coupled systems are referred to with the name of the friction force model used, that is, the Bengisu–Akay approach, Brown–McPhee approach, LuGre approach, and modified LuGre approach. Although a case study of a hydraulically actuated planar four-bar mechanism is shown, the methods presented in this study are general and applicable to three-dimensional mechanisms as well. Using the numerical example, the four approaches are compared based on the simulation work cycle, friction force, energy balance, and numerical efficiency.

2 Multibody system dynamics

In this study, the dynamics of a constrained mechanical system is described using a semi-recursive multibody formulation. In this method, the equations of motion of a system are formulated in the relative joint coordinates using the dynamics of an open-loop system. Closed-loop systems are modeled by employing the cut-joint constraints using the penalty-based augmented Lagrangian method [8, 17, 18]. The multibody system is hydraulically actuated and the dynamics of the hydraulic system is described using the lumped fluid theory [56]. It should be noted that the hydraulic cylinder–piston is not considered as separate bodies, and therefore, their masses are assumed to be neglectable. Nevertheless, the internal dynamics of the hydraulic system, including the friction model of a hydraulic cylinder, are computed and the resultant force is fed into the multibody equations of motion in a monolithic approach.

Fig. 1

Illustration of a multibody system

2.1 Semi-recursive multibody formulation

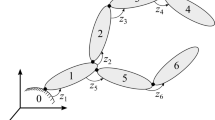
Consider an open-loop system, which has ${N_b}$ bodies. The absolute velocity, ${\mathbf{Z}}_{j}$, and acceleration, ${\dot{\mathbf{Z}}}_{j}$, of the bodies can be described using Cartesian velocities and accelerations [28, 34] as ${\mathbf{Z}}_{j} \equiv \left[ {\dot{\mathbf{s}}}_{j}^{\text {T}}, {\varvec{\upomega }}_{j}^{\text {T}} \right] ^{\text {T}}$ and ${\dot{\mathbf{Z}}}_{j} \equiv \left[ {\ddot{\mathbf{s}}}_{j}^{\text {T}}, {\dot{\varvec{\upomega }}}_{j}^{\text {T}} \right] ^{\text {T}}$. Here, ${\dot{\mathbf{s}}}_{j}$ and ${\ddot{\mathbf{s}}}_{j}$ are, respectively, the velocities and accelerations of a point on body $j \in \left[ 1, {N_b} \right]$, which are instantaneously coincident with the origin of the inertial reference frame, and ${\varvec{\upomega }}_{j}$ and ${\dot{\varvec{\upomega }}}_{j}$ are their angular counterparts. The kinematics for an open-loop system, shown in Fig. 1a, can be calculated, for example, from the base to the leaves using classical kinematic relations [19]. In Fig. 1, the relative joint coordinates, ${z}_{j}$, represent the position of the bodies. The absolute velocities and accelerations can be recursively expressed with respect to the previous bodies as [34]

$$\begin{aligned}&{\mathbf{Z}}_{j} = {\mathbf{Z}}_{j-1} + {\mathbf{b}}_{j} {{\dot{z}}}_{j}, \end{aligned}$$

(1)

$$\begin{aligned}&{\dot{\mathbf{Z}}}_{j} = {\dot{\mathbf{Z}}}_{j-1} + {\mathbf{b}}_{j} {\ddot{z}}_{j} + {\mathbf{d}}_{j}, \end{aligned}$$

(2)

where ${{\dot{z}}}_{j}$ and ${\ddot{z}}_{j}$ are, respectively, the relative joint velocities and accelerations, and ${\mathbf{b}}_{j}$ and ${\mathbf{d}}_{j}$ are vectors that depend on the joint-type connecting bodies ${j-1}$ and j [19]. As the system may branch, the indexes $j-1$ and j may not be successive.

A velocity transformation matrix, ${\mathbf{R}} \in {{\mathbb {R}}}^{6 {N_b} \times {N_b}}$, can map the absolute velocities, ${\mathbf{Z}} = \left[ {\mathbf{Z}}_{1}^{\text {T}}, {\mathbf{Z}}_{2}^{\text {T}}, \hdots , {\mathbf{Z}}_{N_b}^{\text {T}} \right] ^{\text {T}}$, into a set of relative joint velocities, ${\dot{\mathbf{z}}} = \left[ {{\dot{z}}}_{1}, {{\dot{z}}}_{2}, \hdots , {{\dot{z}}}_{N_b} \right] ^{\text {T}}$, as [34]

$$\begin{aligned} {\mathbf{Z}}= & {} {\mathbf{R}} {\dot{\mathbf{z}}} = {\mathbf{T}} {\mathbf{R}}_{\text {d}} {\dot{\mathbf{z}}}, \end{aligned}$$

(3)

$$\begin{aligned} {\dot{\mathbf{Z}}}= & {} {\mathbf{R}} {\ddot{\mathbf{z}}} + {\dot{\mathbf{R}}} {\dot{\mathbf{z}}} = {\mathbf{T}} {\mathbf{R}}_{\text {d}} {\ddot{\mathbf{z}}} + {\mathbf{T}} {\dot{\mathbf{R}}}_{\text {d}} {\dot{\mathbf{z}}}, \end{aligned}$$

(4)

where ${\mathbf{T}} \in {{\mathbb {R}}}^{6 {N_b} \times 6 {N_b}}$ is the constant path matrix that represents the topology of the open-loop system and ${\mathbf{R}}_{\text {d}} \in {{\mathbb {R}}}^{6 {N_b} \times {N_b}}$ is a diagonal matrix whose elements are vectors ${\mathbf{b}}_{j}$, arranged in an ascending order. In Eq. (4), the term ${\dot{\mathbf{R}}} {\dot{\mathbf{z}}}$ can be expressed in terms of vectors ${\mathbf{d}}_{j}$ using Eq. (2) [19].

In an open-loop system, the virtual power of the inertia and external forces can be written as [34]

$$\begin{aligned} \sum _{j=1}^{N_b} {\mathbf{Z}}_{j}^{*{\text {T}}} \left( {\bar{\mathbf{M}}}_{j} {\dot{\mathbf{Z}}}_{j} - {\bar{\mathbf{Q}}}_{j} \right) = 0, \end{aligned}$$

(5)

where an asterisk (*) denotes the virtual velocities, and the mass matrix ${\bar{\mathbf{M}}}_{j}$ and force vector ${\bar{\mathbf{Q}}}_{j}$ can be expressed as

$$\begin{aligned} {\bar{\mathbf{M}}}_{j} = \begin{bmatrix} {m_j} {\mathbf{I}}_{3} &{} - {m_j} {\widetilde{\mathbf{g}}}_{j}\\ {m_j} {\widetilde{\mathbf{g}}}_{j} &{} {\mathbf{J}}_{j} - {m_j} {\widetilde{\mathbf{g}}}_{j} {\widetilde{\mathbf{g}}}_{j} \end{bmatrix}, \end{aligned}$$

(6)

and

$$\begin{aligned} \begin{aligned} {\bar{\mathbf{Q}}}_{j} = \begin{bmatrix} {\mathbf{f}}_{j} - {\widetilde{\varvec{\upomega }}}_{j} \left( {\widetilde{\varvec{\upomega }}}_{j} {m_j} {\mathbf{g}}_{j}\right) \\ {\varvec{\uptau }}_{j} - {\widetilde{\varvec{\upomega }}}_{j} {\mathbf{J}}_{j} {\varvec{\upomega }}_{j} + {\widetilde{\mathbf{g}}}_{j} \left( {\mathbf{f}}_{j} - {\widetilde{\varvec{\upomega }}}_{j} \left( {\widetilde{\varvec{\upomega }}}_{j} {m_j} {\mathbf{g}}_{j}\right) \right) \end{bmatrix}, \end{aligned} \end{aligned}$$

(7)

where ${m_j}$ and ${\mathbf{J}}_{j}$ are, respectively, the mass and inertia tensor of body j, ${\mathbf{I}}_{3}$ is a ${\left( 3 \times 3\right) }$ identity matrix, the vector ${\mathbf{g}}_{j}$ is the position of the center of mass of body j, a tilde ($\sim$) denotes the skew-symmetric matrix of a vector, and ${\varvec{\uptau }}_{j}$ and ${\mathbf{f}}_{j}$ are, respectively, the vector of external moments with respect to the center of mass and external forces applied on body j. By substituting Eqs. (3) and (4) in Eq. (5), the equations of motion for the open-loop system can be written as [34]

$$\begin{aligned} {\mathbf{R}}_{\text {d}}^{\text {T}} {\mathbf{T}}^{\text {T}} {\bar{\mathbf{M}}} {\mathbf{T}} {\mathbf{R}}_{\text {d}} {\ddot{\mathbf{z}}} = {\mathbf{R}}_{\text {d}}^{\text {T}} {\mathbf{T}}^{\text {T}} \left( {\bar{\mathbf{Q}}} - {\bar{\mathbf{M}}} {\mathbf{T}} {\dot{\mathbf{R}}}_{\text {d}} {\dot{\mathbf{z}}} \right) , \end{aligned}$$

(8)

where ${\ddot{\mathbf{z}}} \in {{\mathbb {R}}}^{N_b}$ is the vector of the relative joint accelerations, and ${\bar{\mathbf{M}}} \in {{\mathbb {R}}}^{6 {N_b} \times 6 {N_b}}$ and ${\bar{\mathbf{Q}}} \in {{\mathbb {R}}}^{6 {N_b}}$ are, respectively, a diagonal matrix and a column vector, whose elements are ${\bar{\mathbf{M}}}_{j}$ and ${\bar{\mathbf{Q}}}_{j}$.

By following the penalty-based augmented Lagrangian method [17, 18], a set of m loop-closure constraints, ${{\varvec{\Phi }}} = \mathbf{0}$, are incorporated in Eq. (8) and the equations of motion for the closed-loop system can be written as [18, 49]

$$\begin{aligned} {\mathbf{M}}^{\Sigma } {\ddot{\mathbf{z}}} + {{\varvec{\Phi }}}_{\mathbf{z}}^{\text {T}} \alpha {{\varvec{\Phi }}} + {{\varvec{\Phi }}}_{\mathbf{z}}^{\text {T}} {\varvec{\uplambda }} = {\mathbf{Q}}^{\Sigma }, \end{aligned}$$

(9)

where ${\mathbf{M}}^{\Sigma } = \left( {\mathbf{R}}_{\text {d}}^{\text {T}} {\mathbf{T}}^{\text {T}} {\bar{\mathbf{M}}} {\mathbf{T}} {\mathbf{R}}_{\text {d}} \right)$, ${\mathbf{Q}}^{\Sigma } = \left[ {\mathbf{R}}_{\text {d}}^{\text {T}} {\mathbf{T}}^{\text {T}} \left( {\bar{\mathbf{Q}}} - {\bar{\mathbf{M}}} {\mathbf{T}} {\dot{\mathbf{R}}}_{\text {d}} {\dot{\mathbf{z}}} \right) \right]$, $\alpha$ is a penalty factor that can be set to the same value for all constraints, ${{\varvec{\Phi }}}_{\mathbf{z}}$ is the Jacobian matrix of ${{\varvec{\Phi }}} \left( {\mathbf{z}} \right) = \mathbf{0}$, and ${\varvec{\uplambda }}$ is the vector of Lagrange multipliers that are iterated at each time-step (k) as

$$\begin{aligned} {\varvec{\uplambda }}_{k}^{(h+1)} = {\varvec{\uplambda }}_{k}^{(h)} + \alpha {{\varvec{\Phi }}}_{k}^{(h+1)}, \end{aligned}$$

(10)

where h is the iteration step. The value of ${\varvec{\uplambda }}_{k}^{(0)}$ is the final value of ${\varvec{\uplambda }}_{k-1}$ from the previous time-step. For simplicity, the constraints are assumed to be holonomic. An example of a closed-loop system is shown in Fig. 1b.

In this study, an implicit single-step trapezoidal rule as in [7] is used. In this method, the relative joint velocities, ${\dot{\mathbf{z}}}$, and accelerations, ${\ddot{\mathbf{z}}}$, are corrected using mass–damping–stiffness–orthogonal projections as [9, 17]

$$\begin{aligned}&\left[ {\mathbf{W}} + {\frac{\Delta t^{2}}{4}} {{\varvec{\Phi }}}_{\mathbf{z}}^{\text {T}} \alpha {{\varvec{\Phi }}}_{\mathbf{z}} \right] {\dot{\mathbf{z}}} = {\mathbf{W}} {\dot{\mathbf{z}}}^{'} - {\frac{\Delta t^{2}}{4}} {{\varvec{\Phi }}}_{\mathbf{z}}^{\text {T}} \alpha {{\varvec{\Phi }}}_{t}, \end{aligned}$$

(11)

$$\begin{aligned}&\left[ {\mathbf{W}} + {\frac{\Delta t^{2}}{4}} {{\varvec{\Phi }}}_{\mathbf{z}}^{\text {T}} \alpha {{\varvec{\Phi }}}_{\mathbf{z}} \right] {\ddot{\mathbf{z}}} \nonumber \\&\quad = {\mathbf{W}} {\ddot{\mathbf{z}}}^{'} - {\frac{\Delta t^{2}}{4}} {{\varvec{\Phi }}}_{\mathbf{z}}^{\text {T}} \alpha \left( {\dot{{\varvec{\Phi }}}}_{\mathbf{z}} {\dot{\mathbf{z}}} + {\dot{{\varvec{\Phi }}}}_{t} \right) , \end{aligned}$$

(12)

where ${\dot{\mathbf{z}}}^{'}$ and ${\ddot{\mathbf{z}}}^{'}$ are, respectively, the relative joint velocities and accelerations obtained from the Newton–Raphson iteration, $\Delta t$ is the time-step, ${\mathbf{W}} = {\mathbf{M}} + {\frac{\Delta t}{2}}{\mathbf{C}} + {\frac{\Delta t^{2}}{4}}{\mathbf{K}}$, with ${\mathbf{C}}$ and ${\mathbf{K}}$ representing, respectively, the contributions of damping and stiffness in the system, and ${{\varvec{\Phi }}}_{t}$ is the partial derivative of the constraints with respect to time t.

2.2 Modeling of hydraulic systems

In this study, the lumped fluid theory [56] is used to describe the hydraulic pressures in a hydraulic circuit. In this approach, a hydraulic circuit is partitioned into discrete volumes where the pressures are assumed to be equally distributed. Thus, the effect of acoustic waves is assumed to be negligible. The modeling concept is illustrated in Fig. 2, where one incoming flow, ${Q_{k 1}}$, and two outgoing flows, ${Q_{k 2}}$ and ${Q_{k 3}}$, are associated with a volume, ${V_k}$. The pressure, ${p_k}$, within a hydraulic volume, ${V_k}$, can be expressed as a function of the effective bulk modulus, ${B_{e_k}}$, volume, ${V_k}$, and incoming and outgoing flows using the following differential equation

$$\begin{aligned} {\dot{p}}_k = \frac{B_{e_k}}{V_k} \sum _{s=1}^{n_f} {Q_{k s}}, \end{aligned}$$

(13)

where ${Q_{k s}}$ is the sum of incoming and outgoing flows related to volume ${V_k}$, and ${n_f}$ is the total number of volume flows going in or out of the volume ${V_k}$. The effective bulk modulus, ${B_{e_k}}$, associated with the volume ${V_k}$ can be expressed as

$$\begin{aligned} {B_{e_k}} = \left( \frac{1}{B_{\mathrm{oil}}} + \sum _{s=1}^{n_c} \frac{V_s}{{V_k}{B_s}} \right) ^{-1}, \end{aligned}$$

(14)

where ${B_{\mathrm{oil}}}$ is the bulk modulus of oil, ${B_s}$ is the bulk modulus of the volume ${V_s}$ that forms the volume ${V_k}$, and ${n_c}$ is the total number of sub-volumes ${V_s}$.

Fig. 2

Modeling concept of hydraulic actuators

2.2.1 Throttle and directional control valves

In this study, a semi-empirical modeling approach [26] is used to describe the valves in the system. In this approach, the volume flow rate, ${Q_{t}}$, through a simple throttle valve can be expressed as

$$\begin{aligned} {Q_{t}} = {C_{v_t}} {{\text {sgn}}({\Delta p})} {\sqrt{\mid \Delta p \mid }}, \end{aligned}$$

(15)

where ${C_{v_t}}$ is the semi-empirical flow rate coefficient of the throttle valve, ${\Delta p}$ is the pressure difference over the valve, and ${{\text {sgn}}({\Delta p})}$ is the signum function which determines the sign of ${\Delta p}$. ${C_{v_t}}$ can be calculated as

$$\begin{aligned} {C_{v_t}} = {C_d} {A_t} \sqrt{\frac{2}{\rho }}, \end{aligned}$$

(16)

where ${\rho }$ is the oil density, ${A_t}$ is the area of the throttle valve, and ${C_d}$ is the flow discharge coefficient.

Similarly, the volume flow rate, ${Q_{d}}$, through a directional control valve can be expressed as

$$\begin{aligned} {Q_{d}} = {C_{v_d}} {U} {{\text {sgn}}({\Delta p})} {\sqrt{\mid \Delta p \mid }}, \end{aligned}$$

(17)

where ${C_{v_d}}$ is the semi-empirical flow rate constant of the valve, and U is the relative spool position. The value of ${C_{v_d}}$ can be obtained from the manufacturers’ catalogues. The volume flow is assumed to be laminar for pressure differences of less than 2 bar, and Eqs. (15) and (17) are modified such that the volume flow and pressure difference follow a linear relation. The spool position can be described using the following differential equation

$$\begin{aligned} {\dot{U}} = \frac{{U_{\mathrm{ref}}} - {U}}{\tau }, \end{aligned}$$

(18)

where ${U_{\mathrm{ref}}}$ is the reference voltage signal for the reference spool position, and ${\tau }$ is the time constant. The value of ${\tau }$ can be obtained from the Bode-diagram of the valve, which describes the dynamics of the valve spool.

2.2.2 Double-acting hydraulic cylinder

The motion of a double-acting hydraulic cylinder, shown in Fig. 3, causes volume flows that can be written as

$$\begin{aligned} {Q_{in}} = {{\dot{x}}}{A_1}, {Q_{out}} = {{\dot{x}}}{A_2}, \end{aligned}$$

(19)

where ${Q_{in}}$ and ${Q_{out}}$ are, respectively, the incoming and outgoing volume flow rates of the cylinder, ${{\dot{x}}}$ is the piston velocity, and ${A_1}$ and ${A_2}$ are, respectively, the piston and piston-rod areas of the cylinder. The force, ${F_{cyl}}$, produced by a cylinder can be written in terms of its dimensions, chamber pressures, and the seal friction as

$$\begin{aligned} {F_{cyl}} = {p_1}{A_1} - {p_2}{A_2} - {F_{\mu }}, \end{aligned}$$

(20)

where ${p_1}$ and ${p_2}$ are, respectively, the pressures on the piston and piston-rod sides of the cylinder, and ${F_{\mu }}$ is the total friction force caused by sealing.

3 Friction force models

Friction force is defined as a force that opposes the relative motion between two surfaces in contact. In the literature, several friction force models have been proposed. These models capture a combination of the Coulomb, stiction, viscous, and Stribeck effects. However, most of the friction models in the static friction model category may suffer from numerical instability because of the discontinuity of the friction force at zero relative tangential velocity. To overcome this numerical inconvenience, many alternative continuous friction models have been developed, for example, as shown in Fig. 4. In the category of static friction models, the Bengisu–Akay and Brown–McPhee friction models [10, 16] are considered in this work.

Fig. 3

Schematic figure of a hydraulic cylinder

Fig. 4

Representation of the classical Stribeck friction model (left [14]), and two alternative friction models (middle [37] and right [10, 16]) to overcome discontinuity at zero relative tangential velocity

The friction models in the dynamic friction category consider the pre-slip displacement [11]. It is for this reason that these models eliminate the discontinuity of the friction force at zero relative tangential velocity. In general, they consider the evolution of friction force based on the actual state of contact and the contact history [38]. In a dynamic model, an extra state variable, such as the average bristle deflection [21], is used, which represents the behavior of surface asperities during the contact [38]. During the sticking phase, the bristles behave like springs. In the category of dynamic friction models, the LuGre and modified LuGre friction models [21, 57] are considered in this work.

3.1 Bengisu–Akay friction model

An approximation of the friction force can be presented by the Coulomb friction law, which established that the magnitude of the friction force depends on the relative tangential velocity between the surfaces in contact. Furthermore, it has been established that the static friction is greater than the kinetic or Coulomb friction and it decreases continuously with the increment of relative tangential velocity. This effect is known as the Stribeck effect [29], as shown in Fig. 4. By considering the numerical stability at zero relative tangential velocity, the friction force can be modeled using two equations, one for the slope and the other for the Stribeck effect, as [10, 37]

$$\begin{aligned} {\mathbf{F}}_{\mu } = {\left\{ \begin{array}{ll} \left( - \frac{{F}_{s}}{{{v}_{s}}^2} \left( {\left| {\mathbf{v}}_{t}\right| } - {{v}_{s}} \right) ^2 + {F}_{s} \right) {\text {sgn}}({\mathbf{v}}_{t}) &{} {\left| {\mathbf{v}}_{t}\right| } < {{v}_{s}}, \\ \left( {{F}_{c}} + {\left( {F}_{s} - {F}_{c}\right) e^{- \xi \left( {\left| {\mathbf{v}}_{t}\right| } - {{v}_{s}} \right) }} \right) {\text {sgn}}({\mathbf{v}}_{t}) &{} {\left| {\mathbf{v}}_{t}\right| } \ge {{v}_{s}}, \end{array}\right. } \end{aligned}$$

(21)

where ${{F}_{c}}$ is the Coulomb friction, ${F}_{s}$ is the static friction, ${\mathbf{F}}_{\mu }$ is the total friction force, ${{v}_{s}}$ is the Stribeck velocity, ${\mathbf{v}}_{t}$ is the relative tangential velocity between the two surfaces in contact, and $\xi$ is a positive parameter that represents the negative slope of the sliding regime. Note that ${{F}_{c}} = {\mu }_{c} \left| {\mathbf{F}}_{n}\right|$ and ${{F}_{s}} = {\mu }_{s} \left| {\mathbf{F}}_{n}\right|$, where ${\mu }_{c}$ and ${\mu }_{s}$ are the coefficients of Coulomb and static frictions, respectively, and ${\mathbf{F}}_{n}$ is the normal contact force.

It should be noted that the viscous friction is not considered in Eq. (21). However, for a hydraulic cylinder where lubricants are present, as in this study, the viscous friction cannot be ignored. Therefore, a corrected version of the Bengisu–Akay friction model is presented in this study by incorporating the viscous friction as

$$\begin{aligned} {\mathbf{F}}_{\mu } = {\left\{ \begin{array}{ll} \left( - \frac{{F}_{s}}{{{v}_{s}}^2} \left( {\left| {\mathbf{v}}_{t}\right| } - {{v}_{s}} \right) ^2 + {F}_{s} \right) {\text {sgn}}({\mathbf{v}}_{t}) &{} {\left| {\mathbf{v}}_{t}\right| } < {{v}_{s}}, \\ \left( {{F}_{c}} + {\left( {F}_{s} - {F}_{c}\right) e^{- \xi \left( {\left| {\mathbf{v}}_{t}\right| } - {{v}_{s}} \right) }} \right) {\text {sgn}}({\mathbf{v}}_{t}) + {f({\mathbf{v}}_{t})} &{} {\left| {\mathbf{v}}_{t}\right| } \ge {{v}_{s}}, \end{array}\right. } \end{aligned}$$

(22)

where the function ${f({\mathbf{v}}_{t})}$ describes the viscous friction. In lubricated contacts, viscous friction is generally considered to be linear viscous friction as [21, 38]

$$\begin{aligned} {f({\mathbf{v}}_{t})} = {\sigma }_{2} {\mathbf{v}}_{t}, \end{aligned}$$

(23)

where ${\sigma }_{2}$ is the coefficient of viscous friction. The effect of viscous friction is crucial, especially, in the presence of fluid lubricant or at high relative velocity [37]. A representation of this model is shown on the right side of Fig. 4. It should be noted that if the slope at ${\mathbf{v}}_{t} = 0$ in Eq. (22) is large, small time-steps are required to properly capture the friction effects at low velocity. This may burden the computational efficiency.

3.2 Brown–McPhee friction model

A suitable alternate method to the classical Stribeck friction model that avoids the discontinuity at zero relative tangential velocity has been presented by Brown and McPhee [16]. This model incorporates the Coulomb, stiction, and viscous friction, and it is valid for both positive and negative relative tangential velocity. This velocity-dependent continuous differential model can be written as [16]

$$\begin{aligned} \begin{aligned}&{\mathbf{F}}_{\mu } = \left( {{F}_{c}} \tanh {\left( 4 \frac{{\left| {\mathbf{v}}_{t}\right| }}{{{v}_{s}}}\right) } + \left( {F}_{s} - {F}_{c}\right) \frac{\frac{{\left| {\mathbf{v}}_{t}\right| }}{{{v}_{s}}}}{\left( \frac{1}{4}\left( \frac{{\left| {\mathbf{v}}_{t}\right| }}{{{v}_{s}}} \right) ^2 + \frac{3}{4} \right) ^2} \right) \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad {\text {sgn}}({\mathbf{v}}_{t}) + {\sigma }_{2} {\mathbf{v}}_{t} \tanh {\left( 4 \right) }. \end{aligned} \end{aligned}$$

(24)

In Eq. (24), the Coulomb friction term approaches ${F}_{c}$ as ${\left| {\mathbf{v}}_{t}\right| }$ increases from zero to ${{v}_{s}}$. Similarly, the static friction term, which represents the stiction and Stribeck effect, has its maximum value as $\left( {F}_{s} - {F}_{c}\right)$ at ${\left| {\mathbf{v}}_{t}\right| } = {{v}_{s}}$ and it then decreases to zero for larger relative tangential velocity, where the Coulomb and viscous friction is dominant. Here, the viscous friction term is linearly scaled with velocity and physically corresponds to thin-film viscous friction [16]. A representation of this model is shown on the right side of Fig. 4. This model is suitable for real-time simulations and optimization problems [16].

3.3 LuGre friction model

In LuGre friction model, the friction is considered as an interaction of the bristles between two surfaces, as shown in Fig. 5, and the model utilizes the average bristle deflection. The LuGre (Lund–Grenoble) model [21] is an extension of the Dahl model [20] that captures the Stribeck and stiction effects. When a tangential force is applied, the bristles start to deflect like a spring, giving rise to the sticking phase. The moment the tangential force is sufficiently large, some of the bristles deflect so much that they start to slip [21].

Fig. 5

Interaction of elastic bristles on one surface with rigid bristles on another surface

The average bristle deflection is quantified by introducing an internal state variable, ${\mathbf{q}}$, such that the model can be expressed as [21, 37]

$$\begin{aligned} {\dot{\mathbf{q}}} = {\mathbf{v}}_{t} - \frac{{\sigma }_{0} {\left| {\mathbf{v}}_{t}\right| }}{g({\mathbf{v}}_{t})} {\mathbf{q}}, \end{aligned}$$

(25)

with

$$\begin{aligned} {g({\mathbf{v}}_{t})} = {{F}_{c}} + {\left( {F}_{s} - {F}_{c}\right) e^{-\left( { \frac{{\left| {\mathbf{v}}_{t}\right| }}{{v}_{s}}}\right) ^{n}}}, \end{aligned}$$

(26)

where ${\mathbf{q}}$ is the average bristle deflection, ${\dot{\mathbf{q}}}$ is the rate of average bristle deflection, ${\sigma }_{0}$ is the stiffness of the elastic bristles, the function ${g({\mathbf{v}}_{t})}$ describes the Stribeck effect [21, 53], and n is the exponent that affects the slope of the Stribeck curve. The total friction force, ${{\mathbf{F}}_{\mu }}$, generated from the bending of the bristles can be written as

$$\begin{aligned} {{\mathbf{F}}_{\mu }} = {\sigma }_{0} {\mathbf{q}} + {\sigma }_{1} {\dot{\mathbf{q}}} + {\sigma }_{2} {\mathbf{v}}_{t}, \end{aligned}$$

(27)

where ${\sigma }_{1}$ is the damping of the elastic bristles, which can be a constant or a function of ${\mathbf{v}}_{t}$.

3.4 Modified LuGre friction model

In this model, the LuGre friction model (Sect. 3.3) is modified by incorporating the dynamics of the lubricant film formation [57]. The lubricant film dynamics is computed using a first-order lag element in which the time constant is varied between the deceleration, acceleration, and dwell periods [57]. Thus, in this model, the friction is obtained as a combination of the bristle model (Sect. 3.3) and the lubricant film dynamics.

Similar to the LuGre friction model, the average bristle deflection is quantified by an internal state variable, ${\mathbf{q}}$, such that [57]

$$\begin{aligned} {\dot{\mathbf{q}}} = {\mathbf{v}}_{t} - \frac{{\sigma }_{0} {\left| {\mathbf{v}}_{t}\right| }}{g({\mathbf{v}}_{t}, {\mathbf{h}})} {\mathbf{q}}, \end{aligned}$$

(28)

with

$$\begin{aligned} {g({\mathbf{v}}_{t}, {\mathbf{h}})} = {{F}_{c}} + {\left[ (1-{\left| {\mathbf{h}}\right| }) {F}_{s} - {F}_{c}\right] e^{-\left( { \frac{{\left| {\mathbf{v}}_{t}\right| }}{{v}_{s}}}\right) ^{n}}}, \end{aligned}$$

(29)

where ${\mathbf{h}}$ is the dimensionless lubricant film thickness parameter, and the function ${g({\mathbf{v}}_{t}, {\mathbf{h}})}$ describes the Stribeck effect. The lubricant film dynamics can be written as [52, 57]

$$\begin{aligned} {\dot{\mathbf{h}}} = \frac{1}{\tau _{h}} \left( {\mathbf{h}}_{ss}- {\mathbf{h}}\right) , \end{aligned}$$

(30)

with

$$\begin{aligned}&{\tau _{h}} = {\left\{ \begin{array}{ll} {\tau _{hp}} &{} \left( {\left| {\mathbf{v}}_{t}\right| } \ne 0, \quad {\left| {\mathbf{h}}\right| } \le {\left| {\mathbf{h}}_{ss}\right| } \right) ,\\ {\tau _{hn}} &{} \left( {\left| {\mathbf{v}}_{t}\right| } \ne 0, \quad {\left| {\mathbf{h}}\right| } > {\left| {\mathbf{h}}_{ss}\right| } \right) ,\\ {\tau _{h0}} &{} \left( {\left| {\mathbf{v}}_{t}\right| } = 0 \right) , \end{array}\right. } \end{aligned}$$

(31)

$$\begin{aligned}&\left| {{\mathbf{h}}_{ss}}\right| = {\left\{ \begin{array}{ll} {K_{f}} {\left| {{\mathbf{v}}_{t}}\right| }^{\frac{2}{3}} &{} \left( {\left| {\mathbf{v}}_{t}\right| } \le {\left| {\mathbf{v}}_{b}\right| } \right) ,\\ {K_{f}} {\left| {{\mathbf{v}}_{b}}\right| }^{\frac{2}{3}} &{} \left( {\left| {\mathbf{v}}_{t}\right| } > {\left| {\mathbf{v}}_{b}\right| } \right) , \end{array}\right. } \end{aligned}$$

(32)

$$\begin{aligned}&{K_{f}} = \left( 1- \frac{{F}_{c}}{{F}_{s}}\right) {\left| {{\mathbf{v}}_{b}}\right| }^{-\frac{2}{3}}, \end{aligned}$$

(33)

where ${\tau _{hp}}$, ${\tau _{hn}}$, ${\tau _{h0}}$ are, respectively, the time constants for the acceleration, deceleration, and dwell periods, ${{\mathbf{h}}_{ss}}$ is the dimensionless steady-state lubricant film thickness parameter, ${K_{f}}$ is a proportional constant, and ${{\mathbf{v}}_{b}}$ is the velocity at which the magnitude of the steady-state friction force becomes almost minimum [52, 57]. In Eq. (31), ${\left| {\mathbf{h}}\right| } \le {\left| {\mathbf{h}}_{ss}\right| }$ represents the acceleration period and ${\left| {\mathbf{h}}\right| } > {\left| {\mathbf{h}}_{ss}\right| }$ represents the deceleration period. Here, it is assumed [57] that the lubricant film thickness increases with velocity only in the negative resistance regime, that is, ${\left| {\mathbf{v}}_{t}\right| } \le {\left| {\mathbf{v}}_{b}\right| }$, otherwise, it has a constant maximum value, as shown in Eq. (32). The total friction force, ${{\mathbf{F}}_{\mu }}$, generated from the bending of the bristles and lubricant film dynamics can be written as

$$\begin{aligned} {{\mathbf{F}}_{\mu }} = {\sigma }_{0} {\mathbf{q}} + {\sigma }_{1} {\dot{\mathbf{q}}} + {\sigma }_{2} {\mathbf{v}}_{t}. \end{aligned}$$

(34)

4 Coupling the dynamics of the multibody and hydraulic systems

In this section, the multibody formulation in Sect. 2.1 is extended to incorporate the dynamics of the hydraulic system, introduced in Sect. 2.2, with the friction force models of a hydraulic cylinder, introduced in Sect. 3, in a monolithic approach [32, 49]. The force vector, ${\mathbf{Q}}^{\Sigma }$, in Eq. (9), is incremented with the pressure variation equations and friction force model such that the combined system of equations can be written as

$$\begin{aligned} \left. \begin{aligned} {\mathbf{M}}^{\Sigma } {\ddot{\mathbf{z}}} + {{\varvec{\Phi }}}_{\mathbf{z}}^{\text {T}} \alpha {{\varvec{\Phi }}} + {{\varvec{\Phi }}}_{\mathbf{z}}^{\text {T}} {\varvec{\uplambda }}&= {\mathbf{Q}}^{\Sigma } \left( {\mathbf{z}}, {\dot{\mathbf{z}}}, {\mathbf{p}}, {\mathbf{F}}_{\mu } \right) \\ {\varvec{\uplambda }}^{(h+1)}&= {\varvec{\uplambda }}^{(h)} + \alpha {{\varvec{\Phi }}}^{(h+1)} \\ {\dot{\mathbf{p}}}&= {{\mathbf{u}}_{0}} \left( {\mathbf{p}}, {\mathbf{z}}, {\dot{\mathbf{z}}} \right) \end{aligned} \, \right\} , \end{aligned}$$

(35)

where ${\mathbf{M}}^{\Sigma }$ and ${\mathbf{Q}}^{\Sigma }$ are the respective accumulated mass matrix and accumulated external force vector as shown in Eq. (9), ${\mathbf{z}} \in {{\mathbb {R}}}^{N_b}$ is the vector of the relative joint coordinates, ${\dot{\mathbf{p}}}$ is the time derivative of the vector of hydraulic pressures, ${\mathbf{p}}$, and ${{\mathbf{u}}_{0}} \left( {\mathbf{p}}, {\mathbf{z}}, {\dot{\mathbf{z}}} \right)$ are the pressure variation equations. Here, it is assumed that the dependency of ${\mathbf{Q}}^{\Sigma }$ with respect to ${\mathbf{z}}$, ${\dot{\mathbf{z}}}$, ${\mathbf{p}}$, and ${\mathbf{F}}_{\mu }$, and the dependency of function ${{\mathbf{u}}_{0}}$ with respect to ${\mathbf{z}}$, ${\dot{\mathbf{z}}}$, and ${\mathbf{p}}$ are known. In static friction models, such as the Bengisu–Akay and Brown–McPhee models, the inclusion of friction force, ${\mathbf{F}}_{\mu }$, in Eq. (35) is a straightforward task, where ${{\mathbf{F}}_{\mu }}$ is dependent on ${\mathbf{z}}$ and ${\dot{\mathbf{z}}}$. However, in dynamic friction models, such as the LuGre and modified LuGre models, the inclusion of ${\mathbf{F}}_{\mu }$ in Eq. (35) utilizes extra state variables to describe the friction, such as

$$\begin{aligned}&\left. \begin{aligned}&{\dot{\mathbf{q}}} = {{\mathbf{u}}_{1}} \left( {\mathbf{q}}, {\mathbf{z}}, {\dot{\mathbf{z}}} \right) \end{aligned} \right\} \qquad (\text {LuGre friction model}), \nonumber \\ \end{aligned}$$

(36)

$$\begin{aligned}&\left. \begin{aligned} {\dot{\mathbf{q}}}&= {{\mathbf{u}}_{2}} \left( {\mathbf{q}}, {\mathbf{z}}, {\dot{\mathbf{z}}}, {\mathbf{h}} \right) \\ {\dot{\mathbf{h}}}&= {{\mathbf{u}}_{3}} \left( {\mathbf{h}}, {\mathbf{z}}, {\dot{\mathbf{z}}} \right) \end{aligned} \right\} (\text {modified LuGre friction model}),\nonumber \\ \end{aligned}$$

(37)

where ${{\mathbf{u}}_{1}} \left( {\mathbf{q}}, {\mathbf{z}}, {\dot{\mathbf{z}}} \right)$ and ${{\mathbf{u}}_{2}} \left( {\mathbf{q}}, {\mathbf{z}}, {\dot{\mathbf{z}}}, {\mathbf{h}} \right)$ are the equations of average bristle deflection variation in the LuGre and modified LuGre friction models, respectively, and ${{\mathbf{u}}_{3}} \left( {\mathbf{h}}, {\mathbf{z}}, {\dot{\mathbf{z}}} \right)$ are the equations of lubricant film thickness variation. The state variables in Eqs. (36) and (37) can be integrated over time in two ways. In the first approach, which is employed in this study, the frictional state variables can be added to the state variables of the coupled equations of motion in Eq. (35) and integrated as shown in this section. In the second approach, the frictional state variables can be integrated locally during resolution of the friction problem [38]. The use of dynamic friction models can introduce numerical stiffness to the system, which may decrease the numerical efficiency of the simulation.

In this study, coupled systems are integrated [55] using an implicit single-step trapezoidal rule, as in [7]. It has already been established in [7, 40] that the trapezoidal rule performs satisfactorily for coupled multibody and hydraulic systems by considering position and pressure as the primary variables instead of accelerations and pressure derivatives. Similarly, average bristle deflection for the LuGre friction model and average bristle deflection and lubricant film thickness for the modified LuGre friction model are considered as primary variables when applying the trapezoidal rule. The implementation details of the trapezoidal rule can be followed from Appendix A. By following Appendix A, the residual vector, $\left[ {\bar{\mathbf{f}}} \left( {\mathbf{x}} \right) \right]$, can be written as

(38)

(39)

(40)

where ${\varvec{\uplambda }}$ is obtained as shown in Eq. (10), whereas the approximated tangent matrix, $\left[ \frac{\partial {\bar{\mathbf{f}}} \left( {\mathbf{x}} \right) }{\partial {\mathbf{x}}} \right]$, can be numerically obtained, as in [32, 49], by using the forward differentiation rule as

$$\begin{aligned} \frac{d f \left( x_{0} \right) }{dx} \approx \frac{f \left( x_{0} + \epsilon \right) - f \left( x_{0} \right) }{\epsilon }, \end{aligned}$$

(41)

where $\epsilon$ is the differentiation increment. To avoid ill-conditioning of the tangent matrix, $\left[ \frac{\partial {\bar{\mathbf{f}}} \left( {\mathbf{x}} \right) }{\partial {\mathbf{x}}} \right] _{k+1}^{(h)}$, $\epsilon$ is computed as [49]

$$\begin{aligned} \epsilon = 1 \times 10^{-8} \text {max} \left( 1 \times 10^{-2}, {\mid x_{0} \mid } \right) , \end{aligned}$$

(42)

where $1 \times 10^{-2}$ limits the minimum value for the differentiation increment to $1 \times 10^{-10}$. In the above friction-based approaches, that is, Eqs. (A.2)–(A.4), ${\dot{\mathbf{z}}}$ and ${\ddot{\mathbf{z}}}$ are corrected using mass–damping–stiffness–orthogonal projections [9, 17], as shown in Eqs. (11) and (12).

5 A case study of a hydraulically actuated four-bar mechanism

In this study, a hydraulically actuated four-bar mechanism, as shown in Fig. 6, is used to illustrate the effect of friction models of a hydraulic cylinder on the four-bar mechanism. The four-bar mechanism is modeled using a semi-recursive formulation, as explained in Sect. 2.1. As can be seen in Fig. 6, three relative joint coordinates, ${z_{1}}$, ${z_{2}}$ and ${z_{3}}$, are used in modeling of the planar structure, and two loop-closure constraints are used for the cut-joint (revolute joint) at point E. The mechanism has one degree of freedom. Note that ${z_{1}}$, ${z_{2}}$ and ${z_{3}}$ represent, respectively, the positions of the crank, coupler, and rocker in the inertial reference frame, XYZ. Their initial values are considered as $60^{\text {o}}$, $-37.90^{\text {o}}$, and $-93.58^{\text {o}}$, respectively. In the integration process, the initial values of the relative joint velocities are considered to be $0^{\text {o}}$/s to avoid instabilities. The crank, coupler, and rocker are assumed to be rectangular beams, whose masses and lengths are, respectively, $m_1 = 16$ kg, $m_2 = 64$ kg, and $m_3 = 40$ kg, and $L_1 = 2$ m, $L_2 = 8$ m, and $L_3 = 5$ m. The mass moment of inertia of the bodies is considered as $\frac{m{L}^2}{12}$. In the XYZ frame, the locations of points E, F and G are, respectively, ${\mathbf{r}}_{E} = \left[ 10, 0, 0 \right] ^{\text {T}}$ m, ${\mathbf{r}}_{F} = \left[ \frac{L_1}{2} \cos {(z_1)}, \frac{L_1}{2} \sin {(z_1)}, 0 \right] ^{\text {T}}$ m and ${\mathbf{r}}_{G} = \left[ - \frac{L_1}{2}, 0, 0 \right] ^{\text {T}}$ m. Point F is located at the center of mass of the crank.

Fig. 6

Four-bar mechanism actuated by a double-acting hydraulic cylinder

The four-bar mechanism, as shown in Fig. 6, is hydraulically actuated using a hydraulic circuit that consists of a pump, a tank, a directional control valve, a throttle valve, a double-acting hydraulic cylinder, and connecting hoses. For simplicity, leakage in the hydraulic components is neglected. Following the lumped fluid theory, the hydraulic circuit is partitioned into discrete volumes (shown in Fig. 6), ${V_1}$, ${V_2}$, and ${V_3}$, whose respective pressures ${p_1}$, ${p_2}$, and ${p_3}$ are computed as

$$\begin{aligned} \left. \begin{aligned} {{{\dot{p}}}_1}&= \frac{B_{e1}}{V_1} \left( {Q_{d1}} - {Q_{t}} \right) \\ {{{\dot{p}}}_2}&= \frac{B_{e2}}{V_2} \left( {Q_{t}} - {A_{2}} {{\dot{s}}} \right) \\ {{{\dot{p}}}_3}&= \frac{B_{e3}}{V_3} \left( {A_{3}} {{\dot{s}}} - {Q_{3d}} \right) \end{aligned} \, \right\} , \end{aligned}$$

(43)

where ${Q_{d1}}$ and ${Q_{3d}}$ are the volume flow rates from the directional control valve (Eq. 17), ${Q_{t}}$ is the volume flow rate from the throttle valve (Eq. 15), ${B_{e1}}$, ${B_{e2}}$, and ${B_{e3}}$ are the effective bulk modulus of the respective control volumes (Eq. 14), ${A_{2}}$ and ${A_{3}}$ are the areas of the piston and piston-rod sides, respectively, and ${{\dot{s}}}$ is the actuator velocity. For the presented hydraulic circuit, the control volumes can be written as

$$\begin{aligned} \left. \begin{aligned} {V_1}&= {V_{h_1}} \\ {V_2}&= {V_{h_2}} + {A_{2}} {l_2}\\ {V_3}&= {V_{h_3}} + {A_{3}} {l_3} \end{aligned} \, \right\} , \end{aligned}$$

(44)

where ${V_{h_1}}$, ${V_{h_2}}$, and ${V_{h_3}}$ are the volumes of the respective hoses, and ${l_2}$ and ${l_3}$ are the chamber lengths of the piston and piston-rod sides, respectively, which can be calculated as ${l_2} = \left( ({l_2})_{t = 0} + {\mid {\mathbf{s}} \mid }_{t = 0} - {\mid {\mathbf{s}} \mid } \right)$ and ${l_3} = \left( ({l_3})_{t = 0} - {\mid {\mathbf{s}} \mid }_{t = 0} + {\mid {\mathbf{s}} \mid } \right)$, where ${\mid {\mathbf{s}} \mid }$ is the actuator length of the hydraulic cylinder. The values of ${\mathbf{s}}$ and ${{\dot{s}}}$ are, respectively, calculated as

$$\begin{aligned} \left. \begin{aligned} {\mathbf{s}}&= {\mathbf{r}}_{F} - {\mathbf{r}}_{G}\\ {{\dot{s}}}&= \frac{d{\mid {\mathbf{s}} \mid }}{dt} = {\dot{{\mathbf{s}}}} \cdot \frac{{\mathbf{s}}}{{\mid {\mathbf{s}} \mid }} = {\dot{\mathbf{r}}}_{F} \cdot \frac{{\mathbf{s}}}{{\mid {\mathbf{s}} \mid }} \end{aligned} \, \right\} , \end{aligned}$$

(45)

where ${\dot{\mathbf{r}}}_{F}$ is the velocity vector of point F calculated using classical kinematic relations, as in [19, 30]. The force, ${F_c}$, produced by the hydraulic cylinder (Eq. 20) is expressed as ${\mathbf{F}}_{c} = \left[ \frac{s_{\text {X}}}{{\mid {\mathbf{s}} \mid }}{F_c}, \frac{s_{\text {Y}}}{{\mid {\mathbf{s}} \mid }}{F_c}, \frac{s_{\text {Z}}}{{\mid {\mathbf{s}} \mid }}{F_c} \right] ^{\text {T}}$, where ${s_{\text {X}}}$, ${s_{\text {Y}}}$, and ${s_{\text {Z}}}$ are the components of vector ${\mathbf{s}}$ in the inertial reference frame, XYZ. From the static configuration at $t=0$, $({F_c})_{t=0} = 681.23$ N, $({p_1})_{t=0} = ({p_2})_{t=0}$, and $({p_2})_{t=0} = \left( ({F_c})_{t=0} + {A_{3}} ({p_3})_{t=0} \right) /{A_{2}}$, where the friction force is assumed as zero and $({p_3})_{t=0}$ as 3.5 MPa. The system is hydraulically actuated for 10 s using the reference voltage signal, $U_{\mathrm{ref}}$, as

$$\begin{aligned} U_{\mathrm{ref}} = {\left\{ \begin{array}{ll} 0 &{} t< 1 \text {s}, 2.5 \text {s} \le t< 5 \text {s}, t \le 9 \text {s},\\ 10 &{} 1 \text {s} \le t< 2.5 \text {s},\\ -10 &{} 5 \text {s} \le t < 8 \text {s}, \end{array}\right. } \end{aligned}$$

(46)

where t is the simulation run time. The parameters of the hydraulic circuit are shown in Table 1.

Table 1 Parameters of the hydraulic system

Table 2 Parameters of friction models of a hydraulic cylinder

In this study, the coupled system is integrated by incorporating the friction models of the hydraulic cylinder, as shown in Sect. 4. The parameters of the friction models are shown in Table 2, where the values are selected based on typical values found in the literature. Static friction models, that is, the Bengisu–Akay model and the Brown–McPhee friction model, do not require integration of additional variables other than the positions and pressures of the coupled system. On the other hand, dynamics friction models, that is, the LuGre model and the modified LuGre friction model, require additional variables to be integrated along with the coupled equations of motion. In the proposed integration scheme, the set of variables used to solve the equations of the coupled system (Sect. 4) are

$$\begin{aligned} \left. \begin{aligned} {\mathbf{x}}&= \left[ {\mathbf{z}}^{\text {T}}, \; {\mathbf{p}}^{\text {T}} \right] ^{\text {T}}\\&\quad \quad (\text {Bengisu--Akay and Brown--McPhee approaches})\\ {\mathbf{x}}&= \left[ {\mathbf{z}}^{\text {T}}, \; {\mathbf{p}}^{\text {T}}, \; {\mathbf{q}}^{\text {T}} \right] ^{\text {T}}\\&\quad \quad (\text {LuGre approach})\\ {\mathbf{x}}&= \left[ {\mathbf{z}}^{\text {T}}, \; {\mathbf{p}}^{\text {T}}, \; {\mathbf{q}}^{\text {T}}, \; {\mathbf{h}}^{\text {T}} \right] ^{\text {T}}\\&\quad \quad (\text {modified LuGre approach})\\ \end{aligned}\, \right\} . \end{aligned}$$

(47)

In the trapezoidal integration scheme, the error tolerance for the position is $1 \times 10^{-7}$ rad; for the average bristle deflection and lubricant film thickness, it is $1 \times 10^{-7}$ m; and for the pressure $1 \times 10^{-2}$ Pa. The penalty factor, $\alpha$, in Eq. (9) is considered as $1 \times 10^{11}$ in this study. The voltage, which represents the relative spool position, is integrated using the trapezoidal rule, and the error tolerance is considered to be $1 \times 10^{-7}$ V. All the approaches in this study are implemented in the Matlab environment.

6 Results and discussion

This section presents simulation results of the hydraulically actuated four-bar mechanism, shown in Fig. 6, and demonstrates the effect of friction models of the hydraulic cylinder on the four-bar mechanism. The simulation frames of the four-bar structure at different instants of time, representing the positions of the bodies, are shown in Fig. 7. Here, the four coupled system approaches, namely, the Bengisu–Akay approach, Brown–McPhee approach, LuGre approach, and modified LuGre approach, are compared based on the simulation work cycle, friction force, energy balance, and numerical efficiency. In this study, all the simulations are run with a time-step of 1 ms.

Fig. 7

Position of the four-bar mechanism at every second during the simulation run

Fig. 8

The work cycle representation of the four-bar mechanism with a time-step of 1 ms

6.1 The work cycle representation

In the presented case study, the hydraulic cylinder tilts the four-bar structure outward between 1 and 2.5 s and inward between 5 and 8 s. In the subsequent plots, the regions between the opening and closing of the directional control valve are highlighted in purple. For demonstration, only the crank angle is presented in Fig. 8a. However, the coupler and rocker angles follow a similar pattern. Similarly, only pressure $p_3$ is presented in Fig. 8b; pressures $p_1$ and $p_2$ follow a similar pattern. Even though the differences in the relative joint coordinates and pressures may be small, they differ based on the friction model utilized in the modeling. Such small differences can be an important aspect to consider in applications where high precision and/or low vibration is a pre-requisite. Thus, the friction model can significantly affect the control system performance. It should be noted that the semi-recursive multibody formulation utilizes the full set of relative joint coordinates in the equations of motion.

Fig. 9

Comparison of friction models of the hydraulic cylinder with a simulation time-step of 1 ms

6.2 Friction force

A comparison of the friction force models of the hydraulic cylinder is shown in Fig. 9. The friction forces in all four approaches are continuous at zero relative piston velocity, thus, avoiding numerical instabilities. Figure 9b compares the friction–velocity characteristics of the approaches. The curves corresponding to the Bengisu–Akay and Brown–McPhee approaches match with their definitions, as described in Sect. 3, that is, they describe the Coulomb, stiction, Stribeck, and viscous friction effects. The LuGre and modified LuGre approaches evaluate the friction behavior by using extra state variables, such as the average bristle deflection in the LuGre approach and the average bristle deflection and lubricant film thickness in the modified LuGre approach. As shown in Fig. 9b, the latter two approaches can incorporate pre-slip displacement and frictional lag. The pre-slip displacement implies a small motion of the bristles in the elastic range, when the applied force is less than the break-away force [38]. It can help to determine the static friction as well as the Stribeck effect in the steady state. Frictional lag is a delayed behavior of the friction force with respect to velocity such that the friction force is higher for acceleration than during deceleration.

6.3 Energy balance

The energy balance in the approaches is analyzed by comparing the potential energy, kinetic energy, and work done by the hydraulic cylinder. The energy comparison is shown in Fig. 10, where the energy balance in all four studied approaches showed good agreement with respect to each other. With the Bengisu–Akay approach, the peak energy drift is 0.45 J, which is 0.37% of the maximum cylinder work, 121.02 J, whereas with the Brown–McPhee approach, the peak energy drift is 0.45 J, which is 0.37% of the maximum cylinder work, 120.99 J. With the LuGre approach, the peak energy drift is 0.44 J, which is 0.36% of the maximum cylinder work, 120.94 J, and in the modified LuGre approach, the peak energy drift is 0.44 J, which is 0.36% of the maximum cylinder work, 120.97 J. It should be noted that in all four approaches, the peak energy drift occurred at the opening of the directional control valve at around 1 s. An analogy can be drawn between the hydraulic system and a stiff spring supporting the four-bar structure.

Fig. 10

Comparison of energies with a simulation time-step of 1 ms

6.4 Numerical efficiency

The numerical efficiencies of all four approaches are compared in Figs. 11 and 12, and the average and maximum iterations and total integration time are shown in Table 3. The maximum number of iterations occurred during the opening and closing of the directional control valve. Otherwise, the iterations are mostly one iteration in the Bengisu–Akay and Brown–McPhee approaches and two iterations in the LuGre and modified LuGre approaches. During closing of the directional control valve, the LuGre and modified LuGre approaches required more iterations than the Bengisu–Akay and Brown–McPhee approaches (Fig. 11).

Fig. 11

Number of iterations in the Newton–Raphson method with a time-step of 1 ms

Fig. 12

Comparison of the cumulative integration time with a simulation time-step of 1 ms

Table 3 Comparison of the numerical efficiencies

The integration time of the LuGre and modified LuGre approaches is greater than that of the Bengisu–Akay and Brown–McPhee approaches, which is in agreement with the literature [37, 38]. The poor numerical efficiency of the LuGre and modified LuGre approaches can be attributed to the numerical stiffness introduced by use of extra state variable(s), such as average bristle deflection in the LuGre approach and average bristle deflection and lubricant film thickness in the modified LuGre approach. The poor numerical efficiency of the Bengisu–Akay approach compared with the Brown–McPhee approach is attributed to the change in friction equations during the simulation. The Brown–McPhee approach is relatively the most efficient approach and is a potential candidate for real-time applications [16]. Real-time capabilities can be achieved by implementing the approach in a lower language, such as C++ or Fortran, and by limiting the number of iterations to a lower value.

7 Conclusion

In simulation of coupled multibody and hydraulic systems, an important aspect in the modeling is the nonlinearity and numerical stiffness introduced by the friction model of a hydraulic cylinder. The objective of this paper was to couple various friction models of a hydraulic cylinder with the equations of motion of a hydraulically actuated multibody system in a monolithic framework. The study considered two static friction models: the Bengisu–Akay model and the Brown–McPhee model, and two dynamic friction models: the LuGre model and the modified LuGre model. Within the monolithic framework, the multibody system was described using a semi-recursive formulation and the hydraulic actuator was described using the lumped fluid theory. A hydraulically actuated four-bar mechanism was examined as a case study and the four approaches were compared based on the work cycle, friction force, energy balance, and numerical efficiency.

The relative joint coordinates and hydraulic pressures were affected by the friction force model selected. This is a significant aspect that should be considered in modeling, especially, in applications where high precision and/or low vibration is a pre-requisite. The Bengisu–Akay and Brown–McPhee approaches showed traditional friction–velocity characteristics, namely the Coulomb, stiction, Stribeck, and viscous friction effects. The LuGre and modified LuGre approaches demonstrated frictional phenomena such as pre-slip displacement and frictional lag. All four approaches studied showed acceptable results for energy balance. The modified LuGre approach had the poorest numerical efficiency, which was attributed to the solution of additional state variables: average bristle deflection and fluid film thickness. The Bengisu–Akay approach was more efficient than the LuGre approach but less efficient than the Brown–McPhee approach because of the change in friction equation during the simulation. It can be concluded that the Brown–McPhee approach appears to be numerically the most efficient approach and it was well able to describe usual friction characteristics in dynamic simulation of hydraulically actuated multibody systems.

In future work, the Brown–McPhee approach could be implemented in a lower language, such as C++ or Fortran, to assess real-time capabilities further. The methods presented in this study may be extended to study of state and force estimators. Studies may also be directed toward coupling the dynamic friction models with other multibody formulations. Future studies can investigate the comparative responses of multibody systems based on the high and low magnitudes of the stiffness/damping of dynamic friction models of a hydraulic cylinder and based on throttling in pressure lines. This can lead to a possible source for a stick-slip behavior between the hydraulic cylinder and piston. Furthermore, static friction models that introduce discontinuity at zero relative velocity can be considered in future studies to demonstrate the numerical instability caused by them.

Appendix A: Numerical integration scheme

In this study, coupled systems are integrated using an implicit single-step trapezoidal rule. By applying the rule ${\mathbf{z}}_{k+1} = {\mathbf{z}}_{k} + \frac{\Delta t}{2} \left( {\dot{\mathbf{z}}}_{k} + {\dot{\mathbf{z}}}_{k+1} \right)$ to positions, ${\mathbf{z}}_{k+1}$, velocities, ${\dot{\mathbf{z}}}_{k+1}$, pressures, ${\mathbf{p}}_{k+1}$, average bristle deflections, ${\mathbf{q}}_{k+1}$, and lubricant film thicknesses, ${\mathbf{h}}_{k+1}$, the velocities, accelerations, pressure derivatives, rate of average bristle deflections, and lubricant film thickness derivatives at time-step $\left( k+1 \right)$ can be, respectively, written as

$$\begin{aligned} \left. \begin{aligned} {\dot{\mathbf{z}}}_{k+1}&= \frac{2}{\Delta t} {\mathbf{z}}_{k+1} - \left( \frac{2}{\Delta t} {\mathbf{z}}_{k} + \dot{\mathbf{z}}_{k} \right) = \frac{2}{\Delta t} {\mathbf{z}}_{k+1} + {\hat{\dot{\mathbf{z}}}}_{k} \\ {\ddot{\mathbf{z}}}_{k+1}&= \frac{4}{\Delta t^{2}} {\mathbf{z}}_{k+1} - \left( \frac{4}{\Delta t^{2}} {\mathbf{z}}_{k} \right. \\&\left. \qquad + \frac{4}{\Delta t} \dot{\mathbf{z}}_{k} + \ddot{\mathbf{z}}_{k} \right) = \frac{4}{\Delta t^{2}} {\mathbf{z}}_{k+1} + {\hat{\ddot{\mathbf{z}}}}_{k} \\ {\dot{\mathbf{p}}}_{k+1}&= \frac{2}{\Delta t} {\mathbf{p}}_{k+1} - \left( \frac{2}{\Delta t} {\mathbf{p}}_{k} + \dot{\mathbf{p}}_{k} \right) = \frac{2}{\Delta t} {\mathbf{p}}_{k+1} + {\hat{\dot{\mathbf{p}}}}_{k} \\ {\dot{\mathbf{q}}}_{k+1}&= \frac{2}{\Delta t} {\mathbf{q}}_{k+1} - \left( \frac{2}{\Delta t} {\mathbf{q}}_{k} + \dot{\mathbf{q}}_{k} \right) = \frac{2}{\Delta t} {\mathbf{q}}_{k+1} + {\hat{\dot{\mathbf{q}}}}_{k} \\ {\dot{\mathbf{h}}}_{k+1}&= \frac{2}{\Delta t} {\mathbf{h}}_{k+1} - \left( \frac{2}{\Delta t} {\mathbf{h}}_{k} + \dot{\mathbf{h}}_{k} \right) = \frac{2}{\Delta t} {\mathbf{h}}_{k+1} + {\hat{\dot{\mathbf{h}}}}_{k} \end{aligned} \, \right\} . \end{aligned}$$

(A.1)

By introducing Eq. (A.1) into Eqs. (35)–(37), the dynamic equilibrium, established at time-step $\left( k+1 \right)$, for the coupled system can be written as

$$\begin{aligned} \begin{aligned}&\begin{aligned} {\mathbf{M}}^{\Sigma } {\mathbf{z}}_{k+1} + {\frac{\Delta t^{2}}{4}}&\left( {{\varvec{\Phi }}}_{{\mathbf{z}}}^{\text {T}}\right) _{k+1} \left( \alpha {{\varvec{\Phi }}}_{k+1} + {\varvec{\uplambda }}_{k+1} \right) - \\&\left. \begin{aligned} {\frac{\Delta t^{2}}{4}} \left( {\mathbf{Q}}^{\Sigma }\right) _{k+1} + {\frac{\Delta t^{2}}{4}} {\mathbf{M}}^{\Sigma } \hat{\ddot{\mathbf{z}}}_{k} = 0 \\ {\varvec{\uplambda }}_{k+1}^{(h+1)} = {\varvec{\uplambda }}_{k+1}^{(h)} + \alpha {{\varvec{\Phi }}}_{k+1}^{(h+1)} \\ {\frac{\Delta t}{2}} {\mathbf{p}}_{k+1} - {\frac{\Delta t^{2}}{4}} \left( {{\mathbf{u}}_{0}}\right) _{k+1} + {\frac{\Delta t^{2}}{4}} \hat{\dot{\mathbf{p}}}_{k} = 0 \end{aligned} \, \right\} \\ \end{aligned} \\&(\text {Bengisu--Akay and Brown--McPhee approaches}), \end{aligned} \end{aligned}$$

(A.2)

$$\begin{aligned} \begin{aligned}&\begin{aligned} {\mathbf{M}}^{\Sigma } {\mathbf{z}}_{k+1} + {\frac{\Delta t^{2}}{4}}&\left( {{\varvec{\Phi }}}_{{\mathbf{z}}}^{\text {T}}\right) _{k+1} \left( \alpha {{\varvec{\Phi }}}_{k+1} + {\varvec{\uplambda }}_{k+1} \right) - \\&\left. \begin{aligned} {\frac{\Delta t^{2}}{4}} \left( {\mathbf{Q}}^{\Sigma }\right) _{k+1} + {\frac{\Delta t^{2}}{4}} {\mathbf{M}}^{\Sigma } \hat{\ddot{\mathbf{z}}}_{k} = 0 \\ {\varvec{\uplambda }}_{k+1}^{(h+1)} = {\varvec{\uplambda }}_{k+1}^{(h)} + \alpha {{\varvec{\Phi }}}_{k+1}^{(h+1)} \\ {\frac{\Delta t}{2}} {\mathbf{p}}_{k+1} - {\frac{\Delta t^{2}}{4}} \left( {{\mathbf{u}}_{0}}\right) _{k+1} + {\frac{\Delta t^{2}}{4}} \hat{\dot{\mathbf{p}}}_{k} = 0 \\ {\frac{\Delta t}{2}} {\mathbf{q}}_{k+1} - {\frac{\Delta t^{2}}{4}} \left( {{\mathbf{u}}_{1}}\right) _{k+1} + {\frac{\Delta t^{2}}{4}} \hat{\dot{\mathbf{q}}}_{k} = 0 \end{aligned} \, \right\} \\ \end{aligned} \\&(\text {LuGre approach}), \end{aligned} \end{aligned}$$

(A.3)

$$\begin{aligned} \begin{aligned}&\begin{aligned} {\mathbf{M}}^{\Sigma } {\mathbf{z}}_{k+1} + {\frac{\Delta t^{2}}{4}}&\left( {{\varvec{\Phi }}}_{{\mathbf{z}}}^{\text {T}}\right) _{k+1} \left( \alpha {{\varvec{\Phi }}}_{k+1} + {\varvec{\uplambda }}_{k+1} \right) - \\&\left. \begin{aligned} {\frac{\Delta t^{2}}{4}} \left( {\mathbf{Q}}^{\Sigma }\right) _{k+1} + {\frac{\Delta t^{2}}{4}} {\mathbf{M}}^{\Sigma } \hat{\ddot{\mathbf{z}}}_{k} = 0 \\ {\varvec{\uplambda }}_{k+1}^{(h+1)} = {\varvec{\uplambda }}_{k+1}^{(h)} + \alpha {{\varvec{\Phi }}}_{k+1}^{(h+1)} \\ {\frac{\Delta t}{2}} {\mathbf{p}}_{k+1} - {\frac{\Delta t^{2}}{4}} \left( {{\mathbf{u}}_{0}}\right) _{k+1} + {\frac{\Delta t^{2}}{4}} \hat{\dot{\mathbf{p}}}_{k} = 0 \\ {\frac{\Delta t}{2}} {\mathbf{q}}_{k+1} - {\frac{\Delta t^{2}}{4}} \left( {{\mathbf{u}}_{2}}\right) _{k+1} + {\frac{\Delta t^{2}}{4}} \hat{\dot{\mathbf{q}}}_{k} = 0 \\ {\frac{\Delta t}{2}} {\mathbf{h}}_{k+1} - {\frac{\Delta t^{2}}{4}} \left( {{\mathbf{u}}_{3}}\right) _{k+1} + {\frac{\Delta t^{2}}{4}} \hat{\dot{\mathbf{h}}}_{k} = 0 \end{aligned} \, \right\} \\ \end{aligned} \\&(\text {modified LuGre approach}). \end{aligned} \end{aligned}$$

(A.4)

Equations (A.2)–(A.4) are nonlinear system of equations that can be represented as ${\bar{\mathbf{f}}} \left( {\mathbf{x}}_{k+1} \right) = \mathbf{0}$, where ${\mathbf{x}} = \left[ {\mathbf{z}}^{\text {T}}, {\mathbf{p}}^{\text {T}} \right] ^{\text {T}}$ for the Bengisu–Akay and Brown–McPhee approaches, ${\mathbf{x}} = \left[ {\mathbf{z}}^{\text {T}}, {\mathbf{p}}^{\text {T}}, {\mathbf{q}}^{\text {T}} \right] ^{\text {T}}$ for the LuGre approach, and ${\mathbf{x}} = \left[ {\mathbf{z}}^{\text {T}}, {\mathbf{p}}^{\text {T}}, {\mathbf{q}}^{\text {T}}, {\mathbf{h}}^{\text {T}} \right] ^{\text {T}}$ for the modified LuGre approach. Such nonlinear systems of equations can be solved iteratively using the Newton–Raphson method as [32, 49]

$$\begin{aligned} \left[ \frac{\partial {\bar{\mathbf{f}}} \left( {\mathbf{x}} \right) }{\partial {\mathbf{x}}} \right] _{k+1}^{(h)} \Delta {\mathbf{x}}_{k+1}^{(h)} = - \left[ {\bar{\mathbf{f}}} \left( {\mathbf{x}} \right) \right] _{k+1}^{(h)}, \end{aligned}$$

(A.5)

where $\left[ {\bar{\mathbf{f}}} \left( {\mathbf{x}} \right) \right]$ is the residual vector and $\left[ \frac{\partial {\bar{\mathbf{f}}} \left( {\mathbf{x}} \right) }{\partial {\mathbf{x}}} \right]$ is the approximated tangent matrix.