Learning-based nonlinear model predictive control with accurate uncertainty compensation

Abstract

A learning-based nonlinear model predictive control (LBNMPC) method is proposed in this paper for general nonlinear systems under system uncertainties and subject to state and input constraints. The proposed LBNMPC strategy decouples the robustness and performance requirements by employing an additional learned model and introducing it into the MPC framework along with the nominal model. The nominal model helps to ensure the closed-loop system’s safety and stability, and the learned model aims to improve the tracking behaviors. As a core of the learned model construction, an online parameter estimator is designed to deal with system uncertainties. This estimation process effectively evaluates both the current and historical effects of uncertainties, leading to superior estimating performance compared with conventional methods. By constructing an invariant terminal constraint set, we prove that the LBNMPC is recursively feasible and robustly asymptotically stable. Numerical verifications for a two-link manipulator are conducted to validate the effectiveness and robustness of the proposed control scheme.

1 Introduction

Model predictive control (MPC) technique has received extensive attention over the recent decades [1,2,3], given its optimizing ability with respect to user-defined cost functions and its constraint handling ability regarding state and input constraints. Balancing the robustness and performance requirements is a challenging task in the design of advanced MPC schemes [4]. Though robust MPC methods [5], such as the min–max MPC [6] and tube-based MPC [7], can ensure robustness and constraint handling requirements, these methods usually over-prioritize robustness properties, causing performance degradation and conservativeness. Several control strategies for uncertain systems have been investigated recently [8,9,10,11]. Considering the efficiency and capability against uncertainties [12,13,14], adaptive MPC methods were proposed to reduce system conservativeness and improve the closed-loop performance in [15,16,17]. Moreover, a learning-based MPC (LBMPC) was proposed in [18] for linear systems. LBMPC combines the advantages of both the adaptive control and robust MPC, making it possible to improve performance under system uncertainties while guaranteeing robustness and safety requirements. The main principle of LBMPC is to minimize a cost function by using two parallel models: i) the learned model, which is modified online for performance enhancement purposes; ii) the nominal model, which is employed to ensure safety and stability [19]. This strategy, to some extent, decouples and balances the robustness and the performance of the closed-loop system. Given these merits, LBMPC has been employed in various practical applications [20,21,22].

However, existing LBMPC schemes [18,19,20,21,22] are only designed for linear nominal models. Moreover, only conventional certainty-equivalence (CE)-based adaptive control [23] or statistic-based estimation methods [24] were employed in the existing LBMPC frameworks. It is well understood that adaptive controllers synthesized through the CE principle cannot guarantee the convergence of parameter estimation errors to zero unless reference signals additionally satisfy the strong persistent-excitation (PE) conditions [25]. Therefore, the CE-based adaptive law may lead to poor transient performance and fail to estimate the true values of unknown parameters. Recently, the concurrent-learning adaptive control (CLAC) method was proposed to address the drawbacks of CE-based adaptive controllers [26]. State in a nutshell, this design innovatively uses specially selected and online recorded data concurrently with instantaneously incoming measurements for adaptation. Thus, the CLAC strategy can effectively estimate the unknown parameters based on both the current and historical effects, resulting in superior estimation performance under relaxed excitation conditions. However, how to embed the CLAC technique into the MPC framework (especially for discrete models) is still an open problem.

Motivated by these facts, a learning-based nonlinear MPC (LBNMPC) scheme with a concurrent-learning estimator is proposed in this paper for uncertain nonlinear systems, subject to input and state constraints. To meet the robustness and performance requirements of the closed-loop system simultaneously, an additional learned model enriched by the learning-based uncertainty estimator is introduced into the MPC framework. The main contributions are in order:

• (1) In contrast to existing LBMPC schemes [18, 22] that only consider linear nominal models, this work deals with nonlinear nominal models, and the stability and robustness of the closed-loop system can still be strictly guaranteed by utilizing robust MPC theory. The terminal penalty and inequality constraints force the system states in a terminal region, and the recursive feasibility of the system guarantees the asymptotic stability of the closed-loop system.

• (2) A novel concurrent-learning estimator is designed in a discrete-time form and introduced into the LBNMPC. By employing both instantaneous and historical state data (the historical state data are recorded online), this estimator ensures superior estimation performance compared with conventional methods. It guarantees the exponential convergence of parameter estimation errors, subject to the satisfaction of a relaxed excitation condition.

The remainder of this paper is organized as follows. Section 2 establishes the main framework of our LBNMPC algorithm. Section 3 analyzes the recursive feasibility and stability of the LBNMPC. Section 4 presents the adaptive estimation procedure with stability analysis. In Sect. 5, numerical simulations are illustrated to show the advantages of LBNMPC. Finally, the paper ends with some conclusions in Sect. 6.

Notations. ${\mathbb{R}}_{ \ge a}$ signifies a set of numbers that their real parts are greater than a. The operation $||x||_{Q}^{2}$ means $||x||_{Q}^{2} = x^{T} Qx$, where $Q$ is a positive-definite matrix. The operator ${\mathbb{X}} \oplus {\mathbb{Y}} =$ $\{ x + y|x \in \,\,{\mathbb{X}},y \in \,\,{\mathbb{Y}}\}$ denotes the Minkowski sum, where x and y are elements in the sets ${\mathbb{X}}$ and ${\mathbb{Y}}$, respectively. The operator ${{\mathbb{X}} \ominus {\mathbb{Y}}}$ means ${{\mathbb{X}} \ominus {\mathbb{Y}}} = \{ z \in {\mathbb{R}}^{n} :z \oplus {\mathbb{Y}} \subseteq {\mathbb{X}}\}$[27]. We also denote ${\text{int}} ({\mathcal{F}})$ as the interior of the set ${\mathcal{F}}$. Also, $\lambda_{\min } (\cdot)$ and $\lambda_{\max } (\cdot)$ denote the minimum and maximum eigenvalues of corresponding matrices.

1.1 Definitions

A function $\varpi :{\mathbb{R}}_{ \ge 0} \to {\mathbb{R}}_{ \ge 0}$ is type-$\mathcal{K}$ if it is continuous, strictly increasing, and $\varpi (0) = 0$. Moreover, the function $\varpi$ belongs to class $\mathcal{K}_{\infty }$ if $\varpi (s) \to \infty$ for $s \to \infty$ [27]. Furthermore, a function $\beta :{\mathbb{R}}_{ \ge 0} \times {\mathbb{R}}_{ \ge 0} \to {\mathbb{R}}_{ \ge 0}$ is a $\mathcal{K}\mathcal{L}$ function if $\beta \left( {,t} \right)$ is type-$\mathcal{K}$ for $t \ge 0$, $\beta \left( {s,} \right)$ is nonincreasing for $s \ge 0$, and $\beta \left( {s,t} \right) \to 0$ as $t \to \infty$. Finally, a set is a $\mathcal{C}$-set if it is compact and convex, and it is a $\mathcal{P}\mathcal{C}$-set once it contains the origin.

1.2 LBNMPC strategy

As the main contribution of this work, a LBNMPC framework is developed in this section for general nonlinear systems under system uncertainties. The LBNMPC scheme aims to minimize the quadratic objective function consisting of a stage cost and a terminal cost, subject to nonlinear dynamics, state constraints, input constraints, and a terminal inequality constraint.

1.3 Problem statement

A LBMPC method was proposed in Ref. [18] to improve the system performance while ensuring robustness. It considers a linear nominal model and a learned model with uncertainties. The linear nominal model is used to guarantee the stability of the system. An identification tool is employed for the learned model to improve performance. The LBMPC was implemented in heating, ventilation, and air-conditioning systems in Ref. [20] and the real-time control of quadrotor helicopters in Refs. [19, 21], and [22]. However, all these elegant results are built on linear nominal models. Considering that many practical systems have strong nonlinear properties, this paper aims to address the optimal control problem for nonlinear systems subject to multiple constraints and system uncertainties. The main challenge comes from how to make a balance between adaptability and robustness while strictly guaranteeing the closed-loop stability. Motivated by these facts, a LBNMPC scheme with a high-performance learning estimator is proposed in this paper to solve optimal control problems for uncertain nonlinear systems under constraints. Firstly, the optimal control problem is formulated as follows.

Consider a discrete-time nonlinear system as follows

$$ x^{ + } = f(x,u) + w(x,u) $$

(1)

where $x \in {\mathbb{R}}^{n}$ is the state vector, $u \in {\mathbb{R}}^{m}$ is the control input vector, and $x^{ + } \in {\mathbb{R}}^{n}$ denotes the successor state of x. Besides, $f(\cdot)$ denotes the nominal model of the system which is assumed to be twice continuously differentiable, and $w(\cdot)$ is the uncertainty dynamics of the system.

Without loss of generality, we assume the system’s equilibrium $(x_{e} ,u_{e} )$ is the origin. The system in (1) is subject to the state and control constraints: $x \in {\mathbb{X}}$ and $u \in {\mathbb{U}}$. Here ${\mathbb{X}} \subset {\mathbb{R}}^{n}$ and ${\mathbb{U}} \subset {\mathbb{R}}^{m}$ are $\mathcal{P}\mathcal{C}$-sets. Besides, the uncertainty dynamics is assumed to be bounded for $x \in {\mathbb{X}}$ and $u \in {\mathbb{U}}$. Thus there exists a $\mathcal{C}$-set ${\mathbb{W}}$ such that $w(x,u) \in {\mathbb{W}}$ when $x \in {\mathbb{X}}$ and $u \in {\mathbb{U}}$.

The LBNMPC is constructed to handle the stabilization issue of (1). As mentioned in introduction, a nominal model and a learned model are employed for controller design. The nominal model of (1) is described by

$$ \bar{x}^{ + } = f(\bar{x},\bar{u}) $$

(2)

where $\overline{x}$ and $\overline{u}$ are the state and input of the nominal model. The learned model is defined by

$$ \hat{x}^{ + } = f(\hat{x},\hat{u}) + \hat{w}(\hat{x},\hat{u}) $$

(3)

where $\hat{x}$ and $\hat{u}$ are the induced state and control input based on the learned model, and $\hat{w}$ denotes the estimation of w.

In our LBNMPC, an iterative optimization procedure is required to obtain the control sequence via optimizing a finite-horizon quadratic cost function, which is defined as follows with an initial state $x_{0}$ and a desired state $x_{e}$

$$ V_{N} (x,k,{\text{u}};x_{0} ,x_{e} ) \triangleq V_{f} (x(N);x_{e} ) + \mathop \sum \limits_{k = 0}^{N - 1} l(x(k) - x_{e} ,u(k)) $$

(4)

where N is the prediction horizon, $l(x,u)$ is the stage cost defined by $l(x,u) \triangleq \,\,||x||_{Q}^{2} + ||u||_{R}^{2}$ with Q and R are positive-definite weight matrices. Besides, we denote

$$ {\text{u}}(x,k;x_{0} ,x_{e} ) \triangleq \{ u(x,0;x_{0} ,x_{e} ),u(x,1;x_{0} ,x_{e} ), \ldots ,u(x,N - 1;x_{0} ,x_{e} )\} $$

as the control sequence for the whole prediction horizon. Moreover, $V_{f} (\cdot)$ is the terminal cost function depicted as

$$ V_{f} (x,x_{e} ) = \,\,||x - x_{e} ||_{P}^{2} $$

(5)

where P is the terminal penalty matrix. We also define a terminal constraint set by

$$ x(N) \in \Omega $$

(6)

It is designed to draw the states at the end of the finite prediction horizon to a neighborhood of the origin [28]. The construction process of this terminal constraint set $\Omega$ is described in detail in the following subsection.

1.4 Construction of terminal constraint set

In Ref. [29], a novel robust MPC was proposed for a linear system with additive uncertainties to track changing targets. This controller has the ability to steer the uncertain system to a neighborhood of the target. Reference [30] designed MPC method for constrained systems with detailed stability and optimality analysis. Reference [31] introduced a robust MPC approach to guarantee the feasibility and robustness of linear systems under bounded disturbances and various constraints. Reference [32] presented a maximal output admissible set for linear MPC methods. Reference [33] proved the asymptotic closed-loop stability of the nonlinear MPC. These results provide fundamental design principles for the construction of terminal constraints and showcase how to ensure stability and feasibility of robust MPC controllers under disturbances and constraints.

Specifically, the terminal constraint set aims to block the move at the end of the prediction horizon and restrict the inherent behavior of the finite-horizon control. It is critical in providing stability, safety, robustness, and feasibility of MPC [34]. The terminal penalty matrix $P$ and the terminal constraint set $\Omega$ can be determined off-line. To this end, we consider the Jacobian linearization of the nominal dynamics at the equilibrium $(x_{e} ,u_{e} )$:

$$ \overline{x}^{ + } = A\overline{x} + B\overline{u} $$

(7)

where $A = (\partial f/\partial \overline{x})(x_{e} ,u_{e} )$ and $B = (\partial f/\partial \overline{u})(x_{e} ,u_{e} )$.

Assuming this linearized system is controllable, then there exists a local linear feedback controller $\overline{u} = K(\overline{x} - x_{e} ) \in {\mathbb{U}}$ such that $A^{*} = A + BK$ is asymptotically stable, where K is the feedback gain (K is a positive-definite matrix). Then, the terminal penalty matrix P and the matrix K can be determined by solving the following equation [28]

$$ (A^{ * } )^{T} PA^{ * } - P = - (Q^{ * } + \tau I) $$

(8)

where $Q^{*} = Q + K^{T} RK$, and $\tau$ is a user-defined positive constant.

To guarantee the stability of the system, the invariant terminal constraint set $\Omega$ is designed as

$$ \Omega (x) = \{ x|V_{f} (x,x_{e} ) \le \alpha \} $$

(9)

where $\alpha$ is a constant and computed by the method proposed in Ref. [28].

Remark 1

Note that the local linear feedback controller is only applied to calculate the terminal penalty matrix P and the terminal constraint set $\Omega$ off-line and ensure the system asymptotic stability [33]. It is not directly employed to the actual control system. Besides, it should be emphasized that the terminal constraint set $\Omega$ chosen by the linear feedback control is invariant for the nonlinear system under the MPC control law.

1.5 LBNMPC Strategy

The LBNMPC strategy proposed in this paper inspires from the tube MPC, a type of robust MPC, which can ensure the nonlinear system’s real trajectory lies in a tube that surrounds the nominal trajectory. The width of the tube is restricted in a set ${\mathbb{C}}$, and the constraints set ${\mathbb{X}}$ are shrunk by the width of the tube. Thereby, the nominal trajectory lies in ${{\mathbb{X}} \ominus }{\mathbb{C}}$ and the real trajectory lies in ${\mathbb{X}}$. Similarly, for LBNMPC, the nominal and real trajectories lie in ${{\mathbb{X}} \ominus }{\mathbb{C}}$ and ${\mathbb{X}}$, respectively.

Given the nominal model in (2) and learned model in (3), our LBNMPC is formulated as:

$$ V_{N} (\hat{x},k,{\tilde{\text{u}}};x_{0} ,x_{e} ) \triangleq V_{f} (\hat{x}(N);x_{e} ) + \mathop \sum \limits_{k = 0}^{N - 1} l(\hat{x}(k) - x_{e} ,\tilde{u}(k)) $$

(10)

$$ \hat{x} = x,{\overline{x}} = x $$

(11)

$$ {\overline{x}^{ + }} = f({\overline{x}},\tilde{u}) $$

(12)

$$ \hat{x}^{ + } = f(\hat{x},\tilde{u}) + \hat{w}(\hat{x},\tilde{u}) $$

(13)

$$ \overline{x} \in {{\mathbb{X}} \ominus }{\mathbb{C}},\tilde{u} \in {{\mathbb{U}} \ominus }K{\mathbb{C}} $$

(14)

$$ \overline{x}(N) \in \Omega $$

(15)

where ${\tilde{\text{u}}}$ is the control sequence and the first element of it (i.e., $\tilde{u}$) is applied to both the nominal model and learned model. The set ${\mathbb{C}}$ is defined as ${\mathbb{C}}_{0} = \{ 0\}$, ${\mathbb{C}}_{k} = \oplus_{j = 0}^{k - 1} (A + BK)^{j} {\mathbb{W}}$ [18]. Also, $\overline{x}(N) \in \Omega$ denotes the terminal constraints and $\Omega$ is an invariant set restricted by the local linear feedback controller [35]. In addition, Eq. (11) indicates that, after the optimal control input is applied to the system, the observed state x should be fed to both the nominal state $\overline{x}$ and the learned state $\hat{x}$ to construct the subsequent optimization problem.

Remark 2

The terminal invariant set denotes a set that for all $x \in \Omega$, there exists a control $u \in {\mathbb{U}}$ such that $x^{ + } \in \Omega$ [36, 37]. Therefore, all trajectories of the system always stay in $\Omega$ if they are starting from $\Omega$.

The solution of the above problem is denoted as $\phi (k;x,{\tilde{\text{u}}})$ with the initial state $x_{0}$ and the control sequence ${\tilde{\text{u}}}$. The state constraint $\overline{x}(k) \in {{\mathbb{X}} \ominus }{\mathbb{C}}$, control constraint $\tilde{u}(k) \in {{\mathbb{U}} \ominus }K{\mathbb{C}}$, and terminal inequality constraint $\phi (N,\overline{x},{\tilde{\text{u}}}) \in \Omega$ lead to the control set ${\text{U}}_{N} (\overline{x},x_{e} )$ as follows

$$ {\text{U}}_{N} (\overline{x},x_{e} ) \triangleq \{ {\tilde{\text{u}}}|\tilde{u}(k) \in {{\mathbb{U}} \ominus }K{\mathbb{C}},\overline{x}(k) \in {{\mathbb{X}} \ominus }{\mathbb{C}},\forall k \in \{ 0,1, \cdots ,N - 1\} ,\phi (N,\overline{x},{\tilde{\text{u}}}) \in \Omega \} $$

(16)

The optimal control problem $P_{N} (x,k;x_{0} ,x_{e} )$ is defined by

$$ \begin{aligned} P_{N} (x,k;x_{0} ,x_{e} ):V_{N}^{0} (x)& = \min \{ V_{N} (\hat{x},k,{\tilde{\text{u}}};x_{0} ,x_{e} )|{\tilde{\text{u}}} \\ &\quad \in {\text{U}}_{N} (\bar{x},x_{e} )\} \\ \end{aligned} $$

(17)

The initial solution of $P_{N} (x,k;x_{0} ,x_{e} )$ is

$$ {\tilde{\text{u}}}^{0} (x,k,x_{0} ,x_{e} ) \triangleq \left\{ {\tilde{u}^{0} (0;x,k,x_{0} ,x_{e} ),\tilde{u}^{0} (1;x,k,x_{0} ,x_{e} ), \cdots ,\tilde{u}^{0} (N - 1;x,k,x_{0} ,x_{e} )} \right\} $$

(18)

And the associated state sequence is

$$ {\text{x}}^{0} (x,k,x_{0} ,x_{e} ) \triangleq \left\{ {x^{0} (0;x,k,x_{0} ,x_{e} ),x^{0} (1;x,k,x_{0} ,x_{e} ), \cdots ,x^{0} (N - 1;x,k,x_{0} ,x_{e} )} \right\} $$

(19)

Then, the first element $\tilde{u}^{0} (0;x,k,x_{0} ,x_{e} )$ is applied to the LBNMPC. At the next sampling instant, this procedure operates repeatedly for the successor state.

Remark 3

The difference between the LBNMPC and other MPC methods is that the LBNMPC is formulated based on two models (nonlinear nominal and learned models) simultaneously, which makes it possible for dealing with uncertainties while preserving the properties of robust MPC.

Remark 4

Note that in the LBNMPC, the cost function is constructed by the states of the learned model, while the constraints are imposed on the nominal model. This design ensures robustness when the learned model does not match the true dynamics.

Remark 5

An important characteristic of LBNMPC is that the system safety, stability, and robustness are only related to the state, input, and terminal constraints based on the nominal model. Therefore, the safety & robustness requirement (guaranteed by the nominal model) and the performance enhancement (provided by the learned model) can be decoupled. As a result, the LBNMPC can make a trade-off between the system’s robustness and performance.

2 Stability analysis

In this section, the conditions for guaranteeing the stability of LBNMPC are presented in detail. It is noteworthy that the stability and robustness of the LBNMPC scheme are independent to the system uncertainties and the learning tools that are involved in the learned model. Some necessary definitions are given as follows for the subsequent stability analysis.

Definition 1

[38], Asymptotically Stable: The system is said to be asymptotically stable (AS) about $x_{e}$ on ${\mathcal{F}} \subseteq {\mathbb{R}}^{n}$, if there exists a type-$\mathcal{K}$ function $\varpi$ such that for $x_{k} \in {\mathcal{F}}$, the condition $|x_{k} - x_{e} |\,\, \le \varpi \left( {|x_{k} - x_{e} |\,,k} \right)$ holds for $k \ge 0$.

Definition 2

[39], Robustly Asymptotically Stable: The system is said to be robustly asymptotically stable (RAS) about $x_{e}$ on ${\text{int}} ({\mathcal{F}})$ with respect to measurement error (additive disturbance) e_k, if there exists a $\mathcal{K}\mathcal{L}$ function $\beta$ and for each $\varepsilon > 0$ and compact set $\ell \subset {\text{int}} ({\mathcal{F}})$, there exists $\delta > 0$ such that for all the measurement errors e_k satisfying i)$\max_{k} ||e_{k} || < \delta$; ii) $x_{k} \in \ell$ and $||x_{k} - x_{e} || \le \beta \left( {||x_{k} - x_{e} ||,k} \right) + \varepsilon$ for all $k \ge 0$.

Remark 6

The main difference between AS and RAS is that the RAS considers the measurement error (additive disturbance), and it guarantees the asymptotic stability of system with respect to the disturbance.

Definition 3

[40], Persistent Excitation: A bounded signal $g(\cdot)$: ${\mathbb{R}} \to {\mathbb{R}}^{n \times m}$ is said to be persistent exciting (PE) if there exist positive constants a and $\gamma$ such that for arbitrary $t \ge 0$, one has $\int_{t}^{t + \gamma } {g(\tau )g^{T} (\tau )d\tau \ge aI}$.

Definition 4

[41], Finite Excitation: A bounded signal $g(\cdot)$: ${\mathbb{R}} \to {\mathbb{R}}^{n \times m}$ is said to be finite exciting (FE) if there exist positive constants a and $\gamma$ such that in time interval $[t,t + \gamma ]$, one has $\int_{t}^{t + \gamma } {g(\tau )g^{T} (\tau )d\tau \ge aI}$.

Remark 7

The main difference between PE and FE is that PE requires the signal to be excited over the whole time, while FE just requires the signal to be excited over a finite-time interval. PE means the satisfaction of FE over the whole time. The PE condition is much stronger than the FE condition from the standpoint of practical engineering.

2.1 Stability of open-loop system

The trajectory generated by (12) with feasible solutions can satisfy the terminal inequality constraint in (15) and ensure the boundedness of the objective function in (10). Therefore, feasibility at each time step should be analyzed. We assume that the feasible point is p_n; the system state and input predicted by the nominal model are denoted as $\overline{x}(x,k,x_{0} ,x_{e} ,p_{n} ) \in {{\mathbb{X}} \ominus {\mathbb{C}}}$, $\overline{u}(x,k,x_{0} ,x_{e} ,p_{n} ) \in {{\mathbb{U}} \ominus }K{\mathbb{C}}$, respectively. By introducing the uncertain modeling error (denoted as $d_{n} \in {\mathbb{W}}$) into the nominal model, $\overline{x}^{ + } = f(\overline{x},\overline{u}) + d_{n}$ should be considered for stability analysis. For the next feasible point $p_{n + 1}$, we have $\overline{x}(x,k,x_{0} ,x_{e} ,p_{n + 1} ) = \overline{x}(x,k,x_{0} ,x_{e} ,p_{n} ) + d_{n + 1}$ and $\overline{u}(x,k,x_{0} ,x_{e} ,p_{n + 1} ) = \overline{u}(x,k,x_{0} ,x_{e} ,p_{n} ) + Kd_{n + 1}$, $d_{n + 1} \in {\mathbb{W}}$. Thus, $\overline{x}(x,k,x_{0} ,x_{e} ,p_{n + 1} ) \in {{\mathbb{X}} \ominus }({\mathbb{C}} \oplus {\mathbb{W}}) \oplus {\mathbb{W}}$, which implies $\overline{x}(x,k,x_{0} ,x_{e} ,p_{n + 1} ) \in {{\mathbb{X}} \ominus {\mathbb{C}}}$. Similarly, we have $\overline{u}(x,k,x_{0} ,x_{e} ,p_{n + 1} ) \in {{\mathbb{U}} \ominus }K{\mathbb{C}}$. As a result, for the next feasible point $p_{n + 1}$, the associated state and input are still feasible.

Lemma 1

Considering a set of states ${\mathcal{X}}_{N}$ satisfying (20) that leads to at least one control sequence ${\tilde{\text{u}}}$ meeting the state, control, and terminal constraints. Then, for the nominal system, the feasibility of the open-loop optimal control problem at k = 0 implies its feasibility for all k > 0.

$$ x \in {\mathcal{X}}_{N} \triangleq \{ x|{\text{U}}_{N} \ne \emptyset \} $$

(20)

Proof

Under the condition that there exists an optimal control sequence ${\tilde{\text{u}}}^{*} (x,k,x_{0} ,x_{e} )$ for the optimal control problem $P_{N} (x,k;x_{0} ,x_{e} )$ with the associated state sequence ${\overline{\text{x}}}^{*} (x,k,x_{0} ,x_{e} ) \in \mathcal{X}_{N}$ at $[k,k + N]$, the state ${\overline{\text{x}}}^{*} (x,k + N,x_{0} ,x_{e} )$ belongs to the terminal constraint set $\Omega$ due to the system feasibility. For the next optimal control problem $P_{N} (x,k + \sigma ;x_{0} ,x_{e} )$ ($\sigma > 0$ is a small sampling step), the initial state satisfies $\overline{x}^{0} (x,k + \sigma ,x_{0} ,x_{e} ) = {\overline{\text{x}}}^{*} (x,k + \sigma ,x_{0} ,x_{e} )$. Then, a candidate control sequence ${\tilde{\text{u}}}(x,k + \sigma ,x_{0} ,x_{e} )$ under the local linear feedback controller for the problem $P_{N} (x,k + \sigma ;x_{0} ,x_{e} )$ at $[k + \sigma ,k + \sigma + N]$ can be chosen as.

$$ {\tilde{\text{u}}}(x,k + \sigma ,x_{0} ,x_{e} ) = \left\{ \begin{array}{l} {\tilde{\text{u}}}^{*} (x,k,x_{0} ,x_{e} ) \, {\varvec{for}} \, [k + \sigma ,k + N] \hfill \\ K\overline{x}^{0} (x,k + \sigma ,x_{0} ,x_{e} ) \, \user2{for }(k + N,k + \sigma + N] \hfill \\ \end{array} \right. $$

(21)

Note that the terminal constraints set $\Omega$ is an invariant set restricted by the local linear feedback controller. Therefore, the initial state $\overline{x}^{0} (x,x + \sigma ,x_{0} ,x_{e} ) = {\overline{\text{x}}}^{*} (x,k + N,x_{0} ,x_{e} ) \in \Omega$ indicates that $\overline{x}^{0} (x,k + \sigma + N,x_{0} ,x_{e} ) \in \Omega$ [42,43,44]. This completes the proof.

To sum up, for each prediction horizon of the optimal control problem in (10)–(15) with feasible solutions, the terminal penalty $V_{f} (\hat{x}(N);x_{e} )$ considered in (10) and the terminal constraints in (15) can force the states at the end of the prediction horizon lie within a terminal region.

2.2 Stability of closed-loop system

We choose the cost function $V_{N} (\hat{x},k;x_{0} ,x_{e} )$ as the Lyapunov function to analyze the closed-loop stability. Note that the cost function is related to the learned states at each prediction horizon. After solving the optimal control problem for each prediction horizon, the state $x^{0} (x,k + 1,x_{0} ,x_{e} )$ for next prediction horizon can be acquired by the real system model based on the solution of ${\tilde{\text{u}}}^{*} (x,k,x_{0} ,x_{e} )$. Then, we consider the following assumptions.

Assumption 1 [45]:

a)$f(\cdot)$ is Lipschitz continuous in ${\mathbb{X}} \times {\mathbb{U}}$, $l(\cdot)$ and $V_{f} (\cdot)$ are continuous. b)$\Omega \subset {\mathbb{X}}$, $\Omega$ is closed and compact. c) $u = k_{f} (x) \in {\mathbb{U}}$, $\forall x \in \Omega$. d)$f(x,k_{f} (x)) \in \Omega$, $\forall x \in \Omega$.

Assumption 2

[42]: For the stage cost $l(\cdot)$ and the terminal cost $V_{f} (\cdot)$, there exist $\mathcal{K}_{\infty }$ functions $\alpha_{l}$ and $\alpha_{f}$ satisfying

$$ l(x,\tilde{u}) \ge \alpha_{l} (|x|),\forall x \in \mathcal{X}_{N} ,\tilde{u} \in {\mathbb{U}} $$

(22)

$$ V_{f} (x) \le \alpha_{f} (|x|),\forall x \in \Omega $$

(23)

where $x \in {\mathcal{X}}_{N} \triangleq \{ x|{\text{U}}_{N} \ne \emptyset \}$ since the set ${\text{U}}_{N}$ satisfies the state constraint, input constraint, and terminal constraint.

Lemma 2

[45, 46]: If the cost function satisfies the following condition: There exists a $u = k_{f} (x) \in {\mathbb{U}}$ such that $V_{f} (f(x,k_{f} (x));x_{e} ) + l(x - x_{e} ,k_{f} (x)) \le V_{f} (x,x_{e} )$ for all $x \in \Omega (x_{e} )$. Then, the closed-loop system is AS.

Based on all these preliminaries, we propose the following theorem.

Theorem 1

The cost function $V_{N}^{0} (\cdot)$ satisfies.

$$ V_{N}^{0} (x^{ + } ,k^{ + } ;x_{0} ,x_{e} ) \le V_{N}^{0} (x,k;x_{0} ,x_{e} ) - l(x - x_{e} ,k_{N} (x,k;x_{0} ,x_{e} )) $$

(24)

and the closed-system system is AS.

Proof

The solution of $P_{N} (x,k;x_{0} ,x_{e} )$ is.

$$ {\tilde{\text{u}}}^{0} (x,k,x_{0} ,x_{e} ) \triangleq \left\{ {\tilde{u}^{0} (0;x,k,x_{0} ,x_{e} ),\tilde{u}^{0} (1;x,k,x_{0} ,x_{e} ), \cdots ,\tilde{u}^{0} (N - 1;x,k,x_{0} ,x_{e} )} \right\} $$

(25)

The associated state sequence is

$$ {x}^{0} (x,k,x_{0} ,x_{e} ) \triangleq \left\{ {x^{0} (0;x,k,x_{0} ,x_{e} ),x^{0} (1;x,k,x_{0} ,x_{e} ), \cdots ,x^{0} (N;x,k,x_{0} ,x_{e} )} \right\} $$

(26)

and the first element $\tilde{u}^{0} (0;x,k;x_{0} ,x_{e} )$ is applied to the LBNMPC, and we denote $x^{ + } = x^{0} (1;x,k,x_{0} ,x_{e} )$. Let ${\tilde{\text{u}}}$ denote the following control sequence

$$ {\tilde{\text{u}}}(x,k,x_{0} ,x_{e} ) \triangleq \left\{ {\tilde{u}^{0} (1;x,k,x_{0} ,x_{e} ),\tilde{u}^{0} (2;x,k,x_{0} ,x_{e} ), \cdots ,k_{f} (x^{0} (N;x,k,x_{0} ,x_{e} ))} \right\} $$

(27)

which is feasible for $P_{N} (x,k;x_{0} ,x_{e} )$ but not necessarily optimal. Then, it follows that

$$ \begin{aligned} V_{N}^{0} (x^{ + } ,k^{ + } ,{\tilde{\text{u}}};x_{0} ,x_{e} ) &= V_{N}^{0} (x,k;x_{0} ,x_{e} ) \\ & \quad -\, l(x - x_{e} ,k_{N} (x,k;x_{0} ,x_{e} )) - V_{f} (x^{0} (N;x,k;x_{0} ,x_{e} )) \\ & \quad + \,l\left( {f\left( {x^{0} (N;x,k;x_{0} ,x_{e} ),k_{f} (x^{0} (N;x,k,x_{0} ,x_{e} ))} \right)} \right) \\ & \quad + \,V_{f} \left( {f\left( {x^{0} (N;x,k;x_{0} ,x_{e} ),k_{f} (x^{0} (N;x,k,x_{0} ,x_{e} ))} \right)} \right) \\ \end{aligned} $$

(28)

Considering that $V_{N}^{0} (x^{ + } ,k^{ + } ;x_{0} ,x_{e} ) = V_{N}^{0} (x^{ + } ,k^{ + } ,{\text{u}};x_{0} ,x_{e} ) \le V_{N}^{0} (x,k,{\tilde{\text{u}}};x_{0} ,x_{e} )$, it can be obtained from (28) that

$$ V_{N}^{0} (x^{ + } ,k^{ + } ;x_{0} ,x_{e} ) \le V_{N}^{0} (x,k;x_{0} ,x_{e} ) - l(x - x_{e} ,k_{N} (x,k;x_{0} ,x_{e} )) $$

(29)

Therefore, the cost function is nonincreasing, and the closed-loop system is AS.

[18, 42, 45]. If there exists an additive disturbance $w \in {\mathbb{W}}$, then the asymptotic stability condition for the closed-loop system is modified as: There exists a $u = k_{f} (x) \in {\mathbb{U}}$ such that

$$ V_{f} (f(x,k_{f} (x)),w;x_{e} ) + l(x - x_{e} ,k_{f} (x)) \le V_{f} (x,w,x_{e} ) + \delta , \, \forall w \in {\mathbb{W}} $$

(30)

for all $x \in \Omega (x_{e} )$, where $\delta \in (0,\infty )$. Then, the LBNMPC is RAS with

$$ V_{N}^{0} (x^{ + } ,k^{ + } ,w;x_{0} ,x_{e} ) \le V_{N}^{0} (x,k,w;x_{0} ,x_{e} ) - l(x - x_{e} ,k_{N} (x,k;x_{0} ,x_{e} )) + \delta , \, \forall w \in {\mathbb{W}} $$

(231)

Therefore, the LBNMPC is RAS when i) Assumption 1 and Assumption 2 are satisfied; ii) the system uncertainty is bounded; iii) the terminal cost and the terminal invariant set force the state within the neighborhood of origin at the end of each prediction horizon; iv) the closed-loop system is feasible.

3 Concurrent-learning estimator

From Section III, the robustly asymptotic stability has been guaranteed with the nonlinear nominal model. However, the performance of LBNMPC requires the accurate estimation of the unmodeled dynamics. Some examples to this end are given in [20, 47, 48]. In this section, a novel concurrent-learning-based estimation strategy is proposed and its convergence property is proved.

3.1 Estimator development

We aim to develop an estimator to compensate the uncertain dynamics: $w(x,u)$. In many applications, $w(x,u)$ satisfies an affine representation, i.e., there exists a regressor matrix $z(x,u) \in {\mathbb{R}}^{n \times p}$ and an unknown constant vector $\phi \in {\mathbb{R}}^{p}$, such that $w(x,u) = z(x,u)\phi$. And here p is the total number of unknown parameters. In fact, when $w(x,u)$ cannot satisfy the affine representation, a single-layer neural network can be employed to reconstruct $w(x,u)$. Specifically, based on the Weierstrass approximation theorem [49], $w(x,u)$ can be reconstructed by a very similar form with the affine representation:

$$ w(x,u) = z(x,u)\phi + \varepsilon $$

(32)

But now $z(x,u) \in {\mathbb{R}}^{n \times p}$ is a set of basis functions, $\phi \in {\mathbb{R}}^{p}$ is a governed vector which contains the weights of corresponding basis functions, and $\varepsilon$ is the reconstruction error. It has been well-understood that, by properly choosing a large enough set of basis functions, the reconstruction error $\varepsilon$ is bounded in ${\mathbb{X}} \times {\mathbb{U}}$ and can be arbitrarily small and negligible. Based on these facts, we assume the uncertain dynamics in our paper satisfies $w(x,u) = z(x,u)\phi$, and no matter $z(x,u)$ is a regressor matrix or a set of user-defined basis functions. And the objective of the estimator is to evaluate the true value of $\phi$.

Based on $w(x,u) = z(x,u)\phi$, Eq. (1) can be rewritten as follows

$$ x^{ + } = f(x,u) + z(x,u)\phi $$

(33)

Then, we design the following filtered variables:

$$ x_{f}^{ + } = - \mu_{f} x_{f} + x $$

(34)

$$ z_{f}^{ + } = - \mu_{f} z_{f} + z $$

(35)

$$ f_{f}^{ + } = - \mu_{f} f_{f} + f $$

(36)

where $\mu_{f}$ is the estimator coefficient satisfying $0 < \mu_{f} < 1$. Thus $x_{f}^{ + }$, $z_{f}^{ + }$ and $f_{f}^{ + }$ are bounded variables when x_f, z_f, and f_f are bounded. Substituting (34)–(36) into (1) yields

$$ (x_{f}^{ + } )^{ + } - f_{f}^{ + } - z_{f}^{ + } \phi = - \mu_{f} \left( {x_{f}^{ + } - f_{f} - z_{f} \phi } \right) $$

(37)

We denote $y = x_{f}^{ + } - f_{f} - z_{f} \phi$, and then (37) indicates

$$ y^{ + } = - \mu_{f} y $$

(38)

Since y is an exponentially vanishing term which converges to zero quickly, we have $x_{f}^{ + } - f_{f} - z_{f} \phi \approx 0$. Then, the estimation of $\phi$ (denoted by $\hat{\phi }$) can be divided into two terms

$$ \hat{\phi } = \hat{\phi }_{1} + \hat{\phi }_{2} $$

(39)

And the successors of $\hat{\phi }_{1}$ and $\hat{\phi }_{2}$ are designed as

$$ \hat{\phi }_{1}^{ + } - \hat{\phi }_{1} = - \frac{{k_{I} }}{{\lambda_{Z} }}(z_{f}^{T} z_{f} \hat{\phi }_{1} - z_{f}^{T} \beta ) $$

(40)

$$ \hat{\phi }_{2}^{ + } - \hat{\phi }_{2} = - \left( {\frac{{k_{I} }}{{\lambda_{Z} }}\sum\limits_{i = 1}^{q} {z_{{^{f} }}^{T} (t_{i} )z_{f} (t_{i} )} } \right)\hat{\phi }_{2} + \frac{{k_{I} }}{{\lambda_{Z} }}\sum\limits_{i = 1}^{q} {z_{f}^{T} (t_{i} )\beta (t_{i} )} $$

(41)

where k_I is a user-defined positive constant, $\beta = x_{f}^{ + } - f_{f}$, $\lambda_{Z} = 1 + \lambda_{\max } (\varphi )$, and $\varphi = 1/\lambda_{Z} (z_{f}^{T} z_{f} + \sum\nolimits_{i = 1}^{q} {z_{{^{f} }}^{T} (t_{i} )z_{f} (t_{i} )} )$ is employed for ease of notation. Besides, t_i denotes a set of past time indexes with $0 \le t_{i} < t$, $i = 1,2,...,q$, and here q is a constant which denotes the total number of historical data points. Based on (40) and (41), the estimator $\hat{\phi }$ follows:

$$ \hat{\phi }^{ + } - \hat{\phi } = - \frac{{k_{I} }}{{\lambda_{Z} }}z_{f}^{T} z_{f} \hat{\phi } - \frac{{k_{I} }}{{\lambda_{Z} }}\left( {\sum\limits_{i = 1}^{q} {z_{{^{f} }}^{T} (t_{i} )z_{f} (t_{i} )} } \right)\hat{\phi } + \frac{{k_{I} }}{{\lambda_{Z} }}z_{f}^{T} \beta + \frac{{k_{I} }}{{\lambda_{Z} }}\sum\limits_{i = 1}^{q} {z_{{^{f} }}^{T} (t_{i} )} \beta (t_{i} ) $$

(42)

Equation (42) shows that not only real-time data but past measurements are concurrently introduced into the estimator, and the motivation of this design will be explained in the convergence analysis.

3.2 Convergence analysis

Theorem 2

Consider the nonlinear system with uncertain dynamics as in (1), design the learning-based estimator as in (42). Then the estimation error $\tilde{\phi } = \hat{\phi } - \phi$ is bounded. Moreover, if $\lambda_{\min } (\varphi ) > 0$, $\tilde{\phi }$ exponentially converges to zero.

Proof

Based on the fact that $\beta = x_{f}^{ + } - f_{f} = z_{f} \phi$, we have.

$$ \begin{aligned} \hat{\phi }_{1} ^{ + } - \hat{\phi }_{1} = & - k_{I} (z_{f}^{T} z_{f} \hat{\phi }_{1} - z_{f}^{T} \beta ) = - k_{I} z_{f}^{T} (z_{f} \hat{\phi }_{1} - z_{f} \phi ) \\ & = - k_{I} z_{f}^{T} z_{f} \tilde{\phi } \\ \end{aligned} $$

(43)

$$ \hat{\phi }_{2}^{ + } - \hat{\phi }_{2} = - \frac{{k_{I} }}{{\lambda_{Z} }}\left( {\sum\limits_{i = 1}^{q} {z_{{^{f} }}^{T} (t_{i} )z_{f} (t_{i} )} } \right)\hat{\phi }_{2} + \frac{{k_{I} }}{{\lambda_{Z} }}\sum\limits_{i = 1}^{q} {z_{{^{f} }}^{T} (t_{i} )} \beta (t_{i} ) = - \frac{{k_{I} }}{{\lambda_{Z} }}\left( {\sum\limits_{i = 1}^{q} {z_{{^{f} }}^{T} (t_{i} )z_{f} (t_{i} )} } \right)\tilde{\phi }_{2} $$

(44)

Therefore, one has

$$ \hat{\phi }^{ + } - \hat{\phi } = - k_{I} \varphi \tilde{\phi } $$

(45)

Then, consider the following storage function:

$$ V = (1/k_{I} )\tilde{\phi }^{T} \tilde{\phi } $$

(46)

The successor value of V is $V^{ + } = (\tilde{\phi }^{ + } )^{T} \tilde{\phi }^{ + } /k_{I}$. Accordingly,

$$ \begin{gathered} V^{ + } - V = (\hat{\phi }^{ + } - \phi )^{T} (\hat{\phi }^{ + } - \phi ) - (\hat{\phi } - \phi )^{T} (\hat{\phi } - \phi ) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = (\hat{\phi }^{ + } - \phi )^{T} (\hat{\phi } - \phi ) - (\hat{\phi } - \phi )^{T} (\hat{\phi } - \phi ) + (\hat{\phi }^{ + } - \phi )^{T} (\hat{\phi }^{ + } - \hat{\phi }) \hfill \\ {\kern 1pt} \, = (\hat{\phi }^{ + } - \hat{\phi })^{T} \tilde{\phi } + (\hat{\phi }^{ + } - \hat{\phi })^{T} (\hat{\phi }^{ + } - \hat{\phi }) + \tilde{\phi }^{T} (\hat{\phi }^{ + } - \hat{\phi }) \hfill \\ \, = \tilde{\phi }^{T} (\varphi^{2} - 2\varphi )\tilde{\phi } \hfill \\ \end{gathered} $$

(47)

Since $\varphi$ is positive-definite and $\lambda_{\max } (\varphi ) < 1$, we have $\varphi^{2} - 2\varphi \le 0$. On this basis, Eq. (47) indicates $V^{ + } - V \le 0$. So the estimation error $\tilde{\phi }$ is bounded. Furthermore, if $\lambda_{\min } (\varphi ) > 0$, then it is obvious that $V^{ + } - V \le - a\tilde{\phi }^{T} \tilde{\phi }$, where $a$ is a positive constant. Thus, $\tilde{\phi }$ could exponentially converge to zero. The proof is complete.

Remark 8

Unlike the conventional CLAC that relies on the accurate approximation of immeasurable variables (i.e., the variable $x^{ + }$ in this paper), the proposed estimator adopts filtered states and regressor matrices in (34)–(36) and therefore circumvents the variable approximation requirements.

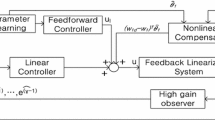
In summary, the detailed design procedure of the LBNMPC is described in this subsection. The detailed implementation procedure of the LBNMPC scheme is presented in Table 1, and the optimal control problem can be solved by the solver MOSEK [50]. For a better understanding of the proposed controller, the architecture of the LBNMPC is illustrated in Fig. 1 as well.

Table 1 Architecture of LBNMPC

Fig. 1

The architecture of the LBNMPC with uncertainty learning

Remark 9

In Theorem 2, we show that the estimation error $\tilde{\phi }$ can exponentially converge to zero, subject to the satisfaction that $\lambda_{\min } (\varphi ) > 0$. Recall the definition of FE conditions, this requirement can be guaranteed if $z_{f}$ satisfies a FE condition. To ensure $\varphi$ is full rank if $z_{f}$ satisfies a FE condition, a simplest way is to add all incoming data of $z_{f}$ into $\varphi$ until $rank(\varphi ) = p$ (therefore, $\lambda_{\min } (\varphi ) > 0$). A more sophisticated method is to design a selection algorithm, and some examples are shown in [26, 33]. Moreover, without the past measurements $\sum\nolimits_{i = 1}^{q} {z_{{^{f} }}^{T} (t_{i} )z_{f} (t_{i} )}$ and $\sum\nolimits_{i = 1}^{q} {z_{{^{f} }}^{T} (t_{i} )\beta (t_{i} )}$, one can only ensure $\mathop {\lim }\limits_{t \to \infty } z_{f} \tilde{\phi } = 0$ from (47). Under this condition, $z_{f}$ is required to satisfy the PE condition as in Definition 3 to ensure the convergence of $\tilde{\phi }$. Note that this is a common requirement in conventional estimator/identifier designs. However, PE conditions are quite strong from the standpoint of practical engineering. In this paper, we relax the PE condition to the FE condition by employing past measurements.

4 Applications to the control of a two-link manipulator

In this section, the effectiveness of the proposed LBNMPC scheme is validated via numerical simulations. A typical two-link robot manipulator model [51] is considered as follows

$$ \left\{ \begin{gathered} \dot{x}_{1} = x_{2} \hfill \\ M(x_{1} ,x_{2} )\dot{x}_{2} + \left( {V(x_{1} ,x_{2} ) + F(x_{1} ,x_{2} )} \right)x_{2} + C(x_{1} ,x_{2} ) = u \hfill \\ \end{gathered} \right. $$

(48)

where $x_{1} = [\begin{array}{*{20}c} {q_{1} } & {q_{2} } \\ \end{array} ]^{T}$ and $x_{2} = [\begin{array}{*{20}c} {q_{3} } & {q_{4} } \\ \end{array} ]^{T}$ denote the position and velocity vectors, respectively. Besides,$u = [\begin{array}{*{20}c} {u_{1} } & {u_{2} } \\ \end{array} ]^{T}$ is the control torque vector, and

$$ M = \left[ {\begin{array}{*{20}c} {p_{1} + 2p_{3} \cos (q_{2} )} & {p_{2} + p_{3} \cos (q_{2} )} \\ {p_{2} + p_{3} \cos (q_{2} )} & {p_{2} } \\ \end{array} } \right] $$

$$ F = \left[ {\begin{array}{*{20}c} {p_{4} } & 0 \\ 0 & {p_{5} } \\ \end{array} } \right]\;C = \left[ {\begin{array}{*{20}c} {p_{6} \tanh (q_{3} )} \\ {p_{7} \tanh (q_{4} )} \\ \end{array} } \right]\;V = \left[ {\begin{array}{*{20}c} { - p_{3} \sin (q_{2} )q_{4} } & { - p_{3} \sin (q_{2} )(q_{3} + q_{4} )} \\ {p_{3} \sin (q_{2} )q_{3} } & 0 \\ \end{array} } \right] $$

where the parameters $p_{1} ,p_{2} ,p_{3} ,p_{4} ,p_{5} ,p_{6} ,p_{7}$ are set to 3.473, 0.196, 0.242, 5.3, 1.1, 8.45, and 2.35, respectively. The continuous-time system in (48) is discretized using Euler approximation as

$$ \left\{ \begin{array}{l} x_{1} (k + 1) = T_{s} x_{2} (k) + x_{1} (k) \hfill \\ x_{2} (k + 1) = T_{s} f(k) + T_{s} g(k)u(k) + x_{2} (k) \hfill \\ \end{array} \right. $$

(49)

where $T_{s}$ is the sampling period, $f(k) = - M^{ - 1} [(V + F)x_{2} (k) + C]$, $g(k) = - M^{ - 1}$.

In this simulation case, we assume that the parameters $p_{5}$ and $p_{7}$ are unknown for controller design and thus they need to be estimated by the proposed learning procedure. The initial guesses of them are $\hat{p}_{5} (0) = 0.6$ and $\hat{p}_{7} (0) = 1.8$. The parameter $k_{f}$ in the filtered regressor is selected as $k_{f} = 0.2$. The prediction horizon is set to N = 7, and the weighting matrices Q and R are chosen as $Q = 3000 \times I_{4 \times 4}$ and $R = I_{2 \times 2}$. The constant $\alpha$ is computed as $\alpha = 1.34$. Through the Jacobian linearization of the nominal system at the origin, the matrices A and B are calculated by (7) as

$$ {\text{A}} = \left[ {\begin{array}{*{20}c} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & { - 4.62} & {2.59} \\ 0 & 0 & {10.32} & { - 23.39} \\ \end{array} } \right]{\text{ B = }}\left[ {\begin{array}{*{20}c} 0 & 0 \\ 0 & 0 \\ {0.34} & { - 0.75} \\ { - 0.75} & {6.78} \\ \end{array} } \right] $$

The terminal penalty matrix P and the local linear feedback gain K are calculated by (8) as

$$ P = \left[ {\begin{array}{*{20}c} {307.70} & {0.73} & {6.86} & {0.76} \\ {0.73} & {300.39} & {0.72} & {0.34} \\ {6.86} & {0.72} & {6.49} & {0.72} \\ {0.76} & {0.34} & {0.72} & {0.33} \\ \end{array} } \right] \, K = \left[ {\begin{array}{*{20}c} {173.20} & {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - 1.02} & {163.89} \\ \end{array} } & { - 0.60} \\ \end{array} } \\ {1.02} & {\begin{array}{*{20}c} {173.20} & {1.46} & {169.98} \\ \end{array} } \\ \end{array} } \right] \, $$

The set ${\mathbb{U}}$ is selected as ${{\mathbb{U}} = [ - 5,5]}$. The set ${\mathbb{W}}$ is chosen via the algorithm in [52] that exploits ${\mathbb{W}}$ based on the Taylor reminder theorem with a “safety-margin’’ [18]. Then, the set ${\mathbb{C}}$ can be calculated by its definition (${\mathbb{C}}_{0} = \{ 0\}$, ${\mathbb{C}}_{k} = \oplus_{j = 0}^{k - 1} (A + BK)^{j} {\mathbb{W}}$[18]). Therefore, the constraint in (14) can be determined, which ensures the closed-loop system's safety. This reflects the main characteristic of LBNMPC that decouples the system's safety and the performance enhancement. The desired trajectory is $x_{d} = [0.5\sin (0.5k),0.5\cos (0.5k),0.25\cos (0.5k),$$- 0.25\sin (0.5k)]^{T}$, and the initial state is $x_{0} = [0.5,0.2,0.05,0.1]^{T}$.

Under these conditions, the simulation results under LBNMPC without the estimation procedure are presented in Fig. 2a, while the results with the uncertainty learning method are shown in Fig. 2b. The thin solid lines in Fig. 2 represent the reference trajectories. It can be observed that the system states can successfully track the desired trajectories in both cases. Moreover, it can be seen from Fig. 3 that the LBNMPC leads to superior performance than that of the one without parameter estimation.

Fig. 2

Tracking performance by LBNMPC with/without uncertainty learning

Fig. 3

Tracking errors by LBNMPC with/without uncertainty learning

The uncertainty learning performance for the unknown parameters $p_{5}$, $p_{7}$ is presented in Fig. 4a. The solid lines in Fig. 4a depict the real values of $p_{5}$, $p_{7}$, and the dashed lines denote the estimated values $\hat{p}_{5}$, $\hat{p}_{7}$. It can be seen from Fig. 4a that the estimated parameters can converge to their real values. The estimation errors ($\tilde{p}_{5}$ and $\tilde{p}_{7}$) in Fig. 4b show that the proposed uncertainty learning scheme can ensure the estimation errors converge to zero.

Fig. 4

Uncertainty estimation results

The optimal control sequence is presented in Fig. 5. The control sequence in Fig. 5 satisfies the input constraints formulated in (14). The cost function variations are presented in Fig. 6. The cost function decreases gradually and finally converges to zero, reflecting the asymptotic stability of the LBNMPC approach.

Fig. 5

Results for the control torque performance

Fig. 6

The cost function variations

In addition to the unknown parameters, the robustness of the LBNMPC is verified under external disturbances on velocity measurements. Two difference cases are considered here: i) Case 1: the velocity measurements are polluted by a zero-mean Gaussian noise with a standard deviation as 1.0 × 10–3; ii). Case 2: the velocity measurements are polluted by a zero-mean Gaussian noise with a standard deviation as 3.0 × 10–3. The simulation results are shown in Fig. 7. Figures 7a and 7c show the tracking trajectories under case 1 and case 2, respectively. The thin solid lines are the desired trajectories. Figures 7b and 7d show the corresponding tracking errors. It can be seen that the position states can precisely track the reference trajectories with good performance even under polluted velocity measurements. All these results show that the proposed LBNMPC approach can maintain good performance under disturbances.

Fig. 7

Tracking performance by LBNMPC under disturbances

To evaluate the properties of the proposed LBNMPC in detail, we also consider a stabilization case by setting $x_{d} = [\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ \end{array} ]^{T}$. The results are given in Fig. 8. One can see that all the states can converge to the origin under the proposed controller. Figure 8b illustrates the tracking errors and the terminal region $\Omega$. It shows that the closed-loop system satisfies the constraints in (15), validating the stability and convergence properties of our LBNMPC.

Fig. 8

Tracking performance under $x_{d} = [\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ \end{array} ]^{T}$

Moreover, two different MPC approaches are also employed for comparison: i) the adaptive model predictive control (AMPC) with the proposed estimation procedure, and ii) the nonlinear model predictive control (NMPC) without uncertainty compensation. The comparative results of tracking trajectories and cost functions are presented in Figs. 9 and 10, respectively. It can be observed that both the LBNMPC and AMPC have good performance in tracking the desired trajectories, while the NMPC leads to larger tracking errors. Moreover, it can be seen from Fig. 10 that the proposed LBNMPC controller leads to a less cost than the AMPC and NMPC.

Fig. 9

Comparative tracking trajectories under various MPC controllers

Fig. 10

The values of cost function under different MPC controllers

To sum up, the proposed LBNMPC is capable of achieving good performance, subject to uncertainties, disturbances, and various constraints.

5 Conclusion

A LBNMPC method was proposed in this paper to solve the optimal control problems of nonlinear systems subject to multiple constraints and system uncertainties. The control strategy was based on two models, i.e., the nonlinear nominal model and the learned model. The nominal model guarantees the stability and robustness of the LBNMPC, while the learned model improves the control performance via a novel concurrent-learning estimator. The key feature of our estimator is that it includes not only real-time data but also past measurements into the estimating framework, achieving precise estimation under a relaxed excitation condition. We showed that our LBNMPC could decouple the robustness and performance and ensure the feasibility, stability, and convergence of the closed-loop system. Extensive simulations and comparative analyses illustrated that LBNMPC could lead to superior tracking performance and robustness compared with other methods.