Controlling grazing-induced multistability in a piecewise-smooth impacting system via the time-delayed feedback control

Abstract

Grazing events may create coexisting attractors and cause complex dynamics in piecewise-smooth dynamical systems. This paper studies the control of grazing-induced multistability in a soft impacting oscillator by using the time-delayed feedback control. The control switches from one of the coexisting attractors to a desired one to suppress complex dynamics near grazing events. We use path-following (continuation) techniques for non-smooth dynamical systems to investigate robustness of the controller and the parameter dependence of the controlled system. In particular, several newly developed computational methods are used, including a numerical method for analysing non-smooth delay equations and a method for calculating the Lyapunov exponents and the grazing point estimation. Numerical simulations demonstrate that the delayed feedback controller is effective, and a proper selection of the control gain and delay time can simplify the complex dynamics of the system near grazing.

1 Introduction

Impacting systems are very common and important components in many engineering applications, such as self-propelled capsule systems [1, 2], rotor systems [3, 4], energy harvesting [5], mechanical bearings [6], manufacturing cutting [7], and oil and gas drilling [8,9,10]. Impacting systems show many complex nonlinear phenomena, e.g. chaotic motion, multistability, and grazing and sliding events [11], which can be exploited during design. For example, Liu et al. [12] and Liao et al. [13] suggested that the efficiency of the vibro-impact drilling can be improved by choosing the most efficient operational mode among possible coexisting attractors. For the self-propelled capsule system in [1], Guo et al. validated the mathematical model by comparing it with experimental results. Then, the numerical results obtained from the model were used to optimise the progression speed and energy efficiency of the capsule prototype. In [14], Páez Chávez et al. studied the mathematical model of a Jeffcott rotor within a snubber ring with anisotropic supports, and the model was used to predict the onset of impacts between the rotor and the snubber ring. The present work will study a periodically excited system with soft impacts, which can represent a wide range of mechanical collisions. Here, soft impact, in contrast to hard impact [15], refers to a collision that has a finite nonzero contact time and the colliding body penetrates the base typically modelled as a one-sided spring. This type of soft impact is a representative model for mechanical collisions. Its nonlinearity brings complex phenomena into a system’s dynamics, such as grazing-induced multistability [16, 17].

‘Grazing’ refers to the scenario when the colliding body encounters the impact with zero transversal velocity. Near-by trajectories experience qualitatively different forces: some will not impact, others will have an impact with nonzero transversal velocity. When an attractor encounters a grazing event, it may change qualitatively (see, e.g. [18,19,20]), which is called a discontinuity-induced (or, short, discontinuous or non-smooth) bifurcation. Nordmark [21] and Pavlovskaia et al. [22] analyse what dynamics occurs near grazing events. The textbook [11] classifies grazing bifurcations also for other piecewise-smooth systems. Their analysis finds coexistence of multistable attractors, chaotic motions and vulnerable attractors, which can be easily perturbed by any variations of system parameters or any external disturbances. Detection of grazing events helps predicting the performance behaviour of an impacting system. For example, Lamba and Budd [23] studied the grazing bifurcation of an impacting system through calculating its Lyapunov exponents (LEs), and the bifurcation was observed as a jump in LEs. In [21], Normark investigated the grazing bifurcation of a single-degree-of-freedom oscillator subjected to a rigid amplitude constraint and the singularities caused by grazing impacts by controlling a system parameter. Foale and Bishop [24] studied grazing bifurcations for two different models of the impact oscillator. They presented numerical evidence that the observed discontinuous bifurcations were limits of standard bifurcations of smooth dynamical systems as the impact was hardened. In [25], Dankowicz and Zhao studied three different bifurcation scenarios associated with grazing conditions for a periodic response of an impact microactuator, a discontinuous jump to an impacting periodic response, a continuous transition to an impacting chaotic attractor and a discontinuous jump to an impacting chaotic attractor, by using the concept of discontinuity mappings. Furthermore, Ing et al. [16, 26] carried out experimental investigations on different bifurcation scenarios of an impact oscillator with a one-sided elastic constraint, leading to smooth (that is, classical) and non-smooth bifurcations. In the present work, the same oscillator will be studied. Our research will focus on how to remove the complexity of its near-grazing dynamics, ideally through a non-invasive approach, without affecting its original dynamics. Specifically, coexisting attractors caused by grazing events, can be reduced to one of attractors, through the delay feedback controller, and without introducing any external attractors, or changing any existing attractors.

Multistable impact motions may have negative effects [27], such as degrading efficiency or reducing service life for the system, which should be avoided. Control of multistable impact motions, especially the near-grazing dynamics, has been studied extensively by many researchers in the past decade. For example, the linear augmentation feedback control law was adopted to control switching between coexisting attractors in a soft impacting system [17]. De Souza et al. used both, a perturbation method [28] and a feedback damping controller [29], to control chaotic attractors in an impacting system. Liu et al. [30] proposed an intermittent control method for non-autonomous dynamical systems to switch between coexisting attractors. A class of control strategies was developed by Dankowicz et al. [31,32,33] to ensure the persistence of desired attractors near the grazing bifurcation of an impact oscillator. Veldman et al. [34] introduced an impulsive control method to bring a single-degree-of-freedom system from an undesired to a desired attractor.

The present study investigates delayed feedback control, as introduced by Pyragas [35], for a periodically excited system with soft impacts (which we will simply call impact oscillator). Pyragas-type delayed feedback control has input $u(\tau )$ of the form

$$\begin{aligned} u(\tau )=K(y(\tau -\tau _d)-y(\tau ))\text{, } \end{aligned}$$

where $y(\tau )$ is some output of the system, $\tau$ is the time and $\tau _d$ is a time delay. The control’s aim is to achieve the switching from one of its coexisting attractors to a target attractor. If $\tau _d$ is equal to the forcing period and the system with delayed feedback control shows periodic motion with period $\tau _d$, the control effort $u(\tau )$ is zero (hence, called non-invasive). Delayed feedback control was originally proposed by Pyragas [35] for controlling chaos. In [36], Pyragas et al. controlled a chaotic electronic oscillator successfully by using the time-delayed feedback controller. In [37], a modified delay feedback control using the act-and-wait concept was proposed to reduce the dimension of phase space of the time-delayed feedback systems. Yamasue et al. [38] used time-delayed feedback control to stabilise irregular and non-periodic cantilever oscillations in amplitude modulation atomic force microscopy experiments. In this paper, we will investigate how time-delayed feedback control suppresses multistability of the impact oscillator close to grazing. The combination of soft impacts, grazing and delay requires several new computational techniques for analysing piecewise-smooth delay differential equations (DDEs). We will adapt path-following (continuation) methods [39], use a recently introduced computational method for calculating LEs in piecewise-smooth DDEs and an accurate algorithm for computing grazing events [40] in DDEs.

The rest of this paper is organised as follows. Section 2 introduces the mathematical model for a periodically forced mechanical oscillator subjected to a one-sided elastic force and some mathematical preliminaries for delayed feedback control. Section 3 studies the performance of the delayed feedback control for controlling multistability near grazing events in the impact oscillator dynamics. In Sect. 4, the further analysis of the impact oscillator under the delayed feedback control is carried out by using path-following methods. Finally, conclusions are drawn in Sect. 5.

2 Mathematical model and concepts

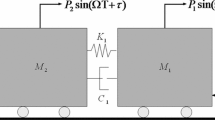
The impact oscillator shown in Fig. 1 represents a mechanical system encountering intermittent so-called soft impacts, which will be used in this work. Soft impacts occur in mechanical systems when an object hits an obstacle of negligible mass but non-negligible stiffness. In Fig. 1, the object is modelled by the block of mass m and the obstacle is modelled by a spring with one-sided stiffness $k_2$ (a backlash spring). The collision occurs when the distance g between block and spring reaches zero. Since during non-impact period the backlash spring is relaxed, the forces on the mass depend continuously on g, and hence on the position y of the block. However, the spring constants exerted by the backlash spring are discontinuous, i.e. 0 for $g>0$, $k_2$ for $g=0$. Thus, the system can operate under either no contact or contact mode with the secondary spring at any time. The nondimensional equations of motion of the impact oscillator can be written in a compact form as [26, 41]

$$\begin{aligned} {\left\{ \begin{array}{ll} x'(\tau )=v(\tau ),\\ v'(\tau )=a\omega ^2\sin (\omega \tau )-2\zeta v(\tau )-x(\tau )\\ \qquad \qquad \quad -\beta (x(\tau )-e) H(x(\tau )-e), \end{array}\right. } \end{aligned}$$

(1)

where $H(\cdot )$ stands for the Heaviside step function, and $x'$ and $v'$ denote the differentiation with respect to the nondimensional time $\tau$. We observe that despite the presence of H the right-hand side of Eq. (1) is continuous in x. This is typical for models with soft impacts where the point mass encounters a spring when crossing a critical position $x_\mathrm {crit}$ (in Eq. (1) $x_\mathrm {crit}=e$). The variables and parameters of the system can be nondimensionalised as follows

$$\begin{aligned} \begin{array}{r@{}lcr@{}lcr@{}lcr@{}l} \omega _{n}=&{} \sqrt{\dfrac{k_{1}}{m}}, &{} &{} \tau =&{} \omega _{n}t, &{} &{} \omega =&{} \dfrac{\Omega }{\omega _{n}}, &{} &{} \zeta =&{} \dfrac{c}{2m\omega _{n}},\\ x=&{} \dfrac{y}{y_{0}}, &{} &{} e=&{} \dfrac{g}{y_{0}}, &{} &{} a=&{} \dfrac{A}{y_{0}}, &{} &{} \beta =&{} \dfrac{k_{2}}{k_{1}}, \end{array} \end{aligned}$$

where $y_{0}>0$ is an arbitrary reference distance, $\omega _{n}$ is the natural frequency, $\omega$ is the frequency ratio, $\beta$ is the stiffness ratio, $\zeta$ is the damping ratio, a is the nondimensionalised forcing amplitude, and e is the nondimensionalised gap.

Fig. 1

Physical model of the soft impact oscillator

In order to suppress the near-grazing multistability of the impact oscillator, a delay feedback controller [36] is applied to system (1) by adding an input $u(\tau )$ to the forcing, such that the new system can be written as

$$\begin{aligned} {\left\{ \begin{array}{ll} x'(\tau )=v(\tau ),\\ v'(\tau )\!=\!\left( a\omega ^2\sin (\omega \tau )+u(\tau )\right) -2\zeta v(\tau )-x(\tau )\\ \qquad \qquad \quad \beta (x(\tau )-e)-H(x(\tau )-e), \end{array}\right. }\nonumber \\ \end{aligned}$$

(2)

where

$$\begin{aligned} u(\tau )=K\left( v(\tau -\tau _{d})-v(\tau )\right) {,\quad }\tau \ge 0\text{, } \end{aligned}$$

(3)

is the time-delayed feedback control. In Eq. (3), $K\ge 0$ is the control gain, setting the coupling strength between the impact oscillator output $v(\tau -\tau _d)-v(\tau )$ and the control input $u(\tau )$, and $\tau _{d}>0$ is a tunable time delay (in contrast to a lag introduced by the control loop, which is assumed to be zero here). Since the purpose of this present work is to control the system to a period-1 response, the delay term $\tau _d$ is set to one period of the external excitation $\tau _d=T:=2\pi /\omega \text{. }$

2.1 Construction of the stroboscopic map

To calculate the LEs, a stroboscopic map needs to be constructed to obtain a discrete-time system. For the piecewise-smooth DDEs (2), a constant phase surface can be defined as

$$\begin{aligned} P^{T}_s:=\{ (y, \tau )\in \mathbb {R}^{2}\times \mathbb {R}^{+}|~ \tau =\tau _{0}+kT,~ k\in \mathbb {Z}^{+}\},\nonumber \\ \end{aligned}$$

(4)

and the relevant continuous stroboscopic map is

$$\begin{aligned} P_D:~P^{T}_s\rightarrow P^{T}_s, \end{aligned}$$

(5)

which is defined by the semiflow described by the piecewise-smooth DDE system (2). The two regions are determined by the Heaviside step function on their right-hand side of system (2). Since the system’s dynamics can be described using the stroboscopic map (5), we use the definition of LEs for discrete-time dynamical systems.

Definition 2.1

[42] For any initial condition $x_{0}\in P^T_s$, let $\{x_{m}\}^{\infty }_{m=0}$ be the corresponding orbit of the map $P_{D}$, and let $\lambda ^{m}_{0 },\cdots ,\lambda ^{m}_{n}$ be the n largest in modulus eigenvalues of $D (P_{D})^{m}(x_{0})$, sorted such that $|\lambda ^m_0|\ge \ldots \ge |\lambda ^m_{n}|$. The LEs of $x_{0}$ are

$$\begin{aligned} \vartheta _{i}:=\lim _{m\rightarrow \infty }\ln |\lambda ^{m}_{i}|^{\frac{1}{m}},i=1,\ldots ,n \end{aligned}$$

(6)

whenever the limit exists for $x_0$ and for all $i\le n$.

Fig. 2

(Colour online) Bifurcation diagram of the impact oscillator computed for $\zeta =0.01$, $e=1.28$, $a=0.49$, $\beta =28$ and varying frequency of external excitation $\omega$. The period-7, period-4 and period-3 attractors are denoted by green, red and blue dots, respectively. Additional panels below present the corresponding periodic orbits and Poincaré sections for $\omega =0.845$, $\omega =0.851$, $\omega =0.8513$, $\omega =0.8528$ and $\omega =0.8538$. The desired attractor for control purpose, i.e. an unstable period-1 orbit, is shown in red dashed line. The location of the impact boundary is indicated by the vertical blue lines

2.2 Construction of basins of attraction

Similarly, the relevant continuous stroboscopic map of the uncontrolled system (1) can be constructed as

$$\begin{aligned} P :~P^{T}_s\rightarrow P^{T}_s, \end{aligned}$$

(7)

which is defined as a semiflow with two dimensions. The basin of attraction of a compact invariant subset $A\subset M$ of system (1) is defined as

$$\begin{aligned} \mathcal {B}(A):=\{y\in M: (P)^{\tau }(y)\in A, \tau \rightarrow +\infty \}, \end{aligned}$$

(8)

where the manifold M is two dimensional.

According to the construction of the maps P and $P_{D}$, the basin of a compact invariant subset $A\subset M$ of system (2) can be defined as

$$\begin{aligned} \mathcal {B}_{d}(A):=\{y\in M:(P_D)^{\tau }\circ P(y)\in A~\mathrm {for}~\tau \rightarrow \infty \}.\nonumber \\ \end{aligned}$$

(9)

Thus, by monitoring the evolution of the basin (9) through varying system parameters and comparing with the basin (8) for the system (1), multistability in the system (2) can be observed.

2.3 Construction of the Jacobian matrix

In order to construct the Jacobian matrix of the map (5), we write system (2) as a nonlinear DDE of the form

$$\begin{aligned} q'=f(\tau ,q,q(\tau -\tau _d)) \end{aligned}$$

(10)

by inserting Eqs. (3) into (2). For this DDE $\tau$ is in $\mathbb {P}$, where $\mathbb {P}$ is an interval of $\mathbb {R}^{+}$ unbounded on the right, and $f:\mathbb {P}\times \mathbb {R}^{2} \times \mathbb {R}^{2} \rightarrow \mathbb {R}^{2}$ is a piecewise-smooth function based on the Heaviside step function. Take $N\in \mathbb {Z}^{+}$ sufficiently large, and define the grid points $\tau ^{i}_{d}:=i\frac{\tau _{d}}{N}$, $i=0,\ldots ,N$, and $y_{i}(\tau ):=q(\tau -\tau ^{i}_{d})$ for all $\tau \ge 0$, $i=0,\ldots ,N$, where $\tau _d:=T$. The DDE (10) can be approximated as a $2(N+1)$-dimensional piecewise-smooth discretised system, as studied in [43]. Thus, in detail, for any time interval $[\tau _{m},\tau _{m}+\tau _{d}]$, where $\tau _{m}=\tau _{1}+(m-1)T$, $\tau _{1}=\tau _{0}$ and $m\in \mathbb {Z}^{+}$, the solution of DDE (10) can be approximated by N steps of size $h=\frac{\tau _{d}}{N}$ by using numerical integration. During each numerical integration, when the system encounters the impact event, it switches directly to the relevant function based on the Heaviside step function, ensuring that the convergence rate of the modified Euler integration is ${{\,\mathrm{\mathcal {O}}\,}}(h)$ [40]. As a consequence, this convergence rate can guarantee the accuracy of the following numerical calculations. If the modified Euler integration formula [44] gives a single step of size as

$$\begin{aligned} y_{0}(\tau _{m}+h)=&\,y_{0}(\tau _{m})+\tfrac{h}{2} \big [f(\tau _{m},y_{0}(\tau _{m}),y_{0}(\tau _{m}-hN))\nonumber \\&+ f(\tau _{m+1},y_{0} \nonumber \\&(\tau _{m+1}),y_{0}(\tau _{m}-h(N-1)))\big ], \end{aligned}$$

(11)

applying the recursion (11) $N+1$ times, we obtain the discretised the map $P_D$ as a map $F_{P}:\mathbb {R}^{2(N+1)}\rightarrow \mathbb {R}^{2(N+1)}$, mapping $Y_{m}: =(y_{N}^{T}(\tau _{m}),\cdots ,y_{1}^{T}(\tau _{m}),y_{0}^{T}(\tau _{m}))^{T}\in \mathbb {R}^{2(N+1)}$ to $Y_{m+1}=F_{P}(Y_{m})$, where $Y_{m+1}: =(y_{N}^{T}(\tau _{m}+\tau _{d}),\cdots ,y_{1}^{T}(\tau _{m}+\tau _{d}), y_{0}^{T}(\tau _{m}+\tau _{d}))^{T} \in \mathbb {R}^{2(N+1)}$. When an arbitrary perturbation $\delta Y$ is applied, the variational equation for $F_{P}$ can be written as

$$\begin{aligned} \delta Y_{m+1}=\sum ^{N+1}_{i=1}\frac{\partial F_{P}(Y_{m})}{\partial y_{i-1}(\tau _{m})}\delta y_{i-1}(\tau _{m}), \end{aligned}$$

(12)

where $\delta Y_{m}:=(\delta y_{N}^{T}(\tau _{m}),\cdots ,\delta y_{1}^{T}(\tau _{m}),\delta y_{0}^{T}(\tau _{m}))^{T} \in \mathbb {R}^{d(N+1)}$ and $\delta y_{i}(\tau ):=\delta y(\tau -\tau _d^i)$, $i=0,\cdots ,N$. As Eq. (12) can be obtained by linearising the variational equation of the nonlinear differential equation as

$$\begin{aligned} \frac{\mathrm {d} }{\mathrm {d}\tau }\delta y_{0}(\tau )= & {} \frac{\partial f(\tau ,y_{0}(\tau ),y_{N}(\tau ))}{\partial y_{0}}\delta y_{0}(\tau ) \nonumber \\&+\frac{\partial f(\tau ,y_{0}(\tau ),y_{N}(\tau ))}{\partial y_{N}}\delta y_{N}(\tau ), \end{aligned}$$

(13)

using the modified Euler integration formula, Eq. (13) can be discretised in the same way as Eq. (11). Iterating this process for $N+1$ times, the approximation of Jacobian matrix $J_m$ of the map $P_{D}$, applied to $\delta Y_m$, equals $\delta Y_{m+1}$, such that $J_m$ can be assembled through the relation

$$\begin{aligned} \delta Y_{m+1}=J_{m}\delta Y_{m}\text{. } \end{aligned}$$

Then, for an arbitrary sufficiently small $\delta > 0$, through selecting an arbitrary initial separation vector (e.g. $\delta Y_{1}=(0, \cdots , 0, 0, \delta )^{T}$) and renormalisation, and calculating the leading LEs of the map $P_{D}$ along approximate trajectory $y_i(\tau _m)$ using Gram-Schmidt orthonormalisation and Eq. (6). For a detailed description of the calculation steps, readers can refer to [40].

3 Numerical investigation of the delay feedback controller

We start with the bifurcation analysis of near-grazing dynamics of the impact oscillator without the delayed feedback control, as given in Eq. (1). Figure 2 shows the bifurcation diagram of the system (1) with excitation $\omega \in [0.845,0.854]$ as the bifurcation parameter. Our calculation was run for 350 cycles of external excitation, and the data for the first 300 cycles were omitted to ensure the steady-state response, whereas the last 50 values of the displacement x at $\tau =\tfrac{2n_s\pi }{\omega }$, $n_s\in \mathbb {Z}^{+}$ were plotted in the bifurcation diagram for each value of the bifurcation parameter. For the range $\omega \in [0.851,0.8512]$, we find coexisting attractors: one period-7, one period-4 and one period-3 orbits, shown as green, red and blue dots, respectively. The additional panels of Fig. 2 show the continuous-time trajectories of the orbits and the corresponding discrete orbits of the stroboscopic map for $\tau _0=0$. At $\omega =0.845$ (first row), the system presents a period-1 (blue) and a period-7 (green) attractors. At $\omega =0.8510$ (second row), there are a period-3 (blue), a period-7 (green) and a period-4 (red) orbits. At $\omega =0.8513$ (third row), the system has a period-3 (blue) and a period-7 (green) responses, which both persist throughout the entire parameter range. Note that at the rightmost of this row, we include the unstable period-1 response (red dashed line), which is the desired target for the delayed feedback controller to suppress this grazing-induced complex dynamics. At $\omega =0.8528$ (fourth row), a new period-7 response (red) can be observed coexisting with the period-3 (blue) and the period-7 (green) orbits. At $\omega =0.8538$ (fifth row), only period-7 (green) and period-3 (blue) attractors are left. Basins of attraction of the impact oscillator are presented in Fig. 3 computed using DYNAMICS-WIN [45] showing the evolution of all these attractors as the frequency of excitation $\omega$ varies.

Fig. 3

(Colour online) Basins of attraction for frequencies $\omega$ highlighted in Fig. 2: a $\omega = 0.851$ with a period-3 (blue dots, black basin), a period-4 (green dots, red basin) and a period-7 attractors (black dots, white basin), b $\omega = 0.8513$ with a period-3 (blue dots, black basin) and a period-7 attractors (black dots, red basin), c $\omega = 0.8528$ with a period-3 (blue dots, red basin), a period-7 (black dots, white basin) and a new period-7 attractors (green dots, black basin). The other parameters are $\zeta =0.01$, $e=1.28$, $a=0.49$ and $\beta =28$

Fig. 4

(Colour online) a Bifurcation diagram and b the largest LEs of impact oscillator with the delayed feedback control for varying control gain $K\in [0,\, 0.8]$. c The maximum displacement, Max(x), for varying control gain $K\in [0.148,\, 0.420]$. System parameters are $\zeta =0.01$, $e=1.28$, $a=0.49$, $\beta =28$, $\omega =0.8528$ and $\tau _{d}=\frac{2\pi }{\omega }$

Fig. 5

(Colour online) Basins of attraction of impact oscillator with delay feedback control, (2)–(3), and different control gains K: a $K=0.0015$ (period-3: green dots with cyan basin, period-7: red dots with orange basin), b $K=0.04$ (period-4: red dots with orange basin, chaos: purple dots with cyan basin) and c $K=0.32$ (period-1: red dot with orange basin). Additional panels demonstrate the phase trajectories of the impact oscillator. The location of the impact boundary is denoted by the vertical blue lines. The other parameters of the system are $\zeta =0.01$, $e=1.28$, $a=0.49$, $\beta =28$ and $\omega =0.8528$

Since the system has multiple attractors at $\omega =0.8528$, the delay feedback control (3), $u(\tau )=K\left( v(\tau -\tau _{d})-v(\tau )\right)$ with $\tau _d=2\pi /\omega$ was applied to suppress this multistable regime. The period-1 orbit is stable only for control gains K in a certain range. Figure 4a shows a bifurcation diagram of the controlled impact oscillator when varying the bifurcation parameter $K\in [0,\, 0.8]$. Our calculations were run for 80 periods of the external excitation with $K=0$ to ensure that the system (1) settles down to its steady state, and then switched the controller (3) on and kept the system (2) under a particular value of the control gain K running for 600 periods, whereas the last 80 values of oscillator’s displacement x at $\tau =\tfrac{2n_s\pi }{\omega }$, $n_s\in \mathbb {Z}^{+}$ were plotted in the bifurcation diagram. Figure 4b shows the corresponding LE diagram of the controlled impact oscillator when varying the control parameter K. Likewise, the calculations for the LEs were run for 80 periods of external excitation with $K=0$ initially, followed by another 600 periods calculations with a certain value of K, where the first 200 periods were omitted to ensure the steady-state response of the controlled oscillator while the remaining 400 periods were used to calculate the LEs as studied in Sect. 2.3. It can be seen from the figures that, when $K<0.148$, the system presents multi-periodic responses. For example, when $K=0.0015$, the system has a period-3 attractor, which is a small perturbation of the period-3 attractor in the uncontrolled system (see inset in Fig. 4a). For $K\in (0.04,\, 0.148)$, we observe some chaotic motions, as indicated by the positive leading LEs, shown in Fig. 4b. For $K\in [0.148,0.42]$, the control stabilises the desired period-1 motion at grazing. The leading LE is smaller than 0, as expected for stable periodic motion, for $K\in [0.148,0.42]$. For $K>0.42$, the desired period-1 motion loses its stability via a Neimark–Sacker bifurcation and transitions into chaos via torus breakup. As can be seen from the figure, the chaotic motions have periodic windows and their corresponding LEs are around 0 (see inset in Fig. 4b) indicating that the system was not successfully controlled. In addition, the maximum displacement, Max(x), for varying control gain $K\in [0.148,\, 0.42]$ is presented in Fig. 4c to demonstrate that the desired period-1 orbit was indeed in the critical state of grazing.

To demonstrate global stability of the delayed feedback control strategy for suitable control gains K, we present the basins of attraction for various control gains K in Fig. 5. The computation procedure for these basins is given as follows: From any initial value ($x_0,v_0$), the trajectory of the system (1) at the moment $\tau _{0}+T$ was calculated, and then was inserted into the system (2) with a certain value of the control gain K. As the trajectory converged to an attractor, this initial value was marked by a specific colour in the phase plane. As the control gain K is set to its nonzero value only for $\tau >T=\tau _d=2\pi /\omega$, the basins of attraction are subsets of $\mathbb {R}^2$, even though the controlled system is a DDE. In Fig. 5a, there are two coexisting attractors for $K=0.0015$, a period-3 (green dots with cyan basin) and a period-7 (red dots with orange basin) attractors. Both attractors are small perturbations of attractors existing in the uncontrolled system. For $K=0.04$, as shown in Fig. 5b, the system is bistable consisting of a period-4 (red dots with orange basin) and chaotic attractors (purple dots with cyan basin). The basin of the chaotic attractor is noticeably smaller than the basin of the period-3 attractor in Fig. 5a. At $K=0.32$, the system is monostable with the desired period-1 attractor only (see Fig. 5c).

According to the above results, when $K\in [0.148,0.42]$, the delay feedback controller can stabilise the impact oscillator on the target period-1 orbit. Figure 6 presents the time profiles of displacement of the system and its external excitation with the control signal u as a demonstration of controlling from different coexisting attractors. As can be seen from the figure, the controller was switched on at the 81th period of the external excitation, and for all the coexisting attractors at $\omega =0.8528$, including a period-3 and two period-7 attractors, the system was successfully driven to the desired period-1 motion at grazing with one impact per period of excitation.

Fig. 6

Time profiles of displacement of the impact oscillator and the external excitation including the control signal u. Grey line indicates the time when the delay feedback control was switched on. Before this time, the gain $K=0$ and the uncontrolled oscillator is on its a period-3, b first period-7 and c second period-7 attractors. The parameters of the controlled impact oscillator are $\zeta =0.01$, $e=1.28$, $a=0.49$, $\beta =28$, $\omega =0.8528$ and $K=0.32$

4 Path-following study of the delay feedback controller

In this section, we will investigate the periodically forced impact oscillator with path-following (continuation) methods, considering the time-delayed feedback controller introduced previously (see system (2) with (3)). As mentioned before, this model is a piecewise-smooth dynamical system with delay, for which no specialised software package for numerical continuation is available to the best of our knowledge. Therefore, in order to carry out a detailed path-following study of the impact oscillator with time-delayed feedback control we will employ the numerical approach proposed in [39].

Fig. 7

(Colour online) a Continuation of period-1 solutions of the (uncontrolled) impact oscillator (1) with respect to the excitation frequency $\omega$, for the parameter values given in Fig. 2. The vertical axis presents the time the oscillating mass is in contact with the secondary spring $k_{2}$ (see Fig. 1). The labels GR1, PD1 and PD2 stand for grazing and period-doubling bifurcations detected at $\omega \approx 0.85061$, $\omega \approx 0.85113$ and $\omega \approx 0.91440$, respectively. Solid and dashed branches mark stable and unstable solutions, respectively. Furthermore, impacting solutions are represented by the green line, while non-impacting orbits correspond to the red branch (before the grazing bifurcation GR1). Panel b depicts a phase plot corresponding to the test point P1 ($\omega =0.8528$), where two periodic solutions coexist, one stable (in blue, solid line) and one unstable (in black, dashed curve)

Fig. 8

(Colour online) a Two-parameter continuation of the period-doubling bifurcations found in Fig. 7, with respect to frequency $\omega$ and amplitude a of excitation. The intersection with the horizontal line $\omega =0.8528$ defines the period-doubling points PD1 and PD2 detected before. Panels b–d display phase plots corresponding to the test points P1 ($\omega =0.72$, $a=1.25$), P2 ($\omega =0.8$, $a=0.92$) and P3 ($\omega =0.9$, $a=0.7$), respectively. These panels present the system response without control (in blue) and with control (in black), using the control parameters $K=0.32$ and $\tau _{d}=\frac{2\pi }{\omega }$

Fig. 9

(Colour online) Continuation of the periodic response of the controlled impact oscillator (2) with respect to the control delay $\tau _{d}$, for the parameter values given in Fig. 2, showing the contact time on the vertical axis. The period-doubling (PD3) and grazing (GR2) bifurcations are located at $\tau _{d}\approx 0.47404$ and $\tau _{d}\approx 1.78922$, respectively. Lateral panels present phase portraits for different values of the control delay $\tau _{d}$

Fig. 10

(Colour online) a Two-parameter continuation of the period-doubling and grazing bifurcations found in Fig. 9, with respect to the control delay $\tau _{d}$ and control gain K. Panels b–d display phase plots corresponding to the test points P1 ($\tau _{d}=0.62$, $K=0.23$), P2 ($\tau _{d}=1.3$, $K=0.3$) and P3 ($\tau _{d}=2.1$, $K=0.4$), respectively

4.1 Defining systems for continuation

The numerical approach presented in [39] is based on the chain approximation [46] using a higher-order approximation scheme of the original DDE by introducing a finite sequence of Taylor expansions as follows. Let us consider a general DDE of the form

$$\begin{aligned} \dot{q}(t)=f(t,q(t),q(t-\tau _{d})), \end{aligned}$$

(14)

which defines a system of delay differential equations (DDEs) with constant delay $\tau _{d}>0$, where $f:\mathbb {R}\times \mathbb {R}^d\times \mathbb {R}^d\rightarrow \mathbb {R}^d$ is a sufficiently smooth function. Let us now take $N\in {{\,\mathrm{\mathbb {N}}\,}}$ sufficiently large and define the grid points $t_{i}:=i\frac{\tau _{d}}{N}$, $i=0,\ldots ,N$. Furthermore, define $u_{i}(t):=q(t-t_{i})$ for all $t\ge 0$, $i=0,\ldots ,N$. In this setting, we obtain via Taylor expansion to order M with

$$\begin{aligned} u_{i-1}(t)= & {} q\left( t-\left( t_{i}-\frac{\tau _{d}}{N}\right) \right) =u_{i}\left( t+\frac{\tau _{d}}{N}\right) \nonumber \\= & {} \sum ^{M}_{k=0}\frac{1}{k!}u^{(k)}_{i}(t)\left( \frac{\tau _{d}}{N}\right) ^k + {{\,\mathrm{\mathcal {O}}\,}}\left( \left( \frac{\tau _{d}}{N}\right) ^{M+1}\right) , \text{ and } \nonumber \\ \end{aligned}$$

(15)

$$\begin{aligned} \dot{u}_{0}(t)=f(t,u_{0}(t),u_{N}(t)), \end{aligned}$$

(16)

for all $t\ge 0$, $i=1,\ldots ,N$, $M\ge 1$. After neglecting the ${{\,\mathrm{\mathcal {O}}\,}}$-terms, we obtain from (15) a system of dN differential equations of order M. In this way, a piecewise-smooth dynamical system of dimension d with constant delay can be approximated by a piecewise-smooth system of ODEs of dimension $d(NM+1)$ for large N, which then allows the study of the resulting model in the framework of hybrid dynamical systems [47]. Choosing order $M=2$, the defining system for periodic orbits of an impact oscillator with time-delayed feedback control (2) can be approximated by the following piecewise-smooth system of ODEs [39] on the interval [0, 1]:

$$\begin{aligned} z'(\tau )&=f(z(\tau ),\phi (z(\tau ),\alpha ),\alpha ), \quad \text{ where } \nonumber \\ \phi (z,\alpha )&={\left\{ \begin{array}{ll} 0&{} \text{ if } x-e<0\, (no contact ),\\ \beta (x-e) &{} \text{ if } x-e\ge 0\, (contact ), \end{array}\right. }\nonumber \\ z&:=(x,r,s,u_{0},\ldots ,u_{N},w_{1},\ldots ,w_{N})^T\in \mathbb {R}^{2N+4}{,\quad }\nonumber \\ \alpha&:=(\omega ,a,\beta ,\zeta ,e,K,\tau _{d})\in \left( \mathbb {R}^+_{0}\right) ^7 \end{aligned}$$

(17)

and

$$\begin{aligned} f(z,\alpha ,\phi )&:= \begin{pmatrix} \tau _{d}u_{0}\\ r+\omega \tau _{d} s-r\left( r^2+s^2\right) \\ s-\omega \tau _{d}r-s\left( r^2+s^2\right) \\ \tau _{d}\left( a\omega ^2r+K\left( u_{N}-u_{0}\right) -2\zeta u_{0}-x-\phi \right) \\ \left( w_{i}\right) _{i=1,\ldots ,N}\\ \left( 2N^2\left( u_{i-1}-u_{i}-\dfrac{1}{N}w_{i}\right) \right) _{i=1,\ldots ,N} \end{pmatrix}\text{. } \end{aligned}$$

(18)

The argument $\phi$ of the right-hand side f defines the no contact and contact operation modes of the impact oscillator, respectively. In the approximating system (17), we have introduced a time re-scaling $\tau \leftarrow \tau /\tau _{d}$ such that the approximation of the history $q(\tau -t)$ for $t\in [0,\tau _d]$ by Taylor expansion (15) is always over the unit interval, regardless the value of the delay $\tau _{d}$. Furthermore, in the approximating system (17) we have that $u_{0}(\tau )=v(\tau )$ and

$$\begin{aligned} u_{i}(\tau )\approx & {} v(\tau -\tau _{i}), \text{ for } \text{ all } \tau \in [0,1], \nonumber \\ \tau _{i}= & {} \frac{i}{N}, i=1,\ldots ,N. \end{aligned}$$

(19)

The approximation of the history of q by $u_i$ on the evenly spaced grid of $\tau _i$ on [0, 1] with order $M=2$ is a special case of the pseudospectral approximation of DDEs by ODEs, as used for bifurcation analysis in MATCONT by [48]. The spectral approximation from [48] has no advantage over the low-order approximation (19) for our problem, because the history segment is only differentiable once with Lipschitz continuous derivative, whenever the contact threshold $x=e$ has been crossed during the previous time interval of length $\tau _d$. Thus, the proposed second-order approximation has the most suitable order M.

In what follows, all numerical continuation results will be obtained from the approximating model (17) (with $N=15$) via the continuation platform COCO [49]. Specifically, we will make use of the COCO-toolbox ‘hspo’, which implements a segment-specific discretisation strategy in the framework of multisegment boundary-value problems, thus allowing the numerical continuation of periodic solutions for piecewise-smooth dynamical systems. In this way, a locus of grazing periodic orbits can be computed by introducing an extra solution segment with a terminal point satisfying the condition $x'=0$, where the mass velocity becomes zero. Here, a grazing solution can be detected via the auxiliary boundary condition $x-e=0$, and therefore a locus of such orbits can be obtained by freeing two parameters during the continuation process, using the COCO-command ‘coco xchg pars’. On the other hand, simulations generated via direct numerical integration will be computed for the original DDE model (2) using the MATLAB solver ‘dde23’, in combination with its built-in event location routines [50, 51] to detect accurately collisions with the impact boundary $x=e$.

4.2 Continuation of periodic orbits

We will first investigate the behaviour of the impact oscillator (1) (without control), considering the dynamical scenario analysed in Fig. 6 as starting point. Figure 7a shows the periodic response of system (1) with respect to the excitation frequency $\omega$, showing in the vertical axis the time the oscillating mass is in contact with the secondary spring $k_{2}$ (see Fig. 1). As can be seen in this bifurcation diagram, low values of $\omega$ produce oscillations of small amplitude, with no contact with the secondary spring. A critical point, however, is found at $\omega \approx 0.85061$, where a grazing bifurcation (labelled GR1) of limit cycles occurs. Here, the system presents a periodic solution making tangential contact with the impact boundary $x=e$. Shortly after the GR1 point, a period-doubling bifurcation (PD1) is detected for $\omega \approx 0.85113$. At this value, the period-1 solution loses stability and a family of stable period-2 solutions is born. The unstable period-1 orbit recovers stability at $\omega \approx 0.91440$, where another period-doubling bifurcation (PD2) occurs. Using direct numerical integration we find further attractors of higher period between the period-doubling points PD1 and PD2, as can be seen in Fig. 7b (see also Fig. 2). Here, a (stable) period-7 solution is depicted together with the original (unstable) period-1 orbit computed at the test point $\omega =0.8528$ (P1). The purpose of the time-delayed feedback control is to stabilise this period-1 response, as discussed before, for the parameter window defined by the period-doubling points PD1 and PD2.

The presence of the stable more complex (period-7) response in the range between PD1 and PD2 suggests that the period-doubling bifurcations PD1 and PD2 are the boundary of a parameter region with more complex system responses in two parameters. We will now investigate these period-doubling bifurcations by tracing them in two parameters (frequency $\omega$ and amplitude a of excitation) via two-parameter continuation. The result is presented in Fig. 8. We observe that the bifurcation points PD1 and PD2 belong to the same branch of period-doubling bifurcations in the two-parameter plane, bounding the isola plotted in panel (a), located between the two extremes of $\omega$ on this curve at $\omega \approx 0.66708$ and $\omega \approx 0.91456$, which define the window of existence of this isola. Inside the isola, the period-1 solution is unstable. The time-delayed feedback control stabilises the period-1 response, as verified at three test points (P1, P2, P3) within the isola, where the uncontrolled response (in blue, see Fig. 8b–d) ranges from periodic to chaotic motion, while the controller in all these cases is able to stabilise the original period-1 orbit (in black).

Next, let us investigate the periodic response of the impact oscillator with time-delayed feedback control using the approximating system (17) and the continuation platform COCO. For this case, the numerical continuation of period-1 solutions of the impact oscillator with time-delayed feedback control is shown in Fig. 9, for the range $0<\tau _{d}\le 3$, using the (unstable) period-1 orbit shown in Fig. 7b as starting solution. As expected, a family of unstable period-1 orbits is found for small time delay $\tau _{d}$. This orbit becomes stable at $\tau _{d}\approx 0.47404$, where a period-doubling bifurcation is located. As the time delay grows, another bifurcation (GR2) is found at $\tau _{d}\approx 1.78922$, where the periodic orbit makes tangential contact with the impact boundary $x=e$. This point, therefore, defines a boundary between impacting and non-impacting motion, as can be seen from the right phase plots in Fig. 9. This numerical investigation indicates that the time-delayed feedback controller is able to not only stabilise the desired period-1 motion but also control impacting regimes in the system.

Next, we will carry out a two-parameter continuation of the detected bifurcations above with respect to the main control parameters, i.e. the time delay $\tau _{d}$ and the control gain K. Figure 10 shows the resulting red and green curves that represent the two-parameter continuation of the period-doubling and grazing bifurcations found in Fig. 9. The bifurcation curves divide the two-dimensional parameter space into three regions. The first region, to the left of the period-doubling curve, corresponds to operation points for which the period-1 response is unstable in the controlled system. Crossing this line from the right produces a supercritical period-doubling bifurcation, due to which stable period-2 solutions are created, as the one computed in Fig. 10b, for the test point P1 ($\tau _{d}=0.62$, $K=0.23$). The region between the period-doubling and grazing curves provides parameter values producing stable period-1 responses, as discussed before, see for instance the solution calculated at the test point P2 ($\tau _{d}=1.3$, $K=0.3$), shown in Fig. 10c. The third region, located to the right of the grazing curve, defines operation points yielding period-1 non-impacting solutions, similar to the test point P3 ($\tau _{d}=2.1$, $K=0.4$), see Fig. 10d.

5 Conclusions

This paper presents a numerical study of controlling grazing-induced multistability in a periodically forced impacting system by using time-delayed feedback control. The control aims to switch the system from undesired coexisting attractors to a desired period-1 response, thus suppressing the complex dynamics caused by grazing or crossing the contact threshold. In our numerical investigations, we use a newly developed numerical approach for analysing non-smooth delay equations, a computational method for calculating the Lyapunov exponents and a grazing point estimation algorithm. In addition, path-following (continuation) techniques for non-smooth dynamical systems were employed to analyse the bifurcations of the controlled system dynamics.

In the first part of the numerical study, a scenario with grazing-induced multistability with coexisting period-3, period-4 and period-7 attractors was investigated. Basins of attraction reveal the complex dynamics of the system during grazing events. Apart from these stable coexisting attractors, an unstable period-1 orbit exists. This orbit was used as the desired attractor for the system with the delayed feedback control. It was found that the delayed feedback control is effective when its control parameter is $K\in [0.148,0.42]$, and the system can be driven to a globally stable period-1 motion with grazing and one impact per period of excitation. As the control gain increases ($K>0.42$), the controller destabilises the period-1 motion through a Neimark–Sacker bifurcation and the system can bifurcate to chaos via torus breakup.

In the second part of this study, we used continuation techniques for non-smooth dynamical systems to identify the parameter window defined by two period-doubling points at where the desired (unstable) period-1 orbit exists. Then, a two-parameter continuation for the frequency and the amplitude of excitation was carried out for tracing the period-doubling bifurcation bounding a region of instability for period-1 orbits. We further investigated the periodic response of the impact oscillator when subject to delayed feedback control. The results show that the control is able to not only stabilise the desired period-1 motion but also control impacting regimes in the system. By varying the main control parameters, the time delay $\tau _d$ and the control gain K, a two-parameter region between the period-doubling and grazing curves that produces the desired stable period-1 responses was obtained.