Suppression of a nonplanar motion in an externally excited string by the addition of viscosity based on velocity feedback control

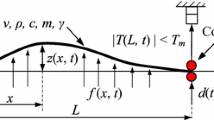
Abstract

This study concerns the out-of-plane motion of a vertically disposed string with one end fixed and the other subjected to a harmonic excitation. Excited in its primary resonance, the string can vibrate in the direction orthogonal to the excitation direction through nonlinear coupling effects and has out-of-plane motion. To suppress this out-of-plane motion, we propose a boundary control method that modifies the boundary condition of the fixed upper end, i.e., we move the fixed upper end in the direction orthogonal to the external excitation. The unstable range for trivial steady state motion in this direction, which exists in the neighborhood of the primary resonance condition, changes to a stable range under suitable feedback gain. The out-of-plane motion is then suppressed for any excitation frequency. Experiments conducted using a simple apparatus confirmed the validity of the proposed method adopting boundary control.

Appendices

Derivation of the equations of motion and effect of the stiffness in the string

We derive Eqs. (4 and 5) following section 7 in [9]. By setting the representative length and time as l and $l\sqrt{\rho A/T_0}$, respectively, the nondimensional equations of motion in $\xi$, $\eta$, and $\zeta$-directions are, respectively,

$$\begin{aligned}&\frac{\partial ^2 \xi ^*}{\partial t^{*2}} - \frac{\partial ^2 \xi ^*}{\partial z^{*2}} + \frac{EI}{T_0l^2}\frac{\partial ^4 \xi ^*}{\partial z^{*4}} = (\beta -1)\nonumber \\&\frac{\partial }{\partial z^*}\left[ \left\{ \frac{d \zeta ^*}{dz^{*}} -\left( \frac{d \zeta ^*}{dz^{*}}\right) ^2 \right. \right. \nonumber \\&\left. \left. + \frac{1}{2}\left( \left( \frac{\partial \xi ^*}{\partial z^*}\right) ^2+\left( \frac{\partial \eta ^*}{\partial z^*}\right) ^2\right) \right\} \frac{\partial \xi ^*}{\partial z^*}\right] , \end{aligned}$$

(56)

$$\begin{aligned}&\frac{\partial ^2 \eta ^*}{\partial t^{*2}} - \frac{\partial ^2 \eta ^*}{\partial z^{*2}} + \frac{EI}{T_0l^2}\frac{\partial ^4 \eta ^*}{\partial z^{*4}} = (\beta -1)\nonumber \\&\frac{\partial }{\partial z^*}\left[ \left\{ \frac{d \zeta ^*}{dz^{*}}-\left( \frac{d \zeta ^*}{dz^{*}}\right) ^2 \right. \right. \nonumber \\&\left. \left. + \frac{1}{2}\left( \left( \frac{\partial \xi ^*}{\partial z^*}\right) ^2+\left( \frac{\partial \eta ^*}{\partial z^*}\right) ^2\right) \right\} \frac{\partial \eta ^*}{\partial z^*}\right] , \end{aligned}$$

(57)

$$\begin{aligned}&\frac{\partial ^2 \zeta ^*}{\partial t^{*2}} - \beta \frac{\partial ^2 \zeta ^*}{\partial z^{*2}} = \frac{1}{2}(\beta -1)\nonumber \\&\frac{\partial }{\partial z^*}\left[ \left( \frac{\partial \xi ^*}{\partial z^*}\right) ^2 + \left( \frac{\partial \eta ^*}{\partial z^*}\right) ^2 \right. \nonumber \\&\left. -2\frac{\partial \zeta }{\partial z}\left\{ \left( \frac{\partial \xi ^*}{\partial z^*}\right) ^2 + \left( \frac{\partial \eta ^*}{\partial z^*}\right) ^2\right\} \right] . \end{aligned}$$

(58)

In Eq. (58), because $\beta>>1$, the first term on the left-hand side (i.e., the longitudinal inertia) can be neglected [9]. Also neglecting the higher-order terms, Eq. (58) leads to

$$\begin{aligned} \frac{\partial ^2 \zeta ^*}{\partial z^{*2}} = -\frac{1}{2}\frac{\partial }{\partial z^*}\left\{ \left( \frac{\partial \xi ^*}{\partial z^*}\right) ^2 + \left( \frac{\partial \eta ^*}{\partial z^*} \right) ^2\right\} . \end{aligned}$$

(59)

Considering the boundary conditions in the $\zeta$-direction, $\zeta ^*=0$ at $z^*=0$ and $z^*=1$, yields

$$\begin{aligned} \frac{\partial \zeta ^*}{\partial z^* }= & {} -\frac{1}{2}\left\{ \left( \frac{\partial \xi ^*}{\partial z^*}\right) ^2+\left( \frac{\partial \eta ^*}{\partial z^*}\right) ^2\right\} \nonumber \\&+ \frac{1}{2}\int _0^1\left\{ \left( \frac{\partial \xi ^*}{\partial z^*}\right) ^2+\left( \frac{\partial \eta ^*}{\partial z^*}\right) ^2\right\} dz^*. \end{aligned}$$

(60)

We deal with the case that the coefficient $\frac{EI}{T_0l^2}$ is sufficiently less than 1 as shown in section 7.5 of [9]; for the string used in the present experiment, $\frac{EI}{T_0l^2}={1.03}\times 10^{-5}$. The third terms on the left-hand sides of Eqs. (56 and 57) are then neglected. Regarding the orders of $\xi$, $\eta$, and $\zeta$ as $O(\zeta )=O(\xi ^2)=O(\eta ^2)$, we neglect the terms related to ${\left( \frac{d \zeta ^*}{dz^{*}}\right) }^2$ in Eqs. (56 and 57). Then, substituting Eq. (60) in Eqs. (56 and 57), we obtain Eqs. (4 and 5), in which the viscous damping effect is further considered.

Derivation of the amplitude equations adopting the method of multiple scales

In this appendix, we derive the amplitude equations in the case with feedback control by applying the method of multiple scales. In the case without feedback control, we replace $\mu _{\mathrm {c}}$ with $\mu$. The asterisk is omitted.

1.1 Ordering of the terms

The orders of the terms and the expansion of the approximate solution are fundamentally decided in a traditional manner (e.g., see pp. 290–294 in [9]). Balancing the external excitation with the cubic nonlinear terms, we estimate the leading order of $\xi$ as $O(\epsilon ^{1/3})$. Additionally, considering the contribution of viscous damping, we set the order of the damping ratio $\mu _{\mathrm {c}}$ as $O(\epsilon ^{2/3})$ by balancing the external excitation and damping terms. The balancing is carried out at $O(\epsilon )$. In a similar way, the order of $\eta$ is estimated as $O(\epsilon ^{1/3})$. We rescale by substituting $\epsilon ^{1/3}$ for $\epsilon$ . Then, the leading order of $\xi$ and $\eta$ is $O(\epsilon )$, the excitation amplitude of $\delta _x$ is $O(\epsilon ^3)$, and the damping ratio $\mu _{\mathrm {c}}$ is $O(\epsilon ^2)$. The first and third terms in Eqs. (4 and 5) are then estimated as $O(\epsilon )$ and the other terms as $O(\epsilon ^3)$ . Because the ratio between $O(\epsilon )$ and $O(\epsilon ^3)$ is $\epsilon ^2$, in the expansion for $\xi$ and $\eta$, the ratio of the leading term with $O(\epsilon )$ and the succeeding second term should be $O(\epsilon ^2)$. We therefore employ the asymptotic expansion as Eqs. (10 and 11). According to the above discussion, because the ratio of the fast and slow time scales, $t_0$ and $t_1$, should be $\epsilon ^2$, we introduce $t_2=\epsilon ^2 t$ and set the order of the detuning parameter $\sigma$ to be $O(\epsilon ^2)$ as in Eq. (13).

1.2 Analysis of the first order, $O(\epsilon )$

By substituting Eqs. (10 and 11) in Eqs. (4 and 5), we obtain equations of the first-order term $O(\epsilon )$ for $\xi$ and $\eta$, respectively, as follows:

$O(\epsilon )$:

$$\begin{aligned} {D_0}^2 \xi _1 - {\xi _1}^{\prime \prime }= & {} 0, \end{aligned}$$

(61)

$$\begin{aligned} {D_0}^2 \eta _1 - {\eta _1}^{\prime \prime }= & {} 0, \end{aligned}$$

(62)

where $D_0$ is the derivative with respect to $t_0$. The prime symbol represents the derivative with respect to the dimensionless coordinate ${ z}$. The boundary conditions of the first-order term are expressed as:

$$\begin{aligned} \left\{ \begin{array}{l} \xi _1(0,t) = 0,\, \xi _1(1,t) = 0, \\ \eta _1(0,t) = 0,\, \eta _1(1,t) = 0. \end{array} \right. \end{aligned}$$

(63)

1.3 Analysis of the third order, $O(\epsilon ^3)$

We also obtain equations of the third-order term $O(\epsilon ^3)$ for $\xi _3$ and $\eta _3$, respectively, as follows:

$O(\epsilon ^3)$:

$$\begin{aligned} {D_0}^2 \xi _3 - {\xi _3}^{\prime \prime }= & {} - 2 D_0 D_2 \xi _1 - 2 \hat{\mu } D_0 \xi _1 \nonumber \\&+ \frac{\beta }{2} \int _0^1 \left( {{\xi _1}^{\prime }}^2 + {{\eta _1}^{\prime }}^2 \right) dz \cdot {\xi _1}^{\prime \prime }, \end{aligned}$$

(64)

$$\begin{aligned} {D_0}^2 \eta _3 - {\eta _3}^{\prime \prime }= & {} - 2 D_0 D_2 \eta _1 - 2 \hat{\mu } D_0 \eta _1 \nonumber \\&+ \frac{\beta }{2} \int _0^1 \left( {{\xi _1}^{\prime }}^2 + {{\eta _1}^{\prime }}^2 \right) dz \cdot {\eta _1}^{\prime \prime }, \end{aligned}$$

(65)

where $D_2$ denotes the derivative with respect to $t_2$. The boundary conditions of the third-order term $O(\epsilon ^3)$ are expressed as:

$$\begin{aligned} \left\{ \begin{array}{l} \xi _3(0,t) = 0,\, \xi _3(1,t) = \hat{\delta _x} \cos \nu t, \\ \eta _3(0,t) = -\hat{\alpha } D_0 \eta _{\mathrm {s}},\, \eta _3(1,t) = 0. \end{array} \right. \end{aligned}$$

(66)

1.4 Derivation of the amplitude equations

According to Eqs. (61 and 62), the solutions of the first-order equations are expressed as:

$$\begin{aligned} \xi _1= & {} \varPhi _{11} (z) A(t_2) e^{i \omega _1 t_0} + \mathrm {c.c.}, \end{aligned}$$

(67)

$$\begin{aligned} \eta _1= & {} \varPhi _{11} (z) B(t_2) e^{i \omega _1 t_0} + \mathrm {c.c.}, \end{aligned}$$

(68)

where c.c. denotes the complex conjugate of the preceding term and $\varPhi _{11}$ is determined by solving the boundary value problems

$$\begin{aligned}&\!\!\!&{\varPhi _{11}}^{\prime \prime } + {\omega _1}^2 \varPhi _{11} = 0, \end{aligned}$$

(69)

$$\begin{aligned}&\!\!\!\left\{ \begin{array}{l} \varPhi _{11}(0,t_0) = 0, \\ \varPhi _{11}(1,t_0) = 0. \end{array} \right. \end{aligned}$$

(70)

The solution of Eq. (69) with the boundary conditions of Eq. (70) for the first mode function is

$$\begin{aligned} \varPhi _{11} = \sin \pi z. \end{aligned}$$

(71)

We rewrite Eqs. (67 and 68) as

$$\begin{aligned} \xi _1= & {} A \sin \pi z \cdot e^{i \omega _1 t_0} + \mathrm {c.c.}, \end{aligned}$$

(72)

$$\begin{aligned} \eta _1= & {} B \sin \pi z \cdot e^{i \omega _1 t_0} + \mathrm {c.c.} \end{aligned}$$

(73)

By considering the component with angular frequency $\omega _1$, which resonates under the external excitation, the solutions of Eqs. (64 and 65) are expressed as:

$$\begin{aligned} \xi _3= & {} \varPhi _{3 \xi } (z,t_2) e^{i \omega _1 t_0} + \mathrm {c.c.}, \end{aligned}$$

(74)

$$\begin{aligned} \eta _3= & {} \varPhi _{3 \eta } (z,t_2) e^{i \omega _1 t_0} + \mathrm {c.c.} \end{aligned}$$

(75)

By substituting Eqs. (67, 68, 74, and 75) in Eqs. (64 and 65), we have

$$\begin{aligned}&{\varPhi _{3 \xi }}^{\prime \prime } + {\omega _1}^2 \varPhi _{3 \xi } \nonumber \\&\quad = 2 i \omega _1 \varPhi _{11} D_2 A + 2 i \omega _1 \hat{\mu } \varPhi _{11} A \nonumber \\&\qquad - \frac{3}{2} \beta {\varPhi _{11}}^{\prime \prime } B_{1111} A |A|^2 \nonumber \\&\qquad - \frac{\beta }{2} {\varPhi _{11}}^{\prime \prime } B_{1111} \overline{A} B^2 - \beta {\varPhi _{11}}^{\prime \prime } B_{1111} A |B|^2, \end{aligned}$$

(76)

$$\begin{aligned}&{\varPhi _{3 \eta }}^{\prime \prime } + {\omega _1}^2 \varPhi _{3 \eta } \nonumber \\&\quad = 2 i \omega _1 \varPhi _{11} D_2 B + 2 i \omega _1 \hat{\mu } \varPhi _{11} B \nonumber \\&\qquad - \frac{3}{2} \beta {\varPhi _{11}}^{\prime \prime } B_{1111} B |B|^2 \nonumber \\&\qquad - \frac{\beta }{2} {\varPhi _{11}}^{\prime \prime } B_{1111} A^2 \overline{B} - \beta {\varPhi _{11}}^{\prime \prime } B_{1111} |A|^2 B, \end{aligned}$$

(77)

where $B_{1111}$ is

$$\begin{aligned} B_{1111} = \int _0^1 {\varPhi _{11}^{\prime }}^{2} dz = \frac{\pi ^2}{2}. \end{aligned}$$

(78)

The associated boundary conditions are expressed as

$$\begin{aligned} \varPhi _{3 \xi } (0)= & {} 0,\, \varPhi _{3 \xi } (1) = \frac{ \hat{\delta _x}}{2} e^{i \hat{\sigma } t_2}, \end{aligned}$$

(79)

$$\begin{aligned} \varPhi _{3 \eta } (0)= & {} 0,\, \varPhi _{3 \eta } (1) = 0. \end{aligned}$$

(80)

The solvability conditions of Eqs. (76 and 77) for $\varPhi _{3 \xi }$ and $\varPhi _{3 \eta }$ are

$$\begin{aligned} D_2 A= & {} - \hat{\mu } A + i \Bigl \{ (3 A |A|^2 + \overline{A} B^2 + 2 A |B|^2 ) C_1 \nonumber \\&- \frac{\hat{\delta _x} e^{i \hat{\sigma } t_2}}{4 C_{1111}} \Bigr \}, \end{aligned}$$

(81)

$$\begin{aligned} D_2 B= & {} - \hat{\mu } B + i (3 B |B|^2 + A^2 \overline{B} + 2 |A|^2 B) C_1. \end{aligned}$$

(82)

To transform Eqs. (81 and 82) into an autonomous equation, we introduce $A_0$ and $B_0$ as

$$\begin{aligned} A (t_2)= & {} A_0 (t_2) e^{i \hat{\sigma } t_2}, \end{aligned}$$

(83)

$$\begin{aligned} B (t_2)= & {} B_0 (t_2) e^{i \hat{\sigma } t_2}, \end{aligned}$$

(84)

where $A_0 (t_2)$ and $B_0 (t_2)$ are the complex amplitudes. By substituting Eqs. (83 and 84) in Eqs. (81 and 82), respectively, we have

$$\begin{aligned} D_2 A_0= & {} - \hat{\mu } A_0 + i \Bigl \{ (3 A_0 |A_0|^2 + \overline{A_0} {B_0}^2 \nonumber \\&+ 2 A_0 |B_0|^2) C_1 - \hat{\sigma } A_0 - \frac{\pi \hat{\delta _x}}{4 \omega _1 C_{1111}} \Bigr \}, \end{aligned}$$

(85)

$$\begin{aligned} D_2 B_0= & {} - \hat{\mu }_\mathrm {c} B_0 + i \Bigl \{ (3 B_0 |B_0|^2 + {A_0}^2 \overline{B_0} \nonumber \\&+ 2 |A_0|^2 B_0) C_1 - \hat{\sigma } B_0 \Bigr \}. \end{aligned}$$

(86)

To make it possible to analyze also the trivial $\eta$ [22], we set $A_0$ and $B_0$ as

$$\begin{aligned} A_0= & {} \frac{1}{2} \hat{a} e^{i \gamma }, \end{aligned}$$

(87)

$$\begin{aligned} B_0= & {} \hat{B}_{0 \mathrm {r}} + i \hat{B}_{0 \mathrm {i}}. \end{aligned}$$

(88)

By substituting Eqs. (87 and 88) in Eqs. (85 and 86), we rewrite Eqs. (85 and 86) as:

$$\begin{aligned} D_2 \hat{a}&{=}&{-} \hat{\mu } \hat{a} \nonumber \\&{+} C_1 \Bigl \{ ({\hat{B}_{0 \mathrm {r}}}^2 {-} {\hat{B}_{0 \mathrm {i}}}^2) \sin 2 \gamma {-} 2 \hat{B}_{0 \mathrm {r}} \hat{B}_{0 \mathrm {i}} \cos 2 \gamma \Bigr \} \hat{a} \nonumber \\&- \frac{\hat{\delta }_x}{2 C_{1111}} \sin \gamma , \end{aligned}$$

(89)

$$\begin{aligned} D_2 \gamma= & {} \frac{1}{4} C_1 \Bigl \{ 3 {\hat{a}}^2 + 8 ({\hat{B}_{0 \mathrm {r}}}^2 + {\hat{B}_{0 \mathrm {i}}}^2) \nonumber \\&+ 4 ({\hat{B}_{0 \mathrm {r}}}^2 - {\hat{B}_{0 \mathrm {i}}}^2) \cos 2 \gamma \nonumber \\&+ 8 \hat{B}_{0 \mathrm {r}} \hat{B}_{0 \mathrm {i}} \sin 2 \gamma \Bigr \} - \hat{\sigma } - \frac{\hat{\delta }_x}{2 C_{1111} \hat{a}} \cos \gamma ,\nonumber \\ \end{aligned}$$

(90)

$$\begin{aligned} D_2 \hat{B}_{0 \mathrm {r}}= & {} - \hat{\mu }_\mathrm {c} \hat{B}_{0 \mathrm {r}} - 3 C_1 ({\hat{B}_{0 \mathrm {r}}}^2 + {\hat{B}_{0 \mathrm {i}}}^2) \hat{B}_{0 \mathrm {i}} \nonumber \\&- \left( \frac{1}{2} C_1 {\hat{a}}^2 - \hat{\sigma }\right) \hat{B}_{0 \mathrm {i}}\nonumber \\&+ \frac{1}{4} C_1 {\hat{a}}^2 (\hat{B}_{0 \mathrm {i}} \cos 2 \gamma - \hat{B}_{0 \mathrm {r}} \sin 2 \gamma ), \end{aligned}$$

(91)

$$\begin{aligned} D_2 \hat{B}_{0 \mathrm {i}}= & {} - \hat{\mu }_\mathrm {c} \hat{B}_{0 \mathrm {i}} + 3 C_1 ({\hat{B}_{0 \mathrm {r}}}^2 + {\hat{B}_{0 \mathrm {i}}}^2) \hat{B}_{0 \mathrm {r}}\nonumber \\&+ \left( \frac{1}{2} C_1 {\hat{a}}^2 - \hat{\sigma }\right) \hat{B}_{0 \mathrm {r}} \nonumber \\&+ \frac{1}{4} C_1 {\hat{a}}^2 (\hat{B}_{0 \mathrm {r}} \cos 2 \gamma + \hat{B}_{0 \mathrm {i}} \sin 2 \gamma ). \end{aligned}$$

(92)

Multiplying Eqs. (89–92) by $\epsilon ^3$ and considering $D_2\approx \epsilon ^{-2}d/dt$, we obtain the amplitude equations as

$$\begin{aligned} \frac{da}{dt}= & {} -\mu a + C_1 a \Bigl \{ -2 B_{0 \mathrm {r}} B_{0 \mathrm {i}} \cos 2 \gamma \nonumber \\&+ ({B_{0 \mathrm {r}}}^2 - {B_{0 \mathrm {i}}}^2) \sin 2 \gamma \Bigr \} \nonumber \\&- \frac{\delta _x}{2 C_{1111}} \sin \gamma , \end{aligned}$$

(93)

$$\begin{aligned} \frac{d\gamma }{dt}= & {} \frac{C_1}{4} \Bigl \{ 3 a^2 + 4 ({B_{0 \mathrm {r}}}^2 - {B_{0 \mathrm {i}}}^2) \cos 2 \gamma \nonumber \\&+ 8 B_{0 \mathrm {r}} B_{0 \mathrm {i}} \sin 2 \gamma + 8 ({B_{0 \mathrm {r}}}^2 + {B_{0 \mathrm {i}}}^2) \Bigr \} \nonumber \\&- \sigma - \frac{\delta _x}{2 C_{1111} a} \cos \gamma , \end{aligned}$$

(94)

$$\begin{aligned} \frac{dB_{0 \mathrm {r}}}{dt}= & {} - \mu _\mathrm {c} B_{0 \mathrm {r}} - 3 C_1 ({B_{0 \mathrm {r}}}^2 + {B_{0 \mathrm {i}}}^2) B_{0 \mathrm {i}} \nonumber \\&- \left( \frac{C_1}{2} a^2 - \sigma \right) B_{0 \mathrm {i}} \nonumber \\&+ \frac{C_1}{4} a^2 (B_{0 \mathrm {i}} \cos 2 \gamma - B_{0 \mathrm {r}} \sin 2 \gamma ), \end{aligned}$$

(95)

$$\begin{aligned} \frac{dB_{0 \mathrm {i}}}{dt}= & {} - \mu _\mathrm {c} B_{0 \mathrm {i}} + 3 C_1 ({B_{0 \mathrm {r}}}^2 + {B_{0 \mathrm {i}}}^2) B_{0 \mathrm {r}} \nonumber \\&+ \left( \frac{C_1}{2} a^2 - \sigma \right) B_{0 \mathrm {r}} \nonumber \\&+ \frac{C_1}{4} a^2 (B_{0 \mathrm {r}} \cos 2 \gamma + B_{0 \mathrm {i}} \sin 2 \gamma ). \end{aligned}$$

(96)

We therefore obtain Eqs. (16–19) as the amplitude equations.

Fig. 15

Dimensionalized theoretical frequency response curves corresponding to the experimental frequency response curves shown in Fig. 11

Table 2 Numerical comparisons for the frequency response curves in theoretical and experimental results

Meanwhile, to obtain Eqs. (31–34), we substitute $A_0$ and $B_0$, expressed by

$$\begin{aligned} A_0= & {} \frac{1}{2} \hat{a} e^{i \gamma }, \end{aligned}$$

(97)

$$\begin{aligned} B_0= & {} \frac{1}{2} \hat{b} e^{i \theta }, \end{aligned}$$

(98)

in Eqs. (85 and 86), and we rewrite Eqs. (85 and 86) as

$$\begin{aligned} D_2 \hat{a}&{=}&{-} \hat{\mu } \hat{a} {+} \frac{1}{4} C_1 \hat{a} {\hat{b}^2} \sin 2 (\gamma {-} \theta ) {-} \frac{\hat{\delta }_x}{2 C_{1111}} \sin \gamma ,\nonumber \\ \end{aligned}$$

(99)

$$\begin{aligned} D_2 \gamma= & {} \frac{1}{4} C_1 \Bigl \{3 {\hat{a}}^2 + {\hat{b}^2} \cos 2 (\gamma - \theta ) + 2 {\hat{b}}^2 \Bigr \} \nonumber \\&- \hat{\sigma } - \frac{\hat{\delta }_x}{2 C_{1111} \hat{a}} \cos \gamma , \end{aligned}$$

(100)

$$\begin{aligned} D_2 \hat{b}= & {} - \hat{\mu }_\mathrm {c} \hat{b} - \frac{1}{4} C_1 {\hat{a}^2} \hat{b} \sin 2 (\gamma - \theta ), \end{aligned}$$

(101)

$$\begin{aligned} D_2 \theta= & {} \frac{C_1}{4} \Bigl \{3 {\hat{b}}^2 + 2 {\hat{a}^2} + {\hat{a}^2} \cos 2 (\gamma - \theta ) \Bigr \} - \hat{\sigma }.\nonumber \\ \end{aligned}$$

(102)

Multiplying Eqs. (99–102) by $\epsilon ^3$ and considering $D_2\approx \epsilon ^{-2}d/dt$, we obtain the amplitude equations as

$$\begin{aligned} \frac{da}{dt}= & {} -\mu a + \frac{C_1}{4} a b^2 \sin 2 (\gamma - \theta ) - \frac{\delta _x}{2 C_{1111}} \sin \gamma ,\nonumber \\ \end{aligned}$$

(103)

$$\begin{aligned} \frac{d\gamma }{dt}= & {} \frac{C_1}{4} \Bigl \{ 3a^2 + 2b^2 + b^2 \cos 2 (\gamma - \theta ) \Bigr \} - \sigma \nonumber \\&- \frac{\delta _x}{2 C_{1111} a} \cos \gamma , \end{aligned}$$

(104)

$$\begin{aligned} \frac{db}{dt}= & {} -\mu _\mathrm {c} b - \frac{C_1}{4} a^2 b \sin 2 (\gamma - \theta ), \end{aligned}$$

(105)

$$\begin{aligned} \frac{d\theta }{dt}= & {} \frac{C_1}{4} \Bigl \{ 3b^2 + 2a^2 + a^2 \cos 2 (\gamma - \theta ) \Bigr \} - \sigma . \end{aligned}$$

(106)

We therefore obtain Eqs. (31–34) as amplitude equations.

Fig. 16

Time histories of the displacement of the piezoelectric actuator in the case that $\nu _d / 2 \pi = 40.2 \ \mathrm {Hz}$ and the nondimensional feedback gain ($\alpha = 0.2$)

Comparison of the frequency response curves in theoretical and experimental results

We quantitatively compare the theoretical and experimental frequency response curves for the x-direction. The comparison is being made without control. We obtain Fig. 15a by dimensionalizing Fig. 2 and compare it with Fig. 11. We first focus on the point C. For the theoretical frequency response curves of Fig. 15a, the dimensional $\sigma _C$ is 0.098 Hz; at this point, the amplitude in the x-direction is 3.03 mm. For the experimental frequency response curves of Fig. 11, the corresponding values are 0 Hz and 1.23 mm. We next focus on the point D. For the theoretical frequency response curves of Fig. 15a, the dimensional $\sigma _D$ is 0.423 Hz; at this point, the amplitude in the x-direction is 2.10 mm. For the experimental frequency response curves of Fig. 11, the corresponding values are 0.399 Hz and 0.56 mm. The frequencies at points C and D in the theory are almost same as the experimental frequencies, but there are discrepancies in the response amplitude of 2.5 times at point C and 3.8 times at point D as shown in Table 2. The explanation may be that the damping ratio ($\mu$) is not considered in the theoretical analysis and the tension of string due to initial tension changed during the experiments.

Displacement of the piezoelectric actuator

We show the displacement of piezoelectric actuator under control in the state that the out-of-plane motion is suppressed. The parameters are different from those in the previous experiments. We obtain the time histories when the excitation frequency $\nu _d / 2 \pi = 40.2 \ \mathrm {Hz}$ and the feedback gain $\alpha = 0.2$ (Fig. 16a and b). We observe the reduction of oscillation in the y-direction. At this time, the displacement of piezoelectric actuator $\eta (0,t)$ is shown as Fig. 16c. As seen from Eq. (44), if oscillation in the y-direction is stabilized to be zero, because the feedback is zero, $\eta (0,t)$ should be zero. However, because the displacement and velocity in the y-direction do not become exactly zero, $\eta (0,t)$ remains as in Fig. 16c.

Cross-sectional area of the string

The cross-sectional area of the string is shown in Fig. 17; the string consists of 49 cylindrical small wires with a diameter of $6.0 \times 10^{-5} \ \mathrm {m}$. We estimated the density of the string as $\rho = 8.63 \times 10^3\ \mathrm {kg/m^3}$ by using the actual cross-sectional area of the string.

Fig. 17

Cross-sectional area of the string for experiments. The string consists of 49 small cylindrical wires with a diameter of $6.0 \times 10^{-5} \ \mathrm {m}$. The black colored area is empty