Dynamical similarity of multi-block catenary arches and rocking blocks subjected to horizontal base excitation

Abstract

In this paper, the dynamical similarity of multi-block catenary arches and columns is discussed, which can be used for the simplified design of rocking arches. The basic hypothesis is that the dynamic response of multi-block arches and columns is similar when the shape of the arch follows the thrust line, i.e. it is a catenary arch. It is validated numerically that the responses of slender catenary arches are safe and reliable approximations of those of not slender arches and then that the overturning acceleration (response) spectra of rigid, slender monolithic blocks can be directly applied for catenary arches. The similarity is based on two parameters, on the limit peak ground acceleration (under which the structure will not move at all) and on the frequency parameter (defined by Housner for rigid blocks).

1 Introduction

Static analysis of masonry and stone arches is usually based on the classical thrust line analysis [1, 2] by calculating the limit horizontal self-weight multiplier of these structures. The horizontal limit load can be considered as an acceleration that would transform the arch to a mechanism [3,4,5].

Oppenheim [6] formulated the exact, nonlinear equations of motion for circular arches subjected to base excitation assuming four hinges. He also investigated the response of a circular arch for a step impulse, and the overturning of a planar arch during the first half cycle of the excitation. De Lorenzis et al. [7] extended Oppenheim’s analysis by introducing an impact model, based on Housner’s model [8] for single rocking blocks. It was assumed that the arch moves as a four-hinge mechanism, and the location of the cracks does not change during one half cycle of the motion. Using a new analytical model, De Lorenzis et al. found that for similar arches (obtained by linear scaling) the larger the arch the higher the safety against overturning. They showed that the overturning impulse is proportional to the square root of the arch radii [7]. This model has been extended for rocking frames, pointed arches and arches with geometrical irregularities [9,10,11]. Kollár and Ther [12] presented a new numerical model for planar multi-block arches subjected to horizontal excitation. Using the new model, it was found that circular arches move as a four-hinge mechanism typically only at the beginning of excitation, and several cracks split open during motion; furthermore, that modelling a multi-block circular arch by an SDOF four-hinge mechanism may significantly overestimate its collapse load.

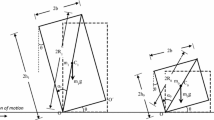
DeJong and Dimitrakopoulos [13] investigated the dynamical equivalency of SDOF mechanisms subjected to gravity load and horizontal ground excitation, $a_{{{\text{g}},}} \left( t \right)$. For gravity load, the structure is in (unstable) equilibrium at $\delta = \varphi$, were $\varphi$ is the generalized displacement. Three examples are shown in Fig. 1. It was proved [13] that for slender structures (i.e. $\delta \ll 1$) and small displacements ($\varphi \ll 1$) the response of the structure depends on three parameters p, $\delta$ and $a_{{{\text{p}},{\text{min}}}}$:

• p is the frequency parameter, defined for rigid blocks by Housner [8],

• δ is the angle of the neutral position (Fig. 1b),

• $a_{{{\text{p}},{\text{min}}}}$ is the horizontal acceleration, which equilibrates the SDOF mechanism subjected to the vertical gravity load at $\varphi = 0$ (Fig. 1c).

Fig. 1

Three examples of SDOF mechanisms: monolithic block (top), rocking frame (middle) and an arch as a four-hinge mechanism (bottom); the SDOF mechanisms (a), their neutral position for gravity load (b), illustration of the horizontal acceleration, a_p,min, which equilibrates the gravity load at φ = 0 (c)

For the rigid block, these parameters are given by Housner [8]:

$$ p = \sqrt {\frac{3g}{{4R}}} = \sqrt {\frac{3g}{{2\sqrt {H^{2} + B^{2} } }}} , \delta = \tan^{ - 1} \frac{B}{H}, a_{{{\text{p}},{\text{min}}}} = g\frac{B}{H}. $$

(1)

The normalized displacement $\varphi /\delta$ depends on two parameters only $p$ and $a_{{{\text{p}},{\text{min}}}}$. The frequency parameter, p, can be interpreted (at least for slender structures) in the following way: $p^{2}$ is equal to the (normalized) acceleration of the mechanism at $\varphi = 0$ subjected to gravity load only (Fig. 1a, $p^{2} = - \ddot{\varphi}/\delta$). The three parameters can be unambiguously calculated for SDOF mechanisms [13]. (For an arch, first the location of the four opening interfaces is determined, and then they are assumed to be unchanged during motion.)

The safety of a rocking block can be represented by the overturning curve, introduced by Housner and developed for different signals by several researchers: Housner and Yim et al. plotted the overturning curve for a single rectangular pulse and a half sine [8, 14], Voyagaki et al. [15] investigated the effect of a range of idealized single-lobe pulses, while others [16,17,18,19,20,21,22] applied full-cycle pulses where impact plays an important role. The overturning curve for harmonic shaking [23, 24] and synthetic and real earthquake records were also defined [14, 21, 25,26,27,28]. The overturning curve has several possible representations, here, following [12, 28, 29] the overturning acceleration (response) spectra (OAS) will be used, where the frequency parameter is shown on the horizontal axis, while a_p /a_p,min is on the vertical axis (Fig. 2). a_p is the maximum peak ground acceleration, and $a_{{{\text{p}},{\text{min}}}}$ is the limit acceleration, if a_p < a_p,min the block will not move at all.

Fig. 2

The overturning acceleration (response) spectrum (OAS) of a rigid block for a sine signal (a) and for an earthquake record (b). Acceleration and block size which belong to a blue dot represent an unsafe structure. The half diameter of the block is $R = \sqrt {B^{2} + H^{2} } /2$ (Fig. 18 of [29])

The curve separates the safe and unsafe parameter range, where overturning does or does not occur. For any signal and any block slenderness, the OAS can be calculated to check overturning; for a given block size, the maximum acceleration (a_p) can be determined for which the block is safe.

The overturning acceleration (response) spectra (OAS) of slender rigid, monolithic blocks can be applied conservatively for multi-block columns [29], because of the following reasons:

• OAS of slender blocks are close to each other [13, 21, 28], and the OAS of a very slender block is, in general, a safe approximation of that of not slender blocks (Fig. 3a).

• Single monolithic blocks are mostly more vulnerable for overturning than multi-block columns with the same overall dimensions [29,30,31] (Fig. 3b).

Fig. 3

Comparison of the OAS of a slender monolithic block with those of less slender blocks (a) and with those of multi-block columns (b) (based on Fig. 19 of [29])

The overturning acceleration (response) spectra (OAS) can be calculated for any signal and any column slenderness and any number of components, nevertheless, for a conservative design it is sufficient to consider the OAS of slender, monolithic blocks only. As a consequence, if for a given location the signal (or earthquake record) is given for which overturning must be inspected, the corresponding OAS of a slender, monolithic block can be used for the design of any multi-block column. When there are several site-specific earthquake records a characteristic OAS should be used, which—according to [28, 32]—can be reasonably well represented by two parameters: the peak ground acceleration and the replacement impulse duration.

The nonlinear dynamic response of masonry structures can also be investigated by numerical methods which can take into account large displacements and rotations of the blocks including the possibility of complete detachment. Applying the discrete element method (DEM), Lemos [33] gives a brief overview of the analyses, reviewing the former results of several researchers. Essential assumptions are described and the potential of the DEM for static and dynamic analysis of masonry structures are presented for various 2D and 3D structures. The potential of the DEM is also illustrated by defining the possible minimum thickness of skewed masonry arches [34] and the effect of the backfill material at masonry arch bridges [35]. Recently, complete masonry towers were investigated numerically by applying the non-smooth contact dynamics (NSCD) method [36, 37]. In their model, the masonry was divided into rigid blocks, simple contact laws were applied, and the damping was neglected. The effect of the friction coefficient as a main parameter was investigated thoroughly to illustrate different collapse mechanisms, clearly illustrating the sensitivity of the results to the input parameters.

2 Problem statement

Since there is a dynamical equivalency of SDOF rocking structures [13], the question arises: can the OAS of (slender, rigid) monolithic blocks be applied also to multi-block arches?

Recently, a model was presented for multi-block arches subjected to earthquakes, where several (more than four) cracks may appear during motion [12]. It was found that for circular arches considering a SDOF four-hinge mechanism may significantly overestimate the collapse load of multi-block arches (Fig. 4). It was also found that while the overturning curves of single blocks and arches with symmetrically located four hinges are similar; for multi-block arches (where several hinges may occur), they can be very different. Hence, it seems that the answer to the above question is no. As will be discussed below, under certain circumstances, a positive answer can be given.

Fig. 4

Comparison of the results (a) of a four-hinge mechanism (SDOF) and the results of the multiple crack model (MDOF) for a circular arch (b) (Fig. 19 of [12])

3 Catenary arch as a key to similarity: research aim

Symmetrical catenary arches are considered, which consist of rigid (brick or stone) blocks, and which are subjected to arbitrary horizontal base excitation. During motion, any interface may split open or close and the crack pattern may change with time (Fig. 5).

Fig. 5

Multi-block catenary arch (a) and two of the possible mechanisms (b, c)

Although there is no equivalency of multi-block columns and arbitrary shape arches, our aim is to show that catenary arches behave similarly as straight columns. Furthermore, we wish to show that the response of an MDOF catenary arch can be conservatively approximated by the response of a monolithic rigid block; and the OAS of slender blocks can be applied for the verification of overturning of catenary arches.

According to the authors’ knowledge, the response of multi-block catenary arches was not investigated before and their key role in the possible modelling of arches for overturning was not recognized.

Why are we considering catenary arches, why do we expect similar behaviour of MDOF arches and monolithic columns? The reason is that straight columns and catenary arches have the important common feature that their thrust line (i.e. the path of the resultant normal force) for gravity load runs through the centres of the cross sections. As a consequence, even for very slender structures there is a limit ground acceleration, under which the structure will not move. On the contrary, for not catenary arches, as well as for not straight columns the thrust line differs from the axis and there is a minimal thickness (minimal slenderness), where an arbitrarily small horizontal acceleration results in the development of a mechanism, and if the thickness is smaller than the minimal one, the structure collapses under gravity loads. This is illustrated in Fig. 6.

Fig. 6

Thrust limes (dashed lines) for columns and arches subjected to gravity loads. For straight columns and catenary arches (a), the slenderness may tend to zero, while for curved columns and circular arches (b), there is a minimum thickness where the thrust line touches the contour of the cross sections

The expressions of the main characteristics of a rigid block are given by Eq. (1). When the block is slender ($B \ll H$), these expressions become

$$ p \approx \sqrt {\frac{3g}{{2H}}} , \delta \approx \frac{B}{H}, a_{{{\text{p}},{\text{min}}}} = g\frac{B}{H}, $$

(2)

where H is the height, B is the width (thickness) of the block and g is the acceleration of gravity. Similarity can be expected only if in the limit (for slender arches) size and thickness affect the parameters of an arch analogously to Eq. (2).

For SDOF systems, e.g. for four-hinge mechanisms of arches the similarity was already proved, but real arches may behave in a more complex manner. First ${a}_{\mathrm{p},\mathrm{min}}$ of a symmetric, slender arch is investigated.

When the thickness of the arch is small compared to its size, it can be treated as a curved bar given by the axis and the cross-sectional properties. Let the function of the axis be proportional to the size.

For gravity load, the bending moment and the normal force in the arch can be calculated as

$$ M_{g} = f_{1} dl^{2} g, N_{g} = f_{2} dlg, $$

(3)

where l is the span, d is the thickness, f₁ and f₂ are functions which belong to an arch of unit length. The eccentricity is

$$ e = \frac{{M_{g} }}{{N_{g} }} = \frac{{f_{1} }}{{f_{2} }}l $$

(4)

which is independent of d.

The arch is statically indeterminate and hence the internal forces cannot be determined unambiguously from the equilibrium equations. For symmetrical loading, they contain two parameters, one due to uniform bending, the other one due to equal and opposite horizontal reaction forces [2]. When these parameters can be chosen in such a way that $f_{1} \equiv 0$, the arch is called catenary and the eccentricity is zero everywhere. If $f_{1} \equiv 0$ does not hold, then, for a small d, the eccentricity may exceed the half thickness, thus the arch cannot carry its self-weight and $a_{{{\text{p}},{\text{min}}}}$ does not exist. A slender arch can carry its self-weight only if $f_{1} \equiv 0$, i.e. when it is a weighted catenary arch.

For horizontal earthquake excitation, the bending moment and the normal force in the arch can be given as

$$ M_{a} = f_{3} dl^{2} a_{{\text{p}}} , N_{a} = f_{4} dla_{{\text{p}}} , $$

(5)

where $f_{3}$ and $f_{4}$ are again functions which belong to an arch of unit length and $a_{{\text{p}}}$ is the acceleration of the ground motion. For small d, the arch can resist only a small acceleration, and as a consequence $N_{a} \ll N_{g}$. When both loads act, for a slender catenary arch we obtain

$$ e = \frac{{M_{a} }}{{N_{g} }} = \frac{{f_{3} dl^{2} a_{{\text{p}}} }}{{f_{2} dlg}} = \frac{{f_{3} }}{{f_{2} }}\frac{{a_{{\text{p}}} }}{g}l. $$

(6)

$M_{a}$ is antisymmetric and $N_{g}$ is symmetric, and hence e is antisymmetric as well (see Fig. 7a). The values of maximum eccentricities are obtained by evaluating Eq. (6) at their locations:

$$ \overline{e} = \frac{{\overline{f}_{3} }}{{\overline{f}_{2} }}\frac{{a_{{\text{p}}} }}{g}l,\; \overline{\overline{e}} = - \frac{{\overline{{\overline{f}}}_{3} }}{{\overline{{\overline{f}}}_{2} }}\frac{{a_{{\text{p}}} }}{g}l. $$

(7)

Fig. 7

Eccentricity of a catenary arch considering horizontal excitation (a) and the corresponding four-hinge mechanisms (b)

Again, since the arch is statically indeterminate the internal forces cannot be determined unambiguously from the equilibrium equations. For antisymmetric bending moment, they contain one parameter, which corresponds to a linearly varying bending moment [2]. To reach the collapse load, this parameter is chosen in such a way that the values of the maximum positive ($\overline{e}$) and negative ($\overline{\overline{e}}$) eccentricities are identical. By so doing, the calculation of $M_{a}$ is unambiguous.

$a_{{\text{p}}} = a_{{{\text{p}},{\text{min}}}}$ when the arch becomes a four-hinge mechanism (Fig. 7b), i.e. when

$$ d = 2\overline{e} = 2\overline{\overline{e}} = 2\frac{{\overline{f}_{3} }}{{\overline{f}_{2} }}l\frac{{a_{{{\text{p}},{\text{min}}}} }}{g}. $$

(8)

Thus, we have

$$ a_{{{\text{p}},{\text{min}}}} = Cg\frac{d}{l}, $$

(9)

where C is a constant. Note that this expression is similar to that obtained for a block (Eq. (2)), $a_{{{\text{p}},{\text{min}}}}$ is proportional to the thickness and for a given slenderness (d/l) independent of the size. Also, note that for slender arches the locations of the hinges along the axis are symmetric.

For a given four-hinge mechanism, the similarity to the rigid block was proven [13] and we have for a slender arch (see Eq. (2))

$$ p\sim \frac{1}{\sqrt l }, \delta \sim \frac{d}{l}. $$

(10)

4 Definitions, assumptions and hypotheses

To reach our research aim, first the following definitions are given:

Thrust line. The path of the resultant normal force [2].

Weighted catenary arch (or simply catenary arch). An arch where the thrust line for gravity load runs through the centres of the cross sections. If the load is uniformly distributed along the arc-length, the thrust line is hyperbolic cosine (regular catenary, cosh(cx)/c).

Replacement catenary arch. The replacement catenary arch is a (weighted) catenary arch of uniform thickness, which can be used safely for the design of arbitrary arches subjected to base excitation. An obvious choice is the catenary arch of maximum uniform thickness, which can be drawn within the contour of an arch (Fig. 8). (The mass distribution of the replacement catenary arch and the original arch are identical, the thickness plays a role in the geometry of the mechanism, since the hinges occur at the contour.)

Fig. 8

An arch and its possible replacement catenary arch

Critical four-hinge mechanism. The critical four-hinge mechanism is obtained from the static analysis of arches for the given vertical gravity load and the horizontal load obtained from the minimum horizontal acceleration, which results in a four-hinge mechanism (Fig. 9a). (The hinges may occur at the interfaces.)

Fig. 9

Critical four-hinge mechanism (a) and critical optimal four-hinge mechanism (b)

Critical optimal four-hinge mechanism. Same as the critical four-hinge mechanism, but the cracks (and hinges) occur at the locations of the maximum eccentricities (Fig. 9b). (The critical and the critical optimal four-hinge mechanisms are identical, if there are infinitely high number of blocks.) The locations of the hinges are given by parameters ${c}_{3}$ and ${c}_{3}{^{\prime}}$ (see Fig. 9b).

Limit peak ground acceleration. The limit peak ground acceleration is the value of the (horizontal) ground acceleration under which the arch will not move et al. (It is equal to ${a}_{\mathrm{p},\mathrm{min}}$ defined in Sect. 1, when the SDOF structure is the critical optimal four-hinge mechanism.)

Neutral position of an arch. Position of a four-hinge mechanism of an arch subjected to gravity load only, which is in (unstable) equilibrium (Fig. 10). It is described by the inclination δ of the left rigid part of the mechanism.

Fig. 10

Neutral position of a four-hinge mechanism

Slenderness of an arch. The thickness to span ratio: d/l (Fig. 11).

Fig. 11

Geometry of an arch with uniform thickness

Shallowness of an arch. The height to span ratio: f/l (Fig. 11).

The assumptions in calculating the arch are identical to those of [12]:

• only the planar displacements of the arch are considered,

• rocking occurs at the outermost corners of the blocks,

• there is no sliding between blocks,

• damping during motion is neglected, however, at the closing of interfaces there is a loss in energy due to inelastic impact (Housner’s model),

• the change in geometry (second-order effects) is taken into account.

An important feature of catenary arches that for gravity load and horizontal excitation their bending moment curves are anti-symmetrical, and hence for slender arches the location of the hinges of the four-hinge mechanism are symmetrical ($c_{3} = c_{3} ^{\prime}$). Note also that the more slender the arch the smaller the energy dissipation during impact is [12], for very slender catenary arches the energy dissipation is negligible.

To demonstrate the dynamical similarity of multi-block catenary arches and monolithic rocking blocks, the following hypotheses will be investigated:

Hypothesis 1

The OAS of the four-hinge mechanism of a very slender catenary arch is a safe and reliable approximation of those of not slender catenary arches.

Hypothesis 2

The OAS of the critical optimal four-hinge mechanism of a slender catenary arch is in general a safe approximation of that of the same arch with possible multiple cracks.

Hypothesis 3

The OAS of a slender monolithic block is a safe approximation of that of catenary arches with the same frequency parameter. The more slender the arch the closer are the OAS.

Note that Hypotheses 1 and 2 are the generalizations of the observations made for columns: see the two bullet points in Sect. 1 (Fig. 3). These will be validated in this paper.

Hypothesis 3 is a consequence of the first two hypotheses as explained below. The dynamical equivalency of SDOF structures [13] does not contain the impact during motion. For slender structures, however, there is no energy dissipation, and hence it can be stated that due to the dynamical equivalency: the OAS of a slender monolithic block and that of the critical optimal four-hinge mechanism of a slender catenary arch are identical provided that their limit peak ground acceleration (a_p,min) and their frequency parameter (p) are identical. This statement together with the first two hypotheses results in the third hypothesis. Nonetheless, the third hypothesis will be validated numerically as well.

If the above hypotheses are valid the possible collapse of MDOF catenary arches can be determined on the basis of the OAS of slender monolithic blocks.

5 Effect of size and slenderness

As it was discussed above, the main characteristics of the critical optimal four-hinge mechanism of a catenary arch are $p$, $a_{{{\text{p}},{\text{min}}}}$, $\delta$ and the locations of the hinges, given by $c_{3}$ and $c_{3} ^{\prime}$ (Fig. 9b). If the distribution of the mass is given the function of the axis of a catenary arch can be unambiguously prescribed by the span and the shallowness, i.e. by l and f.

Now it is presented, how these parameters depend on the size and slenderness of the structure.

Size effect. For a given shape (slenderness (d/l) and shallowness (f/l) are given): $c_{3} ,c_{3} ^{\prime}$, $a_{{{\text{p}},{\text{min}}}}$ and $\delta$ are independent of the size, while the frequency parameter is inversely proportional to the square root of size:

$$ a_{{{\text{p}},{\text{min}}}} = {\text{uniform}},\quad \delta = {\text{uniform}},\quad { }p\sim \frac{1}{\sqrt l }\sim \frac{1}{\sqrt f }\quad \left( {{\text{size}}\,{\text{ effect}}} \right), $$

(11)

(The moments due to the gravity loads are proportional to $l^{3}$ while the rotational inertia is proportional to $l^{4}$, hence the (normalized) acceleration of rotation (i.e. p²), is proportional to $l^{3} /l^{4} = 1/l$.)

Equation (11) holds both for slender (see Eqs. (9) and (10)) and not slender arches.

Slenderness effect for a given size. The effect of slenderness was derived for slender catenary arches, i.e. for $d/l \ll 1$, and are given by Eqs. (9) and (10). $a_{{{\text{p}},{\text{min}}}}$ and $\delta$ are proportional to the thickness, while $c_{3}$ and the frequency parameter are unaffected by the thickness. Note that for not slender arches expressions in Eqs. (9) and (10) can be used only as approximations.

6 Calculation of the dynamic parameters of an arch

Heyman [1] gives a procedure to determine the limit peak ground acceleration (${a}_{\mathrm{p},\mathrm{min}}$), and the geometry of the corresponding critical optimal four-hinge mechanism, when the thrust line touches the contour (Fig. 12). When the four-hinge mechanism is known using nonlinear geometrical equations and static equilibrium the angle of the neutral position ($\delta$) can be directly calculated. These straightforward calculations are not presented here.

Fig. 12

Thrust line of an arch subjected to gravity load and a horizontal acceleration $a_{{\text{p}}}$

To calculate the frequency parameter ($p$), two slightly different expressions are given in [12] Appendix A, which for slender arches are identical. The application of the second one (Eq.A-10 of [12]) is recommended (see also Eq. 17 of [13]), it is:

$$ p = \sqrt {\frac{{\overline{B}_{{\text{v}}} }}{{\overline{A}\delta }}}. $$

(12)

The rotation of the left segment of the four-hinge mechanism is denoted by $\varphi$ (Fig. 13a). $\overline{B}_{{\text{v}}}$ is the moment which equilibrates the mechanism subjected to gravity loads at $\varphi = 0$ (Fig. 13b). $\overline{A}$ is the rotational inertia of the four-hinge mechanism. It may be observed that their ratio is the angular acceleration of the left segment:

$$ \frac{{\overline{B}_{{\text{v}}} }}{{\overline{A}}} = \ddot{\varphi }, $$

(13)

when the structure is at the $\varphi = 0$ position and it is loaded by the gravity load (Fig. 13b). To evaluate $p$, either $\ddot{\varphi}$ is determined directly, and $p = \sqrt {\ddot{\varphi}/\delta }$ or all the parameters are evaluated in Eq. (12).

Fig. 13

Illustration of the calculation of the frequency parameter

7 Verification of the hypotheses

In the numerical calculation of the multi-block arches, the model presented in [12] is applied, i.e. only planar displacements are considered, any number of interfaces may split open and close, Housner’s model is applied for inelastic impact, and the second-order effects are taken into account.

For a few cases, the arch characteristics are given in Table 1 by the dimensionless parameters $c_{1} - c_{4}$, where the arch characteristics are calculated as

$$ p = \sqrt {\frac{g}{{c_{1} f}}} , \quad a_{{{\text{p}},{\text{min}}}} = c_{2} \frac{dl}{{f^{2} }}g, \quad \delta = \frac{d}{{c_{4} l}}. $$

(14)

Table 1 Constants of Eq. (14) and Fig. 9b for the four-hinge mechanisms of catenary arches: $p = \sqrt {g/\left( {c_{1} f} \right)}$, $a_{{{\text{p}},{\text{min}}}} = c_{2} gdl/f^{2}$ (mass is uniform along the arc—hyperbolic shape)

These expressions were constructed in such a way that $c_{1} - c_{4}$ are unaffected by the size, and for slender structures they do not depend on the slenderness [see Eqs. (11) and (12)]. Note that for the application of OAS only two parameters, p and $a_{{{\text{p}},{\text{min}}}}$ are required.

To verify the hypotheses, several thousand time-history analyses were carried out for different arch geometries and signals. Although the existing numerical comparisons are not all conclusive, our results so far strengthen the hypotheses.

In the following, the effect of three different excitations will be investigated, which are shown in Fig. 14a–c: sine curve, a square signal and a step impulse.

Fig. 14

Signals in the numerical calculations. Complete sine (a), square signal (b) and a step impulse (c)

Hypothesis 1

The OAS of arches with three different shallowness and three different slenderness are given in Fig. 15, assuming a four-hinge mechanism (the hinges are at the maximum eccentricities). It can be seen that the OAS of more slender arches are to the left of less slender ones. Hence, the OAS of the four-hinge mechanism of a very slender catenary arch is a safe and reliable approximation of those of not slender catenary arches.

Fig. 15

OAS of optimal critical four-hinge mechanisms of catenary arches with different slenderness, the signals are shown in Fig. 14a–c (parameters of the arches are given in Table 1)

Hypothesis 2

The effect of possible multiple cracks is investigated in Fig. 16, for three different geometries and three different signals. It can be seen that the OAS of the critical optimal four-hinge mechanism of a slender catenary arch is either reasonably close or a safe approximation of that of an arch with possible multiple cracks.

Fig. 16

OAS of optimal critical four-hinge mechanisms and multiple crack models for three different arch geometries (a) and three different excitations (b) (signals are shown in Fig. 14)

Hypothesis 3

The OAS of single rigid blocks and MDOF catenary arches are compared for three different geometries and excitations (Fig. 17). It can be observed that the OAS of a single rigid block is either reasonably close or a safe approximation of that of a catenary arch with possible multiple cracks. The overturning curve of the rigid block seems to be a safe approximation of that of a MDOF catenary arch in a wide ${{a}_{p}/a}_{\mathrm{p},\mathrm{min}}$ range.

Fig. 17

OAS of a multiple crack model catenary arch and a rigid block for three different arch geometries (a) and three different excitations (b) (signals are shown in Fig. 14)

8 Numerical example

The circular arch given in Fig. 18a ($f/l = 0.289$, $d/l = 0.0346$) is investigated for all the three signals shown in Fig. 14. The acceleration under which the circular arch will not move is $a_{{{\text{p}},{\text{min}}}} = 3.036 {\text{m}}/{\text{s}}^{2}$.

Fig. 18

The investigated circular arch (a) and the lower bound (b) and equivalent (c) replacement catenary arches

8.1 Lower bound and equivalent thickness for the replacement catenary arch

As replacement catenary arches a lower bound ($\check{d}$) and an “equivalent” thickness ($\hat{d}$) can be obtained ($\check{d} \le \hat{d}$) as follows:

• As it was stated above, the catenary arch of maximum uniform thickness, which can be drawn within the contour of an arch ($\check{d}$, Fig. 8) is expected to be a safe approximation, i.e. the replacement catenary arch thickness should not be lower than this value.

• The limit peak ground acceleration ($a_{{{\text{p}},{\text{min}}}}$, see the definition above) of the replacement catenary arch is taken to be identical to that of the arch, which results in thickness, $\hat{d}$.

The lower bound and the equivalent thicknesses of the replacement catenary arch are 0.0207 l and 0.0293 l (Fig. 18b, c); their overturning curves are given by dashed and dotted lines in Fig. 19. The results of the simplified calculations are given in Table 2; the details are given below for the lower bound solution.

Fig. 19

OAS of an arch and its replacement rigid blocks for the three signals shown in Fig. 14

Table 2 Comparison of the dynamic characteristics of an arch (Fig. 18) and its simplified models

For the lower bound replacement catenary arch (d/l = 0.0207), p and a_pmin can be calculated numerically, they are:

$$ p = \sqrt {\frac{g}{{c_{1} f}}} = \sqrt {\frac{g}{{c_{1} l\left( {f/l} \right)}}} = \frac{11.82}{{\sqrt l }} \left[ {\frac{1}{{\text{s}}}} \right], a_{{{\text{p}},{\text{min}}}} = c_{2} \frac{dl}{{f^{2} }}g = c_{2} \left( \frac{l}{f} \right)^{2} \frac{d}{l}g = 2,163\frac{{\text{m}}}{{{\text{s}}^{2} }}, $$

(15)

where c₁ = 0.2437, c₂ = 0.8896, g = 9.81 m/s².

The OAS of a rigid block and the arch (with these p and $a_{{{\text{p}},{\text{min}}}}$ values) are presented in Fig. 19. For all the three signals, the OAS of the rigid block is a safe approximation of that of the arch, provided that p and $a_{{{\text{p}},{\text{min}}}}$ are calculated by Eq. (15). Since for a rigid block $p = \sqrt {0.75g/R}$), we may write: $R = \frac{0.75}{{c_{1} \left( {f/l} \right)}}l = 0.0528l$.

We may observe that for this geometry even the block determined from the equivalent thickness of the arch results in a safe approximation due to the effects of the applied simplifications, namely that.

• a four-hinge mechanism is investigated instead of the MDOF arch,

• a very slender structure is considered instead of the real one.

The determination of the geometry of the replacement arch is not the task of this paper, whether the response of a block based on the “equivalent” thickness can be in general used for an arbitrary geometry safely can be answered only after extensive numerical investigations.

9 Proposed design method

Now it is demonstrated, how the safety of an arch can be determined, if the characteristic OAS of a rigid, monolithic slender block for a given site is given [28], as shown in Fig. 20d. The peak ground acceleration (a_p) is determined under which the circular arch shown in Fig. 20a is safe, where the total size is $l = 10.0$, $f/l = 0.289$, $d = 0.35$ m.

Fig. 20

Design of an arch if the OAS of a monolithic block for a specific site is known: the arch geometry (a); a possible replacement catenary arch and its frequency parameter and the limit ground acceleration (b) and the evaluation of the characteristic OAS (d) of a slender block (c)

The dimensions of the replacement catenary arch is obtained by geometrical considerations, here the “equivalent” thickness is applied: l = 10 m, f = 2,924 m, d = 0.293 m. For the replacement catenary arch (Fig. 20b), p and $a_{{{\text{p}},{\text{min}}}}$ must be determined numerically (which is based on a simple static analysis), they are $p = 3.705/{\text{s}}$, $a_{{{\text{p}},{\text{min}}}} = 3.036{\text{ m}}/{\text{s}}^{2}$. From the curve of Fig. 20d, we have (at p = 3.705):

$$ \frac{{a_{{\text{p}}} }}{{a_{{{\text{p}},{\text{min}}}} }} = 1.351 \to a_{{\text{p}}} = 3.036 \times 1.351 = 4.102\frac{{\text{m}}}{{{\text{s}}^{2} }}. $$

(16)

This means, that if in the given location the PGA (a_p,max) of possible earthquakes are below 0.418 g, the investigated circular arch may move during the excitation, but it is not going to collapse.

Obviously, for the design procedure, the characteristic OAS (for a slender block) [28] must be known for a specific site, which is not available yet. (They were determined only for one hundred individual records in [28].)

9.1 Comparison with the response spectrum analysis

We would like to emphasize the analogy between the possible design methodology for overturning of rocking multi-block arches (Fig. 20) and columns and the response spectrum analysis (RSA) of elastic (or elastic–plastic) MDOF structures (Table 3) [32]. In both cases,

• instead of the complex structure, a SDOF structure is investigated: for the RSA a spring–dashpot system, which is defined by the period of vibration and the damping ratio, while for the rocking structure a (slender) monolithic block characterized by the frequency parameter and the limit peak ground acceleration;

• the response spectrum of the SDOF structure is calculated: for RSA the (pseudo) acceleration response spectrum (S_d), while for rocking structures the overturning acceleration (response) spectrum (OAS) (Fig. 21);

• the original structure in both cases is evaluated on the basis of the response spectrum of the SDOF structure.

Table 3 Comparison of RSA and the proposed design method for overturning

Fig. 21

The (pseudo) acceleration response spectrum of a SDOF elastic structure (a) and the OAS of the rocking block (b)

An important difference that the RSA—at least for SDOF elastic structures—is “accurate”, while the above procedure for rocking arches contains several conservative approximations: (i) the replacement of the arch by a catenary arch, (ii) then its replacement by a slender monolithic block and (iii) the neglect of the energy dissipation during impact (which is negligible for slender structures only).

10 Discussion

In this paper, the similarity of the responses of monolithic columns and multi-block arches are investigated. It was shown how the OAS of slender monolithic blocks can be applied for multi-block arches. The key of the solution was that there is dynamical similarity of the response of a monolithic column and a multi-block arch if the latter one is a catenary arch.

As it has been shown, the four-hinge mechanism is a good approximation of multi-block catenary arches for overturning. This seems to be in contradiction to the conclusion of [29] where it was stated that considering a SDOF four-hinge mechanism may significantly overestimate the collapse load of multi-block arches. Note that there is no contradiction: this new statement is valid only for catenary arches.

Since most of the arch-shapes do not follow the thrust line, the first step of design is the determination of the replacement catenary arch. In this paper, only an equivalent and a lower bound thickness was given, the lower value (when only that portion of the arch is considered (Fig. 8), which constitutes a catenary arch) is a conservative approach. To reach a better approximation, a refined replacement procedure should be developed. (Since in the recommended design procedure the catenary arch is characterized by two parameters, p and ${a}_{\mathrm{p},\mathrm{min}}$ only, a possible solution can be that these two parameters are approximated directly, without giving the geometry of the “replacement catenary arch”.)

Since it was shown previously that the results of a single block (e.g. its overturning acceleration response spectrum) can be safely used for the design of multi-block columns, and in this article, it was demonstrated that multi-block catenary arches behave analogously to multi-block columns; we may conclude that the results of single blocks can be directly used for the evaluation of multi-block arches as well. Although the existing numerical comparisons are not all conclusive, we are convinced that the presented methodology is the proper approach to the earthquake-resistant design of multi-block arches.